| Содержание
Введение……………………………………………………………………………2
Глава 1. Организация и проведение статистического наблюдения
1.1 Разработка организационно-методологических вопросов……………………4
1.2 Формирование выборки……………………………………………………….7
1.2.1 Выбор метода и способа выборочного наблюдения, расчет объема выборки…………………………………………………………………………...7
1.3 Выводы по результатам статистического наблюдения………………….......9
Глава 2. Корреляционно-регрессионный анализ
2.1 Исследование парной корреляции…………………………………………..12
2.2 Уравнение (модель) множественной регрессии……………………………28
2.2.1 Формирование модели множественной регрессии…………………….28
2.2.2 Оценка адекватности модели множественной регрессии……………..29
2.2.3 Оценка влияния факторных признаков на результативный признак…32
Глава 3. Оценка взаимосвязи между качественными признаками……………...35
Глава 4. Общий вывод по результатам выполнения курсовой работы…………39
Список использованной литературы……………………………………………...40
Приложение
Введение
Изучение спроса на предприятиях общественного питания является актуальным, так как конкуренция между предприятиям этого типа в г.Радужный достаточно высокая и поэтому необходимо учитывать и анализировать формирование спроса на предприятии, т.к. от него зависит размер получаемой прибыли.
Целью курсовой работы является изучение спроса на предприятии общественного питания на примере предприятия «Источник» в г. Радужный.
Для достижения поставленной цели необходимо решить следующие задачи:
- формирование выборки;
- проведение статистического наблюдения;
- построить модель парной регрессии между признаками;
- построить модель множественной регрессии между факторами;
- оценить взаимосвязи вариационных признаков;
- оценить взаимосвязи альтернативных признаков.
Для решения поставленных задач, были использованы такие программные пакеты как Microsoft Word, Microsoft Excel.
Применение данных программ позволило значительно сократить время обработки данных, получить наиболее точные результаты, имеющие графическую интерпретацию.
Глава 1. Организация и проведение статистического наблюдения
1.1. Разработка организационно-методических вопросов
Целью наблюдения данной работы является изучение спроса на предприятии общественного питания на примере предприятия «Источник» в г. Радужный.
Перед проведением статистического наблюдения необходимо выполнить следующие действия: составить программу наблюдения, организационный план и анкеты.
Программа наблюдения
В процессе наблюдения необходимо получить информацию по следующим признакам:
Качественные признаки:
· Удовлетворенность качеством приобретаемой посетителями продукции предприятия «Источник»;
· Ассортимент продукции, приобретаемой посетителями;
· Приоритетность выбора посетителями типа предприятия общественного питания;
· Предпочтение посетителей относительно выбора месторасположения предприятия;
· Удовлетворенность посетителей предоставлением дополнительных услуг предприятием общественного питания;
· Цель посещения предприятия общественного питания;
Количественные признаки:
· Частота посещения посетителями предприятия общественного питания «Источник»;
· Стоимость одного заказа, сделанного посетителем;
· Удовлетворенность посетителей санитарно-гигиеническими норма предприятия «Источник»;
· Удовлетворенность посетителей соблюдение их прав как потребителей продукции предприятия общественного питания;
· Количество порций заказываемых посетителем за один визит предприятия общественного питания «Источник»;
Организационный план
1. объект наблюдения: посетители предприятия общественного питания г. Радужный;
Единица наблюдения: посетитель предприятия общественного питания «Источник» г. Радужный;
2. цели наблюдения: изучить изучение спроса на предприятии общественного питания «Источник» для дальнейшего анализа и прогноза;
задачи наблюдения:
- сформировать выборочную совокупность;
- провести статистическое наблюдение;
3. органы наблюдения, осуществляющие подготовку и проведение наблюдения и несущие ответственность за эту работу: студентка группы М-31 Мингалиева Полина.
4. время и сроки наблюдения: 12.04.08 – 5.05.08.
Критический момент – 5 мая 2008 года, 18 часов 15 минут.
5. место проведения статистического наблюдения: г.Радужный, 1 квартал, 65
6. подготовительные работы к наблюдению: подготовка анкеты, предварительная смета расходов (табл.1)
Таблица 1.
Смета расходов
| Наименование расхода
|
Количество
|
Цена 1 ед., руб.
|
Стоимость, руб.
|
| 1. Разработка программы и формуляра
|
Электро-
энергия
|
0,8 кВт/ч*12ч= 9,6 кВт/ч
|
1,42
|
13,63
|
| Работа на компьютере
|
4 ч
|
20
|
80
|
| Продолжение таблицы 1
|
| 2.Тиражирование материала
|
анкеты
|
60 шт.
|
2,50
|
275
|
| курсовой проект
|
50 листов
|
| 3.Транспортные расходы
|
внутригородской
|
2 поездки
|
7
|
64
|
| междугородний
|
2 поездки
|
25
|
| 4.Заработная плата
|
стипендия
|
8 часов
|
7
|
56
|
| ИТОГО
|
488,63
|
7. порядок проведения наблюдения: заполнение анкет проводится в зале предприятия общественного питания «Источник» в момент, когда посетители сделали заказ и ожидают его исполнения, сбор данных проводится со слов посетителей, обработка данных (выявление взаимосвязи между конкретными признаками, формирование выборочной совокупности, построение моделей парной и множественной регрессии) осуществляется после заполнения всех анкет по адресу 1 квартал, 12 «а», 55 .
8.
Порядок проведения наблюдения.
Объект наблюдения: посетители предприятия общественного питания
г. Радужный.
Данное статистическое наблюдение можно отнести:
- по форме представления – специально организованное наблюдение;
- по времени регистрации – прерывное единовременное, т.к. статистическое наблюдение проводится один раз;
- по степени охвата единиц статистической совокупности – несплошное выборочное наблюдение;
- по источнику информации – опрос;
- по способу сбора информации – корреспонденский (анкеты заполняются регистратором со слов опрашиваемого).
Опросные анкеты будут заполнялись в течение одного дня с 10:00 до 19:00 22 апреля 2008 г.
8)
Порядок приема и сдачи материалов наблюдения. Прием и сдача материалов на статистическую обработку осуществляется студенткой гр. М-31 Мингалиевой П.
9)
Порядок получения представления предварительных и окончательных данных. По итогам статистического наблюдения было получено 60 заполненных анкет.
1.2. Формирование выборки
1.2.1. Выбор метода и способа выборочного наблюдения
Для формирования выборки необходимо определиться с методом и способом выборочного наблюдения. В данном случае выбирается бесповторный метод, т. к. он дает более точные результаты по сравнению с повторным методом (при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности). При бесповторном методе отобранная единица не возвращается в генеральную совокупность, и тем самым вероятность попасть в выборку для оставшихся единиц увеличивается с каждым шагом отбора, нежели при повторном методе.
Затем определяется способ выборочного наблюдения. Существуют различные способы формирования выборочной совокупности: собственно-случайный отбор, механический отбор, типический отбор и серийный отбор.
В моей выборке используется типический отбор, так как население г.Радужного разбивается по возрастным группам и из них я беру группу людей в возрасте от 20 до 49 лет среди которых будет проводится опрос, численность этих возрастных групп приведены в таблице 2.
Для проведения статистического наблюдения с целью получения сведений по качественным признакам нам необходимо определить объем выборочной совокупности, то есть сколько необходимо опросить человек всего из группы, t(коэффициент доверия) равен 2.
Таблица 2
Численность населения г.Радужного по возрастной группе от 20 лет до 49лет
(по данным администрации г.Радужный)
| Возраст, лет.
|
Численность населения, чел.
|
| 1
|
2
|
| Всего
|
9867
|
| 20-24
|
1255
|
| 25-29
|
1398
|
| 30-34
|
1447
|
| 35-39
|
1469
|
| 40-44
|
2013
|
| 45-49
|
2285
|
Среднее количество потребителей на предприятии общественного питания «Источник» составляет 20 человек за 1 день. Возьмем из них 15 человек и посмотрим максимум и минимум их суммы заказа (800 и 500 рублей). Ориентируясь на эти данные вычислим необходимые нам показатели:

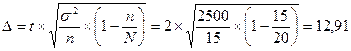
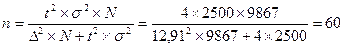
Таким образом, мы вычислили, что нам необходимо опросить 60 человек.
Теперь определим, сколько человек необходимо опросить из каждой возрастной группы.
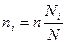 , где , где
 - объем выборки из i группы - объем выборки из i группы
 - общий объем выборки - общий объем выборки
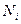 - объем i группы - объем i группы
 - объем генеральной совокупности - объем генеральной совокупности
 человек необходимо опросить из возрастной группы от 20 до 24 человек необходимо опросить из возрастной группы от 20 до 24
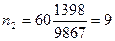 человек необходимо опросить из возрастной группы от 25 до 29 человек необходимо опросить из возрастной группы от 25 до 29
 человек необходимо опросить из возрастной группы от 30 до 34 человек необходимо опросить из возрастной группы от 30 до 34
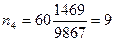 человек необходимо опросить из возрастной группы от 35 до 39 человек необходимо опросить из возрастной группы от 35 до 39
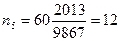 человек необходимо опросить из возрастной группы от 40 до 44 человек необходимо опросить из возрастной группы от 40 до 44
 человек необходимо опросить из возрастной группы от 45 до 49 человек необходимо опросить из возрастной группы от 45 до 49
1.3. Выводы по результатам статистического наблюдения
Опрос проводился среди жителей г. Радужный в количестве 60 человек (приложение 1). В ходе наблюдения ошибки не выявлены. По окончанию опроса были получены данные, которые были занесены в таблицу 3.
Таблица 3.
Итоговая таблица результатов статистического наблюдения
| № вопроса
|
Формулировка вопроса
|
Вариант ответа
|
Количество ответов
|
% доля
|
| 1
|
Как часто вы посещаете предприятие общественного питания (в месяц)?
|
а
б
в
|
14
28
18
|
23,33
46,66
30
|
| 2
|
Вы предпочитаете посещать предприятие общественного питания, расположенное…
|
а
б
в
|
21
21
18
|
35
35
30
|
| 3
|
Вы посещаете предприятие общественного питания для того чтобы …
|
а
б
в
|
21
25
14
|
35
41,66
23,33
|
| 4
|
На какую стоимость заказа на 1 человека Вы рассчитываете, когда идете в предприятие общественного питания?
|
300 руб.
1000 руб.
1500 руб.
2000 руб.
2500 руб.
3000 руб.
|
14
9
12
7
9
9
|
23,33
15
20
11,66
15
15
|
| 5
|
Сколько порций Вы заказываете, когда приходите на предприятие общественного питания «Источник»?
|
а
б
в
г
|
14
16
21
9
|
23,33
26,66
35
15
|
| 6
|
считаете ли Вы ассортимент предоставляемой продукции предприятий общественного питания «Источник» достаточно разнообразным?
|
а
б
|
34
26
|
56,66
43,33
|
| 7
|
Какие предприятий общественного питания Вы предпочитаете в основном посещать?
|
а
б
|
35
25
|
58,33
41,66
|
| 8
|
Удовлетворяет ли Вас качество предоставляемой предприятием общественного питания «Источник» продукции?
|
а
б
в
|
42
0
18
|
70
0
30
|
| 9
|
сколько раз Вы замечали при посещении предприятий общественного питания «Источник» не соблюдение по отношению у Вам санитарно-гигиенических условий?
|
а
б
в
|
37
23
0
|
61,66
38,33
0
|
| 10
|
Вы предпочитаете в основном посещать предприятий общественного питания, которые предоставляют дополнительные услуги (бильярд, караоке)?
|
а
б
в
|
30
18
12
|
50
30
20
|
| 11
|
Сколько раз Вы сталкивались с нарушением прав потребителей на предприятии общественного питания «Источник»?
|
а
б
в
|
16
18
26
|
26,66
30
43,33
|
По данным представленным в таблице 3 видно, что:
· 23,33% жителей посещают предприятия общественного питания 1 раз в месяц, 46,66 % делают это 4 раза в месяц, а оставшиеся 30 % более 4 раз;
· 35% жителей посещают предприятия общественного питания вблизи дома, 35% в центре города, 30% в зависимости от того, где находятся в данный момент;
· 35% жителей посещают предприятия общественного питания отпраздновать какое-либо мероприятие, 41,66% для того, чтобы отдохнуть и 23,33% заходят, чтобы перекусить;
· 23,33% жителей, посещая предприятия общественного питания рассчитывают на сумму в 300 руб.,15% - 1000 руб., 20% - 1500, 11,66% - 2000 руб., 15 %– 2500 руб., 15% - 3000 руб.;
· 23,33% приходя на предприятие «Источник» заказывают 3-5 порций, 26,66% - 6-7 порций, 35% - 9-11 порций, 15% - 12-14 порций
· 56,66% жителей считают ассортимент предприятия общественного питания разнообразным и только 43,33% не считают его таковым;
· 58,33% жителей предпочитают посещать предприятия быстрого питания и 41,66% - предприятия специализирующие на приготовлении блюд какой-либо определенной кухни;
· 70% посетителей предприятия «Источник» ответили, что их удовлетворяет качество предоставляемой продукции, 0% - не удовлетворяет и 30% - не всегда удовлетворяет;
· 61,66% ни разу не замечали не соблюдение санитарно-гигиенических условий, а 38,33% сталкивались с не соблюдение санитарно-гигиенических условий 1 раз, и никто не сталкивался в таким явлением более 1 раза
· 50% любят посещать предприятий общественного питания, которые предоставляют дополнительные услуги (бильярд, караоке), 30% не любят таких заведений, 20% выбирают куда пойти в зависимости от планов
· 26,66% ни разу не сталкивались с нарушением прав потребителей, 30% - 1 раз и 43,33% - более 1 раза
Глава 2. Корреляционно-регрессионный анализ
В этой главе проводится исследование парной корреляции, формирование модели парной регрессии и множественной регрессии.
2.1 Исследование парной корреляции
Для изучения влияния частоты посещений на спрос на предприятии общественного питания «Источник» построим график-поле корреляции, чтобы проверить как проявляется связь между признаками.

Рис 1.
Из ходя из графика на рисунке 1 можно сделать вывод, что связь между признаками существует и имеется линейная зависимость, т.к. большинство точек попали в область ++
Оценим степень тесноты связи с помощью линейного коэффициента корреляции на основе данных таблицы 4:
 или или  , ,
 - среднее значение соответствующего факторного признака; - среднее значение соответствующего факторного признака;
 - среднее значение результативного признака; - среднее значение результативного признака;
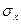 - среднее квадратическое отклонение соответствующего факторного признака; - среднее квадратическое отклонение соответствующего факторного признака;
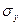 - среднее квадратическое отклонение соответствующего результативного признака; - среднее квадратическое отклонение соответствующего результативного признака;
n
– число наблюдений.
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1≤ r ≤ 1.
Таблица 4
Расчетные значения
| Возраст населения
|
Численность населения
|
Частота посещений предприятий, кол-во раз в мес. x
|
x2
|
Спрос на предприятии, порции y
|
y2
|

|
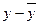
|

|
| 20-24
|
7
|
4
|
16
|
7
|
49
|
-0,83
|
-1,5
|
0,45
|
| 25-29
|
9
|
8
|
64
|
10
|
100
|
3,17
|
1,5
|
5,55
|
| 30-34
|
9
|
8
|
64
|
13
|
169
|
3,17
|
4,5
|
16,65
|
| 35-39
|
9
|
4
|
16
|
7
|
49
|
-0,83
|
-1,5
|
0,45
|
| 40-44
|
12
|
4
|
16
|
10
|
100
|
-0,83
|
1,5
|
-0,45
|
| 45-49
|
14
|
1
|
1
|
4
|
16
|
-3,83
|
-4,5
|
14,85
|
| итого
|
60
|
29
|
177
|
51
|
483
|
37,5
|

Чтобы использовать формулу для линейного коэффициента корреляции рассчитаем дисперсию:


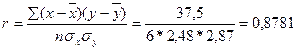
Данный коэффициент попадает в интервал  - это говорит о том, что связь между признаками сильная, а положительный знак коэффициента говорит о том, что связь прямая.- это говорит о том, что связь мед++тной группы от 20 до 24ся актуальным, так как - это говорит о том, что связь между признаками сильная, а положительный знак коэффициента говорит о том, что связь прямая.- это говорит о том, что связь мед++тной группы от 20 до 24ся актуальным, так как
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
При линейной однофакторной связи t-критерий можно рассчитать по формуле:
 , ,
где (n - 2)
– число степеней свободы при заданном уровне значимости α
и объеме выборки n
.
Полученное значение tрасч
сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01)
Подставляем данные в формулу:
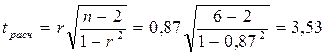
Получаем, что tрасч
>
tтабл
=
2,7764[1]
, линейный коэффициент считается значимым, а связь между x
и y
– существенной, т.е. мы можем исключить случайную ошибку и сказать, что коэффициент однозначно отражает связь между изучаемыми признаками.
Рассчитаем коэффициент детерминации, который показывает долю вариации результативного признака под влиянием вари признака-фактора. В нашем случае 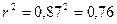 , т.е. спрос на 76% зависит от частоты посещаемости предприятия. , т.е. спрос на 76% зависит от частоты посещаемости предприятия.
С помощью мастер диаграмм строим графическую зависимость по данным таблицы 5, показывающую влияния частоты посещений на спрос на предприятии общественного питания «Источник» (рис.2). Добавляем линию тренда и величину достоверности аппроксимации (показывает точность описания уравнения регрессии)-R2
.
Таблица 5
Распределение значений частоты посещений предприятий общественного питания и спроса на предприятии среди населения в возрасте от 20 до 46лет
| Возраст населения
|
Численность населения, n
|
Частота посещения предприятия х
|
Спрос на предприятии у
|
| 20-24
|
7
|
4
|
7
|
| 25-29
|
9
|
8
|
10
|
| 30-34
|
9
|
8
|
13
|
| 35-39
|
9
|
4
|
7
|
| 40-44
|
12
|
4
|
10
|
| 45-49
|
14
|
1
|
4
|

Рис 2
В основе зависимости спроса от частоты посещений предприятия лежит прямолинейная связь
, которая может быть выражена простым линейным уравнением регрессии:
ŷ = a0
+ a1
x,
где ŷ - теоретические расчётные значения результативного признака (спрос на предприятиях), полученные по уравнению регрессии;
a0
, a1
- коэффициенты (параметры) уравнения регрессии;
х – частота посещений предприятий.
Параметры уравнения a0
, a1
находят методом наименьших квадратов (МНК - метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), то есть в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi
от выровненных ŷ :
S(yi
– ŷ)2
= S(yi
– a0
– a1
xi
)2
® min
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
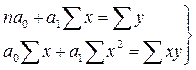
Решим эту систему в общем виде:
 ; ; 
Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:
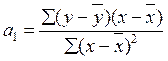 , ,  , ,
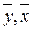 - средние значения результативного и факторного признаков соответственно. - средние значения результативного и факторного признаков соответственно.
Определим значения a0
, a1
данным рассчитанным в таблице 6, подставим их в уравнение связи ŷ = a0
+ a1
x, и найдем значения ŷ, зависящие только от заданного значения х.
Получаем:
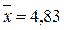
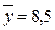

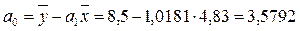
Таблица 6
Расчетные значения
| Возраст населения
|
Численность населения
|
Частота посещений предприятий, кол-во раз в мес. x
|
Спрос на предприятии, порции y
|
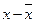
|

|
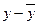
|

|
| 20-24
|
7
|
4
|
7
|
-0,83
|
0,6889
|
-4,5
|
1,245
|
| 25-29
|
9
|
8
|
10
|
3,17
|
10,0489
|
-0,5
|
4,755
|
| 30-34
|
9
|
8
|
13
|
3,17
|
10,0489
|
-0,5
|
14,265
|
| 35-39
|
9
|
4
|
7
|
-0,83
|
0,6889
|
-4,5
|
1,245
|
| 40-44
|
12
|
4
|
10
|
-0,83
|
0,6889
|
-4,5
|
-1,245
|
| 45-49
|
14
|
1
|
4
|
-3,83
|
14,6689
|
-7,5
|
17,235
|
| итого
|
60
|
29
|
51
|
36,8334
|
37,5
|
Таким образом, регрессионная модель зависимости спроса от частоты посещений может быть записана в виде конкретного простого уравнения регрессии: 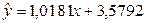 . .
Проверка адекватности модели может быть дополнена нахождением значения средней ошибки аппроксимации:
 , ,
где y – значение результативного признака;
 - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии. - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии.
Таблица 7
Расчетные значения
| Возраст населения
|
Численность населения, ni
|
Частота посещений предприятий,х
|
Спрос на предприятии общественного питания уi
|

|
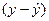
|

|
| 20-24
|
7
|
4
|
7
|
7,6516
|
-0,6516
|
-0,09308571
|
| 25-29
|
9
|
8
|
10
|
11,724
|
-1,724
|
-0,1724
|
| 30-34
|
9
|
8
|
13
|
11,724
|
1,276
|
0,098153846
|
| 35-39
|
9
|
4
|
7
|
7,6516
|
-0,6516
|
-0,09308571
|
| 40-44
|
12
|
4
|
10
|
7,6516
|
2,3484
|
0,23484
|
| 45-49
|
14
|
1
|
4
|
4,5973
|
-0,5973
|
-0,149325
|
| итого
|
60
|
29
|
51
|
-0,17490257
|
Рассчитанные данные в таблице 7подставляем в формулу и получаем:

Полученная величина  не превышать допустимого значения средней ошибки 12% - 15%, а это значит, что данная модель адекватна и соответствует фактическим данным. не превышать допустимого значения средней ошибки 12% - 15%, а это значит, что данная модель адекватна и соответствует фактическим данным.
Определим значимость коэффициентов с помощью t-критерия Стьюдента. При этом вычисляются расчетные значения t-критерия:
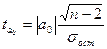
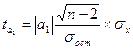
n-объем выборки
 - среднеквадратическое отклонение результативного признака у от выровненных значений - среднеквадратическое отклонение результативного признака у от выровненных значений 
 среднеквадратическое отклонение факторного признака х от общей средней среднеквадратическое отклонение факторного признака х от общей средней 
Таблица 8
Расчетные значения
| Возраст населения
|
Численность населения, ni
|
Частота посещений предприятий,х
|
x2
|
Спрос на предприятии общественного питания уi
|

|
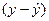
|

|
| 20-24
|
7
|
4
|
16
|
7
|
7,6516
|
-0,6516
|
0,424583
|
| 25-29
|
9
|
8
|
64
|
10
|
11,724
|
-1,724
|
2,972176
|
| 30-34
|
9
|
8
|
64
|
13
|
11,724
|
1,276
|
1,628176
|
| 35-39
|
9
|
4
|
16
|
7
|
7,6516
|
-0,6516
|
0,424583
|
| 40-44
|
12
|
4
|
16
|
10
|
7,6516
|
2,3484
|
5,514983
|
| 45-49
|
14
|
1
|
1
|
4
|
4,5973
|
-0,5973
|
0,356767
|
| итого
|
60
|
29
|
177
|
51
|
11,321268
|
Данные рассчитанные в таблице 8 подставим в формулы и получим:
 
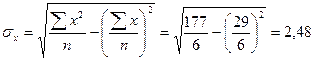

tрасч
>
tтабл
=
2,7764[2]
, то можно говорить о значимости коэффициента а0
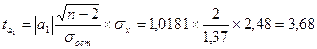
tрасч
>
tтабл
=
2,7764, то можно говорить о значимости коэффициента а1
В ходе проведения регрессионного анализа рассчитывают дополнительные показатели:
а) определяют коэффициент детерминации, который показывает долю вариации результативного признака под влиянием вариации признака фактора: R
=
r
2
.
В данном случае r2
=0,7569, или, иначе говоря, на 75,69 % от частоты посещений предприятия общественного питания «Источник» зависит его спроса.
б) Для удобства интерпретации параметра a1
используют коэффициент эластичности (Эx
). Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:
 , ,
где x
ср
, y
ср
– среднее значение соответственно факторного и результативного признаков;
a
– коэффициент регрессии при соответствующем факторном признаке.
Рассчитаем коэффициент эластичности:
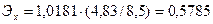
Это означает, что при изменении частоты посещений предприятий на 1%, спрос изменить на 0,5785%
Таким образом, построенная регрессионная модель 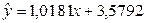 в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю генеральную совокупность. в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю генеральную совокупность.
Для изучения влияния стоимости заказа на спрос на предприятии общественного питания «Источник» построим график-поле корреляции, чтобы проверить как проявляется связь между признаками.

Рис. 3
Исходя из графика на рис.3 можно сделать вывод, что связь между признаками существует и имеется линейная зависимость, т.к. большинство точек попали в область ++
Оценим степень тесноты связи с помощью линейного коэффициента корреляции:
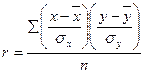 или или  , ,
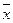 - среднее значение соответствующего факторного признака; - среднее значение соответствующего факторного признака;
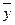 - среднее значение результативного признака; - среднее значение результативного признака;
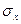 - среднее квадратическое отклонение соответствующего факторного признака; - среднее квадратическое отклонение соответствующего факторного признака;
 - среднее квадратическое отклонение соответствующего результативного признака; - среднее квадратическое отклонение соответствующего результативного признака;
n
– число наблюдений.
Таблица 9
Расчетные значения
| Возраст населения
|
Численность населения
|
Стоимость заказа на 1 чел, руб. x
|
x2
|
Спрос на предприятии, порции y
|
y2
|

|

|

|
| 20-24
|
7
|
2000
|
4000000
|
7
|
49
|
283,34
|
-1,5
|
-425,01
|
| 25-29
|
9
|
2500
|
6250000
|
10
|
100
|
783,34
|
1,5
|
1175,01
|
| 30-34
|
9
|
3000
|
9000000
|
13
|
169
|
1283,34
|
4,5
|
5775,03
|
| 35-39
|
9
|
1000
|
1000000
|
7
|
49
|
-716,66
|
-1,5
|
1074,99
|
| 40-44
|
12
|
1500
|
2250000
|
10
|
100
|
-216,66
|
1,5
|
-324,99
|
| 45-49
|
14
|
300
|
90000
|
4
|
16
|
-1416,66
|
-4,5
|
6374,97
|
| итого
|
60
|
10300
|
22590000
|
51
|
483
|
13650
|
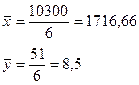
Чтобы использовать формулу для линейного коэффициента корреляции рассчитаем дисперсию по даным приведенным в таблице 9:
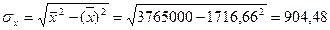


Данный коэффициент попадет в интервал  - это говорит о том, что связь между признаками сильная, а положительный знак коэффициента говорит о том, что связь прямая.- это говорит о том, что связь мед++тной группы от 20 до 24ся актуальным, так как Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального. - это говорит о том, что связь между признаками сильная, а положительный знак коэффициента говорит о том, что связь прямая.- это говорит о том, что связь мед++тной группы от 20 до 24ся актуальным, так как Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
При линейной однофакторной связи t-критерий можно рассчитать по формуле:
 , ,
где (n - 2)
– число степеней свободы при заданном уровне значимости α
и объеме выборки n
.
Полученное значение tрасч
сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01)
Получаем:

tрасч
>
tтабл
=
2,7764[3]
, линейный коэффициент считается значимым, а связь между x
и y
– существенной, т.е. мы можем исключить случайную ошибку и сказать, что коэффициент однозначно отражает связь между изучаемыми признаками.
Рассчитаем коэффициент детерминации, который показывает долю вариации результативного признака под влиянием вариации признака-фактора. В нашем случае  , т.е. спрос на 76,73% зависит от частоты посещаемости предприятия. , т.е. спрос на 76,73% зависит от частоты посещаемости предприятия.
С помощью мастер диаграмм строим графическую зависимость по данным таблицы 10, показывающую влияния стоимости заказа на спрос на предприятии общественного питания «Источник» (рис.4). Добавляем линию тренда и величину достоверности аппроксимации (показывает точность описания уравнения регрессии)-R2
.
Таблица 10
Распределение значений стоимости заказа, сделанного на предприятии общественного питания «Источник» и спроса на предприятии среди населения в возрасте от 20 до 46лет
| Возраст населения
|
Численность населения, n
|
Стоимость заказа на 1 чел, руб. x
|
Спрос на предприятии у
|
| 20-24
|
7
|
2000
|
7
|
| 25-29
|
9
|
2500
|
10
|
| 30-34
|
9
|
3000
|
13
|
| 35-39
|
9
|
1000
|
7
|
| 40-44
|
12
|
1500
|
10
|
| 45-49
|
14
|
300
|
4
|

Рис. 4
В основе зависимости спроса от стоимости заказа лежит прямолинейная связь
, которая может быть выражена простым линейным уравнением регрессии:
ŷ = a0
+ a1
x,
где ŷ - теоретические расчётные значения результативного признака (спрос на предприятиях), полученные по уравнению регрессии;
a0
, a1
- коэффициенты (параметры) уравнения регрессии;
х – частота посещений предприятий.
Параметры уравнения a0
, a1
находят методом наименьших квадратов (МНК - метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), то есть в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi
от выровненных ŷ :
S(yi
– ŷ)2
= S(yi
– a0
– a1
xi
)2
® min
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

Решим эту систему в общем виде:
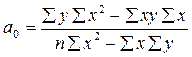 ; ; 
Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:
 , ,  , ,
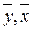 - средние значения результативного и факторного признаков соответственно. - средние значения результативного и факторного признаков соответственно.
Определим значения a0
, a1 по
данным рассчитанным в таблице 11, подставим их в уравнение связи ŷ = a0
+ a1
x, и найдем значения ŷ, зависящие только от заданного значения х.
Получаем:
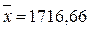
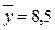

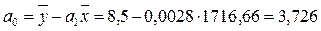
Таблица 11
Расчетные значения
| Возраст населения
|
Численность населения
|
Стоимость заказа, руб. x
|
Спрос на предприятии, порции y
|
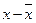
|
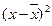
|
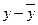
|
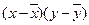
|
| 20-24
|
7
|
2000
|
7
|
283,34
|
80281,5556
|
-1,5
|
-425,01
|
| 25-29
|
9
|
2500
|
10
|
783,34
|
613621,5556
|
1,5
|
1175,01
|
| 30-34
|
9
|
3000
|
13
|
1283,34
|
1646961,556
|
4,5
|
5775,03
|
| 35-39
|
9
|
1000
|
7
|
-716,66
|
513601,5556
|
-1,5
|
1074,99
|
| 40-44
|
12
|
1500
|
10
|
-216,66
|
46941,5556
|
1,5
|
-324,99
|
| 45-49
|
14
|
300
|
4
|
-1416,66
|
2006925,556
|
-4,5
|
6374,97
|
| итого
|
60
|
10300
|
51
|
4908333,334
|
13650
|
Таким образом, регрессионная модель зависимости спроса от частоты посещений может быть записана в виде конкретного простого уравнения регрессии:  . .
Проверка адекватности модели может быть дополнена нахождением значения средней ошибки аппроксимации:
 , ,
где y – значение результативного признака;
 - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии. - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии.
Таблица 12
Расчетные значения
| Возраст населения
|
Численность населения, ni
|
Стоимость заказа на 1 чел, руб. x
|
Спрос на предприятии общественного питания уi
|

|
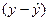
|

|
| 20-24
|
7
|
2000
|
7
|
9,326
|
-2,326
|
-0,33228571
|
| 25-29
|
9
|
2500
|
10
|
10,726
|
-0,726
|
-0,0726
|
| 30-34
|
9
|
3000
|
13
|
12,126
|
0,874
|
0,067230769
|
| 35-39
|
9
|
1000
|
7
|
6,526
|
0,474
|
0,067714286
|
| 40-44
|
12
|
1500
|
10
|
7,926
|
2,074
|
0,2074
|
| 45-49
|
14
|
300
|
4
|
4,566
|
-0,566
|
-0,1415
|
| итого
|
60
|
10300
|
51
|
-0,20404065
|
Подставив данные полученные в таблице 12 получаем:

Величина 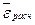 не превышать допустимого значения средней ошибки 12% - 15%, это значит, что данная модель адекватна, соответствует фактическим данным. не превышать допустимого значения средней ошибки 12% - 15%, это значит, что данная модель адекватна, соответствует фактическим данным.
Определим значимость коэффициентов с помощью t-критерия Стьюдента по данным таблицы 13. При этом вычисляются расчетные значения t-критерия:


n-объем выборки
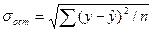 - среднеквадратическое отклонение результативного признака у от выровненных значений - среднеквадратическое отклонение результативного признака у от выровненных значений 
 среднеквадратическое отклонение факторного признака х от общей средней среднеквадратическое отклонение факторного признака х от общей средней 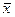
Таблица 13
Расчетные значения
| Возраст населения
|
Численность населения, ni
|
Стоимость заказа на 1 чел, руб. x
|
Спрос на предприятии общественного питания уi
|
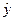
|
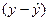
|
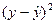
|
| 20-24
|
7
|
2000
|
7
|
9,326
|
-2,326
|
5,410276
|
| 25-29
|
9
|
2500
|
10
|
10,726
|
-0,726
|
0,527076
|
| 30-34
|
9
|
3000
|
13
|
12,126
|
0,874
|
0,763876
|
| 35-39
|
9
|
1000
|
7
|
6,526
|
0,474
|
0,224676
|
| 40-44
|
12
|
1500
|
10
|
7,926
|
2,074
|
4,301476
|
| 45-49
|
14
|
300
|
4
|
4,566
|
-0,566
|
0,320356
|
| итого
|
60
|
10300
|
51
|
11,547736
|
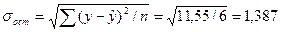 
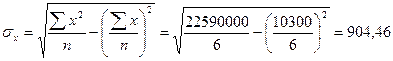

tрасч
>
tтабл
=
2,7764[4]
, то можно говорить о значимости коэффициента а0

tрасч
>
tтабл
=
2,7764, то можно говорить о значимости коэффициента а1
В ходе проведения регрессионного анализа рассчитывают дополнительные показатели:
а) определяют коэффициент детерминации, который показывает долю вариации результативного признака под влиянием вариации признака фактора: R
=
r
2
.
В данном случае r2
=0,7673, или, иначе говоря, на 76,73 % от стоимости заказа посетителей предприятия общественного питания «Источник» зависит его спроса.
б) Для удобства интерпретации параметра a1
используют коэффициент эластичности (Эx
). Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:
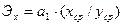 , ,
где x
ср
, y
ср
– среднее значение соответственно факторного и результативного признаков;
a
– коэффициент регрессии при соответствующем факторном признаке.
Рассчитаем коэффициент эластичности:
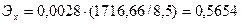
Это означает, что при изменении частоты посещений предприятий на 1%, спрос изменить на 0,5654%
Таким образом, построенная регрессионная модель  в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю генеральную совокупность. в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю генеральную совокупность.
2.2.
Уравнение (модель) множественной регрессии
2.2.1 Формирование модели множественной регрессии
Рассмотрим связь между уровнем спроса (результативный признак) и влияющими на него факторами: частотой посещения предприятия общественного питания; стоимость одного заказа по данным таблицы 14.
Таблица 14
Исходные данные
| Возраст населения
|
Численность населения
|
Спрос на предприятии, порции y
|
Стоимость заказа, руб. x1
|
Частота посещений х2
|
| 20-24
|
7
|
7
|
2000
|
4
|
| 25-29
|
9
|
10
|
2500
|
8
|
| 30-34
|
9
|
13
|
3000
|
8
|
| 35-39
|
9
|
7
|
1000
|
4
|
| 40-44
|
12
|
10
|
1500
|
4
|
| 45-49
|
14
|
4
|
300
|
1
|
| итого
|
60
|
51
|
10300
|
29
|
В связи с трудоемкостью работ проведем нахождение параметров уравнения множественной регрессии и самой модели множественной регрессии с помощью программы Microsoft Excel.
С помощью программы анализ данных проведем анализ множественной регрессии( таблица 15)
Таблица 15
| ВЫВОД ИТОГОВ
|
| Регрессионная статистика
|
| Множественный R
|
0,8926
|
| R-квадрат
|
0,7967
|
| Нормированный R-квадрат
|
0,6611
|
| Стандартная ошибка
|
1,8317
|
| Наблюдения
|
6
|
| Дисперсионный анализ
|
| |
df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
2
|
39,4342
|
19,7171
|
5,8765
|
0,0917
|
| Остаток
|
3
|
10,0658
|
3,3553
|
| Итого
|
5
|
49,5000
|
| |
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение
|
3,4764
|
1,6479
|
2,1097
|
0,1254
|
-1,7678
|
8,7207
|
-1,7678
|
8,7207
|
| Стоимость заказа, руб. x1
|
0,0014
|
0,0023
|
0,6117
|
0,5840
|
-0,0058
|
0,0086
|
-0,0058
|
0,0086
|
| Частота посещений х2
|
0,5476
|
0,8262
|
0,6628
|
0,5549
|
-2,0819
|
3,1771
|
-2,0819
|
3,1771
|
В данном случае уравнение регрессии будет иметь вид:

Так как квадрат множественного коэффициента линейной корреляции R=79% > 70%, то модель считается адекватной.
2.3.2 Оценка адекватности модели множественной регрессии
После нахождения уравнения (модели) множественной регрессии осуществляется проверка модели на адекватность и правильности выбора формы связи следующим образом:
1. Рассчитывается коэффициент F-критерия Фишера:
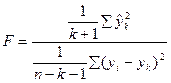 , ,
где  - теоретическое значение результативного признака, полученное по уравнению регрессии; - теоретическое значение результативного признака, полученное по уравнению регрессии;
n
– объем исследуемой совокупности;
k
– число факторных признаков в модели.
Величина F
табл
находится по таблицам при заданном уровне значимости α
(α=0,05 или α=0,01) и числе степеней свободы v
1
=
k
-1
, v
2
=
n
–
k
.
Таблица 16
| №
|
Спрос на предприятии, порции y
|
Стоимость заказа на 1 чел, руб. x1
|
Частота посещений х2
|

|
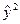
|

|
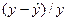
|

|
| 1
|
7
|
2000
|
4
|
33,6668
|
1133,4534
|
-26,6668
|
-3,80954
|
711,11822
|
| 2
|
10
|
2500
|
8
|
42,8572
|
1836,7396
|
-32,8572
|
-3,28572
|
1079,5956
|
| 3
|
13
|
3000
|
8
|
49,8572
|
2485,7404
|
-36,8572
|
-2,83517
|
1358,4532
|
| 4
|
7
|
1000
|
4
|
19,6668
|
386,78302
|
-12,6668
|
-1,80954
|
160,44782
|
| 5
|
10
|
1500
|
4
|
26,6668
|
711,11822
|
-16,6668
|
-1,66668
|
277,78222
|
| 6
|
4
|
300
|
1
|
8,224
|
67,634176
|
-4,224
|
-1,056
|
17,842176
|
| ∑
|
51
|
10300
|
29
|
6621,46881
|
-14,46265
|
3605,239236
|
Подставим расчетные значения из таблицы 16 в формулу:

F
табл
= 7,71[5]
(при α = 0,05;  ) )
F
расч
<
F
табл
, поэтому связь признается не существенной и доля вариации, обусловленная регрессией не превышает случайной ошибки.
Рассчитывается значение средней ошибки аппроксимации по данным таблицы 16:
 , ,
где y
– значение результативного признака;
 - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии. - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии.
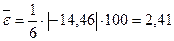
Ошибка аппроксимации не должна превышать допустимого значения (12% - 15%). В нашем случае она равна 2,41%, значит построенная нами модель адекватна.
2. Рассчитывается t-критерий Стьюдента:
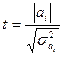 , ,
Дисперсия коэффициента регрессии 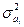 может быть рассчитана по способу, выработанному методикой экспериментирования, заключающейся в том, что величина дисперсии коэффициента может быть приближенно определена по выражению: может быть рассчитана по способу, выработанному методикой экспериментирования, заключающейся в том, что величина дисперсии коэффициента может быть приближенно определена по выражению:
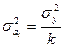 , ,
где 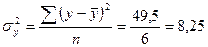 - дисперсия результативного признака; - дисперсия результативного признака;
k
– число факторных признаков в уравнении.

Частота посещений предприятия:

Стоимость заказа:
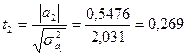
Параметр модели признается статистически не значимыми, т.к. tр
< tкр
при α = 0,05 и v = n-k-1=3 (tкр
= 3.1825[6]
), это говорит о том, что на основе этой модели нельзя делать прогноза на будущее.
2.2.3 Оценка влияния факторных признаков на результативный признак
Влияние факторных признаков на результативный признак определяется посредством исчисления последующих показателей:
1. Частный коэффициент эластичности
, который показывает на сколько процентов в среднем изменится анализируемый показатель с изменением на 1% i-того фактора при фиксированном значении других факторов.
 , ,
ai
– коэффициент регрессии в i-том факторе;
xi
– среднее значение i-того фактора;
yi
– среднее значение результативного показателя.
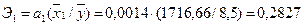
Это говорит о том, что при изменении частоты посещений на 1%, спрос измениться на 0,2827%

Это говорит о том, что при изменении стоимости заказа на 1%, спрос измениться на 0,3111%
Значительное изменение уровня спроса на предприятии будет наблюдаться при изменении частоты посещений предприятия.
2. β – коэффициент, который показывает, на какую часть среднеквадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.
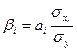 , ,
 - среднее квадратическое отклонение i-того фактора; - среднее квадратическое отклонение i-того фактора;
 - среднее квадратическое отклонение показателя. - среднее квадратическое отклонение показателя.
частота посещений предприятия.

стоимость заказа
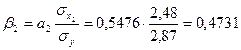
Т.к. 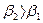 , то стоимость заказа влияет сильнее на спрос, чем частота посещений предприятия. , то стоимость заказа влияет сильнее на спрос, чем частота посещений предприятия.
3. Частный коэффициент детерминации показывает, насколько процентов вариация результативного признака объясняется вариацией i-того признака, входящего во множественное уравнение регрессии.
 , ,
 - парный коэффициент корреляции между результативным и i-м факторным признаками; - парный коэффициент корреляции между результативным и i-м факторным признаками;
 - соответствующий коэффициент уравнения множественной регрессии в стандартизированном масштабе. - соответствующий коэффициент уравнения множественной регрессии в стандартизированном масштабе.


При изменении стоимости заказа, уровень спроса на предприятии изменяется на 41,54%, а при изменении частоты посещений на 38,64%.
4. Множественный коэффициент детерминации (R2
), представляющий собой множественный коэффициент корреляции в квадрате, характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель.
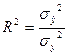 или или  , ,
где 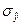 - дисперсия переменной y
, объясненная факторными переменными, включенными в анализ; - дисперсия переменной y
, объясненная факторными переменными, включенными в анализ;
 - общая дисперсия переменной y
; - общая дисперсия переменной y
;
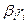 - показатель силы влияния соответствующего фактора на данный показатель. - показатель силы влияния соответствующего фактора на данный показатель.

На основе данного коэффициента можно сделать вывод о том, что спрос предприятии зависит от изменений факторных признаков, входящих в многофакторную регрессионную модель на 80,18%.
5. 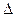 коэффициент показывает какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. коэффициент показывает какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов.

частота посещений предприятия
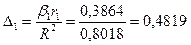
стоимость заказа
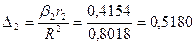
Можно сделать вывод, что на 48,19% спрос зависит от частоты посещений предприятия и на 51,8% от стоимости заказа.
ГЛАВА 3. Оценка взаимосвязи между качественными признаками
В этой главе рассматривается взаимосвязь качественных признаков. Для оценки взаимосвязи качественных признаков используют ряд показателей.
1. Коэффициенты ассоциации и контингенции.
Эти коэффициенты используют для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп.
При исследовании связи числовой материал располагают в виде 4-х клеточной корреляционной таблицы (таблица 4-х полей), которая показывает связь между явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).
Таблица 14
Таблица для вычисления коэффициентов ассоциации и контингенции
| A
|
b
|
a + b
|
| C
|
d
|
c + d
|
| a + c
|
b + d
|
a + b + c + d
|
где a, b, c, d
– частоты появления сочетаний признаков.
Коэффициенты ассоциации и контингенции определяются по следующим формулам.
Коэффициент ассоциации: 
Коэффициент контингенции: 
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтверждённой, если Ка
> 0,5 или Кк
> 0,3.
Таблица 15
| Тип предприятия
|
Разнообразен ли ассортимент?
|
Всего
|
| Да
|
Нет
|
| Бистро
|
25
|
12
|
37
|
| специализированное
|
14
|
9
|
23
|
| Итого
|
39
|
21
|
60
|
Данные таблицы 15 подставим в формулу:


Так как, Кас
> Кконт
, но Ка
< 0,5 и Кк
< 0,3, следовательно связь между типом предприятием и разнообразностью ассортимента отсутствует.
Когда каждый из качественных признаков состоит более, чем из двух групп, то для определения тесноты связи применяют коэффициент взаимной сопряжённости Пирсона-Чупрова.
Для расчёта коэффициента взаимной сопряжённости строится следующая таблица.
Таблица 17
Вспомогательная таблица для расчёта коэффициента
взаимной сопряжённости
| у х
|
1
|
2
|
3
|
Всего
|
| 1
|
nxy
|
nxy
|
nxy
|
nx
|
| 2
|
nxy
|
nxy
|
nxy
|
nx
|
| 3
|
nxy
|
nxy
|
nxy
|
nx
|
| Всего
|
ny
|
ny
|
ny
|
n
|
Этот коэффициент взаимной сопряжённости вычисляется по следующей формуле:
Коэффициент Пирсона: 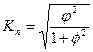
Коэффициент Чупрова:  , ,
φ2 – показатель взаимной сопряжённости (определяется как сумма отношений квадратов частот каждой клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки; вычитая из этой суммы 1, получают величину φ2
):
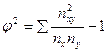
К1 – число значений (групп) первого признака;
К2 – число значений (групп) второго признака.
Чем ближе величины Кп и Кч к 1, тем связь теснее.
Таблица18
| Цель посещения
|
Путь преодолеваемый посетителями
|
Всего
|
| В близи дома
|
В центре города
|
По ситуации
|
А4
|
В5
|
| Отпраздновать к-л событие
|
111
1212
113
|
10
100
3,44
|
0
0
0
|
21
14,44
|
0,687
|
| Отдохнуть
|
0
0
0
|
19
361
12,44
|
2
4
0,2
|
20
12,64
|
1,58
|
| Перекусить
|
0
0
0
|
0
0
0
|
18
324
11,7
|
18
11,7
|
0,65
|
| Всего
|
11
|
29
|
20
|
60
|
2,917
|
Примечание: 1- частоты ; 2 - их квадраты; 3 - квадраты частот, делённые на суммы частот по столбцу; 4 – сумма частот, сумма результатов деления (А), 5 - результат деления нижнего числа на верхнее.
Данные таблицы 18 подставим в формулу:
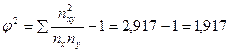
k1
= k2
= 3


Таким образом, можно сделать вывод, о том, что связь между изучаемыми признаками существует.
Теперь рассмотрим взаимосвязь между качеством продукции и предоставлением предприятием дополнительных услуг
Таблица 19
| Посещение предприятий с дополнительными услуга
|
Удовлетворяет ли Вас качество продукции?
|
Всего
|
| Да
|
нет
|
Не всегда
|
А4
|
В5
|
| Да
|
321
10242
22,263
|
0
0
0
|
1
1
0,07
|
33
22,33
|
0,67
|
| Нет
|
14
196
4,26
|
0
0
0
|
0
0
0
|
14
4,26
|
0,3
|
| Зависит от цели посещения
|
0
0
0
|
0
0
0
|
13
169
12,07
|
13
12,07
|
0,92
|
| Всего
|
46
|
0
|
14
|
60
|
1,89
|
Примечание: 1- частоты ; 2 - их квадраты; 3 - квадраты частот, делённые на суммы частот по столбцу; 4 – сумма частот, сумма результатов деления (А), 5 - результат деления нижнего числа на верхнее.
Данные таблицы 19 подставим в формулу:

k1
= k2
= 3
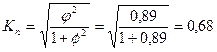

Таким образом, можно сделать вывод, о том, что связь между изучаемыми признаками существует связь.
Глава 4. Общий вывод по результатам выполнения курсовой работы
В данной курсовом проекте были выявлены взаимосвязи между спросом на предприятии общественного питания «Источник» г. Радужный и рядом качественных и количественных признаков по средством методов статистического анализа.
Была проведена выборка, которая составила 60 человек, из которых 7 человек из возрастной группы от 20 до 24; 9 человек из возрастной группы от 25 до 29; 9 человек - от 30 до 34 лет; 9 человек - от 35 до 39; 12 человек - от 40 до 44; 14 человек - от 45 до 49.
На основе данных полученных после опроса, была изучена взаимосвязь между факторными признаками (частотой посещаемости предприятия общественного питания «Источник» и стоимости заказа посетителем) и спросом на предприятии. В итоге были выяснено, что стоимость заказа влияет сильнее на спрос, чем частота посещений предприятия, т.е. на 48,19% спрос зависит от частоты посещений предприятия и на 51,8% от стоимости заказа.
При оценке взаимосвязи качественных признаков было выяснено, что существует связь между предоставлением дополнительных услуг и качеством приобретаемой посетителями продукции, т.к. 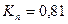 и и  . .
Таким образом, предприятию общественного питания «Источник» в г.Радужный необходимо учитывать и анализировать формирование спроса, т.к. он лежит в основе получаемой прибыли предприятия, поэтому в ходе анкетирование были заданы общие вопросы, из которых стало известно, что посетители были бы довольны, если бы предприятие «Источник» расширило круг предоставляемых услуг, включив в него дополнительные, в качестве которых выступают бильярд или караоке.
Список использованной литературы
1. Громыко Л.В. Теория статистики. – М.: ИНФРА-М, 2002.
2. Гусаров В.М., Статистика: Учеб. Пособие для вузов. – М.: ЮНИТИ-ДАНА, 2002.
3. Елисеева И.И., Юзбашев М.М. «Общая теория статистики», М.: Финансы и статистика, 2002.
4. Ефимова М.Р., Петрова Е.В., Румянцева Б.И. Общая теория статистики. – М.: Статистика, 2000.
5. Новокупова И.Н. Статистика (методические указания к курсовой работе). - Владимир, 2005.
6. «Практикум по теории статистики»., под ред. Р.А. Шмойловой, М.: Финансы и статистика, 2001.
7. «Теория статистики», учебник под ред. Р.А. Шмойловой, М.: Финансы и статистика, 2000.
8. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. – М.: ИНФРА – М., 1998.
[1]
Громыко Л.В. Теория статистики. – М.:ИНФРА-М, 2002 (приложение 9)
[2]
Громыко Л.В. Теория статистики. – М.: ИНФРА-М, 2002 (Приложение 9)
[3]
Громыко Л.В. Теория статистики. – М.: ИНФРА-М, 2002 (Приложение 9)
[4]
Громыко Л.В. Статистика. – М.: ИНФРА-М, 2002 (Приложение 9)
[5]
Громыко Л.В. Статистика. – М.: Финансы и статистика, 2000 (Приложение 8)
[6]
[6] Громыко Л.В. Статистика. – М.: Финансы и статистика, 2000 (Приложение 9)
|