| Лекція 18
Збудження об’ємних резонаторів.
1.
Доведемо ортонормованість власних функцій резонатора.
 , ,  , бо задача про власні коливання розв’язується без струмів. Для другого коливання: , бо задача про власні коливання розв’язується без струмів. Для другого коливання:  . .
 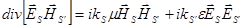 , ,
  . .
Проінтегрувавши обидві рівності по всьому об’єму та врахувавши властивості  векторного добутку, отримаємо: векторного добутку, отримаємо:
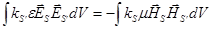 , ,
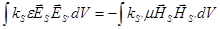 . .
Враховуючи, що  та позначивши та позначивши 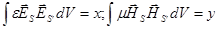 маємо лінійну однорідну систему відносно маємо лінійну однорідну систему відносно  з коефіцієнтами з коефіцієнтами  та та 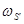 : :
 . Система має нетрівіальні розв’язки якщо . Система має нетрівіальні розв’язки якщо  ; ;  . Тоді . Тоді  , тобто , тобто  . Таким чином маємо ортонормованість власних функцій резонатора з нормою . Таким чином маємо ортонормованість власних функцій резонатора з нормою  , яку легко знайти. , яку легко знайти.
2.
Знайдемо поля  та та  всередині резонатора при наявності струмів. всередині резонатора при наявності струмів.
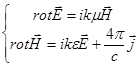 - рівняння Максвела. - рівняння Максвела.
Псевдовектор
в математиці – вектор, що змінює свій напрямок при інверсії системи координат (напрямок, векторний добуток). У фізиці псевдовектор змінює напрямок при інверсії часу  . Наприклад, при інверсії часу електрон починає обертатися в протилежному напрямку, а відповідно змінює і напрямок МП. . Наприклад, при інверсії часу електрон починає обертатися в протилежному напрямку, а відповідно змінює і напрямок МП.
Таким чином, МП – псевдовектор, ЕП – вектор. Звідси можна зробити висновок, що гамільтоніан не може містити  (щоб він був інваріантний до інверсії часу). Ще один висновок – що немає магнітного п’єзоефекту
. (щоб він був інваріантний до інверсії часу). Ще один висновок – що немає магнітного п’єзоефекту
.
 Існує іще одна класифікація: Існує іще одна класифікація:
соленоїдальні та потенціальні.
Потенціальний (поздовжній):
 - немає вихорів. - немає вихорів.
 Соленоїдальний (поперечний): Соленоїдальний (поперечний):
 - немає вузлів. - немає вузлів.
Записавши  ми зробили помилку, бо не врахували потенційні поля, пов’язані з електростатичними полями зарядів, що збуджують струми. ми зробили помилку, бо не врахували потенційні поля, пов’язані з електростатичними полями зарядів, що збуджують струми.
Отже,  , ,  , де , де  , ,  . Взагалі то, . Взагалі то,  , бо магнітних зарядів не існує. Проте, є припущення про існування магнітних зарядів – монополь Дірака
; тоді , бо магнітних зарядів не існує. Проте, є припущення про існування магнітних зарядів – монополь Дірака
; тоді  . .
 , ,
 . .
Підставимо в рівняння Максвела: 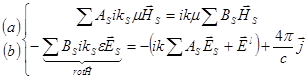 . Прирівнявши відповідні коефіцієнти при базисних функціях . Прирівнявши відповідні коефіцієнти при базисних функціях  та та  , одержимо , одержимо  - з рівняння а). Оскільки - з рівняння а). Оскільки  , то , то  . .
 . .  ; ; 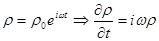 . .
Таким чином, для гармонічних полів:  . Тоді . Тоді  . Використаємо . Використаємо  , ,  . .  , ,  бо бо  . Таким чином, довели строге рівняння Пуансона для електростатичної частини полів. . Таким чином, довели строге рівняння Пуансона для електростатичної частини полів.
Проінтегруємо  по по  , попередньо помноживши на , попередньо помноживши на  : :

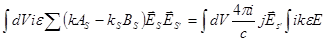
 . .
В результаті отримаємо:  , маємо систему двох рівнянь з двома невідомими. Амплітуда , маємо систему двох рівнянь з двома невідомими. Амплітуда  . .
Ми отримали формулу для резонансного збудження. Тут не враховано дисипацію
, тому можливо  . Якщо дисипацію врахувати наступним чином: . Якщо дисипацію врахувати наступним чином:  , то отримаємо Лоренцівську резонансну криву: , то отримаємо Лоренцівську резонансну криву:  . .
|
 ,
,  .
. . Система має нетрівіальні розв’язки якщо
. Система має нетрівіальні розв’язки якщо 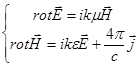 - рівняння Максвела.
- рівняння Максвела. Існує іще одна класифікація:
Існує іще одна класифікація:  Соленоїдальний (поперечний):
Соленоїдальний (поперечний): 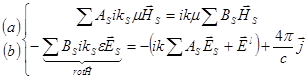 . Прирівнявши відповідні коефіцієнти при базисних функціях
. Прирівнявши відповідні коефіцієнти при базисних функціях  .
. , маємо систему двох рівнянь з двома невідомими. Амплітуда
, маємо систему двох рівнянь з двома невідомими. Амплітуда