| 4.
5. Методы приближенного расчета безусловного отношения правдоподобия.
(Схемы совместного обнаружения – оценивания)
Во многих случаях непосредственно выполнить интегрирование многомерной функции правдоподобия по распределению неизвестных параметров не удается. В этом случае используется один из двух возможных методов приближенного расчета безусловного отношения правдоподобия, приводящих к двум существенно различным по виду, но по существу эквивалентным структурным схемам устройства обработки. Принципиальной особенностью этих схем является возможность одновременно с решением о наличии сигнала получить оценку его априори неизвестных параметров, что оправдывает название “схемы совместного обнаружения – оценивания
”.
4.1 Многоканальная схема совместного обнаружения – оценивания.
Возможность вычисления безусловного отношения правдоподобия с помощью многоканальной схемы базируется на замене интегралов конечными суммами и состоит в следующем.
Пусть область изменения неизвестного параметра представляет некоторый отрезок  . Разобьем этот отрезок на . Разобьем этот отрезок на 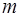 интервалов интервалов 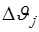 , границы которых обозначим , границы которых обозначим 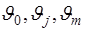 . Тогда . Тогда 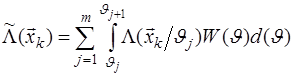 (4.1), (4.1),
где  - априорное распределение неизвестного параметра. - априорное распределение неизвестного параметра.
Будем считать, что функция  непрерывна по непрерывна по  . Тогда согласно обобщенной теореме о среднем для каждого интервала . Тогда согласно обобщенной теореме о среднем для каждого интервала 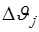 существует принадлежащее этому интервалу значение параметра существует принадлежащее этому интервалу значение параметра  , обеспечивающее выполнение условия , обеспечивающее выполнение условия  , где , где  - отношение правдоподобие, рассчитанное при значении параметра - отношение правдоподобие, рассчитанное при значении параметра  . Поэтому сумма (4.1) может быть представлена в виде . Поэтому сумма (4.1) может быть представлена в виде 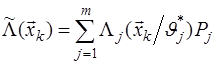 (4.2), (4.2),
где 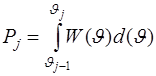 – вероятность того, что параметр – вероятность того, что параметр  принадлежит принадлежит  интервалу. Из формулы (4.2) следует, что безусловное отношение правдоподобия представляет собой выборочное среднее значений парциальных статистик. интервалу. Из формулы (4.2) следует, что безусловное отношение правдоподобия представляет собой выборочное среднее значений парциальных статистик.
Соответствующую формуле (4.2) схему обработки можно представить в виде некоторого 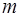 - канального устройства, каждый канал которого настроен на некоторое фиксированное значение неизвестного параметра - канального устройства, каждый канал которого настроен на некоторое фиксированное значение неизвестного параметра 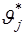 . Очевидно, что при . Очевидно, что при  , т.е. при неограниченном увеличении числа , т.е. при неограниченном увеличении числа 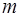 интервалов разбиения, сумма (4.2) независимо от способа разбиения сходится к значению интеграла (4.1), т.е. при интервалов разбиения, сумма (4.2) независимо от способа разбиения сходится к значению интеграла (4.1), т.е. при  изображенная на рис.4.1 схема реализует обработку, близкую к оптимальной. изображенная на рис.4.1 схема реализует обработку, близкую к оптимальной.
Поскольку, как отмечено выше, способ разбиения диапазона значений неизвестного параметра на интервалы 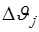 мало влияет на характеристики алгоритма этот способ может выбираться исходя из удобства расчетов; например исходя из условия, чтобы вероятность мало влияет на характеристики алгоритма этот способ может выбираться исходя из удобства расчетов; например исходя из условия, чтобы вероятность  попадания параметра для всех интервалов была одинаковой: попадания параметра для всех интервалов была одинаковой:  . .
Если неизвестный параметр  является измеряемым, т.е. его значение после обнаружения сигнала представляет самостоятельный интерес, то максимально правдоподобная оценка этого параметра соответствует значению параметра является измеряемым, т.е. его значение после обнаружения сигнала представляет самостоятельный интерес, то максимально правдоподобная оценка этого параметра соответствует значению параметра  , при котором , при котором 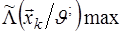 . Выбор номера соответствующего канала и выдачу на выход оценки неизвестного параметра . Выбор номера соответствующего канала и выдачу на выход оценки неизвестного параметра 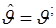 обеспечивают схема поиска максимума и ключ, открываемый в момент принятия решения об обнаружении сигнала. обеспечивают схема поиска максимума и ключ, открываемый в момент принятия решения об обнаружении сигнала.
Рассмотренная схема позволяет дать приближенную количественную оценку влияния априорной неопределенности на параметры обнаружителя, использующего статистику безусловного отношения правдоподобия. Для этого проанализируем ход накопления статистики  в каналах, содержащих и не содержащих сигнал. в каналах, содержащих и не содержащих сигнал.
Обозначим через  индекс канала, содержащего сигнал. Очевидно, что формула (4.2) может быть представлена в виде двух слагаемых индекс канала, содержащего сигнал. Очевидно, что формула (4.2) может быть представлена в виде двух слагаемых
 (4.3) (4.3)
В каналах, где сигнал от цели отсутствует, среднее значение статистики 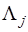 на любом шаге равно единице: на любом шаге равно единице: 
(тождество отражает условие нормировки плотности 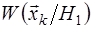 ). Следовательно, мат. ожидание второго слагаемого формулы (4.3) равно ). Следовательно, мат. ожидание второго слагаемого формулы (4.3) равно  . В канале, содержащем цель, . В канале, содержащем цель, 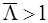 , поэтому отношение правдоподобия этого канала нарастает (в среднем) по геометрической прогрессии , поэтому отношение правдоподобия этого канала нарастает (в среднем) по геометрической прогрессии 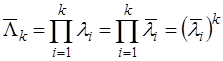 (мат. ожидание произведения независимых величин равно произведению их мат. ожиданий). Следовательно мат. ожидание статистики (4.2) может быть записано в виде: (мат. ожидание произведения независимых величин равно произведению их мат. ожиданий). Следовательно мат. ожидание статистики (4.2) может быть записано в виде:
 Рис.4.2. Рис.4.2.
Таким образом, “вклад” канала, содержащего сигнал, в безусловное отношение правдоподобия  по мере наблюдения нарастает, т.е. суммарный отклик схемы (4.2) стремится к отклику канала, “согласованного” с сигналом (схема как бы настраивается на истинное значение априори неизвестного параметра, см. рис.4.2). Наличие “пустых” каналов при этом учитывается коэффициентом по мере наблюдения нарастает, т.е. суммарный отклик схемы (4.2) стремится к отклику канала, “согласованного” с сигналом (схема как бы настраивается на истинное значение априори неизвестного параметра, см. рис.4.2). Наличие “пустых” каналов при этом учитывается коэффициентом 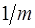 , характеризующим “плату” за априорную неопределенность. За счет этого коэффициента среднее приращение логарифма отношения правдоподобия (информация Кульбака – Леблера) уменьшается примерно на , характеризующим “плату” за априорную неопределенность. За счет этого коэффициента среднее приращение логарифма отношения правдоподобия (информация Кульбака – Леблера) уменьшается примерно на 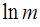 . .
Возможна и другая, эквивалентная, трактовка полученных результатов: уменьшение отношения правдоподобия в 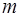 раз равнозначно увеличению в раз равнозначно увеличению в 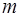 раз решающего порога, что соответствует увеличению длительности наблюдения примерно в раз решающего порога, что соответствует увеличению длительности наблюдения примерно в  раз. раз.
4.2. Следящая (адаптивная) схема совместного обнаружения – оценивания.
Второй возможный подход к приближенному расчету безусловного отношения правдоподобия предусматривает рекуррентный расчет оценок неизвестных параметров в явном виде и подстрой-обнаружителя под эти оценки, поэтому часто его называют адаптивным
.
Обратим внимание, что в задачах обнаружения сигналов возможность получить оценку их параметров до обнаружения
принципиально отсутствует. Ввиду ограниченного времени на наблюдение отводить дополнительное время на получение оценок в большинстве случаев нецелесообразно, поэтому для оценки параметров, как правило используется решающая
выборка. При этом предполагается, что наблюдаемая выборка содержит полезный сигнал, если эта гипотеза не подтверждается, то полученная оценка является псевдооценкой
.
Оператор оценки, т.е. функциональное преобразование 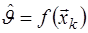 , которому должна подвергаться выборка, в принципе может выбираться из различных соображений, однако чаще всего предпочтение отдается максимально правдоподобным оценкам. При заданном операторе оценки и известном условном распределении выборки , которому должна подвергаться выборка, в принципе может выбираться из различных соображений, однако чаще всего предпочтение отдается максимально правдоподобным оценкам. При заданном операторе оценки и известном условном распределении выборки 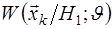 может быть рассчитано условное распределение оценки может быть рассчитано условное распределение оценки 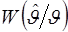 . Затем по формуле Байеса рассчитывается апостериорное распределение неизвестного параметра . Затем по формуле Байеса рассчитывается апостериорное распределение неизвестного параметра
 , ,
где 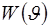 - априорное распределение неизвестного параметра. Усреднением условных функций правдоподобия - априорное распределение неизвестного параметра. Усреднением условных функций правдоподобия 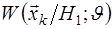 или условного отношения правдоподобия или условного отношения правдоподобия  по апостериорному распределению неизвестного параметра по апостериорному распределению неизвестного параметра 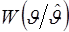 получаем отношение правдоподобия, которое не зависит от неизвестного параметра получаем отношение правдоподобия, которое не зависит от неизвестного параметра  , но зависит от оценки , но зависит от оценки 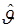 : :
 . .
Если оценка  рассчитана на основании рассчитана на основании 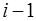 отсчетов входной выборки, предшествующих отсчету отсчетов входной выборки, предшествующих отсчету  , наблюдаемому в данный момент, то оценка , наблюдаемому в данный момент, то оценка  и отсчет и отсчет  взаимно независимы, следовательно отношение правдоподобия факторизуется: взаимно независимы, следовательно отношение правдоподобия факторизуется:
 ,где ,где  - отношение правдоподобия - отношение правдоподобия  - го элемента выборки. - го элемента выборки.
Таким образом, расчет безусловного отношения правдоподобия может выполняться рекуррентно с помощью схемы рис 4.3.
По мере получения новых отсчётов точность оценки  растёт (дисперсия апостериорного распределения уменьшается) и рекуррентный алгоритм сходится к алгоритму, соответствующему точно известным параметрам, т.е. происходит самонастройка алгоритма на истинное значение неизвестного параметра. растёт (дисперсия апостериорного распределения уменьшается) и рекуррентный алгоритм сходится к алгоритму, соответствующему точно известным параметрам, т.е. происходит самонастройка алгоритма на истинное значение неизвестного параметра.
4.3. О роли априорного распределения при синтезе алгоритмов совместного обнаружения – оценивания (адаптивный байесовский подход)
До сих пор мы полагали априорное распределение неизвестных параметров 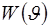 , точно заданным. (Подход к задачам статистических решений, при котором априорное распределение считается известным, называется байесовским
). , точно заданным. (Подход к задачам статистических решений, при котором априорное распределение считается известным, называется байесовским
).
На практике далеко не всегда есть достаточные теоретические или экспериментальные данные для обоснованного выбора того или иного закона распределения 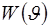 . В связи с этим возникает вопрос о практической ценности алгоритмов обнаружения - оценивания, полученных в рамках байесовского подхода, т.е. о возможности применения таких алгоритмов в случаях, когда априорное распределение отличается от расчетного или неизвестно. . В связи с этим возникает вопрос о практической ценности алгоритмов обнаружения - оценивания, полученных в рамках байесовского подхода, т.е. о возможности применения таких алгоритмов в случаях, когда априорное распределение отличается от расчетного или неизвестно.
Положительный ответ на этот вопрос следует из фундаментального свойства сходимости
байесовских алгоритмов к алгоритмам, соответствующим точно известным параметрам сигнала, причем это свойство сохраняется при любом
априорном распределении. Отмеченная инвариантность позволяет распространить методы байесовской теории на представляющий основной интерес случай, когда априорное распределение  неизвестно. неизвестно.
Соответствующий подход, получивший название адаптивного
байесовского, рассматривает априорное распределение как некоторую весовую функцию, которая лишь задает начальные условия для фильтрации оценок неизвестных параметров и поэтому влияет только на скорость их сходимости. Другая трактовка априорного распределения, возможная в рамках адаптивного байесовского подхода, состоит в том, что оно рассматривается как весовая функция, по которой усредняется условный риск некоторого решающего правила относительно байесовского. Очевидно, что обе трактовки открывают достаточную свободу для выбора функции 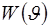 например, из соображений удобства расчета безусловного отношения правдоподобия. например, из соображений удобства расчета безусловного отношения правдоподобия.
Основываясь на изложенном, можно утверждать, что рассмотренные нами алгоритмы совместного обнаружения – оценивания, будучи синтезированными при конкретном виде априорного распределения 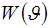 , могут затем применяться безотносительно к его истинному виду, поскольку при достаточно большом времени наблюдения их выходной эффект перестает зависеть от априорной информации, полностью определяется результатами наблюдения и стремится к выходному эффекту оптимального алгоритма. Оба рассмотренных способа вычисления безусловного отношения правдоподобия (с помощью многоканальной схемы или рекурентный) в этом смысле полностью эквивалентны. Выбор того или иного варианта построения схемы определяется из технических, экономических и других соображений. , могут затем применяться безотносительно к его истинному виду, поскольку при достаточно большом времени наблюдения их выходной эффект перестает зависеть от априорной информации, полностью определяется результатами наблюдения и стремится к выходному эффекту оптимального алгоритма. Оба рассмотренных способа вычисления безусловного отношения правдоподобия (с помощью многоканальной схемы или рекурентный) в этом смысле полностью эквивалентны. Выбор того или иного варианта построения схемы определяется из технических, экономических и других соображений.
В заключении отметим, что схемы совместного обнаружения – оценивания могут применяться и в тех случаях, когда неизвестный параметр является мешающим, т.е. не представляет самостоятельного интереса. Оценка параметра на выход схемы при этом не выдается, сам же алгоритм обнаружения остается прежним.
|