| Задача 10 Даны матрицы
1
|
1
|
2
|
2
|
-1
|
1
|
1
|
0
|
0
|
| А=
|
-2
|
0
|
2
|
В=
|
3
|
4
|
-2
|
Е=
|
0
|
1
|
0
|
| 0
|
-1
|
0
|
1
|
0
|
-1
|
0
|
0
|
1
|
Найти матрицу С = 5В – АE + BA -2Е
Решение:
2 -1 1 1 1 2
BA= 3 4 -2 · -2 0 2
1 0 -1 0 -1 0
2•1+(-1)•(-2)+1•0 2•1+(-1)•0+1•(-1) 2•2+(-1)•2+1•0
3•1+4•(-2)+(-2)•0 3•1+4•0+(-2)•(-1) 3•2+4•2+(-2)•0
2•1+(-1)•(-2)+1•0 2•1+(-1)•0+1•(-1) 2•2+(-1)•2+1•0
4 1 2
= -5 5 14
1 2 2
10 -5 5 2 0 0
5В= 15 20 -10 2Е= 0 2 0 АЕ=А,
5 0 -5 0 0 2
1 1 2
т.к. Е – единичная матрица АE = -2 0 2
0 -1 0
| 
|
10-1+4-2
|
-5-1+1-0
|
5-2+2-0
|
| С=
|
15+2-5-0
|
20-0+5-2
|
-10-2+14-0
|
| 5-0+1-0
|
0+1+2-0
|
-5-0+2-2
|
|  11 11
|
-5
|
5
|
| 12
|
23
|
2
|
| 6
|
3
|
-5
|
Задача 20
 Решить систему уравнений методом Гаусса и по формулам Крамера. Решить систему уравнений методом Гаусса и по формулам Крамера.
x + 2y + z = 5
x - y –2z = -1
2x + y + z = 4
Решение:
Метод Гаусса.
| 1
|
2
|
1
|
5
|
1
|
2
|
1
|
5
|
1
|
2
|
1
|
5
|
| 1
|
-1
|
-2
|
-1
|
~
|
0
|
-3
|
-3
|
-6
|
~
|
0
|
-3
|
-3
|
-6
|
| 2
|
1
|
1
|
4
|
0
|
-3
|
-1
|
-6
|
0
|
0
|
2
|
0
|
2z = 0, z = 0; -3y -3∙0 = -6, y = 2; x + 2∙2 + 1∙0 = 5, x = 1.
Решение системы {1;2;0}
По формулам Крамера:

D - определитель матрицы, составленной из коэффициентов при неизвестных,
Dx, Dy, Dz – получаются из в путем замены столбца коэффициентов при соответствующем неизвестном на столбец свободных членов.
| 1
|
2
|
1
|
| Δ=
|
1
|
-1
|
-2
|
= -1+1-8+2-2+2= -6
|
| 2
|
1
|
1
|
| 5
|
2
|
1
|
| Δx
=
|
-1
|
-1
|
-2
|
= -5-1-16+4+2+10 = -6
|
| 4
|
1
|
1
|
X=Δx
/Δ= -6/(-6) = 1
| 1
|
5
|
1
|
| Δy
=
|
1
|
-1
|
-2
|
= -1+4-20+2+8-5 = -12
|
| 2
|
4
|
1
|
Y=Δy
/Δ= -12/(-6) =2
Z=Δz
/Δ= 0/(-6) = 0
| 1
|
2
|
5
|
| Δя
=
|
1
|
-1
|
-1
|
= -4+5-4+10+1-8 = 0
|
| 2
|
1
|
4
|
Решение системы {1;2;0}
Задача 30
На плоскости задан треугольник координатами своих вершин А(2,3), В(-3,1), С(-4,5)
Найти:
- длину стороны АВ
- уравнение стороны АВ
- уравнение медианы АD
- уравнение высоты СЕ
- уравнение прямой, проходящей через вершину С, параллельно стороне АВ
- внутренний угол при вершине А
- площадь треугольника АВС
- координаты точки Е
- сделать чертеж
Решение:
1. Длина стороны АВ:
½АВ½=  » 5,385 » 5,385
2. Уравнение прямой, проходящей через две заданные точки:
 ; ;  ; ; 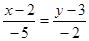
у =  - уравнение прямой АВ, угловой коэффициент kAB
= 2/5 - уравнение прямой АВ, угловой коэффициент kAB
= 2/5
3. Медиана АD делит сторону ВС, противоположную вершине А, пополам.
Координаты середины ВС:
х4
= (х2
+ х3
)/2 = 3,5, у4
= (у2
+ у3
)/2 = 3
D (-3,5;3)
Уравнение прямой, проходящей через две заданные точки, А и D:
 ; ;  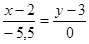 -5,5у = -16,5 -5,5у = -16,5
у = 3- уравнение прямой АD
3. Высота СЕ перпендикулярна АВ, а значит угловой коэффициент высоты СЕ равен
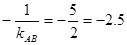
Уравнение прямой, проходящей через заданную точку (х3
ёу3
) и имеющей угловой коэффициент kСЕ
, имеет вид:
у – у3
= kСЕ
(х – х3
); у – 5 = -2,5(х+4)
у = -2,5х -5 – уравнение высоты СЕ.
5. Если прямые параллельны, то их угловые коэффициенты равны. Уравнение прямой, проходящей через точку С (х3
ёу3
) и имеющей угловой коэффициент kАВ
, имеет вид:
у – у3
= kАВ
(х – х3
); у – 5 =  х + х + , ,
у =  х + х + , - уравнение прямой, параллельной АВ. , - уравнение прямой, параллельной АВ.
6. Косинус внутреннего угла при вершине А вычисляется по формуле:
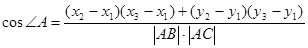 , где , где
 - длины сторон АВ и АС соответственно. - длины сторон АВ и АС соответственно.
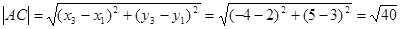
 , ,
ÐА = arc cos 0,7643 = 40о
9'
7. Площадь треугольника АВС вычисляется по формуле:
S = Ѕç(x2
– x1
)(y3
– y1
) – (x3
– x1
)(y2
– y1
)ç;
S= Ѕ ç(-5)·2 – (-2) ·(-6)ç = 22/2 = 11 кв.ед.
8. Координаты точки Е находим, решая совместно уравнения АВ и СЕ, т.к точка Е принадлежит им обоим:
 у = -2,5х -5 у = -2,5х -5
у = 
0,4х +2,2 = -2,5х -5 2,9х = -7,2 х = -2,5
у = 6,25 – 5 = 1,25 Е(-2,5;1,25)
Задача 40
Привести уравнение кривой второго порядка к каноническому виду. Построить кривую.
у2
+ 2x - 2y -1 = 0
Решение:
Выделяем полные квадраты:
у2
- 2у +1 + 2х- 2 = 0
(у - 1)2
= -2(х - 1)
(х - 1) =-1/2(у - 1)2
– это уравнение параболы с центром в точке (1,1), ось симметрии – прямая
у = 1, ветви параболы направлены влево.

Задача 50
Вычислить пределы.
1) 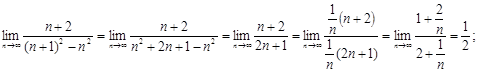
2) 
3) 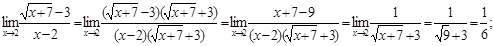
4) 
так как 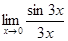 -первый замечательный предел -первый замечательный предел
5)  , (a>0) , (a>0)
Обозначим х-а = t. Если х→а, то t→0, х = t+a, ln x-ln a = 

где 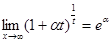 -– второй замечательный предел. -– второй замечательный предел.
Задача 60
Найти производные функций:
1) y = 
y¢ = 
2) у =  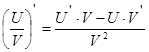

3) y = 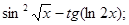
y¢ = 
4) y = ctg(ex
cosx);
y¢= 
Задача 70
Провести полное исследование функции и построить ее график.
у =  ; ;
Решение:
1. Область определения функции: х Î (-¥; +¥).
2. Поведение функции на границах области определения:
 
3. у¢= х3
– х2
= х2
(x-1); у¢= 0, если х1
= 0, х2
= 1;
При х Î (-¥; 0), у¢< 0, функция убывает.
При х Î (0;1), у¢< 0, функция убывает.
В точке х = 0 экстремума нет.
При х Î (1;+∞), у¢> 0, функция возрастает.
В точке х =1 функция имеет локальный минимум.
4. уmin
= 1
/4
- 1
/3
= - 1
/12
.
5. Выпуклость, точки перегиба графика функции:
у²= 3х2
– 2х = x(3x-2).
у²= 0, если 2х(6х -1) = 0, х1
= 0, х2
= 2
/3
;
При х < 0, у²> 0, график вогнутый.
При 0 < х < 2
/3
, у²< 0, график выпуклый.
При х > 2
/3
, у²> 0, график вогнутый.
Точки х1
= 0 и х2
= 2
/3
- точки перегиба графика функции.
у(0) = 0, у(2
/3
) » -0,05
6. Точки пересечения с осями координат:
С осью ОХ. у = 0,  = 0 = 0 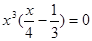 х1
= 0, x2
= 4
/3 х1
= 0, x2
= 4
/3
С осью ОУ. х = 0, у= 0.

Задача 80
Найти частные производные первого и второго порядка функций.
z = x2
∙sin y + y2
∙cos x;
Решение:
 

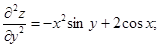
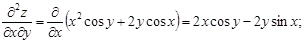
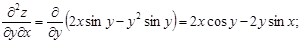
 = = . .
Задача 90
Дана функция . Показать, что . Показать, что 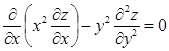
Решение:

 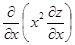 = = 

  = = 
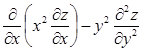 = = - - = 0, что и требовалось доказать. = 0, что и требовалось доказать.
Задача 100
Найти наибольшее и наименьшее значения функции z = x3
+ 8y3
-6xу+1 в прямоугольнике, ограниченном прямыми х = 0, х = 2, у = 1, у = -1.
Решение:
1. Ищем точки экстремумов внутри замкнутой области:

 
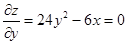
3x2
= 6y, y = 
24y2
= 6x,   
x1
= 0, x2
= 1, y1
= 0, y2
= Ѕ
Точка О(0,0) и точка N (1, Ѕ)
2. Ищем точки экстремумов на границах области:
а) сторона АВ: х= 0, -1 £ у £ 1, z = 8у3
+1;
 24у2
, z¢ = 0, если у = 0, точка (0,0). 24у2
, z¢ = 0, если у = 0, точка (0,0).
б) сторона ВС: у = 1, 0 £ х £ 2, z = х3
– 6х+9;
 3х2
- 6 = 0, х2
= 2 х = ± 3х2
- 6 = 0, х2
= 2 х = ± »±1,4, точка х = -1,4 в замкнутую область не входит. »±1,4, точка х = -1,4 в замкнутую область не входит.
х = 1,4 , – точка К (1,4;1)
в) Сторона CD: х = 2, -1 £ у £ 1,
z = 8 + 8у3
- 12у+1 = 8у3
- 12у+9;
 2у2
= 1, у = 2у2
= 1, у =  - точки M(2;0,7) и Q(2;-0,7) - точки M(2;0,7) и Q(2;-0,7)
г) сторона АD: у = -1, 0 £ х £ 2, z = х3
+ 6х-7;
 3х2
+ 6 ≠ 0, при любых значениях х. 3х2
+ 6 ≠ 0, при любых значениях х.
2. Вычислим значения функции Z в точках А, В, С, D, О, К, M, N, Q.
ZA
= Z(0,-1) = -8+1=-7;
ZB
= Z(0,1) = 8+1=9;
ZC
= Z(2,1) = 8+8-12+1=5;
ZD
= Z(2,-1) = 8-8+12+1=13;
ZK
= Z( ,1) = 2,8+8-8,4+1=3,4; ,1) = 2,8+8-8,4+1=3,4;
ZO
= Z(0,0) = 1;
ZM
= Z(2,0.7) = 8+2,7-8,4+1=3,3;
ZN
= Z(1, ) = 0; ) = 0;
ZQ
= Z(2,-0.7) = 8-2,7+8,4+1=14,7;
Zmin
= -7, Zmax
= 14,7.
Задача 110
Найти формулу вида y = ax + b методом наименьших квадратов по данным опыта (таблицы):
| Х
|
1
|
2
|
3
|
4
|
5
|
| У
|
4,8
|
5,8
|
4,3
|
2,3
|
2,8
|
Решение:
Метод наименьших квадратов дает систему двух линейных уравнений для определения параметров ”a” и “b”:
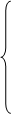 
Подсчитаем суммы:
 1+2+3+4+5=15 1+2+3+4+5=15 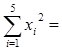 1+4+9+16+25 = 55 1+4+9+16+25 = 55
 4,8+5,8+4,3+2,3+2,8=20 4,8+5,8+4,3+2,3+2,8=20  1·4,8+2·5,8+3·4,3+4·2,3+5·2,8 = 52,5 1·4,8+2·5,8+3·4,3+4·2,3+5·2,8 = 52,5
Подставляем значения сумм в систему уравнений:
52,5 -55a -15b = 0
20 – 15a – 5 b = 0 (*3)
a = -0.75
20 – 15·(-0.75) = 5b; b = 31,25 : 5 = 6,25
Искомая формула: y = -0,75x + 6,25.
Задача 120
Вычислить неопределенные интегралы:
1) 
2) 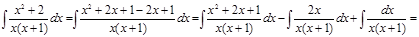


3)  
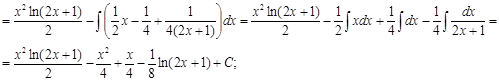
4) 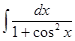 ; Подстановка: t = tg t; x = arctg t, ; Подстановка: t = tg t; x = arctg t,
dx = 

5)  Подстановка: Подстановка: 

Задача 130
Вычислить площадь, ограниченную заданными линиями:
у = х2
, y = 2- x2
Решение:

 S = S = 
S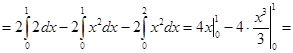

S кв.ед. кв.ед.
Задача 140
Определить объем тела, образованного вращением фигуры, ограниченной заданными линиями:
(у-3)2
+3х = 0, х = -3 вокруг оси Ох
Решение:
V = 
 

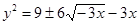
V = 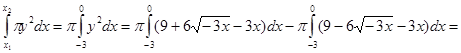

=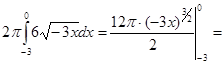 6p∙27 =162p куб.ед. 6p∙27 =162p куб.ед.
Литература:
1. Л.Г. Лелевкина, В.В. Попов «Основы высшей математики». Бишкек, КРСУ, 2005 г.
2. Пискунов Н.С. «Дифференциальное и интегральное исчисление» т.1 М. 1986 г.
|