| Теорія електропровідності напівпровідників та твердих тіл
Зміст
Вступ
1. Елементи зонної теорії твердих тіл
2. Теорія електропровідності напівпровідників
Література
Вступ
Вивчення розділу «Напівпровідники» в шкільному курсі фізики представляє собою важливу і актуальну задачу. Важко уявити собі галузь народного господарства, науки чи техніки де не використовуються прилади які виготовлені із напівпровідникових матеріалів. Завдяки розвитку фізики напівпровідників, в техніці за останнє десятиріччя відбулися революційні зміни: обчислювальні комплекси які займали об’єми 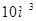 перетворились в мініатюрні комп’ютерні системи які мають набагато ширші функціональні властивості чим їх попередники. На сьогоднішній день технологами створені великі інтегральні схеми, густина активних елементів на яких досягає перетворились в мініатюрні комп’ютерні системи які мають набагато ширші функціональні властивості чим їх попередники. На сьогоднішній день технологами створені великі інтегральні схеми, густина активних елементів на яких досягає 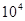 на на  . Все це стало можливим завдяки чітким уявленням про те, що відбувається на міжатомному рівні напівпровідникових структурах. Знайомлячи учнів з основами фізики напівпровідників ми даємо уявленням учням про напрямки розвитку сучасної фізики і покладаємо надію на те що молоде покоління маючи належну природничо – математичну підготовку зробить свій внесок в розвиток даного напряму. . Все це стало можливим завдяки чітким уявленням про те, що відбувається на міжатомному рівні напівпровідникових структурах. Знайомлячи учнів з основами фізики напівпровідників ми даємо уявленням учням про напрямки розвитку сучасної фізики і покладаємо надію на те що молоде покоління маючи належну природничо – математичну підготовку зробить свій внесок в розвиток даного напряму.
В дипломній роботі зроблено спробу систематизувати інформацію про основні етапи розвитку фізики напівпровідників і її практичного застосування; підвищити пізнавальну активність учнів за рахунок поєднання теоретичного і практичного матеріалів.
1. Елементи зонної теорії твердих тіл
Для того щоб визначити властивості кристалу, необхідно знати характер взаємодії всіх частинок (атомних ядер та електронів), його складові. Точний опис цієї взаємодії являє собою дуже складну задачу. Дійсно, кожна частинка (електрон і ядра атома), які входять в склад кристалу об’ємом  , взаємодіють з , взаємодіють з 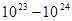 частинок, причому всі вони знаходяться в неперервному і дуже важкому русі. частинок, причому всі вони знаходяться в неперервному і дуже важкому русі.
Квантова механіка дає можливість сформулювати задачу про взаємодію всіх частинок, які складають кристал, у вигляді рівняння Шрьодінгера. Але складене для цього випадку рівняння нерозв’язне.
При описі ряду властивостей кристала (електричні, магнітні, оптичні) потрібно знати насамперед стани валентних електронів в кристалі. Ця обставина значно спрощує задачу, але не дає можливості розв’язати її правильно. Задача ця, яка носить назву багатоелектроної, може бути зведена завдяки ряду спрощень, до так званої одноелектроної задачі про рух одного електрона в самосоглосованому електричному полі кристалу.
Ці спрощення в основному зводяться до наступних положень. По-перше, велика різниться мас атомних ядер та електронів призводить до дуже великої різниці в швидкостях їх руху. Тому при описі руху електрона можна не враховувати рух ядер, а розглядати рух електрона в полі нерухомих ядер. По – друге, повільний рух ядер можна розглядати не в полі, створюваним миттєвим ростошуванням електронів, а в полі, створюваним середнім просторовим розподіленням заряду електронів, так як за час помітного зміщення ядра електрон встигне багаторазово обійти всі точки своєї «орбіти» в кристалі. По – третє, взаємодія кожного електрона з іншими, які залежать від миттєвого розташування всіх електронів, розглядається як взаємодія електрона з самоузгодженим полем, створюваним усередненням просторовим розподіленим полем, створюваним усередненим просторовим розподіленням заряду електронів.
В результаті цих спрощень рівняння Шредінгера стає розв’язуваним. Розв’язання його дає можливі значення енергії електрона в кристалі. Розподілення електронів по цим можливим електричним станам проходить у відповідності з принципом Паулі.
Як відомо, ізольований атом являє собою потенціальну яму, в якій електрон може займати одне з ряду дискретних енергетичних станів.
Якщо зблизити два атоми між собою так, щоб взаємодія між ними ще не з'являлася (для цього відстань між ними 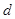 повинно бути більше, чім повинно бути більше, чім 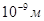 ), то енергетичні рівні електронів в атомах залишаються без змін. ), то енергетичні рівні електронів в атомах залишаються без змін.
Якщо ж відстань між атомами становитиме менш 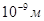 , то в результаті виникненого проміж ними взаємодії зменшиться довжина потенціального бар’єру, які розділяють сусідні атоми. Зниження енергетичного бартеру можливо пояснити притягання електронів одного атома ядром сусіднього. Так як енергія зв’язку електрона з ядром «свого» атома тим більше, чим ближче електрон розташований до ядра, то дія сусіднього атому буде сильніше на зовнішні валентні електрони, чим на електрони внутрішніх електронних оболонок. , то в результаті виникненого проміж ними взаємодії зменшиться довжина потенціального бар’єру, які розділяють сусідні атоми. Зниження енергетичного бартеру можливо пояснити притягання електронів одного атома ядром сусіднього. Так як енергія зв’язку електрона з ядром «свого» атома тим більше, чим ближче електрон розташований до ядра, то дія сусіднього атому буде сильніше на зовнішні валентні електрони, чим на електрони внутрішніх електронних оболонок.
В кристалах атоми розташовані на відстанях 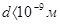 , і тому між ними існує сильна взаємодія. Ця взаємодія і визиває зниження потенціальних бар’єрів між атомами. , і тому між ними існує сильна взаємодія. Ця взаємодія і визиває зниження потенціальних бар’єрів між атомами.
Відстані між сусідніми атомами у кристалі, різні в різних напрямах, але для будь якого із напрямів відстань сусідніми атомами строго однакові (періодична структура). Завдяки цьому можна зобразити енергетичну схему кристала (для визначеного в ньому напряму) у вигляді періодично розташованих потенціальних ям, поділених потенціальними бар’єрами.
При утворенні кристалу різниця між повною енергією електрона в атомі і висотою потенціального бар’єру досить мала, а потенційний бар’єр достатньо малий для того, щоб став тунельний перехід електронів з одного атома в інший. Вірогідність тунельного ефекту велика для валентних валентних електронів і дуже мала (у більшості випадків зникаюче мала) для електронів внутрішніх електронних оболонок. Таким чином, валентні електрони в кристалі не локалізовані у конкретному атомі, а переходять від одного атома до іншого, тобто переміщуються від вузла до вузла кристалічної ґратки. Швидкість цього руху електронів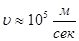 , тому валентний електрон знаходиться в даному вузлі кристалічної ґратки в перебігу , тому валентний електрон знаходиться в даному вузлі кристалічної ґратки в перебігу 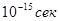 (розмір атому (розмір атому ). Слід зауважити, що перехід електрона з атома в атом проходить без зміни його енергії (він при цьому не отримує і не віддає енергії). ). Слід зауважити, що перехід електрона з атома в атом проходить без зміни його енергії (він при цьому не отримує і не віддає енергії).
На перший погляд можна показати, що такі переходи електрона приводять до порушення принципу Паулі для розподілення електронів кристалу по енергетичним рівням: у будь який момент в атомі можуть знаходитися декілька електронів з однаковими енергіями, так як до утворення кристалу всі вони належали до однакових атомів і мали в них однакові енергії.
Але при утворенні кристалу виникає не тільки зменшення висоти потенційного бар’єру між атомами, але і якісна зміна енергетичних рівнів електронів в атомах. Для з’ясування цього використаємо співвідношення невпевненостей для енергії
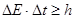
Де  - час знаходження електрона в електричному стані з енергією від - час знаходження електрона в електричному стані з енергією від  до до 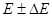 . .
Величина - визначає ширину енергетичного рівня, якщо відомий час перебування на ньому електрона. У ізольованому атомі електрон у нормальному (не збудженому) стані може знаходитись скільки завгодно, і тому, очевидно, ширина енергетичного рівня  скільки завгодно мала. В збудженому стані електрон в ізольованому атомі знаходиться в проміжку часу, тому ширина збудженого енергетичного рівня (по порядку величини) скільки завгодно мала. В збудженому стані електрон в ізольованому атомі знаходиться в проміжку часу, тому ширина збудженого енергетичного рівня (по порядку величини)

В кристалі, ширина енергетичного рівня електрона (того ж порядку величини)
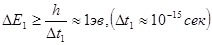
Звідси витікає, що енергетичний рівень електрона при утворенні кристалу з окремих атомів розщеплюється в енергетичну зону. Розщеплення в зону піддані і нормальні і збудженні енергетичні рівні. Таким чином, замість системи дискретних енергетичних рівнів енергії, яким характеризується окремий атом, в кристалі з'являється система енергетичних зон. Ширина енергетичної зони не залежить від розмірів кристалу, а визначається природою атомів, які утворюють кристал, і будовою кристала (міжатомними відстанями в ньому). Ширина енергетичної зони в одному й самому кристалі різна в різних напрямах, оскільки різні міжатомні відстані.
Енергетична зона не є неперервним рядом значень енергії електрона, а являє собою систему дискретних енергетичних рівнів. Число рівнів в енергетичній зоні кристала визначається добутком числа атомів в кристалі на кратність атомного енергетичного рівня, з якого утворилася зона. Під кратністю атомного енергетичного рівня припускається число електронів, котрі можуть знаходитися на цьому рівні з урахуванням принципу Паулі.
Утворення електричних зон можна роздивитися у спрощеній моделі кристалу. В цій моделі реальна періодична «ланка» потенціальних ям атомів, розташованих в атомі в певному напрямі, замінюється «ланкою» прямокутних потенціальних ям, розташованих один від одного на такій ж відстані 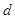 , як і атоми в кристалі. , як і атоми в кристалі.
Прямокутні потенціальні ями розділені потенційними бар’єрами однакової товщини по всій глибині потенційної ями.
Довжина електронів являє собою хвильовий характер. Його можливо представити як росположення груп хвиль з частотами в інтервалі від 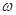 до до 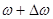 . Максимальна амплітуда цієї групи хвиль співпадає з центром електрону. Це так званий хвильовий пакет. Хвильовий пакет розповсюджується з груповою швидкістю . Максимальна амплітуда цієї групи хвиль співпадає з центром електрону. Це так званий хвильовий пакет. Хвильовий пакет розповсюджується з груповою швидкістю 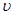 , яка для вільного електрона є миттєвою швидкістю, а для електрона, який рухається періодичному полі кристала, - його середньою швидкістю. , яка для вільного електрона є миттєвою швидкістю, а для електрона, який рухається періодичному полі кристала, - його середньою швидкістю.
Групова швидкість хвилі визначається, як
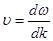 , (1) , (1)
де 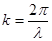 - хвильовий вектор ( - хвильовий вектор ( - довжина хвилі). - довжина хвилі).
Енергія електронної хвилі (електрона) 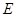 пов’язана з циклічною частотою пов’язана з циклічною частотою 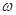 формулою формулою
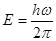 . (2) . (2)
Підставивши 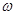 із формули (2) у вираз (1), отримаємо для групової швидкості електронної хвилі (швидкості електрона) вираз із формули (2) у вираз (1), отримаємо для групової швидкості електронної хвилі (швидкості електрона) вираз
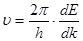 (3) (3)
Енергія вільного електрона 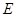 пов'язана з хвильовим вектором рівністю пов'язана з хвильовим вектором рівністю
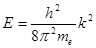 . (4) . (4)
Графік функції 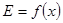 для вільного електрона, який являє собою параболу з вершиною у точці для вільного електрона, який являє собою параболу з вершиною у точці 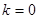 , зображено на малюнку 6 пунктирною лінією. , зображено на малюнку 6 пунктирною лінією.
Для того щоб скласти зображення про характер залежності 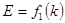 для електрона в кристалі розглянемо його рух в нашому «кристалі». Нехай в ньому е тільки один електрон, який спроможний рухатися по кристалу, і нехай цей електрон починає рухатись під дією сил зовнішнього електричного поля з стану з для електрона в кристалі розглянемо його рух в нашому «кристалі». Нехай в ньому е тільки один електрон, який спроможний рухатися по кристалу, і нехай цей електрон починає рухатись під дією сил зовнішнього електричного поля з стану з 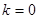 і і 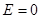 в напрямку, перпендикулярному стінкам потенціальних ям. При цьому електрична хвиля буде частково відбиватися від стінок кожної потенційної ями. Відбиті хвилі відносять частину енергії прямої хвилі, послаблює її. Поки для електронної довжина хвилі її в напрямку, перпендикулярному стінкам потенціальних ям. При цьому електрична хвиля буде частково відбиватися від стінок кожної потенційної ями. Відбиті хвилі відносять частину енергії прямої хвилі, послаблює її. Поки для електронної довжина хвилі її 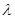 і модуль хвильового вектора і модуль хвильового вектора 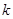 не співпадає умовам брегового віддзеркалення не співпадає умовам брегового віддзеркалення
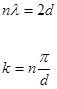 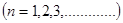 (5) (5)
відбиті хвилі будуть мати різноманітні фази і накладаючись одна на одну.
Внаслідок чого цього пряма хвиля проходить через кристал, майже не відбиваючись, тобто електрон рухається в кристалі, майже як вільний електрон. Графік функції  при цьому дуже мало відрізняються від параболи. при цьому дуже мало відрізняються від параболи.
При подальшому збільшенні модуля хвильового вектора 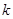 (зменшенні довжини вектора (зменшенні довжини вектора 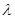 ) енергія відбитих хвиль зростає, а енергія прямої хвилі в залежності від ) енергія відбитих хвиль зростає, а енергія прямої хвилі в залежності від 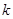 зменшується при порівнянні з темпом росту енергії вільного електрона. Чим менш відрізняється зменшується при порівнянні з темпом росту енергії вільного електрона. Чим менш відрізняється 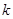 від величини від величини 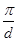 , тим все більш крива , тим все більш крива  відрізняється від параболи. Ця крива зображена на малюнку 6 суцільною лінією. Коли хвильовий вектор стає рівним відрізняється від параболи. Ця крива зображена на малюнку 6 суцільною лінією. Коли хвильовий вектор стає рівним 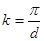 , всі відбиті хвилі опиняються в фазі і інтенсивність відбитої хвилі дорівнює інтенсивності прямої. , всі відбиті хвилі опиняються в фазі і інтенсивність відбитої хвилі дорівнює інтенсивності прямої.
Відхиленні хвилі, внаслідок вторинних віддзеркалень, перетворюються в пряму також швидко, як і пряма – у віддзеркалені: у кристалі виникає стояча електрона хвиля. Стояча хвиля описує такий стан електрона, при якому він однаково вірогідно може рухатись як в прямому, так і в зворотному направлені.
Подальше збільшення хвильового вектору електрона 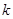 можлива тільки при умові, що енергія його зміниться стрибком на величину можлива тільки при умові, що енергія його зміниться стрибком на величину 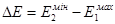 . Після цього модуль хвильового вектору може знову збільшитись від . Після цього модуль хвильового вектору може знову збільшитись від 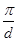 до до 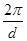 , ф характер зміни енергії електрону в залежності від хвильового вектору буде таким же, як описаний раніше. Коли хвильовий вектор стане рівним , ф характер зміни енергії електрону в залежності від хвильового вектору буде таким же, як описаний раніше. Коли хвильовий вектор стане рівним 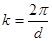 виникає стояча електрона хвиля і знову функція виникає стояча електрона хвиля і знову функція  терпить розрив. Далі це повторюється при значеннях терпить розрив. Далі це повторюється при значеннях 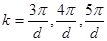 і тому подібне. і тому подібне.
Напрям хвильового вектору співпадає з напрямом швидкості електронної хвилі, тому зміна напряму розповсюдження хвилі на протилежне співпадає зміні знаку хвильового вектору на зворотній. З урахуванням цього можна записати умову брегового віддзеркалення електронних хвиль (умова утворення стоячої хвилі) так:
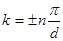 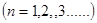 (7) (7)
Станом електрону, характеризуючим значеннями хвильового вектору від 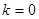 до до 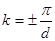 , співпадає деякий інтервал енергій від , співпадає деякий інтервал енергій від до до 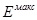 . Цей інтервал енергій складає першу дозволену енергетичну зону кристала. Значенням . Цей інтервал енергій складає першу дозволену енергетичну зону кристала. Значенням 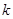 , які лежать в наступному інтервалі від , які лежать в наступному інтервалі від 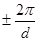 до до 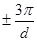 , відповідає третя дозволена енергетична зона і тому подібне. Дозволені енергетичні зони відділені один від одного інтервалами енергій, які електрон, який рухається в кристалі в заданому напрямі, не може мати. Ці інтервали енергій називаються забороненими зонами. , відповідає третя дозволена енергетична зона і тому подібне. Дозволені енергетичні зони відділені один від одного інтервалами енергій, які електрон, який рухається в кристалі в заданому напрямі, не може мати. Ці інтервали енергій називаються забороненими зонами.
Ширина енергетичної зони не залежить від розмірів кристалу, вона залежить від його будови, так як границі зони задаються умовами (7). Для визначеної зони граничні значення хвильового вектору 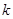 , а отже і енергії, залежать тільки від відстані , а отже і енергії, залежать тільки від відстані 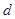 між сусідніми атомами кристала в даному направленні. між сусідніми атомами кристала в даному направленні.
У межах дозволенної зони після зміни хвильового вектора  . Але хвильовий вектор змінюється усередині зони не неперервна, а приймає ряд дискретних значень. При розповсюдженні електронної хвилі (рух електрона) в кристалі, вона випробовує віддзеркалення не тільки від стінок потенційних ям атомів, але і від границь кристалів. Але спільна довжина «ланки» атомів . Але хвильовий вектор змінюється усередині зони не неперервна, а приймає ряд дискретних значень. При розповсюдженні електронної хвилі (рух електрона) в кристалі, вона випробовує віддзеркалення не тільки від стінок потенційних ям атомів, але і від границь кристалів. Але спільна довжина «ланки» атомів 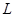 , то умови утворення стоячих електронних хвиль в результаті віддзеркалення їх від границь кристалу запишуться так: , то умови утворення стоячих електронних хвиль в результаті віддзеркалення їх від границь кристалу запишуться так:
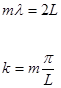  (8) (8)
Стан електрону, який відповідає умовам (8), є стаціонарним. Змінити цей стан електрон в зоні може стрибком (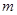 - ціле число). Кількість таких стаціонарних енергетичних станів визначається довжиною ланки атомів - ціле число). Кількість таких стаціонарних енергетичних станів визначається довжиною ланки атомів 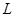 . Максимальна довжина хвилі, при якій утворюється стояча хвиля, дорівнює . Максимальна довжина хвилі, при якій утворюється стояча хвиля, дорівнює 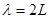 (в довжині «ланки» укладається половина довжини хвилі). Мінімальна довжина хвилі обмежена міжатомним простором і дорівнює (в довжині «ланки» укладається половина довжини хвилі). Мінімальна довжина хвилі обмежена міжатомним простором і дорівнює 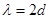 . Відповідно, число стаціонарних станів електрону в енергетичній зоні дорівнює . Відповідно, число стаціонарних станів електрону в енергетичній зоні дорівнює 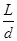 . Але . Але 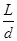 дорівнює числу атомів в «ланці» дорівнює числу атомів в «ланці» 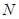 . Таким чином, число стаціонарних станів електрону в розмішеній енергетичній зоні дорівнює числу атомів у відповідній ланки атомів. Ці стани є станами поступального руху електрона. Якщо урахувати , що при будь якому поступальному русі відповідають два значення спіна електрону, то в енергетичній зоні можна «помістити» . Таким чином, число стаціонарних станів електрону в розмішеній енергетичній зоні дорівнює числу атомів у відповідній ланки атомів. Ці стани є станами поступального руху електрона. Якщо урахувати , що при будь якому поступальному русі відповідають два значення спіна електрону, то в енергетичній зоні можна «помістити»  електронів. електронів.
Всі попередньо розглянуті відносно до руху електрона в якомусь даному направленні в кристалі. Для будь якого іншого направлення міжатомна відстань 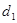 буде іншою, а відповідно, границі енергетичної зони будуть іншими буде іншою, а відповідно, границі енергетичної зони будуть іншими
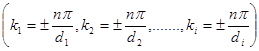 . .
Завдяки цьому в кристалі, границі дозволених зон для будь яких напрямів, як правило не співпадають. Можливо в кристалі і повне перекриття дозволених енергетичних зон для одного напряму з забороненими енергетичними зонами для інших напрямів. Таке перекриття зон спостерігається, окремо, у металів, які належать до II групи періодичної системи елементів Д. І. Менделєєва. Ширина енергетичної зони у трьохмірному кристалі будуть залежити від будови кристалу (від 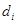 ), а кількість енергетичних рівнів в зоні дорівнює числу атомів в кристалі. ), а кількість енергетичних рівнів в зоні дорівнює числу атомів в кристалі.
Для зображення енергетичних зон кристалу користуються звичайно спрощеною енергетичною схемою.
Так як багато процесів в кристалі (електричні, магнітні, оптичні) пояснюються станом валентних електронів, то на схемі зображують тільки дві дозволені енергетичні зони: валентну зону, яка відповідає нормальним (не збудженим) станом валентних електронів, та найближчу до неї зони збуджених станів цих електронів – збуджену зону, або зону провідності. Називається ця зона, зоною провідності тому, що у відсутності зовнішніх збуджень в ній не має електронів, а коли, отримавши зовні необхідну енергію в цю зону, перейде електрон, то зможе в цій зоні вільно змінювати свою енергію, рухаючись під дією зовнішнього електричного поля, тобто приймати участь у провідності.
Поведінка електронів в заповненій і незаповненій зонах суттєво відрізняються. Зовнішнє енергетичне поле в кристалі може викликати зміну в русі електронів не повністю заповненої зони і не змінює рух електронів в зоні, яка заповнена повністю. Пояснити це можливо наступним чином. Зміна руху електрона пов’язано із зміною його енергетичного стану, а останнє можливо тоді, коли електрон знаходиться у зоні , де є вільні енергетичні рівні, тобто в зоні, яка заповнена не повністю. У повністю заповненій енергетичній зоні немає вільних енергетичних рівнів і тому електрон не змінить свого руху під дією зовнішнього поля. Перейти з одної зони в іншу під дією електричного поля електрон також не може.
Зона теорія пояснює ділення речовин на провідники, напівпровідники і діелектрики перед тим як заповнити валентну зону кристала електронами. Якщо валентна зона кристалу заповнена не повністю , то кристал є провідником. Однак провідником може бути і такий кристал, в якому валентна зона заповнена повністю. При утворенні енергетичних зон в кристалі можливе перекриття валентної зони та збуджених зон. В цьому випадку об’єднана зона стане заповненою не повністю і кристал стане провідником.
Якщо в кристалі повністю заповнена валентна зона відділена від зони провідності забороненої зони, то у відсутності зовнішнього збудження (нагрівання, опромінення та інше) кристал не може проводити електричний струм. Умовно прийнято вважати що напівпровідниками речовини, ширина забороненої в яких менш трьох електронвольт. Діелектриками вважають речовини з шириною забороненої зони більш трьох електронвольт.
2. Теорія електропровідності напівпровідників
Провідність будь якого провідника пропорційна концентрації вільних носіїв заряду в ньому та їх рухомості. Відповідно, температурний хід провідності напівпровідника визначається температурою залежності концентрації та рухомості носіїв в ньому. Температурна залежність концентрації носіїв заряду виражаються наступними формулами
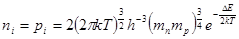 . .
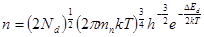 ; (9) ; (9)
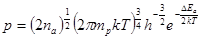 . .
Рухомість вільних носіїв в кристалі визначається розсіянням електронних хвиль на неоднорідностях кристалічної гранки.
У кристалі ці неоднорідності можуть бути лише двох видів: дефекти кристалічної гранки (атоми домішків, відхилення від стехіометрії, дислокації, тріщини, границі кристалічних зерен і тому подібне) і флуктуаційні неоднорідності, які виникають при теплових коливаннях гранки. Одні і ти самі неоднорідності по різному проявляють під час розсіяння носіїв заряду в металі та в напівпровіднику. Так як в металі швидкість електронів завдяки виродженню на порядок вища, чим у напівпровіднику, довжина електронної хвилі в металі відповідно на порядок менша, ніж у напівпровідникові. Неоднорідність атомних розмірів викликають у металі значне розсіяння, але в той час як у напівпровідникові це розсіяння дуже мале.
У атомних напівпровідникових кристалів теплове розсіяння значне при відносно високих температурах. При низьких ж температурах домінує розсіяння на сумішах. При наявності обох механізмів розсіяння результуюча рухомість 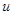 може бути представлена у вигляді може бути представлена у вигляді
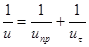 , ,
де  - рухомість носіїв заряду при розсіянні тільки на домішках, - рухомість носіїв заряду при розсіянні тільки на домішках,  - рухомість носіїв заряду при розсіянні тільки на теплових коливаннях. - рухомість носіїв заряду при розсіянні тільки на теплових коливаннях.
Ці дві складові рухомості носіїв ( та та 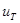 ) змінюються по-різному в залежності від температури. Теоретичний розрахунок показує, що ) змінюються по-різному в залежності від температури. Теоретичний розрахунок показує, що
 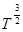 , , 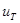 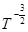
Таким чином, температурний хід рухомості носіїв заряду може бути представлений у вигляді
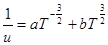 (10) (10)
При низьких температурах домінує перший член, при великих – другий. Залежність (9) напівлогарифмічної системи координат зображена на малюнку 1.

Мал. 1
Положення максимуму на кривій залежить концентрації дефектів у гранці: із збільшенням концентрації дефектів максимум змішується в бік більш високих температур. В таблиці 1 наведені основні величини які характеризують напівпровідники: ширина забороненої зони 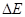 і рухомість носіїв заряду і рухомість носіїв заряду 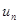 та та  . Всі ці величини приведені для кімнатної температури. . Всі ці величини приведені для кімнатної температури.
| Напівпровідник
|
Ширина забороненої зони
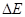 , , 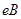
|
Рухомість
|
| Електронів 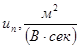
|
Дірок

|
| 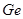
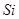
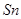
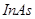
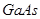

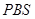
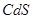
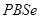
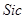
|
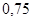
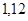
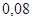
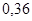
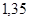
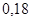
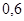

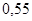
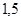
|
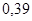
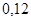
 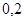

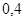
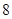
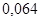
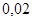
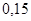
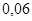
|
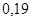
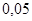
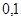
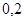
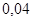
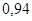
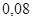
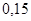
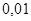
|
Знаючи температуру залежності концентрації вільних носіїв заряду з виразів (9) і їх рухомості (10), можна стверджувати, що температурний хід провідності напівпровідника визначається – експоненціальним множником (9), а тому питома провідність напівпровідника може бути вироджена наступною формулою:
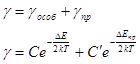 (11) (11)
Де 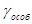 та та 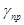 - питомі провідності, які обумовленні власними і домішковими носіями заряду, - питомі провідності, які обумовленні власними і домішковими носіями заряду, 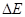 - ширина забороненої зони напівпровідника, - ширина забороненої зони напівпровідника, 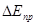 - енергія, яка необхідна для створення домішкового носія заряду, - енергія, яка необхідна для створення домішкового носія заряду, 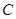 і і 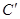 - коефіцієнти, які залежать від природи напівпровідника і слабо залежать від температури. - коефіцієнти, які залежать від природи напівпровідника і слабо залежать від температури.
При відносно низьких температурах звичайно можна знехтувати першим доданком в формулі (11), а при високих, коли настає домішкова виродженність, - другим. В першому випадку провідність буде дорівнювати
 (12а
) (12а
)
в другому
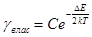 (12б
) (12б
)
Аналізувати температурну залежність провідності напівпровідника зручно за допомогою графіка цієї залежності, отриманого в полу логарифмічної системі координат. Прологарифмувавши формули (12а
) і (12б
), ми отримаємо вираз типу
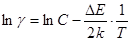 (13) (13)
Якщо по осі абсцис відкласти зворотню температуру, а по осі ординат - 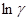 , то графік залежності провідності напівпровідника від температури буде мати вигляд ламаної лінії (малюнок 2). , то графік залежності провідності напівпровідника від температури буде мати вигляд ламаної лінії (малюнок 2).
 
Мал. 2
В області низьких температур у напівпровіднику має місце домішкова провідність (ділянки 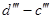 і і 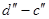 ), збільшення якої в залежності від температури визначається впливом концентрації домішкових носіїв заряду. Ділянки ), збільшення якої в залежності від температури визначається впливом концентрації домішкових носіїв заряду. Ділянки 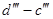 і і 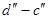 відповідають температурам, при яких всі атоми домішки іонізовані, а власна провідність ще дуже мала. За рахунок зменшення рухомості носіїв, в залежності від температури провідності напівпровідника при цьому декілька зменшуються. При подальшому зростанні температури домінуючий стає власна провідність, яка швидко збільшується зі зміною температури за рахунок росту концентрації власних носіїв заряду. При збільшенні концентрації домішок відповідають температурам, при яких всі атоми домішки іонізовані, а власна провідність ще дуже мала. За рахунок зменшення рухомості носіїв, в залежності від температури провідності напівпровідника при цьому декілька зменшуються. При подальшому зростанні температури домінуючий стає власна провідність, яка швидко збільшується зі зміною температури за рахунок росту концентрації власних носіїв заряду. При збільшенні концентрації домішок 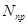 в напівпровіднику, ділянки ломаної лінії в напівпровіднику, ділянки ломаної лінії  змішуються вгору по осі ординат в положення змішуються вгору по осі ординат в положення  , а температура переходу від домішкової провідності до власної зміщується в бік більш високих температур. , а температура переходу від домішкової провідності до власної зміщується в бік більш високих температур.
Хід графіку 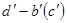 пояснюється наступним чином. При великих концентраціях домішки пояснюється наступним чином. При великих концентраціях домішки 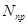 атоми домішки залишаються неповністю іонізованими аж до температури, при якій починає домінувати власна провідність. Таке графічне побудування залежності провідності від температури, як на мал. 2, використовується для експериментального визначення ширини забороненої зони атоми домішки залишаються неповністю іонізованими аж до температури, при якій починає домінувати власна провідність. Таке графічне побудування залежності провідності від температури, як на мал. 2, використовується для експериментального визначення ширини забороненої зони 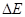 і енергії активації домішкових носіїв і енергії активації домішкових носіїв 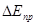 . Як ми можемо побачити із формули (13), кутовий коефіцієнт ділянка домішкової провідності . Як ми можемо побачити із формули (13), кутовий коефіцієнт ділянка домішкової провідності 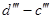 і і 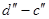 визначає велечіну визначає велечіну 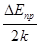 , а кутовий коефіцієнт ділянки власної провідності , а кутовий коефіцієнт ділянки власної провідності 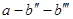 - величіну - величіну 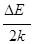 . .
Список літератури
1. Бушманов Б. Н. Хромов Ю. А. – фізика твердого тела. Учебн. пособие для втузов. М., «Высш школа», 1991. 224 с. ил.
2. Вильсон А. – Квантовая теорія металов. Перев. с англ.. В. Левина и Е. Фрейнберга. Гос. узд. техн. – теор. лит., М. – Л., 1999, 227 стр.
3. Волькенштейн Ф. Ф. Электропроводимость полупроводников. Гостехиздат, М. – Л., 2001, 352 стр.
4. Вонсовский С. В. – Вопросы современной квантовой теории электронных проводников. – УФН, 2002, 48, 3, 289 – 388.
5. Гохберг Б. М. – Электропроводимость диэлектриков. Гостехиздат, Л. – М., 1993, 74 (2) стр.
6. Давыдов Б. И. – Советские иследования по электронным проводникам. – УФН, 1997, 33, 2, 157 – 164.
7. Иоффе А. Ф. – Электронные полупроводники. ГТТИ, М. – Л., 1933, 92 стр.
|