| 1. Задача 1. В урне четыре белых и пять черных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что один из этих шаров - белый, а другой - черный.
Решение.
Обозначим через А событие, состоящее в том, что один из этих шаров - белый, а другой - черный.
Вероятность события А найдем используя условную вероятность.
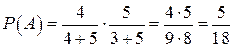 = 0,278 = 0,278
 – вероятность того, что первый шар белый. Вероятность вычислена по формуле классической вероятности. – вероятность того, что первый шар белый. Вероятность вычислена по формуле классической вероятности.
 – вероятность того, что второй шар чнрный. Вероятность вычислена по формуле классической вероятности. – вероятность того, что второй шар чнрный. Вероятность вычислена по формуле классической вероятности.
Ответ: 0,278.
2. Задача 2. Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
Решение.

Пусть событие  состоит в том, что сигнал пройдет с входа на выход. состоит в том, что сигнал пройдет с входа на выход.
 , ,
где  – событие, состоящие в том, что i-ый элемент находится в рабочем состоянии. – событие, состоящие в том, что i-ый элемент находится в рабочем состоянии.
Т.к. события  - независимые совместные события. - независимые совместные события.

Ответ: 0,994.
3. Задача 3. На трех автоматических станках изготавливаются одинаковые детали. Известно, что 30% продукции производится первым станком, 25% - вторым и 45% - третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 0,99 , на втором - 0,988 и на третьем - 0,98. Изготовленные в течение дня на трех станках нерассортированные детали находятся на складе. Определить вероятность того, что взятая наугад деталь не соответствует стандарту.
Решение. Событие А состоит в том, что что взятая наугад деталь не соответствует стандарту.
Гипотезы Н1
, Н2
, Н3
.
 – деталь изготовлена на первом станке; – деталь изготовлена на первом станке;
 – деталь изготовлена на втором станке; – деталь изготовлена на втором станке;
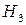 – деталь изготовлена на третьем станке; – деталь изготовлена на третьем станке;
Гипотезы Нi
образуют полную группу событий.
Воспользуемся формулой полной вероятности:
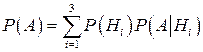 – полная вероятность. – полная вероятность.
 = =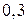 ; ;  = = ; ;
 = =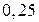 ; ;  = = ; ;
 =0,45; =0,45;  = = ; ;
Тогда
 . = 0,015. . = 0,015.
Ответ: 0,0,015.
4. Задача 4. Игральную кость подбрасывают 12 раз. Чему равно наивероятнейшее число выпадений 6?
Решение.
Найдем  – наиболее вероятное число выпадений 6. – наиболее вероятное число выпадений 6.
Наивероятнейшее число  определяют из двойного неравенства: определяют из двойного неравенства:
 ; ;
 – вероятность появления события в каждом из – вероятность появления события в каждом из  независимых испытаний. независимых испытаний.  – вероятность того, что при одном испытании выпадет 6 (по формуле классической вероятности). – вероятность того, что при одном испытании выпадет 6 (по формуле классической вероятности).  . .  – по условию. – по условию.
 ; ;

Так как  – целое число, то наивероятнейшее число звонков равно – целое число, то наивероятнейшее число звонков равно  . .
Ответ: 2.
5. Задача 5. Дискретная случайная величина  может принимать одно из пяти фиксированных значений может принимать одно из пяти фиксированных значений  , ,  , ,  , ,  , ,  с вероятностями с вероятностями  , ,  , ,  , ,  , ,  соответственно. Вычислить математическое ожидание и дисперсию величины соответственно. Вычислить математическое ожидание и дисперсию величины  . Рассчитать и построить график функции распределения. . Рассчитать и построить график функции распределения.
Решение.
Таблица 1.
| 
|
1
|
4
|
5
|
7
|
8
|
| 
|
0,3
|
0,3
|
0,1
|
0,15
|
0,15
|
Найдем числовые характеристики данного распределения.
Математическое ожидание
  = 4,25 = 4,25
Дисперсию определим по формуле:  . .
  = 24,55. = 24,55.
Тогда 
Найдем функцию распределения случайной величины.
 . .

Построим график этой функции

6. Задача 6. Случайная величина  задана плотностью вероятности задана плотностью вероятности

Определить константу  , математическое ожидание, дисперсию, функцию распределения величины , математическое ожидание, дисперсию, функцию распределения величины  , а также вероятность ее попадания в интервал [0; , а также вероятность ее попадания в интервал [0; ] ]
Решение.
Коэффициент  найдем используя свойство функции плотности распределения: найдем используя свойство функции плотности распределения:  . Так как функция плотности распределения принимает отличные от нуля значения на интервале . Так как функция плотности распределения принимает отличные от нуля значения на интервале  , то , то  . .
Вычислим определенный интеграл:
 . .
Следовательно,  , ,  . .

Математическое ожидание  найдем по формуле: найдем по формуле:
 . .
Т.к. плотность распределения принимает отличное от нуля значения только на отрезке [0,  ], то ], то
 = =  = =
= = =  . .
Вычислили интеграл, используя формулу интегрирования по частям.
Найдем дисперсию  , т.к. плотность распределения принимает отличное от нуля значения только на отрезке , т.к. плотность распределения принимает отличное от нуля значения только на отрезке
[0,  ], то ], то  . .
 = = . .

Найдем  . .
Воспользуемся формулой  = = . .
 = =
Найдем функцию распределения СВ Х.
При
 . . 
При
 . . 
При
 . . 

7. Задача 7. Случайная величина  распределена равномерно на интервале распределена равномерно на интервале  . Построить график случайной величины . Построить график случайной величины  и определить плотность вероятности и определить плотность вероятности  . .
Решение.
Найдем плотность распределения случайной величины  . Случайная величина . Случайная величина  распределена равномерно на интервале распределена равномерно на интервале  , поэтому на этом интервале , поэтому на этом интервале  , вне этого интервала , вне этого интервала  . .
Построим график функции  на интервале на интервале  и в зависимости от числа обратных функций выделим следующие интервалы: и в зависимости от числа обратных функций выделим следующие интервалы:
 ; ;
 ; ;


Так как на интервалах  и и  обратная функция не существует, то для этих интервалов обратная функция не существует, то для этих интервалов  . .

На интервале  одна обратная функция одна обратная функция  , следовательно , следовательно  
На интервале  две обратных функции две обратных функции  и и  , следовательно , следовательно  . .
Найдем производные обратных функций
 ; ;  . .
Учитывая, что  , получим , получим
 ; ;  . .
В результате получим:
 . .
Таким образом, плотность вероятности величины  равна: равна:

8. Задача 8. Двумерный случайный вектор  равномерно распределен внутри области В. Двумерная плотность вероятности равномерно распределен внутри области В. Двумерная плотность вероятности  о любой точке этой области В: о любой точке этой области В:
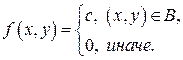
Вычислить коэффициент корреляции между величинами  и и  . .
Решение.
Построим область 

Найдем значение константы 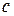 . Воспользуемся свойством функции . Воспользуемся свойством функции 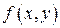

Поскольку  принимает отличные от нуля значения внутри области принимает отличные от нуля значения внутри области  , то получим , то получим
 = =  . .
Следовательно,  . Значит, . Значит, 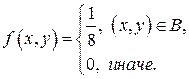
Значение коэффициента корреляции вычислим по формуле

Корреляционный момент вычислим по формуле

 . .
 . .
 . .
 . .
Определим корреляционный момент
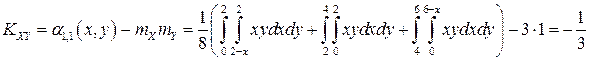

Ответ: 
9. Задача 9. По выборке одномерной случайной величины
1. Получить вариационный ряд;
2. Построить гистограмму равноинтервальным способом;
3. Построить гистограмму равновероятностным способом;
4. Вычислить оценки математического ожидания и дисперсии;
5. Выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия  и критерия Колмогорова ( и критерия Колмогорова ( ) )
| 0,22
|
0,42
|
0,07
|
1,69
|
0,42
|
0,94
|
1,81
|
2,24
|
0,74
|
0,75
|
| 0,80
|
2,59
|
0,55
|
0,43
|
0,51
|
0,38
|
1,41
|
0,73
|
0,03
|
0,96
|
| 0,63
|
0,17
|
0,10
|
0,09
|
1,09
|
1,52
|
2,97
|
0,91
|
1,53
|
0,55
|
| 1,23
|
1,27
|
0,75
|
1,55
|
0,88
|
0,57
|
0,31
|
1,04
|
1,71
|
1,39
|
| 1,16
|
0,86
|
1,13
|
0,82
|
2,02
|
1,17
|
0,25
|
0,64
|
0,07
|
0,11
|
| 1,99
|
0,71
|
2,17
|
0,23
|
2,68
|
1,82
|
1,19
|
0,05
|
1,23
|
4,70
|
| 0,37
|
0,40
|
1,31
|
0,20
|
0,50
|
2,48
|
0,32
|
1,41
|
0,23
|
1,27
|
| 0,33
|
1,48
|
0,52
|
0,68
|
0,30
|
0,40
|
0,24
|
1,52
|
0,17
|
0,17
|
| 0,83
|
1,20
|
0,65
|
0,05
|
1,45
|
0,23
|
0,37
|
0,09
|
3,66
|
0,28
|
| 0,77
|
0,11
|
1,95
|
0,10
|
0,95
|
0,65
|
4,06
|
3,16
|
0,51
|
2,02
|
Решение.
Найдем размах вариации  . .  0,03; 0,03;  4,70; 4,70;
 4,70–0,03 = 4,67. 4,70–0,03 = 4,67.
Вариационный ряд распределения имеет вид:
| 
|
|

|
|
| 0,03
|
1
|
0,86
|
1
|
| 0,05
|
2
|
0,88
|
1
|
| 0,07
|
2
|
0,91
|
1
|
| 0,09
|
2
|
0,94
|
1
|
| 0,1
|
2
|
0,95
|
1
|
| 0,11
|
2
|
0,96
|
1
|
| 0,17
|
3
|
1,04
|
1
|
| 0,2
|
1
|
1,09
|
1
|
| 0,22
|
1
|
1,13
|
1
|
| 0,23
|
3
|
1,16
|
1
|
| 0,24
|
1
|
1,17
|
1
|
| 0,25
|
1
|
1,19
|
1
|
| 0,28
|
1
|
1,2
|
1
|
| 0,3
|
1
|
1,23
|
2
|
| 0,31
|
1
|
1,27
|
2
|
| 0,32
|
1
|
1,31
|
1
|
| 0,33
|
1
|
1,39
|
1
|
| 0,37
|
2
|
1,41
|
2
|
| 0,38
|
1
|
1,45
|
1
|
| 0,4
|
2
|
1,48
|
1
|
| 0,42
|
2
|
1,52
|
2
|
| 0,43
|
1
|
1,53
|
1
|
| 0,5
|
1
|
1,55
|
1
|
| 0,51
|
2
|
1,69
|
1
|
| 0,52
|
1
|
1,71
|
1
|
| 0,55
|
2
|
1,81
|
1
|
| 0,57
|
1
|
1,82
|
1
|
| 0,63
|
1
|
1,95
|
1
|
| 0,64
|
1
|
1,99
|
1
|
| 0,65
|
2
|
2,02
|
2
|
| 0,68
|
1
|
2,17
|
1
|
| 0,71
|
1
|
2,24
|
1
|
| 0,73
|
1
|
2,48
|
1
|
| 0,74
|
1
|
2,59
|
1
|
| 0,75
|
2
|
2,68
|
1
|
| 0,77
|
1
|
2,97
|
1
|
| 0,8
|
1
|
3,16
|
1
|
| 0,82
|
1
|
3,66
|
1
|
| 0,83
|
1
|
4,06
|
1
|
| |
|
4,7
|
1
|
Построим гистограмму равноинтервальным способом. Число интервалов рассчитаем по формуле
 . Длина частичного интервала вычисляется по формуле
. Длина частичного интервала вычисляется по формуле
 . .
Полученные значения запишем в таблицу
| №
|

|

|

|

|

|

|
| 1
|
0,03
|
0,497
|
0,467
|
34
|
0,34
|
0,73
|
| 2
|
0,497
|
0,964
|
0,467
|
27
|
0,27
|
0,58
|
| 3
|
0,964
|
1,431
|
0,467
|
15
|
0,15
|
0,32
|
| 4
|
1,431
|
1,898
|
0,467
|
10
|
0,1
|
0,21
|
| 5
|
1,898
|
2,365
|
0,467
|
6
|
0,06
|
0,13
|
| 6
|
2,365
|
2,832
|
0,467
|
3
|
0,03
|
0,06
|
| 7
|
2,832
|
3,299
|
0,467
|
2
|
0,02
|
0,04
|
| 8
|
3,299
|
3,766
|
0,467
|
1
|
0,01
|
0,02
|
| 9
|
3,766
|
4,233
|
0,467
|
1
|
0,01
|
0,02
|
| 10
|
4,233
|
4,7
|
0,467
|
1
|
0,01
|
0,02
|
Равноинтервальная гистограмма имеет вид:

Построим гистограмму равновероятностным способом.
| №
|

|

|

|

|

|

|
| 1
|
0,03
|
0,17
|
0,14
|
10
|
0,1
|
0,7143
|
| 2
|
0,17
|
0,25
|
0,08
|
10
|
0,1
|
1,2500
|
| 3
|
0,25
|
0,42
|
0,17
|
10
|
0,1
|
0,5882
|
| 4
|
0,42
|
0,57
|
0,15
|
10
|
0,1
|
0,6667
|
| 5
|
0,57
|
0,77
|
0,2
|
10
|
0,1
|
0,5000
|
| 6
|
0,77
|
0,96
|
0,19
|
10
|
0,1
|
0,5263
|
| 7
|
0,96
|
1,27
|
0,31
|
10
|
0,1
|
0,3226
|
| 8
|
1,27
|
1,53
|
0,26
|
10
|
0,1
|
0,3846
|
| 9
|
1,53
|
2,17
|
0,64
|
10
|
0,1
|
0,1563
|
| 10
|
2,17
|
4,7
|
2,53
|
10
|
0,1
|
0,0395
|
Равновероятностная гистограмма имеет вид:

Оценку математического ожидания вычислим по формуле
 1,00. 1,00.
Оценку дисперсии вычислим по формуле:
 , , 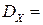 0,82, 0,82,
Построим доверительный интервал для математического ожидания при неизвестной дисперсии:
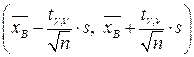
В нашем случае
 1,00, 1,00,  0,82, 0,82,  , ,  , ,  . .
 ; ; 
Доверительный интервал для математического ожидания  . .
Доверительный интервал для дисперсии
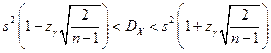 , , 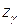 =1,96 ( =1,96 ( ). ).
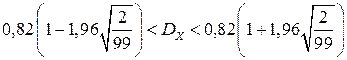

По виду равноинтервальной гистограммы выдвигаем гипотезу о том, что случайная величина X распределена по показательному закону:
H0
: 
H1 : 
Определим оценку неизвестного параметра 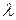

Предполагаемый закон распределения  . Найдем вероятности попадания в каждый из интервалов . Найдем вероятности попадания в каждый из интервалов

Теоретические частоты найдем по формуле

| №
|
Интервалы
[xi
; xi+1
)
|

|

|

|

|

|
| 1
|
0,03
|
0,497
|
0,36
|
36,00
|
-2,00
|
4,00
|
0,1111
|
| 2
|
0,497
|
0,964
|
0,23
|
23,00
|
4,00
|
16,00
|
0,6957
|
| 3
|
0,964
|
1,431
|
0,14
|
14,00
|
1,00
|
1,00
|
0,0714
|
| 4
|
1,431
|
1,898
|
0,09
|
9,00
|
1,00
|
1,00
|
0,1111
|
| 5
|
1,898
|
2,365
|
0,06
|
6,00
|
0,00
|
0,00
|
0,0000
|
| 6
|
2,365
|
2,832
|
0,04
|
4,00
|
-1,00
|
1,00
|
0,2500
|
| 7
|
2,832
|
3,299
|
0,02
|
2,00
|
0,00
|
0,00
|
0,0000
|
| 8
|
3,299
|
3,766
|
0,01
|
1,00
|
0,00
|
0,00
|
0,0000
|
| 9
|
3,766
|
4,233
|
0,01
|
1,00
|
0,00
|
0,00
|
0,0000
|
| 10
|
4,233
|
4,7
|
0,01
|
1,00
|
0,00
|
0,00
|
0,0000
|
| |
|
|
|
|
|
 НАБЛ
= НАБЛ
=
|
1,24
|
Число степеней свободы  определяют по формуле определяют по формуле  . По таблице критерия Пирсона находим: . По таблице критерия Пирсона находим:  . Так как . Так как  , то нет оснований отвергать гипотезу о показательном распределении. Проверим гипотезу о показательном распределении с помощью , то нет оснований отвергать гипотезу о показательном распределении. Проверим гипотезу о показательном распределении с помощью  -критерия Колмогорова. Теоретическая функция распределения F0
(x) показательного закона равна -критерия Колмогорова. Теоретическая функция распределения F0
(x) показательного закона равна
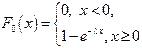
Проверим гипотезу о нормальном распределении с помощью 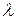 -критерия Колмогорова. Все вспомогательные расчеты сведем в таблицу. -критерия Колмогорова. Все вспомогательные расчеты сведем в таблицу.
| №
|
Интервалы
[xi
; xi+1
)
|
частота в интервале

|

|

|

|
| 1
|
-2,951
|
7
|
34
|
0,34
|
0,36
|
0,02
|
| 2
|
-2,513
|
10
|
27
|
0,61
|
0,59
|
0,02
|
| 3
|
-2,075
|
8
|
15
|
0,76
|
0,73
|
0,03
|
| 4
|
-1,637
|
12
|
10
|
0,86
|
0,82
|
0,04
|
| 5
|
-1,199
|
14
|
6
|
0,92
|
0,88
|
0,04
|
| 6
|
-0,761
|
11
|
3
|
0,95
|
0,91
|
0,04
|
| 7
|
-0,323
|
9
|
2
|
0,97
|
0,93
|
0,04
|
| 8
|
0,115
|
4
|
1
|
0,98
|
0,95
|
0,03
|
| 9
|
0,553
|
16
|
1
|
0,99
|
0,96
|
0,03
|
| 10
|
0,991
|
9
|
1
|
1,00
|
0,97
|
0,03
|
 ; ;  . .
То таблице квантилей распределения Колмогорова по уровню значимости 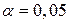 находим критическое значение находим критическое значение  . .
Так как  , то нет оснований отвергать гипотезу о нормальном распределении. , то нет оснований отвергать гипотезу о нормальном распределении.

10. Задача 10. По выборке двумерной случайной величины
1. Вычислить оценку коэффициента корреляции;
2. Вычислить параметры линии регрессии  и и  ; ;
3. Построить диаграмму рассеивания и линию регрессии;
Решение
Найдем числовые характеристики величин  и и  . .
 0,88; 0,88;  0,10. 0,10.
 1,59; 1,59;  . .
 1,76; 1,76;  . .
Корреляционный момент равен:
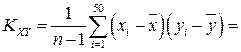 –0,23 –0,23
Найдем уравнения регрессии 
где  ; ; 
Уравнение регрессии имеет вид:
 . .

Коэффициент корреляции равен:
 . .
Найдем интервальную оценку.
 . .
 , ,

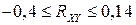
Проверим гипотезу об отсутствии корреляционной зависимости  . .
Проверим нулевую гипотезу  : о равенстве нулю генерального коэффициента корреляции, при конкурирующей гипотезе : о равенстве нулю генерального коэффициента корреляции, при конкурирующей гипотезе  . .
 . .
По таблице критических точек распределения Стьюдента, по заданному уровню  и числу степеней свободы и числу степеней свободы  найдем критическую точку найдем критическую точку  двусторонней критической области. двусторонней критической области.  . .
Так как 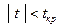 – нулевую гипотезу принимаем. – нулевую гипотезу принимаем.
|