| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
ГОУВПО СФ МЭИ (ТУ)
КАФЕДРА ВТ
Курсовая работа по дисциплине:
«Моделирование систем»
| Группа:
|
АС-08
|
| Преподаватель:
|
Курчавый В.А.
|
| Студент:
|
Мелкумов А.Г.
|
СМОЛЕНСК 2011
Содержание:
Техническое задание: 3
1. Описание работы системы. 4
1.2. Сравнивающее устройство. 5
1.3. Усилитель рассогласования. 6
1.4. Двигатель. 6
1.5. Потенциометр. 7
1.6. Усилитель мощности. 8
1.7. Генератор. 8
1.8. Делитель напряжения. 9
1.9. Структурная схема. 10
2. Синтез корректирующего устройства. 11
3. Расчет параметров корректирующего контура. 17
4. Ввод нелинейностей в систему. 18
5.Моделирование системы. 19
Техническое задание:
1. По заданной функциональной схеме описать принцип действия и сформулировать задачу регулирования. Составить для каждого элемента функциональной схемы уравнение движения. Составить полную структурную схему в операторной форме.
2. Выполнить коррекцию системы – последовательную либо параллельную. При этом показатели качества регулирования должны быть: статическая ошибка – не более 1% от установившегося уровня; перерегулирование – не более 30%. Быстродействие – не оговаривается, но по возможности добиться максимально возможного. Определить быстродействие по переходной функции.
3. Провести расчет параметров корректирующего контура.
4. Ввести нелинейности в характеристики элементов. Нелинейность типа «ограничение» - для усилителя рассогласования. Параметры нелинейности: уровень ограничения +
15 В. Нелинейность типа «зона нечувствительности» - для двигателя.
Параметры нелинейности:
Например: В=10, то А=2.
5. Используя пакет 20-sim выполнить моделирование скорректированной системы. Рассчитать переходную функцию. Сравнить ее с переходной характеристикой пункта 2 и сделать выводы о влиянии нелинейностей на качество процесса регулирования.
1. Описание работы системы.

Рис.1.1. Функциональная схема астатической системы регулирования напряжения генератора постоянного тока.
СУ - сравнивающее устройство;
УР - усилитель рассогласования;
ДВ - двигатель;
П - потенциометр;
УМ - усилитель мощности;
ГН - генератор ;
ДН - делитель напряжения.
Задание на регулирование – U0
– подается на первый вход сравнивающего устройства. На второй вход сравнивающего устройства подается напряжение обратной связи – Uос
. Выходным сигналом сравнивающего устройства является напряжение сигнала ошибки регулирования - Uδ
, которое является входным для усилителя рассогласования. Выходное напряжение усилителя рассогласования – Uур
, поступает на двигатель. Выходным сигналом двигателя является угол поворота вала двигателя - Y, он изменяет угол поворота движка потенциометра, при этом изменяется выходное напряжение потенциометра Uп
. Напряжение Uп
усиливается усилителем мощности – Uум
, и поступает на вход генератора. Выходным сигналом генератора является выходное напряжение генератора Uг
, которое преобразовываясь делителем напряжения, поступает на обратную связь – Uос
, для возможности сравнения с заданием на управление – U0
.
Задача регулирования – поддержание изменения выходной величины Uг
в соответствии с заданием на управление – Uо
.
Принцип регулирования.
Данная система является следящей. Она основана на принципе регулирования по отклонению.
Она содержит: сравнивающее устройство, усилитель рассогласования, двигатель напряжения, потенциометр, усилитель мощности, генератор и делитель напряжения.
Регулятор – сравнивающее устройство, усилитель рассогласования,
двигатель, потенциометр, усилитель мощности и делитель напряжения.
Регулируемая величина – напряжение генератора.
Задание на управление – входное напряжение системы – U0
.
Ошибка регулирования – выходное напряжение сравнивающего устройства - Uδ
.
Данная схема регулирования является астатической. Характерной чертой таких схем является то, что она работоспособна и при нулевом значении ошибки регулирования.
Рис.1.2. Функциональная схема сравнивающего устройства.
Так как сравнивающее устройство представляет собой сумматор напряжений, то уравнение движения будет выглядеть следующим образом:
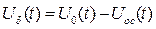
Запишем полученное уравнение движения в операционной форме:
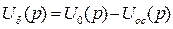
Структурная схема сравнивающего устройства представлена на рисунке 1.3.
     Рис 1.3. Структурная схема сравнивающего устройства.
Рис.1.4. Функциональная схема усилитель рассогласования.
Усилитель рассогласования может описываться пропорциональным или инерционным звеном. Так как по условию, для усилителя рассогласования заданы постоянная времени Тур
и коэффициент передачи Кур
, следовательно, усилитель рассогласования описывается инерционным звеном, и имеет уравнение движения вида:

Запишем полученное уравнение движения в операционной форме:

Преобразуем полученное уравнение:

Полная структурная схема усилителя рассогласования: представлена на рисунке 1.5.
Рис 1.5. Структурная схема усилителя рассогласования.
Рис.1.6. Функциональная схема двигателя.
Двигатель может описываться пропорциональным или инерционным интегральным звеном. По условию, для двигателя задан коэффициент передачи Кдв
(отсутствует постоянная времени), следовательно, двигатель описывается пропорциональным интегральным звеном и имеет уравнение
движения вида:

Запишем полученное уравнение движения в операционной форме, для этого продифференцируем вышестоящее уравнение:

Полная структурная схема двигателя представлена на рисунке 2.6.
Рис 1.7. Структурная схема двигателя.
Рис.1.8. Функциональная схема потенциометра.
Потенциометр описывается пропорциональным звеном. По условию для потенциометра задан коэффициент передачи Кп
. Следовательно, потенциометр имеет уравнение движения вида:

Запишем полученное уравнение движения в операционной форме:

Структурная схема потенциометра представлена на рисунке 1.9.
Рис 1.9. Структурная схема потенциометра.
Рис.1.10. Функциональная схема усилителя мощности.
Усилитель мощности может описываться пропорциональным или инерционным звеном. По условию, для усилителя мощности заданы постоянная времени Тум
и коэффициент передачи Кум
. Следовательно, усилитель мощности описывается инерционным звеном и имеет уравнение движения вида:

Запишем полученное уравнение движения в операционной форме:

Преобразуем полученное уравнение:
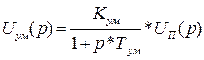
Полная структурная схема усилителя мощности представлена на рисунке 1.11.
Рис 1.11. Структурная схема усилителя мощности.
Рис.1.12. Функциональная схема генератора.
Генератор может описываться пропорциональным или инерционным звеном. По условию, для генератора задан коэффициент передачи Кг
(отсутствует постоянная времени). Следовательно, генератор описывается пропорциональным звеном и имеет уравнение движения вида:

Запишем полученное уравнение движения в операционной форме:

Полная структурная схема генератора представлена на рисунке 1.13.
Рис 1.13. Структурная схема генератора.
Рис.1.14. Функциональная схема делителя напряжения.
Делитель напряжения может описываться пропорциональным звеном. По условию, для делителя напряжения задан коэффициент передачи Кдн
. Следовательно, делитель напряжения имеет уравнение движения вида:

Запишем полученное уравнение движения в операционной форме:

Полная структурная схема делителя напряжения представлена на рисунке 1.15.
Рис 1.15. Структурная схема делителя напряжения.
  
  
Рисунок 1.16 Структурная схема в операторной форме.
Передаточную функцию разомкнутой цепи (без обратной связи) найдём как произведение передаточных функций всех структурных звеньев цепи.


Передаточная функция замкнутой цепи определяется как:

Подставим числовые данные.
Кур
= 20 Кдн
= 0.2
Кум
= 8 Кп
= 0.1
КДВ
= 2 Тур
= 0.175
Кг
= 5 Тум
= 1.5
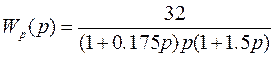

2. Синтез корректирующего устройства.

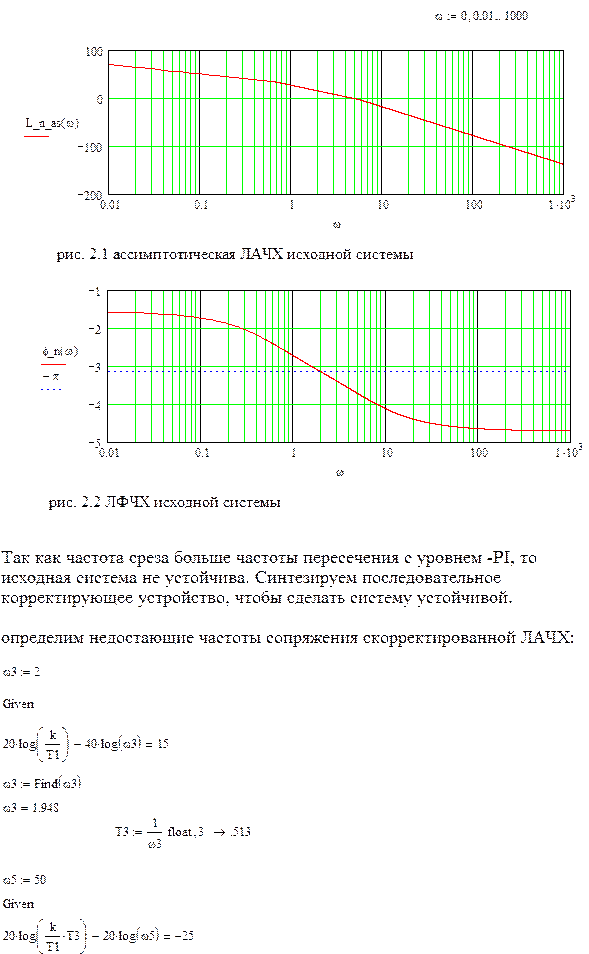




3.
Расчет параметров корректирующего контура.
Передаточная функция корректирующего контура имеет вид:
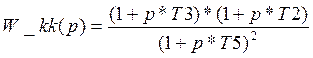
Для реализации этой передаточной функции, используем корректирующий контур следующего вида:

Рис. 3.1 Принципиальная схема корректирующего устройства.
Для этой схемы  . .
 ; ; 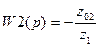 . .
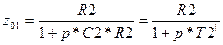 , где , где  . .
 , где , где  . .
Значит  . .
Так как в нашем случае  , то , то  . .
Имеем:  , , 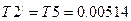 . .
Возьмем  , тогда , тогда  ; ;  . .
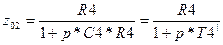 , где , где 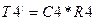 . .
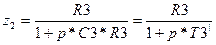 , где , где  . .
Значит  . .
Так как в нашем случае  , то , то  . .
Имеем: 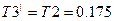 , ,  . .
Возьмем  , тогда , тогда 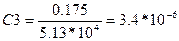 ; ;  . .
Окончательно получаем:
 , , 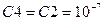 , ,  , ,  . .
4. Ввод нелинейностей в систему.
Введем для усилителя рассогласования нелинейность типа ограничение, которая задается функцией:  , и имеет вид изображенный на рисунке 4.1. , и имеет вид изображенный на рисунке 4.1.

Рис. 4.1. Нелинейность типа ограничение.
Для двигателя введем нелинейность типа зона нечувствительности с ограничением, которая задается функцией: 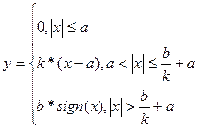 , и имеет вид, изображенный на рисунке 4.2. , и имеет вид, изображенный на рисунке 4.2.

Рис. 4.2 Нелинейность типа зона нечувствительности с ограничением.
Для усилителя рассогласования имеем  , ,  , а коэффициент передачи усилителя рассогласования учтем в его передаточной функции. , а коэффициент передачи усилителя рассогласования учтем в его передаточной функции.
Для двигателя возьмем 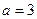 , , 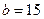 , ,  , а коэффициент передачи двигателя учтем в его передаточной функции. , а коэффициент передачи двигателя учтем в его передаточной функции.
Структурная схема скорректированной системы с учетом нелинейностей изображена на рисунке 4.3.

Рис. 4.3 Структурная схема скорректированной системы с учетом нелинейностей.
5.
Моделирование системы.
Сначала выполним моделирование системы без нелинейностей, чтобы убедиться, что моделирование выполнено правильно. Схема этой системы выполненная в графическом редакторе представлена на рисунке 5.1. Значения параметров элементов этой системы представлены на рисунке 5.2. Начальные условия берем нулевые. График выходной величины представлен не рисунке 5.3. По графику на рисунке 5.3 определяем 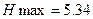 , , 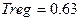 , ,  . Сравнивая эти характеристики с характеристиками переходной функции пункта 2, убеждаемся, что моделирование выполнено правильно. . Сравнивая эти характеристики с характеристиками переходной функции пункта 2, убеждаемся, что моделирование выполнено правильно.

Рис. 5.1 Схема системы без ограничений в графическом редакторе.

Рис. 5.2 Значения параметров элементов системы без ограничений.

Рис. 5.3 Переходная функция системы без ограничений.
Теперь введем в эту систему нелинейности. Схема системы, выполненная в графическом редакторе с учетом нелинейностей, представлена на рисунке 5.4.

Рис. 5.4 Схема системы с учетом нелинейностей.
Нелинейность типа зона нечувствительности с ограничением заменяем двумя нелинейностями: нелинейностью типа зона нечувствительности и нелинейностью типа ограничение, включенными последовательно. Значения параметров элементов для этой схемы представлены на рисунке 5.5. Начальные условия заданы нулевые.

Рис. 5.5 Значения параметров элементов системы с ограничениями.
График переходной функции представлен на рисунке 5.6. По этому графику определим параметры переходной функции. Получаем  , ,  , ,  . .

Рис. 5.6 Переходная функция системы с ограничениями.
Сравнивая две переходные функции, видим, что за счет введения нелинейностей почти в два раза уменьшилось время регулирования и почти исчезло перерегулирование, но зато почти в два раза возросло время нарастания переходного процесса.
В целом качество переходного процесса от введения нелинейностей только повысилось.
|