|
Билет 1.
1. Уравнение Шредингера, его свойства. Статическая интерпретация волновой функции.
Ур-е Шредингера – основное ур-е нерелятивистской квантовой механики, которому подчиняется любая волновая ф-ция
y
(
x
,
y
,
z
,
t
). Частица движется в некотором силовом поле
`
F
(
x
,
y
,
z
,
t
)=
gradU
(
x
,
y
,
z
,
t
) то есть силовое поле задается силовой ф-цией. Нужно найти волновую ф-цию, т.е. решить ур-е Шредингера:
ih
(
¶
y
/
¶
t
)=-(
h
2
/2
m
)
D
y
+
U
(
x
,
y
,
z
,
t
)
y
,
y
(
x
,
y
,
z
,
t
) – искомая волновая ф-ция.
i
=
Ö
-1 – мнимая единица,
h
– константа планка деленная на 2
p
,
m
– масса частицы,
D
- оператор Лапласа,
D
=
¶
2
/
¶
x
2
+…+
¶
2
/
¶
z
2
.
D
y
=
¶
2
y
/
¶
x
2
+…+
¶
2
y
/
¶
z
2
– подставим в уравнение.
U
– силовая ф-ция характеризует поле, в котором движется частица. Это уравнение справедливо для любой частицы, движущейся с малой скоростью. Оно дополняется условиями: 1) Волновая ф-ция
y
должна быть конечна, однозначна, непрерывна. 2) Частные производные должны быть непрерывны. 3) Функция |
y
|2
должна быть интегрируема.
Квадрат модуля волновой функции равен плотности вероятности обнаружения частицы в данной точке пространства  . .
2. Фотопроводимость полупроводников,процессы генерации и рекомбинации носителей заряда
Фотопроводимость полупроводников – увеличение электропроводности полупроводников под действием электромагнитного излучения – может быть обусловлена свойствами, как основного вещества, так и содержащихся в нем примесей. В первом случае при поглощении фотонов, соответствующих собственной полосе поглощения полупроводника, т.е. когда энергия фотона равна или больше ширины запрещенной зоны (
hv
≥
ΔE
), могут совершать перебросы электронов из валентной зоны в зону проводимости, что приведет к появлению добавочных (неравновесных) электронов(в зоне проводимости) и дырок (в валентной зоне). В результате возникает собственная фотопроводимость, обусловленная как электронами, так и дырками.
Если полупроводник содержит примеси, то фотопроводимость может возникать и при
hv
≤
ΔE
: для полупроводников с донорной примесью фотон должен обладать энергией
hv
≥
ΔED
, а для полупроводников с акцепторной примесью -
hv
≥
ΔE
А
. При поглощении света примесными центрами происходит переход электронов с донорных уровней в зону проводимости в случае полупроводника
n
-типа, или из валентной зоны на акцепторные уровни в случае полупроводника
p
-типа. В результате возникнет примесная фотопроводимость, являющаяся чисто электронной для полупроводников
n
-типа и чисто дырочной для
p
-типа.
hv
≥
ΔE
- для собственных полупроводников,
hv
≥
ΔE
П
для примесных полупроводников. Из этого можно определить красную границу фотопроводимости, красная граница фотоэффекта-минимальная частота ν0
света( зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен:
λ0
=
ch
/Δ
E
- для собственных полупроводников
λ0
=
ch
/Δ
E
П
– для примесных полупроводников.
------------------------------------------------------
Билет 2
1.Стационарные состояния, их временная зависимость. Уравнение Шредингера для стационарных состояний.
Стационарные состояния – это состояния с фиксированными значениями энергии. Это возможно, если силовое поле, в котором движется частица, стационарно, т.е. функция
U
=
U
(
x
,
y
,
z
) не зависит явно от времени и имеет смысл потенциальной энергии. Уравнение Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выражается множителем
e
-
iωt
=
e
-
i
(
E
/ħ)
t
, так что Ψ(
x
,
y
,
z
,
t
)=
ψ
(
x
,
y
,
z
)
e
-
i
(
E
/ħ)
t
, где Е- полная энергия частицы, постоянная в случае стационарного поля. Подставляя это выражение в уравнение Шредингера((–ħ2
/2
m
)
ΔΨ
+
U
(
x
,
y
,
z
,
t
)
Ψ
=
i
ħ(∂
Ψ
/∂
t
), где ħ=
h
/(2
π
),
m
–масса частицы,
i
-мнимая единица,
U
-потенциальная функция частицы в силовом поле, в котором она движется
Δ-оператор Лапласа(ΔΨ=∂2
Ψ/∂
x
2
+∂2
Ψ/∂
y
2
+∂2
Ψ/∂
z
2
), Ψ(
x
,
y
,
z
,
t
)-искомая волновая функция частицы) получим:
 разделив на общий множитель
e
-
i
(
E
/ħ)
t
и преобразовав придем к уравнению, определяющему функцию ψ
разделив на общий множитель
e
-
i
(
E
/ħ)
t
и преобразовав придем к уравнению, определяющему функцию ψ
Δψ+(2
m
/ħ2
)(
E
-
U
)
ψ
=0-уравнение Шредингера для стационарных состояний. Это уравнение имеет бесчисленное количество решений, из которых посредством наложения граничных условий отбираются решения, имеющие физич.смысл. Условия: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Т.о. реальный физич.смысл имеют только такие решения, которые выражаются регулярными функциями ψ .
2. Принцип работы лазера. Особенности лазерного излучения. Основные типы лазеров, их применение
.
Лазер – устройство, при прохождении через которое электромагнитные волны усиливаются за счет вынужденного излучения. Лазер – оптический квантовый генератор. Лазер имеет 3 основных компонента: 1) активная среда, 2) система накачки, 3) оптический резонатор. 1-й лазер был рубиновый, активная среда – рубин
Al
2
O
3
. Для оптической накачки использовалась газоразрядная лампа. В кристалле
Al
2
O
3
некоторые атомы
Al
замещены на
Cr
3+
. При облучении рубина цветом атом хрома переходит с уровня 1 на уровень 3, затем происходят переходы либо 3
®
1 (незначительно), либо 3
®
2. Переход 2
®
1 запрещен, поэтому атомы хрома накапливаются на уровне 2, возникает среда с инверсной населенностью. Фотон случайно родившийся при спонтанных переходах может порождать в активной среде множество вынужденных переходов 2
®
1, в результате возникает целая лавина вторичных фотонов, зарождается лазерная генерация. Для выделения направления лазерной генерации используется оптический резонатор. В простейшем случае – пара обращенных друг к другу зеркал на общей оптической оси, между которыми помещается активная среда. Фотоны, которые движутся под углом к оси кристалла выходят из активной среды, а фотоны, которые движутся параллельно оси вызывают вынужденное излучение. Многократно усиленный поток выходит через полупрозрачное зеркало, создавая пучок огромной яркости. Типы лазеров: 1) твердотельные, 2) газовые (гелий-неоновые), 3) полупроводниковые, 4) жидкостные. Применение: обработка, резание, скоростное и точное обнаружение дефектов, в измерительной технике, голография.
|
Билет 4.
1.Квантовая теория свободных электронов в металле. Плотность электронных состояний. Энергия Ферми.
Квантовая теория электропроводности металлов – теория электропроводности основывается на квантовой механике и квантовой статистике Ферми-Дирака. Согласно этой теории выражение для удельной электрической проводимости металлов:
g
=
ne
2
<
lF
>/
m
<
UF
>, где
n
– концентрация электронов проводимости, <
lF
> - средняя длина свободного пробега электронов, имеющего энергию Ферми, <
UF
> - средняя скорость теплового движения такого электрона. Квантовая теория рассматривает движение электронов с учетом их взаимодействия с реальной кристаллической решеткой, а классическая, взаимодействие с идеальной кристаллической решеткой. Классическая теория дает, что
g
~1/
Ö
T
, а квантовая более точно объясняет зависимость
g
от Т, как
g
~1/
T
. Так как согласно классической теории <
U
>~
Ö
T
, то в квантовой теории доказано, что <
UF
> от температура практически не зависит, так как доказано, что с изменением температуры уровень Ферми остается неизменным. Однако с повышением температуы рассеяние «электронных волн» на фотонах возрастает. А это соответствует уменьшению средней длины свободного пробега электронов. Поэтому можно заметить, что сопротивление металла R~1/
g
растет пропорционально Т Энергия Ферми – это максимальная кинетическая энергия, которую могут иметь электроны проводимости в атоме при 0
°
К. Наивысший энергетический уровень, занятый электронами называют уровнем Ферми. Уровню ферми соответствует энергия ферми Е
F
, которую имеют электроны на этом уровне.
2. Радиоактивность. Закон радиоактивного распада. Виды радиоактивных излучений.
Радиоактивностью называется самопроизвольное превращение одних атомных ядер (нестабильных) в другие, сопровождаемое испусканием элементарных частиц. Радиоактивные процессы: 1) α-распад, 2) β-распад, 3) γ-излучение ядер, 4) спонтанное деление тяжелых ядер, 5) протонная радиоактивность. Радиоактивное ядро – материнское, образующееся при распаде – дочернее. Радиоак-ть подразделяют на естественную и искусственную, принципиальных различий в них нет.
Закон радиоактивного распада. Отдельные радиоактивные ядра распадаются независимо друг от друга. Можно считать, что число ядер dN , распадающихся за малый промежуток времени dt, пропорционально как числу имеющихся ядер N, так и dt: dN = - λNdt, где λ – постоянная распада, характерная для каждого рад. препарата (“-“ т.к. убыль числа ядер). Проинтегрируем, получим: N = N0e-λt, где N0 – количество ядер в начальный момент, N – количество нераспавшихся ядер в момент времени t. Это закон рад-ого распада: число нераспавшихся ядер убывает со временем по экспоненте.
Активность А =│dN/dt│=λN – число ядер, распавшихся за ед. времени. [1 Бк (беккерель) =1 распад/с или 1 Ки(кюри) =3,7∙1010 Бк]. Удельная активность – активность на ед. массы рад. препарата.
Период полураспада Т: из условия N0/2 = N0e-λt, откуда Т = ln2/λ = 0,693/λ.
Среднее время жизни τ = (1/ N0)∫0∞tdN = (1/ N0)∫0∞tλNdt = (1/ N0)∫0∞tλN0e-λtdt = 1/λ.
Виды рад. излучений. α-распад. Самопроизвольное испускание ядром α-частицы (ядра 42Не): AZX → A-4Z-2Y+42Не. Спектр излучения α-частицы дискретный (монохромные волны). Масса материнского ядра > массы дочернего. Энергия α-частицы: 4-9 эВ. α-частица, покидая ядро, преодолевает потенциальный барьер, высота которого больше ее энергии. Внутреняя сторона барьера обусловлена ядерными силами, внешняя – кулоновскими. Преодолевает барьер благодаря туннельному эффекту.
β-распад. Самопроизвольный процесс, в котором исходное ядро превращается в другое ядро с тем же массовым числом А, но с Z, отличающимся от исходного на ±1 (испускание е-\е+ или захват). Виды: 1) электронный β--распад (испускается е- и Z→Z+1); 2) позитронный β+-распад (испускается е+ и Z→Z-1); 3) К-захват (ядро захватывает е-, находящийся на К-ой оболочке и Z→Z-1, сопровождается рентгеновским излучением)
γ-излучение. Испускание возбужденным ядром при переходе его в нормальное состояние γ-квантов (их энергия 10кэВ – 5МэВ, спектр дискретный, т.к. дискретны энергетические уровни самих ядер). γ-распад – процесс внутриядерный (β-распад - внутринуклонный). Возбужденные ядра могут переходить в основное состояние, передавая энергию возбуждения внешним е- - внутренняя конверсия электронов (эти е- моноэнергетичны), явление сопровождается рентгеновским излучением.
------------------------------------------------------
Билет 5.
1.Корпускулярно-волновой дуализм материи. Гипотеза де Бройля. Опыты по дифракции микрочастиц.
Де Бройль выдвинул теорию о корп.-волн.дуализме материи, т.е. не только фотоны, но и электроны и любые другие частица материи наряду с корпускулярными обладают также волновыми свойствами. Каждые микрообъект связывают корпуск.характеристики –энергия Е и импульс р, а также волновые – частота ν и длина волны λ. Е=
h
ν,
p
=
h
/λ. Т.о. любой частице обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемо по формуле де Бройля λ=
h
/
p
. Можно добавить то, что на частице вещества переносится связь между полной энергией частицы ε и частотой ν волн де Бройля:
ε
=
h
ν ,
h
-постоянная Планка=6,625·10-34
Дж·с
Волна де Бройля – это волна, связанная с равномерным и прямолинейным движением частицы.
y
=
Acos
(
w
t
-
kx
)
ü
уравнения
y
(
x
,
t
)=
Aexp
(-(
w
t
-
kx
))
þ
волны.
E=h
w
, p=hk,
w
=E/h, k=p/h.
y
(x,t)=Aexp(-i/h(Et-px)) –
плоская
волна
де
Бройля
.
Фазовая и групповая скорости волн де Бройля. Фазовая скорость – скорость распространения фазы .
Et
-
px
=
const
,
Edt
-
pdx
=0, <
u
>=
dx
/
dt
=
E
/
p
= =
mc
2
/
m
u
- средняя скорость волны.
u
ф
=
c
2
/
u
,
u
гр
=
d
w
/
dk
,
E
=
h
w
,
p
=
hk
,
E
2
-
p
2
c
2
=
m
2
0
c
4
;
E
=
c
Ö
(
p
2
+
m
2
0
c
4
).
u
гр
=d
w
/dk=dE/dp= c2p/(2
Ö
(p2
+m2
0
c4
))=pc2/c
Ö
(p2
+m2
0
c4
)=pc2
/mc2
=p/m=m
u
/m=
u
.
u
гр
u
ф
=
c
2
. Дифракция микрочастиц. По идее де Бройля движение электрона или какой другой частицы связано с волновым процессом.
l
=2
p
h
/
p
=2
p
h
/
m
u
(1);
w
=
E
/
h
. Гипотеза была подтверждена экспериментально в 1927 г. исследование отражения электронов от монокристалла никеля, принадлежащего к кубической системе. Узкий пучок моноэнергетических электронов направлялся на пов-ть монокристалла. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру. Интенсивность оценивалась по силе тока. Варьировалась скорость электронов и угол
j
. Рассеяние оказалось особенно интенсивным при угле, соответствующем отражению от атомных плоскостей, расстояние между которыми было известно из рентгенографических исследований. Вычисленная по формуле (1) длина волны примерно равна брэгговской длине волны, где 2
dsin
q
=
n
l
. Этот опыт подтвердил идею де Бройля. Томсон и Тартаковский независимо друг от друга получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Пучок электронов проходил через тонкую фольгу и попадал на фотопластину. Электрон при ударе о фотопластину оказывает на нее такое же действие как и фотон. Полученая таким же способом электрограмма золота сопоставлена с рентгенограммой алюминия. Сходство поразительно. Обнаружили, что дифф. Явления и у атомных и у молекулярных пучков, и длина волны
l
=2
p
h
/
p
. Таким образом было доказано, что волновое сходство присуще отдельному электрону.
|
Билет 3
1. Спонтанное и индуцированное излучение. Коэффициенты «А» и «В» Эйнштейна.
Спонтанный переход – переход атомов с более высоких на более низкие энергетические уровни. Такие переходы приводят к спонтанному испусканию атомами фотонов. Индуцированные переходы – переходы с более низких на более высокие уровни энергии под действием излучения. Для возможности установления равновесия при произвольной интенсивности падающего излучения необходимо существование «испускательных переходов», вероятность ктр. возрастала бы с увеличением интенсивности излучения, т.е. «испуск. переходов», вызываемых излучением. Возникающее при таких переходах излучение назыв. вынужденным или индуцированным.
Вынужденное и вынуждающее излучения являются строго когерентными. Пусть - вероятность вынужденного перехода атома в ед. времени с энергетического уровня - вероятность вынужденного перехода атома в ед. времени с энергетического уровня  на уровень на уровень , ,  -вер-ть обратного перехода. При одинаковой интенсивности излучения -вер-ть обратного перехода. При одинаковой интенсивности излучения  . .  и и  - вероятность вынужденных переходов пропорциональна плотности энергии - вероятность вынужденных переходов пропорциональна плотности энергии  вынуждающего переход магнитного поля, приходящейся на частоту вынуждающего переход магнитного поля, приходящейся на частоту  , соответствующую данному переходу ( , соответствующую данному переходу ( ). Величины ). Величины  назыв. коэф. Эйнштейна. Равновесие между веществом и излучением будет достигнуто при условии, что число атомов назыв. коэф. Эйнштейна. Равновесие между веществом и излучением будет достигнуто при условии, что число атомов  , совершающих в ед. времени переход из состояния n в сост. m, будет равно числу атомов , совершающих в ед. времени переход из состояния n в сост. m, будет равно числу атомов  , совершающих переход в обр. направ. Пусть , совершающих переход в обр. направ. Пусть  , тогда переходы , тогда переходы  смогут происх. только под воздействием излучения, переходы смогут происх. только под воздействием излучения, переходы будут совершаться как вынужденно, так и cпонтан., будут совершаться как вынужденно, так и cпонтан., 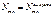 , ,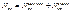
Усл. равновесия: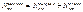 имеем имеем 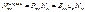 , ,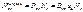
( -числа атомов в сост. m и n). Вероятность спонтанного перехода атома в ед. времени из сост. n в сост m через -числа атомов в сост. m и n). Вероятность спонтанного перехода атома в ед. времени из сост. n в сост m через . Тогда число атомов совершающих в ед. вр. спонтанный переход . Тогда число атомов совершающих в ед. вр. спонтанный переход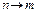 , опр. , опр.  т.е. т.е.
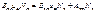 . определяем равновесное значение . определяем равновесное значение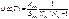 (1), Согласно з-ну Больцмана (1), Согласно з-ну Больцмана  При малых частотах При малых частотах 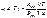 сравнивая с формулой Рэлея-Джинса сравнивая с формулой Рэлея-Джинса 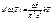 находим, что находим, что 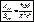 подставляя в (1) получаем формулу Планка. подставляя в (1) получаем формулу Планка.
2. Движение микрочастицы в области одномерного потенциального порога
Одномерный потенциальный порог. 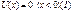
и 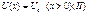 ;Решения ур-ий Шредингера для стац. сост. имеет вид ;Решения ур-ий Шредингера для стац. сост. имеет вид
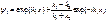 и и  где где 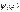 и и 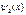
волновые ф-ии частицы в обл-тях I и II соотв. 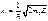 и и 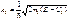 , Вер-ть того что частица отразится от порога опр-ся коэф. отражения , Вер-ть того что частица отразится от порога опр-ся коэф. отражения  , Вероятность прохождения частицы , Вероятность прохождения частицы 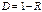 =============================== ===============================

Потенциальный барьер. Пусть ч-ца движущаяся слева направо, встречает на своем пути потенц. барьер высоты 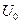 .Рассм. случай .Рассм. случай 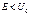 тогда тогда 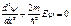 (1) для обл. I и III (1) для обл. I и III
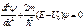 (2) для обл-ти II причем (2) для обл-ти II причем 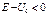 . Будем искать реш. ур-я (1) в виде . Будем искать реш. ур-я (1) в виде 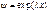 подставляя получаем подставляя получаем  отсюда отсюда 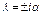 , где , где  , т.о. реш. ур-я (1) имеет вид , т.о. реш. ур-я (1) имеет вид 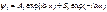 для обл-ти I, для обл-ти I, 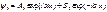 для обл-ти III, аналогично для ур-я (2) для обл-ти III, аналогично для ур-я (2) 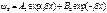 для обл. II, для обл. II, 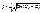 . Заметим,что реш. вида . Заметим,что реш. вида  соотв. волне распростр. в положит. направлении оси х, а реш. вида соотв. волне распростр. в положит. направлении оси х, а реш. вида 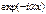 - в противополож. - в противополож.
В обл. III имеется только волна, прошедшая через барьер и распр. слева направо следов. 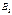 =0. Для того чтобы =0. Для того чтобы  была непрерывна должно вып. усл. была непрерывна должно вып. усл.  и и 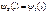 . Для того чтобы . Для того чтобы  не имела изломов необх.: не имела изломов необх.: 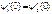 и и 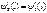 , причем , причем 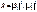 - отношение квадратов модулей амплитуд отраженной и падающих волн определяет вер-ть отражения частицы от потенц. барьера – коэф. отражения. - отношение квадратов модулей амплитуд отраженной и падающих волн определяет вер-ть отражения частицы от потенц. барьера – коэф. отражения. 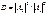 - отнош. квадратов модулей амплитуд прошедшей и падающей волн – вер-ть прохождения частицы через барьер – коэф. прохождения. - отнош. квадратов модулей амплитуд прошедшей и падающей волн – вер-ть прохождения частицы через барьер – коэф. прохождения. . Из ур-ний получившихся из условий непрерывности и гладкости пси-ф-ии, находим . Из ур-ний получившихся из условий непрерывности и гладкости пси-ф-ии, находим
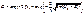 , т.е. вер-ть прохождения частицы через потенц. барьер сильно зависит от ширины барьера
l
и от его превышения над , т.е. вер-ть прохождения частицы через потенц. барьер сильно зависит от ширины барьера
l
и от его превышения над 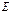 . В случае барьера произв. формы . В случае барьера произв. формы
 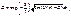 . При преодолении потенц. барьера ч-ца как бы проходит через туннель в этом барьере – рассм. нами явление – туннельный эффект. . При преодолении потенц. барьера ч-ца как бы проходит через туннель в этом барьере – рассм. нами явление – туннельный эффект.
|
| Билет 6
1. Волновая ф-ция, ее статический смысл и условие, которым она должна удовлетворять. Принцип суперпозиции в квантовой механике.
С движением частицы связывается волновой процесс, описываемый волновой ф-цией
y
(
`
r
,
t
)= =
y
(
x
,
y
,
z
,
t
).
y
(
`
r
,
t
)=
y
(
`
r
)
j
(
t
).
dp
=|
y
|2
dV
=|
y
(
`
r
,
t
)|2
dxdydz
– вероятность того, что частица находится в объеме
dV
, определяемая радиусом
`
r
. Таким образом волновая ф-ция не имеет смысла, а квадрат модуля дает плотность вероятности нахождения частицы в пр-ве. Поскольку ф-ция не имеет смысла, то она может быть комплексной:
ò
|
y
|2
dV
=1 (от -
¥
до
¥
) – условие нормировки.
y
- нормированная, если удовлетворяется условие: |
ei
a
|2
=
ei
a
,
e
-
i
a
=1. Требования к волновой ф-ции.
w
=|
y
|2
=
yy
*
,
ò
|
y
|2
dV
=1. 1) Ф-ция должна быть квадратично интегрируема или конечна. 2) ф-ция должна быть однозначна. 3) непрерывность ф-ции вместе с первыми производными. Принцип суперпозиции.
d
w
=|
y
|2
dV
,
y
=
c
1
y
1
+
c
2
y
2
. Если частица может находится в состоянии, описываемом волновой ф-цией
y
1
и
y
2
, то она может находится и в состоянии
y
, являющейся линейной комбинацией этих состояний.
y
=
c
1
y
1
+
c
2
y
2
(с1
и с2
могут быть комплексными), |
c
1
|2
и |
c
2
|2
дают вероятность того, что частица находится в состоянии 1 или в состоянии 2.
2.Эффект Комптона.
Эффектом Комптона наз.упругое рассеяние коротковолнового электромагнитного излучения на свободных электронах вещества, сопровождающееся увеличением длины волны. Комптон экспериментально доказал Δλ=λ`-λ=2λ
c
sin
2
(
θ
/2)( λ`-длина волны рассеянного излучения, λ-длина волны падающего света, λс
- комптоновская длина волны( при рассеянии фотона на электроне λс
=2,426 пм). Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным. Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например на протонах, однако из-за большой массы протона его отдача просматривается лишь при рассеянии фотонов с очень высокой энергией.
------------------------------------------------------
Билет 7
2. Принцип работы лазера. Особенности лазерного излучения. Основные типы лазеров, их применение
.
Лазер – устройство, при прохождении через которое электромагнитные волны усиливаются за счет вынужденного излучения. Лазер – оптический квантовый генератор. Лазер имеет 3 основных компонента: 1) активная среда, 2) система накачки, 3) оптический резонатор. 1-й лазер был рубиновый, активная среда – рубин
Al
2
O
3
. Для оптической накачки использовалась газоразрядная лампа. В кристалле
Al
2
O
3
некоторые атомы
Al
замещены на
Cr
3+
. При облучении рубина цветом атом хрома переходит с уровня 1 на уровень 3, затем происходят переходы либо 3
®
1 (незначительно), либо 3
®
2. Переход 2
®
1 запрещен, поэтому атомы хрома накапливаются на уровне 2, возникает среда с инверсной населенностью. Фотон случайно родившийся при спонтанных переходах может порождать в активной среде множество вынужденных переходов 2
®
1, в результате возникает целая лавина вторичных фотонов, зарождается лазерная генерация. Для выделения направления лазерной генерации используется оптический резонатор. В простейшем случае – пара обращенных друг к другу зеркал на общей оптической оси, между которыми помещается активная среда. Фотоны, которые движутся под углом к оси кристалла выходят из активной среды, а фотоны, которые движутся параллельно оси вызывают вынужденное излучение. Многократно усиленный поток выходит через полупрозрачное зеркало, создавая пучок огромной яркости. Типы лазеров: 1) твердотельные, 2) газовые (гелий-неоновые), 3) полупроводниковые, 4) жидкостные. Применение: обработка, резание, скоростное и точное обнаружение дефектов, в измерительной технике, голография.
2.Деление ядер и цепные реакции. Термоядерный синтез.
Реакция деления ядра заключается в том, что тяжелое ядро под действием нейтронов, а как впоследствии оказалось и других частиц делится на несколько более легких ядер (осколков), чаще всего на ядра, близких по массе. Оно сопровождается испусканием 2-3 вторичных нейтронов, называемых нейтронами деления. Т.к. для средних ядер число нейтронов примерно равно числу протонов, а для тяжелых ядер число нейтронов значительно превышает число протонов, то образовавшиеся осколки деления перегружены нейтронами, в результате чего они и выделяют нейтроны деления. Однако испускание нейтронов деления не устраняет полностью перегрузку ядер-осколков нейтронами. Это приводит к тому, что осколки оказываются радиоактивными.
Испускаемые при делении ядер вторичные нейтроны могут вызвать новые акты деления, что делает возможным осуществления цепной реакции деления - ядерной реакции, в которой частицы, вызывающие реакцию, образуются как продукты этой реакции. Цепная реакция характеризуется коэффициентом размножения
k
нейтронов, который равен отношению числа нейтронов в данном поколении к их числу в предыдущем поколении. Необходимым условием для развития цепной реакции деления является требование
k
≥1. Коэф.размножения зависит от природы делящегося вещества, а для данного изотопа – от его количества, а также размеров и формы активной зоны(пространство, где происходит цепная реакция). Минимальные размеры активной зоны, при которых возможно осуществление цепной реакции, называются критическими размерами. Минимальная масса делящегося вещества, находящегося в системе критических размеров, необходимая для осуществления цепной реакции, называется критической массой.
N
=
N
0
e
(
k
-1)
t
/
T
– число нейтронов в момент времени
t
,
N
0
- число нейтронов в начальный моменты.
k
>1 – саморазвивающиеся реакции,
k
=1 – самоподдерживающаяся реакция,
k
<1 – затухающая реакция.
Реакция синтеза атомных ядер – образование из легких ядер более тяжелых. Реакция синтеза проходящая при сверхвысоких температурах (примерно 107
К и выше) называется термоядерной реакцией.
|
Билет 8.
1.Работа выхода электронов из металла. Термоэлектронная эмиссия. Формула Ричардсона и Ричардсона-Дешмана.
Работа выхода – это работа, которую нужно совершить для удаления электрона с уровня Ферми. Авых
=
D
U
-
EF
,
D
U
зависит от материала, |
D
U
|=
A
+
E
кин
, А=|
D
U
|-
E
кин
, Е
F
– зависит от концентрации свободных электронов
Þ
A
вых
слабо зависит от температуры. Термоэлектронная эмиссия – испускание электронов сильно нагретой поверхностью. Термоэлектронную эмиссию характеризует величина тока насыщения.
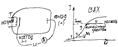
1)
U
- заворачивает электрон, но некоторые электроны, кинетическая энергия которых велика прорываются,
I
>0.
2) Если
U
возрастает, то
I
возрастает, так как содействует росту тока. 3) Линейный участок,
I
~
U
, связана с облаком отрицательного заряда около катода. Оно мешает электрону выскакивать из катода. Рост
U
ведет к уменьшению плотности этого облака
Þ
росту
I
. 4) Насыщение – все кто выскочил из катода, все увлекаются к аноду. Формула Ричардсона-Дешмана.
j
нас
=
A
(
kT
)2
exp
(-
A
вых
/
kT
) идея:
m
u
x
2
/2>
D
U
.
j
нас
повышается при повышении температуры и понижении работы выхода.
2. Структура атомного ядра. Характеристика ядер: заряд, размеры, масса, энергия связи. Свойства и обменные характер ядерных сил.
Атомное ядро состоит из элементарных частиц – протонов и нейтронов. Протон имеет положительный заряд, равный заряду электрона. Нейтрон – нейтральная частица. Протоны и нейтроны называют нуклонами. Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом
Ze
, где
Z
-зарядное число ядра, равное числу протонов в ядре и совпадающее с номером в периодической системе Менделеева. Ядра с одинаковым
Z
, но с разным А называются изотопами, а ядра с одинаковыми А, но с разными
Z
- изобарами. Радиус ядра задается эмпирической формулой
R
=
R
0
A
1/3
, где
R
0
=(1,3÷1,7)10-15
м.
Энергия, которую необходимо затратить на расщепление ядра на отдельные нуклоны, называется энергией связи нуклонов в ядре:
E
св
=[
Zmp
+(
A
-
Z
)
mn
-
m
я
]
c
2
, где
mp
,
mn
,
m
я
- соответственно массы протона, нейтрона и ядра.
Энергия связи ядра
E
св
=[
Zm
Н
+(
A
-
Z
)
mn
-
m
]
c
2
, где
mH
- масса атома водорода.
Δm
=[
Zmp
+(
A
-
Z
)
mn
-
m
я
]-дефект массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра. Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами. Свойства:
1.ядерные силы являются силами притяжения
2.ядерные силы являются короткодействующими – их действие проявляется только на расстоянии 10-15
м. При увеличении расстояния между нуклонами ядерные силы быстро уменьшаются до нуля а при расстоянии, меньших их радиуса действия, оказываются примерно в 100 раз больше кулоновских
3.ядерным силам свойственна зарядовая независимость: ядерные силы, действующие между 2 протонами или 2 нейтронами, одинаковы по величине. Ядер.силы имеют неэлектрическую природу.
4.ядерным силам свойственно насыщение – каждый нуклон в ядре взаимодействует с ограниченным числом ближайших к нему нуклонов.
5.ядерные силы зависят от взаимной ориентации спинов взаимодействующих нуклонов.
6.ядерные силы не являются центральными, т.е. действующими по линии, соединяющей центры взаимодействия нуклонов.
|
Билет 12
1.Прохождение частицы через потенциальный барьер. Туннельный эффект.
Рассмотрим простейший потенциальный барьер прямоугольной формы. Для одномерного (по оси х) движения частицы.
ì
∞,
x
<0 (для области 1)
U
(
x
)=
í
0,0≤
x
≤
l
(для области 2)
î
0,
x
>1 (для области 3)
где
l
-ширина ямы, а энергия отсчитывается от ее дна,
U
-высота. Частица, обладая энергией Е, либо беспрепятственно пройдет над барьером( при Е>
U
), либо отразится от него (при Е<
U
) и будет двигаться в обратную сторону. Для микрочастица, даже при Е>
U
, имеется вероятность отражения от барьера, и при Е<U есть вероятность проникновения через барьер. Это слудет из решения ур-ния Шредингера, описывающего движение микрочастицы
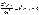 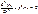
для областей 1 и 3
k
2
=2
mE
/
h
2
; для области 2
q
2
=2
m
(
E
-
U
)/
h
2
Общие решения этих диф.уравнений:
Ψ
1
(
x
)=
A
1
eikx
+
B
1
e
-
ikx
(для области 1);
Ψ
2
(
x
)=
A
2
eiqx
+
B
2
e
-
iqx
(для области2)
Ψ
3
(
x
)=
A
3
eikx
+
B
3
e
-
ikx
(для области 3).
В частности, для области 1 полная волновая, будет иметь вид ψ1
(
x
,
t
)=
ψ
1
(
x
)
e
-(
i
/
h
)
Et
=
A
1
e
-(
i
/
h
)(
Et
-
px
)
+
B
1
x
-(
i
/
h
)(
Et
+
px
)
( в этом выражении первый член представляет собой плоскую волну вдоль х, другой – волну, распространяющаяся в обратную сторону). В области 3 есть только прошедшая сквозь барьер волна и поэтому В3
=0.Для области 2
q
=
iβ
;
β
=√2
m
(
E
-
U
) /
h
.
Получили
Ψ
1
(
x
)=
A
1
eikx
+
B
1
e
-
ikx
,
Ψ
2
(
x
)=
A
2
e
-
βx
+
B
2
eβx
,
Ψ
3
(
x
)=
A
3
eikx
Качественный характер функций ψ1
(х),ψ2
(х),ψ3
(х)(см.рис2), откуда следует, что волновая функция не равна нулю и внутри барьера, а в области3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Т.о. приходим к явлению – туннельный эффект, когда микрочастица может пройти сквозь потенциальный барьер.
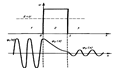
2. Атом во внешнем магнитном поле. Эффект Зеемана.
Эффект Зеемана – расщепление энергетических уровней при действии на атомы магнитного поля. Атом обладающий магнитным моментом, приобретает в магнитном поле дополнительную энергию 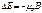 где где  - проекция полного магнитного момента атома на направление поля В . Запишем выражение для энергии каждого подуровня: - проекция полного магнитного момента атома на направление поля В . Запишем выражение для энергии каждого подуровня: 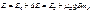 , , 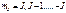 где где 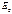 -энергия уровня в отсутствие магн. поля. -энергия уровня в отсутствие магн. поля.
  Отсюда следует, что ур-ни с кв. числом Отсюда следует, что ур-ни с кв. числом 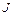 расщепляются в магн. поле на расщепляются в магн. поле на 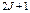 равноотстоящих др. от др. подуровней, причем величина расщепления зависит от множителя Ланде равноотстоящих др. от др. подуровней, причем величина расщепления зависит от множителя Ланде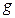 , т.е. интервалы , т.е. интервалы 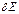 между соседними подуровнями пропорциональны между соседними подуровнями пропорциональны 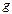 . Возможны только такие переходы между подуровнями, принадлежащими разным уровням, при ктр. вып-ся правила отбора . Возможны только такие переходы между подуровнями, принадлежащими разным уровням, при ктр. вып-ся правила отбора 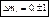 . Компоненты, соотв. . Компоненты, соотв.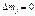 назыв. назыв. 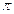 -компонентами, а -компонентами, а 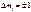 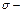 компонентами. При наблюдении перпендикулярно магн. полю присутствуют и компонентами. При наблюдении перпендикулярно магн. полю присутствуют и 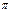 и и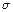 компоненты. При набл. вдоль – только компоненты. При набл. вдоль – только 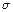 .Частоты .Частоты  зеемановских компонент спектральной линии с частотой зеемановских компонент спектральной линии с частотой 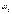 опр. ф-лой опр. ф-лой 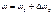 , , 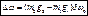 - зеемановское смещение(отн. несмещ. линии) - зеемановское смещение(отн. несмещ. линии)
Простой эффект Зеемана Эффект в ктр. спектральная линия расщепляется на три компоненты. Простой эф. присущ спектральным линиям, не имеющим тонкой структуры. Эти линии возникают при переходах между синглетными ур-нями ( ) ) 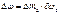 , т.е. , т.е.  (1). Слева (рис.) расщепление ур-ней для перехода (1). Слева (рис.) расщепление ур-ней для перехода  (При включении поля возникают три зеемановские компоненты в соотв с (1)) На рис. справа (При включении поля возникают три зеемановские компоненты в соотв с (1)) На рис. справа но и здесь тоже только три зеемановские компоненты (в соотв. с правилом отбора) но и здесь тоже только три зеемановские компоненты (в соотв. с правилом отбора)
Сложный эффект Зеемана. Когда спектральная линия распадается на число более трех. Это связано с зав-тью расщепления самих ур-ней от множителя Ланде
P.S. Обозначение уровней 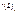 где где 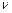 =2s+1, s- спин, L –символ состояния , =2s+1, s- спин, L –символ состояния ,  -квантовое число полного мом -квантовое число полного мом
|
| Билет 10
1.Опыты по рассеянию
a
-частиц. Ядерная модель атома. Постулаты Бора.
α-частицы возникают при радиоактивных превращениях; они являются положительно заряженными частицами с зарядом 2е и массой во много раз больше массы электрона. Пучки α-частиц обладают высокой монохроматичностью.
Резерфорд, исследуя прохождение α-частиц в веществе(через золотую фольгу толщиной 1 мкм), показал, что основная их часть испытывает незначительные отклонения, но некоторые α-частицы резко отклоняются от первоначального направления(даже до 180˚). Т.к. электроны не могут существенно изменить движение столь тяжелых и быстрых частиц, как α-частицы, то Резерфорд сделал вывод что значительное отклонение α-частиц обусловлено из взаимодействием с положительным зарядом большой массы. Однако значительное отклонение испытывают лишь немногие α-частицы; следовательно, лишь некоторые из них проходят вблизи данного положительного заряда. Это означает что положительный заряд атома сосредоточен в объеме, очень малом по сравнению с объемом атома.
На основании своих исследований Резерфорд в 1991г. предположил ядерную (планетарную) модель атома. Вокруг положительного ядра, имеющего заряд
Ze
(
Z
- порядковый номер элемента, е-элементарный заряд), размер 10-15
-10-14
м и массу, практически равной массе атома, в области с линейными размерами порядка 10-10
м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома.
Первый постулат Бора (постулат для стационарных состояний): в атоме существуют стационарные состояния( не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов сопровождается излучением электромагнитных волн. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантовые значения момента импульса, удовлетворяющие условию
me
vrn
=ħ
n
(
n
=1,2,3…) где
me
-масса электрона,
v
-его скорость по
n
-орбите радиуса
rn
,ħ=
h
/(2
π
)
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
hv
=
En
-
Em
равной разности энергий соответствующих стационарных состояний (
En
и
Em
– соответственно энергии стационарных состояний атома до и после излучения(поглощения). При
Em
<
En
происходит излучение фотона, при
Em
>
En
- его поглощение.
2. Примесная проводимость полупроводников. Концентрация основных и неосновных носителей в полупроводнике p-типа. Уровень Ферми примесного полупроводника p-типа. Температурная зависимость проводимости примесного полупроводника p-типа.
Примесная проводимость полупроводников. Примесная проводимость полупроводников возникает, если некоторые атомы данного полупроводника заменить в узлах кристаллической решетки атомами, валентность которых отличается на единицу от валентности основных атомов.
Концентрация основных и неосновных носителей в полупроводниках p-типа.
 В полупроводнике с примесью, валентность которой на единицу меньше валентности основных атомов, имеется только один вид носителей тока – дырки. Такой полупроводник обладает дырочной проводимостью и является полупроводником p-типа. Атомы примеси, вызывающие появление дырок, называют акцепторами. Акцепторные уровни оказывают существенное влияние на электрические св-ва кристалла, если они расположены недалеко от потолка валентной зоны. Образованию дырки отвечает переход э-на из валентной зоны на акцепторный уровень. Обратный переход соответствует разрыву одной из четырех ковал. связей атома примесей с его соседями и рекомбинации образовавшегося при этом электрона и дырки В полупроводнике с примесью, валентность которой на единицу меньше валентности основных атомов, имеется только один вид носителей тока – дырки. Такой полупроводник обладает дырочной проводимостью и является полупроводником p-типа. Атомы примеси, вызывающие появление дырок, называют акцепторами. Акцепторные уровни оказывают существенное влияние на электрические св-ва кристалла, если они расположены недалеко от потолка валентной зоны. Образованию дырки отвечает переход э-на из валентной зоны на акцепторный уровень. Обратный переход соответствует разрыву одной из четырех ковал. связей атома примесей с его соседями и рекомбинации образовавшегося при этом электрона и дырки
Уровень Ферми примесного полупроводника p-типа.
Уровень Ферми располагается в нижней половине запрещенной зоны.
При повышении температуры уровень Ферми(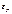 ) в полупроводниках обоих типов смещается к середине запрещенной зоны. ) в полупроводниках обоих типов смещается к середине запрещенной зоны.
Температурная зависимость проводимости примесного полупроводника p-типа.
При повышении температуры концентрация примесных носителей тока быстро достигает вершины. Это значит, что практически освобождаются все донорные или заполняются электронами все акцепторные уровни. По мере роста температуры все больше сказывается собственная проводимость полупроводника, обусловленная переходом электронов из валентной зоны в зону проводимости. → при высоких температурах проводимость полупроводника складывается из примесной и собственной проводимостей. При низких температурах преобладает примесная, а при высоких – собственная проводимость.
|
Билет 11.
1.Тепловое излучение. Интегральные и спектральные характеристики излучения. Закон Кирхгофа. Закон Стефана-Больцмана. Закон смещения Вина.
Тепловое излучение – вид излучения, который может находится в термодинамическом равновесии с излучателем и к анализу такого излучения применимы законы термодинамики.
Спектральная плотность энергетической светимости тела – мощность излучения с единицы площади поверхности тела а интервале частот единичной ширины:
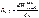 dWν
,
ν
+
dν
изл
-
энергия электромагнитного излучения, испускаемого за единицу времени(мощность излучения) с единицы площади поверхности в интервале частот от ν до ν+
d
ν(Дж/м2
). Интегральная энергетическая светимость можно найти, просуммировав по всем частотам:
dWν
,
ν
+
dν
изл
-
энергия электромагнитного излучения, испускаемого за единицу времени(мощность излучения) с единицы площади поверхности в интервале частот от ν до ν+
d
ν(Дж/м2
). Интегральная энергетическая светимость можно найти, просуммировав по всем частотам:
RT
=∫0
∞
Rν
,
T
dν
. Закон Кирхгофа – отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры
Rν
,
T
/
Aν
,
T
=
rν
,
T
. Закон Стефана-Больцмана
Re
=
σT
4
, т.е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры, σ-постоянная Стефана-Больцмана = 5,67·108
Вт/(м2
·К4
). Закон смещения Вина λмах
=
b
/
T
, т.е. длина волны λмах
, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела, обратно пропорционально его термодинамической температуре,
b
- постоянная Вина =2,9·10-3
м·К. Закон Вина обьясняет, почему при понижении температуры нагретых тел в их спектре сильнее преобладает длинноволновое излучение.
 ==================================================== ====================================================
|
  Билет 12 Билет 12
(2. Статистика Ферми-Дирака. Функция распределения Ф-Д. Вырожденный электронный газ. Энергия Ферми.
Частицы с полуцелым спином называются фермионами. Системы фермионов описываются квантовой статистикой Ф-Д. Фермионы подчиняются правилу Паули: в данном квантовом состоянии системы фермионов не может находиться более 1-й частицы. Ф-ции распределения Ф-Д называются средняя «заселенность» фермионами состояний с данной энергией:
f
Ф
=
D
N
(
Wi
)/
D
gi
, где
D
N
(
Wi
) – число частиц с энергией в интервале от
Wi
до
Wi
+
D
Wi
,
D
gi
– число квантовых состояний в этом интервале энергии. Решение задачи о наиболее вероятном распределении фермионов:
f
Ф=1/(
exp
[(
Wi
-
m
)/
kT
]+1)
m
=(
U
-
TS
+
PV
)/
N
– химический потенциал, работа при увеличении числа частиц в системе на 1,
U
– внутреняя энергия системы,
S
– энтропия,
V
– объем,
p
– давление. Энергия Ферми – максимальная энергия у электрона находящегося на уровне Ферми при
T
=0К. Вырожденный электронный газ: система частиц называется вырожденной, если её св-ва, описываемые квантовыми закономерностями, отличаются от св-в обычных систем, подчиняющихся классическим законам. Параметром вырождения А называется величина: А=
exp
(
m
/
kT
), где
m
- химический эквивалент. Параметр вырождения показывает классический или квантовый случай газа:
EF
/
kT
>1 – квантовая, <<1 – классическая.
))
2.Предельный переход квантовых статических распределений Ферми-Дирака и Бозе-Эйнштейна в классическое распределение Максвелла-Больцмана.
Параметр вырождения.
1) Распределение Ф-Д:
f
Ф
=1/(
exp
[
E
-
EF
/
kT
]+1).
2) распределение Б-Э:
f
Б
=1/(
exp
[
E
-
EF
/
kT
]-1).
3) Распределение М-Б:
f
=
exp
[-
E
/
kT
].
Функции распределения в классической и квантовых статиках, введенные как среднее число частиц в одном состоянии, могут быть выражены единой формулой:
f
=1/(
exp
[
E
-
EF
/
kT
]+
d
). Для Ф-Д:
d
=1, для Б-Э:
d
=-1, для М-Б:
d
=0
EF
=0.
K
– постоянная Больцмана,
T
– абсолютная температура,
EF
– энергия Ферми,
max
E
у
`
e
ферми-газа при
T
=0К. Параметр вырождения:
A
=
exp
(
m
/
kT
). При А<<1 распределение Б-Э и Ф-Д переходят в классическое распределение М-Б.
|
| Билет 13
1. Частица в трехмерном потенциальном ящике. Энергетический спектр частицы. Понятие о вырождении энергетических уровней. Найдем собств. зн-я энергии и соотв. им собств. ф-ии для частицы находящейся в одномерной потенциальной яме с беск. выс. стенками. Пусть движение ограничено непроницаемыми для частицы стенками x=0 и x=l . U=0 при 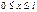 , U=∞ при , U=∞ при 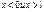 , Ур-е Шредингера , Ур-е Шредингера 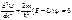 , т.к. за пределы ямы частица вырваться не может, то , т.к. за пределы ямы частица вырваться не может, то 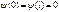 . .
   В области где В области где  , ур-е имеет вид , ур-е имеет вид 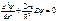 , вводим , вводим 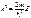 , придем к , придем к  , реш. имеет вид , реш. имеет вид 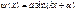 , т.к. , т.к. 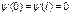 , то , то 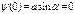 , откуда , откуда 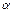 =0 , тогда =0 , тогда 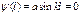 , т.е. , т.е. 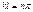 ( (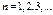 ), откуда ), откуда 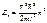 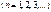 , спектр энергии – дискретный. Подставив зн-е k получим , спектр энергии – дискретный. Подставив зн-е k получим  , для нахождения , для нахождения 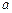 воспользуемся условием нормировки воспользуемся условием нормировки 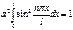 , откуда , откуда 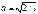 , т.е. , т.е. 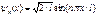
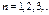 Ч-ца в 3-мер ящ. Ч-ца в 3-мер ящ. 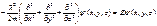
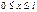 , , 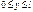 , , 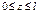 ; ; 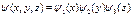 , , 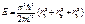 Причем Причем
 при при  будет будет 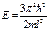 , а при , а при 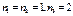 или или 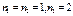 или или 
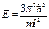 Когда одной энергии соотв. несколько равных сост. называется вырождением, а число этих сост. – кратностью вырождения Когда одной энергии соотв. несколько равных сост. называется вырождением, а число этих сост. – кратностью вырождения
2. Симметрия и законы сохранения в мире элементарных частиц.
Симметрия и законы сохранения в мире элементарных частиц.
Симметрия. Каждой частице соответствует античастица. е+ и р- отличаются от е- и р+ знаком электрического заряда. n от ň знаком магнитного момента. е+ + е- = γ + γ.
Законы сохранения в мире элементарных частиц. В мире элементарных частиц есть ЗС энергии, импульса, момента импульса + всех зарядов: барионного, электрического и трех лептонных.
ЗС барионного заряда B: В = +1 для барионов; В = -1 для антибарионов; для остальных В=0. Для всех процессов с участием барионов и антибарионов суммарный барионный заряд сохраняется.
ЗС лептонных зарядов: электронный Le ( для е и νе (нейтрино)), мюонный Lμ ( для μ и νμ ), таонный Lτ (для τ и ντ ). Le = Lμ = Lτ = +1 (для лептонов); -1 (для антилептонов). Для всех остальных L = 0. Для всех процессов с участием лептонов и антилептонов суммарный лептонный заряд сохраняется.
Существуют ЗС странности S, очарования C, прелести b, изотопического спина
|
Билет 14
1.Частица в одномерной потенциальной яме с бесконечно высокими стенками. Квантование энергии. Плотность вероятности для различных энергетических уровней.
Проведем качественный анализ решений уравнений Шредингера применительно к частице в одномерной прямоугольной потенциальной с бесконечно высокими стенками. Такая яма описывается потенциальной энергией вида(частица движется вдоль оси х):
ì
∞,
x
<0 где
l
-ширина ямы, а энергия
U
(
x
)
í
0,0≤
x
≤
l
отсчитывается от ее дна
î
∞,
x
>1
Уравнение Шредингера для стационарных состояний запишется в виде: (∂2
ψ/∂
x
2
)+(2
m
/ħ2
)(
E
-
U
)
ψ
=0. По условию задачи частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами равна 0. На границах ямы вероятность тоже обращается в 0. Следовательно, граничные условия имеют вид
ψ
(0)=
ψ
(
l
)=0. В пределах ямы(0≤х≤
l
) ур-ние Ш сведется к (∂2
ψ/∂
x
2
)+(2
m
/ħ2
)
Eψ
=0 или (∂2
ψ/∂
x
2
)+
k
2
ψ
=0, где
k
2
=2
mE
/ħ2
.
Общее решение диф.ур-ния ψ(
x
)=
Asinkx
+
BcosKx
. Т.к. ψ(0)=0, то В=0. Тогда
ψ
(
x
)=
Asinkx
. Условие ψ(
l
)=
Asinkl
=0 выполняется только при
kl
=
nπ
, где
n
–целые числа, т.е. необходимо чтобы
k
=
nπ
/
l
Из всего этого следует что
En
=(
n
2
π
2
ħ2
)/(2
ml
2
) (
n
=1,2,3…)
Т.е. стационарное уравнение Ш, описывающее движение частицы в потенциальной яме с бесконечно высокими стенками удовлетворяется только при собственных значениях
En
, зависящих от целого числа
n
.2.
2.Явление радиоактивного распада. Источники радиоактивного излучения. Радиоизотопный анализ.
Радиоактивность – способность некоторых атомов ядер самопроизвольно превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Различают естественную (наблюдается у неустойчивых изотопов, сущ. в природе) и искусственную( у изотопов, полученных в термоядерных реакциях) радиоактивность. Радиоактивное излучение бывает 3 типов:
α
-,
β
- и γ-излучение.
α-Излучение отклоняется электрическим и магнитным полями, обладает высокой ионизирующей и малой проникающей способностью. α-Излучение представляет собой поток ядер гелия.
β-Излучение отклоняется электрическим и магнитными полями, его ионизирующая способность значительно меньше, а проникающая гораздо больше чем у α-частиц. β-Излучение представляет собой поток быстрых электронов.
γ-Излучение не отклоняется электрическим и магнитным полями, обладает относительно малой ионизирующей и очень большей проникающей способностью, при прохождении через кристаллы обнаруживается дифракция. γ-Излучение представляет собой коротковолновое электромагнитное излечение с чрезвычайно малой длиной волны λ<10-10
м и вследствие этого – ярко выраженные корпускулярные свойства, т.е. является потоком частиц – γ-квантов(фотонов).
Радиоактивные распад – естественное радиоактивное превращение ядер, проходящее самопроизвольно. Атомное ядро, испытывающее радиоактивный распад называется материнским, возникающее ядро – дочерним.
N
=
N
0
e
-
λt
– закон радиоактивного распада, согласно которому число нераспавшихся ядер убывает со временем по экспоненциальному закону.
λ
-постоянная для данного радиоактивного вещества величина, наз.постоянной радиоактивного распада.
Единица активности в СИ – беккерель(Бк):1 Бк-активость нуклида, при которой за 1 с происходит один акт распада. До сих пор единица применяется внесистемная единица активности нуклида в радиоактивном источнике – кюри(Ки) 1КИ=3,7·1010
Бк
Билет 15
1.Уравнение Шредингера для гармонического осциллятора и анализ его решений
.
Линейный гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы – является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия осциллятора равна
U
=
mω
0
2
x
2
/2 где ω0
- собственная частота осциллятора,
m
- масса частицы.
Гармонический осциллятор в квантовой механике – квантовый осциллятор – описывается уравнением Шредингера, учитывающим выражение для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются ур-нием Шредингера вида
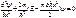
где Е- полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что это уравнение решается
только при собственных значениях энергии
En
=(
n
+½)ħω0
. Эта формула показывает, что энергия квантового осциллятора может иметь только дискретные значения, т.е. квантуется.
Строгое решение задачи о квантовом осцилляторе приводит еще к отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области, в то время как с классической точки зрения она не может выйти за пределы области. Т.о. имеется отличная от нуля вероятность обнаружить частицу в области, которая является классически запрещенной.
2...Представление физических величин операторами. Вычисление средних значений физических величин.
А) Оператор координаты. Действие сводится к умножению волновой функции на эту координату:
x
^
y
=
x
y
,
y
^
y
=
y
y
,
z
^
y
=
z
y
или
x
^=
x
…
б) Оператор проекций импульса. Выражаются с помощью операторов дифференцирования по соответствующим координатам:
P
^
x
=(
h
/
i
)(
¶
/
¶
x
),
P
^
y
=(
h
/
i
)(
¶
/
¶
y
),
P
^
z
=(
h
/
i
)(
¶
/
¶
z
),
`
p
^={
P
^
x
,
P
^
y
,
P
^
z
}.
В) Оператор момента импульса:
`
L
=
`
r
´
`
p
,
Lx
=
ypz
-
zpy
;
Ly
=
zpy
-
xpz
;
Lz
=
xpy
-
ypx
;
L^x
=y^p^z
-z^p^y
=(h/i)(y
¶
/
¶
x-z
¶
/
¶
y).
Г) Оператор кинетической энергии. Определим
T
, пользуясь формулой Т=
p
2
/2
m
,
T
^=
p
^2
/2
m
=-
h
2
/2
m
. Вычисление средних значений:
L
^
y
=
L
y
,<
L
>=
ò
y
*
L
^
y
dV
,
y
(
r
)=
Aexp
(-
r
/
a
)
|
Билет 16
1.Корпускулярно-волновой дуализм материи. Гипотеза де Бройля. Опыты по дифракции микрочастиц
.
Де Бройль выдвинул теорию о корп.-волн.дуализме материи, т.е. не только фотоны, но и электроны и любые другие частица материи наряду с корпускулярными обладают также волновыми свойствами. Каждые микрообъект связывают корпуск.характеристики –энергия Е и импульс р, а также волновые – частота ν и длина волны λ. Е=hν,p=h/λ. Т.о. любой частице обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемо по формуле де Бройля λ=h/p. Можно добавить то, что на частице вещества переносится связь между полной энергией частицы ε и частотой ν волн де Бройля:ε=hν , h-постоянная Планка=6,625·10-34 Дж·с
Волна де Бройля – это волна, связанная с равномерным и прямолинейным движением частицы.
y
=Acos(
w
t-kx)
ü
уравнения
y
(x,t)=Aexp(-(
w
t-kx))
þ
волны.
E=h
w
, p=hk,
w
=E/h, k=p/h.
y
(x,t)=Aexp(-i/h(Et-px)) – плоская волна де Бройля. Фазовая и групповая скорости волн де Бройля. Фазовая скорость – скорость распространения фазы . Et-px=const, Edt-pdx=0, <
u
>=dx/dt=E/p= =mc2/m
u
- средняя скорость волны.
u
ф=c2/
u
,
u
гр=d
w
/dk, E=h
w
, p=hk, E2-p2c2=m20c4; E=c
Ö
(p2+m20c4).
u
гр=d
w
/dk=dE/dp= c2p/(2
Ö
(p2+m20c4))=pc2/c
Ö
(p2+m20c4)=pc2/mc2=p/m=m
u
/m=
u
.
u
гр
u
ф=c2. Дифракция микрочастиц. По идее де Бройля движение электрона или какой другой частицы связано с волновым процессом.
l
=2
p
h/p=2
p
h/m
u
(1);
w
=E/h. Гипотеза была подтверждена экспериментально в 1927 г. исследование отражения электронов от монокристалла никеля, принадлежащего к кубической системе. Узкий пучок моноэнергетических электронов направлялся на пов-ть монокристалла. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру. Интенсивность оценивалась по силе тока. Варьировалась скорость электронов и угол
j
. Рассеяние оказалось особенно интенсивным при угле, соответствующем отражению от атомных плоскостей, расстояние между которыми было известно из рентгенографических исследований. Вычисленная по формуле (1) длина волны примерно равна брэгговской длине волны, где 2dsin
q
=n
l
. Этот опыт подтвердил идею де Бройля. Томсон и Тартаковский независимо друг от друга получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Пучок электронов проходил через тонкую фольгу и попадал на фотопластину. Электрон при ударе о фотопластину оказывает на нее такое же действие как и фотон. Полученая таким же способом электрограмма золота сопоставлена с рентгенограммой алюминия. Сходство поразительно. Обнаружили, что дифф. Явления и у атомных и у молекулярных пучков, и длина волны
l
=2
p
h/p. Таким образом было доказано, что волновое сходство присуще отдельному электрону.
2. Собственная проводимость полупроводников. Концентрация электронов и дырок в чистых полупроводниках. Уровень Ферми в чистых полупроводниках. Температурная зависимость проводимости беспримесных полупроводников.
Проводимость полупроводников.
Полупроводниками являются кристаллические вещества, у которых при 0К валентная зона полностью заполнена электронами, а ширина запрещенной зоны невелика. Характерная черта – проводимость растет с повышением температуры.
Собственная проводимость возникает в результате перехода электронов с верхних уровней валентной зоны в зону проводимости. При этом в зоне проводимости появляется несколько носителей тока – электронов, занимающих место вблизи дна зоны; одновременно в валентной зоне освобождается такое же число мест на верхних уровнях, в результате чего появляются дырки.
Типичные полупроводники – кремний и германий. На рис.  - атомные остатки(ктр. остаются после удаления валентных э-нов) «-» - валентные э-ны, двойные линии – ковал. связь. При достаточно высокой температуре тепловое движение может разорвать отдельные пары, освободив один э-н . Покинутое место э-ном перестает быть нейтральным, в его окрестности возникает избыточный положительный заряд «+е», т.е. образуется дырка (пунктирный кружок). На это место может перескочить э-н одной из соседних пар. В результате дырка начинает также странствовать по кристаллу, как и освободившийся э-н. - атомные остатки(ктр. остаются после удаления валентных э-нов) «-» - валентные э-ны, двойные линии – ковал. связь. При достаточно высокой температуре тепловое движение может разорвать отдельные пары, освободив один э-н . Покинутое место э-ном перестает быть нейтральным, в его окрестности возникает избыточный положительный заряд «+е», т.е. образуется дырка (пунктирный кружок). На это место может перескочить э-н одной из соседних пар. В результате дырка начинает также странствовать по кристаллу, как и освободившийся э-н.
При встрече своб. э-на с дыркой они рекомбинируют (соединяются). Рекомбинация приводит к одновр. исчезновению своб. э-на и дырки. В собств. полупроводнике идут два процесса одновременно: рождение попарно свободных э-нов дырок и рекомбинация .
 Вероятность первого процесса быстро растет с температурой. Вер-ть рекомбинации пропорциональна как числу дырок, так и числу э-нов. Следов, каждой температуре соотв. опр. равновесная концентрация э-нов и дырок, ктр. изменяется пропорционально T (1) Вероятность первого процесса быстро растет с температурой. Вер-ть рекомбинации пропорциональна как числу дырок, так и числу э-нов. Следов, каждой температуре соотв. опр. равновесная концентрация э-нов и дырок, ктр. изменяется пропорционально T (1)
Концентрация электронов и дырок в чистых полупроводниках.
 Распределение электронов по уровням валентной зоны и зоны проводимости описывается функцией Ферми-Дирака. (на рис.) Уровни зоны проводимости лежат на хвосте кривой распределения, поэтому вероятность их заполнения электронами Распределение электронов по уровням валентной зоны и зоны проводимости описывается функцией Ферми-Дирака. (на рис.) Уровни зоны проводимости лежат на хвосте кривой распределения, поэтому вероятность их заполнения электронами 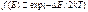 (1). (1).
В собственном полупроводнике одинаковые концентрации э-нов и дырок будут равны 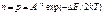 , где А – коэф. пропорциональности. , где А – коэф. пропорциональности.
Уровень Ферми в чистых полупроводниках.
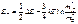 , где ΔЕ – ширина запрещенной зоны, а , где ΔЕ – ширина запрещенной зоны, а 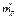 и и 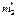 - эффективные массы электрона и дырки. Обычно второе слагаемое пренебрежимо мало, поэтому можно сказать, что уровень Ферми для чистых полупроводников лежит посередине запрещенной зоны. - эффективные массы электрона и дырки. Обычно второе слагаемое пренебрежимо мало, поэтому можно сказать, что уровень Ферми для чистых полупроводников лежит посередине запрещенной зоны.
Температурная зависимость проводимости беспримесных полупроводников.
Электропроводность собственных полупроводников: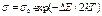 , где , где 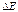 - ширина запрещенной зоны, - ширина запрещенной зоны, 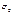 - величина, изменяющаяся с температурой гораздо медленнее, чем экспонента, поэтому ее в первом приближении можно считать константой. - величина, изменяющаяся с температурой гораздо медленнее, чем экспонента, поэтому ее в первом приближении можно считать константой.
|
| Билет 17
1.Уравнение Шредингера для атома водорода. Квантовые числа и их физический смысл.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze(для атома водорода Z=1)
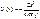 где r-расстояние между электроном и ядром где r-расстояние между электроном и ядром
Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера, учитывающие значение U(r):
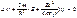
m-масса электрона, Е- полная энергия электрона в атоме.
 В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции ψnlm(r,θ,φ), определяемые 3 квантовыми числами: главным n,орбитальным l и магнитным ml. Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения n=1,2,3….Орбитальное квантовое число l , при заданном n принимает значения l=0,1,…,(n-1) т.е. всего n значений и определяет момент импульса электрона в атоме. Магнитное квантовое число ml, при заданном l может принимать значения ml=0,±1,±2,…,±l, т.е. всего 2l+1 значений. Т.о. магнитное квантовое число определяет проекцию момента импульса на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции ψnlm(r,θ,φ), определяемые 3 квантовыми числами: главным n,орбитальным l и магнитным ml. Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения n=1,2,3….Орбитальное квантовое число l , при заданном n принимает значения l=0,1,…,(n-1) т.е. всего n значений и определяет момент импульса электрона в атоме. Магнитное квантовое число ml, при заданном l может принимать значения ml=0,±1,±2,…,±l, т.е. всего 2l+1 значений. Т.о. магнитное квантовое число определяет проекцию момента импульса на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
2. Эффект Холла в полупроводниках, его практическое применение
Эффект Холла. Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между параллельными току и полю гранями возникает разность потенциалов 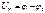 . .
Величина ее определяется выражением UH = RbjB, где b –ширина пластинки, j – плотность тока, B – магнитная индукция поля, R – разный для разных металлов коэффициент пропорциональности, получившей название постоянной Холла.
В полупроводниках. По знаку эффекта Холла в полупроводниках можно судить о принадлежности полупроводника к n или p типу.

На рисунке сопоставлен эффект Холла для образцов с положительными и отрицательными носителями. Направление силы Лоренца изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. Следовательно, при одинаковом направлении тока сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (на рисунке) грани выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом определив знак холловской разности потенциалов, можно установить знак носителей тока.
Билет 18
2.Электрон в периодическом поле кристалла. Образование энергетических зон. Энергетический спектр электронов в модели Кронинга-Пенни.
В основе зонной теории лежит так называемое адиабатическое приближение. Квантово-механическая система разделяется на тяжелые и легкие частицы- ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать. Что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки находятся неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер.
Далее используем приближение самосогласованного поля. Взаимодействие данного электрона со всеми другими заменяется действием на него стационарного эл.поля, обладающего периодичностью кристалл.решетки. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер. Пока атомы изолированы, т.е. находятся друг от друга на макроскопических расстояниях, они имеют совпадающие схемы энергетических уровней. (см.рис). По мере сжатия нашей модели до кристал.решетки, т.е. когда расстояния между атомами станут равными межатомным, взаимодействие между атомами приводит к тому, что энергетические уровни атомов смещаются, расщепляются и расширяются
, образуется зонный энергетический спектр.
Образование зонного энергетического спектра в кристалле является квантово-механическим дефектом и вытекает из соотношения неопределенностей. В кристалле валентные электроны атомов, связанные слабее с ядрами, чем внутренние электроны, могут переходить от атома к атому сквозь потенциальные барьеры, разделяющие атомы, т.е. перемещаться без изменения потенциальной энергии (туннельный эффект).
Энергия внешних может принимать значения в пределах закрашенных областей (см.рис), называемых разрешенными энергетическими зонами. Разрешенные энергетические зоны разделяются зонами запрещенных значений энергии, называемые запрещенными энергетическими зонами.
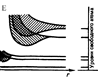
|
Билет №19.
1.Орбитальный, спиновый и полный угловой и магнитный момент электрона.
Электрон обладает собственным моментом импульса
MS
, который называется спином. Его величина определяется по общим законам квантовой механики:
MS
=
`
h
Ö
[
S
(
S
+1)]=
`
h
Ö
[(1/2)*(3/2)]=(1/2)
`
h
Ö
3,
Ml
=
`
h
Ö
[
l
(
l
+1)] – орбитальный момент. Проекция может принимать квантовые значения, отличающиеся друг от друга на
`
h
.
MSz
=
mS
`
h
, (
ms
=
±
S
),
Mlz
=
ml
`
h
. Чтобы найти значение собственного магнитного момента умножим
Ms
на отношение
m
s
к
Ms
,
m
s
– собственный магнитный момент:
m
s
=-eMs
/me
c=-(
е
`
h/me
c)
Ö
[S(S+1)]=-
m
Б
Ö
3,
m
Б
–
Магнетон
Бора
.
Знак (-) потому что
Ms
и
m
s
направлены в разные стороны. Момент Электрона слагается из 2-х: орбитального
Ml
и спинового
Ms
. Это сложение осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов: М
j
=
`
h
Ö
[
j
(
j
+1)],
j
– квантовое число полного момента импульса.
2.Стационарные состояния, их временная зависимость. Уравнение Шредингера для стационарных состояний.
Стационарные состояния – это состояния с фиксированными значениями энергии. Это возможно, если силовое поле, в котором движется частица, стационарно, т.е. функция
U
=
U
(
x
,
y
,
z
) не зависит явно от времени и имеет смысл потенциальной энергии. Уравнение Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выражается множителем
e
-
iωt
=
e
-
i
(
E
/ħ)
t
, так что Ψ(
x
,
y
,
z
,
t
)=
ψ
(
x
,
y
,
z
)
e
-
i
(
E
/ħ)
t
, где Е- полная энергия частицы, постоянная в случае стационарного поля. Подставляя это выражение в уравнение Шредингера( –ħ2
/2
m
-
ΔΨ
+
U
(
x
,
y
,
z
,
t
)
Ψ
=
i
ħ(∂
Ψ
/∂
t
), где ħ=
h
/(2
π
),
m
–масса частицы,
i
-мнимая единица,
U
-потенциальная функция частицы в силовом поле, в котором она движется
Δ-оператор Лапласа(ΔΨ=∂2
Ψ/∂
x
2
+∂2
Ψ/∂
y
2
+∂2
Ψ/∂
z
2
),Ψ(
x
,
y
,
z
,
t
)-искомая волновая функция частицы) получим:
 разделив на общий множитель
e
-
i
(
E
/ħ)
t
и преобразовав придем к уравнению, определяющему функцию ψ
разделив на общий множитель
e
-
i
(
E
/ħ)
t
и преобразовав придем к уравнению, определяющему функцию ψ
Δψ+(2
m
/ħ2
)(
E
-
U
)
ψ
=0-уравнение Шредингера для стационарных состояний. Это уравнение имеет бесчисленное количество решений, из которых посредством наложения граничных условий отбираются решения, имеющие физич.смысл. Условия: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Т.о. реальный физич.смысл имеют только такие решения, которые выражаются регулярными функциями ψ .
Билет 21.
1.Предельный переход квантовых статических распределений Ферми-Дирака и Бозе-Эйнштейна в классическое распределение Максвелла-Больцмана.
Параметр вырождения.
1) Распределение Ф-Д:
f
Ф
=1/(
exp
[
E
-
EF
/
kT
]+1).
2) распределение Б-Э:
f
Б
=1/(
exp
[
E
-
EF
/
kT
]-1).
3) Распределение М-Б:
f
=
exp
[-
E
/
kT
].
Функции распределения в классической и квантовых статиках, введенные как среднее число частиц в одном состоянии, могут быть выражены единой формулой:
f
=1/(
exp
[
E
-
EF
/
kT
]+
d
). Для Ф-Д:
d
=1, для Б-Э:
d
=-1, для М-Б:
d
=0
EF
=0.
K
– постоянная Больцмана,
T
– абсолютная температура,
EF
– энергия Ферми,
max
E
у
`
e
ферми-газа при
T
=0К. Параметр вырождения:
A
=
exp
(
m
/
kT
). При А<<1 распределение Б-Э и Ф-Д переходят в классическое распределение М-Б.
2.Условия возможности одновременного измерения разных величин. Соотношение неопределенностей Гейзенберга.
Если коммутатор [
A
,
B
]не равен нулю, то невозможно одновременно измерить величины. ([
A
,
B
]=
AB
-
BA
)
Гейзенберг предположил, что невозможно определить точно положение и импульс. Неопределенность положения х и рх
удовлетворяют соотношению
ì
Δ
x
·
px
≥ħ/2
í
Δ
y
·
py
≥ħ/2
î
Δ
z
·
pz
≥ħ/2 Обозначив канонически сопряженные величины буквами А и В получим ΔА·ΔВ≥ħ/2. Производные неопределенностей значений двух сопряженных переменных не может быть по порядку величина меньше постоянной Планка ħ. Энергия и время тоже канонически сопряженные величины
Δ
Е·
Δt
.≥ħ
|
Билет №20.
1. Собственные механический и магнитный моменты электрона. Опыт Штерна и Герлаха
Электрон обладает собственным моментом импульса  , не связанным с движ. э-на в пр-ве. Этот собственный момент – спин. Спин характеризует внутр. св-во э-на подобно массе и заряду. , не связанным с движ. э-на в пр-ве. Этот собственный момент – спин. Спин характеризует внутр. св-во э-на подобно массе и заряду.  , , 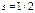 где s – спиновое квантовое число, где s – спиновое квантовое число, 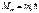 , , 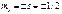 . Электрон наряду с собств. мех. моментом облад. собств. магнитным моментом . Электрон наряду с собств. мех. моментом облад. собств. магнитным моментом  . Причем . Причем 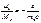 ,тогда ,тогда 
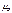 -магнетон Бора (единица магнитного момента) -магнетон Бора (единица магнитного момента) 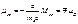 . .
Опыт Штерны и Герлаха. Пучок атомов пропускается через сильно неоднородное поперечное магнитное поле а). Неоднородность достигалась с помощью спец. формы полюсных наконечников б). Далее пучок атомов попадал на фотопластинку Р и оставлял на ней след. Если атомы обладают магнитным моментом, то на них будет действовать сила, пр-я ктр. 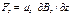  -пр-я магнитного момента атома. При малых -пр-я магнитного момента атома. При малых 
необх. обеспечить дост. большую неоднородность поля, т.е  . в отсутствие магн. поля след пучка на Р имел вид полоски z=0. При включении магнитного поля наблюдалось расщепление пучка в), что являлось следствием квантования пр-ии . в отсутствие магн. поля след пучка на Р имел вид полоски z=0. При включении магнитного поля наблюдалось расщепление пучка в), что являлось следствием квантования пр-ии  . Обнаружилось также, что для разных атомов число компонент, на ктр. расщеплялся пучок, было то четным, то нечетным. Нечетно – у атомов облад. только орбитальным мех. моментом . Обнаружилось также, что для разных атомов число компонент, на ктр. расщеплялся пучок, было то четным, то нечетным. Нечетно – у атомов облад. только орбитальным мех. моментом  , магн. поле снимает вырождение по L и число компонент (значений , магн. поле снимает вырождение по L и число компонент (значений  ) ,будет равно ) ,будет равно 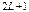 т.е. нечетным. Если же момент = сумме орбитального и спинового, т.е. определяется кв. числом J , то число компонент будет равно 2J+1, и в зав-ти от того, полуцелым или целым будет J , число компонент будет четным или нечетным. т.е. нечетным. Если же момент = сумме орбитального и спинового, т.е. определяется кв. числом J , то число компонент будет равно 2J+1, и в зав-ти от того, полуцелым или целым будет J , число компонент будет четным или нечетным.
2. Контактные явления в полупроводниках. P-n переход, его вольт-амперная характеристика.
Контактные явления в полупроводниках.
Если привести два разных полупроводника в соприкосновение, между ними возникает разность потенциалов, которая называется контактной. В результате в окружающем пространстве возникает электрическое поле. Контактная разность потенциалов обусловлена тем, что при соприкосновении поверхностей часть электронов переходит из одного полупроводника в другой.
Внешняя контактная разность потенциалов:  ; ;
  Внутренняя разность потенциалов: Внутренняя разность потенциалов: 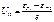 . .
p-n переход, его вольтамперная характеристика.
p-n переход – тонкий слой на границе между двумя областями одного и того же кристалла, отличающимися типом примесной проводимости.
В р-области основные носители тока – дырки (акцепторы становятся отрицательными ионами). В n-области – электроны, отданные донорами в зону проводимости.
 Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют друг с другом.→ меньше носителей и большое сопротивление p-n-перехода. Одновременно на границе между областями возникает двойной электрический слой, образованный отрицательными ионами акцепторной примеси, заряд которых не компенсируется дырками, и положительными ионами донорной примеси, заряд которых теперь не компенсируется электронами. Электрическое поле в этом слое направлено так, что противодействует дальнейшему переходу через слой основных носителей. Равновесие достигается при такой высоте потенциального барьера, при которой уровни Ферми обеих областей располагаются на одинаковой высоте. Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют друг с другом.→ меньше носителей и большое сопротивление p-n-перехода. Одновременно на границе между областями возникает двойной электрический слой, образованный отрицательными ионами акцепторной примеси, заряд которых не компенсируется дырками, и положительными ионами донорной примеси, заряд которых теперь не компенсируется электронами. Электрическое поле в этом слое направлено так, что противодействует дальнейшему переходу через слой основных носителей. Равновесие достигается при такой высоте потенциального барьера, при которой уровни Ферми обеих областей располагаются на одинаковой высоте.
В направлении от p-области к n-области p-n-переход пропускает ток, сила которого быстро нарастает при увеличении приложенного напряжения (прямое направление).
В обратном направлении p-n-переход обладает гораздо большим сопротивлением, чем в прямом. Поле, возникающее в кристалле при наложении обратного напряжения, «оттягивает» основные носители о границы между областями, что приводит к возрастанию ширины переходного слоя, обедненного носителями.
ВАХ p-n-перехода 
|
| Билет 22
1. Статистика Ферми-Дирака. Функция распределения Ф-Д. Вырожденный электронный газ. Энергия Ферми.
  Частицы с полуцелым спином называются фермионами. Системы фермионов описываются квантовой статистикой Ф-Д. Фермионы подчиняются правилу Паули: в данном квантовом состоянии системы фермионов не может находиться более 1-й частицы. Ф-ции распределения Ф-Д называются средняя «заселенность» фермионами состояний с данной энергией:
f
Ф
=
D
N
(
Wi
)/
D
gi
, где
D
N
(
Wi
) – число частиц с энергией в интервале от
Wi
до
Wi
+
D
Wi
,
D
gi
– число квантовых состояний в этом интервале энергии. Решение задачи о наиболее вероятном распределении фермионов:
f
Ф=1/(
exp
[(
Wi
-
m
)/
kT
]+1)
m
=(
U
-
TS
+
PV
)/
N
– химический потенциал, работа при увеличении числа частиц в системе на 1,
U
– внутреняя энергия системы,
S
– энтропия,
V
– объем,
p
– давление. Энергия Ферми – максимальная энергия у электрона находящегося на уровне Ферми при
T
=0К. Вырожденный электронный газ: система частиц называется вырожденной, если её св-ва, описываемые квантовыми закономерностями, отличаются от св-в обычных систем, подчиняющихся классическим законам. Параметром вырождения А называется величина: А=
exp
(
m
/
kT
), где
m
- химический эквивалент. Параметр вырождения показывает классический или квантовый случай газа:
EF
/
kT
>1 – квантовая, <<1 – классическая. Частицы с полуцелым спином называются фермионами. Системы фермионов описываются квантовой статистикой Ф-Д. Фермионы подчиняются правилу Паули: в данном квантовом состоянии системы фермионов не может находиться более 1-й частицы. Ф-ции распределения Ф-Д называются средняя «заселенность» фермионами состояний с данной энергией:
f
Ф
=
D
N
(
Wi
)/
D
gi
, где
D
N
(
Wi
) – число частиц с энергией в интервале от
Wi
до
Wi
+
D
Wi
,
D
gi
– число квантовых состояний в этом интервале энергии. Решение задачи о наиболее вероятном распределении фермионов:
f
Ф=1/(
exp
[(
Wi
-
m
)/
kT
]+1)
m
=(
U
-
TS
+
PV
)/
N
– химический потенциал, работа при увеличении числа частиц в системе на 1,
U
– внутреняя энергия системы,
S
– энтропия,
V
– объем,
p
– давление. Энергия Ферми – максимальная энергия у электрона находящегося на уровне Ферми при
T
=0К. Вырожденный электронный газ: система частиц называется вырожденной, если её св-ва, описываемые квантовыми закономерностями, отличаются от св-в обычных систем, подчиняющихся классическим законам. Параметром вырождения А называется величина: А=
exp
(
m
/
kT
), где
m
- химический эквивалент. Параметр вырождения показывает классический или квантовый случай газа:
EF
/
kT
>1 – квантовая, <<1 – классическая.
2. Контактные явления в полупроводниках. P-n переход, его вольт-амперная характеристика.
Контактные явления в полупроводниках.
Если привести два разных полупроводника в соприкосновение, между ними возникает разность потенциалов, которая называется контактной. В результате в окружающем пространстве возникает электрическое поле. Контактная разность потенциалов обусловлена тем, что при соприкосновении поверхностей часть электронов переходит из одного полупроводника в другой.
Внешняя контактная разность потенциалов: 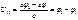 ; ;
Внутренняя разность потенциалов: 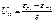 . .
p-n переход, его вольтамперная характеристика.
p-n переход – тонкий слой на границе между двумя областями одного и того же кристалла, отличающимися типом примесной проводимости.
В р-области основные носители тока – дырки (акцепторы становятся отрицательными ионами). В n-области – электроны, отданные донорами в зону проводимости.
 Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют друг с другом.→ меньше носителей и большое сопротивление p-n-перехода. Одновременно на границе между областями возникает двойной электрический слой, образованный отрицательными ионами акцепторной примеси, заряд которых не компенсируется дырками, и положительными ионами донорной примеси, заряд которых теперь не компенсируется электронами. Электрическое поле в этом слое направлено так, что противодействует дальнейшему переходу через слой основных носителей. Равновесие достигается при такой высоте потенциального барьера, при которой уровни Ферми обеих областей располагаются на одинаковой высоте. Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют друг с другом.→ меньше носителей и большое сопротивление p-n-перехода. Одновременно на границе между областями возникает двойной электрический слой, образованный отрицательными ионами акцепторной примеси, заряд которых не компенсируется дырками, и положительными ионами донорной примеси, заряд которых теперь не компенсируется электронами. Электрическое поле в этом слое направлено так, что противодействует дальнейшему переходу через слой основных носителей. Равновесие достигается при такой высоте потенциального барьера, при которой уровни Ферми обеих областей располагаются на одинаковой высоте.
В направлении от p-области к n-области p-n-переход пропускает ток, сила которого быстро нарастает при увеличении приложенного напряжения (прямое направление).
В обратном направлении p-n-переход обладает гораздо большим сопротивлением, чем в прямом. Поле, возникающее в кристалле при наложении обратного напряжения, «оттягивает» основные носители о границы между областями, что приводит к возрастанию ширины переходного слоя, обедненного носителями.
ВАХ p-n-перехода 
|
Билет 23
1.Дискретный испускания и поглощения электромагнитного излучения веществом. Формула Планка для равновесного твердого излучения.
Поместим абсолютно черное тело в куб с зеркальными стенками (отражающими). Равновесное тепловое излучение.
f
w
(
w
,
T
)=(
w
2
/4
p
2
c
2
)
e
,
e
- энергия на частоте
w
,
e
=(1/2)
kT
+(1/2)
kT
=
kT
. Гипотеза Планка состоит в том, что излучение испускается и поглощается порциями энергии (квант энергии).
E
=
h
n
,
h
=6,6*10-34
, Джс – постоянная Планка.
`
h
=
h
/2
p
=1,05*10-34
Джс,
E
=
`
h
w
. Дискретность:
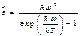
Формула Планка: 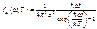
Замечания: R=òfw
(w,T)dw=sT4
Þ s=s(k,c,`h)=5,67*10-8
Вт/м2
Кл4
– постоянная Стефана-Больцмана. Закон Вина: fw
(w,T) Þ jl
(l,Т), djl
/dl=0 Ищем максимум: Þ lmax
=b/T, b= 2,9*10-3
м/Кл.
1. Примесная проводимость полупроводников. Концентрация основных и неосновных носителей в полупроводнике
n
-типа. Уровень Ферми примесного полупроводника
n
-типа. Температурная зависимость проводимости примесного полупроводника p-типа
Примесная проводимость полупроводников.
Примесная проводимость полупроводников возникает, если некоторые атомы данного полупроводника заменить в узлах кристаллической решетки атомами, валентность которых отличается на единицу от валентности основных атомов.
Концентрация основных и неосновных носителей в полупроводниках n-типа.
В полупроводнике с примесью, валентность которой на единицу больше валентности основных атомов, имеется только один вид носителей тока – электроны. Такой полупроводник обладает электронной проводимостью и является полупроводником n-типа. Атомы примеси, поставляющие электроны проводимости, называют донорами.
когда расстояние донорных уровней от дна зоны проводимости гораздо меньше запрещенной зоны, энергия теплового движения даже при обычных температурах оказывается достаточной для того, чтобы перевести электрон с донорного уровня в зону проводимости.
Уровень Ферми примесного полупроводника n-типа.
Уровень Ферми располагается в верхней половине запрещенной зоны.
 При повышении температуры уровень Ферми( При повышении температуры уровень Ферми(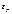 ) в полупроводниках обоих типов смещается к середине запрещенной зоны. ) в полупроводниках обоих типов смещается к середине запрещенной зоны.
Температурная зависимость проводимости примесного полупроводника n-типа.
При повышении температуры концентрация примесных носителей тока быстро достигает вершины. Это значит, что практически освобождаются все донорные или заполняются электронами все акцепторные уровни. По мере роста температуры все больше сказывается собственная проводимость полупроводника, обусловленная переходом электронов из валентной зоны в зону проводимости. → при высоких температурах проводимость полупроводника складывается из примесной и собственной проводимостей. При низких температурах преобладает примесная, а при высоких – собственная проводимость.
Билет 26-2
2. Зонная теория твёрдых тел. Структура зон в металлах, полупроводниках и диэлектриках.
Энергия валентных электронов в кристалле изменяется квазинепрерывно – спектр разрешенных значений энергии состоит из множества близкорасположенных дискретных уровней. В действительности валентные электроны в кристалле движутся не вполне свободно – на них действует периодическое поле решетки, что приводит к тому, что спектр возможных значении энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. В пределах разрешенных зон энергия изменяется квазинепрерывно. Значения энергии, принадлежащие запрещенным зонам, не могут реализоваться.
Валентной зоной (в случае металла ее также называют зоной проводимости) называют разрешенную зону, возникшую уровня, на котором находятся валентные электроны в основном состоянии атома.
Структура зон в металлах, полупроводниках и диэлектриках.

Разрешенную зону, возникшую из того уровня, на ктр. находятся валентные э-ны в осн. состоянии атома будем называть валентной зоной. В случае металла электроны заполняют валентную зону неполностью, поэтому достаточно сообщить э-нам, находящимся на верхних уровнях, совсем небольшую энергию(10-22 эВ), чтобы перевести их на более высокие уровни. В случаях полупроводника и диэлектрика уровни валентной зоны полностью заняты электронами. Для того чтобы увеличить энергию э-на необходимо сообщить ему кол-во энергии не меньшее, чем ширина запрещенной зоны. Электрическое поле сообщить такую энергии э-ну не в состоянии. Если эта ширина невелика (неск. десятых эВ), то энергии теплового движения оказывается достаточно для перевода части э-нов в верхнюю свободную зону. Эти э-ны будут нах-ся в усл-ях аналогичных тем, в ктр. находятся валентные э-ны в металле. Свободная зона окажется для них зоной проводимости. Одновременно станет возможным переход э-нов вал. зоны на ее освободившиеся верхние уровни. Такое в-во – полупроводник. Если ширина запрещенной зоны порядка неск. эВ, тепловое движение не сможет забросить в своб. зону заметное число э-нов. В этом случае кристалл – диэлектрик.
|
Билет 24
1. Зонная теория твердых тел. Структура зон в металлах, полупроводниках и диэлектриках.
В основе зонной теории лежит так называемое адиабатическое приближение. Квантово-механическая система разделяется на тяжелые и легкие частицы- ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать. Что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер. Далее используем приближение самосогласованного поля. Взаимодействие данного электрона со всеми другими заменяется действием на него стационарного эл.поля, обладающего периодичностью кристалл.решетки. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер. Пока атомы изолированы, т.е. находятся друг от друга на макроскопических расстояниях, они имеют совпадающие схемы энергетических уровней. (см.рис). По мере сжатия нашей модели до кристал.решетки, т.е. когда расстояния между атомами станут равными межатомным, взаимодействие между атомами приводит к тому, что энергетические уровни атомов смещаются, расщепляются и расширяются
, образуется зонный энергетический спектр.
Образование зонного энергетического спектра в кристалле является квантово-механическим дефектом и вытекает из соотношения неопределенностей. В кристалле валентные электроны атомов, связанные слабее с ядрами, чем внутренние электроны, могут переходить от атома к атому сквозь потенциальные барьеры, разделяющие атомы, т.е. перемещаться без изменения потенциальной энергии (туннельный эффект).
Энергия внешних может принимать значения в пределах закрашенных областей (см.рис), называемых разрешенными энергетическими зонами. Разрешенные энергетические зоны разделяются зонами запрещенных значений энергии, называемые запрещенными энергетическими зонами.
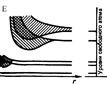 
2. Ядерная модель атома. Постулаты Бора.
На основании своих исследований Резерфорд в 1991г. предположил ядерную (планетарную) модель атома. Вокруг положительного ядра, имеющего заряд
Ze
(
Z
- порядковый номер элемента, е-элементарный заряд), размер 10-15
-10-14
м и массу, практически равной массе атома, в области с линейными размерами порядка 10-10
м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома.
Первый постулат Бора (постулат для стационарных состояний): в атоме существуют стационарные состояния( не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарные состояния атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов сопровождается излучением электромагнитных волн. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантовые значения момента импульса, удовлетворяющие условию
me
vrn
=ħ
n
(
n
=1,2,3…) где
me
-масса электрона,
v
-его скорость по
n
-орбите радиуса
rn
,ħ=
h
/(2
π
)
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
hv
=
En
-
Em
равной разности энергий соответствующих стационарных состояний (
En
и
Em
– соответственно энергии стационарных состояний атома до и после излучения(поглощения). При
Em
<
En
происходит излучение фотона, при
Em
>
En
- его поглощение.
|
|