| Федеральное агентство по образованию.
Государственное образовательное учреждение
высшего профессионального образования
Московский государственный индустриальный университет.
(ГОУ МГИУ)
Кафедра №24 «Бухгалтерского учета, анализа и аудита»
Курсовая работа по статистике
на тему: «Статистическое изучение производительности труда на предприятии»
Ф.И.О. студента: Шленкина Н.Ю.
Номер группы: 4261
Научный руководитель: к.э.н., доцент
Виноградова Е.П.
Москва 2010 г.
Содержание
Введение.......................................................................................................... 3
1. Понятие производительности труда и задачи ее статистического изучения с использованием методов общей теории статистики...................................... 4
2. Расчет показателей выработки продукции и анализ их в динамике........ 6
3. Применение графического метода в анализе выполнения плана и динамики производительности труда........................................................................... 11
4. Факторный индексный анализ производительности труда.................... 12
5. Проведение корреляционного анализа влияния производительности труда на результаты деятельности предприятия........................................................ 19
Заключение.................................................................................................... 30
Список использованной литературы........................................................... 32
Введение
Промышленность - важнейшая отрасль материального производства, в которой создаются все орудия труда и преобладающая часть предметов труда, используемых в других отраслях производственной сферы (в строительстве, сельском хозяйстве и др.). Велика роль промышленности и в создании предметов потребления, т. к. в ходе общественного прогресса все большая частъ потребительских благ подвергается промышленной переработке до того, как поступает в сферу личного и общественного потребления.
Предметом статистики промышленности являются массовые экономические явления, происходящие в промышленности. Статистика промышленности изучает эти явления с количественной стороны.
Главными задачами статистики промышленности являются следующие:
1. Всесторонняя характеристика и анализ деятельности предприятий с использованием современных статистических методов.
2. Оценка эффективности промышленного производства.
3. Выявление внутрипроизводственных резервов и факторов дальнейшего развития промышленного производства.
Производительность труда является одним из важнейших качественных показателей работы предприятия, выражением эффективности затрат труда.
Целью анализа производительности труда является выявление возможностей дальнейшего увеличения выпуска продукции за счет роста производительности труда, более рационального использования работающих и их рабочего времени.
Исходя из указанных целей выделяют, следующие задачи статистического изучения производительности труда в промышленности:
1. измерение уровня производительности труда;
2. изучение выполнения плана и динамики производительности труда;
3. определение степени выполнения норм выработки рабочими;
4. анализ уровня и динамики производительности труда - изучение факторов производительности труда и выявления резервов ее дальнейшего повышения;
5. анализ взаимосвязи производительности труда с другими экономическими показателями, характеризующими результаты работы предприятия.
1. Понятие производительности труда
и показатели производительности труда
Под производительностью труда
(ПТ) понимается его способность производить в единицу рабочего времени определенное количество продукции (работ, услуг) или затрачивать определенное количество времени на производство единицы продукции (работ, услуг).
Рост ПТ определяется либо увеличением выпуска продукции за счет экономии рабочего времени, либо снижением числа работников, занятых производством продукции (работ, услуг).
Прямой величиной производительности труда является показатель выработки:
 , где , где
W – выработка продукции в единицу рабочего времени;
q – выпуск продукции;
T – затраты труда (чел.-часы; чел.-дни; средняя списочная численность рабочих или ППП).
Обратной величиной производительности труда является показатель трудоемкости:
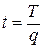 , где , где
T – затраты труда (чел.-часы);
t – трудоемкость изготовления единицы продукции;
q – выпуск продукции.
Покажем расчет прямых и обратных величин производительности труда по данным таблицы 1.1.
Таблица 1.1
Данные для расчета показателей выработки и трудоемкости
| Показатели
|
Условные
обозначения
|
Базисный период
|
Отчетный период
|
Темп роста,
%
|
| Изготовлено деталей, тыс. шт.
|
q
|
195990
|
210155
|
107,3
|
| Затраты труда,
чел.-час.
|
T
|
29211067
|
31093811
|
106,4
|
| Средняя часовая выработка, шт.
|
W
|
0,0067
|
0,0068
|
101,5
|
| Трудоемкость изготовления одной детали, час.
|
t
|
149,04
|
148
|
99,3
|
Показатели выработки за базисный и отчетный периоды соответственно составили:
 шт.; шт.;
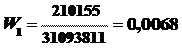 шт. шт.
Показатели трудоемкости соответственно составили:
t
0
= 29211067/ 195990 = 149,04 час.;
t
0
=31093811/ 210155=148 час.
Показатели выработки и трудоемкости взаимосвязаны. Если W0
= 0,0067 то  ; если ; если  то то 

Рис. 1.1. Динамика средней часовой выработки предприятия

Рис. 1.2. Динамика трудоемкости изготовления одной детали
2. Расчет показателей выработки продукции и анализ их в динамике
Абсолютные и относительные статистические величины
Под абсолютными величинами в статистике понимают показатели, которые характеризуют размеры (уровни, объемы изучаемых экономических явлений). Например, объем товарной продукции предприятия, численность промышленно-производственного персонала, размер прибыли и др.
Абсолютные величины в статистике являются исходной базой статистического анализа. Различают индивидуальные и суммарные (итоговые) абсолютные величины. Индивидуальные величины характеризуют конкретную единицу совокупности. Суммарные величины (итоговые) характеризуют всю изучаемую совокупность. Так, абсолютной индивидуальной величиной можно считать, например, выработку конкретного рабочего; суммарной величиной будет являться объем произведенной продукции исследуемой совокупности рабочих.
Абсолютные величины измеряются в натуральных, условно-натуральных и стоимостных единицах. Натуральные величины выражаются в кг, шт., чел. и т.п. При использовании условно-натуральных единиц за условную единицу принимается какая-либо величина, а другие представители данного вида показателей соизмеряются с условной единицей через коэффициенты.
Стоимостные единицы измерения абсолютных величин выражаются в рублях.
В отличие от абсолютных величин, относительные величины являются величинами производными и рассчитываются на основе абсолютных.
В статистическом анализе рассчитывают следующие виды относительных величин: величины динамики, величины выполнения плана, величины планового задания, величины структуры, величины координации, величины интенсивности, величины сравнения.
Относительные величины динамики
– показатели, характеризующие соотношение одноименных величин во времени.

Частное от деления числителя и знаменателя дроби – коэффициент динамики. Коэффициент динамики, выраженный в % – темп роста.
Проведем расчет относительных величин динамики по данным табл. 2.1.
Таблица 2.1
Расчет относительных величин динамики по данным выпуска товарной продукции на промышленных предприятиях
| Предприятие
|
Периоды
|
Товарная продукция
млн у.е.
|
Относительные величины динамики
|
| в коэффициентах
|
в %
|
| №1
|
Базисный
|
14141
|
1,000
|
100
|
| Отчетный
|
14395
|
1,018
|
101,8
|
| №2
|
Базисный
|
25794
|
1,000
|
100
|
| Отчетный
|
23120
|
0,896
|
89,6
|
| №3
|
Базисный
|
81649
|
1,000
|
100
|
| Отчетный
|
86286
|
1,057
|
105,7
|
| №9
|
Базисный
|
195990
|
1,000
|
100
|
| Отчетный
|
210155
|
1,072
|
107,2
|
Вычислим относительные величины динамики с постоянной базой сравнения, приняв за базу сравнения базисный период:





Рис. 2.1. Динамика относительных величин динамики на предприятиях.
Вывод: за рассматриваемый период у всех предприятий, кроме предприятия №2, наблюдается увеличение продукции. Это подтверждают расчетные значения темпов роста, которые превышают 100%. Наиболее значительное увеличение продукции у предприятия №9 – на 7,2% (107,2-100). А у предприятия №2 произошло снижение продукции – на 10,4% (89,6-100).
Относительные величины выполнения плана
– показатели, характеризующие степень выполнения планового задания.

Рассмотрим расчет показателей выполнения плана по данным табл. 2.2.
Таблица 2.2
Расчет относительных величин выполнения плана
и планового задания по данным выпуска продукции на предприятиях
| Предприятие
|
Выпуск продукции, млн. у.е.
|
Процент выполнения плана
|
Процент планового задания
|
| Базисный период
|
Отчетный период
|
| план
|
факт
|
| №1
|
14141
|
14300
|
14395
|
100,7
|
101,1
|
| №2
|
25794
|
24010
|
23120
|
96,3
|
93,1
|
| №3
|
81649
|
85000
|
86286
|
101,5
|
104,1
|
| №9
|
195990
|
208690
|
210155
|
100,7
|
99
,3
|
Вычислим показатели выполнения плана по каждому из предприятий:
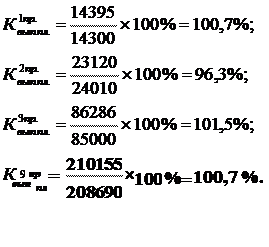
Вывод: более высокий процент перевыполнения плана по выпуску продукции приходится на предприятие №3 – 101,5%. Менее всего был перевыполнен план на предприятии №1 и №9 – на 0,7% (100,7-100). А на предприятии №2 план по выпуску продукции был не выполнен – 96,3%.
Относительные величины планового задания
– показатели, характеризующие степень установления планового задания на отчетный период.

Рассмотрим расчет относительных показателей планового задания по данным таблицы 2.2:




Вывод: более высокий процент установления планового задания приходится на предприятие №3 – 104,1%, в то время как на предприятие №1– 101,1%, №2 – 93,1%, №9 – 99,3%.

Рис. 2.2. Динамика относительных показателей выполнения плана
и планового задания на предприятиях
3. Применение графического метода в анализе выполнения плана и динамики производительности труда
Графики являются средством обобщения и анализа статистических данных.
Графиками в статистике называют условные изображения числовых величин и их соотношений в виде различных геометрических фигур.
С помощью графиков решаются следующие задачи:
- выявляются основные тенденции развития экономических явлений;
- выявляются взаимные связи между явлениями.
При построении графиков (диаграмм) в системе прямоугольных координат необходимо придерживаться следующих правил:
1. Каждый график должен иметь название, которое располагают под ним. В названии в краткой форме следует отразить содержание, место и время явления. Все графики нумеруются.
2. Оси координат должны быть названы и иметь единицы измерения.
3. На числовой оси следует откладывать только целые числа и в равном масштабе (например: 20; 40; 60 и т.д., или 1500; 3000; 4500 и т.д.). Заканчиваться числовая ось должна той величиной, которая немногим больше максимальной величины в исходной совокупности.
4. Если на одной числовой оси необходимо расположить величины, относящиеся к одному и тому же явлению, но резко отличающиеся друг от друга по абсолютному значению, числовую ось можно разорвать знаком (≈), что означает разрыв масштаба.
5. Если необходимо отразить на одном графике (в одной системе прямоугольных координат) два-три явления, то вводят столько же дополнительных числовых осей (осей ординат). Каждая числовая ось должна иметь свою размерность и свой масштаб.
Графики различают по содержанию изображаемых статистических показателей. Изображают следующие виды графиков:
- графики сравнения;
- графики динамики;
- графики структуры;
- графики выполнения плана;
- графики вариационных рядов;
- графики взаимосвязанных показателей.
По видам и способам построения выделяют:
- столбиковые;
- ленточные;
- линейные;
- квадратные;
- круговые;
- секторные диаграммы;
Далее рассмотрим один из видов графиков и соответствующий ему способ графического изображения статистических данных на конкретном примере.
График сравнения. Для построения этого вида графиков используют столбиковые, ленточные, квадратные и круговые диаграммы.
Таблица3.1.
Товарная продукция в фиксированных оптовых ценах предприятия.
| предприятия
|
№1
|
№2
|
№3
|
№9
|
| Товарная продукция
|
14395
|
23120
|
86286
|
210155
|

Рис. 3.1. Товарная продукция в фиксированных оптовых ценах предприятия.
4. Факторный индексный анализ
производительности труда
В практике статистики на промышленном предприятии рассчитывают следующие показатели выработки в зависимости от затрат труда на производство продукции: средняя часовая выработка рабочего, средняя дневная выработка рабочего, средняя месячная (квартальная, годовая) выработка рабочего и средняя месячная (квартальная, годовая) выработка работника промышленно-производственного персонала (ППП).
Взаимосвязь показателей средней выработки представлена на схеме 4.1.
| Средняя месячная (квартальная, годовая) выработка работника ППП (W)
|
=
|
Средняя часовая выработка рабочего (а)
|

|
Средняя продолжительность рабочего дня (b)
|

|
Среднее число дней работы рабочего за месяц (квартал, год) (с)
|

|
Доля рабочих в численности ППП (d)
|
Схема 4.1. Взаимосвязь показателей средней выработки
Используя индексный метод анализа, можно определить влияние в рассмотренных в схеме 3.1 факторов-сомножителей на динамику (изменение) средней месячной (квартальной, годовой) выработка работника промышленно-производственного персонала в отчетном периоде по сравнению с базисным.
Так как W=abcd, то:

 = = 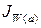  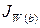  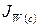  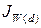
Частное от деления числителя и знаменателя дробей характеризует процентное изменение средней месячной (квартальной, годовой) выработки работника промышленно-производственного персонала под влиянием соответствующего фактора (a, b, c, d).
Разность числителя и знаменателя дробей характеризует абсолютное изменение (в стоимостном выражении) средней месячной (квартальной, годовой) выработки работника промышленно-производственного персонала под влиянием соответствующего фактора (a, b, c, d).
Рассмотрим пример расчета приведенных индексов по данным таблицы 3.1.
Таблица 4.1
Динамика средней годовой выработки
под влиянием различных факторов
| Показатели
|
Единицы
измерения
|
Условные
обозначения
|
Базисный
год
|
Отчетный
год
|
| Товарная продукция в фиксированных оптовых ценах предприятия
|
тыс. у.е.
|
Q
|
195990
|
210155
|
| Средняя списочная численность ППП
в том числе рабочих
|
чел.
чел.
|


|
19386
15624
|
20637
16698
|
| Отработано рабочими человеко-дней
|
чел.-дн.
|
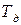
|
3731382
|
3971208
|
| Отработано рабочими человеко-часов
|
чел.-час.
|
|
29211067
|
31093811
|
| Средняя часовая выработка рабочего
|
тыс. у.е.
|

|
6,709
|
6,76
|
| Средняя продолжительность рабочего дня
|
час
|

|
7,828
|
7,829
|
| Среднее число дней работы одного рабочего
за год
|
дн.
|

|
238,82
|
237,83
|
| Доля рабочих в численности ППП
|
|

|
0,806
|
0,809
|
| Средняя годовая выработка работника ППП
|
тыс. у.е.
|
W=abcd
|
10109,1
|
10182,8
|
Общее изменение средней годовой выработки работника ППП в отчетном периоде по сравнению с базисным за счет влияния всех факторов (a, b, c, d) составит:

Изменение средней годовой выработки работника ППП за счет фактора (а), то есть средней часовой выработки, составит:
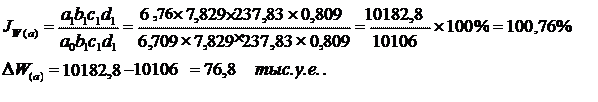 
Изменение средней годовой выработки работника ППП за счет фактора (b), то есть средней продолжительности рабочего дня, составит:
 
Изменение средней годовой выработки работника ППП за счет фактора (с), то есть среднего числа дней работы одного рабочего за год, составит:
  Изменение средней годовой выработки работника ППП за счет фактора (d), то есть доли рабочих в численности ППП, составит:
 

Рис. 4.1. Динамика средней годовой выработки под влиянием различных факторов
Правильность проведенных расчетов подтверждает следующие т6,ождества:
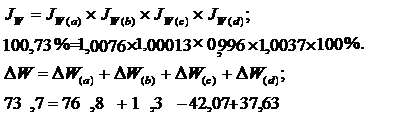
Вывод: средняя годовая выработка работника в отчетном периоде по сравнению с базисным повысилась на 0,73% (100,73%-100%), или на 73,7 тыс. у.е., в том числе:
- за счет увеличения средней часовой выработки рабочего на 0,76% (100,76%-100%) средняя годовая выработка работника увеличилась на 76,8 тыс. у.е.;
- за счет увеличения средней продолжительности рабочего дня на 0,013% (100,013%-100%) средняя годовая выработка работника увеличилась на 1,3 тыс. у.е.;
- за счет снижения среднего числа дней работы одного рабочего за год на 0,4% (99,6%-100%) средняя годовая выработка работника снизилась на 42,07 тыс. у.е.;
- за счет увеличения доли рабочих в численности ППП на 0,37% (100,37%-100%) средняя годовая выработка работника повысилась на 37,63 тыс. у.е.
Таким образом, несмотря на негативное влияние фактора «c» влияние факторов «а», «b» и «d» оказалось решающим, вследствие чего произошло в целом повышение средней годовой выработки работника в отчетном периоде по сравнению с базисным.
Для измерения динамики производительности труда в практике статистики используют три метода: натуральный, трудовой и стоимостной.
Натуральный
метод применяется для измерения динамики производительности труда при условии выпуска одноименной и сравнимой с базисным периодом продукции.
Натуральный метод наиболее точный, поскольку учет продукции ведется в натуральных единицах измерения: штуках, метрах, тоннах и т.п. Уровень производительности труда выражается количеством штук, метров, тонн, произведенных в единицу времени:
Достоинством данного метода является простота расчета, объективность измерения уровня ПТ. Однако сфера применения этого метода весьма ограничена: он может быть использован для анализа динамики ПТ и сравнения ее уровня по бригадам, участкам, предприятиям, в отраслях, где производится однородная продукция или ведется учет затрат рабочего времени по каждому виду производимой продукции. Наиболее широкое применение этот метод получил в добывающих отраслях промышленности.
Индекс производительности труда в этом случае определяется по формуле:
 , где , где
 и и  - выработка продукции соответственно в отчетном и базисном периодах, шт., кг и т.п. - выработка продукции соответственно в отчетном и базисном периодах, шт., кг и т.п.
Трудовой
метод применяется для измерения динамики производительности труда при условии изготовления разноименной, но сравнимой с базисным периодом продукции. Индекс производительности труда определяется по следующей формуле:
 , где , где
 - продукция отчетного периода, шт.; - продукция отчетного периода, шт.;
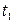 и и 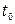 - трудоемкость изготовления единицы продукции соответственно в отчетном и базисном периодах, час. - трудоемкость изготовления единицы продукции соответственно в отчетном и базисном периодах, час.
Трудовой метод измерения динамики производительности труда более широко применим, чем натуральный, так как предусматривает выпуск многономенклатурной, сравнимой с базисным периодом продукции.
Стоимостной
метод применяется для измерения динамики производительности труда, когда учитывается вся продукция предприятия, а не только сравнимая с базисным периодом. Стоимостной метод можно считать универсальным для измерения динамики производительности труда.
Индекс производительности труда в этом случае определяется по формуле:
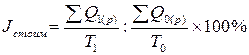 , где , где
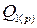 и и  - объем продукции в фиксированных оптовых ценах предприятия соответственно за отчетный и базисный периоды; - объем продукции в фиксированных оптовых ценах предприятия соответственно за отчетный и базисный периоды;
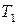 и и 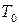 - затраты труда на производство продукции (чел.-часы; чел.-дни; средняя списочная численность рабочих или ППП). - затраты труда на производство продукции (чел.-часы; чел.-дни; средняя списочная численность рабочих или ППП).
Определим по данным таблицы 1.1 индексы производительности труда по натуральному и трудовому методам, а по данным таблицы 4.1 – индекс производительности труда по стоимостному методу.
Тогда индексы соответственно составят:
- по натуральному методу:
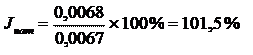 ; ;
- по трудовому методу: 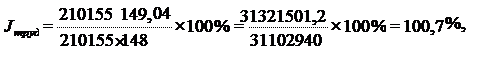
- по стоимостному методу:
индекс часовой выработки рабочих:

индекс дневной выработки рабочих:
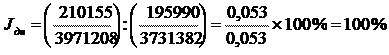
индекс годовой выработки рабочего:

индекс годовой выработки работника ППП:

Важным вопросом в изучении производительности труда на промышленном предприятии является определение степени выполнения норм выработки. Существует 4 способа определения степени выполнения норм выработки рабочими:
1) сопоставлением фактической выработки ( ) с установленной по норме ( ) с установленной по норме ( ); );
2) сопоставлением нормативной трудоемкости (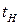 ) с фактической трудоемкостью ( ) с фактической трудоемкостью (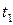 ); );
3) сопоставлением общего количества выработанной продукции ( ) с тем ее количеством, которое могло быть выработано за то же время при установленной норме выработки ( ) с тем ее количеством, которое могло быть выработано за то же время при установленной норме выработки ( ); );
4) сопоставлением количества рабочего времени, положенного по норме на фактически выработанную продукцию ( ), с фактически затраченным временем на ту же продукцию ( ), с фактически затраченным временем на ту же продукцию (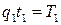 ). ).
5. Проведение корреляционного анализа влияния производительности труда на результаты деятельности предприятия
При изучении взаимосвязей между экономическими явлениями выделяют факторные и результативные признаки. Факторным признаком является тот, который влияет и обуславливает изменение результативного признака. Результативный признак - тот, который изменяется под влиянием факторного признака.
Различают два вида взаимосвязей экономических явлений: функциональные и корреляционные.
При функциональных связях каждому значению факторного признака соответствует вполне определенное значение результативного признака, Функциональные связи можно формализовать, т.е. представить в виде формулы.
При функциональных связях применяется индексный метод анализа.
При корреляционных связях отдельным значениям факторного признака может соответствовать несколько значений результативного признака. Корреляционная связь проявляется в среднем при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и факторным признаком.
При корреляционных связях применяется корреляционный метод анализа.
Связи между явлениями бывают прямые и обратные. При прямых связях с увеличением (уменьшением) факторного признака результативный увеличивается (уменьшается).
В прямой зависимости находится, например, объем выпуска продукции от производительности труда или коэффициента сменности. При обратных связях с увеличением (уменьшением) факторного признака результативный уменьшается (увеличивается). В обратной зависимости находится, например, объем выпуска продукции от величины простоев оборудования, от текучести рабочих кадров и т.п.
По аналитическому выражению связи бывают прямолинейные и криволинейные. Прямолинейные связи выражают уравнением прямой. Криволинейные связи выражают уравнением параболы или гиперболы.
Корреляционный метод анализа взаимосвязи экономических явлений проводят в три этапа.
Прежде чем подробно остановится на каждом из трех этапов корреляционного анализа, обратим внимания на следующее.
В том случае, когда определяется влияние одного фактора на результативный признак, строится однофакторная регрессионная модель (парное уравнение корреляции); когда определяется влияние двух и более факторов на результативный признак - строится многофакторная регрессионная модель (уравнение множественной корреляции).
При подборе факторов для регрессионной модели следует помнить, что факторы не должны находиться в функциональной связи с результативным признаком. В противном случае должен применяться индексный метод анализа, а не корреляционный. Число наблюдений для построения однофакторной регрессионной модели должно быть не менее 10 - 12.
Первый этап корреляционного анализа.
Для определения формы связи между факторным и результативным признаками, т.е. для установления типа аналитической функции связи применяют различные статистические методы. Так, характер и направление связи между изучаемыми экономическими явлениями можно установить, применяя метод статистических группировок. С помощью данного метода наличие связи между явлениями устанавливается визуально.
Для выявления тенденции изменения результативного признака при изменении факторного могут использоваться такие статистические методы, как метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания. Чаще всего для установления формы зависимости между факторным и результативным признаками применяют графический метод.
При прямолинейной форме зависимости между факторным и результативным признаками функция связи имеет вид прямой:  при параболической форме - имеет вид параболы: при параболической форме - имеет вид параболы:  при гиперболической форме - вид гиперболы: при гиперболической форме - вид гиперболы: 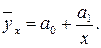
На втором этапе корреляционного анализа
осуществляют решение аналитического уравнения связи путем нахождения его параметров 
Параметр  означает влияние на результативный признак не включенных в регрессионную модель факторов. Как правило, экономической интерпретации параметр означает влияние на результативный признак не включенных в регрессионную модель факторов. Как правило, экономической интерпретации параметр  не подлежит. Параметры не подлежит. Параметры 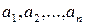 - коэффициенты регрессии, означают величину результативного признака при изменении факторного признака на единицу измерения. - коэффициенты регрессии, означают величину результативного признака при изменении факторного признака на единицу измерения.
В случае прямолинейной формы зависимости параметры аналитического уравнения связи  находятся путем решения следующей системы уравнений: находятся путем решения следующей системы уравнений:
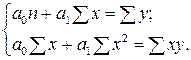
В случае параболической формы зависимости параметры аналитического уравнения связи 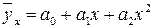 находятся путем решения следующей системы уравнений: находятся путем решения следующей системы уравнений:

В случае гиперболической формы зависимости параметры аналитического уравнения связи  находятся путем решения следующей системы уравнений: находятся путем решения следующей системы уравнений:

Для экономической интерпретации аналитического уравнения связи можно воспользоваться также коэффициентом эластичности:

Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного на 1%..
На третьем этапе корреляционного анализа
осуществляют оценку тесноты связи между факторным и результативным признаками с помощью показателей тесноты связи.
В случае линейной связи между факторным и результативным признаками производят расчеты линейного коэффициента корреляции по формуле:

Линейный коэффициент корреляции варьирует в пределах от -1 до +1. Положительное его значение говорит о прямой связи, отрицательное – об обратной. Близость к нулю говорит о слабой связи, близость к ±1 говорит о существенной связи, при r
= ±1 – связь функциональная.
Для экономической интерпретации линейного коэффициента корреляции применяется коэффициент детерминации:

Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую влиянием соответствующего факторного признака.
В случае криволинейной зависимости (параболической, гиперболической) тесноту связи между факторным и результативным признаками определяют с помощью корреляционного отношения:

Рассмотрим на конкретном примере применение корреляционного метода в изучении взаимосвязи экономических явлений.
Проведем корреляционный анализ влияния производительности труда на динамику рентабельности предприятия.
Определим влияние производительности труда на динамику рентабельности предприятия. Для этого сначала рассчитаем рентабельность каждого предприятия по данным таблицы 5.1.
Таблица 5.1
Данные для расчета рентабельности предприятия
| Предприятие
|
Балансовая прибыль,
у.е.
|
Средняя годовая стоимость основных производственных фондов,
у.е.
|
| №2
|
2452
|
20613
|
| №4
|
12413
|
50829
|
| №6
|
16683
|
37887
|
| №8
|
13153
|
64018
|
| №10
|
4362
|
19928
|
| №12
|
1226
|
10306,5
|
| №14
|
6206,5
|
25414,5
|
| №16
|
8341,5
|
18943,5
|
| №18
|
6576,5
|
32009
|
| №20
|
2181
|
9964
|
| №9
|
13450
|
148192
|
Рентабельность составит:
1 для предприятия №2:  ; ;
2 для предприятия №4:  ; ;
3 для предприятия №6: 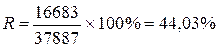 ; ;
4 для предприятия №8:  ; ;
5 для предприятия №10:  ; ;
6 для предприятия №12:  ; ;
7 для предприятия №14:  ; ;
8 для предприятия №16:  ; ;
9 для предприятия №18:  ; ;
10 для предприятия №20: 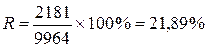 . .
11
для предприятия №9:

Одним из показателей измерения производительности труда является показатель выработки продукции. Рассчитаем показатели выработки для каждого предприятия по данным таблицы 5.2.
Таблица 5.2
Данные для расчета выработки продукции
| Предприятие
|
Товарная продукция,
млн. у.е.
|
Затраты труда,
чел.-час.
|
| №2
|
23120
|
3964008
|
| №4
|
103099
|
8471945
|
| №6
|
89329
|
11753403
|
| №8
|
97097
|
14633487
|
| №10
|
36544
|
3283597
|
| №12
|
11560
|
1982454
|
| №14
|
51549
|
4235973
|
| №16
|
44664
|
5876702
|
| №18
|
48549
|
7316744
|
| №20
|
18272
|
1641799
|
| №9
|
210155
|
31093811
|
Показатель средней часовой выработки составит:
для предприятия №2:  тыс. у.е.; тыс. у.е.;
для предприятия №4:  тыс. у.е.; тыс. у.е.;
для предприятия №6: 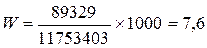 тыс. у.е.; тыс. у.е.;
для предприятия №8:  тыс. у.е.; тыс. у.е.;
для предприятия №10:  тыс. у.е.; тыс. у.е.;
для предприятия №12: 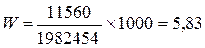 тыс. у.е.; тыс. у.е.;
для предприятия №14:  тыс. у.е.; тыс. у.е.;
для предприятия №16:  тыс. у.е.; тыс. у.е.;
для предприятия №18:  тыс. у.е.; тыс. у.е.;
для предприятия №20:  тыс. у.е. тыс. у.е.
для предприятия №9:  тыс. у.е. тыс. у.е.
Полученные результаты по рентабельности и по средней часовой выработки занесем в таблицу 5.3:
Таблица 5.3
Показатели рентабельности и средней часовой выработки
| Предприятие
|
Рентабельность, %
|
Средняя часовая выработка, тыс. у.е.
|
| №2
|
11,9
|
5,83
|
| №4
|
24,42
|
12,17
|
| №6
|
44,03
|
7,6
|
| №8
|
20,55
|
6,64
|
| №10
|
21,89
|
11,13
|
| №12
|
11,9
|
5,83
|
| №14
|
24,42
|
12,17
|
| №16
|
44,03
|
7,6
|
| №18
|
20,55
|
6,64
|
| №20
|
21,89
|
11,13
|
| №9
|
9,08
|
6,76
|
| Итого:
|
254,66
|
93,5
|
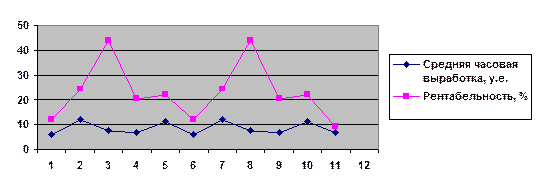
Рис. 5.1. Зависимость рентабельности предприятия
от выработки рабочего
Используя графический метод, по данным таблицы 5.3 определим форму зависимости рентабельности предприятия от средней часовой выработки.
Судя по распределению, зависимость прямолинейная.
Для решения соответствующей системы уравнений построим вспомогательную таблицу 5.4.
Таблица 5.4
| Предприятие, №
|
Выработка,
тыс. у.е. (х)
|
Рентабельность, %
(у)
|
Х*У
|
Х2
|
У2
|
__
УХ
|
| 2
|
5,83
|
11,90
|
69,38
|
33,99
|
141,61
|
20,775
|
| 12
|
5,83
|
11,90
|
69,38
|
33,99
|
141,61
|
20,775
|
| 8
|
6,64
|
20,55
|
136,45
|
44,09
|
422,30
|
21,5
|
| 18
|
6,64
|
20,55
|
136,45
|
44,09
|
422,30
|
21,5
|
| 6
|
7,60
|
44,03
|
334,63
|
57,76
|
1938,64
|
22,345
|
| 16
|
7,60
|
44,03
|
334,63
|
57,76
|
1938,64
|
22,345
|
| 10
|
11,13
|
21,89
|
243,64
|
123,88
|
479,17
|
25,5
|
| 20
|
11,13
|
21,89
|
243,64
|
123,88
|
479,17
|
25,5
|
| 4
|
12,17
|
24,42
|
297,19
|
148,11
|
596,34
|
26,4
|
| 14
|
12,17
|
24,42
|
297,19
|
148,11
|
596,34
|
26,4
|
| 9
|
6,76
|
9,08
|
61,38
|
45,7
|
82,45
|
21,6
|
| Итого
|
93,5
|
254,66
|
2223,96
|
861,36
|
7238,57
|
254,66
|
На основе данных таблицы 5.4 имеем систему уравнений:
_ _
a0
= y – a1
*x
___ _ _ _ _
a1
=(x*y – x * y)/((x2
) – (x) 2
_
x=8.5
_
y=23.15
___
x*y=202.2
_
(x2
)=78.31
_
(x) 2
=72.25
_ _
x * y = 196.8
_
(y2
)=658.05
_
(y) 2
=535.9
a0
= 23.15 – a1
*8.5
a1
=(202.2 – 196.8)/(78.31 – 72.25) = 0.89
a1
= 0.89
a0
= 15.585
Таким образом, найденное аналитическое уравнение связи имеет вид:
 Подставим соответствующие значения x в уравнение и найдем значения Подставим соответствующие значения x в уравнение и найдем значения  : :
yx1
= 15.585+0.89*5.83=20.775
yx2
= 15.585+0.89*5.83=20.775
yx3
= 15.585+0.89*6.64=21.5
yx4
= 15.585+0.89*6.64=21.5
yx5
= 15.585+0.89*7.6=22.345
yx6
= 15.585+0.89*7.6=22.345
yx7
= 15.585+0.89*11.13=25.5
yx8
= 15.585+0.89*11.13=25.5
yx9
= 15.585+0.89*12.17=26.4
yx10
= 15.585+0.89*12.17=26.4
yx
11
= 15.585+0.89*6.76=21.6
Изобразим по найденным значениям 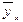 теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 5.1). теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 5.1).
Так как  , то можно считать, что построенное парное уравнение корреляции является искомым. , то можно считать, что построенное парное уравнение корреляции является искомым.
Вывод: с увеличением средней часовой выработки рабочего на 1 тысячу у.е. рентабельность предприятия в среднем возрастает на 0,89.
Для экономической интерпретации аналитического уравнения связи воспользуемся коэффициентом эластичности, который рассчитывается по формуле:

Вывод: увеличение средней часовой выработки рабочего на 1% приводит к увеличению рентабельности предприятия на 0,356%.
Рассчитаем величину линейного коэффициента корреляции для установления тесноты связи между производительностью труда и рентабельностью предприятия:


Вывод: рентабельность предприятия на 19.85% зависит от средней часовой выработки рабочего на предприятии.
Для установления размера вариации рентабельности предприятия от выработки рабочего рассчитаем коэффициент детерминации:
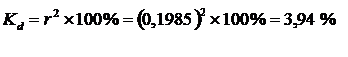
Вывод: на 3.94% вариация рентабельности предприятия объясняется изменением средней часовой выработки рабочего.
Заключение.
Повышение производительности труда - один из объективных экономических законов, присущих каждой общественно-экономической формации. Этот закон выражается в том, что благодаря развитию производительных сил общество сокращает общественно необходимые затраты труда на изготовление различных продуктов, предназначенных для личного или общественного потребления. По мере накопления людьми опыта, знаний, раскрытия законов природы, овладения ими и их использования происходит последовательное повышение производительности труда.
Так, в результате проведенного анализа был сделан вывод, что средняя годовая выработка работника в отчетном периоде по сравнению с базисным повысилась на 0,73% (100,73%-100%), или на 73,7 тыс. у.е., в том числе:
- за счет увеличения средней часовой выработки рабочего на 0,76% (100,76%-100%) средняя годовая выработка работника увеличилась на 76,8 тыс. у.е.;
- за счет увеличения средней продолжительности рабочего дня на 0,013% (100,013%-100%) средняя годовая выработка работника увеличилась на 1,3 тыс. у.е.;
- за счет снижения среднего числа дней работы одного рабочего за год на 0,4% (99,6%-100%) средняя годовая выработка работника снизилась на 42,07 тыс. у.е.;
- за счет увеличения доли рабочих в численности ППП на 0,37% (100,37%-100%) средняя годовая выработка работника повысилась на 37,63 тыс. у.е.
Таким образом, произошло в целом повышение средней годовой выработки работника в отчетном периоде по сравнению с базисным.
При анализе абсолютных и относительных величин было выявлено, что более высокий процент перевыполнения плана по выпуску продукции приходится на предприятие №3 – 101,5%. Менее всего был перевыполнен план на предприятии №1 и №9 – на 0,7% (100,7-100). На предприятии №2 план по выпуску продукции был не выполнен – 96,3%. А более высокий процент установления планового задания приходится на предприятие №3 – 104,1%, в то время как на предприятие №1– 101,1%, №2 – 93,1%, №9 – 99,3%.
При корреляционном анализе влияния производительности труда на динамику рентабельности предприятия было выявлено, что с увеличением средней часовой выработки рабочего на 1 тысячу рублей рентабельность предприятия в среднем возрастает на 0,89. С увеличением средней часовой выработки рабочего на 1% приводит к увеличению рентабельности предприятия на 0,356%.
Производительность труда, вне зависимости от политического устройства, является важнейшим показателем развития экономики.
Рост производительности труда обеспечивает предприятиям и всему общественному производству дальнейшее развитие и благоприятные перспективы, а в сочетании с грамотной маркетинговой и сбытовой политикой, конкурентоспособность, что является непременным условием рыночной экономики. И, в конечном счёте, рост производительности труда ведёт к повышению уровня жизни населения.
Список использованной литературы
1. Т.К. Горемыкина. Статистика. Часть 1. Общая теория статистики: Учебное пособие. – М.: МГИУ, - с. 140, 2007.
2. Т.К. Горемыкина. Статистика. Часть 2. Статистика промышленности: Учебное пособие. – М.: МГИУ, - с. 155, 1999.
3. Я.С.Мелкумов. Социально-экономическая статистика: Учебное пособие. М.: ИНФРА-М, - с. 236, 2008.
|