Контрольная работа: Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
|
Название: Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях Раздел: Рефераты по физике Тип: контрольная работа | ||||||||||||||||
| Задание K 2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
R2 =40см, r2 =25 см, R3 =20 см, x0 =9 см, V0 =8 см/с, x2 =65 см, t1 =1с,
c1 -? c2 -? c3 -? V-? a-?
Уравнение груза 1 имеет вид: (1) x=c2 t2 +c1 t+c0 . Коэффициенты c2 , c1 , c0 могут быть определены из следующих условий: При t=0c x=9 При t=2c x=65. (3) Скорость груза 1 V = Подставляя (2) и (3) в (1) и (4) получим систему уравнений, из которой найдем коэффициенты c2 , c1 , c0
Таким образом, уравнение движения груза 1 имеет вид: x= 10 t2 +8t+9. (5) Скорость груза 1: V = При t=1c V =28см/ c . (6) Ускорение груза 1: a
=
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза V и угловые скорости колес
откуда имеем:
Т.к. V =20t+8 , то
При t=1c Угловое ускорение колеса 3:
Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам:
Задание: Найти скорость 1 тела в конце отрезка s.
Решение: Применим теорему об изменении кинетической энергии системы
T0 =0(т.к. в начальный момент времени система покоилась)
Определим кинетическую энергию системы в конечный момент времени
Определим работу сил в конечный момент времени
A
A
Определим скорость в конечный момент времени
Ответ:
К4. Кинематический анализ многозвенного механизма
a=50см b=30см O1 A=14см O2 B=29см AB=45см BC=54см CD=34см
Найти: 1) скорости точек А, В, С и в механизма и угловые скорости всех его звеньев с помощью плана скоростей; 2) скорости точек А, В, С и в механизма и угловые скорости всех его звеньев с помощью мгновенных центров скоростей; 3) ускорения точек А и В и угловое ускорение звена АВ; 4) положение мгновенного центра ускорений звена АВ; 5) ускорение точки М, делящей звено АВ пополам.
Определние скоростей точек и угловых ускорений звеньев с помощью плана скоростей. Определяем скорости точек. Строим схему механизма в выбранном масштабе (рис1). Вычисляем модуль скорости точки А кривошипа О1 А:
Вектор
Строим план скоростей. Из произвольно выбранного полюса О проводим луч Оа, изображающий в выбранном масштабе скорость точки А. Для определения скорости точки В через полюс О проводим прямую, параллельную скорости перпендикулярную АВ. Получаем точку b; отрезок Оbопределяет скорость точки В. Измеряем длину луча Оb и, пользуясь масштабом скоростей, находим Продолжая построение плана скоростей, находим
Определяем угловые скорости звеньев механизма. Отрезок ab плана скоростей выражает вращательную скорость точки В вокруг точки А: ab= отсюда угловая скорость звена АВ
Аналогично определяются угловые скорости звеньев ВС и ED:
Угловая скорость звена О2 В определяется по вращательной скорости точки В вокруг неподвижного центра О2 .
Определение скоростей точек и угловых ускорений звеньев с помощью мгновенных центров скоростей. а) Определяем положения мгновенных центров скоростей звеньев механизма. Строим схему в выбранном масштабе(рис3) Звенья О1 А, O2 B вращаются вокруг неподвижных центров О1 и О2 .
Рис3 Мгновенный центр скоростей РАВ звена АВ находится на как точка пересечения перпендикуляров, проведенных из точек А и В к их скоростям. Аналогично определяется положение мгновенного центра скоростей РDE . Мгновенный центр скоростей звена АВ находится в бесконечности. Б) Определяем скорости точек . Скорости точек звеньев механизма пропорциональны расстояниям от этих точек до мгновенных центров скоростей соответствующих звеньев. Эти расстояния измеряются на чертеже. Для определения скорости точки В звена АВ имеем пропорции
Следовательно ,
Т.к. мгновенный центр скоростей звена ВС находится в бесконечности, то
Для определения скорости точки Е звена ED имеем пропорции
Следовательно,
Одновременно с определением модулей скоростей точек находим их направления, а также направления вращений звеньев механизма. Например, по направлению скорости точки А и положению мгновенного центра скоростей РАВ устанавливаем, что вращение звена АВ происходит по часовой стрелке. Поэтому скорость точки В при данном положении механизма направлена влево. Аналогично определяем направления вращений остальных звеньев и направления скоростей точек механизма. в) Определяем угловые скорости звеньев механизма Скорость любой точки звена равна произведению угловой скорости этого звена на расстояние от точки до мгновенного центра скоростей:
Угловая скорость звена О2 В определяется по скорости точки В:
Угловая скорость звена ВС равна нулю, т.к. мгновенный центр скоростей звена ВС находится в бесконечности:
Аналогично вычисляем угловую скорость звена ED:
3. Определение ускорений точек A и B и угловое ускорение звена АВ. Определяем С помощью теоремы об ускорениях точек плоской фигуры определяем ускорение точки В:
Т.к. кривошип О1 А вращается равномерно, то ускорение точки А направлено к центру О1 и равно
Центростремительное ускорение точки В во вращательном движении шатуна АВ вокруг полюса А направлено от точки В к точке А и равно
Откладываем от точки В в соответствующем масштабе ускорение полюса Чтобы найти ускорение точки В, необходимо выполнить второе построение, рассматривая эту точку как принадлежащую О2 В. В этом случае
Центростремительное ускорение точки В:
Откладываем от точки В вектор Точка пересечения этой прямой с JK определяет концы векторов Измерением на чертеже получаем
Т.к.
4)Определение положения мгновенного центра ускорений звена АВ. Примем точку А за полюс. Тогда ускорение точки В
Строим параллелограмм ускорений при точке В по диагонали Направление вектора 5) Определение ускорения точки М. Найдем ускорение точки М с помощью МЦУ. Ускорения точек плоской фигуры пропорциональны их расстояниям до мгновенного центра ускорений:
Подставив расстояния, определенные по чертежу К7. Определение абсолютной скорости и абсолютного ускорения точки
OM=Sr(t)=25sin(
v-? a-? Положение точки М на теле в определяется расстоянием Sr=ОМ. При
Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:
Модуль относительной скорости При t=4c
Отрицательный знак у Модуль переносной скорости
Найдем Рассмотрим прямоугольный треугольник АМ=ОА-ОМ. АМ=25-21,65=3,35см.
По теореме Пифагора имеем:
Найдем
При t=4c Знак ”+” у величины Тогда модуль переносной скорости
Модуль абсолютной скорости v найдем способом проекций. Через точку М проводим оси X и Y.
Из треугольника
Тогда
Значит v =
Абсолютное ускорение точки М равно геометрической сумме относительного, переносного и кориолисова ускорений.
Относительное движение. Это движение происходит по закону Sr(t)=25sin( Модуль относительного касательного ускорения где При t=4c
Модуль относительного центростремительного ускорения Переносное движение. Это движение происходит по закону
Модуль переносного вращательного ускорения
Знаки у Тогда Модуль переносного центростремительного ускорения
Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле
В нашем случае Тогда Направление вектора Модуль абсолютной скорости v найдем способом проекций. Через точку М проводим оси X и Y.
Ответ:
|
 x=c2
t2
+c1
t+c0
,
x=c2
t2
+c1
t+c0
,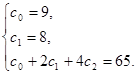
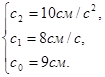
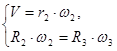
 (7)
(7)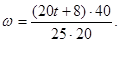

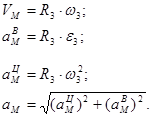 VМ
=
VМ
= Дано
:
Дано
: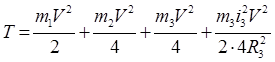
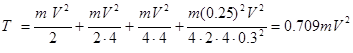
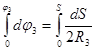



 Дано
:
Дано
:

