| Министерство образования и науки Украины
Донбасская Государственная машиностроительная академия
Контрольная работа по дисциплине
"Информатика"
2009
Задание №1
Выполнить расчеты с использованием финансовых функций. Оформить таблицу и построить диаграмму, отражающую динамику роста вклада по годам (тип диаграммы выбрать самостоятельно).
Определить текущую стоимость обычных ежеквартальных платежей размером 350000 грн. в течение семи лет, если ставка процента - 11% годовых. Рассчитайте, какая сумма на счете, если сумма размером 1000 грн. размещена под 9% годовых на 4 года, а проценты начисляются ежеквартально.
Задание №2
Произвести экономический анализ для заданных статистических данных. Сделать вывод.
| x
|
0,1
|
0,33
|
0,58
|
0,81
|
1,09
|
1,32
|
1,59
|
1,85
|
2,14
|
2,43
|
| y
|
2,7
|
2,38
|
12,39
|
24,72
|
50,62
|
108,91
|
235,84
|
512,48
|
1228,01
|
2931,14
|
Задание №3
Связь между тремя отраслями представлена матрицей затрат А. Спрос (конечный продукт) задан вектором 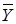 . Найти валовой выпуск продукции отраслей . Найти валовой выпуск продукции отраслей 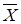 . Описать используемые формулы, представить распечатку со значениями и формулами. . Описать используемые формулы, представить распечатку со значениями и формулами.
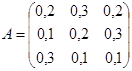 ; ; 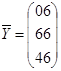
Задание № 4
Решить задачу линейного программирования. Отчет должен содержать следующие разделы:
Условие задачи
Формализация задачи
Графическое решение задачи
Распечатку решения задачи с помощью пакета Microsoft Excel
Экономический вывод
1. На промышленном предприятии изготавливают два продукта: А1 и А2. Эта продукция производится с помощью оборудования И1, И2 и И3, которое в течение дня может работать соответственно 24 000, 32 000 и 27 000 секунд. Нормы времени, необходимого для производства единицы продукции с помощью соответствующего оборудования, даны в таблице 6.
| Изделие
|
Оборудование
|
| И1
|
И2
|
И3
|
| А1
|
3
|
8
|
9
|
| А2
|
6
|
4
|
3
|
Прибыль от производства первого изделия 23 д. е., второго - 12 д. е.
Спланировать производство так, чтобы получить максимальную прибыль, если изделий А2 должно быть выпущено не менее 1000.
Задание №1
Выполнить расчеты с использованием финансовых функций. Оформить таблицу и построить диаграмму, отражающую динамику роста вклада по годам (тип диаграммы выбрать самостоятельно).
1. Определить текущую стоимость обычных ежеквартальных платежей размером 350 000 грн. в течение семи лет, если ставка процента - 11% годовых.
Для решения задачи используем финансовую функцию пакета Microsoft Excel ПЗ. В качестве аргументов:
Норма = 0,11/4 - ставка процента за период (квартал); Кпер = 7´4 - число периодов; Выплата = 350 000 - ежеквартальные выплаты; Бс = 0;
Тип = 0 (выплаты производятся в конце периода).
Результаты решения задачи представлены в таблице 1. Динамика роста стоимости выплат показана на рисунке 1. Таблица 2 содержит расчетные формулы к решению задачи в пакете Microsoft Excel.
2. Рассчитайте, какая сумма на счете, если сумма размером 1000 грн. размещена под 9% годовых на 4 года, а проценты начисляются ежеквартально.
Для решения задачи используем финансовую функцию пакета Microsoft Excel БЗ. В качестве аргументов:
Норма = 0,09/4 - ставка процента за период (квартал); Кпер = 4´4 - число периодов; Выплата = 0 - ежеквартальные выплаты; НЗ = 1000;
Тип = 0 (выплаты производятся в конце периода).
Таблица 1
| Годы
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| Выплата
|
350000
|
350000
|
350000
|
350000
|
350000
|
350000
|
350000
|
| Процент за квартал
|
0,0275
|
0,0275
|
0,0275
|
0,0275
|
0,0275
|
0,0275
|
0,0275
|
| Период в кварталах
|
4
|
8
|
12
|
16
|
20
|
24
|
28
|
| Стоимость, грн.
|
-1 308 799,75
|
-2 483 010,04
|
-3 536 471,28
|
-4 481 600,60
|
-5 329 538,25
|
-6 090 278,84
|
-6 772 789,24
|
| Стоимость, млн. грн.
|
1,309
|
2,483
|
3,536
|
4,482
|
5,330
|
6,090
|
6,773
|
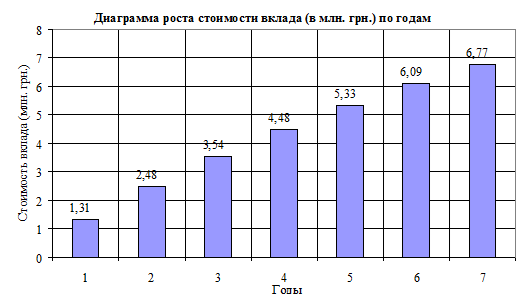
Рисунок 1
Таблица 2
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
| 1
|
Годы
|
1
|
=B1+1
|
=C1+1
|
=D1+1
|
=E1+1
|
=F1+1
|
=G1+1
|
| 2
|
Выплата
|
-350000
|
-350000
|
-350000
|
-350000
|
-350000
|
-350000
|
-350000
|
| 3
|
Процент за квартал
|
=0,11/4
|
=0,11/4
|
=0,11/4
|
=0,11/4
|
=0,11/4
|
=0,11/4
|
=0,11/4
|
| 4
|
Период в кварталах
|
4
|
=C1*4
|
=D1*4
|
=E1*4
|
=F1*4
|
=G1*4
|
=H1*4
|
| 5
|
Стоимость, грн.
|
=ПЗ (B3; B4; B2;;)
|
=ПЗ (C3; C4; C2;;)
|
=ПЗ (D3; D4; D2;;)
|
=ПЗ (E3; E4; E2;;)
|
=ПЗ (F3; F4; F2;;)
|
=ПЗ (G3; G4; G2;;)
|
=ПЗ (H3; H4; H2;;)
|
| 6
|
Стоимость, млн. грн.
|
=В5/10^6
|
=C5/10^6
|
=D5/10^6
|
=E5/10^6
|
=F5/10^6
|
=G5/10^6
|
=H5/10^6
|
Таблица 3
| А
|
B
|
C
|
D
|
E
|
| 1
|
Годы
|
1
|
=B1+1
|
=C1+1
|
=D1+1
|
| 2
|
Первоначальная сумма
|
-1000
|
-1000
|
-1000
|
-1000
|
| 3
|
Выплата
|
0
|
0
|
0
|
0
|
| 4
|
Процент за квартал
|
=9%/4
|
=9%/4
|
=9%/4
|
=9%/4
|
| 5
|
Период в кварталах
|
=B1*4
|
=C1*4
|
=D1*4
|
=E1*4
|
| 6
|
Стоимость, грн.
|
=БЗ (B4; B5;; B2;)
|
=БЗ (C4; C5;; C2;)
|
=БЗ (D4; D5;; D2;)
|
=БЗ (E4; E5;; E2;)
|
Результаты решения задачи представлены в таблице 4. Динамика роста стоимости показана на рисунке 2. Таблица 3 содержит расчетные формулы к решению задачи в пакете Microsoft Excel.
Таблица 4
| Годы
|
1
|
2
|
3
|
4
|
| Первоначальная сумма
|
1000
|
1000
|
1000
|
1000
|
| Выплата
|
0
|
0
|
0
|
0
|
| Процент за квартал
|
0,0225
|
0,0225
|
0,0225
|
0,0225
|
| Период в кварталах
|
4
|
8
|
12
|
16
|
| Стоимость, грн.
|
1 093,08
|
1 194,83
|
1 306,05
|
1 427,62
|
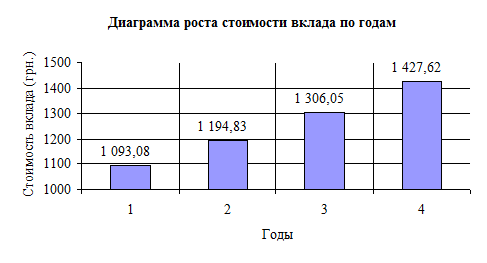
Рисунок 2
Задание №2
Произвести экономический анализ для заданных статистических данных. Сделать вывод.
| x
|
0,1
|
0,33
|
0,58
|
0,81
|
1,09
|
1,32
|
1,59
|
1,85
|
2,14
|
2,43
|
| y
|
2,7
|
2,38
|
12,39
|
24,72
|
50,62
|
108,91
|
235,84
|
512,48
|
1228,01
|
2931,14
|
Точечный график строится через меню:
Вставка > Диаграмма > Стандартная - Точечная.
На рисунке 3 показана точечная диаграмма с линией тренда, построенной на основе предположения линейной зависимости между параметрами Х и Y; на рисунке 4 - на основе предположения логарифмической зависимости; на рисунке 5 - на основе предположения степенной зависимости; на рисунке 6 - на основе предположения экспоненциальной зависимости; на рисунке 7 - на основе предположения полиномиальной зависимости 2-й степени; на рисунке 8 - на основе предположения полиномиальной зависимости 6-й степени.
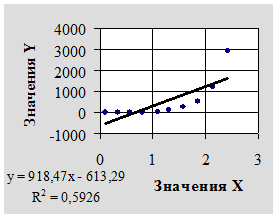
Рисунок 3
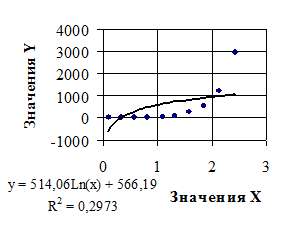
Рисунок 4
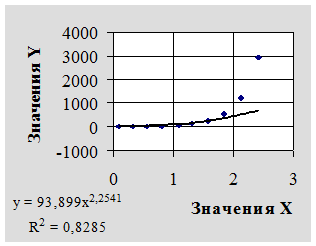
Рисунок 5
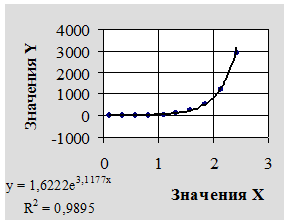
Рисунок 6
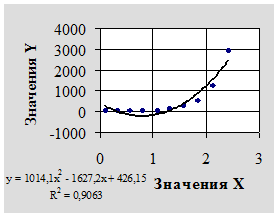
Рисунок 7
Вывод: проанализировав величину коэффициента достоверности аппроксимации R2
, делаем вывод, что исходные данные можно описать экспоненциальной моделью y = 1,6222e3,1177
x
.
Задание №3
Связь между тремя отраслями представлена матрицей затрат А
. Спрос (конечный продукт) задан вектором 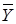 . Найти валовой выпуск продукции отраслей . Найти валовой выпуск продукции отраслей 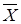 . Описать используемые формулы, представить распечатку со значениями и формулами. . Описать используемые формулы, представить распечатку со значениями и формулами.
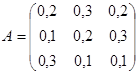 ; ; 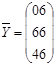
Вектор валового выпуска определяется по формуле
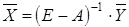 , ,
гдеЕ
- единичная матрица,
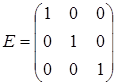 . .
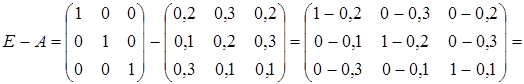
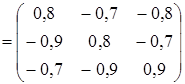 . .
Определитель матрицы Е-А
определяем в пакете Microsoft Excel с помощью функции МОПРЕД:
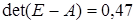 . .
Обратную матрицу 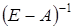 находим функцией МОБР: находим функцией МОБР:
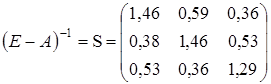 . .
Умножение обратной матрицы на вектор-столбец 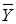 выполняем при помощи функции МУМНОЖ: выполняем при помощи функции МУМНОЖ:
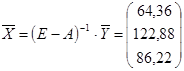 . .
Таблицы 4 и 5 содержат соответственно значения и формулы листа Microsoft Excel.
Таблица 4
| А
|
В
|
С
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
| 1
|
0, 20
|
0,30
|
0,10
|
6,00
|
| 2
|
A=
|
0,10
|
0, 20
|
0,30
|
Y=
|
66,00
|
| 3
|
0,30
|
0,10
|
0,10
|
46,00
|
| 4
|
Решение
|
| 5
|
1,00
|
0,00
|
0,00
|
0,80
|
-0,30
|
-0,10
|
| 6
|
E =
|
0,00
|
1,00
|
0,00
|
E-A =
|
-0,10
|
0,80
|
-0,30
|
det (E-A) =
|
0,47
|
| 7
|
0,00
|
0,00
|
1,00
|
-0,30
|
-0,10
|
0,90
|
| 8
|
| 9
|
1,46
|
0,59
|
0,36
|
1,00
|
0,00
|
0,00
|
| 10
|
S=
|
0,38
|
1,46
|
0,53
|
E=
|
0,00
|
1,00
|
0,00
|
| 11
|
0,53
|
0,36
|
1,29
|
0,00
|
0,00
|
1,00
|
| 12
|
| 13
|
64,36
|
| 14
|
X=
|
122,88
|
| 15
|
86,22
|
Таблица 5
| А
|
В
|
С
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
| 1
|
0, 20
|
0,30
|
0,10
|
6,00
|
| 2
|
A=
|
0,10
|
0, 20
|
0,30
|
Y=
|
66,00
|
| 3
|
0,30
|
0,10
|
0,10
|
46,00
|
| 4
|
| 5
|
1,00
|
0,00
|
0,00
|
=B5-B1
|
=C5-C1
|
=D5-D1
|
| 6
|
E =
|
0,00
|
1,00
|
0,00
|
E-A =
|
=B6-B2
|
=C6-C2
|
=D6-D2
|
det (E-A) =
|
=МОПРЕД (G5: I7)
|
| 7
|
0,00
|
0,00
|
1,00
|
=B7-B3
|
=C7-C3
|
=D7-D3
|
| 8
|
| 9
|
{=МОБР (G5: I7) }
|
{=МУМНОЖ (G5: I7; B9: D11) }
|
| 10
|
S=
|
E=
|
| 11
|
| 12
|
| 13
|
{=МУМНОЖ (B9: D11; G1: G3) }
|
| 14
|
X=
|
| 15
|
Задание №4
Решить задачу линейного программирования. Отчет должен содержать следующие разделы:
Условие задачи
Формализация задачи
Графическое решение задачи
Распечатку решения задачи с помощью пакета Microsoft Excel
Экономический вывод
1. На промышленном предприятии изготавливают два продукта: А1 и А2. Эта продукция производится с помощью оборудования И1, И2 и И3, которое в течение дня может работать соответственно 24 000, 32 000 и 27 000 секунд. Нормы времени, необходимого для производства единицы продукции с помощью соответствующего оборудования, даны в таблице 6.
| Изделие
|
Оборудование
|
| И1
|
И2
|
И3
|
| А1
|
3
|
8
|
9
|
| А2
|
6
|
4
|
3
|
Прибыль от производства первого изделия 23 д. е., второго - 12 д. е.
Спланировать производство так, чтобы получить максимальную прибыль, если изделий А2 должно быть выпущено не менее 1000.
2. Обозначим выпуск первого изделия как х1
, выпуск второго изделия как х2
.
На выпуск единицы изделия А1 на первом типе оборудования И1 расходуется 3 с, на выпуск х
1
изделий - 3х
1
с. На выпуск единицы изделия А2 на первом типе оборудования И1 расходуется 6 с, на выпуск х
2
изделий - 6х
2
с. Фонд времени для оборудования И1 составляет 24000 с. Уравнение системы ограничений (СОГ) имеет вид:
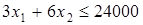 . .
На выпуск единицы изделия А1 на втором типе оборудования И2 расходуется 8 с, на выпуск х
1
изделий - 8х
1
с. На выпуск единицы изделия А2 на втором типе оборудования И2 расходуется 4 с, на выпуск х
2
изделий - 4х
2
с. Фонд времени для оборудования И2 составляет 32000 с. Уравнение СОГ имеет вид:
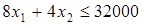 . .
На выпуск единицы изделия А1 на третьем типе оборудования И3 расходуется 9 с, на выпуск х
1
изделий - 9х
1
с. На выпуск единицы изделия А2 на третьем типе оборудования И3 расходуется 3 с, на выпуск х
2
изделий - 3х
2
с. Фонд времени для оборудования И3 составляет 27000 с. Уравнение СОГ имеет вид:
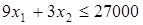 . .
Т.к. х
1
, х
2
- выпуск изделий, то он неотрицателен:
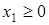 , , 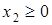
Дополнительное условие - выпуск изделия А2 не должен менее 1000 единиц:
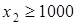 . .
Т.о., целевая функция имеет вид:
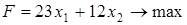
при СОГ:
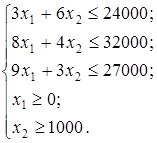
После решения уравнений СОГ принимает вид:
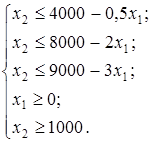
Графическое решение задачи показано на рисунке 8. Очевидно, что критическая точка максимума целевой функции 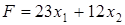 имеет координаты имеет координаты 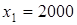 , , 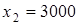 . .
В этом случае значение целевой функции
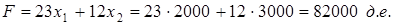
Решение задачи в пакете Microsoft Excel представлено на в таблицах 7 и 8.
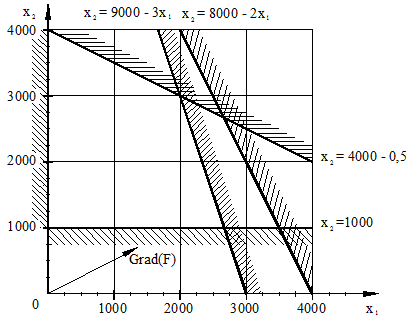
Рисунок 8
Вывод
Максимальная прибыль в 82 000 грн. от использования оборудования типов И1, И2, И3 для производства изделий А1, А2 происходит при выпуске 2000 изделий А1 и 3000 изделий А2.
При этом оборудование И1 и И3 работает постоянно, а И2 недогружено в течение 4000 с.
Таблица 7
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
| 1
|
Переменные
|
| 2
|
x1
|
x2
|
| 3
|
Значения
|
2000
|
3000
|
| 4
|
Нижняя граница
|
0
|
1000
|
| 5
|
Решение
|
| 6
|
Коэффициенты целевой функции
|
23
|
12
|
Значение F:
|
82000
|
| 7
|
Действительный фонд времени
|
Возможный фонд времени
|
Излишки времени
|
| 8
|
И1
|
3
|
6
|
24000
|
24000
|
0
|
| 9
|
Нормы времени И2
|
8
|
4
|
28000
|
32000
|
4000
|
| 10
|
И3
|
9
|
3
|
27000
|
27000
|
0
|
Таблица 8
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
| 1
|
Переменные
|
| 2
|
x1
|
x2
|
| 3
|
Значения
|
2000
|
3000
|
| 4
|
Нижняя граница
|
0
|
1000
|
| 5
|
Решение
|
| 6
|
Коэффициенты целевой функции
|
23
|
12
|
Значение F:
|
=D3*D6+E3*E6
|
| 7
|
Действительный фонд времени
|
Возможный фонд времени
|
Излишки времени
|
| 8
|
И1
|
3
|
6
|
=D3*D8+E3*E8
|
24000
|
0
|
| 9
|
Нормы времени И2
|
8
|
4
|
=D3*D9+E3*E9
|
32000
|
4000
|
| 10
|
И3
|
9
|
3
|
=D3*D10+E3*E10
|
27000
|
0
|
|