| КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ (КИМЫ) И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ ТЕСТИРОВАНИЯ
План
1. Шкалирование результатов тестирования.
2. Статистические характеристики теста.
1.
Шкалирование результатов тестирования
Начнем с привычных шкал термометра, вольтметра или обыкновенной школьной линейки. По положению ртутного столбика, стрелки вольтметра или штрихов линейки мы узнаем температуру, напряжение или длину, т.е. измеряем определенные характеристики определенных объектов. Результатом измерения является число. В реальной жизни не всегда удается выполнить измерение непосредственно. Часто для измерения доступны лишь некоторые функции интересующих нас латентных параметров объекта, и оценивание этих параметров производится путем определенной математической обработки косвенных измерений. Примером такой ситуации является и обработка результатов тестирования с целью оценивания подготовленности участников тестирования или трудности заданий. Раскрытие смысла этих параметров и разработка средств и методов их оптимального оценивания и являются основными объектами теории моделирования и параметризации педагогических тестов.
С математической точки зрения, процесс измерения есть отображение состояния измеряемого объекта на некоторое множество действительных чисел (или на некоторое множество точек числовой оси), называемое шкалой
.
Однако шкала – это не просто определенное множество – дискретное или сплошь заполняющее некоторый промежуток. Важнейшей отличительной чертой шкалы является набор тех соотношений между ее элементами (отсчетами), которые имеют содержательный смысл и разумное толкование в рамках этой шкалы.
Существует много различных шкал, в том числе, в педагогике. Но нас будут интересовать только четыре вида.
1. Порядковые
шкалы, где результаты измерений осмысленно можно только сравнивать между собой. Примером может служить принятая в школе система оценок, выставляемых ученикам в зависимости от их успехов в учебе. Из соотношения отметок b
1
< b
2
для учеников А1
и А2
можно лишь заключить, что А1
учится хуже А2
.
Если же, например, b
1
-
b
2
=
1, то утверждение "успехи А1
на 1 выше, чем успехи А2
"
не объясняет, каково различие между учениками и, по существу, лишено смысла. То же можно сказать и относительно шкалы первичных баллов (в абсолютном или относительном выражении) как для участников тестирования, так и для тестовых заданий. Максимум, что можно сделать в рамках этих шкал, это упорядочить участников тестирования или тестовые задания в порядке возрастания (или убывания) оценок соответствующих латентных параметров.
Основными статистиками порядковых шкал являются медиана, квантили и ранговая корреляция.
2. Шкала более высокого уровня называется интервальной
,
или метрической
.
Ее отличительной чертой является наличие метрики. Это означает, что для любых отсчетов b
1
и b
2
содержательный смысл имеют не только соотношения типа b
1
<
b
2
или b
1
-
b
2
,
но и разность b
2
-
b
1
.
При этом |b
2
-
b
1
| трактуется как расстояние (между двумя элементами метрического множества), выраженное в определенных единицах и, главное, имеющее осмысленное толкование. Специфика шкалы состоит в отсутствии нулевого штриха, то есть в отсутствии начала отсчета. Поэтому метрическая шкала прекрасно подходит для фиксации взаимного положения измеряемых объектов (относительно друг друга), но она не в состоянии информировать о местоположении объекта в некоторой единой системе координат (удалении от начала отсчета). С математической точки зрения указанная ситуация означает, что на множестве определена метрика, единица измерения расстояния, но нет понятия нормы (определено понятие "расстояние", но нет понятия "длина"). Например, при строительстве гидросооружений важно измерять превышения (разности высот) между определенными точками (взаимное положение по высоте, имеющее конкретную гидродинамическую трактовку), но не сами высоты. Превышение между двумя точками, имеющие высоты, например 48 м. и 45 м., имеет то же смысл, что и превышение между точками с высотами 5 м. и 2 м. В противоположность этому разности между первичными баллами 48-45 и 5-2 невозможно сравнивать осмысленно.
По такой же, по существу, шкале, по которой измеряются превышения, измеряются и латентные параметры трудность задания (d
) и уровень знаний (Q), но только единицей измерения расстояний служат не метры, а логиты.
Таблица 1.1
| Разность Q - d
|
Вероятность
верного
решения, Р
|
Информация
в ответе,
=pq
|
Относительная
эффективность
в процентах
|
| 5
|
0,99
|
0,01
|
4
|
| 4
|
0,98
|
0,02
|
8
|
| 3
|
0,95
|
0,05
|
20
|
| 2
|
0,88
|
0,11
|
44
|
| 1
|
0,73
|
0,20
|
80
|
| 0
|
0,50
|
0,25
|
100
|
| -1
|
0,27
|
0,20
|
80
|
| -2
|
0,12
|
0,11
|
44
|
| -3
|
0,05
|
0,05
|
20
|
| -4
|
0,02
|
0,02
|
8
|
| -5
|
0,01
|
0,01
|
4
|
Таблица 1.1 указывает соотношение между разностями Q - d
в логитах и их трактовкой в виде вероятности того, что задание трудности d
будет верно выполнено участником с уровнем подготовленности Q. Данные этой таблицы никак не изменятся, если к величинам Q и d
прибавить любую константу. Последний столбец таблицы 1.1 содержит произведения р(1 - р), которые можно трактовать как количество информации о разности Q - d
, которое содержится в соответствующем элементе матрицы ответов. Содержание этого столбца мы используем позже, но уже сей час полезно отметить, что информативность ответов зависит только от расстояния |Q - d
| между Q и d
и заметно падает с увеличением этого расстояния. Так, одно задание максимальной эффективности равносильно (с точки зрения поддержания одной и той же точности измерения) около 25 заданий минимальной эффективности.
3. Метрическая (интервальная) шкала
, в которой определено начало отсчета, называется шкалой нормированной. В такой шкале определено не только понятие метрики, по и понятие нормы, позволяющее измерять "длины" (то есть определенно» местоположение относительно нуля, на чала отсчета). Поэтому и такой шкале имеет смысл говорить не только о разностях типа Q - d
,
но и о каждой величине Q или d
в отдельности. Такая шкала является наиболее привлекательной, а ее построение в теории педагогических измерений представляет собой определенную революцию в этой теории, поскольку позволяет преодолеть основной ее недостаток – зависимость оценок одного индивидуума от использованного теста и контингента всех участников тестирования или определенной группы участников.
4. Кроме перечисленных "количественных" шкал, выделяют еще номинальную шкалу
,
основанную на качественных переменных, не поддающихся количественному измерению. Примером может служить пол участников тестирования, принадлежность определенному региону России и т.п. Числа по-прежнему используются в номинальных шкалах, но служат они всего лишь для различения отдельных фактов, как бы для их названия. Поэтому никаких содержательных соотношений, кроме а =
b
или а
¹
b
, между такими числами нет. При этом выбор чисел вместо реальных имен или других способов идентификации, конечно, не обязателен, поскольку речь не идет о том, на сколько отличаются друг от друга объекты или события, обладающие каким-либо свойством или признаком.
Если признаков, различающих объекты или события, только два, то номинальная шкала называется дихотомной
. Примером могут служить элементы матрицы ответов участников тестирования на задания теста: правильное выполнение задания ("да") обозначается единицей, ошибочное ("нет") – нулем. При этом разность 1-0 не имеет никакого смысла, и сами цифры 1 и 0 можно заменить любыми другими, например, цифрами 9 и 5, символами "+", "-", словами "да", "нет", "зачет", "незачет" и т.п.
Соответствующие номинальным шкалам данные состоят из наблюдаемых значений частот или табличных сведений о числе появлений каждой из разновидностей изучаемой переменной. Для характеристики номинальных данных часто используются такие (дескриптивные) статистики, как пропорция и процентное отношение.
Использование той или иной шкалы из перечисленных четырех накладывает отпечаток и на применимость тех или иных методов математической обработки, которой обычно подвергаются исходные данные. Например, регрессионный анализ применим только по отношению к количественно выраженным переменным, измеряемым, по крайней мере, в метрической шкале. Примерно тоже самое можно сказать и относительно наиболее известных методов корреляционного анализа. Сказанное не означает, что результаты тестирования, отнесенные к порядковым или даже номинальным шкалам, нельзя анализировать количественно. Однако методы такого анализа должны быть, в общем случае, специальными и от личными от тех, которые используются для переменных в шкалах метрических и нормированных. Например, даже такую общепринятую оценку центра рассеяния переменной как арифметическая средняя часто бывает более обоснованным заменить медианой вариационного ряда, если переменные отнесены к шкале порядковой, а не метрической.
Таким образом, содержательная интерпретация результатов математической обработки данных тестирования может быть дана лишь в том случае, если методы этой обработки адекватны тем шкалам, к которым отнесена исходная информация.
2.
Статистические характеристики теста
После сбора эмпирических данных начинается этап математико-статистической обработки, которая проводится, как правило, с помощью специального программного обеспечения. В практическом плане применение программного обеспечения сопряжено с некоторыми трудностями. В частности, необходимо использование компьютерной техники, приобретение программных продуктов, создание специальной группы технического сопровождения. Однако, как показывает опыт, все эти трудности могут быть преодолены даже силами небольшого преподавательского коллектива, особенно в тех случаях, когда подсчет статистики осуществляется на небольших выборках в 50-100 человек.
Этап математико-статистической обработки можно разбить на 10 шагов.
Первый шаг.
Первый шаг связан с формированием матрицы тестовых результатов, в которой количественные данные представляются в систематизированной и сжатой форме, чтобы обеспечить их дальнейшую обработку и интерпретацию. Формирование матрицы начинается с выбора определенного правила для оценки ответов учеников на задания теста. Обычно результаты ответов оцениваются дихотомически, а именно за каждый правильный ответ учащийся получает один балл, а за неправильный ответ или за пропуск задания — нуль баллов.
Если символом Ху
обозначить результат выполнения Х
-м испытуемым у
-го задания теста, то в сокращенной форме приведенное выше правило можно записать в виде:
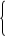 l, если ответ Х
-го испытуемого на у
-е задание верный; l, если ответ Х
-го испытуемого на у
-е задание верный;
0, если ответ Х
-го испытуемого на у
-е задание неверный.
После выбора оценочного правила эмпирические данные сводятся в матрицу. Строки матрицы, состоящие из нулей и единиц, соответствуют ответам учеников на различные задания теста. По столбцам располагаются профили ответов испытуемых на каждое задание теста.
Из дидактических соображений для иллюстрации математико-статистических методов выбрана небольшая матрица, когда 12 учеников отвечали всего на 10 заданий теста (табл. 2.1).
Однако все формулы и подсчеты, обсуждаемые в разделе, могут быть распространены на любые выборки испытуемых и применимы к тестам любой длины.
Второй шаг.
На втором шаге из матрицы тестовых результатов устраняются строки и столбцы, состоящие только из нулей или только из единиц. В приведенном выше примере таких столбцов нет, а строк только две, последние в матрице тестовых результатов. Одна из них, нулевая строка, соответствует ответам 11-го испытуемого, который не смог выполнить правильно ни одного задания в тесте. В этом случае вывод довольно однозначен. Если сложилась такая ситуация, то тест непригоден для оценки знаний 11-го ученика. Для выявления его уровня знаний тест необходимо облегчить, добавив несколько очень легких заданий, которые, скорее всего, большинство остальных испытуемых группы выполнит правильно.
Таблица 2.1.
Матрица результатов тестирования
| Номер испытуемого i
|
Номер задания j
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
| 2
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
| 4
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
| 5
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
| 6
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
| 7
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
| 8
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
| 9
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
| 10
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
| 11
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 12
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
Столь же непригоден, но уже по другой причине тест для оценки знаний 12-го ученика, который выполнил правильно все без исключения задания теста. Причина непригодности теста — его излишняя легкость, не позволяющая выявить истинный уровень подготовки 12-го ученика. Его результаты указывают лишь на знание предложенного в тесте материала, но не позволяют установить границу между освоенным и неосвоенным содержанием курса. Возможно, 12-й ученик знает много чего другого и в состоянии выполнить по контролируемым разделам содержания гораздо более трудные задания, которые просто не были включены в тест. В эту, казалось бы, привычную для традиционного контроля и желаемую для педагога ситуацию, когда испытуемый справился со всем объемом контролируемого материала, необходимо привнести элементы тестовой науки. Хотя традиционный и тестовый контроль служат одной и той же цели – оценке знаний испытуемых, между ними есть существенные различия не только по форме проведения, но и по качеству получаемых оценок. В отличие от традиционных тестовые методы контроля позволяют ответить на наиболее важный вопрос: насколько точна оценка знаний каждого испытуемого и следует ли ей вообще доверять?
Сама по себе постановка вопроса никак не связана с недостатками тестовых методов, поскольку ошибка (погрешность) измерения существует всегда и везде. В том числе и в процессе тестовых измерений возникает ряд погрешностей, мешающих получить истинные баллы учеников. Существование погрешностей приводит к мысли об относительной точности оценок, которая варьирует и которую можно счесть как достаточной, так и не позволяющей доверять полученным оценкам.
Обычно, если нормативно-ориентированный тест сделан хорошо, то достаточной точностью обладают примерно 70% результатов, находящихся в центре распределения, а примерно 5% самых слабых и 5% самых сильных результатов вообще нельзя доверять, так как они отражают истинный уровень знаний учеников с очень большой ошибкой измерения. Именно по этим соображениям профессионально организованные тестовые службы при обработке отбрасывают не менее 3 или 5% результатов на концах распределения. К сожалению, в нашей стране зачастую тестовые оценки испытуемых выставляются без учета теоретических ограничений на возможные диапазоны их применения.
Причина такого положения – практическое незнакомство большинства преподавателей с основами тестовой теории, незнание основных ее положений. Особенно пагубно это незнание сказывается на качестве тестов, разрабатываемых в нашей стране. Нередко автор теста, если его выполнили все или почти все испытуемые группы, расценивает свою работу как успех. У этой тенденции есть свои печальные следствия. Тестовые оценки, полученные со значительной ошибкой измерения, порождают у преподавателей многочисленные сомнения в возможностях педагогических тестов. В сущности, здесь виноваты не тесты, а отсутствие должного профессионализма их разработчиков, но об этом почему-то никто не думает, особенно в тех случаях, когда ругают педагогические тесты.
При правильном положении вещей последние две строки матрицы должны быть удалены, и матрица тестовых результатов примет вид, приведенный в табл. 2.2.
Таблица 2.2.
Матрица результатов после удаления строк
| Номер испытуемого i
|
Номер задания у
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
| 2
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
| 4
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
| 5
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
| 6
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
| 7
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
| 8
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
| 9
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
| 10
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
Третий шаг.
Третий шаг связан с подсчетом индивидуальных баллов испытуемых и количеством правильных ответов испытуемых на каждое задание теста. Индивидуальный балл испытуемого получается суммированием всех единиц, полученных им за правильно выполненные задания теста. Например, 4-й испытуемый выполнил правильно 9 заданий, поэтому его индивидуальный балл равен 9. В строке ответов 2-го испытуемого стоят всего две единицы — его индивидуальный балл Х2
=
2. Для удобства полученные индивидуальные баллы Xi
(i= 1, 2,..., 10) приводятся в последнем столбце матрицы результатов (табл. 2.3).
Таблица 2.3.
Матрица результатов с индивидуальными баллами испытуемых и количеством правильных ответов на задания теста
| Номер испытуемого i
|
Номер задания j
|
Индивидуальный балл (множество Аj)
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
6
|
| 2
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
| 3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
| 4
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
9
|
| 5
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
4
|
| 6
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
4
|
| 7
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
5
|
| 8
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
4
|
| 9
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
9
|
| 10
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
6
|
| Число правильных ответов (множество Аi)
|
9
|
8
|
7
|
6
|
5
|
5
|
3
|
4
|
2
|
1
|
50
|
Число правильных ответов на задания Х
также получается суммированием единиц, но уже расположенных по столбцам. Например, в 1-м столбце стоят 9 единиц — число испытуемых, правильно ответивших на 1-е задание, равно 9. На последнее, 10-е задание ответил правильно только один ученик, поэтому Х10
= 1. Число правильных ответов на каждое задание также помещается в матрицу результатов, обычно оно располагается в последней строке под номером соответствующего задания теста (см. табл. 3).
Четвертый шаг
. На четвертом шаге осуществляется упорядочение матрицы результатов тестирования. Для этого производят перестановку столбцов, располагая числа Л в порядке убывания. Затем меняют местами строки матрицы так, чтобы верхняя строка соответствовала обучаемому с минимальным индивидуальным баллом. Значения X
i
располагают сверху вниз в порядке возрастания. Упорядоченная матрица данных тестирования приведена в табл. 2.4.
Пятый шаг
. На пятом шаге производится графическая интерпретация эмпирических данных. Эмпирические результаты тестирования можно представить в виде полигона, гистограммы, сглаженной кривой (процентилей, огивы) или машинописного графика.
Для построения кривых необходимо упорядочить результаты эксперимента. Их можно записать в виде несгруппированного ряда произвольной формы (табл. 2.5), ранжированного ряда (табл. 2.6), частотного распределения (табл. 2.7) или распределения сгруппированных частот (табл. 2.8).
Таблица 2.5.
Несгруппированный ряд
| Номер
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Балл
|
6
|
2
|
1
|
9
|
4
|
4
|
5
|
4
|
9
|
6
|
Таблица 2.6.
Ранжированный ряд
| Ранг
|
1
|
2
|
3
|
3
|
3
|
4
|
5
|
5
|
6
|
6
|
| Номер
|
3
|
2
|
5
|
6
|
8
|
7
|
1
|
10
|
4
|
9
|
| Балл
|
1
|
2
|
4
|
4
|
4
|
5
|
6
|
6
|
9
|
9
|
Таблица 2.7.
Частотное распределение
| Балл
|
1
|
2
|
4
|
5
|
6
|
9
|
| Частота
|
1
|
1
|
3
|
1
|
2
|
2
|
Таблица 2.8.
Сгруппированное частотное распределение
| Интервал баллов
|
Частота
|
| 1-3
|
2
|
| 4-6
|
6
|
| 7-9
|
2
|
В табл. 2.5 содержатся индивидуальные баллы испытуемых, взятые из последнего столбца матрицы эмпирических результатов выполнения теста (табл. 2.3). В табл. 2.6 эти же баллы расположены в порядке возрастания слева направо и приводятся места (ранги) испытуемых, соответствующие их индивидуальным баллам. Таблица 2.6 удобна для подведения итогов тестирования в повседневной работе педагога, поскольку в небольшом классе такого распределения вполне достаточно для сообщения тестовых результатов ученикам. Балл 6 обеспечивает 1-му испытуемому ранг 5 в группе из 10 учеников. Аналогичным образом можно интерпретировать любую оценку ученика в терминах рангов. Очевидно, что равным баллам приписываются равные ранги. Если список учеников является длинным, то для определения рангов требуется много времени и сил.
Список учеников с полученными тестовыми баллами можно сократить, классифицируя оценки по распределению частот, как, например, в табл. 2.7. В этом случае в верхней строке размещаются только различные оценки, а внизу под каждой оценкой — число ее повторений, которое называется частотой и обычно обозначается символом N.
Сумма всех частот для данного примера N = 1+1+3+1+2+2=10, т.е. равна числу учеников в тестируемой группе.
Для большой группы – скажем, в 100 или более учеников – используют сгруппированное частотное распределение (табл. 2.8). Для построения распределения оценки объединяют в группы. Каждая такая группа называется разрядом оценок. В случае полного размещения оценок по разрядам говорят о распределении сгруппированных частот баллов учеников. Например, для матрицы из табл. 2.4 образовано 3 разряда, представленных в табл. 8. Хотя четкого правила выбора количества разрядов нет, но все же обычно их число стараются варьировать в пределах от 12 до 15. Занижение числа разрядов (менее 12) может существенно исказить результаты тестирования, а его завышение (более 15) затрудняет работу с таблицей.
Полигон частот
. По ряду частотного распределения можно осуществить графическое представление результатов тестирования в виде полигона частот, построенного (рис. 2.1). Для построения полигона частот по горизонтальной оси откладываются тестовые баллы, а по вертикальной – частота появления каждого балла у тестируемой выборки учеников.
Рис. 2.1.
Полигон для распределения табл. 7
Гистограмма представляет собой последовательность столбцов, каждый из которых опирается на единичный (разрядный) интервал, а высота его пропорциональна частоте наблюдаемых баллов. Например, для рассматриваемого примера табл. 7 гистограмма приведена на рис. 2.2. Середина столбца совмещается с серединой интервала разряда, который выбран длиной в один балл.

Рис. 2.2. Столбиковая гистограмма
В данном случае в качестве разрядного выбран единичный интервал.
Гистограмма может быть построена и для сгруппированных данных. В этом случае она выглядит так, как на рис. 2.3 (нижняя гистограмма для гипотетического набора данных), где для сравнения вверху приведена гистограмма для несгруппированных данных.

Рис. 2.3.
Гистограммы распределения несгруппированных и сгруппированных данных
Для сравнения двух или более распределений обычно используют полигоны частот, так как при наложении гистограмм получается довольно запутанная картина. Например, с помощью полигонов можно сравнить результаты выполнения теста учащимися различных, в данном случае трех, классов, имеющих одинаковое количество учеников (рис. 2.4).

Рис. 2.
4
.
Гистограмма эмпирического распределения
На рис. 2.4 отчетливо проглядывает значительное сходство в результатах тестирования у первых двух классов, имеющих довольно похожие полигоны распределения оценок.
Шестой шаг
. На шестом шаге оцениваются меры центральной тенденции совокупности результатов, полученные при выполнении теста. Меры центральной тенденции предназначены для выявления «центрального положения», вокруг которого в основном группируется множество значений рассматриваемого распределения данных. Если предположить, что множество результатов расположено на прямой, то «центральное положение» имеет точка, вокруг которой по тому или иному признаку группируются все результаты выполнения теста. При анализе результатов тестирования можно использовать разные подходы к определению центра распределения. Наиболее простой способ основан на выявлении моды распределения.
Мода
– это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для данных табл. 2.7 модой является балл 4, потому что он встречается чаще (3 раза) любого другого значения балла. Не всякое распределение имеет единственную моду.
Среднее выборочное
(среднее арифметическое) определяется суммированием всех значений совокупности и последующим делением на их число. Для совокупности индивидуальных баллов ??
Х2
,...,
XN
группы ?? испытуемых среднее значение X
будет
 (1) (1)
Среднее арифметическое индивидуальных баллов испытуемых для рассматриваемого выше примера матрицы (табл.3 или 4) будет

Вычисление среднего значения легко произвести на любом калькуляторе или ПЭВМ. Процесс вычисления значительно упрощается, если отдельные значения в совокупности повторяются, как, например, в табл. 7. Для данных таблицы сумма всех результатов определяется умножением каждого значения балла на его частоту и последующим суммированием полученных произведений. Тогда среднее значение будет

В отличие от моды на величину среднего влияют значения всех результатов. Таким образом, среднее арифметическое характеризует всю совокупность значений. Оно обобщает индивидуальные особенности составляющих распределения, в нем уравниваются отдельные значения рассматриваемой величины.
Получаемые результаты в процессе разработки теста требуют специальной интерпретации и размышления.
Интерпретация мер центральной тенденции.
Меры центральной тенденции в определенной степени помогают при оценке качества теста в том случае, когда она проводится по результатам апробации теста на репрезентативной выборке учеников. Обычно считают, что хороший нормативно-ориентированный тест обеспечивает нормальное распределение индивидуальных баллов репрезентативной выборки учеников, когда среднее значение баллов находится в центре распределения, а остальные значения концентрируются вокруг среднего по нормальному закону, т.е. примерно 70% значений в центре, а остальные сходят «на нет» к краям распределения, как на рис. 2.5.

Рис. 2.5.
Нормальная кривая распределения индивидуальных баллов
Если тест обеспечивает близкое к нормальному распределение баллов, то это означает, что на его основе можно определить устойчивое среднее значение баллов, которое принимается в качестве одной из репрезентативных норм выполнения теста. Обратный вывод, вообще говоря, неверен: устойчивость тестовых норм вовсе не предполагает обязательного нормального распределения эмпирических результатов выполнения теста.
Может сложиться представление о том, что существует жесткая связь между нормальным распределением частот и практически любыми эмпирическими данными по тесту.
На самом деле это не так, поскольку нормальная кривая – это изобретение математиков, которое в сглаженном, идеальном виде описывает реальный полигон частот. На практике никогда не была и не будет получена совокупность данных, распределенных точно по нормальному закону. Просто иногда полезно, допуская определенную ошибку, утверждать, что эмпирические данные распределены по нормальному закону, и описывать полигон частот сглаженной кривой.
Нормальное распределение унимодально и симметрично, т.е. половина результатов, расположенная ниже моды, в точности совпадает с другой половиной, расположенной выше, а мода и среднее значение равны. Отсутствие полной симметрии в полигоне частот на практике приводит к смещению моды относительно среднего значения.
В малых выборках мода, как и среднее значение, теряет свою стабильность, хотя причиной нестабильности может служить и неправильный подбор по трудности заданий в тесте. Например, если по репрезентативной выборке получилась гистограмма с бимодальным распределением (рис. 2.6), то среднее значение распределения, находящееся в центре, никак не может служить нормой выполнения теста. Скорее всего, тест был сконструирован неудачно, что послужило причиной отсутствия нормального распределения эмпирических результатов выполнения теста.

Рис. 6.
Гистограмма бимодального распределения
Смещение среднего значения влево или вправо, как на рис. 2.7 и 2.8, говорит о слишком трудной либо соответственно слишком легкой подборке заданий теста.
Таким образом, правильно сконструированный нормативно-ориентированный тест на репрезентативной выборке учеников должен обеспечивать близкое к симметричному распределению индивидуальных баллов, когда мода и среднее значение примерно равны, а остальные результаты расположены вокруг среднего по нормальному закону.

Рис. 7.
Гистограмма распределения баллов по трудному тесту

Рис. 8.
Гистограмма распределения баллов по легкому тесту
Седьмой шаг.
На седьмом шаге определяются описательные характеристики, служащие мерами изменчивости в группе данных по тесту. Введение характеристик связано с необходимостью выявления дополнительных оснований для обоснованного сравнения различных распределений по тестам. При сравнении нескольких распределений с одинаковыми средними с помощью дополнительных характеристик можно выявить существенные различия в структуре, указывающие на значительные отличия в качестве тестов.
Наиболее важная характеристика указывает на особенности разброса эмпирических данных вокруг среднего значения баллов по тесту. Отдельные значения индивидуальных баллов могут быть тесно сгруппированы вокруг своего среднего балла либо, наоборот, сильно удалены от него. Поэтому необходимы оценки характеристик распределения, отражающие вариацию, или, как говорят иначе, изменчивость баллов по тесту.
Для характеристик степени рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия, стандартное отклонение.
Размах
измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Например, распределения индивидуальных баллов табл. 6 размах равен ??.
Вариационный размах легко вычисляется, но используется крайне редко при характеристике распределения баллов по тесту. И для этого есть веские основания. Во-первых, размах является весьма приближенным показателем, так как не зависит от степени изменчивости промежуточных значений, расположенных между крайними значениями в распределении баллов по тесту. Во-вторых, крайние значения индивидуальных баллов, как правило, ненадежны, поскольку содержат в себе значительную ошибку измерения. В этой связи более удачной мерой считается дисперсия.
Дисперсия
.
Подсчет дисперсии основан на вычислении отклонений каждого значения показателя от среднего арифметического в распределении. Для индивидуальных баллов значения отклонений несут информацию о вариации совокупности значений баллов N
учеников, т. е. отражают меру неоднородности результатов по тесту. Совокупность с большей неоднородностью будет иметь большие по модулю отклонения, наоборот, для однородных распределений отклонения должны быть близки к нулю. Знак отклонения указывает место результата ученика по отношению к среднему арифметическому по тесту. Для ученика с индивидуальным баллом выше среднего значение разности несут информацию о вариации совокупности значений баллов N
учеников, т. е. отражают меру неоднородности результатов по тесту. Совокупность с большей неоднородностью будет иметь большие по модулю отклонения, наоборот, для однородных распределений отклонения должны быть близки к нулю. Знак отклонения указывает место результата ученика по отношению к среднему арифметическому по тесту. Для ученика с индивидуальным баллом выше среднего значение разности  будет положительно, а для тех, у кого результат ниже будет положительно, а для тех, у кого результат ниже , отклонение , отклонение  меньше нуля. меньше нуля.
Например, в распределении баллов со средним значением  из табл. 6 отклонения будут: из табл. 6 отклонения будут:
• для 3-го ученика 
• для 2-го  ; ;
• для 5-, 6-и 8-го  ; ;
• для 7-го  ; ;
• для 1- и 10-го  ; ;
• для 4- и 9-го  . .
Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. В рассматриваемом примере сумма отклонений

что, конечно, не позволяет оценить меру неоднородности распределения, поскольку отрицательные и положительные слагаемые уничтожают друг друга. Для преодоления этого эффекта каждое отклонение возводят в квадрат и находят сумму квадратов отклонений: Тогда сумма вида

будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой – в случае близких результатов испытуемых по тесту.
Для рассматриваемого примера

Величина суммы зависит также от размера выборки учеников, выполнявших тест. Зависимость здесь вполне очевидна: чем больше учеников, тем больше положительных слагаемых в сумме, характеризующей вариацию баллов по тесту. Поэтому при сравнении мер изменчивости распределений, отличающихся по объему, возникает препятствие, которое снимается путем деления каждой суммы на N
-
1, где N
– число учеников, выполнявших тест. Определяемая таким образом мера изменчивости называется дисперсией. Она обычно обозначается символом  и вычисляется по формуле и вычисляется по формуле
 (2) (2)
Для рассматриваемого примера

В примере  вычислялась просто в силу того, что среднее арифметическое было целым числом. На практике, как правило, приходится иметь дело с дробными значениями вычислялась просто в силу того, что среднее арифметическое было целым числом. На практике, как правило, приходится иметь дело с дробными значениями  , что делает использование формулы (2) крайне утомительным. , что делает использование формулы (2) крайне утомительным.
Стандартное отклонение
.
Кроме дисперсии, для характеристики меры изменчивости распределения удобно использовать еще один показатель вариации, который называется стандартным отклонением. Стандартное отклонение равно корню квадратному из дисперсии:
 (3) (3)
Для рассматриваемого примера 
Стандартное отклонение не следует путать со средним отклонением, последнее находится по формуле
 (4)
(4)
и является средним значением суммы отклонений, взятых по модулю.
Интерпретация
.
Дисперсия играет важную роль в оценке качества нормативно-ориентированных тестов. Слабая вариация результатов испытуемых указывает на низкое качество теста. Основания для подобного вывода вполне прозрачны. Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовки в тестируемой группе, т.е. о той ситуации, которая диаметрально противоположна основной цели создания нормативно-ориентированного теста.
Излишне высокая дисперсия, характерная для случая, когда все учащиеся отличаются по числу выполненных заданий, также грозит неприятными последствиями и требует переработки теста. Превышение разумных пределов величины дисперсии приводит к искажению вида распределения, которое начинает существенно отличаться от планируемой теоретической нормальной кривой.
При переработке теста следует руководствоваться простым правилом: если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, а дисперсия растет, то это означает, что происходит повышение дифференцирующей способности теста и процесс улучшения теста.
Конечно, использовать какой-либо из существующих критериев для проверки нормальности распределения в практике довольно неудобно. Поэтому зачастую непрофессионалы в оценке характера распределения руководствуются простым соотношением. Для этого величину X
сравнивают с утроенным стандартным отклонением. Если это равенство выполняется, т.е. если
??,
то дисперсия оптимально высока и можно принять гипотезу о нормальности распределения.
??
нормальной кривой, оценивается с помощью асимметрии. Наличие асимметрии легко установить визуально, анализируя полигон частот или гистограмму. Более тщательный анализ можно провести с помощью обобщенных статистических характеристик, предназначенных для оценки асимметрии в распределении.
На рис. 2.9 представлены кривые распределения с отрицательной, нулевой и положительной асимметрией (слева направо) соответственно

Рис.2.9.
Отрицательная, нулевая, положительная асимметрия.
Наиболее удачная формула для подсчета асимметрии имеет вид
Асимметрия (5) (5)
где – индивидуальный балл i
-го ученика; – индивидуальный балл i
-го ученика; – среднее значение баллов по тестируемой группе; – среднее значение баллов по тестируемой группе; – куб стандартного отклонения; N
– число учеников. После подстановки данных из рассматриваемого выше примера (табл. 3) величина асимметрии будет равна – куб стандартного отклонения; N
– число учеников. После подстановки данных из рассматриваемого выше примера (табл. 3) величина асимметрии будет равна

Интерпретация
.
При интерпретации полученного значения асимметрии 0,2 необходимо обратить внимание на то, что вклад положительных значений кубов разностей  будет больше кубов отрицательных значений, но ненамного, поэтому величинa асимметрии получилась положительной и небольшой. Таким образом, асимметрия распределения положительна, если основная часть значений индивидуальных баллов лежит справа от среднего значения, что обычно характерно для излишне легких тестов. Асимметрия распределения баллов отрицательна, если большинство учеников получили оценки ниже среднего балла. Эффект отрицательной асимметрии встречается в излишне трудных тестах, не сбалансированных правильно по трудности при отборе заданий в тест. будет больше кубов отрицательных значений, но ненамного, поэтому величинa асимметрии получилась положительной и небольшой. Таким образом, асимметрия распределения положительна, если основная часть значений индивидуальных баллов лежит справа от среднего значения, что обычно характерно для излишне легких тестов. Асимметрия распределения баллов отрицательна, если большинство учеников получили оценки ниже среднего балла. Эффект отрицательной асимметрии встречается в излишне трудных тестах, не сбалансированных правильно по трудности при отборе заданий в тест.
В хорошо сбалансированном по трудности тесте, как уже отмечалось ранее, распределение баллов имеет вид нормальной кривой. Для нормального распределения характерна нулевая асимметрия, что вполне естественно, так как при полной симметрии каждое значение балла, меньшее  , уравновешивается другим симметричным, большим, чем , уравновешивается другим симметричным, большим, чем  . .
Эксцесс
.
С помощью эксцесса можно получить представление о том, являются ли полигон частот или гистограмма островершинными или плоский. На рис. 2.10 изображены три кривые, отличающиеся по эксцессу.
 Рис. 2.10.
Островершинная, средневершинная и плоская кривые. Рис. 2.10.
Островершинная, средневершинная и плоская кривые.
Первая кривая (А)
– островершинная, имеет явно выраженный положительный эксцесс, вторая кривая (В) –
средневершинная, имеет нулевой эксцесс, характерный для нормальной кривой, третья кривая (С) – плосковершинная, кривые такого типа имени эксцесс меньше нуля.
Обычно эксцесс вычисляется по формуле
Эксцесс , (6) , (6)
где все обозначения остались прежними. Для рассматриваемого примера (см. табл. 2.6) эксцесс будет

Интерпретация
.
При интерпретации полученных оценок эксцесса необходимо помнить о том, что понятие «эксцесс» применимо лишь к унимодальным распределениям. Более того, интерпретация результата, указывающего на крутизну кривой распределения, возможна в сравнительно небольшой окрестности моды и теряет свой смысл по мере удаления вдоль кривой.
В том случае, когда распределение данных бимодально (имеет две моды), необходимо говорить об эксцессе в окрестности каждой моды. Бимодальная конфигурация указывает на то, что по результатам выполнения теста выборка учеников разделилась на две группы. Одна группа справилась с большинством легких, а другая с большинством трудных заданий теста. Один из наиболее важных выводов в случае бимодального распределения нацелен на коррекцию трудности заданий теста. По-видимому, в тесте недостаточно представлены задания средней трудности, позволяющие выровнять распределение баллов, приблизив его к нормальной кривой.
В заключение необходимо провести проверку значимости найденных значений асимметрии и эксцесса. Для этого необходимо добавить информацию о принимаемом уровне риска допустить ошибку в статистическом выводе. Наиболее приемлемым для педагогических измерений является уровень в 5%, который допускает ошибку в пяти случаях из ста.
Девятый шаг.
Девятый шаг предназначен для вычисления показателей связи между результатами учеников по отдельным заданиям теста. При оценке качества заданий важно понять, существует ли тенденция, когда одни и те же ученики добиваются успеха в какой-либо паре заданий теста. Либо, наоборот, такой тенденции, указывающей на связь результатов, нет, и состав учеников, добивающихся успеха, полностью меняется при переходе от одного задания к другому в тесте.
Очевидно, для ответа на поставленные вопросы необходимо провести анализ данных, собрав их в таблицу. Однако такой визуальный анализ данных – дело достаточно утомительное, а для больших выборок и просто невозможное. Поэтому обычно ответ на вопрос о существовании связи между двумя наборами данных получают с помощью корреляции.
Корреляция
.
Корреляция в широком смысле слова означает связь между явлениями и процессами, Однако для исследования связи установить ее наличие недостаточно, необходимо также правильно выбрать ее вид и форму показателя, предназначенного для оценки меры связи между явлениями.
Связь между двумя наборами данных ??
можно выразить графически с помощью диаграммы рассеяния (рис. 2.11).

Рис. 2.11.
Диаграмма рассеяния, показывающая связь результатов тестирования группы школьников по математике (
X
)
с результатами тестирования по физике (
Y
).
Диаграмма указывает на наличие слабой положительной связи, однако не позволяет ввести обобщенную ее меру.
Примеры различного вида диаграмм, позволяющих графически интерпретировать характер связи между наборами данных X
и Y
,
приведены на рис. 2.12.

Рис.2.12.
Графическая интерпретация видов связи.
Коэффициент корреляции Пирсона
.
Для повышения сопоставимости оценок показателей связи по выборкам с различной дисперсией ковариацию делят на стандартные отклонения. Таким образом,  необходимо разделить на необходимо разделить на  и и  , где , где и и  – стандартные отклонения по множествам X и Y соответственно. В результате получается величина, которая называется коэффициентом корреляции Пирсона – стандартные отклонения по множествам X и Y соответственно. В результате получается величина, которая называется коэффициентом корреляции Пирсона : :
 (8) (8)
Интерпретация
.
Анализ значений коэффициента корреляции в табл. 10 позволяет выделить задания 3 и 8 теста. По данным таблицы, задание 3 отрицательно коррелирует с заданиями 7, 8, 9 и 10 теста. О том, что «виновато» третье, а не другие задания теста, свидетельствует анализ значений коэффициента корреляции в столбцах с номерами семь, девять и десять. В них просматривается только один минус на месте, соответствующем заданию теста 3, которое в свою очередь отрицательно коррелирует с четырьмя заданиями теста.
Аналогичная ситуация наблюдается в столбце, соответствующем заданию 8 теста. Отрицательные значения коэффициента корреляции указывают на определенный просчет разработчиков в содержании заданий 3
и 8 теста. Наиболее распространенная причина – отсутствие предметной чистоты содержания – нередко встречается при разработке самых разных тестов.
Понятно, что предметная чистота – скорее идеализируемое, чем реальное требование к содержанию любого теста. Например, в тесте по физике всегда встречаются задания с большим количеством математических преобразований, в тесте по биологии – задания, требующие серьезных знаний по химии, в тесте по истории – задания рассчитанные на выявление культурологических знании, и т п. Поэтому говорить об отсутствии пересечения содержания заданий одной учебной дисциплины с содержанием другой в чистом виде не приходится. Можно лишь стремиться к тому, чтобы при выполнении каждого задания доминировали знания по проверяемому предмету.
По-видимому, противоположная ситуация наблюдалась в заданиях 3 и 8, отрицательные значения корреляции по которым указывают на отсутствие связи их содержания с содержанием других заданий теста.
Таким образом, задания 3 и 8 для повышения гомогенности содержания необходимо удалить из теста. Конечно, окончательное решение остается за автором, поскольку оно бессмысленно без тщательного анализа содержания заданий теста. Правда, подобное решение об удалении заданий может быть принято в том случае, когда эмпирические результаты собраны по репрезентативной выборке учеников. Если представительность выборки не достигнута, то появление минусов может не отражать ни в коей мере реальную ситуацию с содержанием заданий теста.
Анализ 9-го столбца с максимальной суммой 4,6495, приведенной в конце, указывает на наличие ряда довольно высоких значений коэффициента корреляции (<р9
8
= 0,6124; <р97
-0,7638; <р9
10
-0,6667), каждое из которых может получить различную трактовку в зависимости от вида разрабатываемого теста.
Для тематических тестов высокая корреляция между задания ми неизбежна, так как задания отражают слабо варьирующее, исходное содержание, что вполне оправдано назначением теста.
Однако для итоговых тестов высокой корреляции между заданиями по возможности стараются избегать тестов, оценивающих одинаковые содержательные элементы, поскольку вряд ли имеет смысл включать в итоговый тест несколько заданий. Поэтому в итоговых тестах обычно стремятся к невысокой положительной корреляции, когда значения коэффициента варьируют в интервале (0; 0,3) и каждое задание привносит свой специфический вклад в общее содержание теста.
Десятый шаг.
На десятом шаге с помощью подсчета значений коэффициента бисериальной корреляции оценивается валидность отдельных заданий теста.
Коэффициент бисериальной корреляции
используется в том случае, когда один набор значений распределения задается в дихотомической шкале, а другой – в интервальной. Тогда в качестве показателя связи между распределениями выбирают бисериальный коэффициент. Под эту ситуацию подпадает подсчет корреляции между результатами выполнения каждого задания (дихотомическая шкала) и суммой баллов испытуемых (интервальная или квазиинтервальная шкала) по заданиям теста.
Формула для подсчета, полученная по результатам вывода, имеет вид
 (9) (9)
где — среднее значение индивидуальных баллов испытуемых, выполнивших верно у-е задание теста; — среднее значение индивидуальных баллов испытуемых, выполнивших верно у-е задание теста; — среднее значение индивидуальных баллов испытуемых, выполнивших неверно у-е задание теста; — среднее значение индивидуальных баллов испытуемых, выполнивших неверно у-е задание теста; — стандартное отклонение по множеству значений индивидуальных баллов; — стандартное отклонение по множеству значений индивидуальных баллов; — число испытуемых, выполнивших верно у-е задание теста; — число испытуемых, выполнивших верно у-е задание теста; — число испытуемых, выполнивших неверно у-е задание теста; N —
общее число испытуемых, — число испытуемых, выполнивших неверно у-е задание теста; N —
общее число испытуемых,  ; и —
ордината нормированного нормального распределения в точке, за которой лежит 100% площади под нормальной кривой. ?? ?? ?? ; и —
ордината нормированного нормального распределения в точке, за которой лежит 100% площади под нормальной кривой. ?? ?? ??  ?? ?? ?? ??
Вычисление по формуле (9) требует использования специальных таблиц для нахождения ординат стандартной нормальной кривой и определенной математической подготовки.
Интерпретация.
Анализ значений коэффициента бисериальной корреляции в табл. 5.11 указывает на два довольно неудачных задания теста. Это те же самые третье  и восьмое и восьмое  = 0,26] задания. Полученный вывод дает ценную информацию о низкой валидности заданий 3 и 8 теста. Эти задания следует признать неудачными и для улучшения теста их необходимо удалить. = 0,26] задания. Полученный вывод дает ценную информацию о низкой валидности заданий 3 и 8 теста. Эти задания следует признать неудачными и для улучшения теста их необходимо удалить.
В целом задание можно считать валидным, когда значение  Под этот критерий подпадают все, кроме двух заданий (третьего и восьмого) рассматриваемого примера матрицы теста. Под этот критерий подпадают все, кроме двух заданий (третьего и восьмого) рассматриваемого примера матрицы теста.
Оценка валидности задания позволяет судить о том, насколько задание пригодно для работы в соответствии с общей целью создания теста. Если эта цель – дифференциация учеников по уровню подготовки, то валидные задания должны четко отделять хорошо подготовленных от слабо подготовленных учеников тестируемой группы.
Решающую роль в оценке валидности задания играет разность  . Чем выше значение этой разности, тем лучше работает задание на общую цель дифференциации испытуемых, выполняющих тест. Значит ?? . Чем выше значение этой разности, тем лучше работает задание на общую цель дифференциации испытуемых, выполняющих тест. Значит ??
|