| СОДЕРЖАНИЕ
1. Полные системы булевых функций
2. Сокращенные и тупиковые дизъюнктивные нормальные формы
3. Алгоритм Квайна и Мак-Класки минимизации булевой функции
4. Геометрическое представление логических функций
5. Геометрический метод минимизации булевых функций
6. Минимизация булевой функции с помощью карты Карно
7. Построение оптимальных контактно-релейных схем
Упражнения
Библиографический список
1. Полные системы булевых функций
Напомним, что булевой функцией называют функцию  , у которой все независимые аргументы , у которой все независимые аргументы  и сама функция являются логическими переменными, принимающими только два значения: 0 и 1. Эти функции могут быть заданы аналитически в виде пропозициональной формулы (ПФ) геометрически или с помощью таблиц истинности. Например, все элементарные булевы функции двух переменных представлены таблицей истинности 1. и сама функция являются логическими переменными, принимающими только два значения: 0 и 1. Эти функции могут быть заданы аналитически в виде пропозициональной формулы (ПФ) геометрически или с помощью таблиц истинности. Например, все элементарные булевы функции двух переменных представлены таблицей истинности 1.
Таблица 1
| №
|
X1
= 0
X2
= 0
|
0
1
|
1
0
|
1
1
|
fk
(X1
, X2
)
|
| 1
|
0
|
0
|
0
|
0
|
f1
= 0
|
| 2
|
0
|
0
|
0
|
1
|

|
| 3
|
0
|
0
|
1
|
0
|

|
| 4
|
0
|
0
|
1
|
1
|

|
| 5
|
0
|
1
|
0
|
0
|
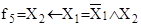
|
| 6
|
0
|
1
|
0
|
1
|
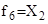
|
| 7
|
0
|
1
|
1
|
0
|

|
| 8
|
0
|
1
|
1
|
1
|
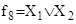
|
| 9
|
1
|
0
|
0
|
0
|
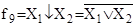
|
| 10
|
1
|
0
|
0
|
1
|

|
| 11
|
1
|
0
|
1
|
0
|

|
| 12
|
1
|
0
|
1
|
1
|
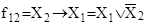
|
| 13
|
1
|
1
|
0
|
0
|
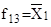
|
| 14
|
1
|
1
|
0
|
1
|

|
| 15
|
1
|
1
|
1
|
0
|

|
| 16
|
1
|
1
|
1
|
1
|
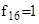
|
Функция f1
называется нулевой; f16
– единичной; f2
– конъюнкцией; f8
– дизъюнкцией; f11
и f13
– отрицаниями Х1
и Х2
соответственно; f12
и f14
– импликациями; f3
и f5
– коимпликациями; f10
– эквиваленцией; f7
– сложением по модулю два или разделительной дизъюнкцией; f9
– стрелкой Пирса (функцией Вебба); f15
– штрихом (функцией) Шеффера.
Функцию, полученную из элементарных путем перенумерации аргументов и подстановки вместо аргументов в некоторых других булевых функций, называют суперпозицией функций. Нетрудно убедиться, что любая булева функция от n аргументов является суперпозицией элементарных функций, заданных табл. 1. Например, функция

является суперпозицией элементарных функций: отрицания, дизъюнкции, конъюнкции и импликации.
Система булевых функций называется полной, если любая булева функция является суперпозицией этих функций.
В последнем столбце таблицы 1 показано, что все элементарные функции двух переменных, следовательно, и любые булевы функции, могут быть записаны с помощью трех логических операций 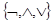 . Поэтому справедлива следующая теорема . Поэтому справедлива следующая теорема
Теорема.
Отрицание, дизъюнкция и конъюнкция образуют полную систему булевых функций
Этот набор булевых функций наиболее удобен для построения сложных булевых функций и чаще всего используется в приложениях, однако он не является минимальным и может быть еще сокращен.
Полная система булевых функций называется базисом, если она перестает быть полной при удалении хотя бы одной из этих функций.
Согласно этому определению система булевых функций 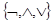 не является базисом. Действительно, применяя законы де-Моргана не является базисом. Действительно, применяя законы де-Моргана
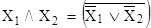 , ,  , ,
конъюнкцию в булевой функции можно заменить на дизъюнкцию и отрицание, а дизъюнкцию – на конъюнкцию и отрицание. Следовательно, отрицание и дизъюнкция (отрицание и конъюнкция) также образуют полную систему булевых функций. Нетрудно убедиться, что наборы 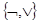 и и 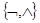 являются базисными, так как их дальнейшее сокращение без нарушения полноты системы невозможно. являются базисными, так как их дальнейшее сокращение без нарушения полноты системы невозможно.
Для проверки полноты заданной системы булевых функций может быть использовано следующее очевидное утверждение:
Если система  - полная и любая из функций f1
, f2
,...,fm
может быть выражена с помощью суперпозиций через функции g1
, g2
,…, gk
, то система - полная и любая из функций f1
, f2
,...,fm
может быть выражена с помощью суперпозиций через функции g1
, g2
,…, gk
, то система 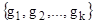 также полная. также полная.
Пример
1
. Доказать полноту системы 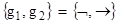 . .
Для доказательства воспользуемся системой  , полнота которой уже доказана, эти функции можно выразить через g1
и g2
по формулам: , полнота которой уже доказана, эти функции можно выразить через g1
и g2
по формулам:
f1
=g1
, 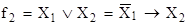 , ,
следовательно система функций  является полной. является полной.
В общем случае для проверки полноты системы булевых функций используется критерий полноты Поста. Прежде чем его сформулировать, напомним некоторые определения [3].
Функция f = (Х1
,Х2
,...,Хn
) называется функцией, сохраняющей константу
0 (1 ), если
f(0,0, ...0) = 0, (f(l, 1....1) = 1).
Функция f (X1
,X2
,...,Xn
) называется самодвойственной,
если
f (X1
,X2
,..., Xn
) =  . .
Функция f (X1
,X2
,...,Xn
) называется монотонной,
если для любых двух наборов X = (X1
,X2
,…,Xn
) и Y = (Yl
,
Y2
,...,Yn
), таких, что X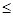 Y (для любого i Xi Y (для любого i Xi
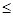 Yi
) имеет место неравенство: Yi
) имеет место неравенство:
f (X1
,X2
,..., Xn
) 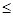 f (Yl,
Y2
,...,Yn
). f (Yl,
Y2
,...,Yn
).
Функция f (X1
,X2
,..., Xn
) называется линейной,
если
f (X1
,X2
,..., Xn
) = 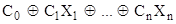 , ,
где 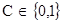 . .
Первые четыре свойства проверяются с помощью таблицы истинности, а для проверки линейности функции необходимо построить многочлен Жегалкина.
Например, из табл. 1 следует, что f2
= X1
ÙX2
и f8
= X1
ÚX2
– функции, сохраняющие константу 0; f10
= X1
↔X2
– функция, не сохраняющая константу 0, но сохраняющая константу 1; f7
= X1
 X2
- несамодвойственная функция; f2
, fg
– монотонные функции; f14
= X1
→X2
– немонотонная функция, так как монотонность нарушается на набоpax (0, 0) и (1, 0); f3
- нелинейная функция, так как соответствующий ей многочлен Жегалкина X1
+ X2
+ X1
X2
– нелинеен. X2
- несамодвойственная функция; f2
, fg
– монотонные функции; f14
= X1
→X2
– немонотонная функция, так как монотонность нарушается на набоpax (0, 0) и (1, 0); f3
- нелинейная функция, так как соответствующий ей многочлен Жегалкина X1
+ X2
+ X1
X2
– нелинеен.
Теорема Поста.
Система в = {f1
, f2
, ... fm
} булевых функций является полной тогда и только тогда, когда среди функций этой системы существуют: функция, не сохраняющая константу 0, функция, не сохраняющая константу 1, а также нелинейная, несамодвойственная и немонотонная функции.
Пример 2.
Доказать полноту системы 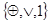 . .
Решение.
Пусть K0
– класс функций, сохраняющих константу 0; К1
– класс функций, сохраняющих константу 1; Кл
, Kc
, Км
– классы линейных, самодвойственных и монотонных функций соответственно.
Составим таблицу Поста следующего вида.
Таблица 2
| №
|
φi
|
K0
|
К1
|
Кл
|
Kc
|
Км
|
| 1
|
X1
 X2 X2
|
+
|
–
|
+
|
–
|
–
|
| 2
|
X1
Ú X2
|
+
|
+
|
–
|
–
|
+
|
| 3
|
1
|
–
|
+
|
+
|
–
|
–
|
Знак "+", стоящий на пересечении i- й строки и j-гo столбца этой таблицы, показывает, что функция φi
– принадлежит соответствующему классу, записанному в j-ом столбце,
Из табл. 1 видим, что φ1
=
f7
не сохраняет константу 1 и не является монотонной, φ2
= f8
– нелинейная и несамодвойственная функция, φ3
= f16
не сохраняет константу 0. Следовательно, все условия теоремы Поста выполнены, и заданная система 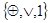 является полной. является полной.
Пример 3.
Доказать, что система {|} является базисом.
Решение.
Рассматриваемая система состоит из одной функции f15
(функции Шеффера). Из табл. 1 видим, что f15
– функция, не сохраняющая 0 и 1, немонотонная (монотонность нарушается на наборах (1, 0) и (1, 1), несамодвойственная, так как  , a двойственная функция , a двойственная функция  нелинейная, так как многочлен Жегалкина для этой функции имеет вид: 1 + X1
X2
. Следовательно, система {f15
} = {|} удовлетворяет всем условиям теоремы Поста и является базисом. нелинейная, так как многочлен Жегалкина для этой функции имеет вид: 1 + X1
X2
. Следовательно, система {f15
} = {|} удовлетворяет всем условиям теоремы Поста и является базисом.
Исследуя различные наборы функций, можно показать, что для множества булевых функций двух переменных существуют 17 различных базисов, в каждом из которых нельзя вычеркнуть ни одну функцию без потери полноты. Наиболее распространенными из них являются конъюнктивный базис Буля
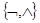 , дизъюнктивный базис Буля , дизъюнктивный базис Буля
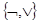 . импликативныи базис . импликативныи базис
 . базис Шеффера
{|}, базис Жегалкина . базис Шеффера
{|}, базис Жегалкина
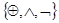 . .
Таким образом, для
аналитического задания булевой функции можно использовать различные языки формул. Критерием выпора должен служить характер рассматриваемой задачи.
2. Сокращенные и тупиковые дизъюнктивные нормальные формы
Известно [4], что всякую булеву функцию можно записать, причем единственным образом, в ДНФ, то есть в виде дизъюнкции элементарных конъюнкций (суммы произведений). В связи с этим можно ставить вопрос об отыскании для заданной функций такой ДНФ, которая была бы наиболее простой по сравнению с ее другими ДНФ.
ДНФ называется минимальной,
если она содержит по сравнению с другими эквивалентными ей формами минимальное количество букв (при подсчете учитывается каждое вхождение буквы в формулу).
В простейших случаях минимизацию функции можно осуществить, выписав все ДНФ для этой функции и выбрав, из них минимальную. Однако такой примитивный метод очень трудоемок, и мы рассмотрим ниже более оптимальные способы решения этой задачи.
Элементарную конъюнкцию φк
назовем импликантой
булевой функции f, если не существует такого двоичного набора переменных, при котором функция φк
принимает значение 1, а функция f – значение 0, то ecть φk
Ú f = f.
Для того чтобы проверить является ли заданная элементарная конъюнкция импликантой функции f, следует всем переменным, которые входят в эту конъюнкцию без знака отрицания, придать значение 1, а тем переменным, которые входят с отрицанием –
значение 0. Тогда элементарная конъюнкция будет иметь истинностное значение 1. После этого следует, проверить, принимает ли функция f значение 1 при любых значениях остальных переменных. В дальнейшем для упрощения записибулевых функций знаки коньюнкции будем заменять знаками умножения или просто опускать.
Пример 4.
Проверить, являются ли одночлены 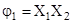 и и 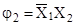 импликантами булевой функции импликантами булевой функции
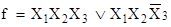 . .
Решение.
Полагая в первом случае Х1
= 1, X2
= 1, имеем φ1
= l и φ2
= l и
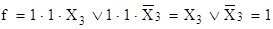 , ,
следовательно, φ2
– импликанта заданной функции.
Во втором случае полагаем X1
= 0, X2
= l. Тогда
φ2
= 1, а  , ,
следовательно, φ2
не является импликантой функции f.
Справедливы следующие утверждения:
1. Если  импликанты булевой функции f, то импликанты булевой функции f, то  и и  также являются ее импликантами. также являются ее импликантами.
2. Если функция  есть импликанта функции f, то функции есть импликанта функции f, то функции 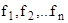 также являются импликантами функции f. также являются импликантами функции f.
Элементарная конъюнкция, входящая в ДНФ булевой функции, называется ее простой импликантой,
если никакая ее часть не является импликантой этой функции.
Сокращенной ДНФ
данной булевой функции называется ее ДНФ, составленная только из простых импликант.
Для приведения булевой функции к сокращенной ДНФ используется, так называемое правило склеивания.
Оно заключается в следующем. Логическую сумму двух элементарных конъюнкций, отличающихся только знаком отрицания над одной из переменных, можно заменить одной элементарной конъюнкцией, которая является общей частью рассматриваемых слагаемых, т.е.
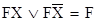 . .
Например,
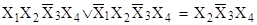
Для любой заданной функции сокращенная ДНФ является единственной. Однако онa может быть избыточной вследствие тогo, что некоторые простые импликанты этой суммы покрываются совокупностями других слагаемых. Такие импликанты называют лишними,
и они могут быть удалены без нарушения равносильности формул.
Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой ДНФ
Исключение лишних импликант из сокращенной ДНФ проводится с помощью правила поглощения:
дизъюнкцию двух элементарных конъюнкций, из которых одна полностью содержится и другой, можно заменить конъюнкцией, имеющей меньший ранг, например, X Ú XF = X,
 . .
Правила склеивания, и поглощения легко доказываются с помощью таблиц истинности. Кроме этих правил, при минимизации функции могут быть использованы любые известные равносильности.
Пример 5.
Упростить булеву функцию  . .
Решение.
Эта функция содержит только простые импликанты, т. е. является сокращенной Однако она избыточна, так как одночлен Х1
X2
можно удалить, не разрушая равносильности. После этого получим функцию:
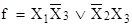 . .
Пример 6.
Найти минимальную ДНФ для функции
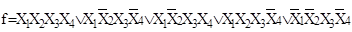 . .
Решение.
Склеивая первый и третий одночлены по переменкой Х2
, получим Х1
X3
X4
. Из первого и четвертого, а затем из второго и третьего слагаемых после склеивания получим соответственно X1
X2
X3
,  и т. д. Окончательный список импликант имеет вид и т. д. Окончательный список импликант имеет вид
В этом списке имеется два одночлена X1
X3
и Х2
Х3
Х4
, которые не поглощают других одночленов из этого списка, следовательно, являются простыми импликантами. Поэтому сокращенная ДНФ имеет вид
 , ,
οна же является и минимальной
В общем случае процесс построения минимальных ДНФ может быть охарактеризован следующей схемой.
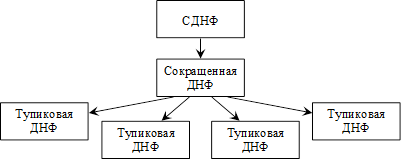
Рис. 1
Сначала получают сокращенную ДНФ. Далее однозначный процесс переходит в ветвящийся процесс построения всех тупиковых ДНФ и, наконец, из тупиковых ДНФ выделяются минимальные. Самым трудоемким этапом этого процесса является построение тупиковых ДНФ. Его можно немного упростить, заранее удалив часть членов сокращенной ДНФ, не участвующих в построении тупиковых ДНФ и тем самым сократить количество просматриваемых подмножеств
Проблема минимизации является важнейшей для технических приложений логических функций и ей посвящено много работ, в которых предложены различные алгоритмы решения этой задачи. Рассмотрим подробнее один из таких алгоритмов.
3. Алгоритм Квайна и Мак-Класки минимизации булевой функции
Этот алгоритм используется наиболее часто, так как он может быть реализован на ЭВМ, и при его применении практически отсутствуют ограничения на число переменных. Минимизацию функции в этом методе рекомендуется выполнить в следующей последовательности.
1. Привести булеву функцию к СДНФ.
2. В СДНФ произвести все возможные склеивания Полученная после этого ДНФ является сокращённой, но среди простых импликант могут оказаться лишние.
3. Перейти от сокращённой ДНФ к минимальной, т.е. исключить лишние импликанты. Для этого рекомендуется воспользоваться импликантой матрицей,
в которой каждой строке соответствует простая импликанта, а каждому столбцу – конституента ( элементарная конъюнкция, содержащая все переменные) СДНФ заданной функции Эта матрица заполняется следующим образом под конституентами, в которые входит данная простая импликанта, ставится метка "1" Для нахождения минимального покрытия функции необходимо удалить из таблицы некоторые лишние простые импликанты С этой целью реализуется следующий алгоритм.
1. Выделение ядра Квайна.
Если в каком-либо столбце импликантной матрицы имеется только одна 1, то импликанта, находящаяся в соответствующем столбце, не является лишней и должна быть включена в минимальное покрытие функции. Такие импликанты называются существенными,
а их совокупность называют ядром
Квайна.
Вычёркивая строки, в которых находятся существенные импликанты, и столбцы, покрываемые этими импликантами, получаем матрицу меньших размеров Если в ней имеются столбцы, содержащие по одной 1, то операцию выделения существенных импликант следует повторить.
2 Сжатие по столбцам или строкам.
Из матрицы вычёркивается тот столбец, в который полностью входит какой-либо другой столбец и та строка, которая полностью покрывается другой.
После выполнения всех указанных действий в матрице останутся только те простые импликанты, которые входят в минимальное покрытие функции. Соединив эти импликанты и найденные ранее существенные импликанты знаками дизъюнкций, получим минимальную ДНФ заданной функции.
Пример 7
Минимизировать булеву функцию
 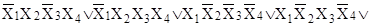
 . .
Решение.
Функция задана в ДНФ, поэтому займемся сразу отысканием простых импликант, проводя операцию склеивания. Для этого представим каждую элементарную конъюнкцию двоичным набором, ставя на k-ом месте 0, если Хk
входит с отрицанием, 1 – если без отрицания и знак "–", если эта переменная не входит в конъюнкцию Тогда функция примет вид:
 . .
Разобьем эти наборы на классы, в каждом из которых содержатся наборы с одинаковым числом единиц и расположим их в порядке возрастания суммы всех чисел набора (рис 2 а
)
Для исключения переменных по правилу склеивания сравним все наборы всех смежных классов. Если при этом какая-либо переменная исключается, то в разряд, соответствующий этой переменной, записываем прочерк. Например, двоичные наборы 0100 и 0101 образуют набор 010–. Все полученные наборы опять разбиваем на классы. Объединяем снова наборы из двух смежных классов, причём сравнению подлежат только те, у которых прочерк находится в одном и том же разряде, получаем новый набор импликант (рис. 2 в
). Нетрудно убедиться, что дальнейшее объединение наборов невозможно, следовательно, все полученные импликанты – простые.
Построим импликантную матрицу (табл. 3 а
). Выделяя столбцы, содержащие по одной единице, находим существенные импликанты, образующие ядро Квайна: 0–0– –0–0. При этом первая из них является существенной для 0000, 0001, 0100, 0101, а вторая – для 0000, 0010, 1000, 1010. Вычёркивая столбцы с этими конституентами и строки с существенными импликантами, получим табл. 3 б
. В этой таблице нет столбцов, содержащих только одну единицу, следовательно существенных импликант в этой таблице нет и ядро Квайна состоит из двух импликант, найденных выше: 0–0– и –0–0.
Переходим к операциям сжатая по строкам и столбцам. Вторая строка табл. 3 б
поглощает первую, а четвёртая – третью, поэтому первую и третью строки можно вычеркнуть (табл. 3 в
).
В табл. 3 в
первый столбец полностью входит в четвёртый, а второй – в третий, После вычеркивания четвертого и третьего столбцов таблица принимает вид 3 г
. Из этой таблицы видно, что импликанта 111– является лишней, так как не содержит единиц ни в одном столбце, а две остальные входят в минимальное покрытие. Таким образом, заданная функция имеет четыре простых импликанты: 0–0–, –0–0, 1––0 и –111. Объединяя их знаком дизъюнкции, получаем минимальную ДНФ в виде
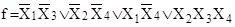 . .
Алгоритм Квайна позволяет получать минимальные дизъюнктивные нормальные формы заданных функций Однако в ряде случаев минимальные конъюнктивные нормальные выражения оказываются "меньше" дизъюнктивных, поэтому при решении задач минимизации желательно получить не только дизъюнктивные, но и конъюнктивные нормальные формулы и выбрать из них наименьшее. Методы получения минимальных конъюнктивных выражений двойственны рассмотренным выше методам и мы не будем на них останавливаться.
4. Геометрическое представление логических функций
Обозначим через Еn
множество всех наборов (α1
,..., αη
), состоящих из чисел ноль и единица. Множество Еn
называется n
-мерным кубом,
а набор (α1
, ..., αη
) - вершинами
куба.
Пусть σ1
, ..., σr
- фиксированный набор чисел из 0 и 1. Множество всех вершин (α1
,..., αη
) куба Еn
таких, что αi
1
= σ1
, αi
2
= σ2
, ... , αir
= σr
, 1 < i1
< i2
< ...< ir
, называется (n – r) - мерной гранью.
Очевидно, что (n – r)-мерная грань является (n – r) - подкубом куба Еn
.
Например, в трехмерном кубе Е3
наборы (0,0,1) и (0,0,0) образуют одномерную ( n = 3, r = 2) грань (ребро), а наборы (1,0,0), (1,0,1), (1,1,0), (1,1,1) - двухмерную грань.
Пусть f(X1
,X2
,…,Xn
) - произвольная булева функция. Ей сопоставляется в соответствие подмножество Νf
вершин куба Еn
, таких что (α1
, ..., αη
)  Nf
тогда и только тогда, когда f(α1
, ..., αη
) = l Очевидно, что по подмножеству Nf
исходная функция f(X1
, X2
., ... , Χn
) восстанавливается однозначно. Таким образом геометрический способ задания булевой функции заключается в задании множества вершин n
-
мерного куба Еn
, в которых данная функция истинна. Nf
тогда и только тогда, когда f(α1
, ..., αη
) = l Очевидно, что по подмножеству Nf
исходная функция f(X1
, X2
., ... , Χn
) восстанавливается однозначно. Таким образом геометрический способ задания булевой функции заключается в задании множества вершин n
-
мерного куба Еn
, в которых данная функция истинна.
Пример 8.
Пусть функция f(X1
, X2
, Х3
) задана табл. 4. Составить для нее множество Nf
.
Таблица 4
| X1
|
X2
|
X3
|
f(X1
, X2
, Х3
)
|
| 0
|
0
|
0
|
1
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
0
|
| 1
|
0
|
0
|
1
|
| 0
|
1
|
1
|
0
|
| 1
|
0
|
1
|
1
|
| 1
|
1
|
0
|
1
|
| 1
|
1
|
1
|
1
|
Решение.
Очевидно, что Nf
= {(0,0,0), (1,0,0), (1,0,1), (1,1,0), (1,1,1)}. Множество Nf
изображено на рис. 3.
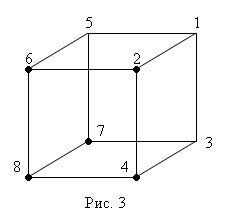
Напомним [1], что для любой булевой функции существует ее представление в СДНФ. Причём в алгоритме построения СДНФ используется только те наборы значений, при которых функция равна единице [3]. Это позволяет проинтерпретировать геометрическое представление функции следующим образом. Рассмотрим трёхмерный куб и занумеруем вершины так, как показано на рис. 4.
 Тогда его грани (двумерные подкубы) можно рассматривать как
Ребрами данного куба ( одномерными подкубами) будут, например,  , и т.д. , и т.д.
Пример 9.
Построить модель куба, соответствующего функции:
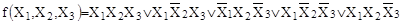 . .
Решение.
Первому слагаемому соответствует вершина 2, второму – вершина 6, третьему – вершина 3, четвертому – вершина 8, пятому – вершина 4 (рис. 5).

Пример 10.
Дана модель куба с помеченными вершинами (рис. 6). Составить СДНФ для данной булевой функции
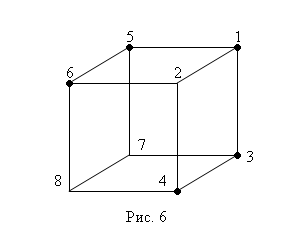
Решение
. Вершине 1 соответствует конъюнкция 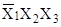 , вершинам 3 и 4 конъюнкция , вершинам 3 и 4 конъюнкция 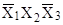 и и  соответственно; вершинам 5 и 6 - конъюнкции соответственно; вершинам 5 и 6 - конъюнкции  и и  . Следовательно, искомая СДНФ имеет вид . Следовательно, искомая СДНФ имеет вид
 . .
Заметим, что для функций, зависящих от четырёх и более переменных, геометрическое представление применяется очень редко, т.к. трудно построить наглядную модель n-мерного куба при n > 3. Поэтому в этом и следующих параграфах мы будем рассматривать только булевы функции трех аргументов, хотя все изложенное справедливо для других функций, зависящих от большого числа аргументов.
Перейдем теперь к геометрической постановке задачи минимизации булевых функций.
5. Геометрический метод минимизации булевой функции
Рассмотрим элементарную конъюнкцию ранга r (т.е. содержащую r пропозициональных переменных)

где ε = 0,1;  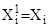 . Очевидно, что множество Nk
, соответствующее конъюнкции К, есть (3 – r)-мерная грань. Число r называется рангом
этой грани. . Очевидно, что множество Nk
, соответствующее конъюнкции К, есть (3 – r)-мерная грань. Число r называется рангом
этой грани.
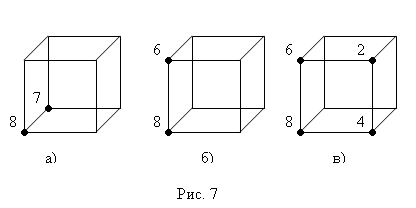
Пример 11
. Конъюнкциям
 , ,
 , ,
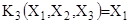
соответствуют грани (рис. 7 а
, б
, в
) , Nk
1
={7,8}, Nk
2
={8,6}, Nk
3
={6,2,4,8}, имеющие ранги 2, 2, и 1. Первые две грани являются одномерной гранью (ребром), а третья - двумерной гранью.
Отметим очевидные свойства введенного соответствия между булевой функцией f и подмножеством Nf
.
Если  , то , то
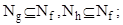
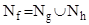 . .
В частности, если f(X1
, Χ2
, X3
) обладает ДНФ, т. е. 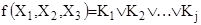 , то , то  и и 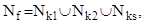 т.е. ДНФ функции f соответствует покрытие множества Ν, гранями т.е. ДНФ функции f соответствует покрытие множества Ν, гранями 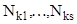 . .
Пример 12.
Рассмотрим представленную в СДНФ функцию
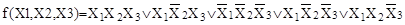 . .
модель куба, для которой построена на рис. 3. С помощью таблицы истинности может быть показано, что данная функция представима также ДНФ
 . .
Этим ДНФ соответствуют два покрытия множества Nf
:
 , ,
 , ,
где Nk1
={2}, Nk2
={6}, Nk3
={3}, Nk4
={8}, Nk5
={4}, Nk10
={2,6,8,4}, Nk20
={4,3}. Одно из этих покрытий - точечное, второе состоит из ребра и двумерной грани.
Пусть ri
- ранг гpани Νki
(он равен рангу конъюнкции ki
). Число r, определенное формулой
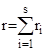 , ,
называется рангом
покрытия
. Тoгда задача о минимизации булевой функции принимает следующую геометрическую постановку: для данного множества Nf
, найти такое покрытие гранями, принадлежащими Nf
,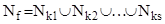 , чтобы его ранг был наименьшим. , чтобы его ранг был наименьшим.
Приведем также определения сокращенной и тупиковой ДНФ c геометрической точки зрения.
Грань Nk
, содержащаяся в Nf
, называется максимальной
относительно Nf
, если не существует грани  , такой, что , такой, что
1) 
2) размерность грани  больше размерности грани Nk
. больше размерности грани Nk
.
Пример 13
. Пусть f(X1
, Х2
, X3
) – функция, заданная табл. 4 и 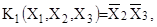 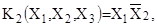  Тогда грани Νk
1
и Nk
3
являются максимальными, a Nk
2
не максимальна для Nf
, т. к. Тогда грани Νk
1
и Nk
3
являются максимальными, a Nk
2
не максимальна для Nf
, т. к.  и размерность Nk
3
больше размерности Nk
2
. и размерность Nk
3
больше размерности Nk
2
.
Конъюнкция К, соответствующая максимальной грани Nk
, называется простой импликантой
функции f.
ДНФ, являющаяся дизъюнкцией всех простых импликант функции f, называется сокращенной ДНФ
.
Покрытие множества Nf
, состоящее из максимальных относительно Nf
граней, называется неприводимым
, если совокупность граней, получающаяся из исходной путем выбрасывания любой грани, не будет покрытием Nf
.
ДНФ, соответствующая неприводимому покрытию множества Nf
называется тупиковой
в геометрическом смысле.
Теорема
. Понятия тупиковой ДНФ и тупиковой ДНФ в геометрическом смысле эквивалентны.
Алгоритм минимизации функций, зависящих от трех переменных, состоит в следующих четырех шагах:
1. Нанести множество Nf
, на трехмерный куб. Использовать или табличное задание функции, отметив вершины, в которых f(X1
, Χ2
, Χ3
) = 1, или СДНФ функции и тогда каждому слагаемому СДНФ поставить в соответствие вершину (см. раздел 5).
2. Если отмеченными окажутся все вершины куба, то данная функция тождественно истинна
3. Если отмечены все вершины какой-либо грани, то для построения минимальной формы заменить все четыре вершины одной переменной – названием грани.
4. Если отмечены вершины какого-либо ребра, то в минимизированной форме им соответствует конъюнкция – название ребра.
Чтобы получить минимизированную форму, надо выбирать ребра, покрывающие вершины, так, чтобы меньшим числом ребер покрыть все отмеченные вершины.
Пример 14
. Минимизировать функцию f(X1
, X2
, Х3
), заданную табл. 4.
Решение
. Множество Nf
для указанной функции изображено на рис. 3. Так как вершины 2, 4, 6, 8 принадлежат одной грани Χ1
, вершины 7 и 8 принадлежат ребру , то минимизированная форма функции f имеет вид , то минимизированная форма функции f имеет вид
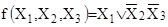 . .
Пример 15.
Минимизировать записанную в СДНФ функцию
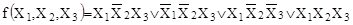 . .
Решение.
Отметим на модели куба элементарные конъюнкции: первой конъюнкции соответствует вершина 6, второй – вершина 5, третьей – вершина 8, четвертой – вершина 2 (рис 8). Таким образом, множество Nf
–построено. Ни одна грань не отмечена полностью, поэтому переходим к шагу 4 алгоритма.

Рис. 8
Вершины 5 и 6 принадлежат одному ребру 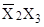 , вершины 6 и 8 – ребру , вершины 6 и 8 – ребру 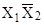 , следовательно, минимизированная форма имеет вид: , следовательно, минимизированная форма имеет вид:
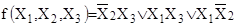 . .
Пример 16
. Минимизировать функцию f(X1
,X2
,X3
), заданную табл. 5.
Таблица 5
| Х1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
| Х2
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
| Х3
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
| f(X1
,X2
,X3
)
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
Решение
. Построим модель куба, соответствующего этой функции (рис.9).

Рис. 9
Грани (1, 2, 3, 4) соответствует X2
, грани (2, 4, 6, 8) – Х1
, следовательно, минимизированная форма имеет вид
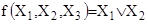 . .
Отметим, что при n = 3 геометрический метод минимизации булевых функций аналогичен минимизации с помощью прямоугольной таблицы, называемой, минимизирующей картой (картой Карно).
6.
Минимизация
булевой функции с помощью карты Карно
Карта Карно представляет собой таблицу для задания логических функций в СДНФ. Например, для функции, заданной табл. 5, карта Карно представлена в табл. 6.
Расположение клеток в таблице позволяет легко определить склеивающиеся между собой члены, так как каждой клетке карты Карно соответствует вершина куба. Допускающие склеивание конституенты располагаются в соседних ячейках по строкам и столбцам, или в виде квадратов и им соответствует одна импликанта, ранг которой меньше, чем ранги склеиваемых конституент. Заметим, что соседними считаются не только рядом стоящие ячейки, но и ячейки, находящиеся на противоположных концах любого столбца и любой строки.
Таблица 6
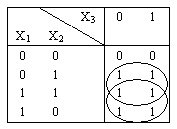
Так, склеивая конституенты, расположенные во второй и третьей строках табл. 6, получаем импликанту – – X2
, а конституентам двух последних строк соответствует импликанта Х1
– –. Следовательно, минимальная форма заданной булевой функции имеет вид (см. пример 16)
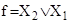 . .
Пример 17.
Минимизировать с помощью карты Карно функцию f(X1
, Х2
, Χ3
), заданную табл. 4.
Решение.
Построим для  минимизирующую карту (табл. 7) минимизирующую карту (табл. 7)
Таблица 7
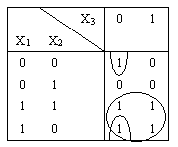
Объединим соседние клетки, соответствующие единичным значениям функции f, в максимальные интервалы, как показано в табл. 7. Сопоставим каждому максимальному интервалу импликанты Χ1
и  . Следовательно, минимальная форма имеет вид: . Следовательно, минимальная форма имеет вид:
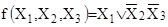 . .
Пример 18.
Минимизировать булеву функцию
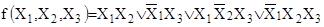 . .
Решение.
Используя таблицы истинности, построим для заданной функции f карту Карно (табл. 8).
Объединим соседние клетки, соответствующие единичному значению функции, в максимальные интервалы, как показано в табл. 8. Следовательно, минимальная форма данной функции имеет вид
Таблица 8

 . .
Если булева функция f зависит от четырех аргументов, то с помощью минимизирующей карты можно находить сокращенную ДНФ.
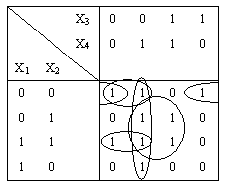
Пример 19.
Пусть функция f(X1
, X2
, Х3
, Х4
) задана та6л. 9. Построить сокращенную ДНФ.
Решение.
Максимальные интервалы, соединяющие клетки, соответствующие единичным значениям функции f, выбираются так, как показано в табл. 9. Сопоставляя им простые импликанты, получим сокращенную ДΗΦ.
Таблица 9
7. Построение оптимальных контактно-релейных схем
Проблема проектирования логических схем сводится к отысканию оптимальной эквивалентной схемы, состоящей из возможно меньшего числа элементов. С математической точки зрения эта проблема сводится к задаче минимизации булевой функции, соответствующей заданной схеме. Для построения оптимальной схемы необходимо сделать следующее.
1. По заданной схеме составить соответствующую ей булеву функцию.
2. Привести эту функцию к ДНФ.
3. Минимизировать записанную в ДНФ булеву функцию одним из описанных выше способов
4. Построить релейно-контактную схему, соответствующую минимальной ДНФ.
Приведем примеры.
Пример 20.
Построить оптимальную релейно-контактную схему, эквивалентную схеме на рис. l0.
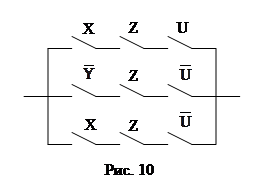
Решение
.
1. Составим по этой схеме булеву функцию
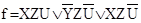 . .
2. Эта функция записана в ДНФ, поэтому предварительных ее преобразований не требуется.
3. Склеиваем первый член с третьим:
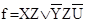 . .
4. Строим релейно-контактную схему, соответствующую полученной функции:

В упрощенной схеме вместо 9 контактов используются только 5.
Пример 21.
Построить оптимальную релейно-контактную схему, эквивалентную схеме на рис. 12.

Решение.
1. Заданной схеме соответствует булева функция
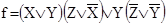 . .
2. Представим эту функцию в ДНФ
 . .
3. Склеивая второй член с четвертым, а затем проводя операцию поглощения, получим
 . .
4. Строим оптимальную релейно-контактную схему (рис. 13).

Упражнения
1. Минимизировать с помощью карт Карно следующие булевы функции:
а) 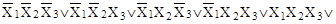
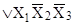 ; ;
б) 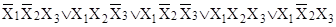 ; ;
в) 
  ; ;
г) 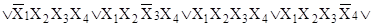  ; ;
д)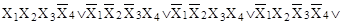 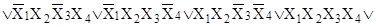 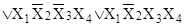 ; ;
е)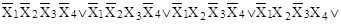  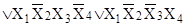 . .
2. Минимизировать булевы функции методом Квайна:
а) 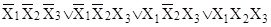 ; ;
б) 
 ; ;
в) 
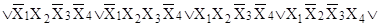
 ; ;
г) 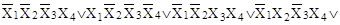
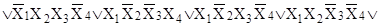
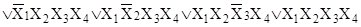 . .
3. Построить для булевой функции  модель куба и минимизировать её. Функция f задана табл. 10, 11, 12. модель куба и минимизировать её. Функция f задана табл. 10, 11, 12.
Таблица 10
| X1
|
X2
|
X3
|
f(X1
,X2
,X3
)
|
| 0
|
0
|
0
|
1
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
1
|
| 1
|
0
|
0
|
0
|
| 0
|
1
|
1
|
1
|
| 1
|
0
|
1
|
1
|
| 1
|
1
|
0
|
0
|
| 1
|
1
|
1
|
1
|
Таблица 11
| X1
|
X2
|
X3
|
f(X1
,X2
,X3
)
|
| 0
|
0
|
0
|
0
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
1
|
| 1
|
0
|
0
|
1
|
| 0
|
1
|
1
|
0
|
| 1
|
0
|
1
|
0
|
| 1
|
1
|
0
|
1
|
| 1
|
1
|
1
|
1
|
Таблица 12
| X1
|
X2
|
X3
|
f(X1
,X2
,X3
)
|
| 0
|
0
|
0
|
1
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
1
|
| 1
|
0
|
0
|
1
|
| 0
|
1
|
1
|
1
|
| 1
|
0
|
1
|
0
|
| 1
|
1
|
0
|
1
|
| 1
|
1
|
1
|
0
|
4. Построить для булевой функции f(X1
,X2
,X3
), записанной в СДНФ, модель куба и минимизировать функцию f:
a) 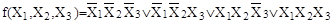 ; ;
б) 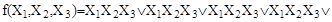  ; ;
в) 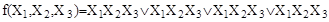 . .
5. Для заданной модели куба (рис. 14 а
, б
, в
) записать булеву функцию  в СДНФ и минимизировать её. в СДНФ и минимизировать её.
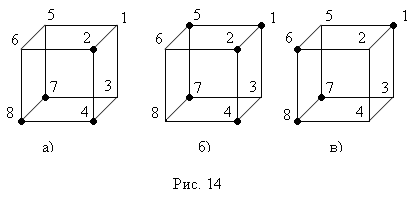
6. Построить оптимальные контактно-релейные схемы для схем, заданных на рис. 15–18.


 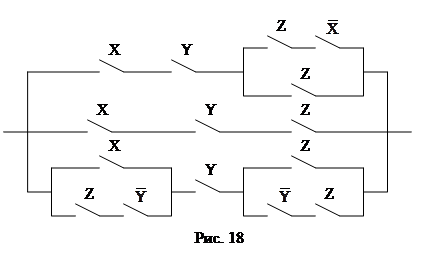
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Нефедов В.Н. Курс дискретной математики / В.Н. Нефедов, В.А. Осипова: Изд-во МАИ, 1992. 262 с.
2. Яблонский С.В. Введение в дискретную математику / С.В. Яблонский. Μ.: Наука, 1979. 272 с.
3. Леденева Т.М. Специальные главы математики. Дискретная математика: учеб. пособие / Т.М. Леденева. Воронеж: ВГТУ, 1997. 130 с.
4. Кретова Л.Д. Элементы математической логики: методические указания к практическим и индивидуальным занятиям / Л.Д. Кретова, Н.Б. Ускова, В.В. Посметьев. Воронеж: ВГТУ, 2005. 21 с.
|