| А.В. Андрейчиков О.Н. Андрейчикова
АНАЛИЗ, СИНТЕЗ, ПЛАНИРОВАНИЕ РЕШЕНИЙ В ЭКОНОМИКЕ
Рекомендовано Министерством образования Российской Федерации в качестве учебника
для студентов высших учебных заведений, обучающихся по специальности "Информационные системы в экономике"
МОСКВА
"ФИНАНСЫ И СТАТИСТИКА-2000
РЕЦЕНЗЕНТЫ:
кафедра "Информационные системы в экономике"
Тверского государственного технического университета (зав. кафедрой доктор технических наук, профессор Б. В. Палюх
);
зам. директора по научной работе Санкт-Петербургского института информатики и автоматизации РАН доктор технических наук, профессор А. В. Смирнов
Работа выполнена при финансовой поддержке Волгоградского государственного технического университета
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ................................................................................................................................................................................................... 1
К ЧИТАТЕЛЮ................................................................................................................................................................................................... 2
ПРЕДИСЛОВИЕ................................................................................................................................................................................................ 4
ГЛАВА 1. АНАЛИЗ ЗАДАЧ И МЕТОДОВ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ.......................................................................... 5
1.1. Эволюция теории принятия решений. ЭВМ в принятии решений...................................................................................... 5
1.2. Схема процесса принятия решений................................................................................................................................................ 6
1.3. Классификация задач принятия решений.................................................................................................................................... 7
1.4. Классификация методов принятия решений.............................................................................................................................. 8
1.5. Характеристика методов теории полезности......................................................................................................................... 10
ГЛАВА 2.
ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ МЕТОДА АНАЛИЗА ИЕРАРХИЙ........................................................... 14
2.1. Иерархическое представление проблемы, шкала отношений и матрицы парных сравнений......................... 14
2.2. Собственные векторы и собственные значения матриц. Оценка однородности суждений............................. 17
2.3. Синтез приоритетов на иерархии и оценка ее однородности......................................................................................... 19
2.4. Учет мнений нескольких экспертов............................................................................................................................................. 21
2.5. Методы сравнения объектов относительно стандартов и копированием................................................................ 23
2.6. Многокритериальный выбор на иерархиях с различным числом и составом альтернатив под критериями.............................................................................................................................................................................................................. 27
2.7. Методика решения прикладных задач на ЭВМ...................................................................................................................... 32
2.7.1. Выбор и прогнозирование наилучшего обеспечения банковского кредита........................................................................... 32
2.7.2. Функционально-стоимостный анализ промышленной продукции........................................................................................... 40
2.7.3. Рациональное распределение ресурсов между альтернативами............................................................................................ 46
ГЛАВА 3.
АНАЛИТИЧЕСКОЕ ПЛАНИРОВАНИЕ НА ОСНОВЕ МЕТОДА АНАЛИЗА ИЕРАРХИЙ............................ 51
3.1. Принципиальные подходы к решению задач планирования........................................................................................... 51
3.2. Представление процесса планирования в виде иерархии................................................................................................. 52
3.3. Способы определения желаемых сценариев........................................................................................................................... 59
3.4. Методика решения прикладных задач на ЭВМ...................................................................................................................... 63
3.4.1. Прогнозирование профессиональной занятости населения крупных городов..................................................................... 63
3.4.2. Планирование предприятием производственной деятельности в условиях конкуренции............................................... 68
3.4.3. Планирование развития отрасли...................................................................................................................................................... 75
ГЛАВА 4.
МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ............................... 84
4.1. Элементы теории нечетких множеств........................................................................................................................................ 84
4.2. Нечеткие операции, отношения и свойства отношений................................................................................................... 85
4.3. Многокритериальный выбор альтернатив на основе пересечения нечетких множеств..................................... 87
4.4. Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения............................. 88
4.5. Многокритериальный выбор альтернатив с использованием правила нечеткого вывода................................ 89
4.6. Многокритериальный выбор альтернатив на основе аддитивной свертки............................................................... 91
4.7. Ранжирование альтернатив на множестве лингвистических векторных оценок................................................. 92
4.8. Методика решения прикладных задач на ЭВМ...................................................................................................................... 93
4.8.1. Многокритериальный выбор методом максимннной свертки в сфере банковского кредитования.............................. 93
4.8.2. Выбор конкурентоспособного товара методом нечеткого отношения предпочтения................................................... 98
4.8.3. Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера.............................................................................................................................................................................................................. 100
4.8.4. Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки...................................................... 108
4.8.5. Выбор предприятия для кредитования методом лингвистических векторных оценок................................. 110
4.8.6. Сравнительный анализ различных методов принятия решений............................................................................................ 111
Глава 5.
МЕТОДЫ
КОМБИНАТОРНО-МОРФОЛОГИЧЕСКОГО АНАЛИЗА И СИНТЕЗА
РАЦИОНАЛЬНЫХ СИСТЕМ................................................................................................................................................................................................................. 120
5.1. Классификация задач анализа и синтеза систем.............................................................................................................. 121
5.2. Постановка задач анализа и синтеза систем...................................................................................................................... 121
5.4. Кластерный анализ морфологических множеств............................................................................................................... 128
5.5. Синтез новых и рациональных систем на морфологических множествах........................................................... 145
5.6. Методика решения прикладных задач на ЭВМ.................................................................................................................... 167
5.6.1. Анализ и синтез систем на основе функционально-стоимостного подхода...................................................................... 167
5.6.2. Рациональное распределение ресурсов в системах................................................................................................................... 172
Глава 6.
ЭВРИСТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА СИСТЕМ................................................................................................. 176
6.1. Классификация эвристических методов синтеза............................................................................................................... 177
6.2. Фонд эвристических приемов....................................................................................................................................................... 178
6.3. Метод "мозгового штурма"............................................................................................................................................................ 179
6.4. Методы ассоциаций и аналогий................................................................................................................................................. 180
6.5. Синектика............................................................................................................................................................................................... 182
6.6. Методы контрольных вопросов и коллективного блокнота.......................................................................................... 182
6.7. Метод "матриц открытия"............................................................................................................................................................... 183
6.8. Алгоритм решения изобретательских задач........................................................................................................................... 183
6.9. Автоматизация эвристических методов синтеза новых систем................................................................................ 185
Глава 7.
АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ ПРИНЯТИЯ, ПЛАНИРОВАНИЯ И СИНТЕЗА РЕШЕНИЙ... 190
7.1. Необходимость автоматизации процессов принятия, планирования и синтеза решений............................. 191
7.2. Предпосылки создания диалоговых систем синтеза и принятия решений............................................................ 191
7.3. Классификация систем принятия и синтеза решений...................................................................................................... 192
7.4. Принципы разработки программных средств........................................................................................................................ 194
7.5. Основные правила разработки систем...................................................................................................................................... 194
7.6. Требования к методам защиты информации........................................................................................................................ 195
7.7. Функции и структура автоматизированной системы принятия, планирования и синтеза решений........ 196
ПРИЛОЖЕНИЕ............................................................................................................................................................................................. 200
К ЧИТАТЕЛЮ
Перед Вами, уважаемый читатель, учебник для экономической специальности "Информационные системы в экономике". Возможно, бегло пролистав его, Вы начнете сомневаться в его статусе и принадлежности. И в самом деле, учебник обычно пишется под утвержденную программу курса, а ее наличие Вам неизвестно (в действительности ее нет). Кроме того, оказывается, по Вашему мнению, что использованный математический аппарат по сложности существенно выше среднего, общепринятого для экономистов.
После того как я поделился подобными своими сомнениями в редакции, мне был задан вопрос: "А купили бы Вы этот учебник для себя?" Ответ был однозначным: "Купил бы и куплю при любой цене". И вот почему. Учебной программы и учебника нет. Но это не вина авторов. Возможно, их учебник и подтолкнет специалистов из Учебно-методического объединения при Министерстве образования Российской Федерации к разработке и утверждению программы.
Сложная математика, много формул? Но ведь это только для российских и других посткоммунистических экономистов, и то не для всех, она сложная. Когда в течение 75 лет основная задача нашей экономики состояла главным образом в объяснении уже принятых вышестоящим руководством решений, математике и ее прикладным возможностям не было места и ничего не оставалось, как заниматься не очень нужными практике, придуманными математиками самими для себя мало кому понятными моделями и алгоритмами. В зарубежной же науке никогда не было и нет деления на "экономику" (без математики) и "математическую экономику". Хорошее, близкое к требованиям математических факультетов университетов владение аппаратом экономико-математического моделирования — стандарт западного экономического образования.
По мере становления в нашей стране рыночной экономики ситуация начала меняться. Стало очевидным, что бизнес будет платить и уже во многих случаях платит за обоснованные расчетами и анализом (далеко выходящими за рамки четырех действий арифметики) инвестиционные проекты, прогнозы, рекомендации по снижению и предотвращению риска и пр. В этих условиях экономика от апологетико-вербальной ориентации начала поворачиваться к естественно-научным дисциплинам, хотя, конечно, никогда ее положения нельзя ставить в один ряд с точными законами естествознания.
Необходимость математизации экономики на современном этапе становится все более ясной не только ученым, но и практикам и, как следствие, руководителям системы высшего образования. Без этого невозможна интеграция нашей экономики в мировую экономическую систему: мы просто не будем их понимать. Однако, как и во многом другом, на этом пути есть свои проблемы.
Большинство наших экономистов не владеют в должной мере современными экономико-математическими методами. Отсюда трудности в качественной подготовке молодых кадров, боязнь формул. Совершенно неприемлемо, когда аспиранты (по специальности "Экономико-математические методы") допускают в диссертациях порой грубые математические ошибки, и последние исправляются по подсказке научного руководителя или оппонентов "в пожарном порядке".
Предлагаемый вниманию читателей учебник написан на высоком математическом уровне. Может ли он вызвать трудности при изучении методов компьютерного моделирования экономических процессов? Да, может. Прежде всего тем, что далеко выходит за рамки четырех действий арифметики. Он отражает чрезвычайно широкое проникновение экономико-математических методов во все сферы принятия решений, причем не только экономической ориентации. По этой причине его следует рекомендовать в первую очередь, как отмечают сами авторы, преподавателям и аспирантам. Тем и другим, скорее всего, потребуется еще адаптировать материал учебника к читаемым курсам, рабочим программам и уровням подготовки студентов, темам диссертаций аспирантов.
В чем специфика учебника?
При широком, воистину энциклопедическом охвате изучаемой проблематики изложение материала во многих местах, по-видимому, неизбежно становится поверхностным, обзорным, с необходимостью ссылок на дополнительные источники. Нарушается очень важный принцип самодостаточности учебника, причем многие из ссылок оказываются в настоящее время для разных категорий читателей практически недоступными. Например, при характеристике методов теории полезности, стремясь, вероятно, ничего не упустить, авторы сводят всю информацию о фундаментальном направлении — функции полезности по Дж. Нейману — О. Моргенштерну к краткой ссылке на их известную монографию. Но она издавалась у нас в стране в 1970 г. ("Теория игр и экономическое поведение": Пер. с англ. — М.: Наука). Где сейчас найти ее студентам? Эта теория и ее возможные прикладные направления в области моделирования рисковых ситуаций в экономике и бизнесе вполне заслуживают, по нашему мнению, самостоятельной публикации с должной адаптацией для студентов и аспирантов. То же можно сказать о нереализованных возможностях практических приложений теории нечетких множеств, например, в страховом деле или при оптимизации организационных структур — задач более важных, чем представленная в учебнике о замещении вакантной должности бухгалтера на фирме.
Это, безусловно, недостатки, которые могут поставить читателя перед определенными трудностями восприятия материала.. Однако достоинства учебника во много крат большие. Учебник написан математически грамотно, что для литературы по экономике, к сожалению, не всегда возможно считать само собою разумеющимся. Широк охват проблематики, где читатель может найти практически почти все, что в настоящее время относят к сфере моделирования управленческих решений.
Содержание учебника апробировано при чтении курсов "Методы теории принятия решений", "Информационные системы стратегического прогнозирования и планирования", "Математическое моделирование экономических процессов", "Теория оптимального управления экономическими процессами" по специальности "Информационные системы в экономике" в Волгоградском государственном техническом университете.
С учетом всех достоинств и недостатков, надо полагать, читатель сам сделает свой выбор.
Нам пора перестать различать экономику без математики и математическое в нее "вторжение". Экономика с той долей математики, которая диктуется содержательной сущностью проблемной области исследования, должна стать не только стандартом западного, но и, наконец, российского образования. Данный учебник вносит несомненный вклад в решение этой проблемы.
Б. А. ЛАГОША, доктор экономических наук, профессор
Нашим родителям посвящается
ПРЕДИСЛОВИЕ
Развитие микроэкономики, макроэкономики и прикладных дисциплин предполагает значительно более высокий уровень их формализации, определяемый прогрессом в области фундаментальной и прикладной математики — теории принятия решений, теории игр, математического программирования, математической статистики и др. В настоящее время экономическая теория на микро- и макроуровнях не может не включать в себя математические модели и методы как естественные и необходимые элементы.
В XX в. математические методы моделирования в экономике применялись широко и эффективно во многих странах мира. Разработчики этих методов были удостоены Нобелевской премии по экономике (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон, Л. Канторович и др.).
В последнее десятилетие российские ученые подготовили ряд учебников и пособий, направленных на повышение математической и компьютерной культуры нового поколения экономистов. Эта учебная литература широко используется при изучении различных экономических специальностей.
Сегодня любые предприятие, фирма или акционерное общество используют вычислительные машины в своей повседневной деятельности для ведения бухгалтерского учета, контроля за выполнением заказов и договоров, подготовки деловых документов. Помимо традиционных сфер применения ЭВМ по обработке рутинной информации, компьютер может оказывать существенную помощь человеку при решении творческих задач. К таким задачам можно отнести анализ, планирование и синтез рациональных решений при исследовании сложных систем в условиях неопределенности, когда недостаток информации компенсируется формализованно представленными знаниями экспертов. Одновременно возрастают необходимость в квалифицированных специалистах по экономической информатике и требования к уровню их подготовки. Такой специалист должен уметь формулировать требования к программным средствам, оценивать их качество и эффективность, выбирать программные средства, наиболее соответствующие запросам пользователей, разрабатывать новые программные продукты и уметь адаптировать готовые информационные системы к конкретным условиям применения.
Данный учебник может быть использован в курсах "Методы теории принятия решений", "Информационные системы стратегического прогнозирования и планирования", "Математическое моделирование экономических процессов", "Теория оптимального управления экономическими процессами" по специальности "Информационные системы в экономике". Учебник написан на основе преподавания этих дисциплин в Волгоградском государственном техническом университете.
В учебнике изложены основные методы анализа, планирования и синтеза рациональных решений в условиях неопределенности. Методы реализованы на ЭВМ и прошли практическую апробацию в различных сферах экономики и управления. Теоретический материал подкреплен практическими примерами, позволяющими лучше усвоить излагаемый материал. Приведены алгоритмы, которые могут реализовываться студентами на ЭВМ. В конце каждой главы для закрепления материала приводятся основные понятия, контрольные вопросы и задания по теме, а также список литературы.
Учебник может использоваться преподавателями, работающими в области компьютерного моделирования экономических процессов.
Книга будет полезной и руководителям различного ранга. В этой связи следует отметить, что описанные в книге системы целесообразно использовать для решения задач социально-экономического прогнозирования и планирования развития промышленных отраслей, предприятий и в других службах, образующих инфраструктуру городов, областей и регионов.
Авторы признательны рецензентам Московского государственного университета экономики, статистики и информатики, доктору экономических наук, профессору Б. А. Лагоше и кандидату технических наук, доценту А. А. Емельянову за ценные замечания, высказанные при прочтении рукописи учебника.
Авторы также благодарят ректора Волгоградского государственного технического университета доктора химических наук, профессора И. А. Новакова и доктора экономических наук, профессора Л. С. Шаховскую, активно способствовавших опубликованию учебника.
ГЛАВА 1.
АНАЛИЗ ЗАДАЧ И МЕТОДОВ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
Задача принятия решений (ЗПР) — одна из самых распространенных в любой предметной области [1 — 7]. Ее решение сводится к выбору одной или нескольких лучших альтернатив из некоторого набора. Для того чтобы сделать такой выбор, необходимо четко определить цель и критерии (показатели качества), по которым будет проводиться оценка некоторого набора альтернативных вариантов. Выбор метода решения такой задачи зависит от количества и качества доступной информации. Данные, необходимые для осуществления обоснованного выбора, можно разделить на четыре категории: информация об альтернативных вариантах, информация о критериях выбора, информация о предпочтениях, информация об окружении задач.
1.1. Эволюция теории принятия решений. ЭВМ в принятии решений
В своем развитии теория принятия решений прошла через три стадии.
На первой стадии развивался дескриптивный подход
к принятию решений. Здесь усилия ученых были направлены на описание процесса выбора решений человеком в целях определения рационального зерна, характерного для всякого разумного выбора. В результате проведенных исследований оказалось, что большинство людей действуют интуитивно, проявляя при этом непоследовательность и противоречивость в своих суждениях. Положительным аспектом исследований в области дескриптивного подхода явилось то, что удалось дать достаточно четкий ответ на вопрос, что может и чего не может человек, решая задачу выбора [8].
На второй стадии исследователи разрабатывали нормативный подход
к принятию решений. Однако и здесь их постигла неудача, поскольку идеализированные теории, рассчитанные на сверхрационального человека с мощным интеллектом, не нашли практического применения.
На третьей стадии был развит прескриптивный подход к
принятию решений. Он оказался наиболее плодотворным, поскольку предписывал, как должен поступать человек с нормальным интеллектом, желающий напряженно и систематизированно обдумывать все аспекты своей задачи. Прескриптивный подход не гарантирует нахождения оптимального решения в любой ситуации, но обеспечивает выбор такого решения, которое не обременено противоречиями и непоследовательностями. Данный подход предъявляет к человеку серьезные требования по освоению методов и приемов теории принятия решений, а также предписывает проведение многочисленных вычислений, связанных с реализацией этих методов.
Первоначальным импульсом для применения ЭВМ в процессе принятия решений явилась необходимость проведения большого объема вычислений для получения обобщенной оценки путем синтеза всех плюсов и минусов по каждой альтернативе. На этом шаге решением ЗПР занимались специалисты, имеющие широкие знания как в области методов принятия решений, так и в программировании на ЭВМ.
Поскольку на практике указанное сочетание знаний является редким, возникла новая категория специалистов — аналитиков в области принятия решений. Аналитики владели методами принятия решений и навыками программирования и выступали в роли посредников между лицом, принимающим решение (ЛПР), и ЭВМ. Аналитик выполнял следующие функции: уточнял совместно с ЛПР постановку задачи, выбирал метод принятия решений, адекватный задаче, собирал необходимую статистическую и экспертную информацию, строил модель задачи, организовывал обработку накопленной информации на ЭВМ, представлял полученные результаты ЛПР и их интерпретировал.
Следующий шаг в применении ЭВМ для принятия решений был связан с созданием диалоговых систем, позволявших менять интересующие исследователя параметры заложенной в память ЭВМ модели задачи принятия решений, выбирать алгоритм поиска решения или его параметров, исследовать чувствительность полученного решения. Такие системы позволяли получать исчерпывающую информацию для всестороннего обоснования выбираемых решений.
В настоящее время в связи с возросшими возможностями современных ЭВМ разработаны программные информационные системы, обеспечивающие поддержку процесса принятия решений на всех его фазах. Большинство систем принятия решений реализовано на персональных ЭВМ.
1.2. Схема процесса принятия решений
Общая схема процесса принятия решений включает следующие основные этапы:
Этап 1. Предварительный анализ проблемы. На этом этапе определяются:
• главные цели;
• уровни рассмотрения, элементы и структура системы (процесса), типы связей;
• подсистемы, используемые ими основные ресурсы и критерии качества функционирования подсистем;
• основные противоречия, узкие места и ограничения.
Этап 2. Постановка задачи. Постановка конкретной ЗПР включает:
• формулирование задачи;
• определение типа задачи;
• определение множества альтернативных вариантов и основных критериев для выбора из них наилучших;
• выбор метода решения ЗПР.
Этап 3. Получение исходных данных. На данном этапе устанавливаются способы измерения альтернатив. Это либо сбор количественных (статистических) данных [9], либо методы математического или имитационного моделирования, либо методы экспертной оценки [10, 11]. В последнем случае необходимо решить задачи формирования группы экспертов, проведения экспертных опросов, предварительного анализа экспертных оценок.
Этап 4. Решение ЗПР с привлечением математических методов и вычислительной техники, экспертов и лица, принимающего решение. На этом этапе производятся математическая обработка исходной информации, ее уточнение и модификация в случае необходимости. Обработка информации может оказаться достаточно трудоемкой, при этом может возникнуть необходимость совершения нескольких итераций [12] и желание применить различные методы [13 — 16] для решения задачи. Поэтому именно на этом этапе возникает потребность в компьютерной поддержке процесса принятия решений, которая выполняется с помощью автоматизированных систем принятия решений.
Этап 5. Анализ и интерпретация полученных результатов. Полученные результаты могут оказаться неудовлетворительными и потребовать изменений в постановке ЗПР. В этом случае необходимо будет возвратиться на этап 2 или этап 1 и пройти заново весь путь. Решение ЗПР может занимать достаточно длительный промежуток времени, в течение которого окружение задачи может измениться и потребовать корректировок в постановке задачи, а также в исходных данных (например, могут появиться новые альтернативы, требующие введения новых критериев). Задачи принятия решений можно разделить на статические
и динамические.
К первым относятся задачи, которые не требуют многократного решения через короткие интервалы времени. К динамическим относятся ЗПР, которые возникают достаточно часто. Следовательно, итерационный характер процесса принятия решений можно считать закономерным, что подтверждает необходимость создания и использования эффективных систем компьютерной поддержки. ЗПР, требующие одного цикла, можно скорее считать исключением, чем правилом.
1.3. Классификация задач принятия решений
Задачи принятия решений отличаются большим многообразием, классифицировать их можно по различным признакам, характеризующим количество и качество доступной информации. В общем случае задачи принятия решений можно представить следующим набором информации [8, 17, 18]:
<
Т
, A
, К
, X, F, G, D>,
где Т—
постановка задачи (например, выбрать лучшую альтернативу или упорядочить весь набор);
А —
множество допустимых альтернативных вариантов;
К—
множество критериев выбора;
Х—
множество методов измерения предпочтений (например, использование различных шкал);
F
— отображение множества допустимых альтернатив в множество критериальных оценок (исходы);
G
—
система предпочтений эксперта;
D
—
решающее правило, отражающее систему предпочтений.
Любой из элементов этого набора может служить классификационным признаком принятия решений.
Рассмотрим традиционные классификации:
1. По виду отображения F.
Отображение множества А и К
может иметь детерминированный характер, вероятностный или неопределенный вид, в соответствии с которым задачи принятия решений можно разделить на задачи в условиях риска и задачи в условиях неопределенности.
2. Мощность множества К.
Множество критериев выбора может содержать один элемент или несколько. В соответствии с этим задачи принятия решений можно разделить на задачи со скалярным критерием и задачи с векторным критерием (многокритериальное принятие решений).
3. Тип системы
G
.
Предпочтения могут формироваться одним лицом или коллективом, в зависимости от этого задачи принятия решений можно классифицировать на задачи индивидуального принятия решений и задачи коллективного принятия решений.
Задачи принятия решений в условиях определенности.
К этому классу относятся задачи, для решения которых имеется достаточная и достоверная количественная информация. В этом случае с успехом применяются методы математического программирования, суть которых состоит в нахождении оптимальных решений на базе математической модели реального объекта. Основные условия применимости методов математического программирования следующие:
1. Задача должна быть хорошо формализована, т. е. имеется адекватная математическая модель реального объекта.
2. Существует некоторая единственная целевая функция (критерий оптимизации), позволяющая судить о качестве рассматриваемых альтернативных вариантов.
3. Имеется возможность количественной оценки значений целевой функции.
4. Задача имеет определенные степени свободы (ресурсы оптимизации), т. е. некоторые параметры функционирования системы, которые можно произвольно изменять в некоторых пределах в целях улучшения значений целевой функции.
Задачи в условиях риска.
В тех случаях, когда возможные исходы можно описать с помощью некоторого вероятностного распределения, получаем задачи принятия решений в условиях риска. Для построения распределения вероятностей необходимо либо иметь в распоряжении статистические данные, либо привлекать знания экспертов. Обычно для решения задач этого типа применяются методы теории одномерной или многомерной полезности. Эти задачи занимают место на границе между задачами принятия решений в условиях определенности и неопределенности. Для решения этих задач привлекается вся доступная информация (количественная и качественная).
Задачи в условиях неопределенности.
Эти задачи имеют место тогда, когда информация, необходимая для принятия решений, является неточной, неполной, неколичественной, а формальные модели исследуемой системы либо слишком сложны, либо отсутствуют. В таких случаях для решения задачи обычно привлекаются знания экспертов. В отличие от подхода, принятого в экспертных системах, для решения ЗПР знания экспертов обычно выражены в виде некоторых количественных данных, называемых предпочтениями.
Выбор и нетривиальность задач принятия решений.
Следует отметить, что одним из условий существования задачи принятия решений является наличие нескольких допустимых альтернатив, из которых следует выбрать в некотором смысле лучшую. При наличии одной альтернативы, удовлетворяющей фиксированным условиям или ограничениям, задача принятия решений не имеет места.
Задача принятия решений называется тривиальной, если она характеризуется исключительно одним критерием К
и всем альтернативам А
i
приписаны конкретные числовые оценки в соответствии со значениями указанного критерия (рис. 1.1 а).

Рис. 1.1. Выбор альтернативы при одном критерии:
а —
в условиях определенности; б — в условиях неопределенности;
в —
в условиях риска
Задача принятия решений перестает быть тривиальной даже при одном критерии К,
если каждой альтернативе А
i
соответствует не точная оценка, а интервал возможных оценок (рис. 1.1 б) или распределение f
(К/А
i
) на значениях указанного критерия (рис. 1.1 в).
Нетривиальной считается задача при наличии нескольких критериев принятия решений (рис. 1.2) независимо от вида отображения множества альтернатив в множество критериальных оценок их последствий.

Рис. 1.2. Выбор альтернативы с учетом двух критериев: а — в случае непрерывной области альтернатив; б —
в случае дискретных альтернатив
Следовательно, при наличии ситуации выбора, многокритери-альности и осуществлении выбора в условиях неопределенности или риска задача принятия решений является нетривиальной.
1.4. Классификация методов принятия решений
Существует множество классификаций методов принятия решений, основанных на применении различных признаков [10, 19 — 23]. В табл. 1.1 приведена одна из возможных классификаций, признаками которой являются содержание и тип получаемой экспертной информации.
Таблица 1.1
Классификация методов принятия решений
| № п/п
|
Содержание информации
|
Тип информации
|
Метод принятия решений
|
| 1
|
Экспертная информация не требуется
|
Метод доминирования [24, 25]
Метод на основе глобальных критериев [26, 27]
|
| 2
|
Информация о предпочтениях на множестве критериев
|
Качественная информация
Количественная оценка предпочтительности критериев
Количественная информация о замещениях
|
Лексикографическое упорядочение [24,25]
Сравнение разностей критериальных оценок [22,24]
Метод припасовывания [24]
Методы "эффективность-стоимость" [24,28]
Методы свертки на иерархии критериев [29,30]
Методы порогов [24, 31]
Методы идеальной точки [24]
Метод кривых безразличия [10,24] Методы теории ценности [10, 24]
|
| 3
|
Информация о предпочтительности альтернатив
|
Оценка предпочтительности парных сравнений
|
Методы математического программирования [32,33]
Линейная и нелинейная свертка при интерактивном способе определения ее параметров [34]
|
| 4
|
Информация о предпочтениях на множестве критериев и о последствиях альтернатив
|
Отсутствие информации о предпочтениях; количественная и/или интервальная информация о последствиях. Качественная информация о предпочтениях и количественная о последствиях
Качественная (порядковая) информация о предпочтениях и последствиях
Количественная информация о предпочтениях и последствиях
|
Методы с дискретизацией неопределенности [8,26]
Стохастическое доминирование [8,10,22]
Методы принятия решений в условиях риска и неопределенности на основе глобальных критериев [8, 35]
Метод анализа иерархий [36]
Методы теории нечетких множеств [7, 13, 14, 15, 17, 37]
Метод практического принятия решений [8, 24]
Методы выбора статистически ненадежных решений [8,38]
Методы кривых безразличия для принятия решений в условиях риска и неопределенности [8]
Методы деревьев решений [8,37]
Декомпозиционные методы теории ожидаемой полезности [8, 10,11]
|
Используемый принцип классификации позволяет достаточно четко выделить четыре большие группы методов, причем три группы относятся к принятию решений в условиях определенности, а четвертая — к принятию решений в условиях неопределенности. Из множества известных методов и подходов к принятию решений наибольший интерес представляют те, которые дают возможность учитывать многокритериальность и неопределенность, а также позволяют осуществлять выбор решений из множеств альтернатив различного типа при наличии критериев, имеющих разные типы шкал измерения (эти методы относятся к четвертой группе).
В свою очередь, среди методов, образующих четвертую группу, наиболее перспективными являются декомпозиционные методы теории ожидаемой полезности, методы анализа иерархий и теории нечетких множеств. Данный выбор определен тем, что эти методы в наибольшей степени удовлетворяют требованиям универсальности, учета многокритериальности выбора в условиях неопределенности из дискретного или непрерывного множества альтернатив, простоты подготовки и переработки экспертной информации.
Охарактеризовать достаточно полно все методы принятия решений, относящиеся к четвертой группе, в рамках данной работы невозможно, поэтому в дальнейшем рассматриваются только три подхода к принятию решений в условиях неопределенности, которые получили наиболее широкое воплощение в системах компьютерной поддержки, а именно: подходы, основанные на методах теории полезности, анализа иерархий и теории нечетких множеств.
1.5. Характеристика методов теории полезности
Декомпозиционные методы теории ожидаемой полезности получили наиболее широкое распространение среди группы аксиоматических методов принятия решений в условиях риска и неопределенности.
Основная идея этой теории состоит в получении количественных оценок полезности возможных исходов, которые являются следствиями процессов принятия решений. В дальнейшем на основании этих оценок можно выбрать наилучший исход. Для получения оценок полезности необходимо иметь информацию о предпочтениях лица, ответственного за принимаемое решение.
Парадигма анализа решения может быть сведена к процессу, включающему пять этапов [10].
Этап 1. Предварительный анализ. На этом этапе формулируется проблема и определяются возможные варианты действий, которые можно предпринять в процессе ее решения.
Этап 2. Структурный анализ. Этот этап предусматривает структуризацию проблемы на качественном уровне, на котором ЛПР намечает основные шаги процесса принятия решений и пытается упорядочить их в виде некоторой последовательности. Для этой цели строится дерево решений, (рис.1.3).

Рис. 1.3. Фрагмент дерева решений
Дерево решений имеет два типа вершин: вершины-решения (обозначены квадратиками) и вершины-случаи (обозначены кружочками). В вершинах-решениях выбор полностью зависит от ЛПР, в вершинах-случаях ЛПР не полностью контролирует выбор, так как случайные события можно предвидеть лишь с некоторой вероятностью.
Этап 3. Анализ неопределенности. На этом этапе ЛПР устанавливает значения вероятности для тех ветвей на дереве решений, которые начинаются в вершинах-случаях. При этом полученные значения вероятностей подлежат проверке на наличие внутренней согласованности.
Для получения значений вероятности привлекается вся доступная информация: статистические данные, результаты моделирования, экспертная информация и т. д.
Этап 4. Анализ полезности. На данном этапе следует получить количественные оценки полезности последствий (исходов), связанных с реализацией того или иного пути на дереве решений. На рис. 1.3 показан один из возможных путей — от начала до точки G.
Исходы (последствия принимаемых решений) оцениваются с помощью функции полезности фон Неймана — Моргенштерна [39], которая каждому исходу rk
ставит в соответствие его полезность и(
rk
)
. Построение функции полезности осуществляется на основе знаний ЛПР и экспертов.
Этап 5. Процедуры оптимизации. Оптимальная стратегия действий (альтернатива, путь на дереве решений) может быть найдена с помощью вычислений, а именно: максимизации ожидаемой полезности на всем пространстве возможных исходов. Одно из условий постановки задачи оптимизации — наличие адекватной математической модели, которая связывает параметры оптимизации (в данном случае это альтернативные варианты действий) с переменными, входящими в целевую функцию (функция полезности). В методах теории полезности такие модели имеют вероятностный характер и основаны на том, что оценка вероятности ожидаемого исхода может быть использована для введения числовых оценок возможных вероятных распределений на конечном множестве исходов.
Задача выбора наилучшего решения в соответствии с аксиоматикой теории полезности [10] может быть представлена следующим образом:

где и(К) —
многомерная функция полезности;
К—
точка в критериальном пространстве;
f
(
K
/
A
) —
функция плотности условного от альтернативы А
распределения критериальных оценок.
Построение функций полезности является основной и наиболее трудоемкой процедурой методов теории полезности, после этого с помощью такой функции можно оценить любое количество альтернатив.
Процедура построения функции полезности включает пять шагов.
Шаг 1.
Подготовительный. Главная задача здесь — подбор экспертов и разъяснение им того, как следует выражать свои предпочтения.
Шаг 2.
Определение вида функции. Функция полезности должна отражать представления ЛПР и экспертов об ожидаемой полезности возможных исходов. Поэтому множество исходов упорядочивается по их предпочтительности, после чего в соответствие каждому возможному исходу необходимо поставить предполагаемое значение ожидаемой полезности. На этом шаге выясняют, является ли функция полезности монотонной, убывающей или возрастающей, отражает ли она склонность, несклонность или безразличие к риску и т. п.
Шаг 3.
Установление количественных ограничений. Здесь определяется интервал изменения аргумента функции полезности и устанавливаются значения функции полезности для нескольких контрольных точек.
Шаг 4.
Подбор функции полезности. Необходимо выяснить, являются ли согласованными количественные и качественные характеристики, выявленные к данному моменту. Положительный ответ на этот вопрос равнозначен существованию некоторой функции, которая обладает всеми требуемыми свойствами. Если последует отрицательный ответ, то возникает проблема согласования свойств, что предполагает возврат на более ранние шаги.
Шаг 5.
Проверка адекватности. Необходимо убедиться в том, что построенная функция полезности действительно полностью соответствует истинным предпочтениям ЛПР. Для этого применяются традиционные методы сравнения расчетных значений с экспериментальными.
Рассмотренная процедура соответствует задаче со скалярной функцией полезности. В общем случае последняя может быть векторной величиной. Это имеет место, когда ожидаемую полезность невозможно представить единственной количественной характеристикой (задача со многими критериями). Обычно многомерная функция полезности представляется как аддитивная или мультипликативная функция частных полезностей. Процедура построения многомерной функции полезности еще более трудоемка, чем одномерной.
Таким образом, методы теории полезности занимают промежуточное место между методами принятия решений в условиях определенности и методами, направленными на выбор альтернатив в условиях неопределенности. Для применения этих методов необходимо иметь количественную зависимость между исходами и альтернативами, а также экспертную информацию для построения функции полезности. Эти условия выполняются не всегда, что накладывает ограничение на применение методов теории полезности. К тому же следует помнить, что процедура построения функции полезности трудоемка и плохо формализуема.
В настоящее время методы теории полезности достаточно хорошо освещены в отечественной научной и учебной литературе [2, 8, 10, 11, 22]. Особого внимания заслуживают работы отечественных ученых: А. М. Дуброва, Б. А. Лагоши, Е. Ю. Хрусталева [40], а также Н. В. Князевского и В. С. Князевской [41]. На основе этих методов реализованы разнообразные компьютерные системы. Наибольшую популярность приобрела промышленная диалоговая система "Альтернатива — Ф", реализующая методы теории полезности и обеспечивающая решение задач многокритериального выбора в условиях определенности, риска и неопределенности [8].
С учетом сказанного в настоящем учебнике представлены наиболее универсальные и менее освещенные в отечественной учебной литературе подходы к принятию решений в условиях неопределенности. Наиболее подробно нами будут рассмотрены автоматизированные методы анализа иерархий и теории нечетких множеств, а также методология по их применению для решения экономических задач.
Основные понятия
1. Принятие решений.
2. Дескриптивный, прескриптивный и нормативный подходы.
3. Формальная модель задачи принятия решений.
4. Задачи выбора.
5. Ситуация выбора.
6. Метод принятия решений.
Контрольные вопросы и задания
1. Укажите особенности дескриптивного, прескриптивного и нормативного подходов к принятию решений.
2. Дайте характеристику формальной модели задачи принятия решений.
3. Приведите основные классификационные признаки задач принятия решений.
4. Какова роль ЭВМ в принятии решений?
5. Охарактеризуйте нетривиальные задачи принятия решений.
6. Перечислите и укажите отличительные признаки основных методов принятия решений.
Литература
1.
Леонтьев В. В.
Межотраслевая экономика/Под ред. А. Г. Гранберга.— М.: Экономика, 1997. — 471 с.
2.
Ларичев О. И., Браун Р.
Количественный и вербальный анализ решений: сравнительное исследование возможностей и ограничений //Экономика и математические методы. — 1998. — Т. 34. — Вып. 4.—С. 97—107.
3.
Канторович Л. В., Горстко
А
. Б.
Оптимальные решения в экономике. — М.: Наука, 1972. — 231 с.
4.
Федоренко Н. П.
Оптимизация экономики: некоторые вопросы использования экономико-математических методов в народном хозяйстве. — М.: Наука, 1997. — 287 с.
5.
Багриновский К. А., Логвинец В.В.
Интеллектуальная система в отраслевом планировании/Отв. ред. В. Н. Буркова — М.: Наука, 1998.— 136 с.
6.
Медницкий В. Г.
Оптимизация перспективного планирования.— М.: Наука, 1984. — 152 с.
7.
Нечеткие
множества и теория возможностей. Последние достижения: Пер. с англ./ Под ред. Р. Р. Ягера — М.: Радио и связь, 1986. — 408 с.
8.
Борисов А. Н., Виллюмс Э. Р.,
Сукур Л. Я.
Диалоговые системы принятия решений на базе мини-ЭВМ.— Рига: Зинатне, 1986. — 195 с.
9.
Статистические
модели и многокритериальные задачи принятия решений: Сб. статей / Сост. и науч. ред. И. Ф. Шахнов. — М.: Статистика, 1979. — 184 с.
10.
Кини Р. Л., Райфа X.
Принятие решений при многих критериях: предпочтения и замещения: Пер. с англ./ Под ред. И. Р. Шахова. — М.: Радио и связь, 1981. — 560 с.
11.
Райфа Г.
Анализ решений (введение в проблему выбора в условиях неопределенности): Пер. с англ. — М.: Наука, 1977. — 408 с.
12.
Мелихов А. Н., Бернштейн Л. С., Коровин С. Я.
Ситуационные советующие системы с нечеткой логикой. — М.: Наука, 1990. — 272 с.
13.
Беллман Р., Заде Л.
Принятие решений в расплывчатых условиях // Вопросы анализа и процедуры принятия решений: Пер. с англ. — М.: Мир, 1976. — С. 172 — 175.
14.
Кофман А.
Введение в теорию нечетких множеств: Пер. с англ. — М.: Радио и связь, 1982. — 432 с.
15.
Орловский С. А.
Проблемы принятия решений при нечеткой исходной информации. — М.: Наука, 1981. — 208 с.
16.
Юдин Д. Б.
Вычислительные методы теории принятия решений. — М.: Наука, 1989. — 320 с.
17.
Борисов А. Н., Крумберг О.
А., Федоров И. П.
Принятие решений на основе нечетких моделей. — Рига: Зинатне, 1990. — 184 с.
18.
Борисов А. Н.
Методическое обеспечение технологии принятия решений // Системы обработки знаний в автоматизированном проектировании. — Рига: Изд-во Риж. техн. ун-та, 1992. — С. 12—15.
19.
Ларичев О. И.
Человеко-машинные процедуры принятия решений// Автоматика и телемеханика. — 1971. —№ 12. —С. 130 — 142.
20.
Ларичев О. И.
Наука и искусство принятия решений. — М.: Наука, 1979.—200с.
21.
Модели
и методы векторной оптимизации / С.В.Емельянов, В.И.Борисов, А.А.Малевич, А.М.Черкашин// Техническая кибернетика. Итоги науки и техники. — М.: ВИНИТИ, 1973. — Т.5. — С. 386 — 448.
22.
Фишберн П. С.
Теория полезности для принятия решений: Пер. с англ. — М.: Наука, 1977. — 352 с.
23.
Krisher J. P.
An annotated bibliography of decision analytic applications to health care//Operations Research. — 1980. — V. 28. — № 1. — P. 97 — 107.
24.
Ларичев О. И.
Анализ процессов принятия человеком решений при альтернативах, имеющих оценки по многим критериям// Автоматика и телемеханика.—1981.—№8.—С. 131—141.
25.
Подиновский В. В., Ногин В. Д.
Парето-оптимальные решения многокритериальных задач. — М.: Наука, 1982. — 256 с,
26.
Беляев Л. С.
Решение сложных оптимизационных задач в условиях неопределенности. — Новосибирск: Наука, 1978. — 126 с.
27.
Чернов Г.,
Мозес Л.
Элементарная теория статистических решений: Пер. с англ. — М.: Сов. радио, 1962. — 406 с.
28.
Руководство
по системе "Планирование, программирование, разработка бюджета"// Новое в теории и практике управления производством в США / Под ред. Б. З. Мильнера. — М.: Прогресс, 1971. — С. 181 —202.
29.
Борисов В. Н.
Векторная оптимизация систем// Исследование систем: Материалы Всесоюзного симпозиума. — М.: ВИНИТИ, 1971.—С. 106— 114.
30.
Евланов Л. Г.
Теория и практика принятия решений. — М.: Экономика, 1984. — 176 с.
31.
Руа Б.
Классификация и выбор при наличии нескольких критериев (метод ЭЛЕКТРА): Пер. с франц.// Вопросы анализа и процедуры принятия решений. — М.: Мир, 1976. — С. 80 — 107.
32.
Интерактивный
метод решения задачи оптимального проектирования машин / И. И. Артоболевский, С. В. Емельянов, В. И. Сергеев и др.// Докл. АН СССР, 1977. Т. 237. — № 4. — С. 793 — 795.
33.
Ларичев О. И.
Человеко-машинные процедуры принятия решений при альтернативах, имеющих оценки по многим критериям (обзор) // Автоматика и телемеханика. — 1971. — № 12. — С. 130 — 142.
34.
Борисов А. Н., Левченко А. С.
Методы интерактивной оценки решений. — Рига: Зинатне, 1982. — 139 с.
35.
Федулов А. А., Федулов Ю. Г., Цыгичко В. Н.
Введение в теорию статистически ненадежных решений. — М.: Статистика, 1979. — 276 с.
36.
Саати Т.
Принятие решений. Метод анализа иеархий: Пер.с англ. — М.: Радио и связь, 1989. — 316 с.
37.
Заде Л.
Понятие лингвистической переменной и его применение к принятию приближенных решений: Пер. с англ. — М.: Мир, 1976. — 165 с.
38.
Райфа Г.
Анализ решений (введение в проблему выбора в условиях неопределенности): Пер. с англ. — М.: Наука, 1977. — 406 с.
39.
Нейман Дж., фон, Моргенштерн О.
Теория игр и экономическое поведение: Пер с англ. — М.: Наука, 1970. — 707 с.
40.
Дубров А. М., Лагоша Б. А., Хрусталев» Е. Ю.
Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пособие/ Под ред. Б. А. Лагоши. — М.: Финансы и статистика, 1999. — 176 с.
41.
Князевский Н. В., Князевская В. С.
Принятие рискованных решений в экономике и бизнесе: Учеб. пособие. — М.: Контур, 1998. — 160 с.
ГЛАВА 2.
ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ МЕТОДА АНАЛИЗА ИЕРАРХИЙ
Метод анализа иерархий (МАИ) [1,2] предполагает декомпозицию проблемы на все более простые составляющие части и обработку суждений лица, принимающего решение. В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии. Относительная значимость выражается численно в виде векторов приоритетов. Полученные таким образом значения векторов являются оценками в шкале отношений и соответствуют так называемым жестким оценкам.
Можно выделить ряд модификаций МАИ, которые определяются характером связей между критериями и альтернативами, расположенными на самом нижнем уровне иерархии, а также методом сравнения альтернатив.
По характеру связей между критериями и альтернативами определяется два типа иерархий. К первому типу относятся такие, у которых каждый критерий, имеющий связь с альтернативами, связан со всеми рассматриваемыми альтернативами (тип иерархий с одинаковыми числом и функциональным составом альтернатив под критериями). Ко второму типу иерархий принадлежат такие, у которых каждый критерий, имеющий связь с альтернативами, связан не со всеми рассматриваемыми альтернативами (тип иерархий с различными числом и функциональным составом альтернатив под критериями).
В МАИ имеется три метода сравнения альтернатив: попарное сравнение; сравнение альтернатив относительно стандартов и сравнение альтернатив копированием.
Ниже рассматриваются методология МАИ и отличительные особенности его модификаций.
2.1. Иерархическое представление проблемы, шкала отношений и матрицы парных сравнений
Иерархическое представление проблемы
В первой модификации метода рассматривается иерархия с одинаковыми числом и функциональным составом альтернатив под критериями и метод попарного сравнения элементов иерархии. Построение иерархии начинается с очерчивания проблемы исследования. Далее строится собственно иерархия, включающая цель, расположенную в ее вершине, промежуточные уровни (например, критерии) и альтернативы, формирующие самый нижний иерархический уровень.
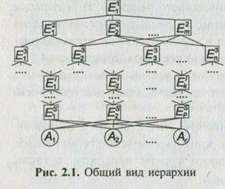
На рис. 2.1 приведен общий вид иерархии, где Е
i
j
— элементы иерархии, А
i
—
альтернативы.
Верхний индекс у элементов указывает уровень иерархии, а нижний индекс — их порядковый номер. Существует несколько альтернативных способов графического отображения иерархии.

На рис. 2.2 приведены три варианта отображения одной иерархии.
Первый вариант — конкретизация (декомпозиция) заданного множества элементов (в частности, критериев). Второй вариант противоположен первому и предполагает синтез более общих элементов из заданных частных. Третий вариант — упорядочение предварительно заданного множества элементов на основе их попарного сравнения.
Шкала отношений
Для установления относительной важности элементов иерархии используется шкала отношений (табл. 2.1). Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа.
Таблица 2.1
Шкала отношений (степени значимости действий)
| Степень значимости
|
Определение
|
Объяснение
|
| 1
|
Одинаковая значимость
|
Два действия вносят одинаковый вклад в достижение цели
|
| 3
|
Некоторое преобладание значимости одного действия над другим (слабая значимость)
|
Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны
|
| 5
|
Существенная или сильная значимость
|
Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий
|
| 7
|
Очевидная или очень сильная значимость
|
Убедительное свидетельство в пользу одного действия перед другим
|
| 9
|
Абсолютная значимость
|
Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны
|
| 2,4,6,8
|
Промежуточные значения между двумя соседними суждениями
|
Ситуация, когда необходимо компромиссное решение
|
| Обратные величины приведен-ных выше ненулевых величин
|
Если действию i
при сравнении с действием j
приписывается одно из определенных выше ненулевых чисел, то действию j
при сравнении с действием i
приписывается обратное значение
|
Если согласованность была постулирована при получении N
числовых значений для образования матрицы
|
Правомочность этой шкалы доказана теоретически при сравнении со многими другими шкалами [2]. При использовании указанной шкалы ЛПР, сравнивая два объекта в смысле достижения цели, расположенной на вышележащем уровне иерархии, должен поставить в соответствие этому сравнению число в интервале от 1 до 9 или обратное значение чисел. В тех случаях, когда трудно различить столько промежуточных градаций от абсолютного до слабого предпочтения или этого не требуется в конкретной задаче, может использоваться шкала с меньшим числом градаций. В пределе шкала имеет две оценки: 1 — объекты равнозначны; 2 — предпочтение одного объекта над другим.
Матрицы парных сравнений
После построения иерархии устанавливается метод сравнения ее элементов. Если принимается метод попарного сравнения, то строится множество матриц парных сравнений. Для этого в иерархии выделяют элементы двух типов: элементы-«родители» и элементы-«потомки». Элементы-«потомки» воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами-«родителями». Матрицы парных сравнений строятся для всех элементов-«потомков», относящихся к соответствующему элементу-«родителю». Элементами-«родителями» могут являться элементы, принадлежащие любому иерархическому уровню, кроме последнего, на котором расположены, как правило, альтернативы. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы (см.
табл. 2.1).
Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент E
1
доминирует над элементом Е2
,
то клетка матрицы, соответствующая строке Е1
и столбцу E
2
,
заполняется целым числом, а клетка, соответствующая строке E
2
и столбцу Е1
,
заполняется обратным к нему числом. Если элемент Е2
доминирует над Е1
,
то целое число ставится в клетку, соответствующую строке Е2
и столбцу Е1
,
а дробь проставляется в клетку, соответствующую строке Е1
и столбцу Е2
.
Если элементы Е1
и Е2
равнопредпочтительны, то в обе позиции матрицы ставятся единицы.
Для получения каждой матрицы эксперт или ЛПР выносит n
(n
–
1)/2 суждений (здесь п —
порядок матрицы парных сравнений).
Рассмотрим в общем виде пример формирования матрицы парных сравнений.
Пусть Е1
,
E
2
,
..., Еп
—
множество из п
элементов (альтернатив) и v
1
,
v
2
, …,
vn
— соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-«родителю»). В этом случае матрица парных сравнений [Е
] имеет следующий вид:

Матрица парных сравнений обладает свойством обратной симметрии, т. е.
aij
=
1/
aji
,
где aij
=
vi
/
vj
При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.
При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более предпочтительна или более вероятна.
2.2. Собственные векторы и собственные значения матриц. Оценка однородности суждений
Собственные векторы и значения матриц
Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [E
], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W
положительной квадратной матрицы [E
] проводится на основании равенства
EW
=
λmax
W
,
(2.1)
где λmax
— максимальное собственное значение матрицы [Е
].
Для положительной квадратной матрицы [Е
] правый собственный вектор W,
соответствующий максимальному собственному значению λmax
, с точностью до постоянного сомножителя С можно вычислить по формуле

где е=
{1,1,1, ....l}Т
– единичный вектор;
k
= 1, 2, 3, ... — показатель степени;
С—
константа;
Т — знак транспонирования.
Вычисления собственного вектора W
по выражению (2.2) производятся до достижения заданной точности:

где l
— номер итерации, такой, что l
= 1 соответствует k
= 1; l
= 2, k
= 2;
l
= 3, k
= 4 и т. д.;
ξ —
допустимая погрешность.
С достаточной для практики точностью можно принять x = 0,01 независимо от порядка матрицы.
Максимальное собственное значение вычисляется по формуле:
λmax
=
eT
[E
]W
Динамические предпочтения и приоритеты
Задача прогнозирования экспертных предпочтений связана с получением оценок приоритетности альтернатив в форме зависимостей от времени. Для этого исходные экспертные оценки должны содержать информацию об изменении предпочтительности одной альтернативы перед другой на некотором временном отрезке. Следовательно, оценка предпочтительности может быть задана не константой, а функцией. Подбор таких функций можно осуществить, либо предоставив в распоряжение эксперта некоторую функциональную шкалу [2], либо путем аппроксимации экспертных оценок, полученных в различные моменты времени. Пример функциональной шкалы показан в табл. 2.2, где функции предпочтительности содержат параметры, подбор которых позволяет более или менее точно описать изменяющиеся суждения и установить область допустимых значений функций в пределах девятибалльной шкалы (см.
табл. 2.1).
Таблица 2.2
Динамические суждения
| Вид функции
|
Описание функции
|
Примечание
|
| const
|
Для всех t
l £ const £ 9
|
Постоянство предпочтений
|
| a
1
(t)+a
2
|
Линейная функция от t
на некотором отрезке, обратная функция - гипербола
|
Линейное возрастание предпочтения одной альтернативы перед другой во времени
|
| b
1
ln(t+
1)+b
2
|
Логарифмический рост
|
Быстрое возрастание предпочтения одной альтернативы перед другой до некоторого t
, после которого следует медленное возрастание
|
| 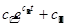
|
Экспоненциальный рост или убывание (с
2
<0), в последнем случае обратная величина – S-образная логистическая кривая
|
Медленное увеличение или уменьшение предпочтения во времени, за которым следует быстрое увеличение (уменьшение)
|
| d
1
t
2
+
d
2
t
+
d
3
|
Парабола с максимумом или минимумом в зависимости оттого, отрицательно или положительно d
1
.
|
Возрастание до максимума, а затем убывание (или наоборот)
|
| f
1
t
n
sin(t+f
2
)+f
3
|
Колебательная функция
|
Колебания предпочтений во времени с возрастающей (п>
0) или убывающей (n
≤
0) амплитудой
|
| Катастрофы
|
Функции, имеющие разрывы, которые следует указать
|
Крайне резкие изменения интенсивности предпочтений
|
Эти функции отражают интуитивные чувства лица, принимающего решения об изменении в тренде: постоянном, линейном, логарифмическом и экспоненциальном, возрастающем до максимума и убывающем или опускающемся до минимума и возрастающем, колебательном и, наконец, допускающем катастрофические изменения.
Для динамических задач матрица парных сравнений содержит функции времени в качестве элементов, поэтому максимальное собственное число λmax
, также собственный вектор W
также будут зависеть от времени, т. е.

Здесь A
(
t
) —
матрица парных сравнений объектов, содержащая информацию об изменении предпочтительности одной альтернативы перед другой на некотором промежутке времени, которая задана функцией из табл. 2.2.
Если порядок матрицы парных сравнений не превышает четырех, для уравнения (2.4) можно получить аналитическое решение [2]. Альтернативным способом является получение A
(
t
)
и W
(
t
)
численными методами. Для этого необходимо иметь в распоряжении информацию о предпочтениях экспертов за определенный период времени. При накапливании такой информации в компьютерной системе становятся возможными прогнозирование предпочтений и оценка ближайших последствий принимаемых решений.
Оценка однородности суждений
В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина aij
ни была взята для сравнения i
-го элемента с j
-м, aij
приписывается значение обратной величины, т. е. аij
= 1/aij
. Отсюда следует, что если один элемент в а
раз предпочтительнее другого, то последний только в 1/а
раз предпочтительнее первого.
При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax
от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (OO) в соответствии со следующими выражениями:

где М(ИО) — среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл. 2.3), полученных в работе [2].
Таблица 2.3
Среднее значение индекса однородности в зависимости от порядка матрицы
| Порядок матрицы (п)
|
М(ИО)
|
Порядок матрицы (и)
|
М(ИО)
|
Порядок матрицы (п)
|
М(ИО)
|
| 1
|
0,00
|
6
|
1,24
|
11
|
1,51
|
| 2
|
0,00
|
7
|
1,32
|
12
|
1,48
|
| 3
|
0,58
|
8
|
1,41
|
13
|
1,56
|
| 4
|
0,90
|
9
|
1,45
|
14
|
1,57
|
| 5
|
1,12
|
10
|
1.49
|
15
|
1,59
|
В качестве допустимого используется значение OO ≤ 0,10. Если для матрицы парных сравнений отношение однородности OO > 0,10, то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.
2.3. Синтез приоритетов на иерархии и оценка ее однородности
Иерархический синтез
Иерархический синтез используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев (элементов), имеющихся в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии. Ниже рассматривается алгоритм иерархического синтеза с учетом обозначений, принятых в предыдущей иерархии (см.
рис. 2.1).
Ш а г 1. Определяются векторы приоритетов альтернатив 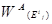 относительно элементов Ei
j
предпоследнего уровня иерархии (i
= S
). Здесь через Ei
j
обозначены элементы иерархии, причем верхний индекс i
указывает уровень иерархии, а нижний индекс j
—
порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив WA
S
относительно уровня иерархии S
осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.2) и (2.3) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:
относительно элементов Ei
j
предпоследнего уровня иерархии (i
= S
). Здесь через Ei
j
обозначены элементы иерархии, причем верхний индекс i
указывает уровень иерархии, а нижний индекс j
—
порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив WA
S
относительно уровня иерархии S
осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.2) и (2.3) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:

Ш а г 2. Аналогичным образом обрабатываются матрицы попарных сравнений собственно элементов E
i
j
.
Данные матрицы построены таким образом, чтобы определить предпочтительность элементов определенного иерархического уровня относительно элементов вышележащего уровня, с которыми они непосредственно связаны. Например, для вычисления векторов приоритетов элементов третьего иерархического уровня (см.
рис. 2.1) обрабатываются следующие три матрицы попарных сравнений:

В матрицах через vj
обозначен вес, или интенсивность, Е
j
-
го элемента.
В результате обработки матриц попарных сравнений определяется множество векторов приоритетов элементов:

Полученные значения векторов 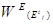 используются впоследствии при определении векторов приоритетов альтернатив относительно всех элементов иерархии.
используются впоследствии при определении векторов приоритетов альтернатив относительно всех элементов иерархии.
Шаг 3. Осуществляется собственно иерархический синтез, заключающийся в последовательном определении векторов приоритетов альтернатив относительно элементов Е
i
j
находящихся на всех иерархических уровнях, кроме предпоследнего, содержащего элементы Е
S
j
. Вычисление векторов приоритетов проводится в направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащими различным уровням. Вычисление проводится путем перемножения соответствующих векторов и матриц.
Общий вид выражения для вычисления векторов приоритетов альтернатив определяется следующим образом:

где  — вектор приоритетов альтернатив относительно элемента E
1
i
-
1
, определяющий j
-й столбец матрицы;
— вектор приоритетов альтернатив относительно элемента E
1
i
-
1
, определяющий j
-й столбец матрицы;
 —
вектор приоритетов элементов E
1
i
-
1
, E
2
i
-
1
,...,
E
n
i
-
1
, связанных с элементом Ej
вышележащего уровня иерархии.
—
вектор приоритетов элементов E
1
i
-
1
, E
2
i
-
1
,...,
E
n
i
-
1
, связанных с элементом Ej
вышележащего уровня иерархии.
Ниже приведен конкретный пример по вычислению векторов приоритетов альтернатив относительно элементов третьего (E
3
j
), второго (Е
2
j
)
и первого (Е1
j
)
уровней иерархии с учетом конкретных связей между элементами иерархии (см.
рис. 2.1).
Определение векторов приоритетов альтернатив для элементов второго уровня осуществляется следующим образом:

Результирующий вектор приоритетов альтернатив относительно корневой вершины иерархии Е
1
1
вычисляется следующим образом:

Рассмотренная модификация МАИ может эффективно применяться при решении широкого класса социально-экономических и управленческих задач.
Оценка однородности иерархии
После решения задачи иерархического синтеза оценивается однородность всей иерархии с помощью суммирования показателей однородности всех уровней, приведенных путем "взвешивания" к первому иерархическому уровню, где находится корневая вершина. Число шагов алгоритма по вычислению однородности определяется конкретной иерархией.
Рассмотрим принципы вычисления индекса ИОИ
и отношения ООИ
однородности иерархии.
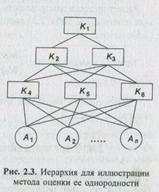
Пусть задана иерархия критериев и альтернатив (рис. 2.3.) и для каждого уровня определен индекс однородности и векторы приоритетов критериев следующим образом:
ИО1
— индекс однородности для 1-го уровня;
{ИО2
, ИО3
} — индексы однородности для 2-го уровня;
{ИО4
, ИО5
, ИО6
} — индексы однородности для 3-го уровня;
{
W
1
} —
вектор приоритетов критериев К
2
и К
3
относительно критерия К
1
;
{
W
2
},{
W
3
} —
векторы приоритетов критериев К
4
, К
5
, К
6
относительно критериев К
2
и К
3
второго уровня.
В этом случае индекс однородности рассматриваемой иерархии можно определить по формуле

где Т — знак транспонирования.
Определение отношения однородности ООИ
для всей иерархии осуществляется по формуле
ООИ
= ИОИ
/ М(ИОИ
),
где М(ИОИ
) — индекс однородности иерархии при случайном заполнении матриц попарных сравнений.
Расчет индекса однородности М(ИОИ
) с учетом экспериментальных данных (см.
табл. 2.3) выполняется по формуле, аналогичной (2.5):

Однородность иерархии считается удовлетворительной при значениях ООИ
≤ 0,10.
2.4. Учет мнений нескольких экспертов
Для повышения степени объективности и качества процедуры принятия решений целесообразно учитывать мнения нескольких экспертов. С этой целью проводится групповая экспертиза, причем множество экспертов может быть подразделено на несколько подмножеств в зависимости от области экспертизы [З], определяемой характером критериев, используемых в иерархии. Оценка весомости критериев и альтернатив с учетом данного подхода предполагает привлечение специалистов-управленцев, маркетологов, производственников, специалистов-теоретиков и т. п. (рис. 2.4).
Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующему соотношению:
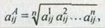 (2.6) (2.6)
где a
А
ij
—
агрегированная оценка элемента, принадлежащего i
-й строке и j
-му столбцу матрицы парных сравнений;
п —
число матриц парных сравнений, каждая из которых составлена одним экспертом.
Логичность критерия (2.6) становится очевидной, если два равноценных эксперта указывают при сравнении объектов соответственно оценки а
и 1/а,
что при вычислении агрегированной оценки дает единицу и свидетельствует об эквивалентности сравниваемых объектов.

Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены на уровне элементов матриц, если однородность составленных матриц достаточна и удовлетворяет условию OO ≤ 0,10. Покажем это на следующем примере.
Пусть заданы суждения двух экспертов в виде матриц попарных сравнений [A1
] и [A2
]:
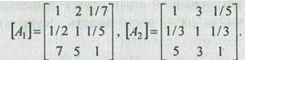
Для этих матриц собственные векторы W
А
i
,
максимальные собственные значения λmax
и оценки однородности (ИО; OO) имеют следующий вид:
для матрицы [A1
]

Для матрицы [A2
],

Осреднение на уровне элементов собственных векторов дает
WA
= {0,184 0,117 0,699}T
.
Осредняя элементы матриц [A1
] [A2
],
получим матрицу [А3
]:

Правый собственный вектор матрицы [А3
] следующий:
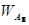 =
{0,184 0,116 0,699}T
.
=
{0,184 0,116 0,699}T
.
Сравнивая два собственных вектора Wa
и 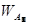 определенных двумя разными способами, можно убедиться в их совпадении, даже несмотря на то, что однородность суждений эксперта, заполнившего матрицу [A2
],
была неудовлетворительной (OO = 0,255 > 0,10).
определенных двумя разными способами, можно убедиться в их совпадении, даже несмотря на то, что однородность суждений эксперта, заполнившего матрицу [A2
],
была неудовлетворительной (OO = 0,255 > 0,10).
В достаточно ответственных задачах при оправданных затратах на экспертизу осреднение суждений экспертов проводится с учетом их квалификации ("веса"). Для определения весовых коэффициентов экспертов целесообразно использовать иерархическую структуру критериев (рис. 2.5).
Расчет агрегированной оценки в случае привлечения п
экспертов, имеющих различную значимость, осуществляется по формуле

где aak
ij
— оценка объекта, проведенная k
-м экспертом с весовым коэффициентом ak
;
при этом а
1
+ а
2
+...+ а
n
= 1.

2.5. Методы сравнения объектов относительно стандартов и копированием
Сравнение объектов относительно стандартов
Во второй модификации рассматривается метод сравнения объектов относительно стандартов. Метод попарного сравнения альтернатив не всегда может быть эффективно применен в некоторых практических ситуациях:
• эксперту может быть предложено для анализа более девяти альтернатив. В этом случае построение однородных матриц попарных сравнений становится затруднительным. Это связано с физическими ограничениями интеллекта человека;
• при добавлении новых альтернатив изменяется порядок ранее прошедших сравнение альтернатив относительно критериев качества. Нарушение порядка альтернатив нежелательно при решении ряда прикладных задач, связанных со значительными финансовыми, материальными и социальными затратами на корректировку последствий принимаемых решений или возможностью возникновения конфликтной ситуации между экспертами, готовящими и обосновывающими решения, и лицами, принимающими решения, несущими ответственность за принятые решения и их последствия;
• альтернативы могут поступать эксперту для сравнения не одновременно, а через определенные промежутки времени. Поэтому в данной ситуации не представляется возможным попарно сравнить объекты.
Для решения проблемы сравнения и оценки альтернатив в указанных ситуациях наиболее целесообразен метод сравнения альтернатив относительно стандартов. Стандарт устанавливает уровень качества объекта относительно критерия качества. Например, критерию "надежность" для объекта "автомобиль" может быть назначено три стандарта, характеризующих соответственно высокий (H — high), средний (М — medium), низкий (L — little) уровень надежности. Каждый стандарт отождествляется, как правило, с некоторым существующим на практике эталоном качества. В качестве таких эталонов принимаются объекты, аналогичные сравниваемым альтернативам. Например, для видов обеспечения банковских кредитов высокий, средний и низкий стандарты по критерию "ликвидность" могут быть отождествлены соответственно с драгоценными металлами, ценными бумагами и недвижимостью.
В иерархической структуре стандарты присваиваются элементам, имеющим непосредственную связь с альтернативами. При этом число стандартов по каждому такому элементу (критерию качества) может быть различно и определяется экспертом с учетом конкретной ситуации. По каждому стандарту экспертом устанавливается относительная степень предпочтения, которая указывает значимость стандарта для эксперта. Численное значение каждого стандарта определяется их попарным сравнением по девятибалльной шкале (см.
табл. 2.1) путем обработки матрицы

Вектор приоритетов стандартов будет иметь следующий вид:
{Н= 0,625 М= 0,257 L= 0,091}T
Из вышеприведенной матрицы следует, что эксперт отдал слабое предпочтение высокому стандарту (Н) перед средним (М), а также среднему перед низким стандартом (L). В то же время предпочтение высокого стандарта (Н) перед низким (L) определено как очень сильное (оценка 7 в матрице).
Рассмотрим правила построения иерархии (рис. 2.6), учитывающей стандарты и алгоритм вычисления векторов приоритетов альтернатив.
Введем следующие обозначения:
С
= {С
0
, C
g
} —
множество стандартов, включающее два подмножества, устанавливающие соответственно основную { С
0
} и дополнительную { С
g
} шкалы. Основная шкала включает градации С
0
=
{Н, М, L}, где Н, М, L — соответственно высокий, средний и низкий уровень стандартов по определенному критерию. Дополнительная шкала может включать градации C
g
=
{НН, НМ, ML, LL}, где НН, НМ, ML, LL — соответственно очень высокое; промежуточное между высоким и средним; промежуточное между средним и низким; очень низкое значение стандартов.
Для конкретного элемента Es
j
,
включенного в иерархию из множества С
, определяется подмножество стандартов Сj
, такое, что Сj
Ì С
, Сj
Î Es
j
.
Например, для элементов иерархии (см.
рис. 2.6)

E
1
s
и Es
p
определены стандарты Н, М, L, а для элемента Е
2
s
—
стандарты Н, НМ, М, ML, L. Следует отметить, что экспертом могут быть назначены различные значения для одних и тех же по наименованию стандартов, относящихся соответственно к элементам E
1
s
и Es
p
.
Вычисление векторов приоритетов альтернатив относительно элементов иерархии,, учитывающей стандарты, осуществляется следующим образом.
Для каждого элемента Es
j
иерархии, непосредственно связанного со стандартами, устанавливается подмножество С
j
Ì С
. Стандарты, входящие в подмножества С
j
, сформированные относительно Es
j
,
попарно сравниваются по девятибалльной шкале предпочтений. Относительные предпочтения стандартов фиксируются в матрицах, обработка которых по итерационному алгоритму, выполняемому в соответствии с соотношениями (2.2) и (2.3), позволяет определить для них правые собственные векторы Ws
j
Î Es
j
.
В собственном векторе верхний индекс указывает на принадлежность вектора уровню стандартов в иерархии.
Лицо, принимающее решение, присваивает каждой альтернативе А
i
значение одного стандарта. Процедура идентификации проводится по всем элементам Es
j
(j
=  ).
В результате идентификации строится матрица [А
] следующего вида: ).
В результате идентификации строится матрица [А
] следующего вида:

В матрице [А
] через wij
обозначено численное значение стандартов, соответствующее альтернативе А
i
и элементу Es
j
иерархии. Таким образом, столбцы в матрице [А
] образуют ненормированные векторы приоритетов альтернатив по соответствующим элементам Es
j
.
Для получения нормированных векторов WA
j
(верхний индекс указывает на то, что ранжируются альтернативы) приоритетов альтернатив матрица [А
] умножается на диагональную матрицу [S
] вида:

Множество нормированных векторов приоритетов альтернатив относительно всех элементов самого нижнего уровня иерархии определяется перемножением матриц
[WA
]=[A]
´
[S].
В полученной матрице [ WA
] столбцами являются нормированные векторы приоритетов альтернатив WA
j
для каждого элемента Es
j
иерархии.
Дальнейшее определение векторов приоритетов альтернатив относительно элементов Ei
j
иерархии, расположенных выше уровня S
,
осуществляется в соответствии с шагами 2 и 3 алгоритма иерархического синтеза (см.
разд. 2.3).
Рассмотрим пример использования метода сравнения альтернатив относительно стандартов, подтверждающий тот факт, что добавление новой альтернативы не нарушает порядок ранее проранжированных альтернатив.
Пусть имеется матрица предпочтений стандартов:

Вектор приоритетов стандартов имеет следующий вид:
Н = 0,696 М = 0,225 L = 0,079.
Рассмотрим четыре альтернативы А
1
,..., А
4
которым поставлены в соответствие следующие значения вектора приоритетов стандартов:
А
1
= 0,225 (М), А
2
=
0,079 (L), А
3
= 0,225 (М), А
4
=0,079 (L),
Нормированный вектор приоритетов рассматриваемых альтернатив следующий:
А
1
А
2
А
3
А
4
W
4
= { 0,370 0,130 0,370 0,130 }Т
.
где Т — знак транспонирования;
(4) — нижний индекс, указывающий число ранжируемых альтернатив.
В соответствии с приведенным вектором альтернативы ранжируются в порядке убывания приоритета: А
1
, А
3
, А
2
, А
4
.
Добавим к рассматриваемому множеству альтернатив новую — А
5
и присвоим ей значение, соответствующее высокому стандарту — Н. Нормированный вектор приоритетов для пяти альтернатив имеет следующий вид:
А
1
А
2
А
3
А
4
A
5
W
5
= {0,137 0,061 0,173 0,061 0,534}T
.
В соответствии с этим вектором альтернативы ранжируются в порядке убывания приоритета следующим образом: А
5
, А
1
, А
3
, А
2
, A
4
. Анализ приведенной последовательности показывает, что добавление новой альтернативы А
5
,
не привело к нарушению порядка у ранее проанализированных альтернатив А
1
, ..., А
4
.
Сравнение объектов методом копирования
В третьей модификации рассматривается определение вектора приоритетов альтернатив методом копирования.
Метод копирования применяется в тех случаях, когда среди анализируемых альтернатив имеются такие, которые идентичны по одним или нескольким анализируемым свойствам (критериям качества). Например, пневматическая виброзащитная система рукавного типа, используемая в рессорном подвешивании пассажирских автобусов, идентична по качеству виброизоляции с металлическим механизмом перескока, реализующим квазинулевую жесткость.
Рассмотрим процедуры сравнения и установления приоритета альтернатив, используемые в методе копирования.
Пусть определено множество альтернатив А
= {а
1
,
а
2
, ..., а
n
}, каждая из которых отличается от всех других альтернатив этого множества уровнем качества по рассматриваемому критерию К
i
и определено другое множество альтернатив В
== {b
1
, b
2
, ...,
bn
}, каждая из которых имеет одинаковые свойства со всеми другими по ранее определенному критерию К
i
.
Предположим, что множество А
имеет хотя бы один элемент а
i
*
,
свойство которого по критерию К
i
идентично свойствам всех альтернатив множества В.
Тогда все альтернативы множества В
являются копиями элемента а
i
*
по критерию К
i
.
При такой ситуации эксперт по критерию Кi
попарно сравнивает только альтернативы множества А.
Далее на основании матрицы попарных сравнений рассчитывается нормированный собственный вектор WA
,
ранжирующий альтернативы множества A
. Всем альтернативам-копиям {b
1
,
b
2
, ...,
bn
} присваивается значение нормированного собственного вектора WA
,
соответствующее элементу ai
*
. В результате получается новый ненормированный вектор приоритетов WAB
всех альтернатив, входящих в множества A
и В.
Вектор WAB
нормируется путем деления каждого значения указанного вектора на сумму всех его значений.
Метод копирования аналогичен методу сравнения альтернатив относительно стандартов в том плане, что позволяет не нарушать порядок ранее проранжированных альтернатив при добавлении новых, являющихся копиями ранее проранжированных альтернатив. Кроме того, число анализируемых альтернатив при добавлении копий может превышать пороговое значение, равное девяти, установленное для метода попарного сравнения.
Рассмотрим пример добавления к ранее проранжированным объектам альтернатив-копий.
Допустим, определены три альтернативы A
1
, А
2
и А
3
,
для которых экспертом установлена относительная степень предпочтений по критерию "надежность функционирования системы". Альтернативы сравниваются попарно в матрице, для которой рассчитывается нормированный собственный вектор, имеющий значения {0,5 0,3 0,2}T
. В приведенном векторе указан знак транспонирования — Т, а порядок значений вектора соответствует весу альтернатив А
1
, А
2
и А
3
.
Предположим, что для анализа поступают две новые альтернативы А
4
, А
5
,
свойства которых по указанному критерию полностью идентичны свойствам альтернативы А
3
.
В этом случае альтернативам-копиям присваиваются веса, соответствующие весу альтернативы А
3
,,
т. е. А
4
=
0,2 и А
5
=
0,2. Новый ненормированный вектор приоритетов альтернатив принимает следующий вид:
{0,5 0,3 0,2 0,2 0,2}T
Значения весов пяти альтернатив после нормирования предыдущего вектора приоритетов имеют следующий вид:
A
1
= 0,35, А
2
== 0,21, А
3
= 0,14, A
4
= 0,14, A
5
= 0,14.
Анализ двух векторов приоритетов, характеризующих соответственно множества из трех и пяти альтернатив, показывает, что добавление альтернатив А
4
, А
5
не нарушило порядок приоритетности альтернатив А
1
, А
2
и А
3
,.
Метод копирования позволяет существенно сократить время экспертов на подготовку исходных данных для анализа и уменьшить вероятность внесения в них как случайных, так и логических ошибок.
2.6. Многокритериальный выбор на иерархиях с различным числом и составом альтернатив под критериями
В четвертой модификации рассматривается метод определения векторов приоритетов альтернатив для иерархий с различным числом и различающимся составом альтернатив под критериями.
В практике принятия решений нередко встречается задача, когда ранжируемые по множеству критериев альтернативы оцениваются экспертом не по всем критериям. Эта задача характерна для ситуаций, в которых множество критериев, выделенных для всех рассматриваемых альтернатив, является избыточным относительно одной или нескольких альтернатив. Таким образом, в рассматриваемом случае эксперт имеет разное количество альтернатив под каждым критерием или под их частью. На рис. 2.7 приведены примеры иерархий, в которых каждый критерий Ej
из множества {Е
1
,
E
2
, ... , Е
p
} имеет разное количество альтернатив из множества {А
1
,А
2
, ... ,Аr
}.
Альтернативы А1
и Аr
; А1
, А2
А
r
; А2
и А
r
оцениваются соответственно относительно элементов (критериев) Е1
, Е2
, Ер
(рис. 2.7а).

Рис. 2.7. Примеры иерархий с разным числом альтернатив под критериями а —
синтез; б — декомпозиция
Рассмотрим методику определения вектора приоритета альтернатив для случая, когда иерархия имеет один уровень критериев, объединенных фокусом (рис. 2.7 б) с учетом значимости критериев, и разное количество альтернатив у каждого критерия. Методика предполагает выполнение ряда процедур по структурированию информации и проведению вычислительных операций.
Процедура 1.
Исходная проблема структурируется в виде иерархии, устанавливающей взаимосвязь между множеством сравниваемых альтернатив {А1
,
A
2
,... , А
r
}и множеством критериев {E
1
, Е2
, ... , Е
p
}.
Процедура 2.
На основе иерархической структуры определяется бинарная матрица [В],
устанавливающая соответствие между альтернативами и критериями. Матрица [В]
содержит элементы bij
= {0,1}. При этом если альтернатива А
i
оценивается по критерию Ej
,
то bij
=
1, в противном случае bij
= 0.
Процедура 3.
Осуществляется экспертная оценка альтернатив по соответствующим критериям. Для этой цели используются метод попарного сравнения, метод сравнения относительно стандартов или метод копирования. На основе экспертных оценок с учетом матрицы [В]
строится матрица [А]
следующего вида:

В матрице [А]
экспертные оценки {aij
} представляют векторы приоритетов альтернатив относительно критериев Ej
.
При этом если альтернатива А
i
не оценивается по критерию Е
j
,
то в матрице [А]
соответствующее значение aij
= 0. Векторы в указанной матрице имеют различное число значений aij
и могут быть нормированными или ненормированными в зависимости от используемого метода сравнения альтернатив.
Процедура 4.
В результате обработки матрицы попарных сравнений критериев Е
j
определяется нормированный вектор приоритетов критериев 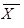 . .
Процедура 5.
Формируются структурные критерии S
и L
,
отображаемые соответствующими диагональными матрицами [
S
]
и [L].
Рассмотрим состав упомянутых матриц.
Матрица [
S
]
имеет следующий вид:

где aij
—
значения векторов приоритетов из матрицы [А].
С помощью матрицы [S]
обеспечивается нормирование векторов приоритетов альтернатив, образующих матрицу [А],
если последняя заполнена методом сравнения относительно стандартов или копирования без предварительного нормирования.
Матрица [L]
имеет следующий вид:

где Rj
—
число альтернатив А
i
,
находящихся под критерием Е
j
,
 —
суммарное число альтернатив, находящихся под всеми критериями. —
суммарное число альтернатив, находящихся под всеми критериями.
Здесь следует отметить, что число N
в матрице [L]
может приниматься равным числу рассматриваемых альтернатив r
,
т.е. N
=
r
.
При этом на конечный результат способ определения N
не оказывает влияния.
Использование структурного критерия L
позволяет эксперту или ЛПР изменять при необходимости вес альтернатив, связанных с соответствующими критериями пропорционально отношению Rj
/
N
.
Этим обеспечивается повышение приоритета альтернатив, образующих большие группы, и снижение приоритета альтернатив в группах с их относительно небольшим числом. Здесь имеется в виду, что группу определяют альтернативы, являющиеся "потомками" по отношению к критерию Ej
.
Необходимость в приведенной вычислительной процедуре обусловлена тем, что у критериев-"родителей" с высоким приоритетом в иерархии может находиться большое число альтернатив-"потомков", а у критериев-родителей" с низким приоритетом — значительно меньшее число альтернатив-"потомков", чем в первом случае. Поэтому в этой ситуации желательно повышение приоритетов альтернатив в большой группе, поскольку, если альтернатив много, каждая из них получит меньший составной приоритет, чем каждая альтернатива, входящая в меньшую группу с низким приоритетом критерия.
На практике возможны также ситуации, прямо противоположные выше охарактеризованной, когда требуется повысить приоритет так называемых редких альтернатив-"потомков", образующих относительно критериев-"родителей" маленькие группы. В этом случае структурная матрица [L
] принимает следующий вид:

Процедура 6.
Определяется вектор приоритетов альтернатив W
относительно критериев. Данная процедура реализуется последовательным перемножением слева направо следующих матриц и векторов:
а) для случая, когда экспертные оценки в матрице [А]
ненормированы:
W=[A] [S][L]
 [B];
(2.7)
[B];
(2.7)
б) для случая, когда экспертные оценки в матрице [А]
нормированы:
W=[A] [L]
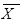 [B].
(2.8)
[B].
(2.8)
В выражениях (2.7) и (2.8) диагональная матрица [В]
предназначена для окончательного нормирования значений вектора приоритетов альтернатив. Эта матрица имеет следующий вид:

где х
i
—
значение ненормированного вектора приоритетов альтернатив, полученное после последовательного перемножения слева направо матриц [
A
], [
S
], [
L
]
и вектора 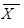 ;
;
r
— число альтернатив.
Рассмотрим пример вычисления вектора приоритета альтернатив.
Допустим, имеется иерархическая система (рис. 2.8), включающая корневую вершину — фокус (Ф), два критерия К1
и К2
и пять альтернатив A
1
, ... ,А5
.
При этом по критерию К1
оцениваются все пять альтернатив, а по критерию К2
—
две альтернативы: А4
и А5
.
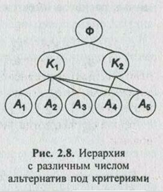
Предположим, что при попарном сравнении альтернатив и критериев получены матрицы, отображающие равную предпочтительность сравниваемых объектов.
Матрицы предпочтений альтернатив относительно критериев K
1
и K
2
соответственно примут вид:

Построим матрицу предпочтений критериев относительно фокуса (Ф):

Правые собственные векторы для приведенных матриц имеют следующий вид:
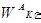 = {0,2 0,2 0,2 0,2 0,2}T
— приоритет альтернатив по критерию K
1
;
= {0,2 0,2 0,2 0,2 0,2}T
— приоритет альтернатив по критерию K
1
;
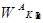 = {0,5 0,5}T
—
приоритет альтернатив по критерию К2
;
= {0,5 0,5}T
—
приоритет альтернатив по критерию К2
;
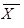 = {0,5 0,5}T
— приоритет критериев относительно фокуса Ф.
= {0,5 0,5}T
— приоритет критериев относительно фокуса Ф.
Поскольку векторы приоритетов альтернатив относительно критериев K
1
и К2
нормированы, результирующий вектор рассчитывается по формуле (2.8).
При этом матрицы [А
] и [L] и вектор 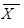 с учетом ранее выполненных расчетов имеют следующий вид:
с учетом ранее выполненных расчетов имеют следующий вид:

Производя последовательные перемножения матриц и вектора слева направо, получим следующие результаты:

Следует отметить, что при неучете структурного критерия L
результирующий вектор приоритетов альтернатив имеет следующий вид:
W'=
[A] 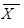 =
{0,1 0,1 0,1 0,35 0,35}T
.
=
{0,1 0,1 0,1 0,35 0,35}T
.
Из сравнительного анализа двух результирующих векторов W
и W'
видно, что в первом случае каждая из альтернатив A
4
,
и A
5
,
(значение 0,286 в векторе) в два раза весомее любой из альтернатив А1
,
A
2
или А3
,
(значение 0,143 в векторе), а во втором случае различие между теми же альтернативами большее и равно 3,5 (значение 0,35 против 0,1) для альтернатив в векторе приоритетов W
'.
Существуют иерархии (рис. 2.9), у которых, в отличие от ранее рассмотренных (приведенной, например, на рис. 2.8), альтернативы сгруппированы в подмножества {А1
, А2
, ..., А
m
},
{А'1
, А'2
, ..., А'
s
},
{А"1
, А"2
,
... , A
"
l
},
а элементы каждого из таких подмножеств связаны, в свою очередь, с определенными группами критериев {K
11
, K
12
,...,K
1
m
}, {K
21
, K
22
,...,
K
2
n
},
{Kn
1
,
Kn
2
,…,
Knp
}.
В этом случае перевернутое иерархическое дерево состоит из ряда самостоятельных иерархических ветвей.
Рассмотрим особенности алгоритма для определения векторов приоритетов альтернатив на иерархиях, состоящих из нескольких ветвей. Для лучшего понимания сущности алгоритма проиллюстрируем его на примере конкретной иерархии (см.
рис. 2.9).

Алгоритм для иерархии с несколькими ветвями
Шаг 1. Вычисляются векторы приоритетов альтернатив относительно критериев К
ij
:

Шаг 2. Строятся r
матриц [А
i
], у
которых наименованиями строк являются альтернативы, а наименованиями столбцов — критерии К
ij
.
При этом если альтернатива А
i
не связана с критерием Kij
,
то в матрице [А
i
] на пересечении соответствующих строки и столбца проставляется нуль.
Шаг 3. Вычисляются r
векторов приоритетов альтернатив WA
i
(
i
= 1,
r
)
относительно критериев К
i
по выражениям:

где [Si
] — матрица для нормирования матрицы [А
i
];
[Li
] —
структурная матрица для изменения веса альтернатив пропорционально отношению R
/
N
(
R
—
число альтернатив, находящихся под критерием К
ij
, N —
суммарное число альтернатив);
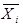 —
вектор приоритетов критериев К
ij
относительно критериев К
i
; —
вектор приоритетов критериев К
ij
относительно критериев К
i
;
[Bi
] — диагональная матрица для получения нормированного вектора WA
i
,
определяемая по выражению (2.9).
Ш а г 4. Вычисляется вектор приоритетов критериев 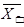 относительно фокуса иерархии К0
.
относительно фокуса иерархии К0
.
Шаг 5. Строится результирующая матрица [A
0
],
у которой наименованиями строк являются все рассматриваемые альтернативы ({А
i
}, i = 1,т,
{А'
i
}, i
= 1,
s
, {А"
i
}, i
= 1
,t
), а наименованиями столбцов — критерии К
i
.
При этом результирующая матрица [Ао
] имеет следующий вид:

Шаг 6. Определяется результирующий нормированный вектор приоритетов W
0
A
всех рассматриваемых альтернатив относительно фокуса иерархии К0
на основании известного выражения:
W0
A
= [
А
0
] [S0
] [L0
]
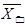 [
В
0
] .
[
В
0
] .
Конец алгоритма.
2.7. Методика решения прикладных задач на ЭВМ
2.7.1. Выбор и прогнозирование наилучшего обеспечения банковского кредита
Метод статических предпочтений и приоритетов
Возвратность кредита представляет собой основополагающее свойство кредитных отношений. Кредитная сделка предусматривает возникновение обязательства ссудополучателем вернуть соответствующий долг. Однако наличие обязательства еще не означает гарантии своевременного возврата. Инфляционные процессы в экономике могут вызывать обесценение суммы предоставленной ссуды, а ухудшение финансового состояния заемщика — нарушение сроков возврата кредита, включающее не только порядок погашения конкретной ссуды исходя из реальных экономических условий, не только юридическое закрепление его в кредитном договоре, но и формы обеспечения полноты и своевременности обратного движения ссуженной стоимости. Под формой обеспечения возвратности кредита следует понимать конкретный источник погашения имеющегося долга, юридическое оформление права кредитора на его использование, организацию контроля банка за достаточностью и приемлемостью данного источника.
Залог имущества клиента — одна из распространенных форм обеспечения возвратности банковского кредита. Предметом залога могут выступить любая вещь или другое имущество, принадлежащее заемщику, на которые в соответствии с законодательством допускается обращение взыскания. Приемлемость товарно-материальных ценностей для залога определяется качеством ценностей и возможностью кредитора осуществлять контроль за их сохранностью. Критериями качества товарно-материальных ценностей являются: быстрота реализации, относительная стабильность цен, долговременность хранения и др. Важно не только определить критерий качества, выбрать в соответствии с ним ценности, но и обеспечить их сохранность. В этой связи наиболее надежным способом обеспечения сохранности заложенных ценностей выступает передача их кредитору, т.е. банку. Одновременно на него переходит обязанность надлежащим образом содержать и хранить предмет заклада, нести ответственность за утрату и порчу.
Рассмотрим пример использования метода анализа иерархий для выбора наиболее надежного обеспечения кредита. Количество и состав рассматриваемых критериев и альтернатив ограничен, поскольку пример носит учебный характер.
В качестве альтернатив примем наиболее часто применяемые в России виды обеспечения кредитов: A
1
— иностранная валюта, А2
— драгоценные металлы, А3
— ценные бумаги, А4
— недвижимость.
Для выбора наиболее рациональной альтернативы используем подход "выгоды — издержки". В соответствии с этим подходом необходимо построить две иерархии, упорядочивающие критерии качества и определяющие общие выгоды и издержки для рассматриваемых альтернатив (рис. 2.10). Наилучшей является альтернатива с наибольшим отношением количественно определенных выгод к издержкам.

В приведенных иерархиях на первом уровне расположены основные факторы, определяющие выгоды и издержки, на втором — критерии качества, характеризующие собственно выгоды и издержки, на третьем — альтернативы, из которых предстоит сделать выбор.
Используя метод попарного сравнения элементов иерархии, построим матрицы парных сравнений для иерархии, отражающей выгоды от обеспечения кредита. Для каждой матрицы рассчитаем нормированный вектор приоритетов (W
), собственное число матрицы (λmax
) и отношение согласованности (ОС).
Рассмотрим матрицы парных сравнений факторов и критериев качества:

Построим матрицы парных сравнений альтернатив относительно критериев качества:

Осуществим иерархический синтез в целях определения вектора приоритета альтернатив относительно факторов и фокуса иерархии.
Вектор приоритетов альтернатив относительно экономического фактора (WA
Э
) определяется путем перемножения матрицы, сформированной из значений векторов приоритетов W
5
, W
6
,
W
7
,
на вектор W
2
,
определяющий значимость критериев качества, расположенных под экономическим фактором:
W
A
Э
= [W5
, W6
, W7
]
´ W2
.

Аналогично определяются векторы приоритетов альтернатив относительно физического фактора (
W
физ
А
юридического фактора (
W
ю
А
)
и фокуса иерархии (
W
ф
А
):

Результирующий вектор приоритетов альтернатив имеет следующие значения:

Анализ значений полученного вектора показывает, что наиболее надежным обеспечением кредита относительно выгод является валюта (альтернатива — А1
)
По изложенному выше алгоритму проводится расчет вектора приоритетов альтернатив для второй иерархии, отражающей издержки от обеспечения кредита.
Результирующие векторы приоритетов альтернатив для двух рассмотренных иерархий и отношения их значений приведены в табл. 2.4.
Таблица 2.4
Значения векторов приоритетов

В результате проведенного анализа можно сделать вывод, что наиболее надежным обеспечением кредита является валюта (А1
). Далее в порядке убывания следуют: драгоценные металлы (А2
), ценные бумаги (А3
) и недвижимость (А4
).
Метод динамических предпочтений и приоритетов
Рассмотрим применение компьютерной системы для поддержки динамических процессов при решении задачи прогнозирования наилучшего обеспечения банковского кредита.
С течением времени приоритет альтернатив может изменяться по тому или иному закону. Для того чтобы определить изменение во времени приоритета альтернатив по комплексу наиболее важных критериев, необходимо определить изменения предпочтений экспертов как по самим критериям, так и по альтернативам. В примере рассматриваются три альтернативы, обеспечивающие банковский кредит: А1
– валюта; А2
– драгоценные металлы;

А3
— недвижимость. Прогнозирование эффективности обеспечения банковского кредита на пятилетие (t
= 1, ...., 5 лет) производится по множеству критериев качества, упорядоченных в иeрархию (рис. 2.11). Экспертно методом парных сравнений установлены динамические предпочтения критериев качества (табл. 2.5) и альтернатив относительно критериев качества (табл. 2.6). Динамические предпочтения установлены на основании функциональной шкалы (см.
табл. 2.2).
Таблица 2.5
Динамические предпочтения критериев качества

При заполнении матриц парных сравнений эксперт отвечает на следующие вопросы: Какой из двух сравниваемых объектов предпочтительнее? По какому функциональному закону идет изменение предпочтительности во времени одного сравниваемого объекта (критерия или альтернативы) над другими? Каковы параметры выбранной функции?
Например, при попарном сравнении альтернатив А1
— валюта и А2
— драгоценные металлы экспертом отдается предпочтение второй, причем прогноз изменения предпочтения описывается экспоненциальной функцией y
21
= 0,01е1.1
t
+2 (см.
табл. 2.6). Параметры функции выбираются с учетом настройки на дискретную девятибалльную шкалу, которая применяется для измерения предпочтений. При этом отсутствию предпочтения соответствует 1, а абсолютному предпочтению — 9.
Таблица 2.6
Динамические предпочтения альтернатив относительно критериев качества

На рис. 2.12 приведен график зависимости y
21
(t
), который показывает, что в начальный момент времени драгоценные металлы предпочтительнее валюты с оценкой 2, затем предпочтительность возрастает с течением времени по экспоненциальному закону: сначала медленно, потом быстро. В конце периода прогнозирования оценка предпочтения близка к 9. Решение задачи численными методами позволяет получить функциональные зависимости векторов приоритетов альтернатив от времени W
(
t
)
по всем критериям (табл. 2.7), входящим в иерархию (см.
рис. 2.11).

Таблица 2.7
Зависимость вектора приоритетов от времени


Графики (рис. 2.13) иллюстрируют функциональные зависимости значений векторов приоритетов рассматриваемых трех альтернатив от времени по критериям "физический износ" и "место хранения". Анализ этих графиков показывает, что по критерию "физический износ" лучшей является альтернатива А2
— драгоценные металлы со значениями, изменяющимися по экспоненциальному закону. С другой стороны, по критерию "место хранения" наиболее предпочтительна валюта со значениями в векторе приоритетов, изменяющимися во времени по логарифмическому закону.

В результате свертки векторов приоритетов альтернатив по всем критериям, входящим в иерархию, получены функциональные зависимости значений результирующего вектора приоритетов альтернатив W
(
t
)
(рис. 2.14) по интегральному критерию "наилучшее обеспечение банковского кредита".
Анализ приведенных графиков показывает, что наиболее предпочтительными являются драгоценные металлы, приоритет которых со временем возрастает по сравнению с валютой.
Экранная форма с ЭВМ, иллюстрирующая этап работы системы поддержки динамических процессов принятия решений при формировании предпочтений, приведена на рис. 2.15.
2.7.2. Функционально-стоимостный анализ промышленной продукции
Функционально-стоимостный анализ (ФСА) — метод комплексного исследования функций объектов — предназначен для обеспечения общественно необходимых потребительских свойств объектов и минимальных затрат на их проявление на всех этапах их жизненного цикла [4 — 7].
Объектами ФСА могут быть изделие, технологический процесс, производственные, организационные, управленческие системы и их отдельные элементы. В методе ФСА анализу подвергаются функции и стоимости функций. Из-за несовершенства объектов, технологических процессов, применяемых материалов затраты могут оказаться излишними. Поэтому цель ФСА — обнаружение, предупреждение, сокращение или ликвидация излишних затрат. Эта цель может быть достигнута путем:
• сокращения затрат при одновременном повышении потребительских свойств объекта;
• повышения качества при сохранении уровня затрат;
• сокращения затрат при обоснованном снижении технических параметров до их функционально необходимого уровня;
• повышения качества при некотором, экономически оправданном увеличении затрат.
Для анализа затрат функций разработаны следующие методы [2, 3]:
1) метод подбора и ориентировочной оценки простейших решений по каждой функции в отдельности;
2) метод ранжирования функций по величине затрат, связанных с выполнением этих функций;
3) метод установления пропорций между затратами на осуществление основных и вспомогательных функций;
4) метод сопоставления затрат на функции с балльными оценками значимости функций;
5) метод исследования факторов снижения затрат на функции.
Для перечисленных выше четвертого и пятого методов на основе МАИ разработаны их модификации. Рассмотрим сущность этих модифицированных методов.
Метод сопоставления затрат на функции с балльными оценками значимости функций.
Он исходит из предположения о том, что нормирующим условием для распределения затрат служит значимость функций. Значимость функций некоторого уровня иерархии функциональной модели определяет их вклад в реализацию функции вышестоящего иерархического уровня, которой они подчинены. Для оценки значимости (Н
i
) i
-й функции в методе ФСА предполагается использовать один из ведущих критериев качества функции, которой он подчинен. Такими критериями являются надежность, точность, быстродействие и т.д. Относительные производственные затраты Zi
на осуществление i
-й функции также выражаются в баллах следующим образом:
Zi
=Ci
×
100/
Собщ
,
(2.10)
где С
i
— затраты на осуществление 1-й функции в рублях;
Сoбщ
— общая стоимость изготовления всего объекта в рублях.
Далее балльные оценки Н
i
и Z
i
сопоставляются с помощью диаграммы "значимость — затраты" и рассчитываются значения удельных относительных затрат на один балл значимости:
zi
=Zi
/Hi
, (2.11)
Неблагополучным соотношением "значимость — затраты" считаются те, у которых Z
i
больше единицы.
Основной недостаток этого метода — большая неопределенность, вкладываемая в определение критерия значимости функции. Поэтому предлагается использовать иерархическое представление значимости функций.
Значимость функций может быть рассчитана по одному ведущему критерию или по комплексу наиболее важных критериев качества, характеризующих главную внешнюю функцию системы в целом. Для первого случае иерархическая система имеет вид, приведенный на рис. 2.16а.
Во втором случае подбирается такой набор наиболее важных критериев качества, с помощью которых может быть оценена как главная внешняя функция, так и функции отдельных элементов, обеспечивающие выполнение первой. Общая схема ранжирования альтернатив-функций (Fi
) по значимости с учетом множества критериев качества (Ki
) приведена на рис. 2.16б.

Рассмотрим пример сопоставления значимости функций и затрат на их осуществление для виброзащитной системы с использованием традиционного и предлагаемого подходов. Виброзащитная система имеет главную функцию, характеризующую систему в целом, и четыре подфункции, определяющие назначение четырех конструктивных элементов, из которых состоит система.
Все подфункции подчинены главной функции — защите от вибраций человека-оператора. Ведущим критерием качества главной функции является качество виброзащитных свойств рассматриваемой технической системы. В результате экспертной оценки относительной значимости функции по критерию "качество виброзащитных свойств" получены следующие данные: H
1
= 40; Н2
= 30; Н3
= 25, Н4
= 5 баллов (сумма баллов по всем функциям должна равняться 100). Относительные производственные затраты на осуществление i
-й функции, выраженные в баллах, имеют следующие значения Z
1
= 30; Z
2
= 50; Z
3
= 5; Z
4
= 15. Диаграмма "значимость — затраты" для рассматриваемой системы виброзащиты приведена на рис. 2.17а. Удельные относительные затраты на один балл следующие: z
1
= 0,75; z2
= 1,66; z
3
= 0,20; z
4
= 3,0. Анализ диаграммы "значимость — затраты" и удельных затрат указывает на целесообразность совершенствования системы по функции F
4
, поскольку для нее удельные затраты значительно превосходят единицу.
Теперь рассмотрим решение этой задачи с использованием метода анализа иерархий (рис. 2. 17б). Значимость функций будем определять по следующим критериям качества K
1
— эффективность; К2
— надежность; К3
— долговечность. Функции оценивались методом попарного сравнения по каждому критерию качества Ki
. В результате иерархического синтеза был получен интегральный вектор приоритетов функций, который установил для них следующую значимость: Н1
= 56, H
2
= 10, H
3
= 30, H
4
= 4. Относительные производственные затраты на осуществление функций оставлены прежними и определены для i
-й функции с учетом (2.10) и (2.11).

Сопоставительный анализ диаграмм показывает, что значимости функций, полученные разными методами, различаются. Удельные относительные затраты распределились по функциям следующим образом: z
1
=
0,53; z
2
=
5,05; z
3
= 0,17; z
4
= 3,57.
Сопоставительный анализ удельных относительных затрат показывает, что согласно первому методу первоочередной функцией для совершенствования является функция F
4
,
а согласно второму методу — F
2
.
Рассмотрим традиционный и модифицированный методы исследования факторов снижения затрат по функциям, которые основан на том, что ожидаемая экономия за счет мероприятий ФСА определяется как уровнем исходных затрат, так и возможными факторами их снижения.
Относительно производственных систем машиностроительного профиля наиболее значимыми факторами экономии затрат являются:
• повышение технического уровня промышленной продукции;
• устранение функционально излишних конструктивных элементов в исходной конструкции;
• повышение обоснованности значений технических параметров на основе технических, технико-экономических и организационно-экономических расчетов;
• применение прогрессивных технологических процессов, заготовок и материалов;
• повышение коэффициента унификации;
• улучшение качества компоновки и технологичности сборки;
• повышение показателей надежности.
Каждый фактор вносит в общую экономию свой вклад, который приближенно оценивается соответствующим процентом снижения фактических затрат на функцию. Схематично в общем виде функциональные затраты и факторы их снижения для i
-й функции приведены на рис. 2.18, где приняты следующие обозначения:

Указанные затраты рассчитываются по известным формулам [1]. Для выявления факторов экономии в традиционном методе ФСА предполагается использовать экспертов, которые имеют знания об альтернативных исполнениях исследуемых функций.
Недостатком данного метода исследования факторов снижения затрат по функциям является то, что в нем отсутствует подход выбора наиболее эффективной альтернативы из множества возможных реализаций i
-го фактора, учитывающий одновременно функциональную эффективность и стоимостные затраты. В связи с этим предлагается лучшие факторы и их альтернативы определять по критерию максимального соотношения уровня технической эффективности к уровню затрат на реализацию функции. Рассмотрим последовательность решения указанной задачи.
Прежде всего следует отметить, что критерий эффективности производственной системы в целом или отдельного ее элемента , является комплексным и включает показатели назначения, надежности, экономичности, патентоспособности и т.п. Поскольку все показатели имеют свои единицы измерения, то при комплексной оценке необходимо использовать безразмерные единицы. Критерий технической эффективности может быть представлен в виде иерархической структуры показателей качества, конкретизирующих обобщенный критерий. В связи с этим для оценки альтернатив факторов по снижению затрат функций целесообразно использовать метод анализа иерархий. После построения иерархической структуры и попарного сравнения альтернатив i
-го фактора относительно критериев самого нижнего иерархического уровня осуществляется вычисление интегрального вектора приоритета W
Т.Э.
альтернатив по целевому критерию технической эффективности исследуемой системы в целом или отдельного ее элемента.
Далее определяются затраты альтернатив факторов по каждой функции. При этом возможны два способа расчета затрат. В соответствии с первым способом вычисляются относительные затраты исходя из стоимостей функций, выраженных в денежных единицах (случай, когда на функциональные элементы системы имеется калькуляция). В соответствии со вторым способом определяются приросты затрат путем попарного сравнения функций системы. Этот способ применяется в ситуациях, когда на элементы системы отсутствует калькуляция, например когда исследуется принципиально новая система.
При использовании второго способа прирост затрат определяется на основе самостоятельной иерархической структуры, для которой рассчитывается вектор приоритета 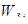 ,
ранжирующий альтернативы, принадлежащие i-
му фактору, относительно вершины иерархической структуры. Вершина иерархии в данном случае определяет затраты на реализацию факторов. Далее берется соотношение соответствующих значений векторов ,
ранжирующий альтернативы, принадлежащие i-
му фактору, относительно вершины иерархической структуры. Вершина иерархии в данном случае определяет затраты на реализацию факторов. Далее берется соотношение соответствующих значений векторов 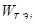 , , 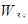 и строится искомый вектор: и строится искомый вектор:

Наиболее значимой альтернативой фактора для улучшения функции по технико-экономическому критерию является та, которая имеет максимальное значение в векторе 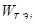 /3i
. /3i
.
Рассмотрим пример определения наиболее значимой альтернативы фактора для улучшения по технико-экономическому критерию функции "перемещать наземным способом от одного до двух человек в диапазоне скоростей от 5 до 200 км/ч", которая относится к легковым автомобилям.
Пусть для улучшения технико-экономических показателей указанной функции используется один фактор: повышение технического уровня базового автомобиля "Москвич" путем использования новых технических идей ведущих мировых автомобильных компаний. Альтернативами данного фактора являются следующие варианты компоновки автомобиля "Москвич": A
1
— "Москвич" — Мерседес, А2
—
"Москвич" — BMW, А3
, —
"Москвич" — Вольво, A
4
— "Москвич" — Фиат, А5
—
"Москвич" — Форд, A
6
—
"Москвич" — Рено.
Иерархическая структура для оценки технической эффективности альтернатив приведена на рис. 2.19. Установление относительной предпочтительности критериев и альтернатив осуществлялось попарным сравнением. Значения векторов приоритетов альтернатив, рассчитанные по всем критериям иерархии, приведены в табл. 2.8, а абсолютные затраты на реализацию альтернатив — в табл. 2.9.

Таблица 2.8
Значения векторов приоритетов альтернатив при оценке их по техническим критериям
| Альтернатива
|
Критерий
|
| K
1
|
K
2
|
K3
|
K4
|
K5
|
K11
|
K12
|
K13
|
K0
|
| A1
|
0,291
|
0,440
|
0,059
|
0,048
|
0,616
|
0,508
|
0,312
|
0,052
|
0,180
|
| A2
|
0,196
|
0,202
|
0,261
|
0,265
|
0,228
|
0,133
|
0,138
|
0,318
|
0,231
|
| A3
|
0,066
|
0,096
|
0,119
|
0,048
|
0,228
|
0,031
|
0,038
|
0,129
|
0,111
|
| A4
|
0,154
|
0,097
|
0,038
|
0,110
|
0,027
|
0,097
|
0,312
|
0,052
|
0,085
|
| A5
|
0,146
|
0,048
|
0,261
|
0,265
|
0,228
|
0,056
|
0,063
|
0,318
|
0,189
|
| A6
|
0,147
|
0,117
|
0,261
|
0,265
|
0,228
|
0,174
|
0,138
|
0,129
|
0,204
|
Таблица 2.9
Абсолютные затраты на альтернативы
| Альтернатива А
i
|
A1
|
A2
|
A3
|
A4
|
A
5
|
A
6
|
| Абсолютные затраты (тыс. руб)
|
150
|
155
|
150
|
50
|
160
|
140
|
Относительные затраты Zi
на i
-ю альтернативу рассчитываются по формуле Zi
= С
i
/Собщ
,
где С
i
— затраты на осуществление i
-й альтернативы; Собщ
— общие затраты на все альтернативы.
Векторы относительных затрат 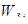 по альтернативам и результирующий вектор, отражающий отношение значений векторов по альтернативам и результирующий вектор, отражающий отношение значений векторов 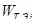 и и 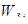 ,
имеют следующий вид: ,
имеют следующий вид:
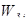 = {0,186 0,193 0,186 0,062 0,200 0,174}T
, = {0,186 0,193 0,186 0,062 0,200 0,174}T
,
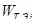 /З
i
= {0,986 1,260 0,597 1,371 0,945 1,772}T
. /З
i
= {0,986 1,260 0,597 1,371 0,945 1,772}T
.
Для последующего расчета отношения "эффективность — затраты" могут использоваться значения прироста затрат, определяемые методом попарного сравнения абсолютных затрат, принадлежащих альтернативам. Для этого вычисляется правый собственный вектор матрицы попарных сравнений, при составлении которой эксперт отвечает на вопросы, какая из двух сравниваемых альтернатив имеет бóльшие затраты и насколько. В табл. 2.10 приведена матрица попарных сравнений альтернатив, построенная по критерию "затраты" на основании сравнения абсолютных затрат.
Таблица 2.10
Матрица попарных сравнений альтернатив
| Какая из сравниваемых модификаций автомобиля
имеет большие затраты ?
|
Правый собственный вектор
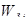
|
| A1
|
A2
|
A3
|
A4
|
A5
|
A6
|
| A1
A2
A3
A4
A
5
A
6
|
1
2
1
1/7
3
1/3
|
1/2
1
1/2
1/7
2
1/3
|
1
2
1
1/7
2
1/3
|
7
7
7
1
8
7
|
1/3
½
½
1/8
1
1/3
|
3
3
3
1/7
3
1
|
0,157
0,236
0,166
0,025
0,328
0,088
|
Результирующий вектор, отражающий отношение значений векторов 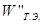 и и 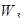 с учетом ранее полученных данных, имеет следующий вид: с учетом ранее полученных данных, имеет следующий вид:
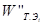 /Зi
= {1,146 1,022 1,495 0,294 1,735 0,431 }T
. /Зi
= {1,146 1,022 1,495 0,294 1,735 0,431 }T
.
Анализ двух результирующих векторов 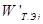 /Зi
и /Зi
и 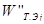 /Зi
показывает, что метод определения затрат существенно влияет на конечный результат. При этом второй подход расчета затрат имеет определенный смысл в тех случаях, когда эксперту важно при решении конкретной задачи выразить свое личное отношение к установлению относительной предпочтительности по каждой альтернативе. /Зi
показывает, что метод определения затрат существенно влияет на конечный результат. При этом второй подход расчета затрат имеет определенный смысл в тех случаях, когда эксперту важно при решении конкретной задачи выразить свое личное отношение к установлению относительной предпочтительности по каждой альтернативе.
При рассмотрении принципиально новых альтернатив, например на уровне новых технологий, затраты для них определяются по многим критериям качества, которые упорядочиваются конкретной иерархией (рис. 2.20).

Далее методом попарного сравнения или методом сравнения относительно стандартов устанавливается степень предпочтения альтернатив и критериев качества. После проведения экспертной оценки осуществляется иерархический синтез, в результате которого рассчитывается интегральный вектор приоритетов альтернатив относительно фокуса иерархии. Для рассматриваемого примера имеем следующий интегральный вектор:
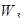 = { 0,328 0,088 0,236 0,166 0,157 0,025}T
. = { 0,328 0,088 0,236 0,166 0,157 0,025}T
.
Окончательный результат получается путем деления значений вектора 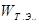 на соответствующие значения вектора на соответствующие значения вектора 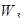 : :
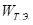 /Зi
={0,549 0,625 0,470 0,512 0,204 8,16}T
. /Зi
={0,549 0,625 0,470 0,512 0,204 8,16}T
.
Анализ последнего вектора позволяет сделать вывод, что лучшей альтернативой является A
6
со значением 8,16.
2.7.3. Рациональное распределение ресурсов между альтернативами
Актуальной является задача распределения ресурсов между альтернативами. В частности, интерес представляют задачи комбинаторной оптимизации, самая простая из которых — определение комбинации (альтернатив, проектов), максимизирующей "общие выгоды" при ограничениях на издержки.
Общая постановка задачи определения комбинации альтернатив с максимальной эффективностью (или эффективностью на единицу требуемого ресурса) заключается в определении сочетаний альтернатив, удовлетворяющих следующим целевым функциям:

при выполнении одного из следующих условий:

где Э — эффективность рассматриваемой комбинации альтернатив, полученной генерацией множества сочетаний с различным числом альтернатив;
Эi
— эффективность i
-й альтернативы, входящей в рассматриваемую комбинацию из п
альтернатив;
РТ
— требуемый ресурс рассматриваемой комбинации альтернатив;
 —
требуемый ресурс i
-й альтернативы, входящей в рассматриваемую комбинацию из п
альтернатив; —
требуемый ресурс i
-й альтернативы, входящей в рассматриваемую комбинацию из п
альтернатив;
Ри
— имеющийся в наличии ресурс рассматриваемой комбинации альтернатив;
 — имеющийся в наличии ресурс i
-й альтернативы, входящей в рассматриваемую комбинацию из п
альтернатив; — имеющийся в наличии ресурс i
-й альтернативы, входящей в рассматриваемую комбинацию из п
альтернатив;
С— заданное пороговое значение ресурса.
Эффективность исходного множества альтернатив рассчитывается на основе МАИ и может быть определена либо на одной иерархии, отражающей критерии эффективности, либо на основе отражения значений векторов приоритетов альтернатив, характеризующих выгоды и издержки, получаемые от их реализации.
Существуют ситуации, в которых при распределении ресурсов руководствуются следующим правилом: делать как можно больше при ограниченных (имеющихся в наличии) ресурсах. Целевая функция в данной задаче — обеспечить

при выполнении одного из условий

где Na
—
число альтернатив;
А
i
—
альтернатива, на которую распределяется ресурс.
Таким образом, для решения задачи комбинаторной оптимизации необходимо прежде всего сгенерировать множество всех возможных сочетаний (комбинаций) из п-
го числа альтернатив. В указанное множество должны входить парные сочетания, тернарные сочетания и далее все п —
1 сочетания, а также сочетание, состоящее из всех п
альтернатив. Максимальное число возможных сочетаний NK
для данной задачи определяется на основе следующей формулы:

где К—
число альтернатив в i
-й комбинации, принимающее значение в диапазоне [0,М
];
М
— максимальное число рассматриваемых альтернатив.
Определим множество комбинаций с различными числом и составом альтернатив.
Допустим, имеется множество из М
альтернатив и каждой альтернативе соответствует ее уникальный порядковый номер.
Требуется из заданного множества получить комбинации всех возможных альтернатив, которые должны удовлетворять следующим условиям: 1) в каждой i
-й комбинации не должно присутствовать одинаковых альтернатив; 2) каждая i-
я комбинация должна отличаться от других не менее чем одной альтернативой; 3) комбинации альтернатив должны содержать в общем случае все единичные, парные, тернарные и другие М-1
и М
сочетания альтернатив. Каждой альтернативе в процессе генерации комбинаций присваиваются два типа признаков: "истина" (И) и "ложь" (Л).
В начальном состоянии всем альтернативам присваивается признак "ложь". В этом случае сгенерированная комбинация содержит нуль альтернатив. Далее осуществляется циклическое изменение признаков альтернатив и генерация из них новых комбинаций по следующим правилам.
Правило 1.
Если альтернатива А1
множества А
имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков у альтернатив. В противном случае, если альтернатива A
1
множества А
имеет признак "И", осуществляем переход к альтернативе А2
.
Правило 2.
Если i
-я альтернатива Ai
множества А
имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков альтернатив. В противном случае изменяем признак i
-й альтернативы А
i
множества А
на "Л" и осуществляем переход к i
+1 альтернативе А
i
+1
.
Правило 3.
Если альтернатива А
N
множества А
имеет признак "Л", то изменяем его на "И" и заканчиваем изменение признаков альтернатив. В противном случае, если альтернатива А
N
имеет значение признака "И", то генерируемая на данной итерации комбинация является последней и содержит все альтернативы множества А.
Таким образом, генерируемая на каждой итерации комбинация включает альтернативы множества А,
имеющие на текущей итерации значение признака "Истина".
В табл. 2.11 приведен пример генерации комбинаций с учетом приведенного выше алгоритма для множества А,
включающего три альтернативы.
Таблица 2.11
Алгоритм генерации альтернатив
| Номер итерации
|
Состояние множества альтернатив А
i
|
Альтернативы, определяющие генерируемую комбинацию
|
| 1
|
А1
"Л"
|
А2
"Л"
|
А3
"Л"
|
-
|
| 2
|
А1
*
"И"
|
A
2
"Л"
|
А3
"Л"
|
A
1
|
| 3
|
А1
"Л"
|
А2
*
"и"
|
А3
"Л"
|
A2
|
| 4
|
А1
*
"И"
|
А2
"И"
|
А3
"Л"
|
А1
А2
|
| 5
|
А1
"Л"
|
А2
"Л"
|
А3
*
"И"
|
А3
|
| 6
|
А1
*
"И"
|
А2
"Л"
|
А
3
"И"
|
A1
A3
|
| 7
|
A1
"Л"
|
А2
*
"И"
|
А3
"И"
|
A
2
A
3
|
| 8
|
А1
*
"И"
|
А2
"И"
|
A3
"И"
|
A1
A2
A3
|
* - отмечен последний изменившийся на итерации признак.
Алгоритм определения комбинации альтернатив, обеспечивающей оптимальное распределение ресурса, имеет следующий вид.
Шаг 1. Определяется М
альтернатив, для каждой из которых устанавливается требуемый ресурс и вычисляется относительная эффективность.
Шаг 2. Генерируются все парные, тернарные, М-1
комбинации альтернатив.
Шаг 3. Для каждой сгенерированной комбинации определяются суммарные значения: требуемого ресурса, относительной эффективности и относительной эффективности на единицу требуемого ресурса.
Шаг 4. Определяется искомая комбинация альтернатив с учетом задаваемой целевой функции.
Рассмотрим пример распределения ресурса на комбинации альтернатив, представляющих компьютерные бухгалтерские программы.
Заданы четыре компьютерные бухгалтерские программы: А1
—
"1C: Бухгалтерия 6.0. ПРОФ" для Windows 95; А2
—
"INFO-Бухгалтер"; А3
—
Комплексная система "INOTEC Бухгалтер"; А4
—
Бухгалтерская система "ПАРУС".
Относительная эффективность (полезность) бухгалтерских программ оценена по комплексу иерархически упорядоченных критериев качества с трех точек зрения: программиста, сопровождающего функционирование программ; бухгалтера, ведущего бухгалтерский анализ на предприятии; руководителя предприятия, использующего результаты бухгалтерского анализа для принятия решений (рис. 2.21).
Методом анализа иерархий определен вектор приоритетов альтернатив, характеризующий их относительную эффективность. Относительная эффективность бухгалтерских программ и требуемые для их приобретения ресурсы (в условных денежных единицах) приведены в табл. 2.12.
Таблица 2.12
Исходные данные по эффективности и требуемому ресурсу
| Параметр
|
Альтернатива Ai
|
| А1
|
А2
|
А3
|
А4
|
| Относительная эффективность
|
0,20
|
0,30
|
0,35
|
0,15
|
| Требуемый ресурс
|
5
|
5
|
10
|
3
|

Таблица 2.13
Результаты распределения ресурса
| Параметр
|
Комбинация альтернатив
|
| А1
А2
|
А1
А3
|
А1
А4
|
A1
A2
A3
|
A1
A3
A4
|
A2
A3
A4
|
A1
A2
A3
A
4
|
| Суммарная, эффективность комбинации
|
0,50
|
0,555
|
0,35
|
0,85
|
0,70
|
0,80
|
1,0
|
| Требуемый ресурс на комбинацию
|
10
|
15
|
8
|
20
|
18
|
18
|
23
|
| Эффективность на единицу ресурса
|
0,050
|
0,037
|
0,044
|
0,043
|
0,039
|
0,044
|
0,043
|
Все возможные комбинации, состоящие из двух, трех и четырех альтернатив, суммарная эффективность комбинаций, требуемый на каждую операцию ресурс и эффективность на единицу ресурса приведены в табл. 2.13.
Требуется определить такие комбинации альтернатив, на которые наиболее целесообразно распределить имеющийся ресурс (15 единиц ресурса) с учетом целевых функций (2.12) и (2.13) при условии min (Ри
- Рт
).
Искомыми комбинациями альтернатив для первой целевой функции является А1
А2
,
а для второй — А1
А3
.
Основные понятия
1. Иерархия.
2. Шкала отношений.
3. Предпочтения.
4. Парные сравнения.
5. Матрицы попарных сравнений.
6. Собственный вектор и собственное значение матрицы попарных сравнений.
7. Однородность суждений.
8. Индекс и отношение однородности матрицы попарных сравнений альтернатив.
9. Синтез приоритетов на иерархии.
10. Однородность иерархии.
11. Принятие решений при учете мнений нескольких экспертов.
12. Сравнение объектов методами стандартов и копирования.
13. Иерархии с различными числом и составом альтернатив под критериями.
14. Многокритериальное прогнозирование социально-экономических систем.
15. Функционально-стоимостный анализ методами анализа иерархий.
16. Рациональное распределение ресурсов методами анализа иерархий.
Контрольные вопросы и задания
1. Какой тип иерархии используется в методе анализа иерархий?
2. Дайте численную и лингвистическую характеристики шкалы отношений.
3. Постройте матрицу попарных сравнений для семи альтернатив.
4. Составьте алгоритм и программу для расчета на ЭВМ собственного вектора и собственного значения матрицы попарных сравнений.
5. Составьте алгоритм и программу для определения индекса и отношения однородности матрицы попарных сравнений.
6. Разработайте универсальный алгоритм и программу для решения задачи синтеза приоритетов для иерархий, элементы которых могут иметь различные связи.
7. Разработайте алгоритм и программу для оценки однородности иерархии, имеющей любую структуру.
8. Разработайте алгоритм и программу для решения задачи синтеза приоритетов на иерархии с учетом мнений нескольких экспертов.
9. В каких ситуациях объекты сравниваются методами стандартов и копирования?
10. Приведите прикладные примеры иерархий с различным числом альтернатив под критериями.
11. Разработайте алгоритм и программу синтеза приоритетов в иерархиях с различным числом альтернатив под критериями.
12. Примените метод анализа иерархий для решения прикладных задач выбора и прогнозирования в различных сферах экономики, например, при снижении риска в антикризисном управлении фирмой.
13. Смоделируйте механизм регионального и городского бюджетов, перераспределите финансовые и другие виды ресурсов, в том числе для реализации крупных региональных программ.
14. Примените метод анализа иерархий для поддержки принятия решений во внешнеэкономической сфере.
15. Разработайте рациональную программу в социальной и инвестиционной сферах.
16. Примените методы принятия решений для разрешения политических и этнических конфликтов.
17. Проведите функционально-стоимостный анализ организационной структуры и управленческой деятельности предприятия.
18. Осуществите рациональное распределение ресурсов с использованием системных методов между альтернативами исследуемой экономической системы.
Литература
1.
Макеев С. П., Шахнов И.Ф.
Упорядочение объектов в иерархических системах // Известия АН СССР, Техническая кибернетика. — 1991.—№ З.—С. 29—46.
2.
Caamu
Т.
Принятие решений. Метод анализа иерархий: Пер. с англ. — М.: Радио и связь, 1989. — 316 с.
3.
Сваткин М. 3., Мацута В. Д., Рахлин К. М.
Группы качества на машиностроительных предприятиях. —Л.: Машиностроение, 1988. — 141 с.
4.
Влчек Р.
Функционально-стоимостный анализ в управлении: Сокр. пер. с чеш. — М.: Экономика, 1986. — 176 с.
5.
Карпунин М. Г., Любинецкий Я. Г., Майданчик Б. И.
Жизненный цикл и эффективность машин. — М.: Машиностроение, 1989. — 312 с.
6.
Карпунин М. Г., Майданчик Б. И.
Функционально-стоимостный анализ в электротехнической промышленности. — М.: Энергоиздат, 1984. —288 с.
7.
Скворцов Н. Н., Омельченко
Л. Н.
Организация функционально-стоимостного анализа на машиностроительных предприятиях. — Киев: Технiка, 1987. — 112 с.
ГЛАВА 3.
АНАЛИТИЧЕСКОЕ ПЛАНИРОВАНИЕ НА ОСНОВЕ МЕТОДА АНАЛИЗА ИЕРАРХИЙ
Планирование является социальным процессом, сводящим то, что считается наиболее вероятным исходом ситуации при заданных текущих действиях, политиках и силах окружающей среды, с тем, что представляется как желательный исход, который, в свою очередь, требует новых действий и политик. Таким образом, планирование — сводящий процесс, поскольку оно уменьшает расхождение между вероятным и желаемым (оптимальным) будущим.
Планирование само по себе является системой, которая имеет назначение (достижение желаемой цели), функции (исследовать среду, ситуацию, структуру, выбрать альтернативы и оценить действия), потоки (информация между специалистами по планированию и пользователями) и структуру (общий план, в пределах которого специалист по планированию сближает наиболее вероятный и желаемый результаты, используя обучение и обратную связь в форме суждений и данных для переоценки результатов).
3.1. Принципиальные подходы к решению задач планирования
Можно выделить три принципиальных подхода к планированию [1-9].
Удовлетворенческое
планирование предполагает достижение неплохих результатов, но не обязательно наилучших. Уровень, которого необходимо достичь для "удовлетворения", определяется как уровень, на который соглашаются лица, принимающие решения. Такое планирование редко приводит к радикальным переменам. Как правило, оно порождает консервативные планы, исправляющие только явные недостатки и не способствующие росту и развитию.
Оптимизационное
планирование направлено на реализацию программ наилучшим образом. Оптимизационное планирование более полезно в тактическом планировании, чем в стратегическом, поскольку первый случай характеризуется полной определенностью исходных данных в настоящем и будущем, а для такой ситуации наилучшим образом приспособлены, как известно, методы оптимизации. Для оптимизационного планирования характерны следующие задачи:
• минимизация ресурса, необходимого для достижения намеченного уровня эффективности;
• максимизация эффективности, которой можно достичь с имеющимся запасом ресурса;
• максимизация отношения эффективности к затратам.
Аналитическое стратегическое
планирование направлено на решение задач, характеризующихся в будущем неопределенностью и незнанием.
Аналитическое стратегическое планирование — процесс обучения и эволюции, т.е. процесс проецирования вероятного или логического будущего (обобщенного сценария) и идеализированных желаемых будущих состояний.
Все планы имеют три общих компонента — начальное состояние, цель (или конечное состояние) и средства, связывающие эти два состояния. Цель процесса планирования — соединить компоненты за наименьшую цену, чтобы достигнуть наибольшей эффективности.
Первый компонент — начальное состояние — определяет начальное состояние людей, управляющих определенными ресурсами; экономическое, политическое и социальное положение общества; ограничения природы и окружающей среды и т.п.
Второй компонент — цель — это желаемая величина, которую надеются достигнуть.
Третий компонент — средства, т. е. сам план, с помощью которого происходит переход от начального состояния к цели.
Выделяются три отличающихся процесса планирования: в прямом направлении, обратном направлении, одновременно в прямом и обратном направлениях.
Процесс планирования в прямом
направлении направлен только в одну сторону. Он представляет собой упорядоченную во времени последовательность событий, которая начинается в момент времени t
= 0 и заканчивается в будущем в момент времени t
= Т.
В прямом процессе рассматриваются текущие факты и предположения, порождающие логический исход (сценарий).
Процесс планирования в обратном
направлении начинается с желаемого исхода в момент времени T, и затем процесс рассматривается в обратном направлении во времени, чтобы оценить факторы и промежуточные исходы, которые требуются для достижения желаемого исхода. Таким образом, обратный процесс планирования обеспечивает средствами контроля и управления прямой процесс при движении в направлении желаемого состояния.
Процесс планирования, осуществляемый одновременно в прямом
и обратном
направлениях, основан на классической теории планирования, которая предполагает наличие двух целей планирования.
Первая цель — это логическая или достижимая цель, при постановке которой подразумевается, что предположения и факторы, воздействующие на исход, останутся существенно неизменными по отношению к настоящему состоянию.
Вторая цель — желаемая, достижение которой требует больших изменений на входах. Эти изменения нужно не только осуществить, но и сделать необратимыми, несмотря на первоначальное поведение системы.
Принцип интегрированного прямого и обратного процессов иерархического планирования осуществляется следующим образом. Сначала проектируется вероятное будущее (первый прямой процесс). Далее в качестве цели принимается желаемое будущее и вырабатываются новые политики (первый обратный процесс), которые присоединяются к набору существующих, и с учетом этих изменений вновь проектируется будущее (второй прямой процесс). Проводится сравнение двух вариантов вероятного будущего и желаемого будущего, соответствующих первому и второму прямому и первому обратному процессам планирования относительно их главных характеристик.
3.2. Представление процесса планирования в виде иерархии
Поскольку в основе стратегического аналитического планирования лежит механизм прямого и обратного процессов, рассмотрим его более подробно с учетом метода анализа иерархий.
Прежде всего следует отметить, что иерархические системы планирования состоят из специфических элементов, имеющих определенное толкование. К указанным элементам относятся: фокус иерархии, акторы, цели, политики, исходы и обобщенный исход. Под фокусом иерархии
понимается общая цель исследуемой проблемы. Данный иерархический уровень может состоять из горизонтов (нескольких интервалов времени). Акторами
называются действующие силы, с различной степенью воздействующие на исход. Цели—
желаемые пределы или величины, которых надеются достигнуть. Под политиками
понимаются санкционированные средства достижения целей, предоставляемые с помощью общепринятых процедур принятия решений. Исходы —
это потенциальные состояния системы, которые получены после применения политик. Обобщенный исход
позволяет интегрировать значения отдельных исходов для оценки последствий принимаемых при планировании решений.
Введем обозначения множеств элементов и собственно элементов, определяющих иерархические уровни. Множества элементов обозначаются прописными буквами русского алфавита, а элементы — строчными буквами:
Фij
—фокус иерархии;
Сij
= {сm
ij
} — множество сил;
АКij
= {акn
ij
} — акторы;
Цij
= {цr
ij
} — пели;
Пij
= {пr
ij
} — политики;
Иij
= {иs
ij
} — исходы;
Прij
= {пpt
ij
} — проблемы.
Для дальнейших рассуждений введем также обозначения, характеризующие интегральную оценку обобщенного исхода (
ОИф
ij
)
и интегральную оценку обобщенного исхода относительно конкретного актора (
ОИАК
ij
).
В приведенных выше обозначениях первый нижний индекс (i
) указывает направление процесса (прямой процесс или обратный), на котором впервые появился элемент иерархии. При этом i
= 1 соответствует процессу планирования в прямом направлении, а i
=2 —
процессу планирования в обратном направлении. Второй нижний индекс j
= 1,
k
указывает порядковый номер процесса планирования в прямом и обратном направлениях. Верхние индексы обозначают порядковый номер элемента на соответствующем уровне или подуровне иерархии.
При исследовании иерархий рассчитываются векторы приоритетов исходов в прямом процессе (
 )
и векторы приоритетов целей (
)
и векторы приоритетов целей (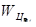 ) или политик (программ) (
) или политик (программ) (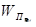 ) в обратном процессе планирования относительно элементов иерархии. Обозначения этих векторов приведены в табл. 3.1, где верхние индексы указывают элементы иерархии, относительно которых они рассчитаны.
) в обратном процессе планирования относительно элементов иерархии. Обозначения этих векторов приведены в табл. 3.1, где верхние индексы указывают элементы иерархии, относительно которых они рассчитаны.
Таблица 3.1
Обозначение векторов приоритетов
| Номер уровня
|
Элемент иерархии, относительно которого определяется вектор приоритетов
|
Обозначение векторов
|
| Вектор приоритетов исходов И1
j
в прямом процессе
|
Вектор приоритетов целей Ц2
j
и политик П2
j
в обратном процессе
|
| 1
|
Фокус
|
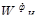
|
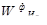 ; ;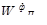
|
| 2
|
Сила
|
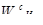
|
-
|
| 3
|
Актор
|
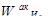
|
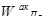 ; ;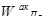
|
| 4
|
Цель
|
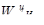
|
- ;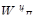
|
| 5
|
Политика
|
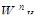
|
-
|
| 6
|
Исход
|
-
|
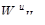 ; ;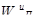
|
| 7
|
Проблема
|
-
|
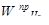 ; ;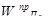
|
Процесс планирования в прямом направлении начинается с определения цели планирования и построения иерархии прямого процесса (рис. 3.1).
В вершине иерархии (уровень 1) устанавливается фокус Ф11
который определяет логическое будущее. Уровень 2 иерархии включает различные экономические, политические, социальные и другие силы, влияющие на исход (этот уровень необязательный). Уровень 3 состоит из акторов, которые манипулируют этими силами (акторы могут включаться в уровень 2 без упоминания сил).
В уровень 4 включаются цели каждого актора. Уровень 5 иерархии содержит политики, которым следует каждый актор для достижения своих целей (этот уровень необязательный). Уровень 6 содержит возможные сценарии, или исходы, за которые борется каждый актор, как за результат реализации своих целей. Уровень 7 иерархии определяется как обобщенный сценарий (исход), который представляет результат реализации всех этих сценариев. Обобщенный сценарий называется также логическим исходом.
Каждый исход в отдельности и обобщенный исход могут быть количественно охарактеризованы по множеству критериев, которые отражают различные аспекты исходов, например политические, экономические, социальные, юридические, технологические и т. д. Значение критерия для исхода определяется относительно текущего состояния по шкале разностей (табл. 3.2).
Таблица 3.2
Шкала разностей
| Разность в значениях
|
Лингвистическая характеристика
|
| 0
|
Значения не изменяются
|
| +2 (-2)
|
Небольшое увеличение (уменьшение) значения
|
| +4 (-4)
|
Большое увеличение (уменьшение) значения
|
| +6 (-6)
|
Значительное увеличение (уменьшение) значения
|
| +8 (-8)
|
Максимальное увеличение (уменьшение) значения
|
| +1,+3,+5,+7
-1,-3,-5,-7
|
Промежуточные значения между двумя смежными суждениями
|
При расчете значения переменной следует ответить на следующие два вопроса: В каком направлении в будущем (увеличится, уменьшится или останется неизменным) произойдет изменение i
-го критерия при реализации рассматриваемого j
-го исхода? Какова интенсивность изменений i-
го критерия? Таким образом, количественная оценка исходов по множеству критериев с использованием шкалы разностей представляет своеобразный метод оценки последствий принимаемых решений при прямом процессе планирования.
Для определения интегральных оценок обобщенного исхода относительно фокуса иерархии ОИф
ij
и относительно конкретного актора ОИак
ij
строится матрица оценки исходов, имеющая следующий вид:
| Критерий
Кi
|
Вес критерия
ri
|
Значение w, вектора приоритетов
|
| w1
|
w2
|
…
|
wi
|
…
|
w
n
|
| K
1
|
r1
|
а11
|
a12
|
…
|
a1j
|
…
|
а
1n
|
| K2
|
r2
|
a21
|
а
22
|
…
|
а
2j
|
…
|
a2n
|
| …
|
…
|
…
|
…
|
…
|
…
|
…
|
...
|
| К
i
|
ri
|
ai1
|
ai2
|
…
|
а
ij
|
…
|
am
|
| …
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
| К
m
|
rm
|
am1
|
а
m2
|
…
|
а
mj
|
…
|
аmn
|
В матрице приняты следующие обозначения Ki
(
i
=
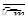 ) —
критерии для оценки исходов; ri
(
i
= ) —
критерии для оценки исходов; ri
(
i
=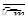 ) —
весовые коэффициенты критериев, отражающие значимость последних в конкретном процессе планирования; wi
(
i
= ) —
весовые коэффициенты критериев, отражающие значимость последних в конкретном процессе планирования; wi
(
i
=
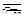 ) —
значения вектора приоритетов вероятных (логических) исходов относительно фокуса иерархии или отдельно взятого актора; а
ij
—
оценка на основе шкалы разностей (см.
табл. 3.2) j
-го исхода по i
-му критерию. ) —
значения вектора приоритетов вероятных (логических) исходов относительно фокуса иерархии или отдельно взятого актора; а
ij
—
оценка на основе шкалы разностей (см.
табл. 3.2) j
-го исхода по i
-му критерию.
Обобщенные веса. А
i
по каждому критерию Ki
(
i
=
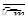 )
определяются следующим образом: )
определяются следующим образом:

Интегральные оценки обобщенного исхода относительно фокуса (верхний индекс ф) или самостоятельного актора (верхний индекс ак) определяются по выражениям:

Переход к обратному процессу осуществляется вследствие того, что в обобщенном сценарии пересекаются противоречивые интересы акторов. В результате может получиться ослабленный вариант того, что каждый актор хочет видеть в качестве исхода. Поэтому один или несколько акторов начинают работать в направлении изменения полученных исходов в сторону желаемых. Для этого ведется работа по изменению и/или добавлению новых целей и политик. Планирование в обратном направлении осуществляется с учетом следующей иерархии (рис. 3.2).

В вершине иерархии устанавливается фокус Ф21
,
отражающий желаемое будущее. В уровень 2 иерархии включаются желаемые исходы, которые хотят реализовать акторы. Желаемые исходы, включенные в этот уровень, могут представлять следующие композиции: 1 — за желаемый исход принят один из вероятных исходов, определенный на предыдущем прямом процессе планирования; 2 — желаемые исходы по числу и наименованию соответствуют вероятным исходам из предыдущего прямого процесса, а отличаются от последних приоритетом сценариев относительно их воздействия на обобщенное желаемое будущее; 3 — в число желаемых исходов включают некоторое подмножество вероятных исходов из предыдущего прямого процесса; 4 — генерируются и рассматриваются новые желаемые исходы, не пересекающиеся с вероятными исходами предыдущего прямого процесса; 5 — множество желаемых исходов формируется на основе вероятных исходов из предыдущего процесса и вновь определенных на данном обратном процессе желаемых исходов.
В уровень 3 включается перечень проблем и ситуаций, которые могут воспрепятствовать реализации сценариев (необязательный уровень).
Уровень 4 образуют акторы, которые влияют на решение проблем. При этом акторы включаются независимо от того, упоминались они или нет в предыдущем прямом процессе. На рис. 3.2 показаны две возможные ситуации, характерные для обратного процесса, которые представлены двумя группами акторов, объединенных вершиной типа "ИЛИ". В первую группу включены исключительно все акторы из предыдущего прямого процесса, а вторая группа состоит из подмножества акторов, принадлежащих предыдущему прямому процессу, и подмножества акторов, впервые включенных в рассмотрение на текущем обратном процессе планирования.
На уровне 5 указываются новые цели акторов, которые не пересекаются с целями предыдущего прямого процесса планирования.
Уровень 6 включает новые политики акторов или политики отдельного актора.
В обратном процессе определяются векторы приоритетов целей относительно фокуса — 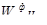 , и отдельных акторов — , и отдельных акторов — 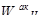 и/или векторы приоритетов политик относительно фокуса — и/или векторы приоритетов политик относительно фокуса — 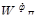 и отдельных акторов — и отдельных акторов — 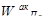 . .
После определения векторов приоритетов целей и политик осуществляется переход ко второму прямому процессу.
Иерархия второго прямого процесса приведена на рис. 3.3.
Уровни 1 и 2 иерархии второго прямого процесса идентичны соответствующим уровням первого прямого процесса. Уровень 3 иерархии второго прямого процесса может отличаться от соответствующего уровня первого прямого процесса тем, что в него включаются новые акторы Акi
21
, определяющие логическое будущее. Таким образом на этом уровне вершиной типа "ИЛИ" объединены две группы акторов, в первую из которых включены исключительно акторы из первого прямого процесса, а во вторую группу добавлены новые акторы.

Обобщающее правило, которого необходимо придерживаться при формировании иерархических уровней акторов j-м
прямом процессе, заключается в том, что определяющие логический исход акторы не могут смениться полностью по сравнению с первым прямым процессом.
Уровни 4 и 5 иерархии второго прямого процесса формируются двумя альтернативными способами. В соответствии с первым способом в эти иерархические уровни включаются цели и политики из предыдущих итераций прямого и обратного процессов. При этом из иерархии обратного процесса добавляются в иерархию следующего за ним прямого процесса наиболее важные цели и политики. В соответствии со вторым способом в иерархию текущего прямого процесса включаются все или наиболее важные цели и политики из предыдущего обратного процесса.
Обобщающее правило, вытекающее из анализа четвертого и пятого иерархических уровней обратного процесса, заключается в том, что иерархия текущего обратного процесса может содержать акторы, цели и политики, полностью отличающиеся от всех соответствующих элементов иерархии всех предыдущих процессов планирования в прямом и обратном направлениях.
Уровень 6 иерархии образуют исходы.
При этом могут рассматриваться либо все ранее определенные исходы в первом прямом процессе, либо в уровень 6 дополнительно к известным добавляют новые исходы.
Уровень 7 иерархии представляет обобщенный сценарий второго прямого процесса.
В результате выполнения второго прямого процесса определяются вектор приоритетов исходов 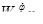 и интегральная оценка обобщенного исхода ОИф
12
. и интегральная оценка обобщенного исхода ОИф
12
.
Затем проводится сравнительный анализ интегральных оценок обобщенных логического и желаемого исходов соответственно для первого — ОИф
11
и второго — ОИф
12
прямых процессов и первого обратного процесса ОИф
21
. В результате сравнительного анализа интегральных оценок обобщенных исходов определяется расстояние между логическим и желаемым будущим. Если от первой итерации не произошло уменьшения расстояния, т. е. не наблюдается приближение логического будущего к желаемому, то проводится вторая итерация обратного процесса. На очередной итерации изменяются приоритеты желаемых будущих состояний и/или проверяются новые цели и политики. Цели и политики, получившие наибольший приоритет, используются на третьей итерации прямого процесса. Далее вычисляется интегральная оценка ОИф
13
логического обобщенного исхода третьего прямого процесса, которая сравнивается с оценкой обобщенного желаемого исхода второго обратного процесса ОИф
22
. Процедура повторяется до тех пор, пока полностью не будет исчерпана возможность поиска путей увеличения сближения логического и желаемого исходов.
Следует иметь в виду, что если приоритет желаемых будущих состояний изменяется при итерациях, то сравнивается оценка обобщенного исхода последнего обратного процесса, в котором приоритеты исходов претерпели изменения, с оценкой обобщенного исхода последнего прямого процесса. Если приоритет желаемых будущих состояний не изменяется при итерациях, то оценка обобщенного исхода, характеризующего указанное желаемое будущее, последовательно сравнивается со всеми предыдущими оценками обобщенных логических исходов.
Характеристика акторов
Результаты, получаемые при прямом и обратном процессах планирования, во многом определяются свойствами акторов. Рассмотрим основные особенности акторов, участвующих в планировании.
По общности преследуемых целей, реализуемых политик и прогнозируемых сценариев акторы можно кластеризовать по трем группам, которые определяют соответствующие виды иерархий. Первую группу определяют акторы, имеющие одинаковые цели, политики и сценарии (рис. 3.4а
), но с различной относительной степенью предпочтительности. Во вторую и третью группу входят акторы с полностью (рис. 3.4 б) или частично (рис. 3.4в) различающимися элементами (целями и т.п.), принадлежащими нижним уровням иерархии. Акторы могут обладать одинаковой или различной силой (весомостью) влияния на конечный результат.
Степень влияния акторов на исход определяется, как правило, их политическим, экономическим, военным, правовым, социальным положением в обществе. По способности или предрасположенности к поиску компромиссного решения акторы, участвующие в конкретном процессе планирования, можно охарактеризовать тремя признаками. Первый признак выделяет группу антагонистически настроенных акторов, не идущих ни на какие компромиссы. Второй признак прямо противоположен первому и определяет группу акторов, стремящихся вырабатывать компромиссные решения. Третий признак объединяет акторов, обладающих свойствами, характерными как для первой, так и для второй указанных групп.
Характером и числом акторов, участвующих в планировании, определяются способы выработки желаемых сценариев. В следующем разделе рассмотрены различные способы определения желаемых сценариев.

3.3. Способы определения желаемых сценариев
Предлагается несколько способов определения желаемых сценариев. Разновидности указанных способов во многом обусловливаются составом и характером акторов, участвующих в процессе планирования. С учетом сказанного в практике планирования выделяются две ситуации, отличающиеся числом акторов, занятых в принятии решений и определяющих принципиальные отличия процедур формирования желательных сценариев. Первая ситуация характеризуется тем, что в процессе выработки и определения предпочтительности желаемых сценариев участвует один актор. В соответствии со второй ситуацией желаемый сценарий определяется с учетом мнений двух или более акторов, находящихся в сложных, возможно противоречивых, отношениях.
Определение желаемых сценариев одним экспертом
При определении желаемых сценариев для ситуаций, в которых процесс планирования осуществляется одним актором, следует придерживаться следующих стратегий.
В соответствии с первой
стратегией проводится построение новой иерархической системы, отличающейся полностью или частично от иерархии предыдущего прямого процесса. Альтернативы в новой иерархии остаются прежними, т. е. они не изменяются по сравнению с предыдущей итерацией процесса. Во вновь формируемую иерархию включают элементы, характеризующие желаемые цели, критерии, политики, и устанавливают их относительную степень предпочтения. Изменению подвергаются также матрицы попарных сравнений альтернатив, при заполнении которых эксперту следует ответить на вопросы: Какая альтернатива из двух сравниваемых более желательна по рассматриваемому критерию? Насколько одна из альтернатив предпочтительнее другой по девятибалльной шкале (см.
табл. 2.1)? Результатом реализации первой стратегии является нормализованный вектор приоритетов желаемых сценариев, рассчитанный относительно фокуса иерархии.
Вторая
стратегия предполагает определение желаемых сценариев по результатам оценки выгод и издержек, которые ожидаются от реализации каждого сценария (исхода). Для решения этой задачи строятся две иерархии, по которым оцениваются относительные выгоды и издержки сценариев. В иерархиях используются все альтернативы-сценарии из предыдущей итерации прямого процесса планирования. При построении и заполнении матриц попарных сравнений альтернатив следует дать ответы на следующие вопросы: Какая из двух сравниваемых альтернатив предпочтительнее и насколько предпочтительнее относительно получения от ее реализации функциональных, экономических, социальных и других выгод (для первой иерархии) и издержек (для второй иерархии)? Результатом проведения второй стратегии первоначально является ненормированный вектор приоритетов альтернатив, рассчитанный по критерию, характеризующему отношение значений ненормированных векторов приоритетов, отражающих выгоды и издержки. Затем ненормированный вектор приводится к нормированному (табл. 3.3) и далее используется в очередном процессе планирования.
Таблица 3.3
Нормирование вектора приоритетов
| Альтернатива-исход (А,)
|
A1
|
А
2
|
A3
|
| Вектор приоритетов выгод
|
0,5
|
0,3
|
0,2
|
| Вектор приоритетов издержек
|
0,2
|
0,3
|
0,5
|
| Ненормированный вектор приоритетов отношений выгод и издержек
|
2,5
|
1,0
|
0,4
|
| Нормированный вектор приоритетов отношений выгод и издержек
|
0,64
|
0,25
|
0,11
|
Третья
стратегия предполагает использование иерархии предыдущего прямого процесса и относящихся к этой иерархии матриц попарных сравнений альтернатив-сценариев со значениями экспертных оценок. Изменению в данном случае подлежат весовые коэффициенты элементов иерархических уровней, кроме уровня альтернатив. При этом весовые коэффициенты будут отражать не наиболее или наименее вероятную их значимость в будущем, как в прямом процессе, а наиболее или наименее желаемую значимость. Уровень акторов из иерархии исключается. Результатом реализации третьей стратегии является нормированный вектор приоритетов альтернатив-исходов относительно фокуса видоизмененной иерархии.
Четвертая
стратегия основана на определении приоритета желаемых сценариев по результатам оценки предполагаемых последствий от реализации каждого рассматриваемого сценария. Оценка последствий осуществляется на матрице специального вида. Наименованиями строк матрицы являются критерии (Ki
), характеризующие будущие важные характеристики исследуемой системы, а наименованиями столбцов — сценарии (А
i
),
взятые из предыдущего прямого процесса. На пересечении строк и столбцов экспертом в матрице зафиксированы оценки (aij
), значения которых определены шкалой разностей (см.
табл. 3.2). Для каждого сценария по матрице рассчитывается интегральная оценка ОА
j

где р, — весовой коэффициент критерия К, (
i
= \,т).
На основании полученной информации об интегральных оценках ОА
j
по каждому сценарию эксперт определяет степень важности желаемых сценариев методом попарных сравнений. При заполнении матриц попарных сравнений предпочтение отдается тем альтернативам, которые имеют большее абсолютное значение интегральной оценки OAj
.
Пример перехода от интегральных оценок сценариев к их вектору приоритетов приведен ниже (табл. 3.4).
Таблица 3.4
Анализ сценариев
| Альтернатива-сценарий (А
j
)
|
А
1
|
A2
|
A3
|
A
4
|
A
5
|
| Интегральная оценка альтернативы OAj
|
-0,2
|
0
|
-2,1
|
+0,5
|
+5,0
|
| Вектор приоритета альтернативы WAj
|
0,03
|
0,10
|
0,02
|
0,25
|
0,6
|
Проектирование желаемых сценариев несколькими экспертами
Процесс разработки желаемых сценариев в соответствии со второй ситуацией, когда планирование контролируют несколько акторов, имеет ряд особенностей.
Прежде всего следует обозначить две принципиально отличающиеся процедуры проведения исследований по планированию в иерархических системах, содержащих несколько акторов. Первая процедура характеризуется тем, что исследование по планированию проводит независимый эксперт, который строит иерархию, определяет акторов, анализирует цели, политики и сценарии, входящие в иерархию. В соответствии со второй процедурой предполагается, что построение иерархии и проведение исследований на ней осуществляют один или несколько акторов, учтенных в рассматриваемой иерархии.
Независимые эксперты имеют возможность формировать желаемые сценарии относительно любого актора, группы акторов или всех акторов, имеющихся в иерархии. При этом они стремятся в наибольшей степени удовлетворить различные интересы наибольшего числа акторов, учитываемых и не учитываемых в конкретной иерархии. Формирование желаемых сценариев актором или группой акторов, непосредственно учтенных в иерархии, осуществляется на основе субъективных представлений об общественных ценностях, к которым следует стремиться в будущем.
На степень объективности желаемых сценариев влияет способ оценки элементов иерархии. При проведении исследований в соответствии с первой вышеупомянутой процедурой оценку всех элементов иерархии проводят независимый эксперт или группа независимых экспертов. Вторая процедура проведения исследований предполагает проведение оценки элементов иерархии либо совместными усилиями акторов и независимых экспертов, либо исключительно заинтересованными в результатах планирования акторами. Отсюда следует, что проведение исследований в целом на иерархических системах независимыми экспертами позволяет формировать более объективные и эффективные желаемые сценарии, чем при проведении аналогичных исследований заинтересованными акторами. В реальных практических ситуациях выработка желаемых сценариев осуществляется с использованием обеих процедур.
Рассмотрим ряд способов формирования желаемых сценариев при наличии нескольких акторов в иерархии процесса планирования.
Первый способ
основан на идее принятия в качестве желаемых сценариев вероятных (логических) сценариев предыдущего прямого процесса со значениями предпочтений одного из акторов. Данная идея основана на предположении, что каждый актор в прямом процессе формирует свои собственные цели и политики, которые для него являются желаемыми. Поэтому в такой ситуации рассматриваемые в иерархии сценарии получат соответствующие предпочтения, удовлетворяющие желаемым целям и политикам для конкретного актора. В качестве примера на рис. 3.5 утолщенными линиями выделена часть иерархии прямого процесса, по которой определяются желаемые исходы относительно актора Акn
.

В табл. 3.5 для сравнения приведено три логических исхода, относящихся к одной иерархии. Один вектор приоритетов построен относительно фокуса иерархии, т. е. с учетом мнений всех акторов, а два других вектора построены относительно двух акторов. Один из векторов приоритетов логических исходов, относящийся к конкретному актору, может рассматриваться последним в качестве желаемого.
Поскольку в данном способе желаемый исход определяется относительно конкретного актора, то возможны различные варианты выбора такого актора, логический исход которого следует принять за желаемый.
Таблица 3.5
Анализ логических исходов
| Исход
|
А1
|
A
2
|
A
3
|
| Вектор приоритетов логических исходов
относительно фокуса
|
0,5
|
0,3
|
0,2
|
| Вектор приоритетов логических исходов
относительно актора (Ak1
)
|
02
|
0,3
|
0,5
|
| Вектор приоритетов логических исходов
относительно актора (Ак2
)
|
0,4
|
0,4
|
0,2
|
В ситуациях, когда актор самостоятельно занимается планированием и имитацией поведения других акторов, желаемым сценарием является, как правило, его логический сценарий, определенный в прямом процессе.
В тех же случаях, когда планированием занимается независимый эксперт, в качестве вектора приоритетов желаемых сценариев может быть выбран вектор приоритетов вероятных (логических) сценариев, соответствующий наиболее влиятельному актору или актору, способному вырабатывать, по мнению эксперта, такие решения, которые в наибольшей степени отвечают наиболее благоприятному развитию общества в будущем — политическому, экономическому, социальному и т. п. Решить проблему о выборе лучшего актора можно на основании расчета обобщенных исходов по каждому актору, отдавая предпочтение тому из них, значение обобщенного исхода у которого наибольшее.
Второй способ
выбора желаемых сценариев основан на идее выработки компромиссных решений между несколькими или всеми акторами.
В том случае, когда планированием непосредственно занимается группа акторов и их не удовлетворяет общий логический исход, исходная иерархия предшествующего прямого процесса преобразуется в новую иерархию. Преобразованная иерархия содержит цели, политики и сценарии, принадлежащие всем заинтересованным акторам, ищущим компромисс.
Определение относительной значимости элементов иерархии проводится в условиях выработки между акторами компромиссных решений и соответствующих экспертных оценок предпочтений. Предполагается также, что сами акторы в данной ситуации имеют либо равную значимость, либо различную значимость, но установленную на основании взаимного согласия.
Если выбор желаемых сценариев по второму способу осуществляется независимым экспертом, то вес акторов по их вкладу в определение более прогрессивного желаемого будущего вычисляется по двум вариантам. В соответствии с первым вариантом относительно каждого актора, включенного в иерархию прямого процесса, рассчитывается оценка обобщенного сценария и больший вес получает тот актор, у которого упомянутая оценка выше. По второму варианту строится иерархическая структура критериев качества акторов, способных определить наилучшее будущее. Альтернативами такой иерархии являются собственно акторы. Пример подобного рода иерархии приведен на рис. 3.6.

3.4. Методика решения прикладных задач на ЭВМ
3.4.1. Прогнозирование профессиональной занятости населения крупных городов
В условиях переходного экономического периода в России назрела проблема профессиональной занятости населения. Особенно остро эта проблема проявляется в отдаленных от столицы России регионах. В частности, в Волгограде для решения этой проблемы создан Центр занятости населения. Помимо решения тактических задач по трудоустройству людей. Центр занимается стратегическим прогнозированием и планированием будущего рынка занятости. Для решения задачи прогнозирования вероятного будущего рынка занятости воспользуемся подходом, основанным на методе анализа иерархий.
Проблема занятости может быть представлена иерархической системой (рис. 3.7). Иерархия включает шесть уровней: фокус, первичные факторы, акторы, цели акторов, контрастные сценарии и обобщенный сценарий.
В иерархии рассматривается пять контрастных сценариев.
1
. Проекция настоящего на будущее.
Предполагается, что ситуация существенно не изменится. Спрос и предложение на рабочую силу останутся в диспропорции.
2
. Всеобщая занятость.
Каждый желающий трудиться сможет получить работу. Спрос и предложение будут находиться в равновесии.
3. Массовая безработица.
Спад производства приведет к дальнейшему высвобождению трудящихся. Процент безработицы существенно увеличится.
4. Рынок высококвалифицированных кадров.
В связи с развитием научно-технического процесса особым спросом на рынке труда будут пользоваться специалисты высокой квалификации.
5. Государственная монополия.
За счет восстановления и расширения государственной монополии на ряд предприятий и отраслей народного хозяйства будут созданы дополнительные рабочие места.

В примере рассматриваются не все матрицы парных сравнений элементов иерархии, а лишь векторы приоритетов для построенных экспертом матриц. Алгоритм проведения исследования представлен шестью укрупненными этапами.
Этап 1. Определение степени влияния факторов на будущее рынка труда.
На втором уровне иерархии есть только одна матрица парных сравнений, определяющая, какой из факторов в большей степени влияет на безработицу:
| Безработица
|
Фактор
|
| Фактор
|
1
|
2
|
3
|
4
|
5
|
W
|
| Экономический
|
1
|
4
|
3
|
5
|
6
|
0,49
|
| Социальный
|
1/4
|
1
|
1/2
|
2
|
4
|
0,15
|
| Технологический
|
1/3
|
2
|
1
|
3
|
4
|
0,22
|
| Политический
|
1/5
|
1/2
|
1/3
|
1
|
2
|
0,09
|
| Демографический
|
1/6
|
1/4
|
1/4
|
1/2
|
1
|
0,05
|
| lmax
=
5,18 ОС = 0,04
|
Из матрицы видно, что эксперты посчитали экономический фактор наиболее доминирующим.
Этап 2. Определение степени влияния акторов на факторы.
Здесь каждая пара акторов сравнивалась относительно степени воздействия на факторы второго уровня. Было построено пять матриц, для которых рассчитывались векторы приоритетов. Ниже приведены результаты расчета:
| Актор
|
Фактор
|
| Экономический
|
Социальный
|
Технологический
|
Политический
|
Демографический
|
| Население
|
0,15
|
0,49
|
0,12
|
0,16
|
0,35
|
| Организации
|
0.26
|
0,20
|
0,61
|
0,30
|
0,21
|
| Инвесторы
|
0,10
|
0,11
|
0,27
|
0,16
|
| Правительство
|
0.44
|
0,13
|
0,54
|
0.18
|
| Центр занятости
|
0,05
|
0,07
|
0,10
|
| lmax
=5,35 ОС=0,08
|
lmax
=5,21 ОС=0,04
|
lmax
=3,09 ОС=0,08
|
lmax
=2,99 ОС=0,0
|
lmax
=5,29 ОС=0,06
|
Этап 3. Определение важности целей акторов.
Цели каждого из пяти акторов сравнивались попарно. В результате получены векторы приоритетов, отражающие упорядочение и веса целей:
| Цель
|
Актор
|
| Население
|
Организации
|
Инвесторы
|
Правительство
|
Центры занятости
|
| Материальное благополучие
|
0,35
|
| Социальная защита
|
0,29
|
| Профессиональный рост
|
0,12
|
| Реализация возможностей
|
0,09
|
| Трудовые ресурсы
|
0,07
|
0,10
|
| Технология
|
0,12
|
0,11
|
| Прибыль
|
0,56
|
0,62
|
| Стабильность
|
0,25
|
0,27
|
| Общественный порядок
|
0,45
|
| Благополучие
|
0,14
|
| Государственный бюджет
|
0,31
|
| Работа
|
0,61
|
| Профессиональный рост
|
0,27
|
| Социальная адаптация
|
0,12
|
Этап 4. Нахождение степени важности акторов относительно факторов влияния на будущее безработицы.
Для определения влияния факторов на будущее безработицы выполним следующие вычисления:

Поскольку на акторы "организации" и "правительство" приходится более 50% воздействия на первичные факторы влияния на безработицу, то в дальнейшем будем использовать эти акторы для получения весов сценариев.
Теперь находим важнейшие цели для акторов, умножая собственный вектор целей на соответствующий вес актора:
для предприятий и организаций

для правительства

Используя четыре цели с максимальными значениями и нормализуя их веса, получим следующий результирующий вектор весов целей:

Полученный нормированный вектор приоритетов будет применен в дальнейшем для получения весов сценариев.
Этап 5. Определение степени влияния сценариев на цели акторов.
Представим результаты обработки матриц парных сравнений:
| Сценарий
|
Цель актора
|
| Прибыль
|
Стабильность
|
Порядок
|
Бюджет
|
| Проекция
|
0,17
|
0,12
|
0,12
|
0,09
|
| Всеобщая занятость
|
0,17
|
0,26
|
0,27
|
0,30
|
| Массовая безработица
|
0,17
|
0,07
|
0,06
|
0,06
|
| Рынок высококвалифицированных
|
0,43
|
0,39
|
0,33
|
0,14
|
| Государственная монополия
|
0,06
|
0,16
|
0,22
|
0,41
|
| lmax
= 5,44 ОС°0,099
|
lmax
= 5,22 ОС=0,049
|
lmax
= 5,43 ОС=0,097
|
lmax
= 5,19 ОС-0,04
|
Для получения весов сценариев относительно фокуса иерархии (будущего рынка безработицы) умножим матрицу, сформированную из значений векторов приоритетов сценариев, на вектор весов целей:

Анализ результирующего вектора приоритетов показывает, что сценарий "рынок высококвалифицированных кадров" имеет наибольший вес и, следовательно, наиболее вероятен.
Этап 6. Определение последствий от принятия наиболее вероятных сценариев и оценка обобщенного сценария.
Зная относительные веса сценариев, полученные на этапе 5, можно сформировать обобщенный сценарий. Обобщенная мера на шкале для переменной состояния получается, если просуммировать произведения весов сценариев (находящихся над наименованиями сценариев в табл. 3.6) на соответствующие значения переменной состояния. Например, для материального благополучия населения имеем
(-1)×0,13 + (+3)×0,237 + (-3)×0,103 + (+3)×0,343 + (+3)×0,185 = 1,856.
Таблица 3.6
Калибровка переменных состояния относительно сценариев (первый прямой процесс)
| Сценарий и его вес
|
| Переменная состояния (критерий для оценки
последствий)
|
Проекция
(0,13)
|
Всеобщая
занятость (0,237)
|
Массовая безработица (0,103)
|
Квалифицированные
кадры (0,343)
|
Государственная
монополия
(0,185)
|
Обобщенный
вес
|
| Население
Материальное благополучие
Социальная защита
Профессиональный рост Реализация возможностей
|
-1
-1
+1
-1
|
+3
+4
-1
- 4
|
-3
-6
-2
-4
|
+3
+1
+6
+5
|
+3
+6
+2
+1
|
+1,856
+1,653
+2,115
+0,410
|
| Организации
Трудовые ресурсы
Технологии
Прибыль
Стабильность
|
+4
-1
+1
-1
|
-3
+4
+2
+5
|
+6
-3
+2
-2
|
+3
+6
+3
+3
|
+1
+4
+3
+4
|
+1,641
+3,307
+2,394
+2,648
|
| Инвесторы
Прибыль
Стабильность
Технология
|
+2
-1
-2
|
+2
+5
+6
|
-1
-2
-3
|
+5
+4
+4
|
+2
+3
+3
|
+2,716 +3,188
+2,780
|
| Правительство
Порядок
Благополучие
Ресурсы
Бюджет
|
-2
-1
+2
-2
|
+5
+3
+1
+4
|
-5
-5
-2
-4
|
+4
+4
+1
+2
|
+5
+4
+6
+3
|
+2,707 +2,178 +1,744 +1,517
|
| !(ентры занятости
Работа
Профессиональный рост Содействие в адаптации
|
+3
+2
+3
|
+1
+1
+1
|
+1
+2
+4
|
+2
+3
+2
|
-1
+2
+1
|
+1,231
+2,103
+1,086
|
| Обобщенное значение для всех сценариев +37,274
|
Интерпретация этого числа такая же ("более, чем сейчас"/ "менее, чем сейчас"), как и при калибровке самих переменных состояний. Таким образом, представляется, что материальное благополучие в будущем будет незначительно повышаться.
Оценка обобщенного сценария в целом получается путем суммирования обобщенных мер для всех переменных состояний. Это значение на обобщенной шкале, равное 37,274, не является "весом", или рангом приоритета. Скорее, оно используется просто как глобальная мера или отметка уровня, по отношению к которой могут измеряться степени сходимости между вероятным и желаемым будущим.
Проведенный анализ калибровочных переменных состояний относительно рассматриваемых сценариев (см.
табл. 3.6) позволяет сделать следующие выводы.
Ситуация с безработицей в ближайшем будущем, вероятно, изменится в лучшую сторону. Процент безработицы приблизится к социально допустимому уровню. Рынок будет ориентирован на высококвалифицированные кадры, которые будут пользоваться особым спросом. Население несколько повысит свое материальное благосостояние, станет более социально защищено и будет вынуждено повышать свою квалификацию. Организации и предприятия будут применять современные технологии, за счет чего повысят прибыль, стабильность и уверенность в будущем. Инвесторы за счет вложения средств в новейшие технологии увеличат собственную прибыль. В целом в государстве установится относительный порядок и улучшится благосостояние населения.
3.4.2. Планирование предприятием производственной деятельности в условиях конкуренции
Предприятие "Волжанин" — ведущий производитель безалкогольных напитков в Нижневолжском регионе. Оно выпускает такую продукцию, как минеральная вода, фруктовые газированные напитки, соки, пиво и т.д. Положение предприятия безалкогольных напитков нестабильно и зависит от текущих экономических условий. Например, исследования, проведенные отделом маркетинга АО "Волжанин", показывают, что потребители становятся более чувствительными к цене и менее лояльны к марке фирмы. В результате доля фирмы на рынке (процент в общем обороте продукции) безалкогольных напитков увеличилась.
Положение АО "Волжанин" в промышленности неустойчиво не только из-за экономических условий и интенсивной конкуренции, но из-за исторического ее доминирования на рынке. Предприятие владеет большой долей на рынке в отрасли, значительно большей, чем ближайшие конкуренты. Уверенное в своей популярности у потребителя предприятие имело возможность требовать и получать много уступок от различных торговцев. Например, оно могло отказывать финансировать рекламу тем торговцам, которые не соглашались на жестко определенные условия содействия, включая выставку товаров в магазине, организацию рекламы по местному телевидению и в газетах и ограничения на рекламу для конкурентов. Отношения между АО "Волжанин" и торговцами постоянно ухудшались, и, наконец, группа крупных торговцев затеяла тяжбу с компанией через федеральную торговую комиссию, приписывая ей нечестную торговую практику и требуя компенсацию за прошлые действия.
Снижение лояльности потребителей к торговой марке предприятия дало торговцам больше подрывных средств для потенциального снижения контроля, которым фирма обладала в отрасли. Например, торговцы могут чаще проводить дополнительное понижение цен или назначать более низкие рыночные цены на товары некоторых конкурентов. Поскольку потребители не так лояльны к марке, как прежде, они будут покупать менее дорогие товары. Такие действия применялись торговцами в отместку за осознанное злоупотребление силой со стороны АО "Волжанин".
В общем, предприятию брошен вызов изменившимся окружением, и оно должно принять решения для успешного выживания в этой новой обстановке. Конкретно, предприятие решило, что, прежде чем возлагать надежды на эффективную конкуренцию ее продукции с другими марками товаров, необходимо улучшить отношения с торговцами. Следует отметить, что это только один компонент более широкого плана, который разрабатывается предприятием для возвращения былого доминирующего положения. Например, предприятие также решило модернизировать упаковку некоторых старых товаров для того, чтобы они приобрели новый более привлекательный вид.
Стратегия завоевания рынка включает специфические договоренности между производителями и торговцами, касающиеся случающегося время от времени снижения цен на товары, специальных предложений (например, два предмета за цену одного), локальной (в противоположность национальной) рекламы, расположения товаров на прилавках и т.д. Предприятие решило разработать новые стратегии завоевания рынка, которые будут находиться в соответствии как с его собственными интересами, так и с интересами торговцев.
Первый прямой процесс планирования:
проектирование методов завоевания рынка при производстве безалкогольных напитков
При первом прямом процессе планирования, который является описательной ветвью метода анализа иерархий, специалисты по планированию построили иерархию окружения, в котором находится АО "Волжанин" (рис. 3.8). Цель прямого процесса— проектирование логического будущего при заданных определенных предположениях о текущих тенденциях.
В рассматриваемом примере предприятие пытается проектировать стратегии завоевания рынка в общеотраслевых масштабах на последующие 10 лет. Его влияние на эти потенциально важные стратегии будет сдерживаться влиянием торговцев и конкурентов, производящих аналогичную продукцию. Следует отметить, что потребители также должны быть включены в список важных акторов. Нужды потребителей отнесены к целям торговцев.
Иерархия имеет следующие уровни:
Уровень 1. Фокус проблемы.
Фокус проблемы — прогнозировать методы завоевания рынка в производстве безалкогольных напитков.
Уровень 2. Акторы.
На этом уровне специалисты по планированию определили акторы влияния на методы завоевания рынка в масштабах отрасли и, кроме того, их относительное влияние. Поэтому здесь уместен был вопрос, каково влияние соответственно торговцев, АО "Волжанин" и конкурентов по отношению к перспективным методам завоевания рынка. Специалисты по планированию смогли определить нормализованные веса каждого актора. Для упрощения процесса изложения матрицы попарных сравнений здесь не определены. Однако краткое описание акторов поможет объяснить приоритеты, которые были получены из попарных сравнений.
Что касается торговцев — владельцев и управляющих магазинами, в которых выставлены и продаются продукты АО "Волжанин" (и ее конкурентов), то хотя они имеют некоторое влияние на выбор стратегий завоевания рынка, но это влияние не так велико, как у производителей и конкурентов.
Если говорить о компании АО "Волжанин", то, несмотря на потерю части былого влияния, она все же считается ведущим производителем в отрасли. Фактически влияние АО на будущее общеотраслевых стратегий завоевания на рынке считается большим, чем совместное влияние конкурентов.
Влияние конкурентов значительно и представляется постепенно возрастающим. Однако, по мнению специалистов по планированию, конкуренты все еще не имеют в руках силы, равной силе рассматриваемого предприятия.

Уровень 3. Цели акторов.
На этом уровне специалисты по планированию спрашивали, какова взаимосвязь между ослаблением влияния АО "Волжанин" и смягчением требований к завоеванию рынка с точки зрения торговцев для каждой пары целей и для каждого из акторов, определенных на уровне 2. Затем планировщики установили приоритеты целей акторов.
Уровень 4. Политики акторов.
На этом уровне специалисты по планированию определили политики, которые применяются акторами для достижения соответствующих целей. Задавался вопрос, как влияет перераспределение мест на прилавках между продукцией АО "Волжанин" и продукцией конкурентов на ослабление рассматриваемого предприятия для каждой цели, установленной на уровне 3. Были определены приоритеты политик, используемых для осуществления целей акторов.
Уровень 5. Исследовательские сценарии.
На этом уровне специалисты по планированию определили три сценария, которые наилучшим образом описывали диапазон альтернативных будущих состояний, и приоритеты сценариев. Дадим краткое описание сценариев.
Сохранять статус-кво —
система возвращения счетов со строгим соблюдением условий, диктуемых стратегией завоевания рынка. В этой системе торговцы платят производителю оптовую цену за товары, не практикуется использование побудительных мотивов (т. е. снижение оптовой цены) кооперации с торговцем в планах завоевания рынка. Торговцы должны платить производителям включенную в цену стоимость завоевания рынка.
Гибкая бесфактурная система —
система с гибким функционированием и без ответных действий (т. е. удержание средств на рекламу) производителей, если торговцы не строго соблюдают условия требований. В такой системе производители будут использовать оптовую цену как побудительный мотив для торговца к кооперации или сами будут инициаторами планов завоевания рынка.
Жесткая бесфактурная система —
система без гибкости в реализации.Если супермаркет применяет только рекламные листки и витринные заголовки для рекламы, но не использует газеты, как того требуют производители, то он не получит соответствующую сумму за участие в рекламе.
Как показано на рис. 3.8, гибкая бесфактурная система представляется наиболее вероятным исследовательским сценарием для будущих стратегий завоевания рынка в отрасли при заданных целях торговцев, АО "Волжанин" и конкурентов. Однако, как уже отмечалось, обобщенный сценарий может включать смесь, или композицию трех сценариев, так как единственный подход не может удовлетворить всех.
Уровень 6. Обобщенный сценарий.
Специалисты по планированию считали, что наиболее вероятным сценарием будет некоторая композиция трех сценариев, выявленных на уровне 5, так как единственный подход не может удовлетворить всех.
Зная относительные веса, приписанные трем сценариям, можно сформулировать обобщенный сценарий, который представляется четырьмя переменными состояниями: доход от продажи, количество выпущенных товаров, сэкономленные средства, связанные с завоеванием рынка, и поток наличных денег.
Сначала необходимо расположить переменные состояния по порядку приоритетов в соответствии с их важностью для АО "Волжанин" (табл. 3.7). Полученный таким образом индекс важности будет использован позднее при оценке степени сходимости между вероятным и желательным будущим, которая достигается путем добавления некоторых определенных при обратном процессе политик. Эти политики будут обсуждаться позднее.
Таблица 3.7
Ранжирование переменных состояния
| Переменная состояния
|
Доход от продажи
|
Объем выпущенных товаров
|
Сэкономленные суммы
|
Поток наличных денег
|
Вектор приоритетов
|
| Доход от продажи
|
1
|
1/3
|
4
|
6
|
0,289
|
| Объем вы
пущенных
товаров
|
3
|
1
|
5
|
7
|
0,554
|
| Сэкономленные
суммы
|
1/4
|
1/5
|
1
|
3
|
0,106
|
| Поток
наличных
денег
|
1/6
|
1/7
|
1/3
|
1
|
0,051
|
Далее переменные состояния используются для получения контуров различных сценариев. Калибровочные числа — целые от -8 до +8. Например, в табл. 3.8 для потока наличных денег второму сценарию — гибкой бесфактурной системе — соответствует -6. Это означает, что у предприятия будет значительно меньше наличных денег, так как торговцы немедленно получат сумму за кооперацию сразу же при выходе на рынок, а не после оплаты счетов за понесенные расходы (если переменная состояния отражает стоимость, а не прибыль, ее увеличение будет отрицательным, а уменьшение — положительным, так что общий результат будет выражать чистый доход).
Таблица 3.8
Калибровка переменных состояния относительно сценариев (первый прямой процесс)
| Переменная состояния
|
Статус-кво (0,10)
|
Гибкая бесфактурная система (0,52)
|
Жесткая бесфактурная система (0,38)
|
Первый прямой процесс
|
| Доход
|
2
|
7
|
5
|
5,74
|
| Объем выпущенных товаров
|
2
|
6
|
4
|
4,84
|
| Сэкономленные суммы
|
-2
|
4
|
5
|
3.78
|
| Поток наличных денег
|
2
|
-6
|
-5
|
-4,82
|
| Обобщение
|
4,49
|
Значения для обобщенной шкалы получаются, если просуммировать произведения весов переменных состояния на значения переменных состояния. Итак, имеем
(0,299) • (5,74) + (0,554) • (4,84) + (0,106) • (3,78)+ (0,051) • (-4,82) = 4,49.
Обратный процесс планирования:
желаемое будущее предприятия АО "Волжанин" и его отношений с торговцами
Обратный процесс — нормативная ветвь метода анализа иерархий, так как в нем идентифицируются политики, которые могут привести к сходимости вероятного и желаемого будущего компании. Кроме идентификации наилучших политик, к которым следует стремиться, в обратном процессе выявляются различные проблемы, могущие возникнуть при осуществлении различных программ выхода на рынок. Обратный процесс имеет следующие уровни (рис. 3.9): уровень 1 —
фокус желаемого будущего; уровень 2 —
желаемые сценарии будущего; уровень 3 —
проблемы и возможности, возникающие при реализации будущего; уровень 4 —
акторы, которые контролируют эти проблемы и возможности; уровень 5 —
цели (или политики) отдельного актора, стремящегося влиять на других акторов. Получив приоритеты этого процесса, можно выбрать политики с наибольшими приоритетами и присоединить их к политикам акторов во втором прямом процессе, чтобы проверить их эффективность по отношению к логическому будущему. В этом случае определение приоритетов осуществляется из этой точки вниз по иерархии.
При проведении обратного процесса специалисты по планированию выбрали для АО "Волжанин" гибкую бесфактурную систему как желательный сценарий, т.е. тот же самый исследовательский сценарий, который представлялся наиболее вероятным будущим при первом прямом процессе. При условии, что вероятное и желаемое будущее методов завоевания рынка совпадают, по мнению специалистов по планированию, имеется большая вероятность, что политики, идентифицированные при обратном процессе, дадут определенную сходимость вероятного и желаемого будущего. Основной заботой специалистов по планированию будет установление того, насколько более сильная сходимость будет получена после добавления этих политик. Для измерения сходимости планировщики должны вернуться к прямому процессу для второй итерации, на этот раз принимая во внимание политики, определенные при обратном процессе.

Второй прямой процесс: измерение сходимости
Планировщики отобрали три политики с наибольшими относительными весами в обратном процессе и ввели их во вторую итерацию прямого процесса для оценки величины сходимости. К отобранным политикам относятся: повышение взаимодействия с торговцами, стимулирование торговцев, прекращение производства некоторых продуктов.
Иерархия второго прямого процесса приведена на рис. 3.10. Уровень 4 теперь включает политики с высоким приоритетом, веса которых были определены в соответствии с их относительным вкладом в цели АО "Волжанин" на уровне 3. Уровень 5 содержит исследовательские сценарии, которые теперь имеют новые веса, полученные в результате добавления политик на уровне 4. На уровне 5 уместен вопрос, какова вероятность осуществления каждого из трех сценариев при более интенсивном взаимодействии с торговцами.
Отметим, что добавление политик повышает вероятность сценария "гибкая бесфактурная система" с 0,52 при первом прямом процессе до 0,66 при втором прямом процессе.

До того как будет установлено, что это единственный сценарий, которого следует придерживаться, такая сходимость может показаться подтверждением эффективности трех новых политик завоевания рынка. Однако истинную сходимость нельзя оценить точно, пока не будет построен новый обобщенный сценарий.
Алгоритм получения этих измерений тот же, что использовался для построения первого обобщенного сценария, за исключением замены весов сценариев над их наименованиями на новые, для отражения исходов второго прямого процесса (табл. 3.9).
Таблица 3.9
Калибровка переменных состояния относительно сценариев (второй прямой процесс)
| Переменная
состояния
|
Статус-кво
(0,07)
|
Гибкая
бесфактурная
система
(0,66)
|
Жесткая
бесфактурная
система
(0,27)
|
Второй прямой
процесс
|
Первый прямой
процесс
|
| Доход
|
2
|
7
|
5
|
6,11
|
5,74
|
| Объем выпущенных
товаров
|
2
|
6
|
4
|
5,18
|
4,84
|
| Сэкономленные суммы
|
-2
|
4
|
5
|
3,85
|
3,78
|
| Поток наличных денег
|
2
|
-6
|
-5
|
-5,17
|
-4,82
|
| Обобщение
|
4,78
|
4,49
|
Сравнение новых весов сценария с теми, что получены ранее (для первого прямого процесса), показывает ценность формулировки нового обобщенного сценария вместо простого измерения повышения вероятности осуществления желаемого сценария.
Отметим, например, что доходы от продажи и количество выпущенных товаров возрастут незначительно. Будет незначительное уменьшение сэкономленных сумм, связанных с завоеванием рынка, и наличных денег, которыми обладает предприятие для инвестиций при заданном увеличении вероятности реализации программы бесфактурной системы по всей отрасли. Итак, не все аспекты обобщенного сценария благоприятны, что свидетельствует о компромиссе, который неизбежно должен быть принят относительно всех проблем планирования.
Политики, определенные в обратном направлении, улучшают обобщенный исход во втором прямом процессе. Обобщенная оценка улучшена на 6,5 % от 4,49 к 4,78, т. е. (4.78 - 4,49) / 4,49 = 0,065.
Прежде чем следовать этим политикам, нужно определить, оправдывают ли издержки незначительное увеличение общих доходов. В случае отрицательного ответа специалистам по планированию необходимо будет провести второй обратный процесс и пересмотреть свои допущения, сформулировать новые суждения и добавить новые политики, которые будут ориентированы на преодоление слабостей политик, определенных ранее, при первом обратном процессе.
3.4.3. Планирование развития отрасли
Рассматривается прикладная задача аналитического (стратегического) планирования развития отрасли виброзащитных систем рессорного подвешивания железнодорожных экипажей, являющейся важной для России, имеющей самую разветвленную сеть железных дорог в мире. Высокие грузонапряженность и скорость движения поездов сравнительно быстро приводят железнодорожный путь в негодность, что повышает аварийность транспорта, снижает сохранность перевозимых грузов, ухудшает комфортабельность перевозок и увеличивает затраты на восстановление пути. Возникающие проблемы могут быть в значительной степени разрешены за счет внедрения в ходовые части подвижных составов новых виброзащитных систем, определяющих динамическое качество составов. Повышение плавности хода и скоростей движения подвижного состава позволит также решить ряд социально-экономических проблем в масштабах страны. Например, скоростной железнодорожный транспорт обеспечит снижение расходов на авиатранспорт за счет его сокращения; улучшение социально-экономического уровня людей; ускорение социально-экономического развития стратегически важных регионов страны и т. п.
Наличие разнообразного парка локомотивов и вагонов требует развития разнообразных технологий виброзащитных систем и разработки ряда организационных мероприятий для воплощения этих технологий в жизнь. Поэтому необходимо проводить системные исследования по планированию рационального развития отрасли виброзащитных технологий. Рассмотренная процедура планирования носит многоитерационный характер и включает два процесса по определению вероятных исходов, выполненных в прямом направлении, и один процесс, выполненный в обратном направлении.
Перейдем к рассмотрению конкретного процесса стратегического планирования.
Первый прямой процесс планирования
Он направлен на определение альтернативных вероятных сценариев развития отрасли виброзащитных систем железнодорожного транспорта.
Иерархическая структура первого прямого процесса планирования приведена на рис. 3.11. Уровень 1 иерархии (фокус) определяет проецируемое будущее развитие виброзащитных систем рассматриваемой отрасли при условии протекания процесса развития без какого-либо вмешательства извне. На уровне 2 расположены акторы, в наибольшей степени определяющие развитие в будущем. Принимаются во внимание четыре актора; Ак1
— Министерство путей сообщения; Ак2
— пользователи транспортом; Ак3
— ученые и проектировщики систем виброзащиты; Ак4
— производственники.
Каждый актор преследует свои цели, ряд из которых пересекается с целями для других акторов. В рассматриваемом примере выделено восемь самостоятельных целей, обозначенных через Цi
, которые определяют уровень 3 иерархии. Уровень 4 содержит вероятные сценарии (альтернативы) развития виброзащитных технологий. При этом предполагается, что развитие отрасли виброзащиты в будущем будет происходить по всем предложенным сценариям, но с разной степенью интенсивности. Замыкает иерархию обобщенный сценарий, отражающий некоторый компромиссный для акторов путь развития отрасли.

После построения иерархии ее элементы оценивались экспертом методом попарного сравнения путем построения соответствующих матриц. На уровне 1 иерархии (см.
рис. 3.11) есть одна матрица парных измерений доминирования, устанавливающая степень влияния акторов на логический исход. При заполнении данной матрицы эксперт отвечал на вопрос, какой из акторов в наибольшей степени определяет наиболее вероятный исход. Матрица и ее собственный вектор имеют следующий вид:
| Вероятное будущее
|
Министерство
|
Пользователи
|
Ученые
|
Производственники
|
Собственный вектор
|
| Министерство
|
1
|
7
|
7
|
1
|
0,436
|
| Пользователи
|
1/7
|
1
|
1/2
|
1/7
|
0,053
|
| Ученые
|
1/7
|
2
|
1
|
1/7
|
0,075
|
| Производственники
|
1
|
7
|
7
|
1
|
0,456
|
| lmax
= 4,06
OO = 0,018
|
Из этой матрицы видно, что логическое будущее в доминирующей степени определяют два актора — Министерство и производственники.
На уровне 3 иерархии рассчитывается значимость целей относительно каждого актора. Здесь число матриц попарных сравнений равно четырем и соответствует числу акторов. Матрицы попарных сравнений целей приведены ниже:
| Какая из целей важнее для министерства?
|
| Министерство
|
Ц1
- комфорт
|
Ц2
- ремонт
|
Ц3
– обслужи-вание
|
Ц4
– перестрой-ка
|
Ц5
– надеж-ность
|
Собственный вектор
|
| Комфорт
|
1
|
1/5
|
1/3
|
1/3
|
1/5
|
0,051
|
| Ремонт
|
5
|
1
|
5
|
5
|
1
|
0,392
|
| Обслуживание
|
3
|
1/5
|
1
|
1/3
|
1/5
|
0,080
|
| Перестройка
|
3
|
1/5
|
3
|
1
|
. 1/3
|
0,137
|
| Надежность
|
5
|
1
|
5
|
3
|
1
|
0,340
|
| lmax
= 5,29 ОО = 0,058
|
| Какая цель важнее для производственников?
|
| Производители
|
Ц4
– Перестройка
|
Ц8
- Экспорт
|
Собственный вектор
|
| Перестройка
|
1
|
7
|
0,875
|
| Экспорт
|
1/7
|
1
|
0,125
|
| lmax
= 2,0 ОО = 0,079
|
| Какая цель важнее для пользователей?
|
| Пользователи
|
Ц1
- Комфорт
|
Ц5
- Надежность
|
Собственный вектор
|
| Комфорт
|
1
|
1/5
|
0,167
|
| Надежность
|
5
|
1
|
0,833 '[
|
| lmax
= 2,0 ОО = 0,0:
|
| Какая цель важнее для проектировщиков и ученых?
|
| Ученые и проектировщики
|
Ц1
- Ком-форт
|
Ц6
- Субсидии на науку
|
Ц7
- Престиж науки
|
Ц5
- Надежность
|
Собственный вектор
|
| Комфорт
|
1
|
1/5
|
1
|
1
|
0,149
|
| Субсидии на науку
|
5
|
1
|
3
|
1
|
0,452
|
| Престиж науки
|
1
|
1/3
|
1
|
1
|
0,164
|
| Надежность
|
1
|
1
|
1
|
1
|
0,235
|
| lmax
= 4,26
ОО = 0,079
|
На уровне 4 определяются матрицы доминирования относительно каждой цели для шести сценариев. Результаты попарных сравнений приведены в табл. 3.10.
На основании вышеизложенного алгоритма иерархического синтеза проводится расчет векторов приоритетов альтернатив-сценариев относительно четырех акторов и фокуса иерархии. Значения векторов приоритетов альтернатив-сценариев даны в верхней части табл. 3.11.


Из анализа этих векторов видно, что наиболее вероятными являются сценарии развития, соответствующие альтернативам А1
, А2
и А3
,.
Причем вероятность развития сценария по альтернативе А1
(статус-кво, т.е. сохранение в будущем такого же положения дел, как в настоящее время) в два раза выше, чем по альтернативам A
2
и А3
.
Сценарии, соответствующие альтернативам А4
, А5
,
и А6
имеют очень малую вероятность реализации в будущем при существующем раскладе сил.
Для анализа последствий от реализации альтернативных вероятных сценариев строится обобщенный сценарий с использованием шкалы разностей.
С этой целью определяется перечень критериев, относительно которых экспертом по шкале +8,+6,..., -6, -8 оцениваются сценарии.
Предложены следующие критерии: число ученых и проектировщиков; профессиональный уровень ученых; благосостояние ученых, проектировщиков и производственников; грузопоток железнодорожного транспорта; надежность функционирования дорожной системы в целом; комфортабельность транспортных средств; затраты на поддержание пути и виброзащитных систем; развитие и престиж науки; развитие технологий; развитие экспорта.
Анализ результатов оценки альтернативных и обобщенных сценариев относительно акторов и фокуса иерархии (см табл. 3.11) позволяет сделать следующие выводы.
Векторы приоритетов альтернатив-сценариев, принадлежащие различным акторам, существенно различаются значениями, характеризующими относительную степень предпочтения альтернатив. Например, для производственников альтернатива А1
) (статус-кво) более чем в 10 раз предпочтительнее альтернативы А6
,
(развитие активных систем), в то время как для ученых альтернатива А6
,
более чем в 2 раза предпочтительнее альтернативы А1
.
Анализ интегральных оценок обобщенных исходов показывает, что наилучшего будущего можно достичь при реализации целей, преследуемых учеными и проектировщиками (значение оценки +21,29). Наиболее вероятное развитие отрасли виброзащитных систем с учетом различной степени влияния на процесс в будущем всех акторов приводит к некоторому компромиссному интегральному обобщенному сценарию со значением, равным +10,476.
Обобщенный вероятный сценарий развития отрасли виброзащитных систем с учетом влияния на процесс всех акторов имеет следующую краткую характеристику, полученную в результате анализа правого крайнего столбца (см.
табл. 3.11). При развитии отрасли виброзащитных систем с учетом сложившейся ситуации в ближайшем будущем будут наблюдаться следующие изменения переменных состояний. Число ученых будет иметь тенденцию к снижению (значение -0,132 = 0,35 • (-2) + 0,165 • (0) + 0,160 • (+2) + + 0,118 • (0) + 0,124 • (+2) + 0,08 • (0)). Наметится небольшое снижение профессионального уровня ученых. Для ученых и производственников несколько повысится благосостояние. Функциональные параметры транспортных средств в целом претерпят изменения как в сторону небольшого улучшения (увеличение грузопотока и комфортабельности), так и в сторону ухудшения — уменьшения надежности. Ожидается незначительное снижение затрат на содержание железнодорожного пути при одновременном увеличении затрат на содержание виброзащитных систем рессорного подвешивания. Будет иметь место некоторое развитие новых технологий и увеличение доходов от экспорта, а также приобретут незначительную положительную тенденцию развитие науки и ее престижность.
На этапе оценки и описания обобщенного логического сценария планирование в прямом направлении завершается. На следующем шаге определяются желаемые альтернативы-сценарии. Нами было отмечено наличие достаточно большого арсенала способов определения желаемых сценариев.
Ниже рассматриваются два подхода по определению желаемых сценариев развития отрасли виброзащитной техники для железнодорожных транспортных средств.
В соответствии с первым подходом в качестве желаемого будущего принимается наиболее прогрессивный обобщенный сценарий, соответствующий в нашем случае вектору приоритетов альтернатив, принадлежащему в первом прямом процессе ученым и проектировщикам. Желаемые альтернативы-сценарии будут иметь в этом случае следующие весовые коэффициенты:
А1
= 0,130; A
2
= 0,150; А3
= 0,238; А4
= 0,073; A
5
= 0,122; A
6
= 0,287. Оценка обобщенного желаемого сценария, проведенная по критериям и переменным состояниям, равна 21,29 (см.
табл. 3.11).
В соответствии со вторым подходом желаемые сценарии выбираются с учетом интересов (целей) всех или части акторов, участвующих в планировании. Ситуация по выработке желаемого сценария может выглядеть следующим образом. Акторы предварительно договариваются между собой о синтезе такого желаемого сценария, который бы позволил в будущем улучшить критерии и переменные состояния по сравнению с вероятным сценарием при условии сохранения интересов и целей каждого актора. При этом независимому эксперту с согласия всех акторов предлагается изменить их значимость в иерархии, использованной в предыдущем прямом процессе, в соответствии с их компетентностью в вопросе определения наиболее благоприятного будущего. Например, ученые и проектировщики значительно более компетентны в вопросе определения наиболее благоприятного будущего, чем производственники и пользователи транспортными средствами, о чем свидетельствуют интегральные оценки обобщенных исходов, соответствующие прогнозам указанных акторов в первом прямом процессе. Расчет весовых коэффициентов желаемых альтернатив-сценариев проводится по известной иерархии (см.
рис. 3.11). При этом вводятся следующие изменения. Фокусом иерархии в данном случае является желаемое будущее - развитие отрасли виброзащитных систем. Приоритет акторов устанавливается с учетом их компетентности в определении наилучшего желаемого будущего. В связи с этим экспертом присвоены акторам следующие веса: Ак1
(Министерство) = 0,32; Ак2
(пользователи) = 0,03; Ак3
(ученые и проектировщики) = 0,37; Ак4
(производственники) = 0,27. Все остальные исходные данные приняты без изменений из первого прямого процесса. Результирующие весовые коэффициенты желаемых сценариев в соответствии со вторым подходом распределены относительно альтернатив следующим образом: А1
= 0,25; А2
=
0,20; А3
= 0,18; А4
= 0,10; A
5
= 0,125; A
6
= 0,15. Оценка обобщенного желаемого сценария, проведенная по ранее введенным критериям и переменным состояния (см.
табл. 3.11), имеет значение +15,24, что в 1,5 раза выше оценки обобщенного вероятного сценария относительно фокуса иерархии (значение +10,476).
Первый обратный процесс планирования.
Он начинается после получения желаемых сценариев. Этот процесс позволяет определить новые цели, политики и их значимость для более эффективного использования в последующем прямом процессе планирования.
Проведенный выше анализ показывает, что наибольший вес по влиянию на развитие исследуемой отрасли имеют такие акторы, как Министерство и производственники. Поэтому в первом обратном процессе целесообразно выработать эффективные политики именно для этих акторов, чтобы они начали влиять на смещение приоритетов в сторону желаемых сценариев.
Для решения данной задачи построена иерархия первого обратного процесса (рис. 3.12). Фокусом иерархии является желаемая стратегия развития отрасли виброзащитных систем. На уровне 2 расположены желаемые сценарии развития отрасли. При этом приняты во внимание шесть сценариев, рассмотренных ранее в первом прямом процессе. Приоритеты желаемых сценариев соответствуют приоритетам вероятных сценариев, определенных относительно ученых и проектировщиков.
На уровне 3 определены основные проблемы, которые возникают при реализации желаемых сценариев. Для определения значимости проблем при их попарном сравнении следует отвечать на вопрос, разрешение какой проблемы предпочтительно для достижения желаемого сценария.
Определено шесть проблем, приводимых ниже.
Проблема 1.
Для достижения желаемых сценариев требуются значительные субсидии на перестройку существующего предприятия.
Проблема 2.
У производственников высокий уровень консервативности мышления в отношении перестройки производства для создания новых изделий.
Проблема 3.
В производственной сфере, требующей перестройки, низкие материальные и моральные стимулы у рабочих и инженерно-технических работников.
Проблема 4.
Существующие в нормативных документах нормы на вибрацию имеют низкий уровень, что не способствует созданию и внедрению в практику более эффективных технических систем.
Проблема 5.
Отсутствует необходимое финансирование научных исследований в области функциональных свойств и надежности новых систем виброзащиты.

Проблема
б.
Отсутствует специальная служба, обеспечивающая контроль за безопасностью эксплуатации скоростных железнодорожных транспортных средств.
На уровне 4 иерархии расположены наиболее значимые акторы (Министерство путей сообщения и производственники), контролирующие существующие проблемы. При установлении степени важности одного актора перед другим здесь следует ответить на вопрос, какой актор в большей степени контролирует проблемы и влияет на их разрешение.
Уровень 5 образован альтернативами-целями, которые необходимо применить во втором прямом процессе для сближения вероятного и желаемого исходов.
Для двух указанных акторов определено шесть новых альтернатив-целей:
А1
—
привлечение инвестиций из военно-промышленного комплекса (ВПК) для создания специальных активных систем виброзащиты, способных одновременно эффективно функционировать на военных и гражданских транспортных средствах;
А2
—
развитие кооперации с иностранными фирмами, создание совместных предприятий и привлечение зарубежных инвестиций;
А3
, —
ужесточение норм на вибрацию;
А4
— организация системы прямых экспортных поставок комплектующих систем виброзащиты без привлечения посредников;
А5
—
разработка на производстве более совершенной системы материального и морального стимулирования труда;
А6
—
проработка вопроса о привлечении инвестиций частных спонсоров.
Для определения относительной важности альтернатив-целей эксперту при составлении матриц попарных сравнений следует ответить на вопрос, какая из двух сравниваемых целей и насколько предпочтительнее для достижения j
-м актором желаемой стратегии развития отрасли виброзащитных систем? В приведенной иерархии (см.
рис. 3.12) акторы имеют различное число целей, поэтому иерархический синтез осуществляется четвертой модификацией метода анализа иерархий.
Результирующий вектор приоритетов альтернатив-целей имеет следующий вид:
 = {0,609; 0,153; 0,042; 0,0139; 0,029; 0,215}Т
. = {0,609; 0,153; 0,042; 0,0139; 0,029; 0,215}Т
.
Анализ приведенного вектора показывает, что наиболее значимыми являются цели, соответствующие альтернативам А1
, A
2
и А4
.
Полученный вектор приоритетов альтернатив-целей необходим для установления относительной значимости целей во втором прямом процессе планирования.
Второй прямой процесс планирования.
Иерархия этого процесса (рис. 3.13) строится с учетом целей, определенных и проранжированных в предыдущем обратном процессе. Актору "Министерство путей сообщения" добавляются четыре альтернативы-цели A1
,
A
2
, А3
,
и А4
(см. рис. 3.12). Актору "производственники" добавляются не все пять новых целей-альтернатив, сгенерированных для него в обратном процессе, а четыре наиболее значимые, соответствующие альтернативам A1
, А2
, А4
и А5
.
Далее методом попарного сравнения устанавливается значимость новых целей относительно целей, принадлежавших иерархии первого прямого процесса. Для этого существующие матрицы парных сравнений целей достраиваются экспертом с учетом значимости новых целей следующим образом:
| Какая цель важнее для производственников в первом прямом процессе?
|
| Производственники
|
Ц4
— перестройка
|
Ц8
— экспорт
|
| Перестройка
|
1
|
7
|
| Экспорт
|
1/7
|
1
|
| Какая цель важнее для производственников во втором прямом процессе?
|
| Производственники
|
1
|
2
|
3
|
4
|
5
|
6
|
| Уменьшение затрат на перестройку производства
|
1
|
4
|
1
|
3
|
3
|
5
|
| Повышение прибыли от экспорта
|
1/4
|
1
|
1/5
|
1
|
1
|
3
|
| Кооперация с иностранными партнерами
|
1/3
|
1
|
1/5
|
1
|
3
|
5
|
| Инвестиции ВПК
|
1
|
5
|
1
|
5
|
3
|
7
|
| Экспорт без посредников
|
1/3
|
1
|
1/3
|
1/3
|
1
|
3
|
| Стимулирование сотрудников
|
1/5
|
1/3
|
1/7
|
1/5
|
1/3
|
1
|

Иерархический синтез приоритетов альтернатив, проведенный для второго прямого процесса, позволил получить следующий вектор приоритетов исходов:

Интегральная оценка обобщенного исхода, полученная относительно фокуса иерархии второго прямого процесса, имеет следующее значение:
ОИф
12
= 19,616.
Анализ интегральных оценок обобщенных вероятных исходов для первого (10,476) и второго (19,616) прямых процессов указывает на уменьшение во второй итерации различия между вероятным и желаемым (21,290) исходами.
Во втором прямом процессе получен достаточно хороший результат по критерию интегральной оценки обобщенного исхода, поэтому итерационный процесс на этом этапе может быть завершен.
Основные понятия
1. Аналитическое планирование.
2. Прямой и обратный процессы.
3. Вероятное (логическое) и желаемое будущее.
4. Стратегическое планирование и практика.
5. Оценка последствий.
6. Конкуренция и стратегическое планирование.
7. Маркетинг и стратегическое планирование.
8. Антикризисное управление предприятий и стратегическое планирование.
Контрольные вопросы и задания
1. Дайте определение иерархическим уровням применительно к задачам аналитического планирования.
2. Охарактеризуйте прямой и обратный процессы аналитического планирования.
3. На основе каких предпосылок и как формируются вероятное (логическое) и желаемое будущее?
4. Разработайте стратегию мотивации труда работников промышленного предприятия.
5. Разработайте подходы для обоснованного развития фирмы или государственного предприятия в условиях нестабильной экономики.
6. Спланируете обоснованный бюджет фирмы или государственного предприятия.
7. Разработайте стратегическую маркетинговую политику предприятия.
8. Оцените последствия развития исследуемого предприятия от принятых стратегических решений.
9. Ответьте для себя на вопрос, как часто следует проводить планирование своей деятельности или деятельности предприятия.
Литература
1. Саати Т., Керне К.
Аналитическое планирование. Организация систем: Пер. с англ. — М.: Радио и связь, 1991. — 224 с.
2. Аганбегян А. Г.
Перспективное отраслевое планирование: Экономико-математические методы и модели. — Новосибирск, 1986. — 192 с.
3. Аганбегян А. Г.
Управление и эффективность. — М.: Экономика, 1981. —71 с.
4. Проблемы
методологии комплексного социально-экономического планирования/ Е. 3. Майминас, В. Л. Тамбовцев, А. Г. Фонатов и др.; Под ред. Н. П. Федоренко и др. — М.: Наука, 1983 . — 415 с.
5. Петраков Н. Я., Ротарь В. И.
Фактор неопределенности и управления экономическими системами / Отв. ред. С. А. Айвазян. — М.: Наука, 1985. — 191 с.
6. Черемных Ю. Н.
Математические модели развития народного хозяйства. — М.: Изд-во МГУ, 1986. — 103 с.
7. Айвазян С. А.
и др. Прикладная статистика: Исследование зависимостей: Справ, изд. / Под ред. С. А. Айвазяна. — М.: Финансы и статистика, 1985. — 487 с.
8. Дубров А. М.
Математико-статистическая оценка эффективности в экономических задачах. — М.: Финансы и статистика, 1982. — 176 с.
9. Анчишкин А. И.
Наука. Техника. Экономика. — 2-е изд. — М.: Экономика, 1989. — 383 с.
ГЛАВА 4.
МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
Элементы теории нечетких множеств могут успешно применяться для принятия решений в условиях неопределенности. Основатель теории нечетких множеств Л. Заде еще в 1965 г. предрекал широкое прикладное значение своей теории, написав по этому поводу следующее: "Фактически нечеткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ".
4.1. Элементы теории нечетких множеств
Рассмотрим основные элементы теории нечетких множеств [l]. Пусть U
—
полное множество, охватывающее все объекты некоторого класса. Нечеткое подмножество F
множества U,
которое в дальнейшем будем называть нечетким множеством, определяется через функцию принадлежности mF
(u
), и
Î U.
Эта функция отображает элементы Ui
, множества U
на множество вещественных чисел отрезка [0,1], которые указывают степень принадлежности каждого элемента нечеткому множеству F.
Если полное множество U
состоит из конечного числа элементов и
i
,
i
= 1, 2, ..., п,
то нечеткое множество F
можно представить в следующем виде:

где "+" означает не сложение, а, скорее, объединение: символ "/" показывает, что значение mF
относится к элементу, следующему за ним (а не означает деление на и
i
).
В случае, если множество U
является непрерывным, F
можно записать как интеграл:

Нечеткие множества широко применяются для формализации лингвистических знаний. Рассмотрим для примера множество процентных ставок, предоставляемых банками по вкладам. Каким образом можно выделить подмножество высоких процентных ставок? В условиях динамично изменяющейся среды не всегда возможно точно ответить на этот вопрос, однозначно выделив множество высоких ставок. При использовании аппарата теории нечетких множеств решить такую задачу можно даже при отсутствии полной количественной информации об окружении. Функция принадлежности для элементов нечеткого множества F
1
,
соответствующих понятию "высокие процентные ставки" (рис. 4.1), будет иметь следующий вид:


Функция принадлежности к нечеткому множеству низких процентных ставок запишется следующим образом:

4.2. Нечеткие операции, отношения и свойства отношений
Операции над нечеткими множествами.
Над нечеткими множествами, как и над обычными, можно выполнять математические операции. Рассмотрим важнейшие из них: дополнение множества, объединение и пересечение множеств.
Операция дополнения
может быть представлена следующим образом:

Операция объединения
будет иметь следующий вид:

Здесь и далее операция v обозначает взятие максимума. Операция пересечения
вычисляется следующим образом:

Здесь и далее символ л обозначает взятие минимума.
Нечеткие отношения.
Нечетким отношением R
между полным множеством U
и другим полным множеством V
называется подмножество прямого декартова произведения U
´
V,
определяемое следующим образом:

где U
= {u1
, u2
,..., и
l
}, V
{v1
, v2
,..., vm
}.
Допустим, что между элементами знаний, представленных нечеткими множествами F
и G
,
существует связь, заданная правилом: "Если F,
то G", при этом F
Í U
, G
Í V.
В логике высказываний для представления правил подобного вида используется операция импликации. В нечеткой логике предложены различные способы реализации импликации. Один из наиболее простых способов заключается в представлении импликации, соответствующей правилу "Если F,
то G", нечетким отношением R
,
которое вычисляется следующим образом [2]:

Свойства нечетких отношений.
1. Объединение отношений
(
R
È
S
)(
u
,
v
)
= R
(
u
,
v
)
Ú S
(
u
,
v
), и
Î U
,
v
Î
V.
2. Пересечение отношений
(
R
Ç
S
)(u
, v
) = R
(
u
,
v
)
Ù
S
(
u
,
v
), и
Î U
,
v
Î V.
3. Операция включения
(R
Í S
) « R
(
u
,
v) £S
(
u
,
v), u
Î
U
,
v
Î V.
4. Свойство идемпотентности
R
Ç
R
=
R
,
R
È
R
=
R
.
5. Коммутативность
R
Ç
S
= S
Ç
R,R
È
S = S
È
R.
6. Ассоциативность
R
Ç
(
S
Ç
Q
) = (
R
Ç
S
)
Ç
Q
.
R
È
(S
È
Q) = (R
È
S
È
Q.
7. Дистрибутивность
R
Ç
(S
È
Q) = (R
Ç
S)
È
(S
Ç
Q).
R
È
(S
Ç
Q) = (R
È
S)
Ç
(S
È
Q).
8. Рефлексивность
Если mR
(и, и) =
1, отношение R
—
рефлексивное.
Если mR
(и, и) <
1, отношение R
— слабо рефлексивное.
Если mR
(и, и)
= 0, отношение R
— антирефлексивное.
Если mR
(и, и)
> 0, отношение R —
слабо антирефлекеивное.
9. Симметричность
mR
(u
, v)
= mR
(v, и); и, v
Î U
.
10. Транзитивность
mR
(
u
, v)
³ mR
(
u
,
z
)
Ù mR
(
z
,
v
);
u
, v
,
z
Î U
.
4.3. Многокритериальный выбор альтернатив на основе пересечения нечетких множеств
Элементы теории нечетких множеств успешно применяются для . принятия решений. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами. Рассмотрим одну из математических постановок задач принятия решений на основе теории нечетких множеств.
В данном случае критерии определяют некоторые понятия, а оценки альтернатив представляют собой степени соответствия этим понятиям. Пусть имеется множество альтернатив А
= {а1
, а2
, ..., а
m
,
} и множество критериев С=
{С1
, С2
, ..., С
n
},
при этом оценки альтернатив по каждому i
-му критерию представлены нечеткими множествами:
С
i
=
{mCi
(a1
)/ mCi
, (a2
)/a2
, …,
mCi
(am
)/am
}
Правило выбора лучшей альтернативы можно представить как пересечение нечетких множеств, соответствующих критериям:
D
= С1
Ç
C
2
Ç
...
Ç
С
n
.
Операция пересечения нечетких множеств может быть реализована разными способами. Иногда пересечение выполняется как умножение, но обычно этой операции соответствует взятие минимума:

Лучшей считается альтернатива a
*
, имеющая наибольшее значение функции принадлежности

Если критерии С
i
имеют различную важность, то их вклад в общее решение можно представить как взвешенное пересечение:
D=C1
a
1
Ç
C2
a2
Ç
...
Ç
n
a
n
,
где аi
-
весовые коэффициенты соответствующих критериев, которые должны удовлетворять следующим условиям:

Коэффициенты относительной важности можно определить, используя процедуру попарного сравнения критериев.
4.4. Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения
Рассмотрим метод принятия решений, предполагающий построение множества недоминируемых альтернатив на основе нечеткого отношения предпочтения [З].
Постановка задачи в краткой форме представляется следующим образом. Пусть задано множество альтернатив А
и каждая альтернатива характеризуется несколькими критериями качества с номерами j
== i
, ..., т.
Информация о попарном сравнении альтернатив по каждому критерию качества j
представлена в форме отношения предпочтения Rj
.
Таким образом, имеется т
отношений предпочтения Rj
на множестве А.
Требуется выбрать лучшую альтернативу из множества {A
,
R
1
,
...,R
m
}.
Метод многокритериального выбора альтернатив на основе нечеткого отношения предпочтения основан на ряде определений.
Определение 1.
Нечетким отношением R
на множестве А
называется нечеткое подмножество декартова произведения А
´
А,
характеризующееся функцией принадлежности mR
: А
´ А
®
[0,1]. Значение mR
(a
, b
) этой функции понимается как степень выполнения отношения а
Ù
b
.
Определение 2.
Нечетким отношением предпочтения на А
называется любое заданное на этом множестве рефлексивное нечеткое отношение, функция принадлежности которого вычисляется следующим образом:

Определение 3.
Пусть А —
множество альтернатив и mR
— заданное на нем нечеткое отношение предпочтения. Нечеткое подмножество недоминируемых альтернатив множества (А,
mR
) описывается функцией принадлежности

Определение 4.
Четко недоминируемыми называются альтернативы, для которых mR
НД
(а) =
1, а множество таких альтернатив

Определение 5.
Носителем нечеткого множества В
с функцией принадлежности mB
(a
) является множество {а
½а
Î А,
mB
> 0}.
Процедура решения задачи выбора выполняется в несколько шагов.
1. Строится нечеткое отношение Q
1
,
которое является пересечением исходных отношений предпочтения:

и определяется нечеткое подмножество недоминируемых альтернатив в множестве (А,
mQ
1
):

2.
Строится нечеткое отношение Q
2
:

и определяется нечеткое подмножество недоминируемых альтернатив в множестве (
A
,
mQ
2
):

Данная функция упорядочивает альтернативы по степени их недоминируемости. Числа wj
в приведенной выше свертке представляют собой коэффициенты относительной важности рассматриваемых критериев, для которых выполняются следующие условия:

3. Отыскивается пересечение множеств mQ
1
НД
и mQ
2
НД
:

4. Рациональным считается выбор альтернатив из множества

Наиболее рациональной альтернативой из множества АНД
является та, которая имеет максимальную степень недоминируемости.
4.5. Многокритериальный выбор альтернатив с использованием правила нечеткого вывода
Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений [2].
Сущность метода, на основе которого реализована компьютерная система, заключается в следующем. Пусть U
—
множество элементов, А —
его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Подмножества Aj
являются значениями лингвистической переменной X.
Допустим, что множество решений характеризуется набором критериев х1
, х2
, ...,
xp
,
т.е. лингвистических переменных, заданных на базовых множествах и1
, и2
,
.... up
соответственно. Например, переменная х1
"качество управления" может иметь значение НИЗКОЕ, а переменная х2
"стоимость" — значение ХОРОШЕЕ и т. д. Набор из нескольких критериев с соответствующими значениями характеризует представления лица, принимающего решение, об удовлетворительности альтернативы. Переменная S "удовлетворительность" также является лингвистической. Ниже приведен пример высказывания :
d
1
:
"Если x
1
= НИЗКОЕ и x
2
= ХОРОШЕЕ, то S
= ВЫСОКАЯ". В общем случае высказывание d
1
имеет вид:
d
1
:
"Если x1
= А1
,
и x
2
= А2
i
и ... хр
= Ар
i
то S
= В
i
".
(4.1)
Обозначим пересечение (x
1
= А1
i
Ç x
2
= А2
i
Ç... хр
= Ар
i
)
через х
= А
i
.
Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности:

Здесь V
=
U
1
´U
2
´...Up
; v
= (
u
1
, и2
...,
up
);
m
Aij
(uj
) — значение принадлежности элемента и, нечеткому множеству Аij
.
Тогда высказывание (4.1) можно записать в виде:

Для придания общности суждениям обозначим базовые множества U
и V
через W
.
Тогда А
i
—
нечеткое подмножество W
,
в то время как В
i
—
нечеткое подмножество единичного интервала I
.
Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации [4]. Нечеткая импликация Лукасевича имеет вид:

где Н —
нечеткое подмножество на W
´ I
, w
Î W
,
i
Î
I.
Аналогичным образом высказывания d
1
,
d
2
,...,
dq
преобразуются в множества Н1
, Н2
, ..., Нq
.
Их пересечением является множество D
:
D
= H1
Ç H2
Ç ... Ç Н
q
и для каждого (w, i)
Î W
´
I

Удовлетворительность альтернативы, которая описывается нечетким подмножеством А
из W,
определяется на основе композиционного правила вывода:
G
= А
°
D,
где G — нечеткое подмножество интервала I
.
Тогда

Сопоставление альтернатив происходит на основе точечных оценок. Для нечеткого множества С
Ì I
определяем a-уровневое множество (a Î [0, 1]):
Сa
= {i | mc
(i) ³ a Î I
}.
Для каждого Сa
можно вычислить среднее число элементов — М(Сa
):
для множества из п
элементов

для Сa
={a
£
i
£
b
}



при 0 £ a
1
£ b
1
£
а2
£
b
2
£
...
£
а
n
£
bn
£
1.
Тогда точечное значение для множества С
можно записать в виде:

где amax
— максимальное значение в множестве С.
При выборе альтернатив для каждой из них находится удовлетворительность и вычисляется соответствующая точечная оценка. Лучшей считается альтернатива с наибольшим ее значением.
4.6. Многокритериальный выбор альтернатив на основе аддитивной свертки
В рассматриваемом методе [3] экспертные предпочтения представлены с
помощью нечетких чисел, имеющих функции принадлежности треугольного вида (рис.4.2).

Пусть имеется множество альтернатив А
= {а1
, а2
, ...,
am
} и множество критериев С = {с1
, с2
, ...,
с
n
}, при этом оценка j
-й альтернативы по i-му
критерию представлена нечетким числом Rij
, a относительная важность i
-го критерия задается коэффициентом a
i
=
1,2 ...,п.
Если коэффициенты а, нормированы, то взвешенная оценка j
-й альтернативы вычисляется по формуле

Если функции принадлежности mRij
(rij
) и ma
i
(ai
) имеют треугольный вид, то для них, как и для нечеткого числа X,
вершина X*,
а также левая Х
¢
и правая X"
границы определяются следующими соотношениями:

Взвешенная оценка j
-й альтернативы R
j
является результатом линейной комбинации нечетких чисел и также будет иметь функцию принадлежности треугольного вида. Вершину и границы нечеткого числа Z == Х
´
Y
,
полученного в результате операций сложения или умножения (символ ´
обозначает обобщенную операцию), можно вычислить следующим образом:
Z
'=
X
¢
´
Y
¢
;
Z
¢¢
=
X
¢¢ ´
Y
¢¢
;
Z
*=
X
*
´
У.
Ранжирование альтернатив с использованием полученных взвешенных оценок возможно на основе их нечеткой композиции:

Здесь mJ
(j
) — нечеткое множество альтернатив, соответствующих понятию "лучшая альтернатива". Лучшей считается альтернатива, имеющая наибольшее значение mJ
(j
).
Приоритет каждой альтернативы вычисляется путем выбора минимума среди точек пересечения правой границы соответствующего ей нечеткого числа R
j
с
границами нечетких чисел, представляющих взвешенные оценки альтернатив, расположенных правее на числовой оси (удовлетворяющих условию rk
>
rj
.).
При этом предполагается, что правая граница области определения нечетких чисел соответствует самым предпочтительным оценкам, а левая — наихудшим.
4.7. Ранжирование альтернатив на множестве лингвистических векторных оценок
Задано множество альтернатив A
== {а1
, а2
, ..., а
m
}
и множество соответствующих исходов S
= [
s
1
,
s
2
, ...,
sm
,}.
Каждый исход sj
характеризуется альтернативой а
i
и вектором лингвистических оценок на множестве критериев К
= [К1
, К2
,
.... К
n
}.
Множество лингвистических векторных оценок исходов К = {
K
(
s
1
),
K
(
s
2
), ...,
K
(
sm
)}
можно упорядочить, введя функцию принадлежности нечеткого отношения порядка m ³
: К
´ К
®
[0,1]. Для i
-го критерия обозначим mi
³
(
Ki
(
sj
),
Ki
(sk
)) через mi
³
(sj
, sk
) Значение этой функции можно вычислить по фоомуле

Степень истинности m < (sj
,
sk
)
нечеткого высказывания sj
<
sk
можно определить как вероятность того, что точное значение s
j
будет меньше точного значения sk
.
Предполагая, что исходы являются независимыми случайными величинами, отношение m < (sj
,
sk
)
можно представить в виде:

где vs
(
x
)
— вероятность того, что в качестве точного значения нечеткого числа s
используется величина х;
ws
(
x
) —
вероятность того, что в качестве точного значения s
используется величина у < х:

Векторные оценки могут быть упорядочены на основе функции принадлежности

где х — обозначает символ обобщенной операции.
Так как между множеством альтернатив и исходив существует взаимно однозначное соответствие, функцию принадлежности нечеткого отношения предпочтения на множестве альтернатив можно представить в виде:

Решение задачи с использованием данного метода включает следующие основные шаги:
• вычисление функций принадлежности m<
с использованием соотношений (4.2);
• построение нечеткого отношения порядка m³
;
• минимизация отношения m³
;
• определение отношений предпочтения на множестве альтернатив и выявление лучшей альтернативы. Для этого вычисляется отношение предпочтения между альтернативой aj
и всеми остальными альтернативами, функция принадлежности которого имеет вид:

где Ij
—
множество индексов альтернатив, с которыми может сравниваться j-я
альтернатива.
Решение задачи ранжирования можно описать соотношениями:

где rj
—
ранг альтернативы.
Наиболее предпочтительная альтернатива имеет самый низкий ранг.
4.8. Методика решения прикладных задач на ЭВМ
4.8.1. Многокритериальный выбор методом максимннной свертки в сфере банковского кредитования
Банковское кредитование
С развитием рыночных отношений процесс кредитования банками предприятий сопряжен с многочисленными факторами риска, способными повлечь за собой непогашение ссуды в установленный срок. При анализе кредитоспособности заемщика определяется возможность своевременного и полного погашения задолженности по ссуде; степень риска, которую банк готов взять на себя; размер кредита, который может быть предоставлен в конкретной ситуации; условия предоставления кредита.
В современных условиях анализ кредитоспособности связан не только с оценкой платежеспособности клиента на определенную дату, но и с выявлением наиболее предпочтительных заемщиков, прогнозированием их финансовой устойчивости в перспективе, учетом возможных рисков по кредитным операциям. Проведение такого всестороннего анализа позволяет банку более эффективно управлять кредитными ресурсами и получать прибыль.
Применяемые банками методы в области кредитования основаны на данных бухгалтерских отчетов, поэтому они позволяют лишь оценить кредитоспособность ссудозаемщика, не обеспечивая выбора наиболее оптимального заемщика в целях минимизации факторов риска для банка и наиболее эффективного планирования своей деятельности в будущем.
Рассмотрим применение метода принятия решений, основанного на теории нечетких множеств в области кредитования, позволяющего повысить обоснованность принимаемых решений и обеспечить выбор наиболее рационального варианта из множества допустимых.
К региональному отделению сберегательного банка России обратились четыре предприятия с просьбой о предоставлении им кредита. Поскольку ресурсы банка ограничены, перед ним стоит задача выбрать одно предприятие, лучшее по комплексу критериев качества. В рассматриваемой задаче предприятия являются альтернативами, из которых предстоит сделать выбор лучшей. Альтернативы обозначим через а1
, ...,
a
4
.
Для оценки кредитоспособности предприятий-заемщиков используем данные их бухгалтерской отчетности (табл. 4.1).
Таблица 4.1
Данные бухгалтерской отчетности
| Финансовый показатель
|
Значение показателя для предприятия, тыс. руб.
|
| a1
|
a2
|
a3
|
a4
|
| Денежные средства (ДС)
|
229,1
|
946,2
|
947,0
|
1442,9
|
| Краткосрочные финансовые вложения (КФВ)
|
394,1
|
462,7
|
466,4
|
2066,0
|
| Дебиторская задолженность (ДЗ)
|
4639,8
|
8391,4
|
8514,5
|
10908,2
|
| Запасы и затраты (33)
|
6028,1
|
21557,6
|
21370,4
|
17424,5
|
| Собственный капитал (СК)
|
12395,8
|
35247,8
|
41244,2
|
53939,4
|
| Краткосрочные обязательства (ОКс)
|
4058,1
|
13834,9
|
16827,1
|
25028,3
|
| Итог баланса (ИБ)
|
16453,9
|
49082,7
|
58071,3
|
78967,7
|
| Валовая выручка (ВВ)
|
59438,9
|
38567,9
|
43589,5
|
28343,6
|
| Прибыль (П)
|
16642,9
|
4442,5
|
65384,2
|
3401,2
|
На основании этих данных рассчитываются финансовые коэффициенты, характеризующие кредитоспособность заемщиков: коэффициент абсолютной ликвидности (F
1
), промежуточный коэффициент покрытия (
F
2
),
общий коэффициент покрытия (
F
3
),
коэффициент финансовой независимости (
F
4
)
коэффициент рентабельности продукции (
F
5
).
Перечисленные коэффициенты являются критериями качества кредитоспособности предприятий и рассчитываются по следующим формулам:

Рассчитанные значения критериев качества для рассматриваемых предприятий приведены в табл. 4.2. Там же даны нормативные значения критериев. Анализ расчетных и нормативных значений критериев показывает, что все предприятия могут претендовать на получение кредита.
Таблица 4.2
Расчетные и нормативные значения критериев качества предприятий
| Критерий качества
|
Значение критерия для предприятия
|
Нормативное значение
|
| а1
|
a
2
|
a3
|
a4
|
| F1
|
0,154
|
0,102
|
0,084
|
0,140
|
0,1-0,25
|
| F2
|
1,297
|
0,71
|
0,59
|
0,57
|
0,5-1,0
|
| F3
|
2,78
|
2,27
|
1,86
|
1.27
|
1,0-2,5
|
| F4
|
0,75
|
0,72
|
0,71
|
0,68
|
0,6
|
| F
5
|
0,28
|
0,115
|
0,15
|
0,12
|
Чем выше, тем лучше
|
Обработка полученной исходной информации с применением математического аппарата теории нечетких множеств проводится в три этапа.
Этап 1. Построение функций принадлежности, соответствующих понятиям "предпочтительный коэффициент абсолютной ликвидности", "желаемый промежуточный коэффициент покрытия", "наилучший коэффициент рентабельности" и т. д. (рис. 4.3). Построение таких функций проводят эксперты, располагающие знаниями в области кредитования предприятий различного функционального назначения.
Этап 2. Определяются конкретные значения функции принадлежности по критериям качества F
1
, ...,
F
5
.
На рис. 4.3 показаны значения функций принадлежности, соответствующие рассматриваемым альтернативам. Нечеткие множества для пяти рассматриваемых критериев, включающие четыре анализируемые альтернативы, имеют следующий вид:
 = 0,61/0,154 + 0,41/0,102 + 0,33/0,084 + 0,46/0,140; = 0,61/0,154 + 0,41/0,102 + 0,33/0,084 + 0,46/0,140;
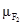 = 1,0/1,297 + 0,71/0,71 + 0,59/0,59 + 0,57/0,57; = 1,0/1,297 + 0,71/0,71 + 0,59/0,59 + 0,57/0,57;
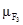 = 1,0/2,78 + 0,91/2,27 + 0,75/1,86 + 0,51/1,27; = 1,0/2,78 + 0,91/2,27 + 0,75/1,86 + 0,51/1,27;
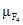 = 1,0/0,75 + 0,96/0,72 + 0,94/0,71 + 0,90/0,68; = 1,0/0,75 + 0,96/0,72 + 0,94/0,71 + 0,90/0,68;
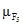 = 0,93/0,28 + 0,38/0,115 + 0,5/0,15 + 0,4/0,12. = 0,93/0,28 + 0,38/0,115 + 0,5/0,15 + 0,4/0,12.

Этап 3. Производится свертка имеющейся информации в целях выявления лучшей альтернативы. Множество оптимальных альтернатив В
определяется путем пересечения нечетких множеств, содержащих оценки альтернатив по критериям выбора.
Если критерии, по которым осуществляется выбор вариантов, имеют одинаковую важность для ЛПР, то правило выбора лучшего варианта имеет вид:
В
= F
1
Ç F
2
Ç F
3
Ç F
4
Ç F
5
.
Оптимальной считается альтернатива с максимальным значением функции принадлежности к множеству В.
Операция пересечения нечетких множеств соответствует выбору минимального значения для j
-й альтернативы:

Для рассматриваемой задачи множество оптимальных альтернатив будет формироваться следующим образом:
В =
{ min { 0,61; 1,0; 1,0; 1,0; 0,93 }
min { 0,41; 0,71; 0,91; 0,96; 0,38 }
min { 0,33; 0,59; 0,75; 0,94; 0,50 }
min { 0,46; 0,57; 0,51; 0,90; 0,40 }}.
Результирующий вектор приоритетов альтернатив имеет следующий вид:
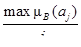 = max {0,61; 0,38; 0,33; 0,4}. = max {0,61; 0,38; 0,33; 0,4}.
Таким образом, лучшей альтернативой является а1
,
которой соответствует значение 0,61. На втором, третьем и четвертом местах находятся соответственно а4
®
0,4, а2
®
0,38, а3
®
0,33.
Выбор лучшего банка для размещения денежных средств физическим лицом
Цель решаемой задачи — выбор лучшего банка для размещения денежных средств физическим лицом. В отличие от предыдущего примера используемые для выбора критерии имеют различную значимость для ЛПР.
Было выбрано три банка: альтернативы а1
,
а2
; и a
3.
Определено шесть критериев выбора:
F
1
— процентная ставка (этот параметр может меняться для различных условий вклада в данном банке, однако задача будет решаться исходя из предположения, что ЛПР определился с условиями вклада и рассматривает альтернативы, удовлетворяющие этим условиям);
F
2
—
расположение банка;
F
3
—
активы банка;
F4
—
политика банка;
F
5
—
ликвидность банка (рассчитывается через коэффициент ликвидности Кл);
f
6
—
репутация банка (оценивается по экспертной шкале).
Значения критериев для всех альтернатив определены в табл. 4.3.
Таблица 4.3
Значения критериев для альтернатив
| Критерий
|
Альтернатива
|
| Банк a
1
|
Банк a2
|
Банк a3
|
| F
1
- процентная ставка, %
|
30
|
35
|
40
|
| F
2
-
расположение
|
Рядом с домом
|
В одном районе
|
В одном городе
|
| F
3
-активы банка, млн руб.
|
15
|
20
|
10
|
| F4
-
политика банка
|
Консервативная
|
Умеренная
|
Рискованная
|
| F
5
- ликвидность (Кл )
|
2
|
2,5
|
1,5
|
| F
6
- репутация (2,3,4,5)
|
5
|
4
|
3
|
Для каждой альтернативы определены конкретные значения, которые представлены следующими нечеткими множествами:
 = {0,05/30 + 0,25/35 + 0,4/40}; = {0,05/30 + 0,25/35 + 0,4/40};
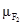 = {0,7/a1
+1,0/a2
+0,3/a3
}; = {0,7/a1
+1,0/a2
+0,3/a3
};
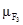 = {0,35/15 + 0,6/20 + 0,2/10}; = {0,35/15 + 0,6/20 + 0,2/10};
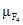 =
{0,25/a1
+ 0,7/a2
+ 0,3/a3
}; =
{0,25/a1
+ 0,7/a2
+ 0,3/a3
};
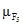 ={0,5/2+0,9/2,5+0,35/1,5}; ={0,5/2+0,9/2,5+0,35/1,5};
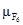 = {1,0/5+0,75/4+0,6/3}. = {1,0/5+0,75/4+0,6/3}.
На рис. 4.4 приведена экранная форма системы принятия решений на нечетких множествах, которая используется для ввода исходной информации о критериях и альтернативах.

Критерии имеют различную значимость при определении наиболее рационального варианта. В связи с этим необходимо определить весовые коэффициенты bi
критериев. Один из возможных способов получения значений весовых коэффициентов заключается в построении матрицы попарных сравнений критериев. Для критериев, использованных при решении задачи выбора лучшего банка, составлена следующая матрица:
| Выбор банка
|
F
1
|
F2
|
F3
|
F4
|
F5
|
F6
|
| F1
|
1
|
7
|
3
|
4
|
1/4
|
1/3
|
| F2
|
1/7
|
1
|
1
|
1/2
|
1/7
|
1/2
|
| F3
|
1/3
|
1
|
1
|
1/2
|
1/4
|
1/2
|
| F4
|
1/4
|
2
|
2
|
1
|
1/5
|
1
|
| F
5
|
4
|
7
|
4
|
5
|
1
|
3
|
| F
6
|
3
|
2
|
2
|
1
|
1/3
|
1
|
Весовой коэффициент критерия bi
определяется на основании вычисленных значений правого собственного вектора матрицы попарных сравнений ai
с последующим умножением на число критериев п.
bi
=
ai
n.
Значения ai
и bi
приведены в табл. 4.4.
Таблица 4.4
Собственный вектор матрицы полярных сравнений критериев и их весовые коэффициенты

Множество оптимальных альтернатив В
с учетом различной важности критериев качества определяется путем пересечения нечетких множеств следующим образом:

Найдем множество оптимальных альтернатив с учетом полученных весовых критериев:
В
= { min { 0,051,062
; 0,70,318
; 0,350,404
; 0,250,589
; 0,52,652
; 1,00,972
}
min { 0,251,062
; 1,00,318
; 0,60,404
; 0,70,589
; 0,92,652
; 0,750,972
}
min { 0,41,062
; 0,30,318
; 0,20,404
; 0,30,589
; 0,352,652
; 0,60,972
}}.
Множество оптимальных вариантов В
имеет вид:

Таким образом, лучшей альтернативой является банк а2
на втором месте банк a
3
самым худшим вариантом для вклада денег является банк а1
.
4.8.2. Выбор конкурентоспособного товара методом нечеткого отношения предпочтения
Под конкурентоспособностью понимают комплекс потребительских, стоимостных и социальных характеристик товара (изделия), определяющих его успех на данном рынке, т. е. способность данного товара быть обмененным на деньги на конкретном рынке в условиях широкого предложения к обмену других конкурирующих товаров-аналогов. Конкурентоспособность — это степень соответствия совокупности свойств объекта ценностной системе рынка. Границы понятия конкурентоспособность
непрерывно расширяются, переходя от конкурентоспособности изделия к конкурентоспособности предприятий и даже государств. Конкурентоспособность обеспечивается высоким технологическим уровнем и качеством, соответствием требованиям и стандартам стран-импортеров, фирм-покупателей, высоким уровнем технологического обслуживания, патентной чистотой и патентной защитой, приемлемой ценой, льготными условиями платежа и т. д.
Проанализируем ряд виброзащитных технологий для выявления наиболее конкурентоспособной на определенном международном рынке.
Защита современных транспортных систем, в частности автомобилей, от механических динамических воздействий обеспечивается виброизоляторами. Виброизоляторы являются комплектующими элементами, которые закупаются на рынке фирмами — производителями автомобилей. Разновидностей виброизоляторов достаточно много. Поэтому перед фирмами изготовителями, с одной стороны, и фирмами-покупателями — с другой, возникает проблема выбора наиболее рациональных элементов для производства и эксплуатации.
Задачу выбора рационального виброизолятора с учетом наиболее важных критериев качества рассмотрим на примере анализа четырех альтернатив: а1
—
пневматического виброизолятора; a
2
— металлического торсионного элемента, работающего на скручивание; a
3
— винтовой пружины; a
4
— резинового элемента.
Для оценки альтернатив используем восемь критериев качества:
F
1
— собственная частота колебаний виброизолятора (
f
,
Гц);
F
2
—долговечность элемента (Т,
лет);
F
3
— габаритный размер (
h
,
метр);
F
4
—
коэффициент передачи на резонансе (
Tz
,
безразмерные единицы);
F
5
—
устойчивость к механическим повреждениям (шкала экспертных оценок);
F
6
—
стоимость (тыс. руб.);
F
7
—
шумоизоляция (дБ);
F
8
— патентная чистота (условные единицы измерения).
На основании функций принадлежности всех альтернатив по восьми критериям определены их конкретные значения, которые представляют собой следующие нечеткие множества:

По этим данным составлены матрицы нечетких отношений предпочтения R
1
,
...,
R
8


Задача выбора решается в соответствии с описанной выше процедурой.
1. Строим нечеткое отношение Q
1
=
R
1
Ç R
2
Ç …Ç R8
:

Находим подмножество недоминируемых альтернатив на множестве {А,
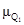 }: }:

по всем i
и j
(i
¹
j
):


2. Строим отношение Q
2
.

Коэффициенты wk
относительной важности критериев имеют следующие значения: w
1
= 0,23, w
2
= 0,09, w
3
= 0,04, w
4
= 0 23 w
5
= 0,04, w
6
= 0,09, w
7
=
0,23, w
8
= 0,04.
Определяем нечеткое отношение Q
2
.

Находим подмножество недоминируемых альтернатив множества [А,
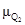 }: }:

по всем i
и j
(i
¹
j
):

3. Результирующее множество недоминируемых альтернатив есть пересечение множеств 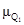 НД
и НД
и 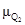 НД
: НД
:

4. Следовательно, рациональным следует считать выбор альтернативы a
1
имеющей максимальную степень недоминируемости.
4.8.3. Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера
Руководство фирмы рассматривает кандидатов на замещение вакантной должности бухгалтера. Задача заключается в том, чтобы, используя описанный выше метод, выявить наилучшего претендента. Обсуждение среди членов руководства фирмы дало следующий результат:
d
1
:
"Если кандидат имеет требуемые квалификацию, образование и опыт ведения бухгалтерского учета, то он — удовлетворяющий (отвечающий требованиям)";
d
2
:
"Если он вдобавок к вышеописанным требованиям умеет работать с современным программным обеспечением (ПО), то он — более чем удовлетворяющий";
d
3
:
"Если он дополнительно к условиям d
2
обладает необходимыми юридическими знаниями, то он — безупречный";
d
4
:
"Если он имеет все оговоренное в d
3
, кроме способности работать с современным ПО, то он — очень удовлетворяющий";
d
5
:
"Если кандидат имеет необходимую квалификацию, имеет опыт ведения бухгалтерского учета, обладает юридическими знаниями, но не имеет высшего образования, он все же будет удовлетворяющим";
d
6
:
"Если он не имеет квалификации и не имеет опыта ведения бухгалтерского учета, то он — неудовлетворяющий".
Анализ приведенных информационных фрагментов позволяет выявить шесть критериев, используемых для принятия решения:
Х1
—
квалификация; Х2
—
образование; Х3
,
— опыт ведения бухгалтерского учета; Х4
, —
умение работать с современным ПО; Х5
—
юридическая грамотность, Y
—
удовлетворительность.
Для формулирования правил следует определить возможные значения лингвистических переменных Xi
и Y,
которые будут использоваться для оценки кандидатов:
d
1
:
"Если Х1
= ПОДХОДЯЩЯЯ и X
2
= ВЫСШЕЕ, и Х3
= ДОСТАТОЧНЫЙ. то Y
= УДОВЛЕТВОРЯЮЩИЙ";
d
2
:
"Если Х1
= ПОДХОДЯЩАЯ и X
2
= ВЫСШЕЕ, и Х3
= ДОСТАТОЧНЫЙ, и X
4
= СПОСОБЕН, то Y
= БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ";
d
3
:
"Если Х1
= ПОДХОДЯЩАЯ и Х2
= ВЫСШЕЕ, и X
3
= ДОСТАТОЧНЫЙ, и Х4
=
СПОСОБЕН, и X
5
= ОБЛАДАЕТ, то Y
= БЕЗУПРЕЧНЫЙ";
d
4
:
"Если Х1
=
ПОДХОДЯЩАЯ и Х2
=
ВЫСШЕЕ, и Х3
=
ДОСТАТОЧНЫЙ, и X
4
=
ОБЛАДАЕТ, то Y
= ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ";
d
5
:
"Если Х1
= ПОДХОДЯЩАЯ и X
2
= НЕ ВЫСШЕЕ, и Х3
= ДОСТАТОЧНЫЙ, и X
5
= ОБЛАДАЕТ, то Y
= УДОВЛЕТВОРЯЮЩИЙ";
d
6
:
"Если Х1
= НЕ ИМЕЕТ и Х3
=
НЕДОСТАТОЧНЫЙ, то Y
= НЕУДОВЛЕТВОРЯЮЩИЙ".
Переменная Y
задана на множестве J
=
{0; 0,1; 0,2; ...; 1}.
Значения переменной Y
заданы с помощью следующих функций принадлежности:
S
=
УДОВЛЕТВОРЯЮЩИЙ определено как mS
(х) = х, х
Î J;
MS
=
БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ — как mMS
(
x
)=
Ö
x
;
x
Î
J
;

VS
=
ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ — как mVS
(
x
) = х2
,
x
Î
J
,
US
= НЕУДОВЛЕТВОРЯЮЩИЙ — как mVS
(
x
) =
1 - х, х
Î
J.
Выбор производится из пяти кандидатов на множестве U
= {
u
1
, и2
,
u
3
,
u
4
,
u
5
}.
В рассматриваемой задаче оценки кандидатов заданы следующими нечеткими множествами:
ПОДХОДЯЩАЯ (квалификация) А
= {0,8/u
1
, 0,61
u
2
, 0,5/
u
3
, 0,1/
u
4
, 0,3/
u
5
};
ВЫСШЕЕ (образование) В
= {0,5/
u
1
,1/
u
2
, 0/
u
3
, 0,5/
u
4
, 1/
u
5
};
ДОСТАТОЧНЫЙ (опыт) С = {0,6/
u
1
, 0,9/и2
, 1/
u
3
, 0,7/
u
4
, 1/
u
5
};
СПОСОБЕН (работать с ПО) D
= {1/
u
1
, 0,3/и2
, 1/
u
3
, 0/
u
4
, 0/
u
5
}',
ОБЛАДАЕТ (юридическими знаниями) Е =
{0/
u
1
, 0,5/
u
2
, 1/
u
3
, 0,8/
u
4
, 1/
u
5
}.
С учетом введенных обозначений правила d
1
, ...,
d
6
принимают вид:
d
1
:
“Если Х= А и В, и С,
то Y
=
S
”
;
d
2
:
"Если Х= А
и В,
и С
, и D,
то Y =
MS
":
d
3
: “
Если X
= А
и В,
и С
, и D
, и E
, то Y
= P
”
;
d
4
:
“
Если X
= А
и B
, и С,
и Е,
то Y
= VS
”
;
d
5
:
“Если X
= A
, и не В,
и С
, и E
, то Y
= S
”
;
d6
:
“Если Х
= не A
и не С
, то Y
= US
”
.
Вычислим функции принадлежности  для левых частей приведенных правил: для левых частей приведенных правил:
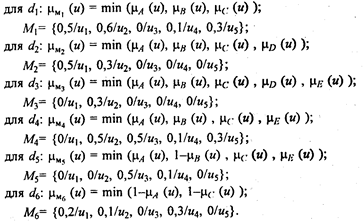
Теперь правила можно записать в виде:
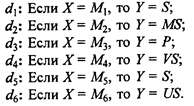
Используя для преобразования правил вида "Если Х
= М,
то Y
= Q
" импликацию Лукасевича mD
(u
, j
) = min(l, 1-mM
/(u
) + mY
(j
)), для каждой пары (
u
,
j
)
Î
U
х J
получаем следующие нечеткие отношения на U
´
J:


В результате пересечения отношений D
1
,
..., D
6
получаем общее функциональное решение:

Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой среде:
Ek
= Gk
° D
,
где Е
k
—
степень удовлетворения альтернативы k
;
Gk
—
отображение альтернативы k
в виде нечеткого подмножества на U
, в —
общее функциональное решение. Тогда

Кроме того, в этом случае 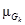 (u
) = 0;
u
¹
uk
, (u
) = 0;
u
¹
uk
,
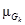 (u
) = 1; u
=
uk
. Отсюда (u
) = 1; u
=
uk
. Отсюда 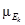 (i
) = (i
) = 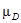 (uk
,
i
) Другими словами, Е
k
есть k-я
строка в матрице D.
Теперь применим описанную выше процедуру для сравнения нечетких подмножеств в единичном интервале для получения наилучшего решения на основе точечных оценок. (uk
,
i
) Другими словами, Е
k
есть k-я
строка в матрице D.
Теперь применим описанную выше процедуру для сравнения нечетких подмножеств в единичном интервале для получения наилучшего решения на основе точечных оценок.
Для первой альтернативы
E
1
={0,5/0; 0,6/0,1; 0,7/0,2; 0,8/0,3; 0,9/0,4; 1/0,5; 1/0,6; 1/0,7; 1/0,8; 0,9/0,9; 0,8/1}.
Вычисляем уровневые множества Ej
a
и мощность такого множества М(Е
a
)
по формуле

 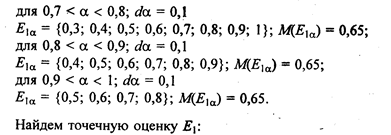

Аналогично находим точечные оценки для других альтернатив:
для второй альтернативы F
(
E
2
)
= 0,656;
для третьей — F
(
E
3
)
= 0,575;
для четвертой — F
(
E
4
)
= 0,483;
для пятой — F
(
E
5
) =
0,562.
В качестве лучшей выбираем альтернативу, имеющую наибольшую точечную оценку. В нашем примере это альтернатива и2
,
следовательно, она и будет наилучшей. Второе место занимает альтернатива u
3
;
третье – u
5
,
четвертое – и1
,
а самой худшей из альтернатив является u
4
.
Формализация знаний с помощью правил позволяет учитывать различную важность критериев и самих правил. Предположим, что в рассмотренной задаче ЛПР считает крайне важным умение кандидата на должность бухгалтера работать с программным обеспечением. Тогда в правилах d
2
и d
3
значением критерия Х4
будет понятие ОЧЕНЬ СПОСОБЕН, описываемое нечетким множеством D
1
следующего вида:

Правило d
4
исключим из рассмотрения, так как теперь кандидат, не владеющий умением работать с ПО, не является ОЧЕНЬ УДОВЛЕТВОРЯЮЩИМ. Тогда соответствующие левым частям правил нечеткие множества М
i
,
i
= 1, .... 6, i
¹ 4, будут иметь вид:


F(u1
)
—0,560; F(u2
)—
0,600; F(u3
)
—0,575; F(u4
)—
0,475; F(u5
)—
0,530.
Сравнение полученных результатов показывает, что с повышением значимости критерия Х4
ранжировка альтернатив несколько изменилась: и1
и u
5
поменялись местами. Этот факт согласуется с исходными данными, так как кандидат и1
имеет максимальное значение по критерию Х4
,
а u
5
-
минимальное.
Для учета различной важности правил будем использовать нормированные весовые коэффициенты, которые можно получить либо путем попарных сравнений, либо путем экспертного назначения весов.
В рассматриваемой задаче возможны различные подходы к выбору кандидата на должность: мягкий, жесткий, рациональный и т. д. Мягкий
подход обычно имеет место в условиях дефицита времени и квалифицированных кадров, основную директиву этого подхода можно сформулировать так: "лишь бы умел что-нибудь делать". При мягком подходе самый большой вес будет иметь правило d
6
а все остальные будут одинаково значимыми. Значения весовых коэффициентов правил приведены в табл. 4.5.
Жесткий
подход к выбору кандидата на должность возможен в случае избытка квалифицированных кадров и ресурса времени, отводимого для выбора. Целью такого подхода является поиск кандидата, наиболее соответствующего идеалу. Назначенные ЛПР экспертные оценки важности правил с использованием 10-балльной шкалы и соответствующие весовые коэффициенты приведены в табл. 4.5.
Таблица 4.5
Оценки важности правил
| Правило
|
d
1
|
d
2
|
d
3
|
d
4
|
d
5
|
d
6
|
| Мягкая экспертная оценка
|
2
|
2
|
2
|
2
|
2
|
10
|
| Коэффициент
|
0,6
|
0,6
|
0,6
|
0,6
|
0,6
|
3
|
| Жесткая экспертная оценка
|
2
|
3
|
10
|
3
|
2
|
0
|
| Коэффициент
|
0,6
|
0,9
|
3
|
0,9
|
0,6
|
0
|
Нечеткие отношения D
1
, ...,
D
6
,
возводятся в степени, соответствующие весовым коэффициентам правил, после чего выполняется их пересечение и получается общее решение D
.
При мягком подходе к принятию решения получены следующие точечные оценки альтернатив: F
(
u
1
) -
0,494; F
(
u
2
) -
0,533; Р(
u
3
) -
0,530; Р(
u
4
) -
0,437; Р(
u
5
) -
0,539. Полученные результаты можно интерпретировать следующим образом: наиболее предпочтительными кандидатами являются u
5
, и2
и u
3
,
за ними следует и1
,
а худшей альтернативой является u
4
.
Таким образом, при мягком подходе лучшие альтернативы становятся слабо различимыми, что выглядит естественно, поскольку все они являются неплохими кандидатами.
При жестком подходе множество точечных оценок альтернатив имеет вид: F
(
u
1
) -
0,555; F
(
u
2
) -
0,828; Р(
u
3
) -
0,549; Р(
u
4
)-
0,512; Р(
u
5
) -
0,558. Абсолютное предпочтение имеет кандидатура и2
,
на втором месте с очень близкими оценками находятся кандидаты u
5
и и1
,
на третьем – u
3
и на последнем – u
4
.
Нетрудно заметить, что при жесткой оценке ослабляются различия между претендентами, далекими от идеала.
Подход с использованием правил, имеющих одинаковую важность, можно считать усредненным,
или рациональным.
Рассмотренный метод принятия решений с использованием правил нечеткого вывода является адаптацией нечеткой логики к процессам принятия решений с исходными данными в виде точечных оценок. В ряде случаев оценивание альтернатив удобнее производить с использованием нечетких чисел, которые являются значениями лингвистических переменных. При этом правила могут применяться не одновременно, а последовательно. Такой подход к компьютерной поддержке процессов принятия решений используется в интеллектуальных системах с нечеткой логикой.
Рассмотрим решение задачи о выборе бухгалтера с использованием такой системы. Для этого введем следующие лингвистические переменные:
ОБРАЗОВАНИЕ (Высшее, Среднее)
ОПЫТ (Отсутствует, Приемлемый, Большой)
УМЕНИЕ РАБОТАТЬ С ПО (Есть, Нет)
ЮРИДИЧЕСКАЯ ГРАМОТНОСТЬ (Есть, Нет)
СПЕЦИАЛИСТ (Удовлетворяющий, Неудовлетворяющий)
КАНДИДАТ (Хороший, Очень хороший. Безупречный).
В скобках приведены возможные значения лингвистических переменных, каждое из которых представлено нечетким числом (множеством). Отношения между лингвистическими переменными задаются с помощью правил:
d
1
:
"Если ОБРАЗОВАНИЕ = Высшее или ОБРАЗОВАНИЕ = Среднее и ОПЫТ = Приемлемый или ОПЫТ == Большой, то СПЕЦИАЛИСТ = Удовлетворяющий, иначе СПЕЦИАЛИСТ = Неудовлетворяющий";
d
2
:
"Если СПЕЦИАЛИСТ = Удовлетворяющий и УМЕНИЕ РАБОТАТЬ С ПО = Есть, то КАНДИДАТ = Хороший";
d
3
:
"Если СПЕЦИАЛИСТ = Удовлетворяющий и ЮРИДИЧЕСКАЯ ГРАМОТНОСТЬ = Есть, то КАНДИДАТ = Очень хороший";
d
4
:
"Если СПЕЦИАЛИСТ = Удовлетворяющий и УМЕНИЕ РАБОТАТЬ С ПО = Есть, и ЮРИДИЧЕСКАЯ ГРАМОТНОСТЬ = Есть, то КАНДИДАТ = Безупречный".
Правила записываются в базу знаний интеллектуальной системы. В процессе решения задачи пользователем задаются исходные данные, которые представляют собой значения лингвистических переменных, соответствующих альтернативам. Обработка этих данных осуществляется посредством процедур нечеткого логического вывода. Результатами работы системы являются нечеткое множество, полученное для заданного кандидата, и мера его сходства с возможными исходами, т. е. нечеткими множествами:
СПЕЦИАЛИСТ (Удовлетворяющий);
СПЕЦИАЛИСТ (Неудовлетворяющий);
КАНДИДАТ (Хороший);
КАНДИДАТ (Очень хороший);
КАНДИДАТ (Безупречный).
Значения лингвистических переменных для альтернатив u
1
, ...,
u
5
приведены в табл. 4.6.
Таблица 4.6
Исходные данные для логического вывода
| Лингвистическая переменная
|
Альтернатива
|
| u1
|
u2
|
u3
|
u
4
|
u
5
|
| ОБРАЗОВАНИЕ
|
Среднее
|
Высшее
|
Не (Среднее или Высшее)
|
Среднее
|
Высшее
|
| ОПЫТ
|
Приемлемый
|
Большой
|
Большой
|
Приемлемый Ç Большой
|
Большой
|
| УМЕНИЕ РАБОТАТЬ C ПО
|
Есть
|
Нет
|
Есть
|
Нет
|
Нет
|
| ЮРИДИЧЕСКАЯ ГРАМОТНОСТЬ
|
Нет
|
Нет Ç Есть
|
Есть
|
Есть
|
Есть
|
На рис. 4.5 показан результат вывода с использованием правила d
1
для альтернативы u
1
.
На рис. 4.6 и 4.7 показаны экранные формы интеллектуальной программной системы нечеткого логического вывода, используемые для ввода исходной информации.


В табл. 4.7. приведены результирующие лингвистические оценки альтернатив, полученные методом нечеткого вывода, и соответствующие им значения мер сходства.
Таблица 4.7
Результаты работы системы нечеткого вывода
| Лингвистическая оценка
|
Альтернатива
|
| u
1
|
u2
|
u3
|
u4
|
u
5
|
| СПЕЦИАЛИСТ (Неудовлетворяющий)
|
0,08
|
0,0
|
0,30
|
0,21
|
0,10
|
| СПЕЦИАЛИСТ (Удовлетворяющий)
|
0,85
|
0,95
|
0,32
|
0,69
|
0,97
|
| КАНДИДАТ (Хороший)
|
0,81
|
0,0
|
0,30
|
0,0
|
0,0
|
| КАНДИДАТ (Очень хороший)
|
0,0
|
0,74
|
0,28
|
0,57
|
0,91
|
| КАНДИДАТ (Безупречный)
|
0,0
|
0,0
|
0,22
|
0,0
|
0,0
|
Полученные результаты позволяют увидеть, что кандидаты u
1
, u
2
, u
4
,
u
5
являются удовлетворяющими специалистами (мера сходства больше 0,5), а кандидат u
3
почти с одинаковым значением меры сходства принадлежит ко всем возможным категориям. При этом значения меры сходства находятся в интервале (0,22 - 0,32), что свидетельствует о весьма слабом сходстве с соответствующими понятиями. Такие результаты скорее следует интерпретировать как неспособность данного объекта вписаться в рамки имеющихся градаций при сформулированном наборе правил, чем как свойство быть похожим на все категории одновременно. Альтернатива u
1
хорошо согласуется с понятием хорошего кандидата, а u
2
и u
5
—
с понятием очень хорошего кандидата. Альтернатива u4
также претендует на роль очень хорошего кандидата, однако сходство с соответствующим нечетким прототипом имеет весьма невысокое.
4.8.4. Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки
Рассмотрим пример применения метода аддитивной свертки для решения задачи по выбору некоторой фирмой, производящей бытовую технику, стратегии расширения своей доли на рынке.
Первоначально определяются альтернативы — возможные стратегии поведения фирмы.
Стратегия а1
—
снижение цены. Это возможно в том случае, когда фирма имеет некоторое преимущество перед конкурентами или может обеспечить снижение себестоимости продукции. Однако реализация этой стратегии может привести к ценовой конкуренции, что само по себе достаточно опасно,
Стратегия а2
—
модификация существующего продукта. Она потребует дополнительных расходов на переналадку производства, но при этом обеспечит некоторое повышение качества продукции. Реализация такой стратегии может привлечь новых покупателей, способствуя новому перераспределению долей рынка между фирмами. Конкуренция в данном случае не является ценовой и столь сильной.
Стратегия а3
—
разработка нового продукта. Эта стратегия потребует дополнительных и значительных расходов, но позволит в случае успеха опередить конкурентов в технологическом развитии и некоторое время быть монополистом на рынке.
Стратегия а4
—
поиск новых рынков сбыта. В этом случае фирма за счет поиска новых рынков и вхождения на них может увеличить объем продаж, но это не повлечет за собой перераспределение старого рынка. При такой стратегии также достаточно велика вероятность возникновения сильной конкурентной борьбы и возрастания расходов на маркетинговые исследования и новые производственные мощности.
Для оценки альтернатив определим следующие критерии:
c
1
— затраты на расширение производства; c
2
— время реализации проекта; c
3
— затраты на маркетинговые исследования; с4
—
управленческие расходы; с5
—
риск от потерь; c
6
— срок окупаемости; c
7
—
качество продукции; c
8
— цена продукции.
Для оценки относительной важности критериев используется лингвистическая переменная W
= {ПРАКТИЧЕСКИ НЕВАЖНЫЙ; НЕ ОЧЕНЬ ВАЖНЫЙ; ДОВОЛЬНО ВАЖНЫЙ; ВАЖНЫЙ; ОЧЕНЬ ВАЖНЫЙ}. Значения термов множества заданы нечеткими числами, которые имеют треугольный вид функций принадлежности (рис. 4.8).

Критерии получили следующие лингвистические оценки относительной важности a = {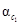 = ВАЖНЫЙ; = ВАЖНЫЙ; 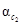 =
ДОВОЛЬНО ВАЖНЫЙ; =
ДОВОЛЬНО ВАЖНЫЙ; 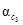 = НЕ ОЧЕНЬ ВАЖНЫЙ; = НЕ ОЧЕНЬ ВАЖНЫЙ; 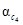 = ВАЖНЫЙ; = ВАЖНЫЙ; 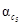 = НЕ ОЧЕНЬ ВАЖНЫЙ; = НЕ ОЧЕНЬ ВАЖНЫЙ; 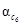 = ДОВОЛЬНО ВАЖНЫЙ; = ДОВОЛЬНО ВАЖНЫЙ; 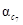 = ВАЖНЫЙ; = ВАЖНЫЙ; 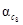 = НЕ ОЧЕНЬ ВАЖНЫЙ}. = НЕ ОЧЕНЬ ВАЖНЫЙ}.
Оценка альтернатив по критериям производится с использованием лингвистической переменной S
== "УДОВЛЕТВОРИТЕЛЬНОСТЬ" = {КРАЙНЕ НИЗКАЯ; НИЗКАЯ; СРЕДНЯЯ; ВЫСОКАЯ; ОЧЕНЬ ВЫСОКАЯ}. Функции принадлежности термов имеют следующий вид:
КРАЙНЕ НИЗКАЯ = {1,0/0,0; 0,0/0,0};
НИЗКАЯ = {0,0/0,0; 1,0/0,2; 0,0/0,4};
СРЕДНЯЯ = {0,0/0,3; 1,0/0,5; 0,0/0,7};
ВЫСОКАЯ = {0,0/0,6; 1,0/0,8; 0,0/1,0};
ОЧЕНЬ ВЫСОКАЯ = {0,0/0,8; 1,0/1,0};
В табл. 4.8 сведены оценки рассматриваемых альтернатив.
Таблица 4.8
Оценка удовлетворительности альтернатив относительно критериев
| Критерий
|
Оценка альтернативы
|
| а1
|
a2
|
a3
|
a4
|
| c1
|
Средняя
|
Средняя
|
Низкая
|
Крайне низкая
|
| c
2
|
Высокая
|
Высокая
|
Средняя
|
Низкая
|
| c
3
|
Высокая
|
Высокая
|
Низкая
|
Крайне низкая
|
| c
4
|
Высокая
|
Низкая
|
Низкая
|
Средняя
|
| c
5
|
Низкая
|
Очень высокая
|
Высокая
|
Средняя
|
| c
6
|
Средняя
|
Средняя
|
Высокая
|
Высокая
|
| c
7
|
Высокая
|
Низкая
|
Низкая
|
Средняя
|
| c
8
|
Высокая
|
Средняя
|
Средняя
|
Средняя
|
Аддитивная свертка представленной информации дала следующий результат:
mJ
(j
) =
{1,0/a1
; 0,75/a2
; 0,68/a3
; 0,58/а
4
}.
что позволяет считать лучшей альтернативой стратегию по снижению цены а1
.
4.
8.5. Выбор предприятия для кредитования методом лингвистических векторных оценок
Решается задача выбора из трех альтернативных предприятий наиболее платежеспособного в целях предоставления кредита. Оценка альтернатив (а
i
) проводится по следующим критериям: с1
—
общая ликвидность; с2
— обеспеченность собственными средствами; с3
— восстанавливаемость платежеспособности.
Сформируем векторный критерий С = {c
1
, с2
,
c
3
}. Оценки возможных исходов по критериям сi
представлены нечеткими числами, заданными на базовом множестве Х
= {1, 2, 3, ..., 10}. Множество лингвистических оценок TS
= {ОН (очень низкий); Н (низкий); С (средний); В (высокий); OВ (очень высокий)}. Функции принадлежности термов имеют вид:
ОН = {1,0/1; 0,8/2; 0,2/3};
Н= {0,8/1; 0,9/2; 0,5/3; 0,2/4};
С = {0,3/3; 0,7/4; 1,0/5; 0,8/6; 0,2/7};
В = {0,2/7; 0,5/8; 0,9/9; 0,8/10};
ОВ = {0,2/8; 0,8/9; 1,0/10}.
Лингвистические векторные оценки альтернатив заданы матрицей:

Суть данной методики заключается в вычислении оценки предпочтительности каждой из альтернатив относительно других. При этом, как и в случае максиминной свертки, сначала вычисляются наихудшие оценки для каждой альтернативы (m<
), а после этого обратные им отношения предпочтительности (m³
), среди которых выбирается максимальное.
Вычислим степень предпочтительности для альтернативы а1
:


Аналогично находятся суммы по критериям c
2
и c
3
. Функция принадлежности m<
(a
1
) вычисляется следующим образом:

Теперь вычислим нечеткое отношение m³
(
a
1
):
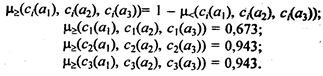
Степень предпочтительности альтернативы а1
равна минимальному из приведенных значений, т. е, m³
(
a
1
)
= 0,673. Для альтернативы а2
получены следующие оценки:

Степень предпочтительности m³
(
a
2
)
= 0,462.
Соответственно для а3
.
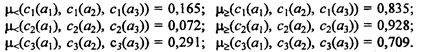
Степень предпочтительности m³
(
a
3
)
= 0,709. Лучшей считается альтернатива, имеющая максимальную степень предпочтительности, т. е. a
3
.
4.8.6. Сравнительный анализ различных методов принятия решений
Теория нечетких множеств, предложенная Л. Заде в 1961 г., к настоящему времени приобрела широкую популярность и получила практическое применение во многих отраслях знаний. В сфере принятия решений на базе этой теории разработан широкий спектр разнообразных методов, только небольшая часть из которых рассмотрена в настоящей книге. Нелегкой проблемой сегодняшнего дня является выбор подходящего метода или программного обеспечения для поддержки процессов принятия решений. Поэтому особую актуальность приобретают проведение сравнительного анализа различных методов и разработка рекомендаций по их применению.
Рассмотрим подходы к решению одной задачи многокритериального выбора в условиях неопределенности с использованием различных методов. При этом будем использовать исходную информацию, полученную от одного и того же высококвалифицированного эксперта. Ранее были рассмотрены задачи в условиях одинаковой и различной важности критериев. Последняя ситуация является более общей, поэтому будем решать задачу в условиях неодинаковой значимости критериев.
Анализ и оценка инвестиционных проектов — одна из самых сложных задач в сфере экономики, производства и управления. Ее сложность обусловлена, с одной стороны, значительной неопределенностью, так как при решении вопроса об инвестициях всегда нужно предвидеть будущее, и с другой стороны — наличием множества заведомо противоречивых критериев. Человеку (ЛПР) свойственно желать получения максимальной прибыли при минимальных затратах, чего, как известно, никому не удавалось достигнуть, поскольку минимальные затраты равны нулю. При решении подобных задач в условиях определенности целевая функция строится на основе независимых, а следовательно, и непротиворечивых критериев. Однако в условиях неопределенности анализ решений производится на основе вербальной экспертной информации, элементы которой могут противоречить друг другу. При этом результаты анализа решений, полученные любыми методами, теряют свою ценность, так как точность и достоверность результата вычислений никогда не могут превзойти точности и достоверности исходных данных.
Итак, инвестор должен осуществить выбор одного из трех проектов: а1
—
проект технологического комплекса для термического обезвреживания и переработки отходов; а2
—
проект завода по производству аэрозольных огнетушителей третьего поколения; a
3
— проект создания инвестиционно-финансовой компании.
Задача анализа проектов может иметь большое количество постановок в зависимости от целей, которые стоят перед инвестором, от объема его финансовых ресурсов, от его склонности к риску, от окружающей обстановки и возможных прогнозов на будущее.
В данном случае главной целью ЛПР является выбор рационального инвестиционного проекта. При этом объем финансовых ресурсов инвестора ограничен, он не склонен к большому риску и имеет не самые худшие виды на будущее. Для выбора сформирован следующий набор критериев: с1
—
рентабельность; с2
—
оценка возможных рынков сбыта; c
3
— первоначальные средства; c
4
—
производственный риск; с5
—
инвестиционный риск. Рациональный выбор связан со стремлением получить решение, характеризующееся приемлемыми оценками по всем критериям, хотя их значимость для ЛПР может быть различной. Примерами альтернативных постановок могут служить задачи выбора проекта с максимальной прибылью или с минимальным риском.
Прежде чем рассматривать решение данной задачи разными методами, дадим характеристику критериев и альтернатив.
Характеристика критериев
Рентабельность инвестиций (
PI
) —
это показатель, позволяющий определить, в какой мере возрастает ценность фирмы (богатство инвестора) в расчете на один рубль инвестиций. Рентабельность показывает меру устойчивости проекта и рассчитывается по формуле

где CFt
—
поступление денежных средств в конце периода t
;
k
—
коэффициент дисконтирования;
I
0
—
первоначальное вложение средств.
При оценке рынков сбыта
учитываются следующие факторы:
- доля рынка, которую в принципе можно захватить;
- потенциальная емкость рынка (общая стоимость товаров, которые покупатели определенного региона могут купить за определенный промежуток времени);
- прогнозируемый объем продаж;
- оценка возможных конкурентов.
Первоначальные средства —
складываются из расходов на строительство и оснащение оборудованием инвестируемых объектов, на подготовку капитального строительства и на дополнительные оборотные средства.
Производственный риск—
связан с возможностью невыполнения фирмой своих обязательств перед заказчиком. Оценка этого показателя зависит от множества факторов риска, которые имеют место на различных стадиях реализации проекта. На подготовительной стадии выделяют следующие риски: удаленность от инженерных сетей, отношение местных властей, доступность подрядчиков на месте и т. д. На стадии строительства отмечают неплатежеспособность заказчика, непредвиденные затраты, в том числе и из-за инфляции, недостатки проектно-изыскательских работ, несвоевременную поставку комплектующих, недобросовестность подрядчика. На стадии функционирования главными рисками считаются: финансово-экономические, социальные, технические, экологические.
Инвестиционный риск —
вызван возможным обесцениванием инвестиционно-финансового портфеля, состоящего из собственных и приобретенных ценных бумаг. Основными составляющими инвестиционного риска являются политический, экономический, социальный, экологический и криминальный риски.
Описание альтернатив
1. Проект по созданию технологии и оборудования для термического обезвреживания и переработки отходов (a
1
). В данном проекте предлагается метод переработки отходов, основанный на их последовательной термической и электрошлаковой обработке. В результате переработки отходов получается шлак — пирозит, который может быть использован в дорожном строительстве, при изготовлении химически стойких облицовочных футеровочных плиток, а также при изготовлении бетона.
Срок реализации проекта 12 месяцев. Срок окупаемости проекта 2—3 года. Требуемый объем инвестиций — 0,4 млн долл. Рассчитанная рентабельность инвестиций составляет 4,362. Ожидаемая прибыль без учета налогов после реализации проекта — 322 000 долл. в год.
Ожидаемый рынок: внутренний рынок России и стран СНГ.
Подготовка и реализация проекта связана с достаточно высокой степенью производственного риска и невысокой степенью инвестиционного риска.
2. Проект по созданию производства аэрозольных огнетушителей третьего поколения (a
2
). В данном проекте предлагается создание производства безопасных для человека огнетушителей АПГ-Зп с беспламенным составом, которые могут работать во взрывоопасных средах. Такие огнетушители могут применяться на производстве и при транспортировке легковоспламеняющихся жидкостей (бензин, ацетон, спирт), на автомобильном и железнодорожном транспорте, на судах морского и речного флотов, на любых электроустановках. Аэрозоль, входящий в состав огнетушителя, не портит помещения, оборудования, мебели и продуктов питания.
Первоначальные инвестиции - 0,28 млн долл.
Срок реализации проекта 12 месяцев.
Срок окупаемости проекта 2 года.
Рентабельность инвестиций составляет 1,62.
Ожидаемая прибыль без учета налогов после реализации проекта — 450 000 долл. в год.
Ожидаемый рынок: внутренний и внешний рынки.
Подготовка и реализация проекта связана с очень высокой степенью производственного риска и средней степенью инвестиционного риска.
3. Проект создания инвестиционно-финансовой компании (a
3
). Компания организовывается для работы по следующим направлениям: доверительное управление имуществом, повышение ликвидности товарно-материальных ценностей, управление дебиторскими задолженностями, консультации и услуги по ценным бумагам.
Первоначальные инвестиции - 0,1 млн долл.
Рентабельность инвестиций составляет 41,62.
Ожидаемая прибыль без учета налогов после реализации проекта — 2 млн долл. в год.
Ожидаемый рынок: часть регионов России.
Подготовка и реализация данного проекта связана с низкой степенью производственного риска и очень высокой степенью инвестиционного риска.
Решение задачи методом максиминной свертки
Оценки альтернатив по заданным критериям представлены следующими нечеткими множествами:

Весовые коэффициенты важности рассматриваемых критериев определены с использованием процедуры парного сравнения и имеют следующие значения:
b = {1,78; 0,68; 0,67; 0,22; 1,65}.
Наиболее важными критериями для ЛПР являются рентабельность и инвестиционный риск, существенно менее важными — размер вложений и оценка рынков, самым меньшим весом обладает производственный риск.
Лучшая альтернатива определяется следующим образом:

Множество оптимальных альтернатив имеет вид:
mD
(a
) = {0,781/a1
; 0,432/a2
; 0,588/a3
}.
Максимальное значение принадлежит а1
,
на втором месте находится a
3
,
а худшей альтернативой является а2
.
Решение задачи с использованием метода отношений предпочтения
На основании функций принадлежности (4.3) построены следующие отношения предпочтения на множестве альтернатив:

Множество недоминируемых альтернатив 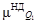 = ||1 1 1||. Значение нормированных на единицу весовых коэффициентов критериев заданы вектором w
= {0,36; 0,14; 0,13; 0,05; 0,32}. Вычислим нечеткое отношение Q
2
: = ||1 1 1||. Значение нормированных на единицу весовых коэффициентов критериев заданы вектором w
= {0,36; 0,14; 0,13; 0,05; 0,32}. Вычислим нечеткое отношение Q
2
:

Находим подмножество недоминируемых альтернатив множества
{А,
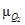 }:
}:
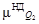 (а
i
)
= || 0,83 0,69 1 ||. Результирующее множество недоминируемых альтернатив — это пересечение множеств (а
i
)
= || 0,83 0,69 1 ||. Результирующее множество недоминируемых альтернатив — это пересечение множеств 

Следовательно, рациональным следует считать выбор альтернативы а3
, имеющей максимальную степень недоминируемости.
Решение задачи с применением нечеткого логического вывода
На основании приведенных выше исходных данных о критериях и альтернативах экспертом сформулированы правила:
d
1
:
"Если с1
= ВЫСОКАЯ, и с2
= ХОРОШАЯ, и с3
=
ПРИЕМЛЕМЫЕ, то Y
= УДОВЛЕТВОРИТЕЛЬНЫЙ";
d
2
:
"Если c
1
= ОЧЕНЬ ВЫСОКАЯ, и c
2
=
ХОРОШАЯ, и c
3
= ПРИЕМЛЕМЫЕ, и c
4
= НИЗКИЙ, и c
5
= ОЧЕНЬ НИЗКИЙ, то Y
= БЕЗУПРЕЧНЫЙ";
d
3
:
"Если c
1
= НИЗКАЯ, и c
2
= ПЛОХАЯ, и с3
= ВЫСОКИЙ, то Y
= НЕУДОВЛЕТВОРИТЕЛЬНЫЙ".
Переменная Y
задана на множестве J
=
{0; 0,1; 0,2; ...;
1}.
Значения переменной Y
заданы с помощью следующих функций принадлежности:
S
= УДОВЛЕТВОРИТЕЛЬНЫЙ, mS
(
x
)
=х,х
Î
J;
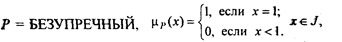
US
=
НЕУДОВЛЕТВОРИТЕЛЬНЫЙ, mUS
(
x
)
= 1-х, x
Î J
. В рассматриваемой задаче оценки инвестиционных проектов заданы следующими нечеткими множествами:
ВЫСОКАЯ (рентабельность) А
= {0,5/а1
; 0,1/а2
; 1/а3
};
ОЧЕНЬ ВЫСОКАЯ (рентабельность)  (
a
)
= (
a
)
=  (
a
); (
a
);
НИЗКАЯ (рентабельность)  (
a
)
= 1 — (
a
)
= 1 — 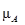 (
a
)
; (
a
)
;
ХОРОШАЯ (оценка рынков сбыта) В
= {0,7/a
1
, 0,5/а2
,
0,2/a
3
};
ПЛОХАЯ (оценка рынков сбыта) 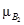 (
a
)
= 1 - (
a
)
= 1 - 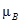 (
a
) (
a
)
ПРИЕМЛЕМЫЕ (первичные средства) G
=
{0,3/a
1
, 0,5/a
2
,1/a
3
};
НИЗКИЙ (производственный риск) D
=
{0,5/a
1
, 0,3/а2
,
0,9/a
3
};
НИЗКИЙ (инвестиционный риск) Е
= {0,6/a
1
, 0,4/а2
,
0,2/a
3
}
ОЧЕНЬ НИЗКИЙ (инвестиционный риск) 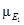 (
a
)
= (
a
)
= 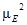 (
a
)
; (
a
)
;
ВЫСОКИЙ (инвестиционный риск) 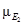 (
a
) =
1- (
a
) =
1- 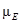 (
a
). (
a
).
Дополнительные градации лингвистических оценок (со словом ОЧЕНЬ) предназначены для учета наиболее важных критериев. В данном случае это рентабельность (c
1
) и инвестиционный риск (c
5
).
С учетом введенных обозначений правила d
1
, ...,
d
3
принимают вид:
Функции принадлежности 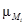 для левых частей приведенных правил имеют вид: для левых частей приведенных правил имеют вид:
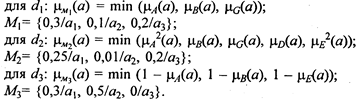
Правила приобретут следующий вид:
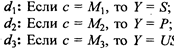
Используя для преобразования правил импликацию Лукасевича, получим нечеткие отношения D
1
, ...
D
3
на U
x
J
и в результате их пересечения функциональное решение D
:

Для альтернатив вычислены следующие точечные оценки:
F(a1
)
= 0,500; F(a2
)
= 0,431; F(a3
)
= 0,600. Максимальную оценку имеет третья альтернатива, следовательно, она является наиболее предпочтительной.
Решение задачи методом аддитивной свертки
Важность критериев была задана нечеткими числами с функциями принадлежности следующего вида:
ВАЖНЫЙ (В)— mB
={0,4; 1/0,7; 0/1};
ОЧЕНЬ ВАЖНЫЙ (OB) — mOB
={0/0,7; 1/1};
НЕ ОЧЕНЬ ВАЖНЫЙ (НОВ) — mHOB
= {0/0,1; 1/0,4; 0/7}.
Для оценки альтернатив использовались лингвистические значения:
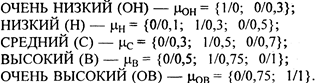
Альтернативы получили следующие оценки по критериям:

Взвешенные оценки альтернатив Ri
имеют следующие функции принадлежности:

Оценки предпочтительности альтернатив равны: m(
a
1
)
= 0,90, m(
a
2
)
= 0,62, m(
a
3
)
= 1,0. Лучшей альтернативой является a
3
, a худшей – а2
.
Решение задачи методом анализа иерархий
На заданном наборе критериев была построена трехуровневая иерархия, на верхнем уровне которой определена цель выбора (с
G
).
На втором уровне находятся обобщенные критерии: прибыль (с
P
) к
и риск (с
R
)
. На третьем уровне иерархии расположены перечисленные выше критерии с1
, ..., с5
.
При этом критерии c
1
, с2
, с3
,
входят в группу критерия cP
,
а критерии с4
, с5
—
в группу критерия cR
. Экспертные предпочтения и полученные приоритеты приведены в матрицах попарных сравнений:

В результате иерархического синтеза получены векторы приоритетов альтернатив:

Альтернативой с наименьшим риском является а1
, а
наибольшую прибыль обеспечивает а3
.
Эта же альтернатива имеет максимальный приоритет относительно цели выбора.
Сравнение полученных результатов
На рис. 4.9 приведены результаты решения задачи выбора рационального инвестиционного проекта, полученные различными методами.

Несмотря на то, что исходная информация во всех рассмотренных примерах является последовательной и непротиворечивой, полученные результаты заметно отличаются. Кроме описанных выше нечетких методов принятия решений, для сравнения использовался метод анализа иерархий, который обычно дает результаты, хорошо согласующиеся с интуитивными представлениями экспертов при рациональном подходе к принятию решений.
Несовпадение результатов, полученных разными методами, объясняется, с одной стороны, разными способами представления экспертной информации, а с другой стороны — различием подходов к принятию решений. Так, в основу метода анализа иерархий и метода отношений предпочтения заложен рационально-взвешенный подход, основанный на попарных сравнениях объектов и нормированных весовых коэффициентах. Максиминная свертка и лингвистическая векторная оценка являются реализациями пессимистического подхода, игнорирующего хорошие стороны альтернатив, когда лучшей считается альтернатива, имеющая минимальные недостатки по всем критериям. Аддитивная свертка предполагает оптимистический подход, когда низкие оценки по критериям имеют одинаковый статус по сравнению с высокими. Нечеткий вывод на правилах реализует эвристический подход.
Анализ приведенных результатов позволяет сделать следующие выводы:
1. Методы принятия решений на нечетких моделях позволяют удобно и достаточно объективно производить оценку альтернатив по отдельным критериям. В отличие от других методов добавление новых альтернатив не изменяет порядок ранее ранжированных наборов. При оценке альтернатив по критериям возможна как лингвистическая оценка, так и оценка на основе точечных оценок с использованием функций принадлежности критериев.
2. Основной проблемой многокритериального выбора с применением нечетких моделей является представление информации о взаимоотношениях между критериями и способы вычисления интегральных оценок. Методы, базирующиеся на разных подходах, дают различные результаты. Каждый подход имеет свои ограничения и особенности, и пользователь должен получить о них представление, прежде чем применять тот или иной метод принятия решений. Наиболее широкие возможности для представления информации дает эвристический подход.
3. Большинство нечетких методов принятия решений показывает слабую устойчивость результатов относительно исходных данных. Исследование рассмотренных методов показало, что наибольшей устойчивостью обладает метод, основанный на правилах.
Анализ нечетких методов принятия решений позволяет сформулировать требования к дальнейшим разработкам в этой области. Это развитие теоретических подходов к описанию сложных взаимоотношений между критериями, более широкое применение интеллектуальных методов на основе нечеткой логики, а также развитие комбинированных методов принятия решений с использованием нечетких представлений.
Основные понятия
1. Нечеткие множества.
2. Нечеткие числа.
3. Лингвистические переменные.
4. Лингвистический критерий.
5. Лингвистическая оценка.
6. Нечеткие операции и отношения.
7. Нечеткие отношения предпочтения.
8. Максиминная свертка нечетких множеств.
9. Нечеткий логический вывод.
10. Композиционное правило вывода.
11. Методология применения методов теории нечетких множеств.
12. Сравнительный анализ методов.
13. Практические результаты применения методов принятия решений.
Контрольные вопросы и задания
1. Перечислите и дайте определения основным элементам теории нечетких множеств.
2. Дайте определение нечетким операциям, отношениям и свойствам отношений.
3. Охарактеризуйте постановку задачи многокритериального выбора альтернатив на основе пересечения нечетких множеств.
4. Составьте алгоритмы и программы многокритериального выбора альтернатив методом максиминной свертки.
5. Постановка задачи выбора альтернатив на основе нечеткого отношения предпочтения.
6. Разработайте алгоритмы и программы для решения задачи многокритериального принятия решений на основе нечеткого отношения предпочтения.
7. Постановка задачи выбора альтернатив с аддитивным критерием.
8. Разработайте алгоритмы и программы для решения задачи многокритериального принятия решений на основе аддитивной свертки предпочтений, заданных нечеткими числами.
9. Постановка задачи принятия решений на основе лингвистической векторной оценки.
10. Разработайте алгоритмы и программы для решения задачи многокритериального выбора с использованием метода лингвистического векторного критерия.
11. Постановка задачи многокритериального выбора с использованием правила нечеткого вывода.
12. Разработайте алгоритмы и программы для решения задачи выбора рациональной альтернативы на основе математического аппарата нечеткого логического вывода.
13. Рассмотрите применение принципов пересечения нечетких множеств в экономических и управленческих задачах принятия решений.
14. Разработайте методику применения метода нечеткого отношения предпочтения для проектирования и выбора конкурентоспособных экономических, технических и управленческих решений.
15. Поставьте задачи из области экономики, наилучшим образом формализуемые математическим аппаратом нечеткого логического вывода.
16. Решите одну задачу различными методами принятия решений, основанными на теории нечетких множеств. Проведите сравнительный анализ полученных результатов. Сделайте вывод о том, какой из методов дает наиболее адекватные результаты в сравнении с вашими представлениями.
Литература
1. Заде Л.
Понятие лингвистической переменной и его применение к принятию приближенных решений: Пер. с англ. — М.: Мир, 1976. — 165 с.
2. Нечеткие множества и теория возможностей. Последние достижения: Пер. с англ. — М.: Радио и связь, 1986. — 408 с.
3. Борисов А. П., Крумберг О. А., Федоров И. П
.
Принятие решений на основе нечетких моделей. — Рига: Зинатне, 1990. — 184 с.
4. Нечеткие множества в моделях управления и искусственного интеллекта/Под ред. Д. А. Поспелова. — М.: Наука, 1986. — 312 с.
Глава 5.
МЕТОДЫ
КОМБИНАТОРНО-МОРФОЛОГИЧЕСКОГО АНАЛИЗА И СИНТЕЗА
РАЦИОНАЛЬНЫХ СИСТЕМ
Методы комбинаторно-морфологического анализа и синтеза предназначены для поиска новых решений на основе разделения рассматриваемой системы на подсистемы и элементы, формирования подмножеств альтернативных вариантов реализации каждой подсистемы, комбинирования различных вариантов решения системы из альтернативных вариантов реализации подсистем, выбора наилучших вариантов решения системы.
Под морфологией здесь понимается структурная форма системы, организованная в соответствии с ее функциями.
Термин морфологический анализ
очень стар и прослеживается от Раймонда Луллия (1235 — 1315 гг.). Луллием была выдвинута идея, названная "Великое искусство", в соответствии с которой путем систематической комбинации относительно небольшого числа принципов возникает возможность разрешить все проблемы философии и метафизики. Однако у Луллия не было вычислительной машины, чтобы использовать все комбинации принципов.
Изучив "Великое искусство" Луллия, Декарт увидел в этом опасность механизации мышления. Он писал: "В молодости из философских наук я немного изучал логику..., но, изучив ее, я заметил, что в логике ее силлогизмы... скорее помогают объяснить другим то, что нам известно, или даже, как в искусстве Луллия, бестолково рассуждать о том, чего не знаешь, вместо того, чтобы изучать это."
Напротив, Лейбниц был верным приверженцем "Искусства" Луллия и говорил о нем с гордостью в своей "Диссертации о комбинаторике", в которой дал обобщение комбинаторному методу.
Повод для отрицательной оценки метода Луллия дали его последователи в XVII и XVIII вв. Так, Свифт в "Путешествии Гулливера" в юмористической манере описывает механическое приспособление, которое случайным образом комбинировало буквы и таким образом "позволило самым невежественным людям писать книги без всякой помощи таланта или науки". Таким образом, "Искусство" Луллия мало-помалу было предано забвению, несмотря на всю его потенциальную ценность. В то же время критика Свифта помогла определить, чем является морфологический анализ. Морфологический анализ никогда не будет чудодейственным средством или развитием идей. Фактически морфологический анализ
есть метод развития творческих способностей, или, точнее, систематическое вспомогательное средство для творчества. Он совершенно не исключает творческого труда человека, а стимулирует его и расширяет его возможности, распространяя на большее . число идей, чем это было бы возможно при более классическом подходе.
Метод морфологического исследования реализуется в два качественно различных этапа [1]. Первый этап предполагает получение описания всех систем, принадлежащих к исследуемому классу, т. е. классифицирование множества систем. Этот этап решения задачи называется морфологическим анализом.
На втором этапе проводятся оценка описаний различных систем исследуемого класса и выбор тех из них, которые в том или ином приближении соответствуют условиям задачи. Этот этап решения называется морфологическим синтезом,
так как в итоге получается целостное описание всей исследуемой системы из частей описания подсистем и отношений между ними.
Подходы и методы синтеза вариантов систем в метризованном морфологическом пространстве развиты в работе [2]. В ней также сформулированы и обсуждены аксиомы метрики в морфологическом пространстве, установлена единственность метрики, удовлетворяющая этим аксиомам.
Ниже будут рассмотрены морфологические методы исследования новых рациональных систем, развитые для реализации на ЭВМ.
5.1. Классификация задач анализа и синтеза систем
Задачи морфологического синтеза отличаются большим разнообразием и классифицируются по различным признакам, характеризующим количество и качество доступной информации. В общем случае задачи морфологического синтеза можно представить следующим набором информации:
<Т, А, К, X,
F
,
G
,
L
, М, N, С, Р,
Y
,
Q
,
D
>
Здесь приняты следующие обозначения :
Т—
постановка задачи (
t
1
—
синтезировать и выбрать наилучший вариант системы; t
2
— упорядочить весь набор синтезированных вариантов; t
3
— синтезировать и выбрать вариант, наиболее близкий по свойствам к заданному техническому заданию или прототипу; t
4
— синтезировать и упорядочить весь набор вариантов по степени сходства к заданному объекту);
А
— множество допустимых альтернатив для реализации функций (обобщенных функциональных подсистем), a1
—
альтернатива реализует одну функцию из рассматриваемой морфологической таблицы, a
2
—
альтернатива реализует более одной функции);
K
— множество критериев оценки альтернатив и выбора варианта системы (k
1
— множество содержит один критерий (скалярный критерий); k
2
— множество содержит несколько критериев (векторный критерий)) ;
X—
множество методов измерения предпочтений альтернатив (x
1
— использование номинальной — классификационной шкалы; x
2
— использование ранговой шкалы; x
3
—
использование количественной шкалы; x
4
—
экспертная оценка с помощью комментариев; x
5
— экспериментальная оценка; x
6
—
оценка на основе продукционных правил);
F
— отображение множества допустимых альтернатив, реализующих функции, в множество критериальных оценок (отображение А
в К
может иметь детерминированный вид (f
1
); вероятностный (
f
2
);
неопределенный (f
3
);
G
—
система предпочтений решающего элемента (
g
1
—
формирование предпочтений одним лицом; g
2
— формирование предпочтений коллективом);
L
—
способы исследования системы (l
1
— исследование целостной системы ; l
2
— исследование системы по частям);
М —
методы оценки вариантов (m
1
, — оценка варианта в целом после его синтеза из частей; т2
—
оценка отдельных подсистем, альтернатив и их сочетаний до начала процедуры синтеза);
N —
процедуры выбора вариантов (n
1
— последовательный перебор всех вариантов по принципу лексикографического упорядочения; n
2
—
последовательный перебор; п3
—
случайное зондирование морфологического множества; n
4
—
детерминированное зондирование);
С —
вид целевой функции (c
1
– аддитивная; с2
—
мультипликативная; c
3
— целевая функция на основе мер сходства и различия);
Р —
число рассматриваемых уровней системы (p
1
— один; p
2
—
более одного);
Y
—
уровень формализации постановки и решения задачи (у1
—
неформализованный эвристический подход; у2
—
формально-эвристический подход; у3
—
полностью формализованный подход);
Q
— Уровень компьютеризации процедур (
q
1
— отсутствует информационно-программная поддержка процедур метода; q
2
— часть или все процедуры реализованы в виде диалоговой компьютерной системы; q
3
— метод реализован в виде интеллектуальной системы);
D
—
решающее правило, отражающее систему предпочтений.
Любой элемент данного набора может служить классификационным признаком для задач комбинаторно-морфологического синтеза.
В последующих разделах рассмотрены различные процедуры обработки информации в созданной автоматизированной системе морфологического синтеза.
5.2. Постановка задач анализа и синтеза систем
Целями морфологического анализа и синтеза систем являются: системное исследование всех мыслимых вариантов решения задачи, вытекающих из закономерностей строения (морфологии) совершенствуемого объекта, что позволяет учесть, кроме известных, необычные варианты, которые при простом переборе могли быть упущены исследователем из вида; реализация совокупности операций поиска на морфологическом множестве вариантов описания функциональных систем, соответствующих исходным требованиям, т. е. условиям задачи. Морфологическое множество вариантов описания функциональных систем представляется морфологической таблицей (рис. 5.1).
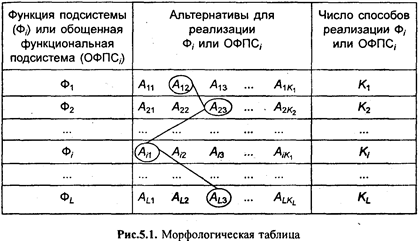
В морфологической таблице цепочкой связанных альтернатив показан один из вариантов рассматриваемой системы. Общее число всевозможных вариантов N
,
образующих морфологическое множество, определяется как декартово произведение множеств альтернатив, образованных каждой строкой морфологической таблицы:

В приведенном выражении приняты следующие обозначения:
K
l
—
число способов (альтернатив) для реализации l
-и функции или обобщенной подсистемы; L —
число всех функций.
Морфологическое множество является областью поиска в пространстве размерностью L.
Генерируемый вариант системы представляет выборку альтернатив по одной из каждой строки морфологической таблицы и в общем виде записывается следующим образом:

Правило генерации вариантов исследуемых систем таково, что каждый целостный вариант отличается от любого другого варианта рассматриваемого морфологического множества хотя бы одной альтернативой Alm
.
Поиск в морфологическом множестве вариантов систем при решении задачи синтеза осуществляется по различным целевым функциям и алгоритмам, которые рассматриваются в последующих разделах данной главы.
Метод морфологического анализа и синтеза реализуется в несколько этапов.
Этап 1. Проводится формирование исходной цели или проблемы, отражающей основные требования к синтезируемому объекту.
Этап 2. Осуществляется построение морфологической таблицы и заполнение ее альтернативами.
Этап 3. Описываются свойства альтернатив морфологической таблицы. Свойства альтернатив могут характеризоваться в шкале наименований классификационными функциональными и структурными признаками или в числовой шкале, отражающей качество альтернатив по различным критериям.
Этап 4. Формируется формализованное поисковое задание и выбирается вид целевой функции.
Этап 5. Реализуется та или иная процедура поиска вариантов решения задачи. Под поиском в данном случае понимается последовательность операций выбора из морфологического множества вариантов описания функциональной системы и операций оценки эффективности и совместимости подсистем, образующих синтезированный целостный вариант. Здесь же определяется соответствие варианта требованиям к искомой функциональной системе — от понятия "подходящее решение" до понятия "оптимальное или рациональное решение".
Рассмотрим методы и подходы по обработке информации на каждом этапе морфологического синтеза систем.
5.3. Подготовка информации для анализа и синтеза рациональных систем
Установление исходной цели синтеза
Формирование исходной цели синтеза может осуществляться с различной степенью полноты и определенности. Если перед исследователем поставлена задача, требующая поиска принципиально новой социально-экономической или организационной системы, то исходная цель будет носить достаточно общий, расплывчатый характер, например: найти принципиально новые средства перемещения людей в черте города, спроектировать эффективную систему расчета с клиентами супермаркета. В то же время, когда процесс синтеза связан с совершенствованием конкретных социально-экономических и других систем-прототипов, исходная цель конкретизируется рядом экономических, социальных и технологических требований, которые могут носить качественный или количественный характер. Последний способ формирования исходной цели синтеза в лучшей степени подлежит формализации, и на его основе реализован ряд подходов по синтезу рациональных вариантов систем. Исходная цель в значительной степени определяет подходы по формированию поисковых заданий и морфологических таблиц.
Способы формирования поисковых заданий
Можно выделить три подхода к формированию формализованных поисковых заданий, на основании которых решаются различные задачи морфологического синтеза. В соответствии с первым подходом поисковое задание формируется на основе качественных классификационных признаков и их значений, характеризующих отдельные подсистемы искомого варианта. При втором подходе поисковое задание формируется на основе количественной экспертной шкалы в виде некоторого множества критериев качества и требуемого уровня их выполнения в искомом решении. Третий подход предполагает выбор оптимального или рационального варианта из морфологического множества без явного выделения поискового задания. Т. е. здесь при поиске требуемого варианта используется лишь информация, характеризующая свойства и качество самих альтернатив, находящихся в морфологической таблице.
Составление поискового задания на основе множества классификационных качественных признаков целесообразно осуществлять с использованием автоматизированных баз данных, накапливающих наиболее важные классификации различных экономических, управленческих и организационных систем.
Автоматизированная база данных должна в этом случае включать признаки и значения признаков для характеристики всех функций (или обобщенных функциональных подсистем), имеющихся в морфологической таблице.
Формирование поисковых заданий на основе количественных признаков имеет ряд особенностей. В этом случае поисковые образы альтернатив, реализующие функции рассматриваемой системы, представляют числовые характеристики, отражающие степень проявления различных свойств. Такими свойствами являются, например, надежность подсистем, их технологичность, стоимость и т. п.
Задание численных значений критериев, характеризующих, с одной стороны, поисковое задание, а с другой — альтернативы морфологической таблицы, может проводиться методом сравнения с эталоном или методом попарного сравнения. На практике в качестве эталона может выступать существующая или гипотетическая альтернатива, свойство которой по i
-му критерию оценивается максимальным значением выбранной числовой шкалы. Например, для шкалы, имеющей значения: 1 — очень плохо, 2 — плохо, 3 — удовлетворительно, 4 — хорошо, 5 — отлично, интересующее исследователя свойство эталона, отраженное i
-м критерием качества, должно быть оценено значением "5 — отлично".
Рассмотрим ряд процедур составления поисковых заданий из критериев качества и их значений для поиска требуемых вариантов на морфологических таблицах методом сравнения с эталоном.
Процедура 1.
В соответствии с этой процедурой поисковое задание формируется непосредственно на морфологической таблице в виде комбинаций альтернатив {A
¢
ij
}, извлекаемых по одной из каждой строки таблицы. Оценка альтернатив, вошедших в поисковое задание, осуществляется по множеству интересующих критериев качества наравне с другими альтернативами {Aij
) из морфологической таблицы. Пример морфологической таблицы с оценкой множеств альтернатив {Aij
} и {A
¢
ij
} методом сравнения с эталоном по пятибалльной шкале приведен на рис. 5.2а.

Получение значений показателей качества для альтернатив при их попарном сравнении основано на расчете собственного вектора матрицы парных сравнений. Матрицы парных сравнений строятся для альтернатив, принадлежащих определенной обобщенной функциональной подсистеме, входящей в морфологическую таблицу. Матрицы попарных сравнений составляются по каждому рассматриваемому критерию качества. В эти матрицы включаются в том числе и альтернативы {A
¢
ij
}, образующие поисковое задание.
Процедура 2.
Поисковое задание формируется в виде некоторого гипотетического идеального варианта, элементы которого A
¢¢
ij
, соответствующие каждой строке морфологической таблицы, имеют по всем заданным критериям качества идеальные, наилучшие предельные свойства. Эти предельные свойства в общем случае определяются субъективными факторами, т. е. представлениями конкретных экспертов.
При использовании метода сравнения альтернатив относительно эталонов гипотетические альтернативы A
¢¢
ij
, образующие поисковое задание, оцениваются по заданному списку критериев качества Ki
наивысшей оценкой из принятой числовой шкалы (рис. 5.2 б).
Для получения численных значений гипотетического поискового задания методом попарного сравнения строятся матрицы попарных сравнений по каждому заданному по условиям задачи критерию качества. В этих матрицах один элемент отводится для идеальной альтернативы. При заполнении матрицы эксперт, сравнивая альтернативы из множества {А
ij
}, из которых будет синтезироваться вариант системы, отвечает на вопрос, какая из двух сравниваемых альтернатив предпочтительнее и насколько. В то же время при сравнении каждой альтернативы из множества {Aij
} с идеальной A
¢¢
ij
эксперт всегда выражает определенную степень предпочтения идеальной альтернативе.
Процедура 3.
Поисковое задание может формироваться на основании желаемого для эксперта качества, которое необходимо иметь в синтезируемых вариантах систем. При формировании поискового задания методом сравнения с эталоном эксперт устанавливает значение желаемого качества в пределах используемой шкалы. Морфологическая таблица и поисковое задание в данном случае аналогичны приведенным на рис. 5.2а.
Аналогично формируется поисковое задание методом попарного сравнения. В каждой матрице парных сравнений один из элементов отводится для альтернативы, отражающей в поисковом задании желаемые свойства. Эти желаемые свойства могут быть соотнесены в конкретном поисковом задании со свойствами альтернатив, участвующих в синтезе. Причем уровень желаемых свойств у альтернатив поискового задания может быть выше, равен или ниже уровня свойств альтернатив, из которых синтезируется вариант системы.
Морфологические таблицы
Морфологические таблицы — эффективное средство представления знаний о множестве социально-экономических или организационных систем. Они позволяют систематизировать достаточно большой объем знаний о морфологии систем в компактном виде. Разработка морфологической таблицы дает возможность формализовать процесс упорядочения множества заключенных в ней вариантов систем. Качество составления морфологической таблицы во многом определяет конечный результат поиска искомого решения проблемы. Разработка морфологических таблиц связана с первым этапом метода морфологического исследования — морфологическим анализом. Целью морфологического анализа является классифицирование исследуемого объекта или множества объектов. Морфологическое классифицирование в общем случае заключается в делении родового понятия таким образом, что последним могут соответствовать как множества известных систем, так и множества потенциальных вариантов, появление которых возможно в будущем.
Формирование конкретных морфологических таблиц для отображения множества технических систем может производиться двумя способами. Выбор способа определяется конечными целями морфологического исследования, характером исходной информации, степенью изученности предметной области, профессиональным уровнем специалистов, их знаниями.
Первый способ основан на проведении функционально-элементного анализа систем. В результате формируется морфологическая таблица, включающая функции или обобщенные функциональные подсистемы и альтернативы, реализующие соответствующие функции. Альтернативы, как правило, оцениваются количественно экспертными оценками по критериям качества для решения задач синтеза рациональных вариантов.
Формирование морфологических таблиц первым способом наиболее предпочтительно в тех ситуациях, когда в исходной информации, характеризующей анализируемую систему, не выражены в явном виде функциональные компоненты, когда специалисты по знаниям недостаточно хорошо ориентируются в анализируемой предметной области и когда при синтезе новых рациональных систем предполагается использовать только количественную экспертную оценку альтернатив по критериям качества.
Второй способ реализуется в два этапа. На первом этапе проводится функциональный анализ таким же образом, как он проводился в первом способе. На втором этапе каждая альтернатива, находящаяся в морфологической таблице, дополнительно характеризуется множеством качественных классификационных признаков, более тонко и полно отражающих отличительные особенности альтернатив.
Второй способ формирования морфологических таблиц используется в следующих ситуациях: при наличии предварительно структурированной информации о системах по функциональным компонентам, при постановке задачи проведения более глубокого исследования морфологического множества вариантов систем и синтеза принципиально новых знаний о структуре систем, при наличии высококвалифицированных специалистов с большим опытом исследовательской работы в анализируемой предметной области, когда требуется исследовать морфологические множества одновременно по количественно оцененным критериям качества и качественным признакам, характеризующим функции и структуру вариантов систем. Рассмотрим более подробно методы разработки морфологических таблиц.
Разработка морфологических таблиц на основе функционально-элементного анализа систем
При разработке морфологических таблиц, предназначенных для синтеза рациональных и оптимальных вариантов по многим критериям качества, классификационные признаки и их значения должны иметь такое содержание, которое позволяло бы оценивать их количественно. Такими основополагающими характеристиками сложных систем являются функции и элементы, реализующие те или иные функции.
При функциональном анализе удобным является принцип выделения и рассмотрения структур с двухуровневой иерархией. Согласно этому принципу первоначально выделяется главная функция (функции) рассматриваемой системы, которая представляет самый верхний иерархический уровень.
Затем устанавливают функциональные элементы, обеспечивающие выполнение главной функции и образующие первый иерархический уровень. Функции, выполняемые элементами первого иерархического уровня, являются подфункциями по отношению к главной функции системы. Далее каждый функциональный элемент первого уровня рассматривается как самостоятельная система, что позволяет выделить конструктивные элементы второго уровня, обеспечивающие функционирование элементов первого уровня. Аналогично производится разделение на функциональные элементы третьего уровня и последующих. Глубина разделения системы определяется в каждом конкретном случае характером и требованиями решаемой задачи.
Таблица 5.1
Планируемые администрацией города альтернативные мероприятия
| Функция (мероприятие)
|
Альтернатива (
Aij
)
|
| Инвестирование из местного бюджета в геологоразве-
дывательные работы
|
А11
-
разведка нефти в пойме Волги
|
A
12
- разведка нефти в степной местности
|
A
13
–
разведка природного газа
|
…
|
A
1
k
- разведка се-росодержащих
руд
|
| Реконструкция предприятий
|
А21
- тракторный завод
|
A
22
-моторный завод
|
А23
-
завод буровой техники
|
…
|
A
2
k
-
обувная фабрика
|
| Капитальные вложения
|
А31
-
строительство моста через Волгу
|
A
32
- строительство телевизионной башни
|
А33
-
реконструкция плотины через Волгу
|
…
|
A
3
l
– строительство Волго-Донского канала-2
|
| Привлечение иностранных инвестиций
|
A
41
- завод по производству упаковки (Германия)
|
А42
-
завод
по производству легковых автомобилей (Южная Корея)
|
A
43
- технологическое оборудование по добыче нефти (Италия)
|
…
|
А4
r
–
технологическое оборудование по производству обуви (Италия)
|
| …
|
…
|
…
|
…
|
…
|
…
|
| Развитие транспортной системы
|
Ak
1
- существенное расширение троллейбусных маршрутов
|
А
k
2
- незначительное расширение троллейбусных маршрутов
|
Ak
3
-
существенное расширение маршрутов маршрутного такси
|
…
|
А
kv
-
внедрение мо- но-рельсового транспорта
|
На основании проведенного анализа формируются строки морфологической таблицы, в которые записываются функции системы или обобщенные функциональные подсистемы, из которых состоит система в целом. Причем строки морфологической таблицы определяются из функций или обобщенных функциональных подсистем, относящихся к одному иерархическому уровню. Наименованиями столбцов являются альтернативы — варианты исполнения функций. Для заполнения морфологической таблицы альтернативами можно использовать различные информационные источники. Пример морфологической таблицы, систематизирующей планируемые администрацией города мероприятия для реализации в ближайшем будущем, приведен в табл. 5.1.
Разработка морфологических таблиц с использованием классификационных признаков
При разработке морфологических таблиц на основе функционального анализа систем достаточно было выявить функции подсистем, образующих исследуемую систему в целом, и подобрать для каждой функции альтернативы конкретных реализаций. Данный вид морфологических таблиц хотя и дает возможность проведения многокритериальной оценки альтернатив и выбора рациональной целостной системы, однако в ряде исследовательских задач недостаточно глубоко вскрывает морфологию системы. Устранить этот недостаток можно путем использования в морфологических таблицах классификационных признаков для описания альтернатив (табл. 5.2).
Чтобы построить морфологические таблицы на основании классификационных признаков, требуется разработать для каждой обобщенной функциональной подсистемы функциональную классификацию. После формирования классификаций осуществляется описание альтернатив каждой функции соответствующими признаками и значениями этих признаков, т. е. составляются классификационные образы альтернатив. Обработка таких морфологических таблиц проводится с использованием подходов кластерного анализа.
Таблица 5.2
Представление знаний об альтернативе в виде множества классификационных признаков
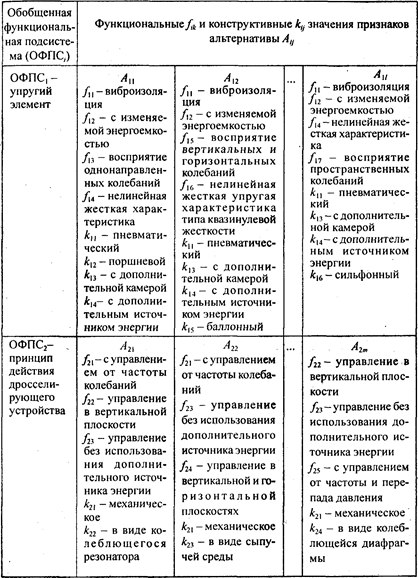
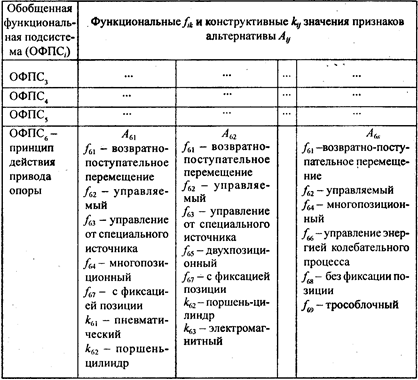
5.4. Кластерный анализ морфологических множеств
Основы кластерного анализа систем
Для выявления закономерностей строения сложных систем целесообразно в первую очередь собранные данные разложить "по полочкам", классифицировать. Вопросы кластерного анализа рассмотрены в учебнике А. М. Дуброва, В. С. Мхитаряна, Л. И. Трошиной [З].
Стремление собрать похожие объекты "в кучу" вполне понятно, поскольку именно классификация помогает исследователю ориентироваться в огромном многообразии объектов и тем самым является средством экономии памяти. В общем виде классификации позволяют, с одной стороны, относить объекты к одному из классов, а с другой — формировать сами "образы", число которых заранее может быть неизвестно.
Таким образом, анализ структуры данных — необходимый этап проводимых исследований. Особую актуальность классификационные построения приобретают при разработке новых информационных технологий, предназначенных для исследования сложных систем.
Рассмотрению подлежат в основном детерминистские методы построения и исследования систем-классификаций, основанные на качественных и количественных признаках.
Системы-классификации
Система
определяется как непустое множество объектов (или несколько таких множеств), между которыми установлены некоторые отношения. Таким образом, в системе набор элементов рассматривается как целостное единство, обладающее интегративными свойствами и противостоящее окружению или среде.
Система может быть представлена пятеркой:

Если хотя бы один член пятерки изменяется во времени или пространстве, то система называется динамичной, в противном случае — статичной.
Системы-классификации — это результат классификационных построений на множествах объектов. Примерами таких систем могут являться множество описаний объектов с заданным отношением эквивалентности, т.е. принадлежности к одному и тому же классу; множество классов с заданным отношением иерархии; множество классификаций с заданным отношением доминирования и т.д. В приведенных примерах указаны системы-модели, т.е. некоторые абстрактные аналоги реальных систем, которые значительно проще последних по большинству аспектов, исключая самые важные для конкретного рассмотрения. Системы-классификации сочетают субъективные и объективные начала, так как человек при классификационных построениях учитывает лишь ограниченное число признаков из бесконечного числа возможных. Таким образом, для бесконечного набора, которым обладает реальный объект, существует также бесконечное множество вариантов выбора ограниченных наборов.
Следовательно, если множество признаков, учитываемое на объектах, является системой описания, а множество значений каждого из учитываемых признаков на конкретных объектах — описанием этих объектов, то аналоги-модели объектов (в частности, системы-классификации) — это системы множеств, каждое из которых есть описание. Система-модель С = С (
I
,
R
,
A
(
S
)
, A
(
ps
)
, A
(
SP
)
)
является образом системы-оригинала С'
= С (
I
', R', А(
S
')
),
A
(
RS
')
, A
(
SR
')
)
. Отображение множества С'
на множество С
является гомоморфным, если С
имеет тот же состав, что и С'
(обратное неверно). Из сказанного видно, что система-модель содержит меньшее число элементов и связей, чем система-оригинал, но все элементы и связи, которые имеются в модели, правильно копируют прототип.
Для выбора "правильной модели" не существует формальной процедуры, она определяется целями классификационных построений и уровнем знаний конкретного исследователя.
Основные этапы построения и исследования систем-классификаций
Первым этапом классификационных построений является глубокое проникновение в суть рассматриваемых явлений и выбор соответствующего принципа классификации.
Второй этап — установление списка признаков и их значений, подлежащих учету на отдельных объектах. В список включаются признаки, наиболее полно характеризующие изучаемые объекты в смысле заданной цели. Из рассмотрения исключаются признаки, имеющие слабые разделительные свойства.
Третий этап — отбор репрезентативной выборки объектов и производство измерений.
Четвертый этап — выбор отношений на множестве описаний объектов; мер, порождающих отношения; решающих правил и критериев эффективности. Здесь же производятся вычисления.
Пятый этап — построение и анализ структурной схемы системы, в которой связи между элементами соответствуют выполнению отношений между ними. Способом представления структурных схем являются графы и дендрограммы.
Шестой этап — интерпретация полученных результатов, т. е. перенос полученных утверждений с системы-модели на систему-прототип.
Первые три этапа построения систем-классификаций составляют творческую часть процедуры классификации, которая целиком зависит от исследователя и не может быть формализована.
На четвертом и пятом этапах классификации требуется перерабатывать большой объем информации по определенным правилам логики. В связи с этим актуальной становится задача формализации процедур на этих этапах и реализации их в виде компьютерных систем.
Виды измерений
Системы, подлежащие классификации, изучаются прежде всего относительно наличия у них характерных свойств или состояний, которые отражаются различными признаками. Значения признаков могут измеряться с различной точностью.
Для измерения признаков применяются шкалы наименований, порядка, отношений, балльные, интервалов.
При использовании шкалы наименований указывается только, одинаковы или нет объекты относительно измеряемого признака.
Порядковые или ранговые признаки сравниваются только по отношению "больше — меньше".
Более точные измерения предполагают и большее число значений. В этом случае используются балльные шкалы. Значения балльной шкалы представляют собой ограниченный дискретный ряд чисел, отстоящих друг от друга на одинаковом расстоянии.
При дальнейшем увеличении точности измерений число значений можно увеличивать, доводя его до максимально осуществимого.
Условно все виды оценок делят на качественные и количественные. В соответствии с рекомендациями, приведенными в работе [4], качественными можно считать только те из них, которые измеряются в шкале наименований.
Формализация обработки качественных признаков
Множество вариантов, систематизированных в морфологических таблицах, может быть отражено списком качественных признаков. Список признаков, определяющий вариант морфологического множества, представляет его признаковый образ. Количество признаковых образов и собственно признаков, используемое в конкретном исследовании, может быть достаточно большим. Это делает морфологическое множество труднообозримым и малодоступным для анализа на умозрительном уровне.
Более четкие результаты могут быть получены при использовании математических методов, специально предназначенных для сжатия информации и количественной характеристики интегрированных свойств анализируемого материала.
Множество образов вариантов систем может быть представлено как матрица, имеющая q
столбцов и р
строк (порядка p
х q
), причем номеру столбца соответствует наименование системы Sj
(j
= 1, 2, ... , q),
а номеру строки — название признака Zi
(i
=1, 2,..., р).
В ряде случаев номеру строки ставится в соответствие значение признака. Информационным содержанием матриц являются указания о присутствии или отсутствии каждого из учитываемых признаков в рассматриваемых системах. При этом если i
-й признак присутствует в j
-й системе, то на пересечении i
-й строки и j
-ro столбца помещается "1", в противном случае — "0".
Любой j
-й столбец матрицы назовем описанием j-
й системы, любую i
-ю строку — описанием i
-го признака. В терминах теории множеств

Формула (5.1) читается: семейство множеств S
,
состоящее из всех S
j
,
таких, у которых элементы j
принадлежат множеству J
.
Аналогично семейство множеств

есть индексированное множество, а I
— индексное множество:

Индексация позволяет различать множества, состоящие из одинаковых элементов.
Пример матрицы образов представлен в табл. 5.3.
Таблица 5.3
Матрица
образов как семейство множеств
| S1
|
S2
|
S3
|
…
|
Sq
|
| Z1
|
0
|
1
|
0
|
…
|
1
|
| Z2
|
1
|
1
|
0
|
…
|
1
|
| Z
3
|
1
|
1
|
1
|
…
|
0
|
| …
|
…
|
...
|
...
|
…
|
…
|
| Zp
|
0
|
0
|
0
|
0
|
0
|
Семейство множеств S
или Z с заданными на них отношениями можно рассматривать как системы, в которых связи между элементами образуют определенную структуру. Следовательно, содержание задач по обработке матриц образов систем включает подбор типов отношений и анализ структуры порождаемых ими систем.
Рассмотрим основные меры, порождающие отношения на множестве исследуемых систем.
Меры сходства и различия.
Мерой сходства (близости) обычно называется величина С (
S
j
,
S
k
), имеющая предел и возрастающая с возрастанием близости объектов. Под мерой сходства будем понимать неотрицательную вещественную функцию С
(Sj
, Sk
), обладающую следующими свойствами:

Здесь Sj
,
Sk
—
множества значений признаков, описывающие сравниваемые объекты. Мера, коэквивалентная мере сходства, называется мерой различия D
(
Sj
,
Sk
)
и обладает свойствами метрики, если:

Свойствами (5.2) обладает, в частности, континуум эквивалентных мер, представляемых формулой
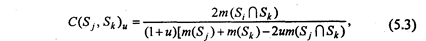
Меры сходства и различия "изобретаются" по специальным правилам [4], а выбор конкретных мер зависит, в первую очередь, от суперзадачи — цели конкретного исследования, а также от шкалы измерений. В табл. 5.4 приведены наиболее распространенные меры сходства и различия для различных значений коэффициента и
(5.3), предназначенные для обработки качественных и количественных признаков.

Вычисление значений меры сходства двух сравниваемых объектов по качественным признакам удобно производить на основе бинарной матрицы, которая в терминах теории множеств задается следующим образом:

Здесь S
—
индексированное множество с элементами Sj
(алфавит описаний), Sj
—
j
-
e
описание объекта; Z
— индексированное множество с элементами Z
i
(алфавит признаков или значений признаков); Z
i
— i
-й признак (значение признака); xiy
—
одно из двух значений {0, 1} i
-гo признака y j-
го объекта (
xij
= 1, если i
-й признак есть у j
-го объекта, в противном случае xij
=
0); J
и I
— индексные множества.
Бинарная матрица для вычисления меры сходства между двумя объектами имеет следующий вид:

Вычисление меры сходства, например, по формуле Чекановского — Серенсена (см.
табл. 5.4) с учетом бинарной матрицы (5.4) осуществляется по следующему выражению:

где xi
1
,
xi
2
—
одно из двух значений {0, 1).
Рассмотрим правила вычисления количества элементов некоторых множеств, получаемых в результате операций над ними. Количество элементов множества S
равно

где р —
общее число элементов множества S;
xi
—
значение i
-ro элемента множества S,
при этом 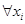 Î S
®
xi
=
1. Î S
®
xi
=
1.
Количество элементов пересечения двух множеств S
1
Ç S
2
равно

где xi
1
,
xi
2
—
соответственно значения i
-го элемента для множеств S1
и S
2
.
Количество элементов объединения двух множеств S
1
È
S
2
равно

Мера включения.
Она отражает различную степень включения одного объекта в другой и позволяет выявить, какой из двух сравниваемых объектов содержит больше специфических признаков, т. е. определить, какой объект более оригинален, а какой — более типичен среди множества анализируемых объектов.
Меры включения множества S
2
в множество S
1
и S
1
в S
2
определяются следующим образом:

Меры включения несимметричны, а включение j
-го описания в самом себе стопроцентно, так как

Для более полного анализа множеств исследуемых объектов рассчитываются меры сходства, различия и включения для всех пар объектов. Полученные после вычислений значения соответствующих мер сводятся в квадратные матрицы порядка q
x g
, номерами строк и столбцов которых являются номера изучаемых объектов.
Отношения мер сходства, включения и иерархии
Отношения мер сходства (различия), включения и иерархии позволяют при обработке множеств исследуемых объектов выявлять наиболее интересные закономерности строения анализируемых множеств. В общем случае под отношением понимается пара <А
, М>,
где М—
множество, на котором отношение определено, а А
— подмножество пар М
x М,
для которых это отношение выполнено. Множество М
называется областью задания отношения А.
Отношения мер сходства и иерархии исследуются на основе матриц сходства множества рассматриваемых объектов, а отношения мер различия и включения исследуются на основе матриц мер различия и включения. При этом матрицы сходства и различия по определению соответствующих мер обладают свойством симметрии относительно главной диагонали, а матрицы мер включения таким свойством не обладают.
Отношения сходства, различия и включения, порождаемые соответствующими мерами, определяются следующим образом:

Здесь j
, k
Î J
;
С
D
, D
D
, B
D
—соответственно отношения сходства, различия и включения; D
— некоторое произвольное число (0 £ D
£ 1,0 для отношения сходства и включения). Записи Sj
С
D
Sk
и Sj
B
D
Sk
означают соответственно то, что S
j
и Sk
находятся в отношении "D
-сходства" и "D
-банальности". Отношение "банальности" или "экзотичности" порождается мерой включения. При этом запись Sj
B
D
Sk
означает, что описание Sj
"банальнее" Sk
при пороге D
. Например, если рассчитанные для пары объектов меры включения имеют следующие значения: W
(S
1
; S
2
) = 0,57, W
(
S
2
;
S
1
)=
0,67, то эти результаты можно интерпретировать следующим образом. Мера включения первого описания во второе (0,67) показывает, что второй объект "оригинальнее", или "экзотичнее", первого. Т. e. описание второго объекта содержит больше специфических признаков, чем описание первого объекта, поскольку первое описание включено во второе на 67 %, а второе включено в первое на 57 %.
Отношение иерархии определяется следующим образом. Если множество H(i)
образовано соединением некоторых классов из множества Н(
i
)
,
то f
: Н(
i
)
®
Н(
j
)
сюръективно: каждому элементу Н(
i
)
соответствует хотя бы один элемент из Н(
j
)
. То обстоятельство, что класс появляется классом более широким, чем Н(
j
)
отображается через отношение иерархии И следующим образом: Н(
i
)
И Н(
j
)
(класс H
(
i
)
подчиняет класс H
(
j
)
).
Множество H
(
i
)
называется сгущением H
(
j
)
, если хотя бы один из классов H
(
i
)
есть соединение классов из H
(
j
)
.
Если И = {Н(1)
,..., H
(
S
)
} есть множество разбиений, таких, что Н(
k
)
сгущение Н(
k
-1)
, где k
Î К
, К
= {
k
½ k
—
целое число, 1 £ k
£ S
},
то в предельном случае Н(1)
состоит из всех классов, содержащих ровно по одному элементу, a H
(
S
)
— из одного класса, совпадающего с исходным множеством исследуемых объектов J.
При этом если задано разбиение, то элементы, входящие в один и тот же класс, являются неразличимыми (эквивалентными). Здесь под разбиением Н
множества J
понимается представление J
в виде совокупности непустых подмножеств Hk
, k
= 1, 2,..., п ,
таких, что

Множество И есть иерархическая система, состоящая из S
уровней. Номеру каждого уровня можно поставить в соответствие его ранг, так как К—
упорядоченное множество, а названия всех классов одного ранга считать категорией.
При практической реализации иерархических классификаций строятся дендрограммы, являющиеся графическим способом изображения системы, что делает наглядной структуру иерархической системы. Последовательный процесс построения сгущений начинается с рассмотрения q
объектов {
q
Î H
(1)
). Таким образом, на первом шаге каждый объект из заданного множества считается классом. Далее два наиболее схожих объекта объединяются в один класс, и общее число последних становится равным q
-
1. Эти классы принадлежат разбиению H
(2)
, являющемуся сгущением Н(1)
. Если число схожих объектов п,
то объединяются любые два из них. Среди оставшихся снова отыскиваются наиболее схожие, которые также объединяются. Аналогичные процедуры осуществляются до тех пор, пока все объекты не попадут в один класс H
(
S
)
.
Одним из наиболее распространенных и простых подходов построения дендрограмм является подход, основанный на использовании матрицы сходства.
Определение сходства каждого вновь образованного класса со всеми остальными может производиться на основе матриц сходства шестью наиболее употребительными методами, которые описываются единой формулой:
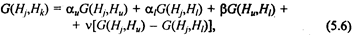
где G
(
Hj
,
Hk
) —
мера сходства или различия классов Hj
и Hk
= {Ни
,
Hl
}.
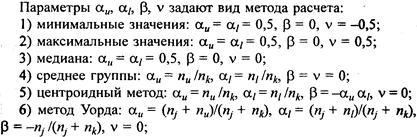
Здесь nu
, nk
— число объектов соответственно u
-го и k-
го классов; п
k
= nu
+ nl
.
Конкретный метод подбирается проектировщиком индивидуально для исследуемой предметной области с учетом ее специфики. Единых правил выбора не существует. Главным критерием для выбора метода классификации может являться хорошая интерпретируемость получаемых результатов, не противоречащих физическому смыслу изучаемой предметной области.
Обобщенные алгоритмы классификационных построений
Алгоритм построения матриц отношений сходства и включения.
Этот алгоритм отличается для указанных двух мер лишь методом расчета значений матриц сходства и включения.
Шаг 1. Формируются два множества: множество исследуемых объектов J
= {
S
1
, S
2
,..., Sq
}
и множество признаков Z
= { Z
1
, Z
2
,
..., Zp
}. Каждый объект Si
описывается подмножеством признаков {Z
i
}
Î Z
, являющимся качественным признаковым образом. Все образы объектов систематизируются в матрицу образов, где представляются индексированными множествами (табл. 5.5).
Шаг 2. Генерируются все парные сочетания объектов, и для каждой пары описаний объектов Si
и S
j
строится индексная матрица В
= ║ xij
║; i
=  ; j
= ; j
=  ; где р —
число строк матрицы образов, соответствующее числу рассматриваемых признаков m
(
Z
).
На основе индексной матрицы рассчитываются меры сходства C
(
Si
,
Sj
)
или включения W
(
Si
, Sj
). Для определения меры сходства может быть использована одна из формул, приведенных в табл. 5.4. Расчет мер включения осуществляется по формулам (5.5). ; где р —
число строк матрицы образов, соответствующее числу рассматриваемых признаков m
(
Z
).
На основе индексной матрицы рассчитываются меры сходства C
(
Si
,
Sj
)
или включения W
(
Si
, Sj
). Для определения меры сходства может быть использована одна из формул, приведенных в табл. 5.4. Расчет мер включения осуществляется по формулам (5.5).
Таблица 5.5
Пример матрицы образов
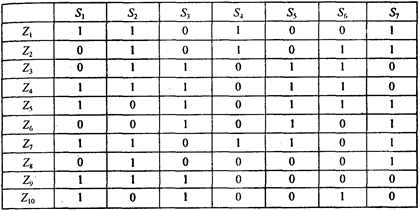
Например, для пары объектов S
1
и S
2
(см.
табл. 5.5) меры сходства и включения имеют следующие значения:
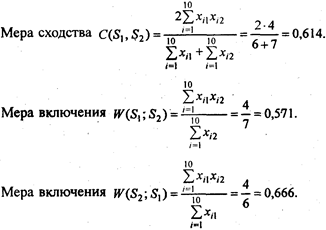
Шаг 3. На основе рассчитанных на шаге 2 значений мер сходства и включения (см.
табл. 5.5) строятся соответствующие матрицы размерностью q
x
q
(табл. 5.6, 5.7).


Матрица мер сходства симметрична относительно главной диагонали, а матрица мер включения таким свойством в общем случае не обладает. В приведенной матрице включения число 0,57 (первый столбец и вторая строка) соответствует W
(
S
1
;
S
2
)
, а число 0,67 (второй столбец и первая строка) соответствует W
(
S
2
,
S
1
).
Таким образом, индекс при названии первого множества в скобках указывает номер столбца, а второго — номер строки матрицы включения. При построении матрицы сходства индекс при первом множестве в мере сходства указывает номер строки матрицы, а при втором — номер столбца.
Шаг 4. Задается отношение сходства или включения в следующем виде:

где Δ — произвольное число (0 £ Δ £ 1,0); i
,
j
Î J
.
Для заданного значения Δ строится матрица сходства [СΔ
] или включения [B
Δ
], в которой все значения, большие или равные Δ, заменяются единицами, а оставшиеся — нулями.
Примеры матриц [С0,60
] и [B
0,67
] Для значений Δ ³ 0,60 и Δ ³ 0,67 приведены в табл. 5.8, 5.9.


Матрицы [С0,60
] и [B
0,67
] отображены соответственно графами и орграфами отношений сходства и включений (рис 5.3). Дуги и стрелки соединяют те объекты, которые имеют единицу на пересечении соответствующих строк и столбцов матриц.

Направление стрелки в графе отношений включения устанавливается таким образом, что она начинается в вершине графа, соответствующей Si
-му объекту, принадлежащему i
-й строке матрицы, и заканчивается в Sj
-м
объекте, принадлежащем j
-му столбцу матрицы. При этом Si
-й и Sj
-й объекты должны быть связаны отношением включения, т. е. иметь на пересечении Si
-го и Sj
-го объектов в матрице отношений включения единицу. Чем больше стрелок входит в тот или иной объект, тем более он оригинален по сравнению с другим объектом. Например, наиболее оригинальным является объект S
2
, так как в него входят три стрелки (рис. 5.3б).
При практическом использовании выше приведенных отношений величину Δ находят путем перебора серии значений, добиваясь при этом установления всех существенных связей.
Алгоритм построения иерархической классификация (дендрограммы)
Приводимый здесь алгоритм построения иерархической классификации основан на анализе значений матрицы сходства. Аналогично проводится построение иерархической классификации на основе меры различия. Рассмотрим пошаговую обработку данных для построения дендрограммы сходства с иллюстрацией ряда процедур на примерах в целях лучшего понимания алгоритма.
Шаг 1. Определяются два множества: множество исследуемых объектов J
= {
S
1
,
S
2
, ...,
Sq
}
и множество признаков Z
= {Z
1
, Z
2
, ...,
Zp
}.
Экспертно формируются индексированные множества по каждому объекту. Строится матрица сходства

где Sij
—
значение меры сходства объекта Si
с объектом Sj
;
q
—
число анализируемых объектов.
Последующую иллюстрацию алгоритма осуществим на примере матрицы сходства {см.
табл. 5.6).
Шаг 2. Просматриваются все элементы матрицы сходства [С
], расположенные выше главной диагонали. Определяется и метится элемент, имеющий максимальное значение меры сходства С
(
Si
, Sj
)max (данный элемент не принадлежит к элементам главной диагонали). Для рассматриваемой матрицы сходства таким элементом является С
(S
4
, S
5
) =
0,75. Если в матрице сходства более одного элемента с одинаковым максимальным значением, то отбирается и метится любой их них.
Шаг 3. Определяются номера i
-й строки j
-го столбца, на пересечении которых расположен отмеченный на шаге 2 элемент. Из матрицы сходства извлекаются все значения, соответствующие i
-й строке и j
-му столбцу, из которых формируются два массива значений мер сходства:
| Hi
=Si
|
S1
|
S2
|
S3
|
S4
|
S5
|
S6
|
S7
|
| С
(S4
,
Si
)
|
0,44
|
0,60
|
0
|
1
|
0,75
|
0,25
|
0,67
|
| C(S5
, Si
)
|
0,55
|
0,5
|
0,73
|
0,75
|
1
|
0,60
|
0,55
|
Ш а г 4. Определяется мера сходства классов G (Н, Н^) одним из методов, описываемых обобщенной формулой (5.6). Используем метод медианы. Тогда

С учетом метода медианы имеем
| Hi
=Si
|
S1
|
S2
|
S3
|
S4
, S5
|
S6
|
S7
|
| С
(S4,5
, Si
)
|
0,50
|
0,55
|
0,37
|
1
|
0,43
|
0,61
|
Полученный массив данных вписывается на место четвертой и пятой строк и четвертого и пятого столбцов вновь формируемой матрицы сходства. Наша исходная матрица сходства примет следующий вид:
| S1
|
S2
|
S3
|
S4,5
|
S6
|
S7
|
| S1
|
1
|
0,62
|
0,50
|
0,55
|
0,55
|
0,5
|
| S2
|
0,62
|
1
|
0,46
|
0,55
|
0,50
|
0,62
|
| S3
|
0,50
|
0,46
|
1
|
0,37
|
0,73
|
0,33
|
| S4,5
|
0,50
|
0,55
|
0,37
|
1
|
0,43
|
0,61
|
| S6
|
0,55
|
0,50
|
0,73
|
0,43
|
1
|
0,36
|
| S7
|
0,50
|
0,62
|
0,33
|
0,61
|
0,36
|
1
|
На данном шаге запоминаются значения индексов вновь образованного класса (
S
4,5
)
и меры сходства, при которой этот класс образовался, — С (
S
4
,
S
5
)
= 0,75.
Шаг 5. Процедура обработки матрицы сходства вновь начинается с шага 2. Итерационный процесс продолжается до тех пор, пока размерность матрицы сходства не уменьшится до 2 х 2. На этом процесс построения иерархической классификации заканчивается.
В результате работы алгоритма определяются перечень индексов классов в том порядке, в котором они объединялись в новые классы, а также уровни сходства, на которых это объединение происходило. Для рассматриваемого примера имеем следующие результаты:

Полученные результаты используются для построения дендрограмм. Дендрограмма делает наглядной структуру иерархической классификации. В данном примере (рис. 5.4) наибольшим сходством обладают классы S
4
и S
5
, наименьшим — классы Н5
= {
S
1
,
S
2
,
S
4
,
S
5
,
S
7
}
и Н2
= {
S
3
, S
6
}
.
Мера сходства на основе экспертной оценки
Для повышения точности определения сходства исследуемых объектов меру сходства можно формировать на основе экспертной оценки.
Экспертная оценка сходства объектов проводится двумя способами.
Способ 1. Для рассматриваемых объектов первоначально определяется множество признаков {fij
}.
На основе множеств признаков и рассматриваемых объектов для последних строится матрица образов, в которой принадлежность признака объекту S
i
отображается единицей, а отсутствие — нулем (табл. 5.10).
Таблица 5.10
Матрица образов анализируемых объектов
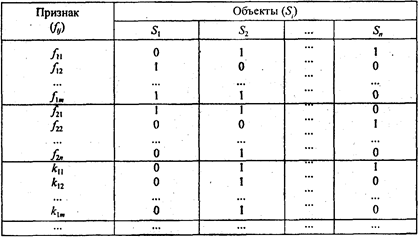
Все значения каждого признака сравниваются попарно экспертом, который формирует матрицы сходства признаков. Далее составляются матрицы сходства объектов по каждому признаку и на их основе рассчитывается интегральная матрица сходства. Значения мер сходства объектов интегральной матрицы определяются по выражению

где Cl
(
Si
,
Sj
) —
значение меры сходства двух объектов по l
-му признаку;
rl
(
Si
,
Sj
) —
весовой коэффициент l
-го признака, характеризующий его вклад в интегральное значение меры сходства

т —
число признаков, по которым оценивается сходство объектов.
Значение С
l
(
Si
,
Sj
)
определено в интервале {0...1}, причем Cl
(
Si
, Sj
) = 1 при i
=j
.
Способ 2. Мера сходства между альтернативами устанавливается экспортно по одному или нескольким критериям качества, таким, как качество выполнения основных функций, надежность, технологичность, экологичность, эстетичность и т. д.
Вычисление интегрального значения меры сходства альтернатив по нескольким критериям качества осуществляется по технологии, аналогичной той, которая использовалась в первом способе. Отличие состоит лишь в том, что во втором способе индекс l
=
1,т
в формуле (5.7) обозначает принадлежность к l
-му критерию качества, а т
-число критериев качества, учитываемых в рассмотрении.
Экспертные методы оценки меры сходства объектов позволяют проводить более точный анализ по сравнению с методом, основанным на обработке качественных бинарных признаков. Однако экспертные методы требуют привлечения высококвалифицированных специалистов, что не всегда бывает возможно, а также существенно повышают время предварительного анализа объектов. Поэтому при анализе большого числа объектов (сотни или тысячи единиц) со значительным числом признаков, характеризующих эти объекты, целесообразно проводить различные классификационные построения в два этапа. На первом этапе, не используя экспертные методы оценки сходства, проводить грубое усечение исходного множества объектов, а на втором — выполнять более тонкие исследования, применяя экспертные методы оценки мер сходства (различия) объектов.
Обработка количественных признаковых образов
В работе [6] введено понятие дескриптивных множеств и определены меры пересечения и объединения двух множеств {
S
1
и S
2
) для случая применения количественных данных:
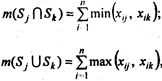
где п —
число признаков, представляющее объединение множеств признаков двух текущих сравниваемых описаний объектов Sj
и Sk
.
При учете данного подхода многие меры сходства, различия, включения и т. д. можно определять для описаний, состоящих из количественных признаков.
Пусть дано два объекта S
1
и S
2
,
которые охарактеризованы экспортно по множеству критериев качества: К1
—
надежность, К2
—
технологичность, К3
—
стоимость, К4
—
компактность. Описания объектов имеют следующие количественные значения критериев:
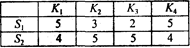
Требуется найти меры сходства и включения описаний S
1
и S
2
.

Из приведенных примеров видно, что при определении числа пересечений двух множеств подсчитывается сумма минимальных значений, образующих эти множества, а при определении числа элементов множества — суммируются все его значения.
Определение оригинальных и типовых систем
На основе матриц сходства и включения можно установить наиболее типовые системы или, напротив, наиболее оригинальные. Выявление указанных закономерностей осуществляется методом определения правого собственного вектора указанных матриц.
При обработке матрицы сходства максимальное значение ее правого собственного вектора будет соответствовать наиболее типовому элементу, т. е. наиболее схожему со всеми остальными рассматриваемыми в этой матрице объектами. Минимальное значение в правом собственном векторе матрицы включения характеризует наиболее оригинальный (экзотичный) объект.
Вычисление правого собственного вектора положительной квадратной матрицы проводится итерационным алгоритмом, использованным для обработки матриц парных сравнений (см.
разд. 2.2).
Кластеризация морфологических множеств
Генерируемые на морфологических таблицах морфологические множества вариантов систем имеют сложную неоднородную внутреннюю структуру. Выявление закономерностей строения исследуемых множеств позволяет более эффективно решать основные задачи по поиску, прогнозированию и планированию рациональных систем. Предварительная кластеризация морфологических множеств с учетом особенностей структуры и свойств вариантов систем помогает во многих задачах преодолеть проклятие размерности, отсеять неинтересные для исследователя варианты систем. Можно выделить два способа формирования классов. Первый способ заключается в том, что классы формируются в процессе конкретного исследования. Второй способ предполагает предварительное задание классов исследователем. При проведении исследований, связанных с выявлением новых классов, применяются методы, позволяющие проводить иерархическое упорядочение морфологических множеств на основе мер сходства; определять подмножества вариантов, наиболее сходных между собой по различным признакам и свойствам; выявлять классы, содержащие наиболее типовые или наиболее оригинальные варианты. Если отряды классов задаются предварительно исследователем, то решается задача идентификации. Цель идентификации — распознавание синтезируемого на морфологической таблице варианта системы и отнесение его к тому или иному классу с учетом решающих правил. Таким образом, осуществляется сортировка синтезируемых вариантов по классам.
Результаты кластеризации в конечном итоге определяются способом описания альтернатив в морфологической таблице, правилом вычисления меры сходства, методом построения иерархической классификации, структурой морфологической таблицы, способом задания классов при решении задачи идентификации.
Решая задачи исследования морфологических множеств на основе методов кластерного анализа, следует различать три существенно отличающихся способа описания альтернатив в морфологической таблице. Способ описания альтернатив обусловливает метод вычисления меры сходства между синтезируемыми вариантами систем. Можно выделить три способа описания альтернатив и соответствующие им правила определения сходства между вариантами.
Первый способ описания каждой альтернативы предполагает указание только ее наименования, например описание альтернативы может быть представлено в виде А
ij
.
При втором способе описания каждая альтернатива имеет наименование и экспертные оценки, указывающие степень сходства со всеми другими альтернативами, принадлежащими одной обобщенной функциональной подсистеме. Третий способ представления предусматривает указание для каждой альтернативы классификационных признаков. Указанная для характеристики альтернатив информация используется при вычислении мер сходства между синтезируемыми вариантами. Вычисление мер сходства осуществляется по различным правилам.
При первом способе
описания альтернатив в виде наименований А
ij
меры сходства между двумя вариантами S'
и S
"
вычисляются по известной формуле

с учетом следующих правил:
• число элементов множества, образующего вариант системы S
¢
или S
¢¢
', равно числу альтернатив А
ij
, входящих в данное множество;
• число пересечений элементов двух множеств S'
и S"
равно числу одинаковых пар альтернатив А
¢
lm
и А
¢¢
lm
, принадлежащих соответственно вариантам S'
и S",
т. е.

При втором способе
описания альтернатив на основе экспертной оценки их степени сходства друг с другом расчет меры сходства между двумя вариантами S
¢
и S"
системы определяется по формулам:


где С
l
(
A
¢
lm
, А
¢¢
lm
)
— экспертное интегрированное значение меры сходства пары альтернатив, принадлежащих l
-и обобщенной функциональной подсистеме;
L
—
число обобщенных функциональных подсистем, образующих вариант системы;
С
i
(
Z
¢
ilm
,
Z
¢¢
ilm
)
— экспертное значение меры сходства пары альтернатив по i
-му классификационному признаку или критерию качества;
ri
—
весовой коэффициент, определяющий вклад в меру сходства i
-ro признака или критерия;
К —
число признаков или критериев, по которым описаны свойства альтернатив А
¢
lm
и A
¢¢
lm
.
При третьем способе
описания вариантов синтезируемых систем определение меры сходства между вариантами осуществляется по выражению (5.9). Вариант системы здесь описан множеством значений признаков Zilm
= {0,1}. Значение признака Zilm
равно единице в описании альтернативы А
lm
, если признак присутствует в ней, в противном случае Zilm
= 0.
Рассмотрим строение морфологических множеств относительно иерархических классификаций. Первоначально исследуем морфологическое множество, включающее варианты, альтернативы которых описаны в соответствии с первым способом, т. е. простым указанием их наименований. При проведении исследований данного типа целесообразно определить наиболее приемлемый метод классификации. Критерием для отбора метода кластеризации может являться хорошая интерпретируемость полученных результатов, т. е. достижение высокой адекватности между моделью-классификацией и реальной системой-прототипом. Проанализируем шесть наиболее простых и распространенных методов иерархической классификации: медианы, максимальных значений, минимальных значений, средней группы, центроиды, Уорда. Осуществим кластеризацию морфологического множества, систематизированного морфологической таблицей (табл. 5.11). Исходное морфологическое множество (табл. 5.12) сформировано алгоритмом лексикографического упорядочения альтернатив.

Объекты морфологического множества состоят из трех функциональных подсистем. С учетом выражения (5.8) и относящихся к нему правил формируется матрица мер сходства вариантов:

Обработка матрицы сходства шестью указанными методами позволяет получить шесть иерархических классификаций (дендрограмм). Анализ дендрограмм (рис. 5.5) показывает, что все методы, кроме метода максимальных значений, дают качественно сходные классификации. В то же время количественные значения уровней сходства у дендрограмм, построенных методами медианы и средней группы, существенно отличаются от дендрограмм, построенных другими методами.

При этом более верные результаты дают методы медианы и средней группы. Действительно, пары объектов S
5
—S
7
,
S
1
—S
3
, S
2
—
S
4
,
S
6
—
S
8
сходны между собой двумя альтернативами, а при наличии в объекте трех функциональных подсистем, реализуемых альтернативами, его сходство с любым другим объектом по двум альтернативам оценивается значением 0,67. Классы, образованные объектами S
5
—S7
и S
1
—S
3
, а также S
2
—
S
4
и S
6
—
S
8
, сходны между собой в среднем одной альтернативой, т. е. G
(
S
5-7
, S
1-3
)
= G
(
S
2-4
,
S
6-8
)
= 0,5.
На вид дендрограммы влияет не только метод определения сходства между классами, но и порядок извлечения классов из матрицы сходства для тех случаев, когда указанные матрицы содержат несколько одинаковых максимальных значений. В этих случаях возможны два способа извлечения классов из матрицы. Первый способ основан на случайном выборе двух классов, на пересечении которых в матрице сходства стоит одно из максимальных значений. Второй способ предполагает осуществление одновременного выбора всех классов, имеющих максимальные значения в матрице сходства.
Наиболее распространен в практике кластерного анализа первый способ извлечения классов из матрицы. Таким образом, при наличии в матрице сходства не единственного максимального значения меры сходства анализируемых классов число дендрограмм, которое может быть построено на основе такой матрицы, также не равно единице. Примером является рассмотренная ранее матрица сходства, имеющая двенадцать пар классов с равным максимальным значением. Следовательно, для такой матрицы уже на первом шаге алгоритма построения иерархической классификации возможны двенадцать вариантов ее построения. При этом на последующих шагах обработки матрицы сходства также не исключена многовариантность при выборе пары классов с максимальным значением. Альтернативная дендрограмма для рассматриваемой матрицы приведена на рис. 5.6. Она построена для случая, когда из матрицы сходства первой извлекалась пара S
1
и S
2
.
| 
|
Сравнительный анализ двух дендрограмм показывает, что их структуры идентичны, однако наблюдается перегруппировка классов на всех иерархических уровнях сходства.
С учетом проведенного анализа можно рекомендовать для исследования морфологических множеств методы медианы и средней группы.
Проанализируем рассматриваемое морфологическое множество на предмет наличия в нем наиболее типичных и оригинальных вариантов. Для этого рассчитаем правый собственный вектор матрицы сходства:

В полученном векторе все значения одинаковы. Следовательно, морфологические множества, содержащие варианты систем, представленные альтернативами, описанными в виде наименований, не содержат наиболее типовых или наиболее оригинальных вариантов. Полученный результат наглядно иллюстрируется графом сходства (рис. 5.7), который построен для максимального порогового значения отношения сходства С
D
= 0,67.
Построение матрицы включения вариантов систем, входящих в рассматриваемое морфологическое множество, показало, что она идентична матрице сходства, т. е. симметрична относительно главной диагонали. Это подтверждает наличие особой специфики у морфологических множеств, полученных методом комбинирования альтернатив.


Иерархическая классификационная структура морфологических множеств определяется прежде всего строением морфологической таблицы. В качестве примера на рис. 5.8 приведены дендрограммы, построенные методом медианы для морфологических множеств, сгенерированных на четырех различных таблицах.
Свойства морфологических множеств изменяются, если альтернативы описаны указанными ранее вторым или третьим способом. В этом случае в морфологических множествах удается выделить наиболее типовые или наиболее оригинальные варианты.
5.5. Синтез новых и рациональных систем на морфологических множествах
Многокритериальный синтез
Морфологический синтез рациональных вариантов по критериям качества начинается с независимой оценки альтернатив, принадлежащих соответствующим функциональным подсистемам. Метод основан на двух предположениях. Первое предположение заключается в том, что альтернативы, принадлежащие одним функциональным подсистемам, можно оценивать независимо от альтернатив, принадлежащих другим функциональным подсистемам. Второе предположение состоит в том, что наилучший целостный вариант системы содержит лучшие альтернативы. Для ряда сложных функциональных систем справедливо второе предположение.
Рассматриваемый подход используется для предварительного усечения исходного морфологического множества. Оставшееся после усечения обозримое подмножество рациональных вариантов исследуется на предмет оценки их эффективности и совместимости отдельных альтернатив.
Морфологический синтез рациональных вариантов может реализоваться по двум направлениям. Первое направление предусматривает поиск наиболее рациональных вариантов в самом морфологическом множестве. При этом максимизируется аддитивная или мультипликативная целевая функция.
Второе направление предполагает поиск в морфологическом множестве вариантов, наиболее сходных с поисковым заданием. Расчет значений целевых функций осуществляется для каждого варианта, синтезируемого на исследуемой морфологической таблице. Для этой цели используется специальный алгоритм генерации всех вариантов систем, содержащихся в морфологической таблице. Алгоритм функционирует по принципу лексикографического упорядочения объектов.
Общее число перебираемых компьютером вариантов определяется здесь декартовым произведением множеств альтернатив, относящихся к каждой функции обобщенной функциональной подсистемы.
Рассмотрим основные положения морфологического синтеза рациональных вариантов систем по множеству критериев на примере синтеза мероприятий для развития инфраструктуры города. Пусть задана морфологическая таблица (рис 5.9), содержащая описания альтернатив. Альтернативы подлежат предварительной оценке по критериям качества. Возможны два способа проведения экспертной оценки. По первому способу оценка альтернатив всех функциональных подсистем осуществляется по единому множеству критериев (частный случай). По второму способу оценка каждой функциональной подсистемы мероприятий и соответствующих ей альтернатив проводится по различным уникальным подмножествам критериев (наиболее общий случай).

В первом и втором способах оценки имеется возможность использовать три вида структур критериев качества, по которым предполагается ранжировать альтернативы и отыскивать рациональные элементы в каждой строке морфологической таблицы. Используемая по усмотрению исследователя структура критериев может представлять один критерий, вектор критериев, иерархическую структуру критериев. Приведенные три вида структур критериев реализуемы методом анализа иерархий.
Далее экспертным путем определяется относительная степень предпочтительности критериев качества между собой для установления их весомости (значимости) при решении конкретной задачи. Следующим этапом является оценка альтернатив относительно критериев самого нижнего иерархического уровня. Степень предпочтительности устанавливается экспертом методом попарного сравнения или методом сравнения относительно стандартов.
По полученным экспертным данным вычисляются векторы приоритетов альтернатив ( ) по всем критериям качества, вплоть до критерия, определяющего фокус (вершину) иерархии. Аналогично рассчитываются векторы, устанавливающие приоритет альтернатив, находящихся во всех остальных строках морфологической таблицы. Для последующего синтеза рациональных целостных вариантов систем в морфологическую таблицу заносятся векторы приоритетов альтернатив по интересующим исследователя критериям качества. ) по всем критериям качества, вплоть до критерия, определяющего фокус (вершину) иерархии. Аналогично рассчитываются векторы, устанавливающие приоритет альтернатив, находящихся во всех остальных строках морфологической таблицы. Для последующего синтеза рациональных целостных вариантов систем в морфологическую таблицу заносятся векторы приоритетов альтернатив по интересующим исследователя критериям качества.
Это могут быть фокусы иерархий критериев или критерии, находящиеся на промежуточных уровнях иерархий. В рассматриваемом примере морфологическая таблица содержит для определенности векторы приоритетов альтернатив относительно всех критериев и фокусов иерархий. Лучшей альтернативой в каждой строке морфологической таблицы по тому или иному критерию является та, которая имеет наибольшее значение в соответствующем векторе приоритетов.
При поиске рациональных вариантов в морфологическом множестве могут решаться две отличающиеся друг от друга задачи.
Решение первой задачи сводится к отысканию в морфологическом множестве одного или нескольких целостных вариантов систем, удовлетворяющих аддитивной или мультипликативной целевой функции. При этом на морфологической таблице генерируются все варианты технических систем алгоритмом полного перебора. Аддитивная и мультипликативная целевые функции в этой задаче определяются следующим образом.
Аддитивная целевая функция.
Найти подмножество S
Î
W
, для элементов которого

где S
— подмножество искомых целостных вариантов систем;
W — морфологические множества всех систем, содержащихся в исследуемой морфологической таблице, имеющие размерность N
,
определяемую по выражению:

L
—
число функций системы (число строк морфологической таблицы);
wlm
, w
*
lm
, — соответственно рассматриваемое и наилучшее интегральные по нескольким критериям качества значения векторов приоритетов, соответствующих альтернативам Alm
, и А
*lm
, входящих в i
-й вариант синтезируемой системы и наилучшей по рассматриваемым критериям альтернативы;
N —
размерность морфологического множества;
Kl
—
число способов (альтернатив А
lm
для реализации i
-й функции системы.
Аддитивные модели базируются на предположении о том, что качество системы (экономической, управленческой и т. д.), т. е. ее ценность, полезность, эффективность, определяется суммой эффектов от каждого ее свойства. Частной и широко применяемой на практике формой выражения аддитивного показателя качества является взвешенная арифметическая (5.10), (5.11). Наряду с аддитивной моделью, базирующейся на применении средневзвешенной арифметической, используются и другие виды показателей качества, основанные на других принципах, например на принципе мультипликативности, т. е. не сложения, а перемножения эффектов. В этом случае показатель качества выражается средневзвешенной, но не арифметической, а геометрической.
Мультипликативная целевая функция.
Найти подмножество S
Î
W
, для элементов которого

Вопрос о том, какая из этих двух средневзвешенных более адекватно отражает поведение человека, принимающего решение с учетом не одного, а нескольких показателей, был предметом научной дискуссии Галилея с Ноццолино еще в 17в. (Галилей отдавал предпочтение среднегеометрическому, а Ноццолино — среднеарифметическому). С тех пор многие ученые — специалисты в области статистики, психофизиологии и другие высказывали различные теоретические доводы в пользу каждой из этих двух средневзвешенных. В различных областях науки и практики аддитивный показатель качества в виде средневзвешенной арифметической используется гораздо чаще, чем другие виды средневзвешенных (например, среднегеометрическая). Однако использование аддитивного показателя качества требует, чтобы между относительными показателями любых свойств существовала независимость по предпочтению.
Решение второй задачи сводится к поиску в морфологическом множестве подмножества вариантов систем, наиболее сходных с поисковым заданием. Целевая функция в этой задаче определяется следующим образом: найти подмножество S
Î
W
, для элементов которого

где С
(Si
1
, S
2
) — мера сходства между описанием рассматриваемого варианта системы Si
1
и описанием поискового задания S
2
;
x
1
lm
,
x
2
l
— числовые значения критериев качества, характеризующие соответственно рассматриваемый вариант системы и поисковое задание;
L —
может иметь два значения и определять либо число обобщенных функциональных подсистем, либо число критериев качества, которыми на количественном уровне охарактеризованы описания Si
1
и S2
;
т —
порядковый номер альтернативы в строке морфологической матрицы.
Первое значение индекс L
имеет в том случае, если x
1
lm
и x
2
l
представляют интегральную оценку по множеству критериев качества, характеризующих альтернативу А
lm
, являющуюся компонентом описания рассматриваемой системы Si
1
и описания системы S
2
,
выступающей в роли поискового задания (это могут быть прототип, идеальная система, желаемая система).
Второе значение индекс L
имеет в случае, когда x
1
lm
и x
2
l
представляют неинтегральные по множеству критериев качества значения, характеризующие в целом альтернативу рассматриваемых вариантов систем и поискового задания. Верхние индексы указывают на принадлежность к рассматриваемому варианту системы (индекс равен единице) и поисковому заданию (индекс равен двум).
Если в выражении (5.12) х1
l
т
и x
2
i
отражают интегральные значения всего множества критериев, характеризующих альтернативы, то при необходимости учета различной степени влияния на меру сходства функциональных подсистем в числитель и знаменатель после знака суммы необходимо добавить весовой коэффициент wl
и присвоить соответствующие значения каждой функциональной подсистеме. Если x
1
lm
и х2
l
,
отражают значения индивидуальных критериев качества, то для учета влияния на меру сходства (5.12) одновременно функциональных подсистем и критериев качества необходимо ввести два весовых коэффициента. В этом случае целевая функция будет иметь следующий вид: найти подмножество S
Î
W
, для элементов которого

где rl
— весовой коэффициент, определяющий вклад в меру сходства критериев качества обобщенной функциональной подсистемы ОФПСl
;
wlp
— весовой коэффициент, определяющий вклад в меру сходства критерия качества К
p
по которому оценивается ОФПСl
;
L
— число обобщенных функциональных подсистем;
P
— число критериев качества, характеризующих альтернативы А
lm
и А
l
,
причем Р =
1,2,..., r
при l
= 1; Р =
1,2,..., s
при l
=
2; Р
= 1,2,..., t
при l
= h
;
x
1
lpm
- оценка по критерию качества Кр
альтернативы А
lm
, участвующей в синтезе и принадлежащей обобщенной функциональной подсистеме ОФПСl
;
x
2
lp
—
оценка по критерию качества Кр
обобщенной функциональной подсистемы ОФПСl
, принадлежащей системе, представляющей поисковое задание.
Рассмотрим примеры синтеза вариантов систем на основе аддитивной целевой функции и на принципе определения меры сходства между вариантом и поисковым заданием. Используем для этой цели ранее построенную морфологическую таблицу (см.
рис. 5.9).
Строго упорядочим по значимости обобщенные функциональные подсистемы (строки) сверху вниз и альтернативы в каждой строке — слева направо. Осуществим синтез всех вариантов систем по лексикографическому принципу, подобному упорядочению слов в словарях. Для каждого варианта рассчитаем значение аддитивной целевой функции по выражению (5.10). Упорядочив варианты в направлении уменьшения значений целевой функции (табл. 5.13), можно определить подмножество наиболее эффективных решений, которые подлежат дополнительному анализу. К таким решениям относятся, например, варианты 16, 10 и 4.
Таблица 5.13
Значения эффективности и сходства синтезированных систем
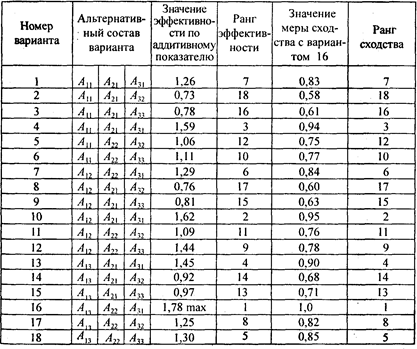
Сформулируем поисковое задание из альтернатив, содержащихся в морфологической таблице. Примем в качестве поискового задания интегральные значения критериев качества, относящиеся к альтернативам, из которых состоит наилучший вариант, синтезированный на основе аддитивной целевой функции. Лучший вариант состоит из альтернатив (А13
, A
22
, А31
).
Расчет мер сходства по формуле (5.13) между лучшим вариантом и всеми остальными синтезированными вариантами (см.
табл. 5.13) позволил проранжировать последние по степени близости к поисковому заданию. Сравнительный анализ результатов показал, что все синтезированные варианты имеют ранг близости к наиболее эффективному решению такой же, как и при расчете их эффективности по аддитивной целевой функции.
Учет при синтезе различного вклада функциональных подсистем в эффективность целостной системы
Функциональные подсистемы, из которых состоит некоторая функциональная система, могут вносить различный вклад в ее эффективность и новизну. Поэтому в таких случаях, помимо оценки относительного вклада в эффективность и новизну альтернатив, необходимо оценивать относительный вклад функциональных подсистем.
Для решения данной задачи выполняются следующие процедуры.
1. Строится морфологическая таблица, наименованиями строк которой являются обобщенные функциональные подсистемы исследуемой системы, а наименованиями столбцов — альтернативы.
2. Морфологическая таблица преобразуется в трехуровневую иерархию в виде перевернутого дерева (рис. 5.10), отражающую множество функциональных реализаций. Фокусом иерархии является наименование исследуемого множества технических систем. Уровень 2 иерархии образуют обобщенные функциональные подсистемы (ОФПСi
), т. е. наименования строк морфологической матрицы. Каждая обобщенная функциональная подсистема конкретизируется своим подмножеством альтернативных функциональных реализаций (Аij
), образующих уровень 3 иерархии.

3. Составляются иерархические структуры критериев качества для определения векторов приоритетов обобщенных функциональных подсистем и альтернатив, конкретизирующих указанные подсистемы. Для оценки обобщенных функциональных подсистем и альтернатив могут использоваться как одинаковые по структуре и содержанию иерархии критериев качества, так и различающиеся.
Следует отметить, что оценка по иерархиям критериев второго типа имеет наибольшее распространение.
4. Для сформированных иерархий рассчитывают векторы приоритетов альтернатив  принадлежащих каждой обобщенной функциональной подсистеме, и вектор приоритетов WОФПС
собственно обобщенных функциональных подсистем. Последний определяет их вклад в эффективность и новизну системы в целом. принадлежащих каждой обобщенной функциональной подсистеме, и вектор приоритетов WОФПС
собственно обобщенных функциональных подсистем. Последний определяет их вклад в эффективность и новизну системы в целом.
Значения векторов приоритетов приписываются соответствующим элементам иерархии (см.
рис. 5.10), отражающей множество функциональных реализаций. При этом рассчитанные векторы нормированы следующим образом:

5. На основании предшествующей информации производится иерархический синтез по алгоритму, предназначенному для осуществления свертки в иерархиях с несколькими ветвями, имеющих различное число альтернатив под критериями. В результате получаем нормированный вектор приоритетов всех альтернатив относительно фокуса иерархии.
6. Полученные значения векторов приоритетов альтернатив заносятся в соответствующие ячейки первоначальной морфологической матрицы, на которой осуществляются комбинаторный синтез систем и вычисление для них значений целевых функций аддитивным или мультипликативным методом.
Рассмотрим пример, иллюстрирующий влияние на результаты комбинаторного синтеза различной степени значимости обобщенных функциональных подсистем.
Зададим морфологическую матрицу размерностью 3х3 (рис. 5.11 а), в которой представлены три обобщенные функциональные подсистемы (ОФПСi
; =  ). Каждая ОФПСi
имеет три альтернативы Aij
(i
=j
= ). Каждая ОФПСi
имеет три альтернативы Aij
(i
=j
=  ). Иерархическое представление матрицы приведено на рис. 5.11б. ). Иерархическое представление матрицы приведено на рис. 5.11б.

Для упрощения примера оценка обобщенных функциональных подсистем и альтернатив производится по одному критерию, характеризующему их эффективность.
При попарном сравнении обобщенных функциональных подсистем эксперт отвечает на вопрос, какая подсистема из двух сравниваемых дает больший вклад в новизну целостной системы. При попарном сравнении альтернатив, принадлежащих определенной подсистеме, эксперт отдает то или иное предпочтение, отвечая на вопрос, какая альтернатива из двух сравниваемых обладает большей эффективностью. Степень предпочтения устанавливается по девятибалльной шкале. В табл. 5.14 приведено четыре варианта векторов приоритетов обобщенных функциональных подсистем и альтернатив, принадлежащих последним. Вариант 1 можно характеризовать тем, что все подсистемы и альтернативы, конкретизирующие соответствующую подсистему, равнопредпочтительны. В варианте 2 равнопредпочтительны между собой только обобщенные функциональные подсистемы. В варианте 3 равнопредпочтительны все альтернативы, принадлежащие соответствующим обобщенным подсистемам, а последние отличаются друг от друга вкладом, вносимым в новизну системы в целом. В варианте 4 отсутствуют равнопредпочтительные элементы. Результирующие векторы приоритетов альтернатив относительно фокуса иерархии (см.
рис. 5.11 б) приведены в табл. 5.15.
Таблица 5.14
Варианты оценки обобщенных функциональных подсистем и альтернатив
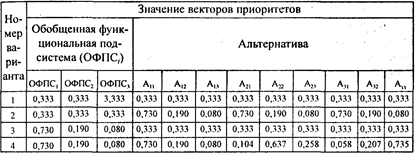
Анализ результатов (см.
табл. 5.14) позволяет сделать следующие выводы. В тех случаях, когда равнопредпочтительны одновременно подсистемы и альтернативы (вариант 1) или только альтернативы (вариант 3), все синтезируемые комбинаторным методом целостные системы будут также равнопредпочтительны. Интегральные значения критерия качества "эффективность системы" для любой целостной системы равны 0,333 как для варианта 1, так и для варианта 3.
Предварительные оценки альтернатив в вариантах 2 и 4 не одинаковы. Учет в иерархическом синтезе различной степени предпочтительности обобщенных функциональных подсистем относительно их вклада в эффективность целостной системы приводит к различным векторам приоритетов альтернатив относительно фокуса иерархии, а следовательно, к различным значениям критерия качества у синтезируемых композиций альтернатив. Например, лучшей для варианта оценки 2 является композиция А11
А21
А31
(значение критерия 0,729), а лучшей для варианта оценки 4 является композиция А11
А22
А33
(значение критерия 0,713).
Для всего морфологического множества вариантов (27 вариантов), синтезированных на морфологической таблице (рис. 5.12), рассчитаны значения критерия качества "эффективность системы" с учетом вариантов 2 и 4 оценки альтернатив и обобщенных функциональных подсистем (см.
табл. 5.15).
Таблица 5.15
Результирующие векторы приоритетов альтернатив по критерию "эффективность"
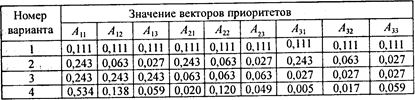
Анализ приведенных графиков (см.
рис. 5.12) показывает, что при установлении равного вклада со стороны обобщенных функциональных подсистем в эффективность целостной системы (кривая 1) можно выделить шесть вариантов систем с существенно более высоким значением этого критерия по сравнению с остальными. Множество этих систем состоит из следующих вариантов:
M
1
= {1, 3, 4, 5, 6, 27}. Указанным вариантам соответствуют следующие комбинации альтернатив: (А11
А21
А32
), (А11
А22
А31
), (А11
А23
A
31
), (
A
12
A
21
A
31
)
, (А13
A
21
А31
), (А11
А21
А31
).
При установлении различного вклада со стороны обобщенных функциональных подсистем в эффективность целостной системы (кривая 2) выделяется девять вариантов конструкций с существенно более высоким значением рассматриваемого критерия по сравнению с остальными.

Множество этих систем состоит из следующих вариантов:
М2
= {1,2, 3,4, 11, 12, 15, 16, 27}.
В заключение можно отметить, что интегральное качество синтезируемой целостной системы определяется, с одной стороны, относительным качеством обобщенных функциональных подсиcтем, а с другой — относительным качеством альтернатив, их реализующих.
Синтез систем на основе качественных классификационных признаков
Синтез вариантов систем на морфологических таблицах можно осуществлять с использованием качественных классификационных признаков, характеризующих свойства альтернатив. Классификационные признаки несут обобщенную специфическую информацию о системах, отличающуюся от рассмотренной ранее информации, определяющей предпочтения по критериям качества. Классификационные признаки могут Сыть использованы в задачах поиска в морфологических множествах вариантов, наиболее сходных по функциям и структуре с заданным известным прототипом или поисковым заданием, отражающим желаемые для исследователя свойства. В таких задачах исследователи и эксперты в большей степени оперируют не количественными данными, а понятиями, имеющими качественный характер. Качественные признаки наиболее информативны и при решении задач синтеза оригинальных (экзотичных) вариантов систем, обладающих свойствами существенной новизны и конкурентоспособности.
Синтез вариантов, сходных с прототипом.
Задачу поиска в морфологическом множестве вариантов систем, наиболее близких к прототипу или поисковому заданию, можно решать на основе мер сходства и различия. Целевая функция в этой задаче имеет следующий вид: найти подмножество S
Î
W
, для элементов которого

где С(
Si
1
,
S
2
)
— мера сходства между описанием синтезированного варианта системы Si
1
и прототипом или поисковым решением S
2
.
Морфологический синтез на основе классификационных признаков с учетом целевой функции, в основе которой лежит мера сходства (5.14), осуществляется следующим образом.
Вначале формируется морфологическая таблица (табл. 5.16), в которой альтернативы Aij
охарактеризованы множеством признаков fij
.
Наличие у альтернативы того или иного признака из указанного множества отмечается в морфологической таблице единицей, а отсутствие — нулем. Прототип, относительно которого вычисляется мера сходства, задается аналогичным образом. Предположим, что прототип синтезирован из альтернатив морфологической таблицы и состоит из композиции А11
А21
А31
. После определения прототипа осуществляется генерация всех вариантов, содержащихся в рассматриваемой таблице. Поисковые образы сгенерированных вариантов сравниваются с образом прототипа (табл. 5.17).

Для каждой пары, состоящей из прототипа и поискового образа варианта, вычисляется мера сходства: C
(
Sl
l
,
S
2
)
=0,87; C
(
Sl
2
,
S
2
) = 0,84; C
(
Sl
18
,
S
2
)
= 0,7. Варианты упорядочиваются по степени близости к прототипу. Подмножество наиболее близких к прототипу вариантов в конечном итоге предоставляется эксперту для более детального анализа.
Выявление в морфологических множествах наиболее оригинальных вариантов.
Прогресс в социально-экономической и технологической сферах определяется внедрением новых эффективных систем. Задача по выявлению и обоснованию новых вариантов систем достаточно трудоемка, так как требует сопоставления систем по большому числу классификационных признаков. Вариант системы, принадлежащей некоторому множеству вариантов, наиболее оригинален, если он в наименьшей степени включен по составу признаков во все оставшиеся варианты из рассматриваемого множества. Формализация процедуры выявления в морфологическом множестве новых, наиболее оригинальных вариантов систем основана на использовании мер включения и сходства.
Поиск наиболее оригинального варианта в морфологическом множестве осуществляется но следующему алгоритму.
Этап 1. На основе морфологической таблицы генерируются все варианты, образующие морфологическое множество.
Этап 2. Для всего морфологического множества вариантов строится матрица включения или матрица сходства.
Этап 3. Вычисляется правый собственный вектор W
матрицы, построенной на предыдущем этапе.
Этап 4. Отыскивается подмножество минимальных значений в векторе W,
которому соответствуют наиболее оригинальные варианты. т.е. ищутся минимумы целевой функции:
Число искомых элементов вектора п
задается исследователем.
Организация данных и процесс их обработки на ЭВМ.
Важнейшим требованием по реализации данного алгоритма выступает требование рациональной организации данных и процесса их обработки с учетом вычислительных ресурсов современных ЭВМ. В соответствии с этим все расчетные операции по синтезу оригинальных решений на морфологической таблице были подвергнуты углубленному анализу и некоторые формулы были существенно модифицированы.
Приведем описание процедуры расчета меры включения множества признаков i
-го решения в множество признаков всех решений, содержащихся в морфологической таблице.
Если морфологическая таблица содержит NS
строк и в каждой строке i
размещается  альтернатив, то число возможных решений альтернатив, то число возможных решений 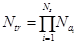 . Для этого множества решений предполагается построить матрицу мер включения, размерность которой будет Ntr
´Ntr
. После этого вычисляется значение меры включения i
-го решения (
Si
)
во все сгенерированные решения (
S
). . Для этого множества решений предполагается построить матрицу мер включения, размерность которой будет Ntr
´Ntr
. После этого вычисляется значение меры включения i
-го решения (
Si
)
во все сгенерированные решения (
S
).
На уровне алгоритмической модели математического обеспечения построение матрицы мер включения не предусматривалось, так как размещение в памяти персональных ЭВМ информации о решениях, число которых превышает 1000, представляется невозможным. С учетом этого формулу вычисления меры включения можно представить следующим образом:
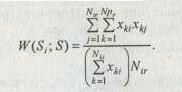
Этот подход к расчету меры включения решает проблему размещения необходимой информации о решениях в памяти ЭВМ. Однако существенным его недостатком является значительное число (Ntr
´Ntr
) выполняемых в рамках одного цикла операций.
В качестве средства решения этой проблемы может выступить следующий подход. Значение меры включения вычисляется для всего множества решений, описание которого по признакам образовано комбинацией описаний входящих в него альтернатив. Таким образом, определенная величина, составляющая меру включения всего решения, может быть отнесена к каждой альтернативе. Это позволит избежать повторного ее расчета при построении целостной меры включения S
i
.
Эти значения могут храниться во внешней памяти ЭВМ. В случае добавления альтернативы к множеству альтернатив в строках морфологической таблицы будет произведен пересчет значений параметров включения только для альтернатив этой строки.
Аналогичные действия будут выполнены и в случае исключения альтернативы из 1-й строки. Представим произведенные над формулой математические преобразования:

где Npr
—
общее число признаков, которыми описаны системы;
Ns
—
число строк в морфологической таблице;
Npj
—
число признаков в строке j
;
xil
и xij
—
значения признака i
соответственно для Sl
и Sj
;
xl
ji
и xk
jl
—
значения признака i
для альтернативы в строке j
, соответствующей Sl
и Sk
;
Индекс k
принимает значения из множества {Р
k
}
номеров альтернатив строки у, входящих в решение Sk
.
Смысл отраженных формулой (5.15) преобразований состоит в следующем. Множество сумм  , а также , а также  может быть разбито, в свою очередь, на большее множество сумм, соответствующих операции не над целостными Si
и Sj
, а над составляющими его альтернативами. Выражение может быть разбито, в свою очередь, на большее множество сумм, соответствующих операции не над целостными Si
и Sj
, а над составляющими его альтернативами. Выражение 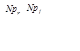 отражает число общих признаков альтернативы в строке j
, входящей в Sl
со всеми альтернативами. отражает число общих признаков альтернативы в строке j
, входящей в Sl
со всеми альтернативами.
Для определения величин, характеризующих операции, выполняемые над описанием по признакам каждой альтернативы, при вычислении меры включения каждого Si
в описание всех S
требуется перейти от формулы, содержащей номера систем, к формулам, основанным на параметрах структуры морфологической таблицы.
Приведем описание формулы, предусматривающей расчеты меры включения W
(
Sl
,
S
)
на основе значения числа общих признаков О
ij
альтернативы А
ij
со всеми альтернативами i
-й строки и числа признаков Zij
альтернативы Aij
.
В соответствии с логикой комбинаторного синтеза целостных технических решений множество S = {Sl
}
включает все альтернативы i
-й строки морфологической таблицы, причем все множество альтернатив из строки i
(A
il
, ... , А
ij
, ..., 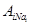 ) может входить во все S
qi
раз, где
) может входить во все S
qi
раз, где

Соотношение (5.15) формально отражает следующий принцип: каждая альтернатива А
ij
i
-й строки входит в Ntr
/
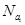 решений, где
решений, где 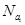 —
число альтернатив в i
-й строке.
—
число альтернатив в i
-й строке.
Таким образом, каждой альтернативе А
ij
i
-й строки можно поставить в соответствие функцию О
ij
= f
(А
il
,..., А
ik
,
..., 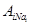 ), характеризующую число общих признаков описания этой альтернативы и описаний множества неповторяющихся альтернатив {А
ij
}, включающего собственно альтернативу Аij
. Указанная функция определяется следующим образом:
), характеризующую число общих признаков описания этой альтернативы и описаний множества неповторяющихся альтернатив {А
ij
}, включающего собственно альтернативу Аij
. Указанная функция определяется следующим образом:

где 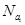 —
число альтернатив в i
-й строке;
—
число альтернатив в i
-й строке;
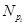 —
число признаков в i
-
й строке;
—
число признаков в i
-
й строке;
х
i
kj
и х
i
kl
—
значение признака k
из множества признаков {xik
}, описывающих альтернативы i
-й строки.
Число признаков, которые включает описание альтернативы А
ij
, является уникальной ее характеристикой. Это число можно определить из соотношения, которое соответствует знаменателю формулы (5.15):

где 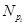 —
число признаков, включаемых описанием альтернативы Ау ;
—
число признаков, включаемых описанием альтернативы Ау ;
х
i
kj
—
значение признака k
из множества признаков {х
i
kj
}, характеризующих альтернативы i
-й строки.
Нормированное значение меры включения Si
в множество S
с учетом приведенных рассуждений может быть рассчитано в соответствии с формулой

где Ns
—
число строк в морфологической таблице;
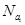 —
число альтернатив в i
-й строке;
—
число альтернатив в i
-й строке;
Ntr
—
число S
, которое может быть получено на морфологической матрице

р
li
—
элемент множества номеров альтернатив, образующих решение Si
.
В результате модификации схемы расчета меры включения предоставляется возможность не производить повторный расчет характеристик О
ij
и Zij
, от которых функционально зависит мера включения W
(
Si
;
S).
Значения О
ij
и Zij
хранятся во внешней памяти ЭВМ и рассматриваются как входные данные для алгоритмической модели процесса функционирования системы морфологического синтеза.
Морфологические методы синтеза рациональных вариантов систем
Отличительной особенностью морфологических методов древовидного, лабиринтного и блочно-лабиринтного синтеза рациональных вариантов систем является то, что в них оценка степени соответствия синтезированного варианта исходной цели синтеза осуществляется непосредственно в ходе процедуры построения искомого варианта, по мере наращивания функциональных подсистем.
Морфологический метод древовидного синтеза.
Он относится к методам морфологического последовательного детерминированного поиска [1] и позволяет существенно уменьшить число операций выбора по сравнению с полным перебором вариантов, содержащихся в морфологической таблице. Общее число операций выбора в методе древовидного синтеза определяется по выражению

где Kl
—
число альтернатив для реализации l
-й обобщенной функциональной подсистемы или функции;
L
—
число обобщенных функциональных подсистем (строк морфологической таблицы).

Метод морфологического древовидного синтеза включает несколько этапов.
Этап 1. Формулируется цель исследования и строится морфологическая таблица для рассматриваемой предметной области (рис. 5.13). Обобщенные функциональные подсистемы, определяющие строки морфологической таблицы, ранжируются системой принятия решений по значимости.
Этап 2. В морфологической таблице выделяются две строки, соответствующие функциональным подсистемам с наивысшей значимостью (рис. 5.13б
). Осуществляется синтез всех парных сочетаний альтернатив, содержащихся в двух выбранных строках таблицы. Для рассматриваемого примера число парных сочетаний альтернатив равно восьми. Полученные парные сочетания альтернатив анализируются исследователем с использованием системы принятия решений по множеству критериев качества. По результатам многокритериального анализа отбирается наиболее рациональный вариант. Допустим, что лучшим является вариант (А11
А42
).
Этап 3. Из морфологической таблицы извлекается очередная по значимости обобщенная функциональная подсистема с альтернативами ее возможной реализации. Проводится комбинирование выделенных на данном этапе альтернатив с рациональным вариантом, полученным на предыдущем этапе. Полученное в результате синтеза множество тернарных комбинаций альтернатив вновь анализируется исследователем с использованием системы принятия решений в целях выявления наиболее рациональной комбинации. Например, лучший вариант на данном этапе может состоять из следующих трех альтернатив — (А11
А42
А32
)
.
Этап 4. Синтез продолжается в соответствии с этапами 2 и 3 вплоть до исчерпания всех обобщенных функциональных подсистем и получения целостного варианта, включающего все подсистемы.
Морфологический метод лабиринтного синтеза.
Данный метод базируется на древовидном методе и относится к классу методов с корректировкой [7].
Идея метода заключается в том, что в процессе поиска рационального решения на морфологической таблице на каждом этапе отбирается не одно, а п
рациональных сочетаний альтернатив.
Наилучшее из этих сочетаний поступает на следующий этап, а п-1
вариантов резервируются.
Если на Р-
м этапе проектировщику не удается получить удовлетворительное решение, комбинируя все альтернативы P
-й обобщенной функциональной подсистемы с наилучшим вариантом, полученным на предыдущем, (Р-1)-м этапе, то организуется просмотр всех п-1
вариантов, зарезервированных на (Р-1)-м этапе со всеми альтернативами Ар
j
, относящимися к Р-
му этапу. Если в этом случае требуемый вариант не отыскивается, то осуществляется возврат на (P
-2)-й этап и организуется последовательный просмотр всех зарезервированных на этом этапе вариантов со всеми альтернативами функциональной подсистемы Р-1
и отбор соответствующего наилучшего (Р
-2)-го варианта. Процедура поиска может продолжаться вплоть до первой и второй по значимости обобщенных функциональных подсистем.
Проиллюстрируем вариант реализации лабиринтного метода синтеза на примере. Предположим, что задана морфологическая таблица, состоящая из четырех строк (рис. 5.14), проранжированных по значимости.
На этапе 1 выполняется полный перебор альтернатив первых двух по значимости обобщенных функциональных подсистем. В результате получается шесть парных сочетаний альтернатив, среди которых для определенности отмечаются два наиболее рациональных варианта: (А11
А22
)
и (
A
12
A
21
)
. Второй по эффективности вариант (A12
A21
)
отмечается в качестве резервного. Проводится согласование наиболее рационального варианта с исходными требованиями на проектирование. При наличии такого соответствия процедура синтеза продолжается на этапе 2, в противном случае уточняются исходные требования и состав морфологической таблицы.
На этапах 2 и 3 синтез осуществляется по тем же правилам, что и на этапе 1. В конечном итоге при прохождении всех обобщенных функциональных подсистем в рассматриваемом примере остается два варианта системы: (А11
А22
А32
А41
)
и (А11
А22
А32
А42
)
. Если хотя бы один из этих вариантов удовлетворяет исходной цели проектирования, то процедура синтеза заканчивается, в противном случае работа продолжается на этапе 4.

Этап 4 предполагает возврат на этап 2 и извлечение зарезервированного варианта, которым является вариант, состоящий из комбинации альтернатив (А11
А22
А31
)
. Этот резервный вариант комбинируется с альтернативами, принадлежащими четвертой строке морфологической таблицы. В результате получаются два новых сочетания из четырех альтернатив, которые проверяются на предмет соответствия техническому заданию. Если такое соответствие есть, то процедура синтеза заканчивается, в противном случае процесс синтеза продолжается. При исчерпании всех резервных вариантов, зафиксированных на втором этапе, работа по поиску решения задачи продолжается с извлечения очередного резервного варианта на первом этапе. Далее процесс повторяется в соответствии с ранее представленным алгоритмом.
Лабиринтный метод синтеза по сравнению с древовидным позволяет повысить вероятность получения наиболее эффективного варианта системы, удовлетворяющего требованиям проектировщика. Это достигается за счет итерационной процедуры возврата к пространству меньшей размерности. При реализации лабиринтного метода на каждом этапе выбор наиболее эффективного и резервных вариантов проводится на основе многокритериального принятия решений методом анализа иерархии или методом, основанным на теории нечетких множеств. Компьютерная реализация лабиринтного метода обеспечивает запоминание всего многоитерационного маршрута прохождения по морфологической таблице. Это позволяет проанализировать принятые ранее решения и выбрать окончательное, наиболее рациональное.
Морфологический метод блочно-лабиринтного синтеза.
Этот метод предполагает конструирование систем на отдельных блоках морфологической таблицы, что позволяет свести решение задачи морфологического синтеза к задаче меньшей размерности [8,9].
Процесс синтеза рационального варианта осуществляется "сверху вниз", т. е. от более обобщенных функциональных подсистем к более конкретным реализациям этих подсистем.
Существуют две модификации метода блочно-лабиринтного синтеза.
Рассмотрим первую модификацию.
Метод состоит из ряда этапов, на каждом из которых осуществляются процедуры структурирования информации, оценки вариантов и принятия решений.
Этап 1. Выбирается объект исследования, формируется исходная цель синтеза системы и составляется список требований, которым должна удовлетворять искомая система. Требования ранжируются по значимости.
Этап 2. Осуществляется построение "скелетной" морфологической таблицы, состоящей из основных (главных) функциональных подсистем рассматриваемой системы и основных вариантов, реализующих выделенные функциональные подсистемы. К основным функциональным подсистемам относятся такие, которые определяют сущность системы в целом и отличают ее от других систем.
Этап 3. Проводится синтез рациональных вариантов на "скелетной" морфологической таблице. Для выполнения этой процедуры используется метод лабиринтного синтеза.
В результате получается так называемая минимальная исследуемая функциональная система, включающая то минимальное количество функциональных подсистем, с помощью которых можно реализовать основную функцию системы в целом. Конечно же, такая функциональная система, как правило, не может удовлетворить всем требованиям задания и подвергается дальнейшему совершенствованию.
Этап 4. В синтезированном на этапе 3 рациональном варианте определяются "слабые" функциональные элементы, не удовлетворяющие в полной мере предъявляемым требованиям. Для улучшения основных "слабых" элементов строятся дополнительные морфологические таблицы. Наименованиями строк этих таблиц являются наименования вспомогательных функциональных подсистем. Эти подсистемы получены в результате декомпозиции "слабых" элементов.
Этап 5. С помощью метода лабиринтного синтеза осуществляется поиск рациональных вариантов на дополнительных морфологических таблицах.
Процедура выявления "слабых" элементов может быть распространена и на рациональные варианты, полученные на дополнительных матрицах.
Этап 6. Проводится компоновка вновь синтезированных на дополнительных морфологических таблицах функциональных подсистем в целостную систему.
В заключение принимается решение о соответствии синтезированного решения исходным требованиям. Если такое соответствие есть, то задача считается решенной, в противном случае проделываются следующие процедуры:
• расширяется число отбираемых (резервируемых) вариантов на промежуточных этапах метода при поиске рациональных вариантов на морфологических таблицах;
• пересматриваются требования исходной цели синтеза;
• составляются новые "скелетные" и (или) дополнительные морфологические таблицы;
• осуществляется варьирование методами синтеза рациональных вариантов.
Рассмотрим кратко вторую модификацию
метода блочно-лабиринтного синтеза.
Этап 1. Проектировщиком выполняются действия, аналогичные тем, которые описаны в первой модификации блочно-лабиринтного метода.
Этап 2. Строится морфологическая таблица. Осуществляется разбиение морфологической таблицы на блоки в соответствии с количеством функциональных подсистем, входящих в целостную систему. Каждый-блок может содержать несколько функциональных подсистем.
Этап 3. Осуществляется синтез подмножеств рациональных вариантов функциональных подсистем в каждом блоке. Если блок содержит одну подсистему, то из множества альтернатив выбирается требуемое подмножество наилучших с использованием системы принятия решений.
Для синтеза рациональных вариантов в блоках, содержащих более двух подсистем, используется метод лабиринтного поиска. Когда же блок содержит два признака, то для выбора рациональных решений несложно использовать метод полного перебора возможных сочетаний альтернатив.
Этап 4. Направлен на формирование новой морфологической таблицы меньшей размерности, чем исходная. Число строк этой таблицы равно числу функциональных подсистем (числу блоков, на которые разбита исходная морфологическая таблица). Альтернативами вновь сформированной морфологической таблицы являются рациональные варианты, синтезированные на отдельных блоках (этап 3).
Этап 5. Предусматривается синтез технической системы в целом, проводимый лабиринтным методом на новой морфологической таблице, и принятие решения о соответствии полученного окончательного решения исходным требованиям.
Применение блочно-лабиринтного синтеза наиболее оправдано для многофункциональных сложных организационных и социально-экономических систем.
Синтез многофункциональных систем при снятых ограничениях на число и характер выполняемых ими функций
Одна из закономерностей развития больших систем, прослеживающаяся особенно ярко в последнее время, — это повышение их сложности и увеличение числа выполняемых ими функций. В зависимости от целей синтеза в исходной постановке задачи на создание многофункциональных систем число и характер выполняемых ими функций могут быть либо строго зафиксированы, либо ограничения на число и характер реализуемых функций отсутствуют. При этом предполагается, что оставляемые в системе функции и элементы, их реализующие, обеспечивают, с одной стороны, нормальную работоспособность системы, а с другой — ее наилучшую эффективность для некоторых определенных в исходном задании условий производства и эксплуатации (определенного сегмента рынка).
Яркими примерами многофункциональных сложных систем в бытовой технике являются аудио- и видеосистемы. Такие системы могут содержать в одном блоке одновременно разное по количеству и составу число таких функциональных элементов, как магнитофон, радиоприемник, лазерный компакт-диск, телевизор, видеомагнитофон, персональный компьютер и т. д.
В связи с установившимися тенденциями развития современных систем актуально решение проблемы по созданию подходов и методов, позволяющих решать задачи синтеза рациональных многофункциональных систем при снятых ограничениях на число и характер выполняемых ими функций. Решение поставленной задачи может быть проведено в три этапа. На этапе 1 выбирается рациональный состав функций Fi
(обобщенных функциональных подсистем). На этапе 2 для каждой функции формируется множество наиболее рациональных альтернатив. На этапе 3 определяется лучшая композиция альтернатив, реализующих исследуемые функции.
Рассмотрим подробнее один из подходов для решения обозначенной задачи.
Решение задачи начинается с построения морфологической таблицы, в строках которой отражены возможные для реализации в проектируемой системе функции (Fi
). Столбцы таблицы заполняются альтернативами (Аij
), обеспечивающими выполнение функций с различной степенью эффективности. В качестве примера рассматривается морфологическая таблица мероприятий, планируемых администрацией города для реализации в ближайшем будущем (табл. 5.18).
Пусть в исходной постановке задачи сняты ограничения на число и характер выполняемых функций в проектируемой целостной системе. При этом требуется синтезировать рациональную систему с учетом конкретной ситуации, сложившейся в городе.
Таблица 5.18
Исходная морфологическая таблица

Сначала исходное множество функций F
={
F
1
,
F
2
,
F
3
}
обрабатывается алгоритмом, обеспечивающим генерацию множества F
={
F
1
,
F
2
,
F
3
,
F
1
F
2
,
F
1
F
3
,
F
2
F
3
,
F
1
F
2
F
3
}
всех единичных, парных, тернарных и т.д. сочетаний элементов из множества F
.
В сформированном множестве не все единичные функции и сочетания этих функций могут обеспечить работоспособность целостной системы. Поэтому отбираются лишь допустимые функции и их сочетания, которые обеспечивают нормальную работу системы. Для рассматриваемой задачи допустимыми функциями являются: F
1
,
F
1
F
2
,
F
1
F
3
,
F
1
F
2
F
3
.
Затем строится иерархическая система критериев качества для выбора наиболее предпочтительного сочетания функций в проектируемой системе.
Один из вариантов иерархии для выбора предпочтительной функции или сочетаний функций приведен на рис. 5.15.

Результаты иерархического синтеза по каждому критерию приведены в табл. 5.19, из которой видно, что приоритет функциональных композиций существенно зависит от критериев.
После установления наиболее эффективных композиций функций строятся морфологические таблицы, систематизирующие варианты реализации функций. Например, для повышения жизненного уровня населения города (см.
табл. 5.19) наиболее эффективными и предпочтительными являются две композиции функций: F
1
F
3
и F
1
F
2
F
3
.
Для этих композиций построены две морфологические таблицы (табл. 5.18, 5.20), элементами которых являются различные альтернативы по реализации соответствующих функций.
Таблица 5.19
Значение векторов приоритетов функциональных композиций
| Критерий качества системы
|
Значение для вектора приоритетов функциональных композиций
|
| F1
|
F1
F2
|
F1
F3
|
F
1
F
2
F
3
|
| Быстрая прибыль
Рабочие места
Экология
Повышение жизненного уровня
|
0,1
0,05
0,5
0,1
|
0,2
0,05
0,1
0,1
|
0,2
0,5
0,2
0,4
|
0,5
0,4
0,2
0,4
|
Таблица 5.20
Исходные данные для синтеза двух функциональных систем
| Функция
|
Альтернатива
|
| F
1
-
реконструкция предприятий
|
А11
- тракторный завод
|
A
12
- моторный завод
|
А13
- завод буровой техники
|
| F
3
-
развитие транспортной системы
|
A
31
- метрополитен
|
А32
-троллейбусные маршруты
|
А33
- маршрутные такси
|
Окончательный синтез комплексных решений на морфологических таблицах может проводиться различными алгоритмами (полный перебор, древовидный или лабиринтный синтез) в зависимости от их размерности. Отобранные в результате синтеза лучшие решения из первой и второй матриц сравниваются между собой по дополнительному комплексу критериев качества в целях выбора окончательного наилучшего варианта.
Синтез многофункциональных систем с различным числом самостоятельных составляющих подсистем
В процессе эвристического поиска новых эффективных систем часто прибегают к следующему правилу проектирования:
"Для эффективной реализации целей синтеза создается один объект, выполняющий несколько функций, благодаря чему отпадает необходимость в других объектах, либо, наоборот, один объект, выполняющий одновременно несколько функций, заменяется несколькими объектами с самостоятельными функциями". Одно из прогрессивных направлений предполагает синтез многофункциональных систем, реализованных минимальным числом подсистем. Такие многофункциональные системы позволяют повысить их производительность и качество в определенных условиях эксплуатации и оказываются более предпочтительными, чем многофункциональные системы, у которых за каждую функцию отвечает самостоятельная подсистема.
Задача многовариантного синтеза таких систем может быть успешно решена на морфологических таблицах. Построение морфологических таблиц и алгоритмов синтеза эффективных вариантов имеет в этих случаях свои особенности, которые рассматриваются ниже.
Предположим, что исходная система выполняет три функции: F
1
,
F
2
и F
3
. Указанные функции в общем случае могут быть реализованы на основе трех или двух альтернативных элементов или же на основе одного элемента (табл. 5.21). Далее генерируются все возможные сочетания функций и для каждого сочетания подбираются альтернативы, которые сводятся в матрицу (табл. 5.22). Верхние индексы в матрице соответствуют порядковому номеру альтернативы, а нижние — номерам функций, которые реализуются альтернативами.
Таблица 5.21
Варианты систем с различным числом элементов

На основании матрицы (см.
табл. 5.22) формируются альтернативные структуры морфологических таблиц для синтеза вариантов систем. В морфологических таблицах число и состав функций соответствуют составу и числу функций исходной системы.
Таблица 5.22
Сочетания функций и их реализации
Синтез систем на основе различного числа элементов осуществляется с помощью альтернативных морфологических таблиц:

Синтез вариантов системы на основе приведенных морфологических таблиц может проводиться двумя способами. В соответствии с первым способом первоначально выбирается наиболее предпочтительная морфологическая таблица, а затем на ней осуществляется синтез и отбор эффективных вариантов. Второй способ предполагает синтез вариантов одновременно на всех морфологических таблицах с последующим усечением множеств вариантов по тем ли иным критериям качества. Поиск эффективных вариантов может быть осуществлен различными методами, например по критерию отношения показателей эффективности и издержек, с учетом эффективного распределения имеющихся ограниченных ресурсов и т.п.
Анализ морфологических множеств по различным комбинациям критериев
При решении ряда задач синтеза систем комбинаторно-морфологическим методом возникает потребность в определении эффективности полученных решений по различным сочетаниям критериев качества. Это особенно актуально в тех случаях, когда синтезируемые системы мало отличаются друг от друга или от конкурирующего объекта по всему комплексу рассматриваемых критериев качества.
Для решения указанной задачи предложена методика исследования морфологических множеств систем, систематизированных в морфологических таблицах по различным сочетаниям критериев качества, которая реализована в виде компьютерной системы. Методика включает шесть процедур.
Процедура 1.
Исследование начинается с формирования морфологической таблицы. Здесь же может быть задан конкурирующий объект в виде комбинации альтернатив, соответствующих обобщенным функциональным подсистемам, образующим строки морфологической таблицы.
Процедура 2.
Формируется исходное множество наиболее важных критериев качества для расчета эффективности отдельных альтернатив морфологической таблицы и синтезированных целостных вариантов. Для каждой обобщенной функциональной подсистемы могут быть определены на основе исходного множества критериев подмножества, состоящие из полностью или частично пересекающихся по содержанию критериев качества.
Процедура 3.
Альтернативы морфологической таблицы оцениваются экспертом попарно или относительно стандартов. На основании экспертных данных по каждой обобщенной функциональной подсистеме вычисляется вектор приоритетов альтернатив по отдельным критериям качества.
Процедура 4.
Алгоритмом полного перебора на морфологической таблице генерируются все возможные варианты систем.
Процедура 5.
Для каждого синтезированного варианта системы генерируются все возможные парные, тернарные и т. д. сочетания критериев качества. По каждому сочетанию критериев качества рассчитываются их суммарные значения, которые присваиваются соответствующим альтернативам.
Процедура 6.
Осуществляется сравнение синтезированных вариантов систем между собой или с заданным конкурирующим объектом. При этом каждая анализируемая пара объектов сравнивается по всем сгенерированным в процедуре 5 сочетаниям критериев качества.
Выбор лучших вариантов производится в соответствии с тремя решающими правилами.
Решающее правило 1.
Требуется найти такое решение в множестве решений, сгенерированных в процедуре 4, эффективность которого имеет максимальное значение по заданному исследователем числу критериев качества, образующих некоторую i
-ю композицию из множества полученных в процедуре 5.
Целевая функция для указанного правила имеет следующий вид:

где Эс
— эффективность синтезированной системы;
а
ij
k
— относительная оценка альтернативы А
ij
по k
-му критерию, являющейся элементом морфологической матрицы и компонентом синтезированной системы.
i
— порядковый номер обобщенной функциональной подсистемы (ОФПСi
), (i =  —
число ОФПС в системе); —
число ОФПС в системе);
j
—
порядковый номер альтернативы, который может иметь различное максимальное значение у каждой ОФПСi
;
k
— критерий качества;
Р —
число критериев качества, учитываемых при вычислении эффективности.
Решающее правило 2.
Для всех единичных критериев, а также сочетаний любых двух, трех, четырех и т. д. вплоть до всего рассматриваемого в задаче множества критериев качества необходимо определить одну или несколько наиболее эффективных систем, удовлетворяющих целевой функции (5.16).
Решающее правило 3.
Для всех единичных критериев, а также сочетаний любых двух, трех, четырех и т.д. вплоть до всего рассматриваемого в задаче множества критериев качества необходимо определить одну или несколько систем со значениями эффективности, максимально превышающими эффективность заданной конкурирующей системы. Целевая функция в данном случае имеет следующий вид:

где aij
k
—
относительные оценки эффективности, относящиеся к альтернативам А
ij
, входящим в композицию синтезируемых систем;
bij
k
—
относительные оценки эффективности, относящиеся к альтернативам, входящим в композицию, представляющую конкурирующую систему.
Рассмотрим пример выявления систем, синтезированных комбинаторно-морфологическим методом, обладающих более высокой эффективностью по ряду критериев по сравнению с заданным конкурирующим образцом.
Таблица 5.23
Морфологическая матрица с высокоэффективным конкурирующим аналогом (
A
11
A
21
A
31
)
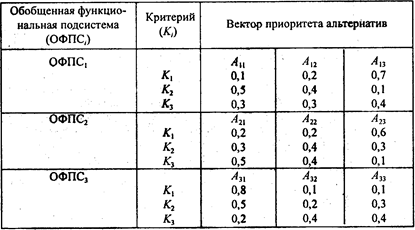
Пусть задана морфологическая таблица (табл. 5.23), содержащая в качестве наименований строк три обобщенные функциональные подсистемы. Каждая подсистема имеет по три альтернативы А
ij
для реализации первых. Все альтернативы оценены по одному множеству критериев качества К1
, К2
и K
3
. Значения критериев качества для альтернатив приведены в соответствующих ячейках матрицы. В качестве конкурирующего варианта определена система, состоящая из альтернатив (
A
11
A
21
A
31
)
. Альтернативы конкурирующего объекта по условию задачи не могут присутствовать в синтезируемых системах, подлежащих сравнению с первым. Таким образом, на морфологической матрице в результате синтеза получено 2×2×2=8 отличающихся друг от друга вариантов.
В табл. 5.24 для синтезированных решений приведены рассчитанные значения их эффективности (Э
c
)
по всем единичным критериям качества, их парным и тернарным сочетаниям. Там же даны значения эффективности по соответствующим критериям для конкурирующего объекта (А11
А21
А31
)
.
Таблица 5.24
Значения эффективности вариантов систем по различным критериям качества
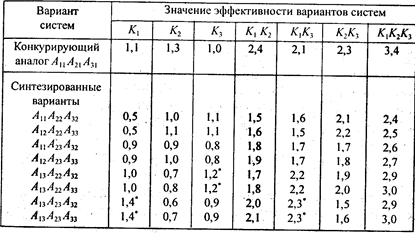
Анализ приведенных результатов показывает, что по критериям К1
и К1
K
3
две новые синтезированные системы: (А13
А23
А32
)
и (А13
А23
А33
)
, а по критерию К3
,
также две системы: (А13
А22
А32
)
и (А13
А22
А33
)
значительно эффективнее конкурирующего объекта. Эти системы отмечены звездочкой (см.
табл. 5.24).
По критерию K2
и сочетаниям критериев К1
К2
, К2
К3
, К1
К2
К3
конкурирующий объект превосходит в эффективности все синтезированные новые варианты систем.
Морфологический синтез систем по критерию комбинационной новизны
Критерий комбинационной новизны численно характеризует для представленного в морфологической таблице класса систем новые сочетания функциональных подсистем. Этот критерий определяется по формуле

где N —
число строк в морфологической таблице (число функциональных подсистем);
Ri
и Р
i
—
номера столбцов морфологической таблицы соответственно в строках R
и Р,
альтернативы из которых вошли в i
-ю систему;
К —
переменная; К =
1, если альтернатива из строки R
и столбца Ri
образовала известную комбинацию с альтернативой из строки Р
и столбца Рi
; К = 0,
если эта комбинация ранее была неизвестна в пределах рассматриваемого класса объектов.
Определение критерия комбинационной новизны для каждой системы осуществляется на основании матриц комбинационных связей альтернатив. Построение указанных матриц ведется в соответствии со следующими принципами. Рассматривается морфологическая таблица, содержащая N
строк. Для всех альтернатив i
-й строки формально отражаются комбинационные связи с альтернативами, содержащимися во всех остальных строках морфологической таблицы:
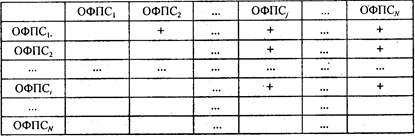
В приведенной матрице плюсами обозначены взаимосвязи между функциональными подсистемами, альтернативы которых необходимо попарно оценить по признаку новизны. Для альтернатив каждой пары функциональных подсистем ОФПСi
и ОФПСj
строятся матрицы комбинационных связей альтернатив К
ij
= {К
lr
ij
}
, l
= 1,..., п
i
;
r
= 1,..., nj
,
где п
i
и п
j
—
соответственно число альтернатив в i
-й и j
-й строках морфологической таблицы. Число матриц К
= {К
ij
}
определяется по формуле
Nk
= N
( N -
1 )/ 2,
где N —
число строк морфологической таблицы.
Рассмотрим пример вычисления критерия комбинационной новизны. Пусть задана исходная морфологическая таблица (табл. 5.25).
Таблица 5.25
Морфологическая таблица
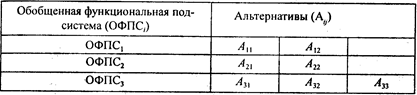
На основании морфологической таблицы с учетом экспертной информации строится Nk
=3(3 -1 )/2=3 матриц {К
lr
ij
}
парных комбинационных связей альтернатив А
ij
. Здесь верхние индексы указывают номера сравниваемых обобщенных функциональных подсистем, а нижние индексы — количество альтернатив двух сравниваемых подсистем.
Матрицы парных комбинаций имеют следующий вид:

Содержание матрицы 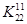 свидетельствует о том, что для альтернативы A
11
известны решения, в которых она участвовала в сочетании с альтернативами A
21
или А22
, а для альтернативы A
12
не известны случаи ее участия в комбинациях с альтернативами A21
и А22
.
Значения критерия комбинационной новизны для 12 синтезированных на морфологической таблице (см.
табл. 5.25) вариантов (Si
) рассчитаны с учетом формулы (5.17): свидетельствует о том, что для альтернативы A
11
известны решения, в которых она участвовала в сочетании с альтернативами A
21
или А22
, а для альтернативы A
12
не известны случаи ее участия в комбинациях с альтернативами A21
и А22
.
Значения критерия комбинационной новизны для 12 синтезированных на морфологической таблице (см.
табл. 5.25) вариантов (Si
) рассчитаны с учетом формулы (5.17):

Большей новизной обладают те решения, у которых наибольшее значение критерия комбинационной новизны. В рассматриваемом случае к таким решениям относятся Sy
,
S
\
g
,
S
^.
5.6. Методика решения прикладных задач на ЭВМ
5.6.1. Анализ и синтез систем на основе функционально-стоимостного подхода
Комбинаторно-морфологический метод синтеза может быть эффективно применен для решения задач функционально-стоимостного анализа и прогнозирования систем. При этом предполагается, что исследуемая система улучшается одновременно по нескольким или всем функциям и по каждой функции имеет более одной альтернативы по ее реализации.
Рассмотрим наиболее характерные случаи синтеза рациональных решений на морфологических таблицах при условии, что в искомое решение обязательно включается по одной альтернативе по всем имеющимся в таблице функциям, т.е. из каждой строки таблицы.
Случай 1.
Каждая альтернатива А
ij
морфологической таблицы имеет оценку ее выгод (достигаемой эффективности) и оценку требуемых для реализации издержек, которые выражены в денежных единицах, т.е. каждой А
ij
Î {Bij
; И
ij
}, где Bij
, И
ij
— значения в денежных единицах выгод и издержек.
Поиск рациональных вариантов решений может быть осуществлен в соответствии со следующими постановками задач.
1. Найти решения, удовлетворяющие одной из приведенных целевых функций:

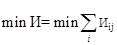
где В, И — значения выгод и издержек для m
-го целостного решения;
Bij
, И
ij
— значения выгод и издержек альтернативы А
ij
(i
=  , п —
число строк морфологической таблицы; j
=
, п —
число строк морфологической таблицы; j
=  , для i
= l; j
= , для i
= l; j
=  , для i
= 2; j
= , для i
= 2; j
= 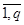 для i
= п). для i
= п).
2.
Найти одно или несколько решений, удовлетворяющих целевой функции

3. Найти одно или несколько решений по отношению выгод к издержкам, удовлетворяющих целевой функции и ограничениям:

На целевую функцию может быть наложено одно из приведенных ограничений:

Здесь а
и b
—
пороговые значения (ограничения) выгод и издержек, выраженные в денежных единицах.
Случай
2.
Каждая альтернатива Аij
морфологической таблицы имеет только экспертную оценку выгод и издержек. Т.е. А
ij
Î {vij
B
, vij
И
}, верхние индексы характеризуют соответственно выгоды (В) и издержки (И).
Поиск рациональных решений осуществляется по следующим целевым функциям.
1. Найти решения, удовлетворяющие одной из приведенных целевых функций


Здесь VВ
,
V
И
—
значения выгод и издержек для т-го
целостного решения, каждая альтернатива А
ij
которого охарактеризована экспертными значениями vij
B
, vij
И
(в частности, значениями нормированного вектора приоритета альтернатив по критерию качества); i
= 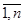 (п —
число строк морфологической таблицы); j
=
(п —
число строк морфологической таблицы); j
= 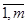 для i
= 1; j
= для i
= 1; j
= 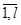 для i
=2; j
= для i
=2; j
=
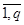 для i
= n
. для i
= n
.
2. Найти рациональные решения по отношению выгод к издержкам, представленному в целевой функции экспертными данными:

С учетом накладываемых на целевую функцию ограничений имеем:

при выполнении одного из приведенных ограничений:

Здесь a
ç
,
b
ç
—
ограничения (пороговые значения) выгод и издержек, выраженные в безразмерной шкале экспертных оценок.
При этом в общем случае значения vij
B
и vij
И
представляют интегральные оценки, принадлежащие вектору приоритетов элементов (альтернатив) i
-й строки матрицы по экономическим, техническим, социальным, управленческим и другим факторам. Данные векторы рассчитываются для каждой строки морфологической матрицы методами анализа иерархических систем.
Случай
3.
Каждая альтернатива А
ij
морфологической матрицы имеет экспертную оценку для оценки выгод (неопределенность по выгодам) от ее реализации и оценку издержек в денежных единицах, т. е.А
ij
Î { vij
B
, И
ij
}.
Поиск рациональных решений осуществляется по следующей целевой функции: найти рациональные решения по отношению выгод, выраженных экспортно, к издержкам, определенным в денежных единицах:

На целевую функцию может быть наложено одно из приведенных ниже ограничений:

Обозначения в целевых функциях и ограничениях соответствуют вышепринятым.
Случай 4.
Каждая альтернатива А
ij
морфологической матрицы имеет оценку выгод в денежном выражении и экспертную оценку издержек (неопределенность по издержкам), т.е. А
ij
Î {вij
, vij
И
}.
Поиск рациональных решений осуществляется по следующей целевой функции: найти рациональные решения по отношению выгод, выраженных в денежных единицах, к издержкам, определенным экспортно:

На целевую функцию может быть наложено одно из приведенных ниже ограничений:

При решении практических задач число искомых рациональных решений задается исследователем и может находиться в пределах от одного до нескольких десятков в зависимости от размерности задачи и конкретных условий ее решения.
Рассмотрим подходы по применению комбинаторно-морфологического метода для проведения функционально-стоимостного анализа систем.
Пусть имеется морфологическая таблица, описывающая множество систем (табл. 5.26).
Каждая система содержит три функциональные подсистемы F,. Подсистемы имеют альтернативные решения, для которых известны значения выгод и издержек, выраженные в денежных единицах (млн руб.) — случай 1. Предположим, требуется синтезировать виброзащитную систему, удовлетворяющую целевой функции:
max В/И при условии В = Вmах. (5.18)
Таблица 5.26
Морфологическая таблица с оценкой альтернатив по критериям выгод (В) и издержек (И)
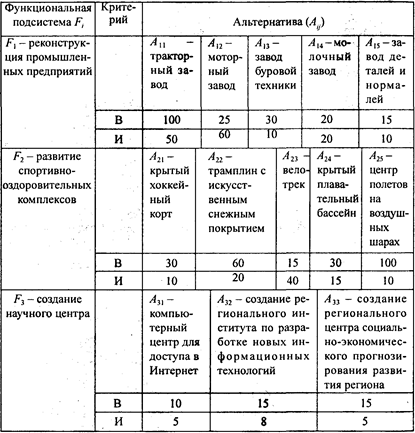
Поиск решений на морфологической матрице методом сканирования позволяет выявить два решения, обеспечивающих максимальную выгоду в размере 215 млн руб.: (А11
А25
А32
) и (А11
А25
A
33
). Однако отношение выгод к издержкам у первого и второго вариантов решения различны и составляют соответственно 215/68 и 215/65. Следовательно, искомым решением является второе.

Для проведения функционально-стоимостного анализа систем в ситуациях, когда отсутствуют количественные данные в денежном выражении по выгодам и издержкам (случай 2), осуществляется предварительная оценка альтернатив. С этой целью строятся два типа иерархий для оценки соответственно выгод и издержек. Если при оценке альтернатив, относящихся к функциональной подсистеме, требуется учесть ее особенности, то для нее строится уникальная иерархия. На рис. 5.16 приведен пример иерархических систем для оценки выгод и издержек от реализации альтернатив. Причем выгоды оцениваются по уникальным иерархиям, относящимся к каждому из трех элементов, а издержки по всем элементам оцениваются по одной иерархии.
Альтернативы каждой строки таблицы оцениваются методами попарного сравнения, относительно стандартов или копирования. Оценка в экспертных единицах проводится по соответствующим иерархиям относительно критериев, непосредственно связанных с альтернативами. Далее вычисляются векторы приоритетов альтернатив относительно корневого показателя для выгод и издержек. Значения векторов приоритетов заносятся в соответствующие ячейки морфологической таблицы (табл. 5.27).
Таблица 5.27
Морфологическая таблица с оценкой альтернатив по критериям выгод (V
B
)
и издержек (
V
И
) и
векторов приоритетов
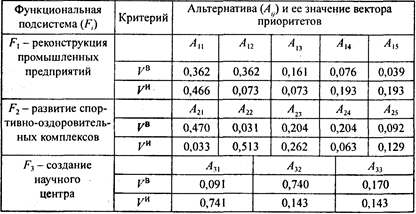
Поиск решений, удовлетворяющих заданной целевой функции max V
В
/
V
И
,
может проводиться по одному из алгоритмов, приведенных в этой главе. На рис. 5.17 показаны абсолютные значения критериев: выгод (d
1
) и издержек (d
2
) и относительные значения отношений выгод к издержкам (d
3
) для 14 наилучших вариантов, синтезированных на рассматриваемой морфологической таблице. Относительные значения d
3
получены путем деления отношений d
1
/
d
2
,
принадлежащих синтезированным вариантам, на максимальное значение (d
1
/d
2
) max.

5.6.2. Рациональное распределение ресурсов в системах
Задача распределения ресурсов на основе метода морфологического синтеза имеет следующую постановку.
Пусть имеется морфологическая таблица, описывающая множество вариантов исследуемой системы. При этом каждая система имеет п
обобщенных подсистем, характеризующих строки таблицы. Каждая обобщенная подсистема может быть реализована конечным числом альтернатив А
ij
. Причем для каждой i
-й строки индекс j
имеет свое максимальное значение. Альтернативам каждой строки присвоены значения относительной эффективности Э
ij
и значения требуемого для реализации ресурса Р
ij
. Задан ресурс (РИ
— имеющийся в наличии ресурс), который необходимо оптимально распределить между альтернативами морфологической таблицы по следующим правилам.
Правило 1.
Распределить ресурс между одной или несколькими комбинациями (количество задается исследователем), включающими в свой состав обязательно по одной альтернативе из
каждой строки морфологической таблицы и удовлетворяющими одной из двух целевых функций — (5.19) или (5.20).
Правило 2.
Распределить ресурс между одной или несколькими комбинациями (количество задается исследователем), включающими в свой состав по одной альтернативе, но не из каждой строки таблицы, а из любого парного, тернарного, n
-1-го сочетания строк морфологической таблицы и удовлетворяющими одной из двух целевых функций — (5.19) или (5.20).
Распределение ресурса по правилу 2 осуществляется в случаях, когда условиями задачи не определено требование обязательного использования всех строк морфологической таблицы в формировании варианта системы или имеющийся ресурс из-за его ограниченности нельзя распределить между всеми строками таблицы.
Обобщенный алгоритм определения комбинации альтернатив, обеспечивающей оптимальное распределение ресурса, включает следующие шаги.
Шаг 1. Определяется морфологическая таблица, состоящая из п
строк, отражающих обобщенные функциональные подсистемы. Для каждой обобщенной функциональной подсистемы задается требуемое число альтернатив Аij
по их реализации.
Каждая альтернатива Аij
характеризуется значениями: Э
ij
— эффективности и Р
Tij
— требуемого ресурса для практической реализации альтернатив.
Задается имеющийся в наличии ресурс РИ
, который необходимо оптимально распределить (по условию задачи ресурса может хватить только на одну комбинацию альтернатив, реализующих все или часть подсистем синтезируемого варианта).
Шаг 2. Методом полного перебора генерируется либо множество всех возможных комбинаций альтернатив с учетом включения в комбинацию всех п
обобщенных функциональных подсистем (правило 1), либо множество всех возможных комбинаций альтернатив, состоящих из всех парных, тернарных и т.д. вплоть до n
-
1 сочетаний обобщенных функциональных подсистем (правило 2).
Шаг 3. Для каждой сгенерированной комбинации альтернатив определяются суммарные значения: требуемого ресурса (РT
), относительной эффективности (Э
) и относительной эффективности на единицу требуемого ресурса (Э/РT
). Указанные значения вычисляются по следующим выражениям:

где п —
число обобщенных подсистем, входящих в сгенерированный вариант системы;
i
— порядковый номер обобщенной подсистемы, входящей в сгенерированный вариант системы;
j
— порядковый номер альтерантивы i
-й обобщенной подсистемы.
Ш а г 4. Определяется искомая комбинация альтернатив с учетом задаваемой целевой функции и ограничений:

Ограничения, накладываемые на целевые функции:

Конец алгоритма.
Рассмотрим пример распределения ресурса на комбинации альтернатив, генерируемых методом морфологического синтеза.
Пусть морфологическая таблица (табл. 5.28) содержит некоторое множество функциональных элементов для синтеза системы продвижения товара на рынок.
Таблица 5.28
Морфологическая таблица распределения ресурсов между альтернативами в системе продвижения товара на рынок
Синтезируемая система реализуется тремя обобщенными функциональными подсистемами: распространения рекламы, стимулирования сбыта в сфере торговли, пропаганды товара. Для каждой подсистемы задано множество альтернатив А
ij
которые характеризуются значениями эффективности Э
ij
и требуемого ресурса PT
для их практической реализации. Требуется найти систему, представленную комбинацией, включающей по одной альтернативе из каждой строки таблицы и удовлетворяющей следующей целевой функции:

при условии Р
T
< РИ
= 36 условных денежных единиц.
Сгенерированные на морфологической таблице все тернарные комбинации (12 вариантов) альтернатив и рассчитанные для них значения требуемого ресурса (РT
), эффективности (Э
) и отношения Э/Р
T
приведены в табл. 5.29. Из ее анализа видно, что имеющийся ресурс, равный 36 условным денежным единицам, можно распределить между девятью комбинациями, кроме комбинаций с порядковыми номерами 6, 9 и 10. Оптимальным вариантом, удовлетворяющим целевой функции (5.21), является комбинация из альтернатив (А11
А22
А31
) с порядковым номером 3 и со значением Э/РT
== 0,060. При этом имеющийся ресурс расходуется не полностью и в резерве остается 36 - 20 = 16 денежных единиц.
Если изменить условия задачи таким образом, что требуется найти комбинацию альтернатив, обеспечивающую достижение максимальной эффективности при прежних условиях Р
T
< РИ
= 36, то искомой комбинацией альтернатив в этом случае будетА11
А21
А32
(порядковый номер 2) со значениями эффективности Э
=
1,8 и требуемого ресурса Р
T
= 35.
Таблица 5.29
Эффективность и требуемые ресурсы тернарных комбинаций альтернатив
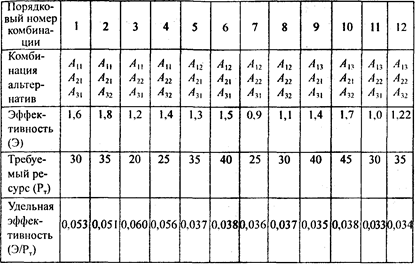
Рассмотрим задачу распределения ресурса между альтернативами рассматриваемой морфологической таблицы систем продвижения товара на рынок для случая, когда имеющегося в наличии ресурса не хватает на три обобщенные функциональные подсистемы. Поэтому на основе морфологической таблицы формируется множество вариантов, состоящее из единичных альтернатив и всех возможных парных сочетаний альтернатив. При этом в каждую комбинацию входит только одна альтернатива из участвующей комбинации обобщенной функциональной подсистемы. Для решения данной задачи используется алгоритм определения комбинации альтернатив с учетом правила 2.
Множество сгенерированных единичных альтернатив и их парных сочетаний альтернатив и рассчитанные для них на основе данных морфологической таблицы (см.
табл. 5.28) значения эффективности Э
, требуемого ресурса Р
T
и отношений Э/РT
приведены в табл. 5.30.
Таблица 5.30
Значения эффективности (Э
), требуемого ресурса (Р
T
) и отношения Э/Р
T
для единичных альтернатив и их парных сочетаний
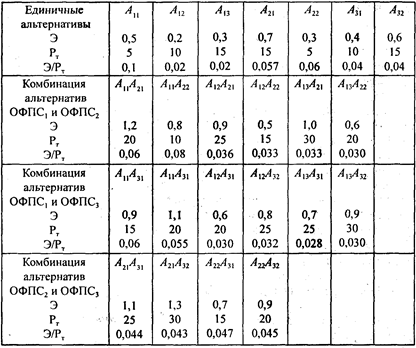
Пусть по условиям задачи требуется найти решения, имеющие максимальное значение удельной эффективности на единицу затрат и при этом удовлетворяющие ряду альтернативных условий: найти max Э/Р
T
при условии выполнения одного из ограничений:
1) Р
T
£ РИ
=15;
2) min(P
И
– PT
), P
И
=15.
Оптимальным решением, удовлетворяющим заданной целевой функции и первому ограничению, является единичная альтернатива А11
со значениями Э/Р
T
= 0,1 и Р
T
= 5. При этом остались неиспользованными 10 единиц ресурса.
Оптимальным решением, удовлетворяющим одновременно рассматриваемой целевой функции и второму ограничению, характеризующему максимальное использование имеющегося ресурса (РИ
), является комбинация альтернатив (А11
А31
) со значениями Э/Р
T
= 0,06 и РИ
= 15.
Основные понятия
1. Комбинаторно-морфологический анализ и синтез.
2. Морфологическая таблица.
3. Морфологическое множество.
4. Кластерный анализ морфологических множеств.
5. Меры сходства и различия.
6. Иерархические классификации — дендрограммы.
7. Оригинальные и типовые решения.
8. Древовидный, лабиринтный и блочно-лабиринтный поиск вариантов.
9. Многокритериальная оценка альтернатив.
10. Морфологическая таблица как иерархическая система.
11. Распределение ресурсов в задачах комбинаторно-морфологического анализа и синтеза.
12. Рациональное распределение ресурсов.
13. Компьютерная система распределения ресурсов методом комбинаторно-морфологического синтеза.
Контрольные вопросы и задания
1. Дайте характеристику основным классификационным признакам, характеризующим задачи комбинаторно-морфологического анализа и синтеза систем.
2. Сформулируйте постановку задачи комбинаторно-морфологического анализа и синтеза систем.
3. Какой вид информации может использоваться в формализованных процедурах морфологического анализа и синтеза?
4. Разработайте алгоритмы и программы кластерного анализа морфологических множеств.
5. Исследуйте морфологические множества экономических систем по отношениям сходства, различия, иерархии. Выявите в морфологических множествах наиболее оригинальные и типовые решения.
6. Сформулируйте основные целевые функции, используемые при синтезе рациональных решений на морфологических множествах.
7. Разработайте алгоритмы и программы синтеза рациональных вариантов на морфологических таблицах с использованием различных целевых функций и подходов по генерации целостных вариантов систем из отдельных компонентов.
8. Укажите особенности синтеза вариантов систем на морфологических таблицах при снятых ограничениях на число и состав функциональных подсистем в целостном варианте.
9. Разработайте прикладную программу для поиска рациональных вариантов экономических систем на основе метода комбинаторно-морфологического анализа и синтеза систем.
10. Разработайте прикладную программу по распределению ресурсов между альтернативами для сложных многокомпонентных систем.
11. Предложите развитие подходов распределения ресурсов для задач, формализуемых комбинаторно-морфологическим методом.
Литература
1.
Одрин В.М.
Морфологический синтез систем: постановка, классификация методов, морфологические методы "конструирования" / Препринт АН УССР. Ин-т кибернетики, 86-3. Киев, 1986. — 37 с.
2.
Дубов Ю.А., Травкин С.И., Якимец В.Н.
Многокритериальные модели формирования и выбора вариантов систем. — М.: Наука, 1986. — 296 с.
3.
Дубров
A
.
M
., Мхитаряч
B
.
C
., Трошин Л.И.
Многомерные статистические методы. — М.: Финансы и статистика, 1998. — 369 с.
4.
Андреев В.Л.
Классификационные построения в экологии и систематике. — М.: Наука, 1980. — 142 с.
5.
Половинкчн А.И.
Законы строения и развития техники: Учеб. пособие. — Волгоград: ВолгПИ, 1985. — 202 с.
6.
Семкчн Б.И.,
Двойченков В.И.
Об эквивалентности мер сходства и различия. // Исследование систем. 1 .Сложные системы. — Владивосток: ДВНЦ,1973. — С. 95 — 104.
7.
Kaufmann A.
Imagination artificielle (Heuristigue automatique) // R.I.R.O. — 1969.— V.3.—№3.—Р.5—24.
8.
Zwicky F.
The morphological approach to discovery, invention research and construction. // Zwicky F., Welson A. New methods of thought and procedure. — Berlin, Springer, 1967. — P. 78 — 297.
9.
Zwicky F.
Entdecken, Erfinden, Forschen im Morphologische Weltbild, Munich et Zurich, 1966; Discovery, Invention, Research through the Morphological Approach, Macmillan, New York, 1969.
Глава 6.
ЭВРИСТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА СИСТЕМ
Под эвристическим синтезом понимается способ решения какой-либо поставленной задачи, включающий совокупность приемов мыслительной деятельности, а также операций по сбору, анализу, обработке и хранению информации. Эвристические методы синтеза [1 — 16] используются при необходимости поиска как можно большего числа новых рациональных решений для реализации полезных функций системы, для устранения или ослабления отрицательного эффекта ненужных и излишних функций, для эффективного синтеза новых или рациональных систем.
Эвристические методы синтеза направлены на реализацию эффективных решений, отвечающих современному уровню развития науки, экономики и систем управления и т.п., за счет увеличения функционально взаимозаменяемых вариантов, позволяющих приблизить синтезируемую систему к минимальным, функционально оправданным затратам.
Эвристический синтез базируется на эвристике — науке о творческом мышлении, кроме того, используются положения таких наук, как психология творчества, системный анализ, исследование операций, теория игр, праксеология и др. Эвристический синтез нередко приводит к получению принципиально новых решений.
В России и за рубежом разработано большое число методов эвристического синтеза для решения задач в различных областях — технике, экономике, управлении, дизайне и др. В этой главе будут даны те эвристические методы, которые наиболее удачно могут быть применены для поиска эффективных экономических, управленческих и организационных решений.
6.1. Классификация эвристических методов синтеза
Наиболее значимым признаком классификации методов эвристического синтеза является наличие или отсутствие алгоритма, организующего мыслительный процесс. По этому признаку можно выделить две группы методов: методы ненаправленного (полуупорядоченного) синтеза, опирающиеся только на простейшие приемы ассоциативного мышления; методы направленного (упорядоченного) синтеза, для которых характерны комплексный подход, системный анализ проблемы и алгоритмизация творческого процесса.
Методы ненаправленного синтеза решений
К методам ненаправленного синтеза решений относятся следующие приемы творчества: аналогия, инверсия, эмпатия, идеализация.
Метод аналогии
предусматривает использование подобного (аналогичного) известного решения, которое "подсказано", например, литературой по экономике, менеджменту, изобразительному искусству или "подсмотрено" в природе.
Для освоения этого метода необходимо обладать (и развивать) наблюдательностью и способностью к переносу опыта.
Метод инверсии
основан на использовании при решении задачи принципов перестановки, переворачивания, выворачивания наизнанку. Этот метод приучает к гибкости мышления, отказу от традиционных стереотипных решений, преодолению психологической инерции.
Метод эмпатии
означает отождествление себя с разрабатываемой системой. При этом исследователь как бы ставит себя на место, например, банка, рекламы, товара и стремится ощутить все действия, которые над ним могут совершаться.
Метод идеализации
связан с желанием получить представление об идеальной системе, полностью отвечающей поставленной цели. Рассматривать идеальные решения часто оказывается полезным, даже если это сопряжено с определенной долей фантазии, поскольку такие решения могут натолкнуть на новую идею.
К методам ненаправленного синтеза с небольшой упорядоченностью мыслительных процессов относятся "мозговой штурм", метод контрольных вопросов, метод гирлянд ассоциаций и метафор, синектика, некоторые разновидности морфологического анализа и синтеза и др. В основе этих методов использованы различного рода "активизаторы" творческого мышления. Например, для настроя мышления на творческий лад применяются эвристические правила "двадцати четырех", "двадцати пяти" и "двадцати шести".
Эвристическое правило "двадцати четырех"
предполагает творческое отношение ко всем задачам, с которыми человек встречается на протяжении 24 часов. Все возникающие при этом,идеи записываются и дополняются новыми.
Эвристическое правило "двадцати пяти"
предполагает для решения той или иной задачи выдвижения не менее 25 идей. Вследствие того, что сгенерировать такое количество идей достаточно трудно, рекомендуется обращаться к личному опыту исследователя, его воспоминаниям об увиденном, прочитанном, услышанном, использовать правило "двадцати шести".
Последнее правило исходит из принципа подсказки: "Подумайте, какое слово, начинающееся на букву А, затем В и т.д., может навести на решение проблемы". (Число 26 — количество букв английского алфавита.) Используя это правило, можно активизировать мозг словами из словаря — в результате какое-то из них может вызвать в сознании неожиданную ассоциацию и привести к решению проблемы.
В методах ненаправленного поиска учитываются особенности человеческой психики. Сама процедура поиска решений указанными методами хотя и производит впечатление детской игры, тем не менее способствует раскрепощению и повышению интеллектуального подъема у специалистов, позволяет преодолеть у последних психологическую инерцию.
Методы направленного синтеза решений
Наиболее эффективны для синтеза новых решений методы направленного синтеза, основанные на научно обоснованных алгоритмах творческого процесса. На одних этапах алгоритмов поле поиска расширяется, на других — сужается. Указанные алгоритмы не имеют жесткой структуры и зачастую называются эвристическими алгоритмами.
Для придания процессу синтеза общей направленности требуется четкая постановка цели и уяснение сущности решаемой задачи. Для этого целесообразно использовать понятия экономического, управленческого или организационного противоречия и идеального конечного результата. Экономическое, управленческое или организационное противоречие характеризует несоответствие между возникшими потребностями общества и возможностями существующих систем. В более узком смысле указанные виды противоречий проявляются при улучшении одних характеристик рассматриваемых систем, повлекшем за собой ухудшение других характеристик.
Идеальный конечный результат (ИКР) — это гипотетическое идеализированное решение, к которому следует стремиться и которое соответствует поставленной цели. ИКР является своего рода критерием синтеза и выбора решений, в соответствии с которым лучшим считается решение, наиболее близкое к ИКР. При использовании ИКР задача рассматривается только с потребительской стороны и поэтому не может заменить социально-экономические оценки вариантов, характеризующие их эффективность.
Современные методы направленного синтеза основаны на сложных алгоритмизированно-процедурных подходах, типизированных способах решения разнообразных изобретательских задач.
Классификация методов эвристического синтеза возможна по ведущему признаку, характеризующему главный активизирующий эффект метода. По этому признаку все методы эвристического синтеза можно разделить на следующие группы.
1. Методы, в которых ведущая роль принадлежит коллективным формам творческой работы. Эти методы основаны на предпосылках о том, что коллективное мышление, организованное по определенным правилам, в условиях благоприятного психологического климата оказывается значительно эффективнее, чем сумма индивидуальных мышлений. Указанное свойство коллективного творчества используется в методах "мозгового штурма", конференции идей, коллективного блокнота, синектики.
2. Методы, основанные на системном анализе комплексных решений, упорядочении признаков частных решений, анализе комплексных решений путем комбинирования частных решений. К этим методам относятся модификации морфологического анализа и синтеза, методы упорядоченных признаков и десятичных матриц поиска.
3. Методы, в которых главное место отводится ассоциативному мышлению, использованию аналогий, метафор и семантических свойств понятий. Это методы фокальных объектов, гирлянд случайностей и ассоциаций.
4. Методы, в которых подсказывается способ разрешения противоречий с помощью эвристических приемов. К их числу относятся алгоритм решения изобретательских задач и библиотека эвристических приемов.
6.2. Фонд эвристических приемов
Для синтеза новых рациональных решений в области экономики или управления целесообразно использовать фонды эвристических приемов. Под эвристическим приемом понимается правило, предписывающее способ преобразования известной системы в новую, более эффективную.
На основе фонда эвристических приемов, адаптированных для решения творческих задач в области экономики и управления (см.
Приложение) целесообразно формировать персональные фонды с учетом особенностей предметной области. При создании персонального фонда необходимо учитывать следующие рекомендации.
1. Изложение эвристических приемов в ряде случаев должно быть ориентировано на интересующий специалиста класс задач и активизировать творческое мышление.
2. Для каждого эвристического приема целесообразно подбирать примеры решения задач из своей области или функционально близких областей. Такие примеры, с одной стороны, являются образцами аналитических задач, помогающими эффективно использовать тот или иной прием при решении новой задачи, а с другой — они могут быть использованы как готовые или полуготовые решения в рассматриваемой задаче.
3. Проведение систематического изучения моментов перехода от известного решения к улучшенным экономическим и управленческим решениям и формулирование новых обобщенных эвристических приемов.
4. Изучение эволюции экономических, управленческих и организационных систем в целях формулирования эвристических приемов, ориентированных на интересующий специалистов класс систем, и подбора для них типичных приемов решения творческих задач.
5. Обобщение опыта удачно решенных задач и формулирование новых эвристических приемов.
6.3. Метод "мозгового штурма"
"Мозговой штурм" — наиболее известный и широко применяемый метод генерирования новых идей путем творческого сотрудничества группы специалистов. Являясь в некотором смысле единым мозгом, группа пытается штурмом преодолеть трудности, мешающие разрешить рассматриваемую проблему. В процессе такого штурма участники выдвигают и развивают собственные идеи для развития других, комбинируют их. Для обеспечения максимального эффекта "мозговой штурм" должен подчиняться определенным правилам и основываться на строгом разрешении во времени процесса выдвижения идей и процесса их обсуждения и оценки. На первой стадии штурма запрещается осуждать выдвинутые идеи и предложения (считается, что критические замечания уводят к частностям, прерывают творческий процесс, мешают выдвижению идей). Роль руководителя группы состоит в том, чтобы активизировать творческое мышление участников заседания, обеспечить выдвижение возможно большего числа вариантов осуществления той или иной функции системы или ее составной части.
После выдвижения идеи выполняются тщательное их обсуждение, экономическая оценка и отбор лучшей.
На стадии обсуждения участники "мозгового штурма" должны развить выдвинутые идеи для нахождения в них рациональных зерен. Участники должны концентрироваться на положительных сторонах идей и развивать их. Поэтому выдвигаемые в процессе обсуждения дополнительные идеи могут базироваться на идеях других участников или, наоборот, служить для них фундаментом, катализатором. Значительный эффект дает комбинирование идей при одновременном выявлении преимуществ и недостатков синтезируемых при этом вариантов.
Метод "мозгового штурма" эффективен прежде всего при решении не слишком сложных задач общего организационного характера, когда проблема хорошо знакома всем участникам заседания и по рассматриваемому вопросу имеется достаточная информация.
При реализации "мозгового штурма" в течение нескольких совещаний необходимо синтезировать 400 — 500 идей для сравнительно сложной задачи.
Метод "мозгового штурма" имеет ряд модификаций.
Индивидуальный
"мозговой штурм" проводится в основном по тем же правилам, что и рассмотренный выше коллективный, но выполняется одним специалистом, который одновременно генерирует идеи, дает им объективную оценку и критикует их, выступает в качестве секретаря сессии. Если лицо, проводящее индивидуальный "мозговой штурм", не узкий специалист по исследуемой проблеме, то целесообразно передавать результаты эксперту для оценки и дальнейшей работы. Такая технология синтеза решений предусматривает длительность сессии не более 3 — 10 мин, при обеспечении высокой самодисциплины. Полученные идеи фиксируются на бумажных или электронных носителях информации, а их оценка проводится через несколько дней после их получения. При проведении индивидуального "мозгового штурма" необходимо обладать навыками постановки вопросов, на которые могут быть даны альтернативные ответы.
Массовый
"мозговой штурм" проводится участниками сессии — массовой (до нескольких сот человек) аудиторией, решающей какую-либо сложную задачу. Отбор идей производится на промежуточных этапах. Участники группируются по 6 — 8 человек, при этом важно, чтобы непосредственное отношение к задаче имел лишь руководитель группы, а остальные члены группы были бы лишь знакомы с нею (иначе могут сыграть негативную роль элементы амбиции специалистов, разработавших ранее этот проект). Штурм проходит в два этапа. На первом этапе оперативными группами проводится прямой коллективный "мозговой штурм". При этом желательно, чтобы задача касалась того участка, на котором работают участники оперативной группы. Длительность первого этапа — не более 15-20 мин. На втором этапе по окончании сессии руководители каждой группы в течение нескольких минут оценивают выдвинутые идеи, отбирают из них наиболее интересные и сообщают их на "пленарном заседании". После завершения работы некоторые идеи начинают внедряться, а другие передаются экспертам для доработки.
Письменный
"мозговой штурм" применяется, когда нет возможности собрать специалистов в одном месте. В этом случае формируется творческое задание в форме довольно подробного вопросника, который отражает в альтернативном виде основные проблемы, требующие решения. В остальном процедура та же, что и при обычном "мозговом штурме". Метод письменного "мозгового штурма" исключает возможность обмена идеями и поэтому тормозит появление оригинальных идей.
Двойной
"мозговой штурм" органически соединяет в себе процессы генерирования идей и их доброжелательной позитивной критики. Сессия делится на два формальных этапа с перерывом между ними в 45 мин.
Первый этап — постановка творческого задания, формулирование участниками своих предложений. На втором этапе проводится неофициальная часть сессии, непринужденное свободное обсуждение. Поощряются обсуждение предложенных идей, их позитивная критика, непринужденное генерирование новых. Третий этап — продолжение выдвижения идей, но более конкретных, практически реализуемых. По окончании сессии экспертами проводится оценка идей, их проработка и внедрение в жизнь.
Обратный
"мозговой штурм" отличается от прямого тем, что здесь большое внимание уделяется критике высказываемых идей. На совещании решаются более узкие, специальные задачи. Содержанием работы на сессии является всесторонний анализ слабых мест в объекте, который необходимо усовершенствовать или заменить новым. В результате составляется своеобразная ведомость всякого рода недостатков в системе. Недостатки оцениваются экспертами, которые исключают ошибочные замечания и выводы. После этого проводится прямой "мозговой штурм" по ликвидации вскрытых недостатков.
Конференция идей —
одна из разновидностей коллективного творчества. От "мозгового штурма" она отличается темпом проведения совещания по выдвижению идей и допущением доброжелательной критики в форме реплик, комментариев. Считается, что критика может даже повысить ценность выдвинутых идей. Поощряется фантазирование и комбинирование идей.
К конференции идей привлекаются руководители и рядовые сотрудники, лица, постоянно имеющие дело с данной проблемой, и новички, которые часто выдвигают новые, свежие идеи. Например, разновидность конференции идей — "дискуссия 66" представляет собой разбивку больших по составу творческих коллективов на мелкие дискуссионные группы по 6 человек, которые в течение 6 мин (отсюда название метода) проводят мини-конференции по четко сформулированной проблеме.
6.4. Методы ассоциаций и аналогий
Методы ассоциаций и аналогий предполагают активизацию в первую очередь ассоциативного мышления человека. К этим методам относятся метод фокальных объектов и метод гирлянд случайных ассоциаций.
Метод фокальных объектов
состоит в перенесении признаков случайно выбранных объектов на совершенствуемый объект, который лежит как бы в фокусе переноса и поэтому называется фокальным. В результате возникает ряд неожиданных вариантов решения. Этот метод дает хорошие результаты при поиске новых модификаций известных систем. Он позволяет, например, быстро найти идеи новых совершенно необычных товаров, способов обслуживания в супермаркетах, новых способов управления.
Метод генерирования случайных ассоциаций
формализован двумя алгоритмами.
Алгоритм 1. Перед началом работы алгоритма задается следующая информация: А
— список объектов; В —
список признаков; С
— матрица связей А
и В,
причем С
ij
= 1, если i
-й объект обладает j
-м признаком, в противном случае С
ij
= 0.
Работа алгоритма заключается в случайном выборе объекта из списка А
и всех его признаков из списка В.
В результате получается случайная ассоциация "объект — признаки". Следующая ассоциация получается независимо от предыдущей.
Алгоритм 2. Входная информация в этом алгоритме совпадает с входной информацией алгоритма 1.
Выполняются следующие процедуры:
1. Случайный выбор из списка А
объекта а.
2. Выбор из списка В
всех признаков объекта а.
Результат — список Ba
.
3. Случайный выбор из списка Ba
признаков b
.
4. Выходные данные: а,
Ba
, b
.
5. Выбор из списка А
всех объектов, обладающих признаком b.
Результат — список А
b
.
6. Случайный выбор из списка А
b
объекта а.
7. Перейти k
раз к процедуре 2.
8. Конец.
На каждой итерации алгоритма пользователю выводится очередная случайная ассоциация "объект — признаки — случайный признак". Результатом работы является гирлянда ассоциаций длины k.
Последовательность объектов в гирлянде характерна тем, что соседние объекты имеют общий признак.
Оригинальность и допустимость идей, получаемых на основе случайных ассоциаций, существенно зависят от входных списков А
и В.
При этом, чем больше пересечение признаков фокального объекта со списком В,
тем больше вероятность получения допустимой идеи и меньше — оригинальной.
Рассмотрим пример генерирования случайных ассоциаций при решении задач по созданию нового потребительского товара.
Исходная информация:
А
= {а1
—
авторучка, а2
—
фонарь, a
3
— радиоприемник, a
4
— часы}.
В
= {b
1
—
стеклянный, b
2
—
светотеплоизлучающий, b
3
— многоцветный, b
4
—
плавающий, b
5
— встроенный, b
6
—
гигантский, b
7
—
миниатюрный, b
8
— источник энергии — тепловая энергия, излучаемая телом человека}.
Матрица С
связей А
и В
для рассматриваемого примера имеет следующий вид:

Выполняемые процедуры:
1. Случайный выбор из списка А
объекта:
a
2
—
фонарь.
2. Выбор из списка В
всех признаков объекта а2
.
 = {b2
, b3
, b4
, b5
, b6
, b7
, b8
}. = {b2
, b3
, b4
, b5
, b6
, b7
, b8
}.
3. Случайный выбор из списка  признака b
: признака b
:
b4
— плавающий.
4. Выходные данные:
a2
— фонарь;
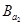 = {b
2
,
b
3
,
b
4
,
b
5
,
b
6
, b7
,
b
8
}. = {b
2
,
b
3
,
b
4
,
b
5
,
b
6
, b7
,
b
8
}.
b4
— плавающий.
5. Выбор из списка А
всех объектов, обладающих признаком b
.
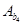 =
{а
1
, a2
,
a3
, a4
}. =
{а
1
, a2
,
a3
, a4
}.
6. Случайный выбор из списка 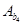 объекта: объекта:
a3
— радиоприемник.
После первой итерации гирлянда случайных ассоциаций имеет следующий вид: а2
—
фонарь, в4
—
плавающий, a3
— радиоприемник.
Признак b
4
является общим для объектов а2
и а3
.
7. Переход к процедуре 2.
Результат — список 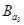 = {b
4
,
b
5
,
b
6
, b7
,
b
8
}. = {b
4
,
b
5
,
b
6
, b7
,
b
8
}.
8. Случайный выбор из списка  признака: b
8
— источник энергии — тепловая энергия. признака: b
8
— источник энергии — тепловая энергия.
9. Выходные данные:
а3
—
радиоприемник;  = {b
4
,
b
5
,
b
6
, b7
,
b
8
}; b
8
— источник энергии — температура тела человека. = {b
4
,
b
5
,
b
6
, b7
,
b
8
}; b
8
— источник энергии — температура тела человека.
10. Выбор из списка А
всех объектов с признаком b
8
:
 = {a2
,
a3
, a4
}. = {a2
,
a3
, a4
}.
11. Случайный выбор из списка  объекта: a4
— часы. После второй итерации гирлянда случайных ассоциаций имеет следующий вид: а2
— фонарь, b
4
—
плавающий, а3
—
радиоприемник, b
8
—
источник энергии — температура тела человека, a
4
— часы. объекта: a4
— часы. После второй итерации гирлянда случайных ассоциаций имеет следующий вид: а2
— фонарь, b
4
—
плавающий, а3
—
радиоприемник, b
8
—
источник энергии — температура тела человека, a
4
— часы.
В результате двух итераций алгоритма возникшие ассоциации от синтезированной гирлянды позволяют сгенерировать следующие идеи потребительского товара:
• фонарь для подводного плавания;
• радиоприемник для плавания с источником энергии от температуры тела человека;
• часы с подзарядом от тепловой энергии, излучаемой телом человека.
6.5. Синектика
Синектика — комплексный метод стимулирования творческой деятельности, использующий приемы и принципы как "мозгового штурма", так и метода аналогий и ассоциаций. Само слово "синектика" — неологизм, означающий объединение разнородных элементов.
В основе метода лежит поиск нужного решения благодаря преодолению психологической инерции, состоящей в стремлении решить проблему традиционным путем. Синектика позволяет выйти за рамки какого-то конкретного образа мыслей и значительно расширяет диапазон поиска новых идей за счет представления привычного непривычным и, наоборот, непривычного — привычным.
При использовании синектики решение проблемы ищет группа специалистов разных специализаций, как владеющих этим методом, так и только приступающих к его овладению. Рекомендуется, чтобы члены синектической группы (кроме руководителя) перед началом работы не знали сути рассматриваемой проблемы, что позволяет абстрагироваться от привычного стереотипа мышления.
Одна из важнейших частей синектической процедуры — выяснение того, как участники представляют себе обсуждаемую проблему. С этой целью они предлагают свои варианты ее определения. Руководитель записывает их на доске, что имеет существенное психологическое значение, поскольку каждый участник начинает воспринимать проблему как свою и делает попытки ее решить. Далее руководитель задает наводящие вопросы, вызывающие ассоциации и аналогии. Метод синектики широко использует личную аналогию (эмпатию). Человек мысленно вживается в образ рассматриваемой системы, стараясь отождествить себя с ней и проанализировать возникающие ощущения. Это помогает при синтезе новых вариантов систем. Эмпатия успешно применяется при решении особо сложных проблем, а также для проверки осуществимости различных идей.
6.6. Методы контрольных вопросов и коллективного блокнота
Метод контрольных вопросов
применяется для психологической активизации творческого процесса. Цель метода состоит в том, чтобы с помощью наводящих вопросов подвести к решению задачи. Метод может применяться как в индивидуальной работе, так и при коллективном обсуждении проблемы, например при "мозговом штурме". Один из широко распространенных вопросников А. Осборна включает девять групп вопросов: 1. Какое новое применение системе можно предложить? 2. На какую другую систему похожа данная система и что можно скопировать? 3. "Какие возможны модификации путем изменения функций? 4. Что можно в системе увеличить? 5. Что можно в системе уменьшить (сжать, ускорить, сузить, раздробить)? 6. Что можно в системе заменить? 7. Что можно в системе преобразовать (схему, порядок работы и т.д.)? 8. Что можно сделать в системе наоборот? 9. Какие новые комбинации элементов системы возможны?
В данных вопросах содержатся рекомендации по апробированию эвристических приемов (инверсия, аналогия, дробление, перенос, динамизация и т.д.) для решения поставленной задачи.
Метод коллективного блокнота
позволяет сочетать независимое выдвижение идей каждым членом рабочей группы с коллективной их оценкой и процессом выработки решения. Метод реализуется следующим образом.
Каждый участник получает блокнот, в котором записывает в общих чертах без применения специальных терминов существо проблемы, а также данные, позволяющие ориентироваться в ней. В течение месяца каждый участник ежедневно заносит в блокнот возникающие по рассматриваемой проблеме идеи, оценивает их и определяет, какие из них могут обеспечить наилучшее решение задачи. Одновременно формулируются наиболее целесообразные направления исследования на последующем этапе работы. Кроме того, в блокноте фиксируются идеи, находящиеся в стороне от основной проблемы, но развитие которых может оказаться полезным для нахождения конечного решения.
Систематизация зафиксированных в блокнотах идей осуществляется руководителем группы, а заключительное творческое обсуждение — всеми членами группы. Выбор окончательного решения проводится методом "мозгового штурма".
6.7. Метод "матриц открытия"
Метод "матриц открытия" получил широкое распространение во Франции. Как и в морфологическом методе синтеза, здесь преследуется цель систематически исследовать все мыслимые варианты, вытекающие из закономерностей строения (морфологии) совершенствуемой системы, выбрать и изучить поле возможных решений. В то же время метод "матриц открытия" проще и дает возможность ограничить количество рассматриваемых вариантов. Суть метода — в построении квадратной матрицы (табл. 6.1), в которой пересекаются два ряда характеристик по вертикали и горизонтали. Ряды могут быть упорядоченными по какому-либо признаку или неупорядоченными. Характеристики могут быть выражены количественно или качественно. В отличие от метода морфологического анализа здесь часть выбранных характеристик может относиться не к системе, а к условиям ее эксплуатации.
Таблица 6.1
Структура "матрицы открытия"
| Влияющий фактор
|
Материалы
|
Оборудование
|
Потребности
|
Рынки
|
| Материалы
|
| Оборудование
|
| Потребности
|
| Рынки
|
Основные этапы метода "матриц открытия" по обработке информации следующие:
• составление перечня элементов, свойств, объектов, фактов, идей и т.п.;
• выработка поля анализа — определение проблемы в наиболее общей и абстрактной форме, уточнение ее, построение структуры поля;
• определение пересечения рядов и столбцов, обнаружение возможных комбинаций;
• изучение выбранных комбинаций и выбор рациональных решений.
Метод "матриц открытия", как правило, не дает законченных решений и служит для систематизации имеющегося материала и определения отправных пунктов дальнейшего исследования. Комбинации характеристик дают возможность для плодотворных ассоциаций, постановки проблем, которые ранее оставались незамеченными.
6.8. Алгоритм решения изобретательских задач
Алгоритм решения изобретательских задач [1, 2] — эвристический метод, ориентированный на идеальный ответ, максимальное использование имеющихся ресурсов, получение решения задачи путем выявления и разрешения внутренних противоречий системы. Наибольшее распространение до настоящего времени этот алгоритм получил в области технического проектирования. Тем не менее основные подходы данного метода могут быть эффективно применены при синтезе новых экономических, управленческих и организационных систем.
Алгоритм решения изобретательских задач может быть использован для решения четырех задач, иерархически упорядоченных по сложности.
Решение задач первого
уровня не связано с устранением противоречий в системе и приводит к мельчайшим усовершенствованиям. Такие задачи под силу каждому специалисту. Здесь объект задачи указан точно и правильно, вариантов изменений мало, а сами изменения перестраивают систему незначительно.
Задачи второго
уровня — с внутрисистемными противоречиями, легко преодолеваемыми с помощью способов, известных применительно к родственным системам. Ответы на задачи этого уровня — мелкие изобретения. Для получения ответа рассматривается несколько десятков вариантов решений.
Задачи третьего
уровня характеризуются тем, что противоречие и способ его преодоления находятся в пределах одной науки. При этом можно полностью изменить один или два функционально значимых элемента системы и частично изменить другие элементы. Количество рассматриваемых вариантов здесь исчисляется сотнями. В итоге получаются решения с высокой степенью новизны и эффективности.
При решении задач четвертого уровня синтезируется новая система. В таких задачах противоречия устраняются средствами, выходящими за пределы науки, к которой относится задача. Число вариантов измеряется тысячами и десятками тысяч. В итоге — создание принципиально новой системы.
Рассмотрим основные этапы и процедуры алгоритма решения изобретательских задач, адаптированных к экономическим, управленческим и организационным проблемам.
Этап 1.
Выбор задачи.
1.1. Определить конечную цель решения задачи:
• Какую характеристику системы необходимо изменить?
• Какие характеристики объекта заведомо нельзя менять при решении задачи?
• Какие расходы снизятся, если задача будет решена?
• Каковы допустимые затраты?
• Какой главный показатель качества необходимо улучшить?
1.2. Проверить обходной путь. Допустим, что задача принципиально не решена. Тогда какую другую задачу необходимо решить, чтобы получить требуемый конечный результат:
• переформулировать задачу, перейдя на уровень надсистемы, в которую входит данная в задаче система;
• переформулировать задачу, перейдя на уровень подсистем, входящих в данную в задаче систему;
• на трех уровнях (надсистема, система, подсистема) переформулировать задачу, заменив требуемое действие обратным.
1.3. Определить, решение какой задачи целесообразнее — первоначальной или одной из обходных. Произвести выбор.
1.4. Определить требуемые количественные показатели.
1.5. Увеличить требуемые количественные показатели, учитывая время, необходимое для реализации изобретенной системы.
1.6. Уточнить требования, выдвинутые конкретными условиями, в которых предполагается реализация изобретенной системы.
1.7. Проверить, решается ли задача прямым применением стандартных решений.
1.8. Применить оператор РВС (размеры, время, стоимость):
• мысленно меняем размеры системы от заданной величины до 0. Как теперь решается задача?
• мысленно меняем размеры системы от заданной величины до ¥. Как теперь решается задача?
• мысленно меняем время процесса (или скорость) от заданной величины до 0. Как теперь решается задача?
• мысленно меняем время процесса от заданной величины до ¥. Как теперь решается задача?
• мысленно меняем стоимость системы или процесса от заданной величины до 0 или от заданной величины до ¥. Как при этом решается задача?
Этап
2.
Построение модели задачи.
2.1. Записать условия задачи, не используя специальные термины.
2.2. Выделить и записать конфликтную пару элементов системы.
2.3. Записать два взаимодействия элементов конфликтующей пары: имеющееся и то, которое надо ввести.
2.4. Записать стандартную формулировку модели задачи, указав конфликтующую пару и внутреннее противоречие системы.
Этап 3.
Анализ модели задачи.
3.1. Выбрать из элементов, входящих в модель задачи, тот, который можно легко изменять, заменять и т.д.
3.2. Записать стандартную формулировку идеального конечного результата (ИКР).
3.3. Выделить ту зону системы или элемента системы, которая непосредственно не обеспечивает достижение требуемого ИКР.
3.4. Сформулировать противоречивые требования к состоянию выделенной зоны системы.
3.5. Записать стандартную формулировку экономического, управленческого или организационного противоречия: выделенная зона системы (указать) должна быть (указать состояние), чтобы выполнять полезное взаимодействие (указать), и должна быть (указать состояние), чтобы предотвращать вредное воздействие (указать).
Этап
4.
Устранение противоречия.
4.1. Рассмотреть простейшие преобразования выделенной зоны:
• разделение противоречивых свойств в пространстве;
• разделение противоречивых свойств во времени;
• разделение противоречивых свойств путем использования переходных состояний, при которых сосуществуют или попеременно появляются противоречивые свойства;
• разделение противоречивых свойств перестройкой структуры (частицы выделенной зоны наделяются имеющимся свойством, а вся выделенная зона в целом наделяется требуемым (конфликтующим) свойством).
4.2. Использовать фонд эвристических приемов для устранения противоречия в системе.
Этап
5.
Предварительная оценка полученного решения.
5.1. Провести предварительную оценку полученного решения.
5.2. Оценить новизну полученного решения.
5.3. Определить подзадачи, которые могут возникнуть при практической реализации полученной идеи.
Этап 6.
Развитие полученного ответа.
6.1. Определить, как должна быть изменена надсистема, в которую входит измененная система.
6.2. Проверить, может ли измененная система применяться по-новому.
6.3. Использовать полученный ответ при решении других экономических, управленческих и организационных задач.
6.9. Автоматизация эвристических методов синтеза новых систем
В настоящее время из эвристических методов наиболее подготовленными к автоматизации являются метод генерирования случайных ассоциаций и алгоритм решения изобретательских задач (см.
разд. 6.4). Программная реализация этих алгоритмов не представляет особого труда. Здесь рассматривается проект оболочки компьютерной системы, реализующей алгоритм решения изобретательских задач (АРИЗ) в области экономики, управления или проектирования организационных структур. Структура данной программной оболочки (рис. 6.1) во многом основывается на структуре системы "Изобретающая машина" (ИМ)[17].
Компьютерная система по решению изобретательских задач включает ряд базовых подсистем. Подсистемы Приемы и Стандарты основаны на эвристических правилах преобразования экономических, управленческих или организационных систем. Подсистема Эффекты должна накапливать информацию об экономических, управленческих или технологических эффектах. В технических приложениях данная подсистема накапливает информацию о физических, химических и геометрических эффектах.
Подсистема АРИЗ достаточно универсальна. Она предназначена для разрешения экономических и управленческих противоречий в различных областях экономики и управления: Профильность подсистемы может меняться за счет ее наполнения разным содержанием в зависимости от типа задач, а также от используемых ресурсов.
Подсистема ФСА служит для проведения функционально-стоимостного анализа исследуемых систем.
Подсистема Самоучитель АРИЗ обеспечивает обучение экономистов и управленцев основам теории решения изобретательских задач и технологии решения задач с использованием ЭВМ.

Подсистема Прогноз позволяет формировать идеи по прогнозированию развития экономико-управленческих систем.
Подсистема Пульсар предназначена для более качественного решения задач по анализу и синтезу алгоритмов работы информационных экономических и управленческих систем.
Архитектура развиваемой оболочки компьютерной системы может быть построена по аналогии с архитектурой системы "Изобретающая машина" и предусматривает следующие блоки (рис. 6.2): обучение основным понятиям, содержащимся в базе знаний, диалог по постановке задачи по результатам диалога, выдача идеи решения задачи, развитие идеи. Пред выдачей идей решения проводится предиалог, целью которого является подготовка ЛПР к пониманию сути идеи решения.

Блок постдиалога обеспечивает привязку идеи решения к задаче пользователя, а блок убеждения формирует файл разбора задач-аналогов.
В тех случаях, когда при получении идеи требуется решение дополнительных задач, управление передается блоку формирования подзадач с последующим выходом на начальный диалог. В остальных блоках проводятся оценка технико-экономического уровня и перспективности идеи, развитие получаемых идей, например, для получения дополнительных эффектов или распространения найденного принципа на другие области экономики и управления.
Для разрешения экономических, управленческих или организационных противоречий с использованием эвристических приемов может быть использована компьютерная экспертная система, основанная на формуле Байеса [18]. Эта экспертная система является инструментальным средством для быстрого создания экспертных систем принятия решений в различных предметных областях.
Модель базы знаний экспертной системы представляется в виде
М
=
{Н
, S, G, P, VH, VS
},

В процессе работы экспертной системы используются следующие зависимости:

Симптом с максимальной ценой в наибольшей мере изменяет априорные вероятности гипотез при подтверждении или отрицании этого симптома. Цены симптомов вычисляются для определения очередного симптома, относительно которого следует задать очередной вопрос пользователю. Вопросы пользователю задаются в виде текста соответствующего симптома. При этом требуется подтвердить или отвергнуть симптом. Ответ пользователя задается в шкале: (-5,..., 0,...,+5), где -5 означает "нет", 0 — "не знаю", +5 — "да". Если ответ пользователя -5 (отрицание соответствующего симптома Si
),
то априорная вероятность гипотезы Н
j
будет P
(
Si
ù Н
j
). Если ответ 0, то вероятность гипотезы Н
j
не изменяется. Если ответ +5, то априорная вероятность гипотезы Н
j
будет P
(
Si
÷ Н
j
). Для определения априорной вероятности гипотезы при остальных ответах пользователя используется кусочно-линейная аппроксимация.
После вычисления вероятности P
(
Hj
÷ R
i
), где Ri
, — ответ пользователя на симптом S
i
,
априорная вероятность Р(Н
j
)
заменяется вычисленной апостериорной вероятностью. Подтверждение (отрицание) симптома S
i
,
связанного с гипотезой Н
j
, является положительным свидетельством для гипотезы Н
j
, если апостериорная вероятность больше априорной. Подтверждение (отрицание) симптома является отрицательным свидетельством для гипотезы, если апостериорная вероятность меньше априорной.
Для каждой гипотезы Н
j
вычисляется два числа: Р
m
ах
(Н
j
) = M
1
j
— апостериорная вероятность гипотезы при всех положительных свидетельствах и Pmin
(Н
j
) = M
2
j
—
апостериорная вероятность гипотезы при всех отрицательных свидетельствах. Имеются три правила формирования результата работы экспертной системы.
Правило 1.
Подтверждение или отклонение гипотезы Н
j
. Если на некотором шаге работы новая вычисленная (апостериорная) вероятность Р
гипотезы Н
j
становится больше Р
aj
+
L
1
(М1
j
- Paj
), то гипотеза подтверждается (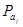 — априорная вероятность гипотезы); если апостериорная вероятность Р
гипотезы Н
j
становится меньше — априорная вероятность гипотезы); если апостериорная вероятность Р
гипотезы Н
j
становится меньше 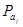 +
L
2
( +
L
2
(
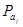 -
M
2
j
), то гипотеза отвергается. Коэффициенты L
1
и L
2
— настроечные параметры. -
M
2
j
), то гипотеза отвергается. Коэффициенты L
1
и L
2
— настроечные параметры.
Правило 2.
Наиболее вероятный результат. Считается, что гипотеза Н
r
наиболее вероятна, если при любых дальнейших ответах пользователя апостериорные вероятности остальных гипотез не могут превысить значение апостериорной вероятности гипотезы Н
r
.
Правило 3.
Если не сработали первые два правила и все вопросы по симптомам исчерпаны, то в качестве результата выдается несколько гипотез с наибольшими апостериорными вероятностями.
После сеанса работы с экспертной системой пользователь имеет возможность получить разъяснение результатов ее работы.
Экспертная система снабжается блоком обучения базы знаний, который позволяет корректировать оценки вероятностей Р+
и Р-
с процедурами заполнения траектории "вопрос — ответ" и подтверждения правильности ответа экспертной системой. Этот блок облегчает построение прикладных экспертных систем, поскольку ошибки первоначального наполнения систем могут исправляться в процессе сеансов работы с опытным экспертом-учителем.
Экспертная система может быть использована для решения широкого круга задач, в частности для синтеза рациональных решений с помощью эвристических приемов. Эвристический прием —
это некоторая рекомендация экономисту-изобретателю, дающая направление изменения прототипа системы в искомое экономическое или управленческое решение. В основе метода эвристических приемов лежит понятие экономического или управленческого противоречия. Противоречие выявляется при анализе прототипа системы и описывается в терминах показателей экономического объекта в виде пары (X,
Y
),
где Х—
показатель, который необходимо улучшить в прототипе; Y
— показатель, который недопустимо ухудшается. При этом для фиксированного Х
в одном прототипе может быть выделено несколько экономических или управленческих противоречий вида (X,
Y
,),
i
=
 . .
Назначение экспертной системы по эвристическим приемам состоит в выдаче рекомендаций изобретателю-экономисту или управленцу по применению наиболее эффективных эвристических приемов для разрешения выявленных в прототипе противоречий.
В качестве гипотез здесь выступают эвристические приемы. Симптомами являются показатель, который необходимо улучшить, — X,
и показатель, который при этом ухудшается, — Y
.
В качестве базы знаний в данной экспертной системе используется таблица взаимосвязей противоречий и эвристических приемов. Интерпретацией симптома является противоречие. Считается, что симптом (X,
Y
) связан с гипотезой Н
, если противоречие разрешается с некоторой вероятностью эвристическим приемом.
Экспертная система при взаимодействии с пользователем работает следующим образом.
Шаг 1. Пользователю предъявляется вопрос относительно некоторого показателя, который необходимо улучшить в прототипе.
Шаг 2. Пользователь, отвечая на указанный вопрос, выбирает этот показатель из меню.
Шаг 3. Система задает пользователю вопрос, ухудшается ли при этом некоторый другой показатель прототипа, и указывает этот показатель.
Шаг 4. Пользователь отвечает на поставленный вопрос по шкале (-5,..., 0,...,+5).
Шаг 5. Экспертная система проверяет решающие правила и либо выдает наиболее достоверный эвристический прием, либо формирует следующий прием.
Компьютеризация эвристических методов синтеза в области экономики и управления находится в стадии зарождения и требует значительных усилий исследователей в дальнейшем развитии этого направления. В перспективе ЭВМ должна помогать человеку не только выполнять рутинную работу, но и способствовать повышению творческой активности при поиске новых рациональных решений [19]..
Основные понятия
1. Эвристические методы.
2. Эвристический прием (правило).
3. Экономическое и техническое противоречие.
4. "Мозговой штурм".
5. Методы ассоциаций и аналогий.
6. Метод синектики.
7. Контрольные вопросы и коллективный блокнот.
8. Метод "матриц открытия".
9. Алгоритм решения изобретательских задач.
10. Автоматизация эвристических методов синтеза новых систем.
Контрольные вопроси а задания
1. Сформулируйте основные классификационные признаки эвристических методов синтеза систем.
2. В чем заключаются основные принципы поиска новых рациональных систем методом, основанным на фонде эвристических приемов?
3. Предложите новые принципы построения компьютерной системы, основанной на использовании фонда эвристических приемов.
4. Дайте характеристики различным методам "мозгового штурма".
5. Предложите вариант создания компьютерной системы для поддержки творческого процесса синтеза новых эффективных систем, осуществляемого методом "мозгового штурма".
6. Разработайте каталоги признаков для решения прикладных задач конкретной экономической предметной области методами ассоциаций и аналогий.
7. Разработайте компьютерную систему синтеза решений на основе метода ассоциаций.
8. Охарактеризуйте особенности метода синектики.
9. Предложите экономические задачи для решения методами контрольных вопросов и коллективного блокнота. Опишите технологию их решения.
10. Разработайте "матрицы открытия" для решения прикладных экономических задач. Осуществите поиск рациональных вариантов, удовлетворяющих исходной постановке задачи.
11. Сформулируйте творческую экономическую задачу. Решите задачу методом АРИЗ. Опишите процесс решения задачи.
Литература
1.
Альтшуллер Г.С.
Алгоритм изобретения. —М.: Московский рабочий, 1973. — 296 с.
2.
Альтшуллер Г.С.
Творчество как точная наука. — М.: Сов. радио, 1979. — 184 с.
3.
Буш Г.Я.
Методологические основы научного управления изобретательством. — Рига: Лиесма, 1974. — 167 с.
4.
Гильде В., Штарке К.
Нужны идеи: Пер. с нем. — М.: Мир, 1973. — 64 с.
5.
Голдовский Б.И;
Вайнерман М.И.
Рациональное творчество. — М.: Речной транспорт, 1990. — 120 с.
6.
Джонс. Дж.К.
Методы проектирования: Пер. с англ.- 2-е изд., доп. — М.: Мир, 1986. — 326 с.
7.
Диксон Д.
Проектирование систем: изобретательство, анализ, принятие решений: Пер. с англ. — М.: Мир, 1969. — 440 с.
8.
Загоруйко Н.Г.
Методы обнаружения закономерностей. — М.: Знание, 1981. —62 с.
9.
Одрин В.М; Картавов В.В.
Некоторые итоги и перспективы развития морфологического анализа систем / Препринт АН УССР. Ин-т кибернетики, 73-62. — Киев, 1973. — 83 с.
10.
Одрин В.М; Картавов В.В.
Морфологический анализ систем. — Киев: Наукова думка, 1977. — 183 с.
11.
Одрин В.М.
Метод морфологического анализа технических систем. — М.: ВНИИПИ, 1989. — 312 с.
12.
Повилейко Р.П.
Классификация методов решения конструкторско-изобретательских задач (десятичные матрицы поиска). // Проблемы информатики. — Новосибирск: Наука, 1972. — Вып.5. — С. 5 — 37.
13.
Повилейко Р.П.
Инженерное творчество. — М.: Знание, 1977. — 62 с.
14.
Техническое
творчество: теория, методология, практика. Энциклопедический словарь-справочник / Под ред. А. И. Половинкина, В. В. Попова. — М.: НПО "Информ-система", 1995. — 408 с.
15.
Титов В.Н.
Выбор целей в поисковой деятельности (методы анализа проблем и поиска решений в технике). — М.: Речной транспорт, 1991.— 125 с.
16.
Тринг М; Лейтуэйт Э.
Как изобретать?: Пер. с англ. — М.: Мир, 1980. — 272 с.
17.
Цуриков В.М.
Проект "Изобретающая машина" - интеллектуальная среда поддержки инженерной деятельности // ТРИЗ. — 1991. — №2.1.—С. 17 -35.
18.
Дворянкин А. М.
Экспертная система для принятия проектных решений // Инновационное проектирование в образовании, технике и технологии: Межвуз. сб. научн. тр. — Волгоград, Изд-во ВолгГТУ, 1996. — С. 25 — 34.
19.
Андрейчиков А. В., Андрейчикова О. Н.
Компьютерная поддержка изобретательства. — М.: Машиностроение, 1998. — 467 с.
Глава 7.
АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ ПРИНЯТИЯ, ПЛАНИРОВАНИЯ И СИНТЕЗА РЕШЕНИЙ
Повышение качества и производительности труда — "вечная" проблема. При этом особенно сложно повысить эффективность творческого труда, к которому относятся процедуры принятия, планирования и синтеза рациональных и новых решений в экономике. Одним из наиболее перспективных способов решения этой проблемы является создание автоматизированных систем.
Создание принципиально новых экономических систем и выработка эффективных управленческих решений всегда будет прерогативой высокотворческих личностей, поскольку даже в суперЭВМ невозможно вдохнуть душу человека и заложить в ее память постоянно развивающуюся модель знаний творческой личности, являющейся частью модели мира. Тем не менее для принятия, планирования и синтеза экономических решений среднего уровня уже сейчас активно разрабатываются компьютерные интеллектуальные системы, способные синтезировать решения более эффективно, чем человек. В настоящее время такие системы развиваются не в направлении подключения дополнительных программных модулей и создания требуемых баз данных, а в радикальном перераспределении вычислительных работ и концентрации пользовательских, поисковых задач синтеза решений в экспертных системах, которые могут рассматриваться как особые комплексные подсистемы со своими информационной базой и программным обеспечением общего и специального назначения.
7.1. Необходимость автоматизации процессов принятия, планирования и синтеза решений
Методы принятия, планирования и синтеза решений основываются на применении знаний (в частности, системы предпочтений) лица или коллектива лиц, ответственных за принимаемое синтезируемое решение.
Однако процедуры выявления знаний, системы предпочтений лица, принимающего решение, настолько сложны, что требуют участия консультанта в процессе оценки, синтеза и выбора решения из множества альтернативных вариантов. Консультант, как правило, хорошо осведомлен о методах принятия и синтеза решений, приемлемых при разных критериях, альтернативах, шкалах критериев, типах оценок и т. п.
Привлекаемые к процессу решения задачи специалисты помогают ЛПР более четко разобраться в сложившейся ситуации выбора решений, обучают его применяемым методам. Опыт консультанта обеспечивает целенаправленность размышлений ЛПР и строгость в структуре получаемых от него оценок. Все это дает пользователям возможность синтеза и выявления наиболее обоснованных вариантов наилучших в некотором смысле решений из множества допустимых.
Выявление данных, знаний и системы предпочтений ЛПР для решения задачи осуществляется путем сбора экспертной информации, объем которой оказывается весьма существенным. Объем экспертной информации, которую необходимо получить и обработать, тем больше, чем выше размерность решаемой задачи.
Разработка универсальных анкет для различных вариантов задач принятия, планирования и синтеза решений невозможна. Следовательно, требуется постоянное участие консультанта, направляющего последовательность рассуждений ЛПР в процессе сбора экспертной информации, что ведет к нарушению принципов конфиденциальности и необходимой документальности информации. Таким образом, если решение, выбранное предлагаемым методом, является неудовлетворительным для ЛПР, консультант не имеет возможности документально точно восстановить процедуру опроса. В результате невозможно обосновать справедливость решения, полученного на основе выявления системы предпочтений пользователя, а также его оценок правдоподобности тех или иных последствий принимаемых решений.
Решение задач в неавтоматизированном режиме не позволяет организовать сбор и обработку исходной информации от нескольких экспертов.
Значительным толчком к разработке диалоговых систем принятия и синтеза решений послужило быстрое развитие персональных ЭВМ, что позволило существенно приблизить ЭВМ к реальному пользователю.
Таким образом, необходимость автоматизации процессов принятия, планирования и синтеза решений предопределена возможностью возложить на ЭВМ роль консультанта по принятию и синтезу решений и тем самым обеспечить конфиденциальность информации и учесть способности каждого ЛПР, рационально распределить функции между пользователем и ЭВМ, обеспечить сбор, накопление, хранение и коррекцию экспертной информации при необходимости повторного решения задачи.
7.2. Предпосылки создания диалоговых систем синтеза и принятия решений
Под диалогом
обычно подразумевается [1, 2] процесс непосредственного и достаточно быстрого обмена сообщениями между двумя субъектами, при котором существует постоянная смена ролей информатора и реципиента (т.е. выдающего и принимающего сообщение соответственно).
Данное определение пригодно для рассмотрения взаимодействия как человека и ЭВМ, так и между людьми. Однако при этом изменяется смысл терминов субъект, информатор
и реципиент.
Исследования диалога человека и ЭВМ в настоящее время ведутся в следующих основных направлениях:
1) моделирование свободной
беседы, неограниченного речевого взаимодействия между двумя субъектами, которому были бы присущи свойства целенаправленности, взаимопонимания, равноценности деятельности и обучения партнеров;
2) технический подход, при котором на первый план выдвигаются свойства быстроты и возможность прямого обмена сообщениями, а также чисто языковое оформление и исключаются из рассмотрения основные свойства первого указанного подхода, такие, как взаимопонимание, равноценность деятельности и возможность обучения партнеров.
Наиболее правомерен подход, предусматривающий сочетание свойств обоих направлений, согласно которому диалогом человека с ЭВМ называется процесс, характеризуемый совокупностью или хотя бы одним из следующих качеств:
• наличие цели взаимодействия у обоих партнеров;
• определенная степень равноценности деятельности в процессе решения задачи;
• обмен сообщениями, направленный на установление понимания одним партнером сообщений другого;
• расширение и усовершенствование знаний (умений) одного партнера за счет знаний (умений) другого, в частности обучение одного партнера другим.
Рассмотрим более подробно эти качества.
Наличие цели взаимодействия у обоих партнеров.
Диалог между двумя людьми предполагает существование у участников цели, ради достижения которой осуществляется обмен сообщениями. При взаимодействии человека с ЭВМ (в задачах принятия, планирования и синтеза решений) цель человека, ответственного за выбор наилучшего решения, состоит в необходимости решить соответствующую задачу принятия, планирования и синтеза рационального решения. Целью компьютерной программной системы может быть оказание помощи лицу, решающему задачу. Реализация этой цели в зависимости от степени "интеллектуальности" ЭВМ допускает либо просто выполнение необходимых трудоемких рутинных расчетов, либо получение от ЛПР всей необходимой информации, хранение больших объемов информации и выдачу результатов решения, либо выбор путей решения задачи, что позволяет заставить пользователя мыслить в процессе решения системно и последовательно.
Равноценность деятельности партнеров по диалогу.
В процессе решения задачи предполагается способность каждого из партнеров совершать действия сходного характера, направленные на достижение поставленной цели. При взаимодействии человека и ЭВМ эта равноценность может проявляться в разумном разделении функций, которое обеспечивает наилучшее сочетание возможностей человека и ЭВМ.
Равноценность деятельности достигается при достижении определенной степени "интеллектуализации" ЭВМ, т.е. при переходе к ЭВМ, как минимум, функций сбора и накопления необходимой экспертной информации, а также обработки и выдачи ее по запросам.
Взаимопонимание партнеров.
Оно достигается при наличии у партнеров системы языковых знаков или кодов, из которых формируются сообщения, и хотя бы частичного понимания каждым из них предметной области. Чем большее количество знаний и умений оказывается общим для обоих партнеров, тем легче достигается понимание ими друг друга. Если же участники диалога не располагают некоторым минимумом общих знаний и/или умений, то необходимо осуществить дополнительное обучение хотя бы одного из них. Важную роль в проблеме взаимопонимания играет язык общения. В последнее время большое внимание уделяется разработке систем с естественным для человека языком общения [1, 3]. Однако требование абсолютной естественности языка подчас не является первостепенным; во многих случаях гораздо важнее четкое и однозначное понимание некоторых фактов и/или команд, чем форма их представления.
Процесс взаимообучения партнеров.Он
разделяется на две фазы:
1) обучение пользователя-профессионала машинным методам и средствам решения задач, осуществляемое вычислительной машиной;
2) обучение ЭВМ путем накопления и обобщения опыта решения задач пользователем в целях сокращения его участия в процессе выработки решения, оказания ему необходимой, деликатной помощи, а также накопления базы экспертной информации.
7.3. Классификация систем принятия и синтеза решений
Существующие интеллектуальные системы в большей степени ориентированы на реализацию методов принятия и синтеза решений, методов оптимизации, эвристических алгоритмов, чем на реализацию функций систем управления базами данных, информационно-поисковых систем и т. п.
Рассмотрим классификацию систем принятия и синтеза решений по основным классификационным признакам.
По характеру поддержки решений
можно выделить два класса систем:
1) системы специального назначения, ориентированные на решение определенного класса задач;
2) универсальные системы, обеспечивающие возможность быстрой настройки на конкретную задачу синтеза или принятия решений.
Основная масса существующих систем соответствует второму классификационному признаку.
По характеру взаимодействия пользователя и системы
можно выделить три класса:
1) системы, инициатором диалога в которых является ЭВМ, а пользователь выступает в роли пассивного исполнителя;
2) системы, в которых пользователь активен и является инициатором диалога;
3) системы, характеризующиеся последовательной передачей управления от пользователя к системе и наоборот.
Безусловно, системы второго класса представляют наибольший интерес, поскольку они дают пользователю полную свободу выбора действий. Однако реализация подобного способа взаимодействия в системах, предназначенных для пользователей-непрофессионалов, должна основываться на естественном языке общения. Достаточный синтаксический и семантический анализ запроса требует очень большого объема оперативной памяти, а также составления универсального тезауруса. Такой способ взаимодействия может быть реализован лишь на ЭВМ пятого поколения, функционирующих на принципах искусственного интеллекта.
Большинство разрабатываемых диалоговых систем относится к третьему классу. Принцип последовательной передачи управления позволяет пользователю взять управление на определенном этапе в свои руки и тем самым как бы вмешаться в процесс решения задачи, изменив его в нужном направлении, путем задания параметров, выбора метода и т. п.
По
наличию и характеру базы данных в системе
различают:
1) системы, не предусматривающие каких-либо способов накопления и хранения информации;
2) системы, имеющие базу данных или совокупность файлов для сбора, накопления и выдачи информации;
3) системы, имеющие развитые системы управления базами данных.
Все указанные системы могут быть использованы для накопления как объективной статистической, так и экспертной информации. При этом накопление объективной информации осуществляется, как правило, на один шаг быстрее, чем экспертной.
По
наличию интеллектуального компонента в системе
различают:
1) системы, не предусматривающие каких-либо способов накопления и обработки плохо формализуемых знаний;
2) системы, имеющие базы знаний, механизмы вывода и объяснения полученных решений.
Появление технологии обработки знаний сделало возможным использование в рамках автоматизированных процедур богатого методического задела из области искусственного интеллекта. В области экономики и управления существует много задач, содержащих как хорошо формализуемые процедуры, на которых применяются традиционные математические методы, так и плохо формализуемые процедуры, характеризующие творческие аспекты исследуемого процесса.
Поэтому модель для решения подобных задач должна представлять собой симбиоз методов обработки знаний и традиционных математических методов. При этом процедуры обработки знаний выступают в качестве среды, не отрицающей или заменяющей уже разработанные фрагменты, а органично интегрирующей их.
Использование в системах принятия и синтеза экономико-управленческих решений теории искусственного интеллекта представляется особенно актуальным и перспективным.
При интеллектуализации экономических информационных систем должны быть обеспечены:
• возможность использования всех способов представления знаний (процедурного, продукционного, семантического);
• реализация хранения и доступа к знаниям в рамках банка знаний;
• многокритериальный анализ альтернатив;
• построение заключений на основе количественного вывода о возможности сочетания реализаций составных частей системы, о значениях характеристик реализаций в нетиповых условиях функционирования и др.;
• обработка не полностью определенной информации в ходе принятия, планирования и синтеза экономико-управленческих решений;
• взаимодействие перечисленных процедур обоснования решений.
7.4. Принципы разработки программных средств
Системы принятия и синтеза решений, реализующие диалоговый принцип взаимодействия, оформляются в виде пакетов прикладных программ, под которыми подразумевается совокупность программ, совместимых между собой и обеспечивающих решение задач из некоторой предметной области [З].
Основные принципы проектирования программных средств применительно к процессам принятия и синтеза решений следующие.
В основе построения пакетов программ лежит принцип конструктивной независимости,
который предполагает разработку универсальной структуры пакета и некоторых его элементов.
Важнейшим принципом построения является модульность программных объектов.
Данный принцип означает дискретность структуры пакета и унификацию программных средств в целях формирования различных вычислительных схем, предназначенных для решения задач синтеза и выбора решений.
Унификация программных средств проявляется в том, что каждая программная единица (модуль) предназначена для выполнения определенных функций и взаимодействует с данными некоторым стандартным способом. В этом заключается очередной технологический принцип построения системы — принцип стандартизации взаимодействия программ с данными,
который предполагает использование единых методики и механизма подключения программных средств к данным.
Принцип машинной независимости
пакетов программ предусматривает возможность эксплуатации разработанного программного и информационного обеспечения при смене типов и поколений вычислительной техники.
Для успешной реализации этого принципа необходимо прежде всего выбрать универсальный алгоритмический язык. В качестве такого языка может быть выбран Си++ в силу его широкой распространенности на современных персональных ЭВМ.
Принцип максимальной независимости от операционных систем
непосредственно связан с принципом машинной независимости и преемственности систем.
Необходимое условие жизнеспособности программного обеспечения — соблюдение принципа расширяемости,
согласно которому пакеты программ являются открытыми системами, допускающими их непрерывное пополнение новыми программными средствами. Реализация этого принципа возможна лишь при соблюдении принципа модульности структуры пакета программ.
При разработке программного обеспечения для решения сложных задач принятия, планирования и синтеза решений, требующих активного вмешательства или непосредственного участия человека в процессе решения, особенно важно следовать принципу коммуникабельности,
который предполагает простоту общения пользователя с пакетом и предусматривает работу в интерактивном режиме.
7.5. Основные правила разработки систем
В процессе разработки диалоговых систем следует учитывать множество требований, которые условно можно подразделить на требования, определяющие принципы проектирования систем, и требования к эксплуатационным характеристикам диалоговых, систем.
Принципы проектирования диалоговых систем.
К ним относятся следующие правила
1. Прежде чем перейти к обсуждению достоинств и недостатков некоторой существующей системы или выдвижению требований к разработке системы с заданными свойствами, пользователь должен познакомиться с какой-либо моделью системы практически.
2. Разработка конкретных диалоговых систем, как правило, нацелена на автоматизацию процедур решения задач определенного класса. Поэтому проектировщику следует максимально использовать опыт работы и методологию, которые применялись пользователями создаваемой системы на практике, а не навязывать новую технологию решения задач.
3. Следует предусмотреть адаптивную обратную связь между пользователем и системой, позволяющую разработчику в интерактивном режиме приспособить систему к реальным условиям решения задачи. Наличие обратной связи дает возможность модифицировать систему с учетом новых требований ЛПР и новых задач.
4. При проектировании систем необходимо предусмотреть методы контроля и защиты информации, включающие следующие процедуры:
• синтаксический, логический и численный контроль информации;
• коррекцию ранее полученной информации;
• прерывание процедуры выполнения с возвратом в подходящую точку алгоритма с восстановлением исходных состояний файлов экспертной информации.
5. В процессе работы системы необходима фиксация ее деятельности с помощью ЭВМ для обеспечения накопления протоколов работы, последующий анализ которых позволяет интерпретировать и аргументировать решения, а также выявить ошибки, подразделяя их на ошибки пользователя и системы.
Требования к эксплуатационным характеристикам диалоговых систем.
К этим требованиям можно отнести следующие.
1. Правила адаптации субъекта к диалоговым системам предназначены для разработки систем, действующих на естественном языке, что является целью большинства исследований по искусственному интеллекту. При этом требование соблюдения таких условий, как участие пользователя в создании системы и обоснованность любых действий системы, определяется в зависимости от ранее указанных особенностей класса решаемых задач и типа предпочтений ЛПР. Эти условия предполагают, что пользователь не является пассивным элементом в системе и все действия разрабатываемой системы необходимо оценивать относительно их воздействия на активно изменяющегося пользователя, пытающегося понять и познать систему.
2. Условия проектирования диалоговых систем, диктующие необходимость снижения умственной нагрузки на пользователя-непрофессионала, предполагают выполнение следующих требований:
• единообразие вычислительных и опросных процедур и терминологии: желательно пользоваться привычной лексикой пользователя, т.е. система должна либо проектироваться для конкретной задачи, либо иметь возможность настраиваться на специфическую терминологию конкретной пользовательской области;
• определение последовательности предоставления информации и возможность получения углубленной информации по мере необходимости;
• обучение, основанное на опыте работы пользователя; предлагается снабдить пользователя подсказками с помощью ЭВМ и обеспечить возможность накопления опыта путем тренировочных просчетов;
• обозримость состояния диалога, которая предполагает использование кратких форм диалога (вопрос — ответ, выбор из меню) либо ответов на ограниченном естественном языке, не допускающем неоднозначное трактование требуемых в конкретной ситуации действий.
Дополнительно необходимо отметить, что помощь, предоставляемая пользователю со стороны системы, должна быть благожелательной, обеспечивать всестороннюю поддержку, выдачу справочной информации любой степени детализации в любой момент по требованию, своевременную ясную и точную диагностику ошибок пользователя с указанием способов их преодоления. Однако эта помощь системы не должна быть избыточной. Таким образом, одновременно с адаптацией пользователя к системе должен происходить и обратный процесс адаптации системы, который позволяет учесть уровень обучения пользователя и тем самым минимизировать его умственную нагрузку путем снижения числа вопросов, сокращения их формулировок и т. п.
7.6. Требования к методам защиты информации
Выбор решений в реальных ситуациях часто базируется на конфиденциальной информации, доступ к которой возможен лишь при получении санкций на использование либо на корректировку ранее накопленной информации. Настоящее условие предусматривает контроль и защиту информации в базе данных, причем данная проблема должна быть решена на этапе проектирования системы.
Различают два вида средств защиты экспертной информации: средства защиты, предоставляемые операционной системой, и программные средства защиты информации.
К средствам защиты экспертной информации, предоставляемым операционной системой
независимо от типа используемой ЭВМ, относятся:
• шифры, пароли, идентификаторы области каждого пользователя, где хранятся его программы и наборы данных;
• идентификаторы магнитных дисков, на которых расположены пользовательские области, откуда пользователь может считывать информацию.
Значения идентификаторов магнитного диска и пользовательской области, а также пароли известны только системному программисту, ответственному за эксплуатацию операционной системы, и непосредственному пользователю.
К числу программных средств
защиты информации можно отнести шифры задач синтеза и принятия решений. Введение шифра задачи обеспечивает конфиденциальность информации по следующим причинам:
• он известен только пользователю и не должен сообщаться системному программисту;
• без ввода шифра невозможен запуск ни одной из программ для соответствующей задачи, а также исключен несанкционированный доступ к экспертной информации, накопленной в системе, стандартными средствами операционной системы.
7.7. Функции и структура автоматизированной системы принятия, планирования и синтеза решений
Структура системы принятия, планирования и синтеза рациональных решений в области экономики и управления приведена на рис. 7.1. Система включает три функциональные подсистемы: принятия решений, аналитического планирования и комбинаторно-морфологического синтеза.
Диалоговый монитор системы организует в соответствии с выбранной пользователем задачей работу всех трех подсистем и их компонентов, в частности: изменение порядка взаимодействия компонентов, добавление новых схем решения функциональных задач, диалоговое управление вызовом очередных компонентов систем. В целом диалоговый интерфейс построен на принципах функционирования экспертной системы, использующей знания о процедурах решения выбранного класса задач.
В рамках данной системы автоматизируются следующие функции экономиста (управленца) — аналитика:
• хранение информации;
• поиск информации по запросам в базах данных и знаний для анализа взаимосвязей объектов, изучения состава объектов, анализа значений характеристик, уточнения функций и условий функционирования исследуемых объектов;
• формирование социально-экономических и технологических требований и критериев качества к исследуемой системе;
• генерация вариантов сложных многокомпонентных систем;
• многокритериальный анализ вариантов и выбор лучшего из них;
• построение планов вычислений и проведение расчетов;
• логический вывод информации на основе имеющихся знаний.
Функциональная подсистема принятия решений
[4, 5]. Она включает в себя компонент математических методов ранжирования альтернатив и распределения ресурсов с учетом многокритериальности, базу данных критериев качества, базу знаний иерархий критериев качества и функций принадлежности, базу знаний решенных задач по принятию решений.

Компонент математических методов реализует методы многокритериального анализа и выбора вариантов, в основе которых лежат методы анализа иерархий и принятия решений на нечетких множествах, а также методы комбинаторики для решения задач оптимального распределения ресурсов.
База данных критериев качества содержит информацию о различных социально-экономических, технологических, экологических, антропогенных и других критериях, которые классифицированы по различным экономическим, управленческим и организационным проблемам. База данных критериев постоянно пополняется новой информацией.
База знаний иерархий критериев качества и функций принадлежности накапливает и хранит знания о наиболее типовых иерархиях и функциях из различных отраслей экономики. Она строится на основе знаний высококвалифицированных специалистов предметных областей и может быть использована при решении типовых задач без существенной корректировки значений функций принадлежности и иерархических структур критериев.
База знаний решенных задач хранит и накапливает информацию о компонентах решенных практических задач по принятию решений. К таким компонентам причислены функции принадлежности по различным критериям; иерархические структуры критериев, экспертные оценки степени предпочтительности исследуемых альтернатив и относительной важности критериев, векторы приоритетов альтернатив по всем рассматриваемым в задаче критериям и для каждого эксперта, участвовавшего в решении задач принятия и обоснования рациональных решений.
Компонент математических методов для поддержки динамических процессов в иерархических системах имеет ряд особенностей, не рассматриваемых ранее. Данный компонент расширен следующими процедурами:
• процедурой подбора функций и построения полиномов, аппроксимирующих динамику изменения предпочтений на основе информации, хранящейся в базе данных;
• процедурой численного решения уравнения (2.4) для матриц произвольной размерности, элементы которых заданы функциями из табл. 2.2;
• процедурой построения регрессионных зависимостей приоритетов от времени на основе информации, содержащейся в базе данных.
Задача прогнозирования решается в системе двумя способами: путем построения аппроксимирующих зависимостей на основе имеющейся в базе данных информации с последующим их использованием для построения динамических матриц парных сравнений на определенном отрезке времени, а также путем экспертной оценки вероятного изменения предпочтений с помощью функциональной шкалы (см.
табл. 2.2) и последующего численного решения уравнения вида (2.4).
Получение динамических приоритетов также возможно путем аппроксимации информации, хранящейся в базе данных, или в результате решения уравнения (2.4).
База данных системы для поддержки динамических процессов принятия решений выполняет две основные функции. Она используется для информационной поддержки пользователя при формировании новых задач в данной предметной области, а также в процессах анализа при извлечении знаний. Представление информации о целях, критериях, альтернативах, экспертах и, наконец, предпочтениях сопряжено со сложностями, поскольку между элементами данных существует множество связей различного характера. В соответствии с основными функциями данные можно разделить на две категории, одна из которых, наиболее общая, обеспечивает информационную поддержку пользователя, а другая, более конкретная, используется в процессах извлечения знаний. К первой категории относится информация об альтернативах, критериях и экспертах. Данные об этих объектах можно организовать в виде пополняемых списков и таблиц. Вторая категория данных содержит ссылки на конкретные альтернативы, критерии и экспертов, участвовавших в решении определенной задачи, а также включает информацию обо всех предпочтениях и приоритетах. Для представления данных первой категории хорошо подходит любая модель, данные второй категории плохо вписываются во все модели. Поэтому для их представления используется собственный формат, названный "файл задачи".
Сравнение реляционной и файловой моделей показало явные преимущества последней по возможностям представления сложных данных, при этом трудоемкость реализации такой системы значительно выше.
Функциональная подсистема аналитического планирования.
Она включает в себя компонент формирования процессов планирования в прямом и обратном направлениях; базу данных наименований сил, акторов, целей акторов, критериев качества, политик, сценариев; базу знаний прямых и обратных иерархических процессов планирования; базу знаний решенных задач. Подсистема аналитического планирования взаимодействует с компонентом математических методов многокритериального выбора альтернатив на иерархических структурах.
Формирование прямого и обратного процессов планирования обеспечивается средствами графического интерфейса и математическим компонентом подсистемы принятия решений. В частности, для этой цели используется метод анализа иерархий. Этот компонент позволяет пользователю формировать процессы планирования и проводить сравнительную оценку обобщенных сценариев, осуществлять калибровку переменных состояний и оценку последствий принимаемых решений.
База данных содержит систематизированную по различным ситуациям планирования развития экономических отраслей информацию: о политических, экономических и социальных силах, действующих в обществе; об акторах, т. е. социальных группах, влияющих на процесс планирования и исходы; о целях акторов, критериях качества, конкретизирующих цели, и о политиках, которые предпринимаются акторами для достижения целей; о вероятных сценариях развития исследуемого процесса.
База знаний иерархий содержит знания о прямых и обратных процессах планирования в виде иерархических систем и векторов . приоритетов элементов, расположенных на иерархических уровнях. Иерархические системы классифицированы по отраслям экономики.
База знаний решенных задач хранит и накапливает всю информацию о каждой задаче планирования, просчитанной данной подсистемой. Накопление подобных знаний позволяет прослеживать динамику планирования близких по содержанию задач планирования и накапливать знания для последующих обобщений в целях создания самообучающейся системы.
Функциональная подсистема комбинаторно-морфологического синтеза
[6]. Она содержит компонент формирования морфологических таблиц; компонент математических методов комбинаторно-морфологического синтеза, распределения ресурсов и подсистем; базу данных критериев качества; базу данных классификационных признаков; базу знаний решенных задач.
Компонент формирования морфологических таблиц обеспечивает ввод в систему таблиц различной структуры и размерности в графическом режиме. Сформированная таким образом морфологическая таблица содержит для решения конкретной задачи всю необходимую информацию о функциональных подсистемах, альтернативах, критериях качества, предпочтениях, параметрах.
Формирование морфологических таблиц для решения задач осуществляется двумя способами: непосредственным вводом новой таблицы пользователем в диалоговом режиме; с использованием базы знаний решенных аналогичных задач и баз данных критериев качества, функциональных подсистем и классификационных признаков. Для оценки альтернатив, систематизированных морфологической таблицей, привлекается подсистема принятия решений.
Компонент математических методов содержит все рассмотренные в предыдущих разделах комбинаторно-морфологические методы синтеза рационального распределения ресурсов между альтернативами и кластерного анализа морфологических множеств.
База данных функциональных подсистем содержит информацию об основных характеристиках элементов, из которых синтезируются сложные экономические, управленческие или организационные системы.
База данных критериев качества позволяет накапливать и отбирать из нее критерии, наиболее важные для решения конкретной задачи. При этом главные критерии не ускользают из поля деятельности исследователя.
База данных классификационных признаков содержит информацию о качественных функциональных, структурных и параметрических признаках и их значениях. Признаки и их значения образуют родовидовые классификации и сгруппированы с учетом различных функциональных подсистем.
База знаний решенных задач накапливает и хранит знания о практически решенных задачах для использования накопленного опыта в типовых ситуациях синтеза рациональных систем. База знаний хранит всю входную и выходную информацию.
Основные понятия
1. Автоматизация процессов принятия, планирования и синтеза экономических решений.
2. Диалоговые компьютерные системы.
3. Классификация компьютерных систем принятия и синтеза экономических решений.
4. Принципы разработки компьютерных систем.
5. Методы защиты информации.
6. Функции и структура автоматизированной системы принятия и синтеза решений.
Контрольные вопросы и задания
1. Дайте обоснование необходимости автоматизации процессов принятия, планирования и синтеза экономических решений.
2. По каким основным признакам классифицируются компьютерные системы принятия и синтеза решений?
3. Каковы правила и принципы разработки программных средств?
4. Приведите основные требования, предъявляемые к методам защиты информации.
5. Предложите новую концептуальную структуру и набор функций автоматизированной системы принятия и синтеза решений для выбранной вами конкретной экономической области.
6. Проведите научное исследование по выявлению процедур эвристических методов, которые целесообразно формализовать в ближайшем будущем и в перспективе (первое десятилетие XXI в.).
Литература
1.
Довгяло А. М.
Диалог пользователя с ЭВМ: Основы проектирования и реализации. — Киев: Наукова думка, 1981. — 232 с.
2.
Сакман Г.
Решение задач в системе человек — ЭВМ. — М.: Мир, 1973.—351 с.
3.
Мишенин А. И.
Теория экономических информационных систем. — М.: Финансы и статистика, 1999. — 243 с.
4.
Андрейчиков А. В., Андрейчикова О.Н.,
Джабер Ф.Ф.
Автоматизированное принятие решений в иерархических системах // Программные продукты и системы. — 1993. — № 3. — С.23 — 29.
5.
Андрейчикова О. Н.
Интеллектуальные системы для поддержки процессов принятия решений: Учеб. пособие. — Волгоград: Изд-во ВолгГТУ, 1996. — 93 с.
6.
Андрейчиков А. В. Анорейчикова О. Н.
Компьютерная поддержка изобретательства. — М.: Машиностроение, 1998. — 476 с.
ПРИЛОЖЕНИЕ
Фонд эвристических приемов
1. Преобразование структуры.
1.1. Исключить наиболее напряженный элемент.
1.2. Исключить элемент при сохранении объектом всех прежних функций.
1.3. Убрать лишние структурные элементы, даже если будет потерян один процент эффекта.
1.4. Обеспечить выполнение одним элементом нескольких функций, благодаря чему отпадет необходимость в других элементах.
1.5. Присоединить к базовой системе дополнительный специализированный элемент.
1.6. Заменить связи между элементами систем.
1.7. Заменить источник финансирования, кредитования и т. д.
1.8. Существенно изменить компоновку системы.
1.9. Сосредоточить органы управления и контроля в одном месте.
1.10. Ввести единую систему управления или финансирования, кредитования и т. д.
1.11. Соединить однородные или предназначенные для смежных операций объекты.
1.12. Объединить в единое целое объекты, имеющие самостоятельное назначение, которое сохраняется после объединения в новом комплексе.
1.13. Использовать принцип агрегирования. Создать базовую систему, на которую можно "навесить" различные (в различных комбинациях) новые функциональные подсистемы.
1.14. Совместить или объединить явно или традиционно несовместимые системы, устранив возникающие противоречия.
1.15. Найти глобально оптимальную структуру.
1.16. Выбрать (придумать) наиболее красивую структуру.
2. Преобразование в пространстве (при проектировании офисов, маркетов и т. п.).
2.1. Изменить традиционную ориентацию в пространстве (положить набок, повернуть низом вверх. Повернуть путем вращения и т. д.).
2.2. Использовать "пустое пространство" между элементами системы (один элемент системы может проходить сквозь полость в другом элементе системы).
2.3. Объединить известные порознь элементы системы с размещением одного внутри другого по принципу "матрешки".
2.4. Заменить размещение по одной линии размещением по нескольким линиям или плоскостям. Инверсия приема.
2.5. Заменить размещение на плоскости размещением по нескольким плоскостям или в трехмерном пространстве. Инверсия приема.
2.6. Изменить направление действия силы.
2.7. Приблизить рабочие органы системы к месту выполнения ими своих функций без передвижения самой системы.
2.8. Заранее расставить объекты так, чтобы они могли вступить в действие с наиболее удобного места и без затрат времени на доставку.
2.9. Перейти от последовательного соединения элементов к параллельному или смешанному. Инверсия приема.
2.10. Разделить объект на части так, чтобы приблизить каждую из них к тому месту, где она работает.
2.11. Разделить систему на две части: объемную и необъемную, вынести объемную часть за пределы, ограничивающие объем.
2.12. Вынести элементы, подверженные действию вредных факторов, за пределы их действия.
2.13. Перенести (поместить) систему или ее элемент в другую среду, исключающую действие вредных факторов. Выйти за традиционные пространственные ограничения.
3. Преобразования во времени.
3.1. Перенести выполнение действия на другое время. Выполнить требуемое действие до начала работы или после ее окончания.
3.2. Перейти от непрерывного действия (процесса) к периодическому, или импульсному. Инверсия приема.
3.3. Перейти от стационарного во времени режима к изменяющемуся.
3.4. Исключить бесполезные (вредные) интервалы времени. Использовать паузу между периодическими действиями для осуществления другого действия.
3.5. По принципу непрерывного полезного действия осуществлять работу системы непрерывно, без холостых ходов. Все элементы системы должны работать с полной нагрузкой все время.
3.6. Изменить последовательность выполнения операций.
3.7. Перейти от последовательного осуществления операций к параллельному (одновременному). Инверсия приема.
3.8. Совместить экономические (технологические, организационные) процессы или операции. Объединить однородные или смежные операции. Инверсия приема.
4. Приемы дифференциации.
4.1. Разделить движущийся поток информации на два или несколько.
4.2. Разделить систему на части.
4.3. Дифференцировать экономические и другие источники; приблизить их к исполнительным органам.
4.4. Сделать автономным управление каждого элемента системы.
4.5. Провести дробление традиционной целостной системы на мелкие однородные элементы, выполняющие однородные функции. Инверсия приема.
4.6. Придать системе блочную структуру, при которой каждый блок выполняет самостоятельную функцию.
4.7. Выделить в системе самый нужный элемент (нужное свойство) и усилить его, улучшить условия его работы.
5. Количественные изменения.
5.1. Резко изменить (в несколько раз) параметры или показатели системы (ее элементов, окружающей среды).
5.2. Увеличить (или уменьшить) в системе число одинаковых или подобных друг другу элементов. Изменить число одновременно действующих или обрабатываемых элементов системы.
5.3. Увеличить (или уменьшить) степень дробления системы.
5.4. Допустить незначительное уменьшение требуемого эффекта.
5.5. Использовать идею избыточного решения (если трудно получить 100 % требуемого эффекта, задаться целью получить несколько больше имеющегося).
5.6. Изменить вредные факторы так, чтобы они перестали быть вредными.
5.7. Уменьшить число функций системы с тем, чтобы она была более специализированной, соответствующей только оставшимся функциям и требованиям.
5.8. Гиперболизировать, значительно увеличить размеры системы и найти ей применение. Инверсия приема.
5.9. Создать местное локальное качество; осуществить локальную концентрацию усилий.
5.10. Найти глобально оптимальные параметры экономической (управленческой, организационной и т. д.) системы по различным критериям качества.
6. Использование профилактических мер.
6.1. Предусмотреть прикрытие и защиту легко повреждающихся элементов.
6.2. Ввести предохранительные устройства или блокировку.
6.3. Выполнить систему модульной, так чтобы можно было заменять отдельные поврежденные части.
6.4. Для сокращения времени простоев и повышения надежности создать легко используемый запас рабочих элементов. Предусмотреть в ответственных частях системы дублирующие элементы.
6.5. Заранее придать системе качества сопротивления нежелательным воздействиям окружающей среды.
6.6. Заранее придать объекту изменения, противоположные недопустимым или нежелательным изменениям, возникающим в процессе работы.
6.7. Придать системе новое свойство, например обеспечить его самовосстановление.
6.8. Выполнить элементы системы взаимозаменяемыми.
6.9. Разделить систему на части так, чтобы при выходе из строя одного элемента система в целом сохраняла работоспособность.
6.10. Для повышения надежности заранее подготовить аварийные средства.
6.11. Обеспечить уменьшение или устранение колебательных и инерционных процессов.
6.12. Использовать объекты живой и неживой природы при формировании зоны эстетического воздействия (создание зеленой изгороди из деревьев и кустарников, маскировка и т. д.).
6.13. Исключить из окружающей предметной среды объекты, вызывающие отрицательные эмоции.
6.14. Осуществить разработку новых технологий, обеспечивающих резкое уменьшение финансовых нарушений в различных сферах деятельности.
7. Использование резервов.
7.1. Использовать периодически возникающие доходы для получения дополнительного эффекта.
7.2. Компенсировать чрезмерный расход прибыли получением какого-либо дополнительного положительного эффекта.
7.3. Устранить вредный фактор (например, за счет компенсации его другим вредным фактором).
7.4. Вместо действия, диктуемого условиями задачи, осуществить противоположное по эффекту действие.
7.5. Выполнивший свое назначение или ставший ненужным элемент использовать для других целей.
7.6. Использовать вредные факторы для получения положительного эффекта.
7.7. Выбрать и обеспечить оптимальные параметры (себестоимость, процентные ставки и др.).
7.8. Уточнить расчетные параметры на основе использования более точных математических моделей и ЭВМ.
7.9. После улучшения какого-либо элемента системы определить, как должны быть изменены другие элементы, чтобы эффективность системы в целом еще более повысилась.
8. Преобразование по аналогии.
8.1. Применить объект, предназначенный для выполнения аналогичной функции, в другой отрасли экономики.
8.2. Использовать в качестве прототипа искомого экономического (управленческого, организационного и т. п.) решения аналогии из близких или отдаленных областей экономики.
8.3. Применить решение, аналогичное имеющемуся в наиболее развитых экономических странах, в научно-фантастической литературе и т. д.
8.4. Использовать аналогии свойств других систем; использовать свойства без самой системы.
8.5. Использовать принцип имитации, заключающийся в создании таких систем, которые по своим свойствам аналогичны другой системе.
8.6. Использовать эмпатию: мысленно превратить себя в систему, с помощью своих ощущений найти наиболее целесообразное решение.
8.7. Вместо недоступной, сложной, дорогостоящей системы использовать ее упрощенные копии, модели, макеты.
Андрейчиков А.В., Андрейчикова О.Н.
А65 Анализ, синтез, планирование решений в экономике — М.: Финансы и статистика, 2000. — 368 с.: ил.
ISBN 5-279-02188-1.
Описаны современные математические и эвристические методы и компьютерные системы, применяемые для анализа, планирования и синтеза экономических решений в условиях неопределенности. Рассмотрены методологические подходы использования этих методов и систем для решения широкого спектра прикладных социально-экономических задач.
Для студентов вузов, обучающихся по специальности "Информационные системы в экономике" и смежным специальностям, а также для аспирантов и преподавателей.
УДК
[
330.44 + 330.46] (0.75.8)
ББК 65.050.03.я73
Учебное издание
Андрейчиков Александр Валентинович
Андрейчикова Ольга Николаевна
АНАЛИЗ, СИНТЕЗ, ПЛАНИРОВАНИЕ РЕШЕНИЙ В ЭКОНОМИКЕ
Заведующая редакцией Л. А. Табакова
Ведущий редактор Л. Д. Григорьева
Редактор А. М. Материна
Художественный редактор Ю. И. Артюхов
Технический редактор Е. В. Кузьмина
Корректоры А. М. Маторина, Н. Б. Вторушина
Обложка и художественное оформление Е
. К. Самойлова
ИБ№3485
Лицензия ЛР 010156 от 29.01.97
Сдано в набор 01.06.99. Подписано в печать 9.12.99
Формат 60х88/16. Гарнитура "Арчал". Печать офсетная
Усл. п. л. 22,54. Уч.-изд. л, 19,92 Тираж 3000 экз. Заказ 2012. "С" 149
Издательство "Финансы и статистика"
101000, Москва, ул. Покровка, 7
Телефон (095) 925-47-08, факс (095) 925-09-57
E-mail: mail@finstat.ru http://www.finstat.ru
Великолукская городская типография
Комитета по средствам массовой информации и связям с общественностью администрации Псковской области
182100, Великие Луки, ул. Полиграфистов, 78/12
Тел./факс: (811-53) 3-62-95
E-mail: VTL@MART.RU
|