| Исследуем сплошной подшипник (Ω
= 360 °С), имеющий размеры D
=
120 мм и В
=
120мм, который работает при нагрузке F
=
40000Н и при скорости N
j
=45,00-1
. Предполагается, что эти рабочие условия являются критическими для теплового баланса. Корпус подшипника, имеющий площадь поверхности А
=
0,3м2
, и неразрезная втулка подшипника изготовлены из алюминиевого сплава. Вал изготовлен из стали. Смазочное масло подают через отверстие размером dL
=5мм, расположенное диаметрально противоположно нагруженной зоне втулки подшипника. В качестве смазки используют масло со степенью вязкости VG 46 (ИСО 3448).
Прежде всего исследуют возможность работы подшипника без смазки под давлением. В этом случае диссипация тепла происходит только путем конвекции. Окружающая температура составляет T
amb
=40o
С, максимальная допустимая температура подшипника T
lim
=70o
С.
Если температура подшипника превысит T
lim
,
то следует предусматривать подачу смазочного материала под давлением с внешним масляным охлаждением. В таких случаях предполагается, что смазочный материал подают в подшипник с избыточным давлением ре
n
= 5 х 105
Па, а температура масла на входе составляет T
е
n
= 60 O
С.
Размеры и рабочие параметры подшипника даны в таблице 1
Таблица 1 – Размеры и рабочие параметры подшипника
| Нагрузка на подшипник
|
F
= 40000 Н
|
| Скорость вала
|
N
J
= 45,00 с-1
|
| Скорость подшипника
|
N
В
= 0 с-1
|
| Угол охвата
|
Ω = 360 о
|
| Максимальный внутренний диаметр подшипника
|
D
max
=120,070х10-3
м
|
| Минимальный внутренний диаметр подшипника
|
D
min
120,050х10-3
м
|
| Диаметр смазочного отверстия
|
d
L
= 5 х10-3
м
|
| Максимальный диаметр вала
|
D
Ј
,max=119,950х10-3
м
|
| Минимальный диаметр вала
|
D
Ј
,min=119,930х10-3
м
|
| Относительная длина подшипника
|
В/
D
= 0,5
|
| Средняя высота неровностей поверхности скольжения подшипника
|
r
zB
= 2 х10-6
м
|
| Средняя высота неровностей поверхности скольжения вала
|
r
zj
= 1 х10-6
м
|
| Коэффициент линейного расширения подшипника
|
α I,В = 23 х10-6
K-1
|
| Коэффициент линейного расширения вала
|
α I,J = 11 х10-6
K-1
|
| Теплоотводящая поверхность корпуса подшипника
|
А
= 0,3м2
|
| Коэффициент теплопередачи
|
k
A
= 20 Вт/(м2
×К)
|
| Температура окружающей среды
|
T
amb
= 40 o
C
|
| Температура смазочного материала на входе подшипника при смазке под давлением
|
Tе
n
= 60 o
C
|
| Избыточное давление подачи смазочного материала при смазке под давлением
|
р
е
n
= 5 х10-5
Па
|
| Объемная удельная теплоемкость смазочного материала
|
Ρ
с=
1,8 х10-6
Дж/( м3
×К)
|
| Предельные значения:
|
| максимальная допустимая удельная нагрузка на подшипник
|
 = 10 х10-6
Па
= 10 х10-6
Па
|
| предельно допустимая температура подшипника
|
T
lim
= 70 o
C
|
| критическая толщина смазочного слоя
|
h
min = 9 х10-6
м
|
| Смазочный материал
|
VG 46
|
Вязкостно-температурная зависимость для масла VG 22 и ρ
= 900 кг/м3
представлена в таблице 1.
Таблица 1–Вязкостно-температурная зависимость для масла VG 46 и ρ
=900 кг/м3
| Tе
ff
, o
C
|
η eff (Tе
ff
), Па×с
|
| 40
|
0,042
|
| 50
|
0,029
|
| 60
|
0,019
|
| 70
|
0,014
|
Проверим ламинарный поток по уравнению
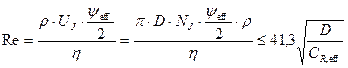
При предполагаемой температуре подшипника Т
B
,0
=
60 °С и предполагаемой плотности смазочного материала ρ
=900кг/м3
. Для вычислений определим, значение  Относительный зазор в подшипнике в соответствии с уравнениями составляет: Относительный зазор в подшипнике в соответствии с уравнениями составляет:
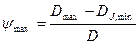



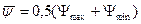

Изменение относительного зазора в результате теплового воздействия составляет в соответствии с уравнением:

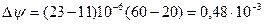 
Эффективный относительный зазор в подшипнике в соответствии с уравнением составляет:
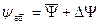

Предполагаемая температура подшипника 
Эффективная динамическая вязкость смазочного материала при T
eff
=60 °С в соответствии с входными параметрами
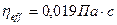
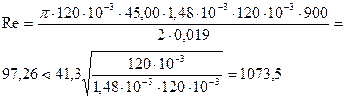

Поток является ламинарным, поэтому настоящий стандарт для данного случая применим. Определим удельную нагрузку на подшипник в соответствии с уравнением :
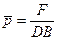

Удельная нагрузка на подшипник  допустима, так как допустима, так как 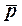 < <
 lim
.
Отвод тепла путем конвекции. lim
.
Отвод тепла путем конвекции.
Эффективная угловая скорость согласно уравнению составляет:
Угловая скорость вала
 
Угловая скорость подшипника

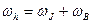
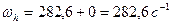
Число Зоммерфельда согласно уравнению :
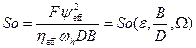
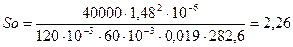
Относительный эксцентриситет является функцией величин So
, B
/
D
, W
и определяется по таблицам
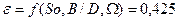
Минимальная толщина смазочного слоя согласно уравнению:
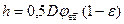

Удельный коэффициент трения согласно уравнению:
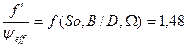
Коэффициент трения
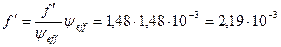
Расход тепла, обусловленный мощностью трения, согласно уравнению:


Расход тепла через корпус подшипника и вал в окружающую среду согласно уравнению составляет:


Из соотношения P
th
,
f
= P
th
,
amb
следует, что
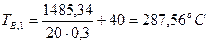
Так как T
B
, 1
> Т
B
,0
, то следует, что температура подшипника Т
B
,0
=60 °С должна быть скорректирована. Скорректированное предположение о температуре подшипника
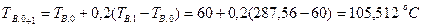
Результаты дальнейшей итерации приведены в таблице 3. На седьмом этапе расчета разность между предполагаемой температурой подшипника Т
B
,0
и расчетной температурой подшипника Т
B
,1
составляет менее 1 °С. Температура подшипника Т
B
рассчитана с достаточной степенью точности. Так как Т
B
> Т
lim
, то диссипация тепла путем конвекции оказывается недостаточной. Поэтому подшипник следует охлаждать смазочным материалом (смазка под давлением)
Таблица 3 – Результаты итераций
| Параметры
|
Единицы измерения
|
Этапы расчета
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| TB
,
0
=Teff
|
°С
|
60
|
105,6
|
198,27
|
91,49
|
266,25
|
136,5
|
| ηeff
|
Па с
|
0,019
|
0,0045
|
0,002
|
0,0065
|
0,002
|
0,0027
|
| Ψeff
|
|
1,48
|
2,03
|
5,28
|
1,86
|
3,96
|
2,4
|
| S0
|
-
|
2,26
|
18
|
96,9
|
10,5
|
154,14
|
41,9
|
| ε
|
-
|
0,425
|
0,82
|
0,966
|
0,716
|
0,95
|
0,883
|
| hmin
|
м
|
51,06
|
22
|
6,4
|
31,7
|
11,88
|
0,017
|
| f'/ψeff
|
-
|
1,48
|
3,1
|
0,5
|
5
|
0,9
|
3,5
|
| Pf
|
Вт
|
1485,3
|
4268,2
|
1064,8
|
6307,6
|
2414
|
5697,2
|
| TB
|
°С
|
287,6
|
751,4
|
217,5
|
1091,3
|
442
|
989,5
|
| TB
,0
|
°С
|
105,5
|
198,27
|
91,49
|
266,2554
|
136,5
|
245,9
|
При расчетах в этом случае используется смазочный материал VG 46 и относительная длинна подшипника В/
D
= 0,5. Но в этом случае не выполняется условие температур ( Разность между предполагаемой температурой подшипника Т
B
,0
и расчетной температурой подшипника Т
B
,1
составляет менее 1 градуса).
Поэтому ведем расчет при VG32 и В/
D
=0,75.
Таблица 1–Вязкостно-температурная зависимость для масла VG 32 и ρ
=900 кг/м3
| Tе
ff
, o
C
|
η eff (Tе
ff
), Па×с
|
| 40
|
0,03
|
| 50
|
0,021
|
| 60
|
0,014
|
| 70
|
0,009
|
Проверим ламинарный поток по уравнению
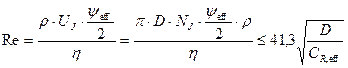
При предполагаемой температуре подшипника Т
B
,0
=
60 °С и предполагаемой плотности смазочного материала ρ
=900кг/м3
. Для вычислений определим, значение 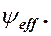 Относительный зазор в подшипнике в соответствии с уравнениями составляет: Относительный зазор в подшипнике в соответствии с уравнениями составляет:

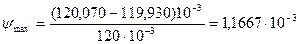
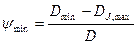
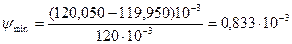

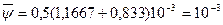
Изменение относительного зазора в результате теплового воздействия составляет в соответствии с уравнением:
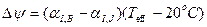
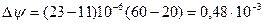 
Эффективный относительный зазор в подшипнике в соответствии с уравнением составляет:

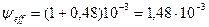
Предполагаемая температура подшипника 
Эффективная динамическая вязкость смазочного материала при T
eff
=60 °С в соответствии с входными параметрами
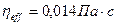
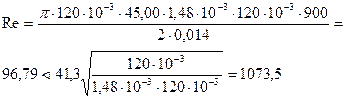

Поток является ламинарным, поэтому настоящий стандарт для данного случая применим. Определим удельную нагрузку на подшипник в соответствии с уравнением :


Удельная нагрузка на подшипник 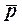 допустима, так как допустима, так как  < <
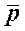 lim
.
Отвод тепла путем конвекции. lim
.
Отвод тепла путем конвекции.
Эффективная угловая скорость согласно уравнению составляет:
Угловая скорость вала
 
Угловая скорость подшипника


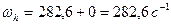
Число Зоммерфельда согласно уравнению :


Относительный эксцентриситет является функцией величин So
, B
/
D
, W
и определяется по таблицам
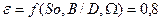
Минимальная толщина смазочного слоя согласно уравнению:
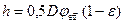

Удельный коэффициент трения согласно уравнению:
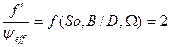
Коэффициент трения

Расход тепла, обусловленный мощностью трения, согласно уравнению:

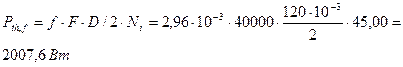
Расход тепла через корпус подшипника и вал в окружающую среду согласно уравнению составляет:
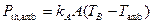
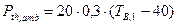
Из соотношения P
th
,
f
= P
th
,
amb
следует, что

Так как T
B
, 1
> Т
B
,0
, то следует, что температура подшипника Т
B
,0
=60 °С должна быть скорректирована. Скорректированное предположение о температуре подшипника

Таблица 4 – Результаты итераций
| Параметры
|
Единицы измерения
|
Этапы расчета
|
| 1
|
2
|
3
|
4
|
| TB
,
0
=Teff
|
°С
|
60
|
122,9
|
187,08
|
123,8
|
| ηeff
|
Па с
|
0,014
|
0,003
|
0,0019
|
0,0026
|
| Ψeff
|
|
1,48
|
2,23
|
3
|
2,25
|
| S0
|
-
|
2,05
|
21,72
|
62,08
|
25,5
|
| ε
|
-
|
0,8
|
0,748
|
0,88
|
0,78
|
| hmin
|
м
|
17,7
|
33,72
|
20
|
29,7
|
| f'/ψeff
|
-
|
2
|
2,6
|
1
|
2
|
| Pf
|
Вт
|
2007,6
|
3932,4
|
2034,7
|
3052,1
|
| TB
|
°С
|
374,6
|
695,4
|
379,12
|
548,68
|
| TB
,0
|
°С
|
122,9
|
187,08
|
123,8
|
157,72
|
Однако и в этом случае не выполняется разность температур ( Разность между предполагаемой температурой подшипника Т
B
,0
и расчетной температурой подшипника Т
B
,1
составляет менее 1 градуса).
Для расчета принимаем VG32 и В/
D
=0,75.
Отвод тепла смазочным материалом (смазка под давлением).
Предполагаемая температура смазочного материала на выходе:

Эффективная температура смазочного слоя:
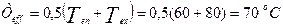
Эффективная динамическая вязкость смазочного материала при T
eff
=70о
С на основании заданных параметров составляет:
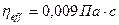
Изменение относительного зазора в результате воздействия температуры согласно уравнению составляет:


Эффективный относительный зазор согласно уравнению:


Число Зоммерфельда :
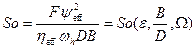
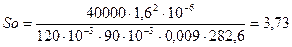
Относительный эксцентриситет:
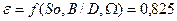
Минимальная толщина смазочного слоя согласно уравнению:
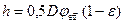

Удельный коэффициент трения:
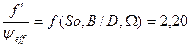
Коэффициент трения составляет:
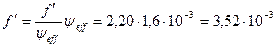
Расход тепла, обусловленный мощностью трения, согласно уравнению:

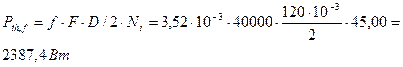
Расход смазочного материала вследствие развития внутреннего давления согласно уравнению:
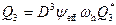

Расход смазочного материала, обусловленного давлением подачи, согласно уравнению:
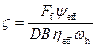
 

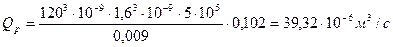
Расход смазочного материала согласно уравнению:
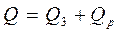

Расход тепла через смазочный материал согласно уравнению:

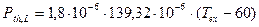
Из соотношения P
th
,
f
= P
th
,
L
получаем:
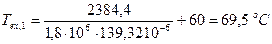
Так как T
ех,
1
< T
ех,
0
, следует предположение, что температура выхода смазочного материала T
ех,
0
= 78 о
С должна быть скорректирована.
Скорректированное предположение о температуре выхода масла:
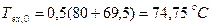
Дальнейшие этапы итерации указаны в таблице 5.
На третьем этапе расчета разность между предполагаемой температурой выхода смазочного материала T
ех
, 0
и рассчитанной температурой выхода T
ех
, 1
составила менее 1 °С.
Следовательно, температура выхода смазочного материала T
ех
рассчитана с достаточной степенью точности.
Так как T
ех
<
T
lim
, то температура выхода смазочного материала находится в допустимых пределах.
Так как h
m
in
>
h
lim
, то минимальная толщина слоя смазочного материала находится в допустимых пределах.
Вместо итерационных расчетов можно воспользоваться методом графической интерполяции. Для этого проводят расчет для ряда предполагаемых температур Т
B
или T
ех
, которые охватывают диапазоны ожидаемых решений.
В таблице 5 представлены расчеты итераций температуры масла на выходе из подшипника
Таблица 4–Результаты итераций температуры масла на выходе из подшипника
| Этапы расчета
|
| 1
|
2
|
3
|
| T
en
|
o
C
|
60
|
60
|
60
|
| T
ex
,0
|
o
C
|
80
|
74,75
|
75,5
|
| T
eff
|
o
C
|
70
|
67,38
|
67,75
|
| η eff
|
Па×с
|
0,009
|
0,010
|
0,0095
|
| Ψ eff
|
-
|
1,6×10-3
|
1,57×10-3
|
1,59×10-3
|
| So
|
-
|
3,73
|
3,23
|
3,49
|
| ε
|
-
|
0,825
|
0,824
|
0,822
|
| h
min
|
м
|
16,8×10-6
|
16,6×10-6
|
16,9×10-6
|
| f΄/
Ψ
eff
|
-
|
2,20
|
2,34
|
2,29
|
| Pf
|
Вт
|
2387,4
|
2491,7
|
2468
|
| Q3
|
м3
/с
|
100×10-6
|
91,4×10-6
|
85,2×10-6
|
| Qp
|
м3
/с
|
39,32×10-6
|
34,4×10-6
|
37,7×10-6
|
| Q
|
м3
/с
|
139,32×10-6
|
125,8×10-6
|
122,9×10-6
|
| T
ex
,1
|
o
C
|
69,5
|
71
|
70,9
|
| T
ex
,0
|
o
C
|
74,75
|
75,5
|
75,45
|
В таблице 6 приведены промежуточные результаты для случая диссипации тепла через смазочный материал (смазку под давлением). На этапе 4 расчета по таблице 6 указаны результаты графического решения
Таблица 6 – результаты итераций диссипации тепла через смазочный материал
| Параметр
|
Единица измерения
|
Этапы расчета
|
| 1
|
2
|
3
|
4
|
| T
en
|
o
C
|
60
|
60
|
60
|
60
|
| T
ex
|
o
C
|
70
|
90
|
110
|
66
|
| T
eff
|
o
C
|
65
|
75
|
85
|
63
|
| ηeff
|
Па×с
|
0.082
|
0.0061
|
0.0048
|
0.013
|
| Ψeff
|
-
|
1.54 10-3
|
1.6 10-3
|
1.78 10-3
|
1.5 1.5610-3
|
| So
|
-
|
0.72
|
1.1
|
1.6
|
2,42
|
| ε
|
-
|
0.447
|
0.53
|
0.64
|
0,78
|
| h
min
|
м
|
51 10-6
|
47 10-6
|
38.410-6
|
20,46 10-6
|
| f΄/
Ψ
eff
|
-
|
7.7 10-3
|
6.5 10-3
|
5.210-3
|
2,3 10-3
|
| Pf
|
Вт
|
2901
|
2449
|
2185
|
2467,4
|
| Q
|
м3
/с
|
115.94
|
168.93
|
194.8
|
127,4
|
| Pth
,
L
|
Вт
|
2086.92
|
9122
|
22225.5
|
2552,3
|
|