Реферат: Теоритические понятие центра тяжести тела

ТЕОРЕТИЧЕСКОЕ ПОНЯТИЕ ЦЕНТРА ТЯЖЕСТИ ТЕЛА.

Рассмотрим сложение параллельных сил. Представим, что к трём точкам А₁ , А₂ и А₃ твердого тела приложены параллельные силы , и , образующие пространственную систему. Равнодействующая двух параллельных сил равна по модулю сумме их модулей, а линия действия делит расстояние между точками приложения слагаемых сил на отрезки, обратно пропорциональные силам (рис. 1).

Точка С, через которую проходит линия действия равнодействующей системы параллельных сил, называется центром параллельных сил.

Формулы координат центра параллельных сил имеют вид:

; ; . (1)

При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести. Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом i от действия на нее Земли обозначим через ΔР _{i ;} , а силу тяжести всего тела – через Р. Силы тяжести элементарных частиц тела направлены приближенно к центру Земли, т. е. образуют систему сходящихся сил. Если размеры рассматриваемого тела малы по сравнению с размерами земного шара, то силы тяжести элементарных частиц тела можно считать системой параллельных сил, направленных в одну сторону.

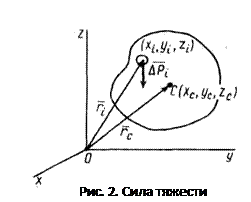Центром тяжести тела называют центр системы параллельных сил, которую приближенно образуют силы тя жести его элементарных частиц.

Радиус-вектор центра тяжести тела вычисляем как радиус-вектор центра параллельных сил (рис. 2) по формуле

(2)

где – радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку; – сила тяжести элементарной частицы; – сила тяжести всего тела; п – число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.

Если в (2) перейти к пределу, увеличивая число элементарных частей п до бесконечности, то после замены _; дифференциалом dP , а суммы – интегралом получим:

(3)

где – радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (2) и (3) получаем:

где x_c , y_c , z_c – координаты центра тяжести; x_i , y_i , z_i — координаты точки приложения силы тяжести .

Используя понятие центра тяжести тела, введем понятие его центра масс . Силы тяжести элементарных частей тела и всего тела можно выразить через их массы Δm_i и М и ускорение силы тяжести g с помощью формул

Подставляя эти значения сил тяжести в (2) и (3) после сокращения на g , которое принимаем одинаковым для всех частей тела, имеем

(4)

и соответственно

(5)

По формулам (4) и (5) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор которой вычисляется по формулам (4) или (5). В проекциях на оси координат из (4) и (5) получаем:

где х_с , у _c , z_c – координаты центра масс тела.

Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам

где – объем элементарной частицы тела; и – соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела

где – объем тела. Подставляя эти значения в (4) и (5), после сокращения на и соответственно получим формулы

и

по которым определяют центр тяжести объема тела.

Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем

где – удельный вес; – площадь элементарной частицы поверхности; S – площадь всей поверхности. После сокращения на для однородной поверхности получим следующие формулы для определения центра тяжести её площади:

и

Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам

и

где – длина элемента линии; l – общая длина линии, центр тяжести которой определяется.

При решении задачи нахождения центра тяжести плоской фигуры используется понятие статического момента площади относительно оси. Это алгебраическая сумма произведений площадей частей плоской фигуры на расстояние их центров тяжести до оси: и . Тогда, если А – площадь всей плоской фигуры,

; .

МЕТОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРОВ ТЯЖЕСТИ (ЦЕНТРОВ МАСС)

1. Метод симметрии. При определении центров тяжести широко используется симметрия тел. Для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии Аналогично для однородного тела, имею щего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.

Примеры:

1) дуга (рис. 3, а.)

2) треугольник – центр пересечения медиан (рис. 3, б.)

3) круговой сектор (рис. 3, в.)

4) параболический треугольник (рис. 3, г)

5) конус (рис. 3, д.)

2. Метод разбиения на части (метод группировки). Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 4. Плоскую фигуру можно разбить на три части, центры тяжести которых С₁ , С₂ и С₃ известны. Они находятся на пересечении диагоналей прямоугольников. Их радиусы-векторы обозначим и площади Общая площадь сложной фигуры будет

Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим.

Радиусы-векторы центров тяжести частей тела выразятся в такой форме:

или

Используя эти формулы для радиуса-вектора всей фигуры, имеем

Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.

3. Метод отрицательных масс. Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 5). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью S ₁ и центром масс С ₁ полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим S ₂ , а ее центр масс – С₂ . Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле

В отличие от обычного метода разбиения на части в данной формуле массы и, следовательно, площади входят со знаком минус. Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.

4. Способ подвешивания. Данный способ рассматривается ниже.