| Федеральное Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу "Общая физика"
ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
НА МАШИНЕ АТВУДА
Преподаватель Студент группы 220201
___________ /____________. / Стороженко Сергей Валерьевич
___________2011 г. 2011 г.
2011
1. ЦЕЛЬ РАБОТЫ
Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1. На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное - по риске на корпусе среднего кронштейна.
Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.
Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средние значения времени < t
> и квадрата времени < t
2
> прохождения грузом с перегрузом пути S:
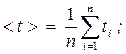
(3.1)
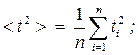
(3.2)
Абсолютная суммарная погрешность измерения времени прохождения пути S:
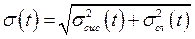 (3.3) (3.3)
Абсолютная случайная погрешность измерения времени прохождения пути S:
σсл
(t
) = t(a, n
) × S
(t
) ; (3.4)
где t(a, n
) - коэффициент Стьюдента
стандартная абсолютная погрешность измерения времени:
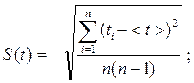
(3.5)
где
ti
- времени прохождения пути при i
–ом
измерении ( i
=1. … , n
),
n
– число измерений, < t
> - среднее значение времени прохождения пути.
Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути S:
σ(t
2
) = 2 <
t
>
σ(t
) (3.6)
Абсолютная погрешность косвенного измерения корня квадратного из расстояния:
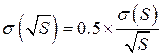
(3.7)
Угловой коэффициент экспериментальной прямой:
b =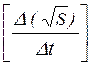 (3.8)
(3.8)
Величина ускорения, определяемого из линеаризованного графика:
a
= 2b2
(3.9)
 Абсолютную случайную погрешность ускорения sсл
(a
) рассчитываем методом наименьших квадратов. Абсолютную случайную погрешность ускорения sсл
(a
) рассчитываем методом наименьших квадратов.
Рассчитываем параметры линеаризованного графика
(y = f(x)
= Ax + B)
и случайные абсолютные погрешности параметров.
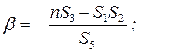
Расчет производится по формулам: (3.10)
 куда входят следующие величины: куда входят следующие величины:
(3.11)
где n
– число экспериментальных точек.
Абсолютная случайная погрешность определения углового коэффициента: sсл
(β
):
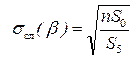
(3.12)
где вспомогательная величина:
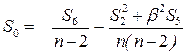
(3.13)
Абсолютная случайная погрешность ускорения:
s
(
a
)
= 4 b
s
(
b
)
(3.14)
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Макет № 82
Измеренные значения и результаты их обработки приведены в таблице 4.1.
Результаты прямых и косвенных измерений Таблица 4.1
| S
1
= 10, см
|
S
2
= 20, см
|
S
3
= 30, см
|
S
4
= 35, см
|
S
5
=42, см
|
| Номер измерения
|
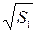 =3,16 см1/2 =3,16 см1/2
|
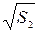 = 4,47 см1/2 = 4,47 см1/2
|
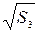 = 5,48 см1/2 = 5,48 см1/2
|
 = 5,92 см1/2 = 5,92 см1/2
|
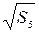 =6,48 см1/2 =6,48 см1/2
|
| t
, c
|
t
2
, c2
|
t
, c
|
t
2
, c2
|
t
, c
|
t
2
, c2
|
t
, c
|
t
2
, c2
|
t
, c
|
t
2
, c2
|
| 1
|
1,558
|
2,427
|
2,425
|
5,881
|
3,186
|
10,150
|
3,297
|
10,870
|
3,627
|
13,155
|
| 2
|
1,423
|
2,025
|
2,178
|
4,744
|
2,964
|
8,785
|
3,017
|
9,102
|
3,538
|
12,517
|
| 3
|
1,446
|
2,091
|
1,856
|
3,445
|
2,585
|
6,682
|
3,015
|
9,090
|
3,145
|
9,891
|
| 4
|
1,341
|
1,798
|
1,554
|
2,415
|
2,662
|
7,086
|
2,783
|
7,745
|
2,775
|
7,701
|
| 5
|
1,376
|
1,893
|
1,396
|
1,949
|
2,505
|
6,275
|
2,694
|
7,257
|
2,530
|
6,401
|
| < t
>, c
|
1,43
|
1,88
|
2,78
|
2,96
|
3,12
|
| < t
2
>, c2
|
2,05
|
3,69
|
7,79
|
8,81
|
11,33
|
Средние значения времени < t
> и квадрата времени < t
2
> прохождения пути S, приведенные в таблице 4.1, рассчитаны по выражениям 3.1 и 3.2 (число точек измерения n=5 ).
Для первой точки измерения
(S
1
= 10 см):
Стандартную абсолютную погрешность измерения времени рассчитываем по формуле 3.5 для числа измерений n=5:
Δt1
= t1
−< t>1
= 1,558−1,43 = 0,13 с; Δt1
2
= ( 0,13)2
= 0,0169 с2
;
Δt2
= t2
−< t>1
= 1,423−1,43 = -0,007 с; Δt1
2
= (-0,007)2
= 0,000049 с2
;
Δt3
= t3
−< t>1
= 1,446−1,43 = 0,016 с; Δt1
2
= (0,016)2
= 0,000256 с2
;
Δt4
= t4
−< t>1
= 1,341−1,43 = -0,089 с; Δt1
2
= (-0,089)2
= 0,00792 с2
;
Δt5
= t5
−< t>1
= 1,376−1,43 = -0,054 с; Δt1
2
= (-0,0584)2
= 0,002916 с2
;
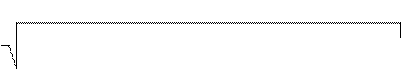
0,0169 +0,000049+0,000256+0,00792+0,002916
S(t)1
= 5x(5-1) = 0,001 с;
Абсолютная случайная погрешность измерения времени прохождения пути определяется по формуле 3.4. При доверительной вероятности a=0,9 и числе измерений n
=5 коэффициент Стьюдента t(a, n
) = 2,1:
σсл
(t
)1
= 2,1×0,001 = 0,0021 c ;
Результаты расчетов погрешностей
прямых и косвенных измерений времени и квадрата времени.
Таблица 4.2
| №
измерения
|
№ опыта
|
t, с
|
Δt, с
|
Δt2
, с2
|
<t>, с
|
S(t), с
|
σ(t),с
|
σ(t2
), с2
|
| 1
|
1
|
1,558
|
0,13
|
0,0169
|
1,43
|
0,001
|
0,0021
|
0,006
|
| 2
|
1,423
|
-0,007
|
0,000049
|
| 3
|
1,446
|
0,016
|
0,000256
|
| 4
|
1,341
|
-0,089
|
0,00792
|
| 5
|
1,376
|
-0,054
|
0,002916
|
| t1
= 1,43 ± 0,0021, с
|
| 2
|
6
|
2,425
|
0,545
|
0,297025
|
1,88
|
0,036
|
0,076
|
0,286
|
| 7
|
2,178
|
0,298
|
0,088804
|
| 8
|
1,856
|
-0,024
|
0,000576
|
| 9
|
1,554
|
-0,326
|
0,106276
|
| 10
|
1,396
|
-0,484
|
0,234256
|
| t2
= 1,88± 0,076 с
|
| 3
|
11
|
3,186
|
0,406
|
0,164836
|
2,78
|
0,012
|
0,0252
|
0,14
|
| 12
|
2,964
|
0,184
|
0,033856
|
| 13
|
2,585
|
-0,195
|
0,038025
|
| 14
|
2,662
|
-0,118
|
0,013924
|
| 15
|
2,505
|
-0,275
|
0,075625
|
| t3
= 2,78 ± 0,0252, с
|
| 4
|
16
|
3,297
|
0,337
|
0,113569
|
2,96
|
0,011
|
0,0231
|
0,14
|
| 17
|
3,017
|
0,057
|
0,003249
|
| 18
|
3,015
|
0,055
|
0,003025
|
| 19
|
2,783
|
-0,177
|
0,031329
|
| 20
|
2,694
|
-0,266
|
0,070756
|
| t4
= 2,96± 0,0231, с
|
| 5
|
21
|
3,627
|
0,507
|
0,257049
|
3,12
|
0,045
|
0,0945
|
0,56
|
| 22
|
3,538
|
0,418
|
0,174724
|
| 23
|
3,145
|
0,025
|
0,000625
|
| 24
|
2,775
|
-0,345
|
0,119025
|
| 25
|
2,530
|
-0,59
|
0,3481
|
| t5
= 3,12 ± 0,0945, с
|
Абсолютную систематическую приборную погрешность измерения времени определяем как половину цены наименьшего деления секундомера :
σсис
(t) = 0,0005 с ;
 Абсолютная суммарная погрешность измерения времени прохождения пути по формуле 3.3 : Абсолютная суммарная погрешность измерения времени прохождения пути по формуле 3.3 :
σ(t)1 = 0,0005²+0,0021² = 0,0021 с;
Так как величина σсис
(t) много меньше величины σсл
(t
)1
(σсис
(t) = 0,0005 с << σсл
(t
)1
= 0,0021 c), то в дальнейшем будем считать, что σ(t
)1
≈ σсис
(t
)1
.
Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути рассчитываем по формуле 3.6 :
σ(t
2
)1
= 2×1,43×0,0021 = 0,006 с2
;
Результаты измерений записываем в виде < t > ± σ(t) :
t1
= 1,43±0,0021 с.
Результаты расчетов случайной, приборной и общей погрешности измерений времени и квадрата времени приведены в таблице 4.2.
Абсолютную погрешность измерения расстояния определяем как половину цены деления линейки:
σ(S) = 0,05 см ;
Абсолютная погрешность косвенного измерения корня квадратного из расстояния по формуле 3.7 :
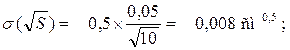
Для остальных точек измерений (при других значениях S) расчет проводится аналогично.
Результаты расчетов приведены в таблицах 4.2 и 4.3.
Таблица 4.3.
| n/n
|
S , см
|
σ(S), см
|
 , см0,5 , см0,5
|
σ( ). см0,5 ). см0,5
|
<t>, c
|
(<t>)2
, c2
|
(<t>)× 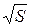 , c× см0,5 , c× см0,5
|
| 1
|
10
|
0,5
|
3,16
|
0,01
|
1,43
|
2,05
|
4,519
|
| 2
|
20
|
0,5
|
4,47
|
0,01
|
1,88
|
3,69
|
8,404
|
| 3
|
30
|
0,5
|
5,48
|
0,01
|
2,78
|
7,79
|
15,234
|
| 4
|
35
|
0,5
|
5,92
|
0,01
|
2,96
|
8,81
|
17,523
|
| 5
|
42
|
0,5
|
6,48
|
0,01
|
3,12
|
11,31
|
20,218
|
| å
|
137
|
25,51
|
12,17
|
33,65
|
65,90
|
| МНК
|
S
6
|
|
S
2
|
|
S
1
|
S
4
|
S
3
|
На основании данных, приведенных в таблицах 4.2, 4.3 строим графики зависимостей S
=
f
1
(
t
)
( рис. 4.1.) и S
=
f
2
(
t
2
)
( рис. 4.2.), на графиках наносим доверительные интервалы.
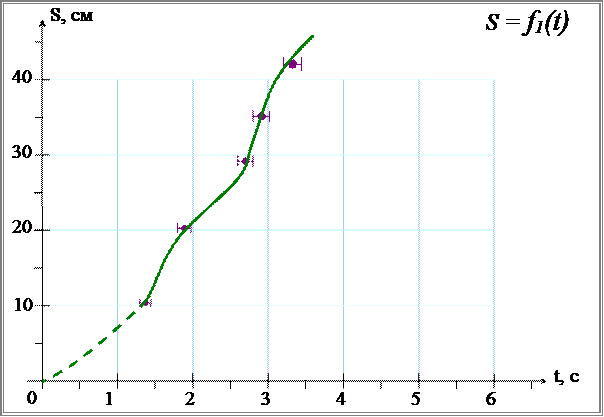
Рисунок 4.1. Зависимость пройденного пути S
от времени t
.
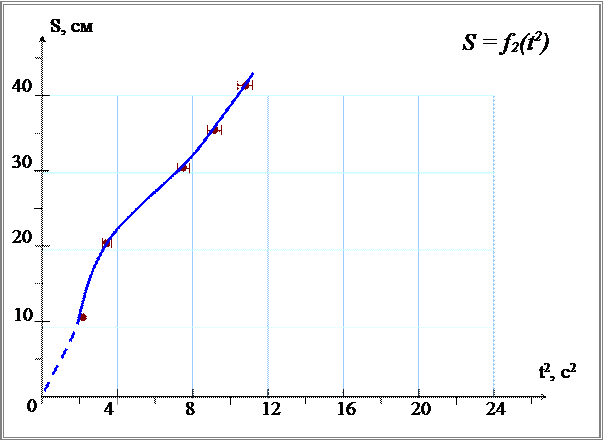
Рисунок 4.2. Зависимость пройденного пути S
от квадрата времени t
2
.
На рис.4.3. представлен линеаризованный график 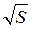 =
f
3
(
t
)
зависимости квадратного корня =
f
3
(
t
)
зависимости квадратного корня 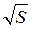 пройденного пути от времени t
. пройденного пути от времени t
.
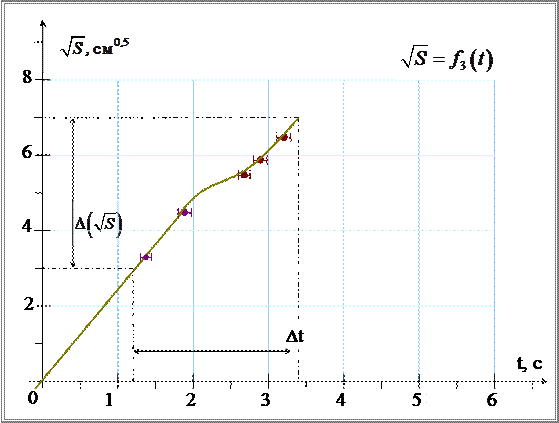
Рисунок 4.3. Зависимость  от времени t
. от времени t
.
На графике (рис. 4.3) видно, что прямая пересекает доверительные интервалы для всех экспериментальных точек.
Определим из графика угловой коэффициент прямой по формуле 3.8:
b
граф
= 4 / 2,3 = 1,73 см0,5
/с ;
Величину ускорения определим по формуле 3.9:
a
граф
= 2×1,732
=5,98 см/с2
;
По методу наименьших квадратов (МНК) рассчитаем параметр b
линеаризованного графика 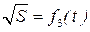 =
b
t
и случайную абсолютную погрешность параметра sсл
(b
). =
b
t
и случайную абсолютную погрешность параметра sсл
(b
).
По формулам 3.11, используя данные таблицы 4.3, определяем значение величин S
1
− S
6
для расчета по МНК (число точек n =5):
S
1
= 12,17 c; S4
= 33,65 c2
;
S
2
= 25,51см1/2
; S
6
= 137 см ;
S
3
= 65,90 c×см1/2
; S
5
= 5×33,65 − 12,17 2
= 20,14 c × см1/2
.
По формуле 3.10 определим параметр b
линеаризованного графика:
b
=
(5×65,90 − 12,17 ×25,51) / 20,14 = 0,94 см1/2
/c.
Угловой коэффициент прямой b
= 0,94 см1/2
/c.
Значение вспомогательной величины S
0
по формуле 3.13:
S
0
= 137/ 3 – (25,512
+ 0,94 2
×20,14 ) / 15 = 1,03 см.
По формуле 3.12 определим погрешность вычисления углового коэффициента прямой:
s
(
b)
= (5×1,032
/20,14) 0,5
=
0,513 см1/2
/c .
Величина ускорения по формуле 3.9 :
a
= 2×0,942
= 1,76 см/с2
.
Абсолютная случайная погрешность ускорения по формуле 3.14 :
s
(
a
)
= 4×0,94×0,513 = 1,93 см/с2
.
Получаем:
a
= (1,76 ± 1,93) см/с2
= (1,76 ± 1,93)×10-2
м/с2
.
5. ВЫВОДЫ
В результате проделанной работы мы смогли в пределах погрешностей измерений построить линеаризованный график зависимости 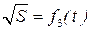 .
Все точки в этой зависимости укладываются на прямую в пределах их погрешностей. .
Все точки в этой зависимости укладываются на прямую в пределах их погрешностей.
Подтвердили справедливость закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда:
при равноускоренном движении с нулевой начальной скоростью справедливо выражение S
= at
2
/2 ,
где S
– путь пройденный телом за время движения t,
a
– ускорение движения.
В ходе работы определена величина ускорения и сделана оценка ее погрешности:
a
= (1,76 ± 1,93) × 10-2
м/с2
.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие силы действуют на груз с перегрузком во время движения?
 На груз с перегрузом во время движения действует сила тяжести F
тяж2
и противоположно направленная сила натяжения нити T2
. На груз с перегрузом во время движения действует сила тяжести F
тяж2
и противоположно направленная сила натяжения нити T2
.
Сила тяжести F
тяж2
= (
M
+
m
)
g
,
где M
– масса груза, m
– масса перегрузка, g
– ускорение свободного падения.
2. Запишите уравнение движения для каждого из грузов.
Уравнение движения грузов имеют вид:
(
M
+
m
)
g
–
T
1
= (
M
+
m
)
a
1
- груз с перегрузом (справа)
Mg
– T
2
= Ma
2
-
груз
(
слева
)
В силу не растяжимости нити a
2
= -
a
1
;
при невесомом блоке T
1
=
T
2
имеем следующие уравнения движения:
(M + m)g
– T
= (M + m)a
Mg
– T
= - Ma
3. Укажите возможные причины, обуславливающие несовпадение теоретических выводов с результатами измерений.
- физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин;
- точность вычислений.
4. Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени?
Систематическая погрешность измерения времени σсис
(t) приводит к тому, что прямая на линеаризованном графике не проходит через начало координат. Величина отрезка, отсекаемого прямой при пересечении с осью t
( от точки пересечения до начала координат), есть величина систематической погрешности измерения времени σсис
(t).
5. Укажите физические допущения, используемые при теоретическом анализе движения грузов в машине Атвуда.
Идеализация движения грузов на машине Атвуда:
- нить и блок невесомы, нить не растяжима, сила трения на оси блока мала, можно пренебречь.
|