| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ»
Филиал в г. Самаре
Кафедра гуманитарных и
социально-экономических дисциплин
КОНТРОЛЬНАЯ РАБОТА
Вариант-21
по дисциплине: Финансово – коммерческие расчёты
на тему: Основные имитационные модели инвестиций
Выполнила:
студентка 4-го курса гр.261
Фомина Е.Н.
Проверил: Рабинович М.Г.
Самара – 2009
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ…………………………………………………………..
|
3
|
| 1. Понятие имитационной модели и имитационного моделирования……………………………………………………….
|
4
|
| 2. Особенности и возможности имитационного подхода…………
|
5
|
| 3. Система массового обслуживания……………………………...
|
6
|
| 4. Вопросы формирования случайных потоков событий…………
|
14
|
| 5. Моделирующие алгоритмы………………………………………
|
19
|
| 6. Моделирование одноканальной СМО…………………………...
|
20
|
| 7. Моделирование многоканальной СМО………………………….
|
22
|
| ЗАКЛЮЧЕНИЕ………………………………………………………
|
24
|
| СПИСОК ЛИТЕРАТУРЫ…………………………………………...
|
25
|
ВВЕДЕНИЕ
В настоящее время российская экономика испытывает существенный дефицит инвестиций. Именно увеличение инвестиционной активности может стать стимулирующим фактором, позволяющим обеспечить стабильный экономический рост. Помимо макроэкономических факторов, определяющих инвестиционный климат в стране, при принятии решений о реализации отдельного инвестиционного проекта наибольшее значение имеет эффективность инвестиций, то есть степень соответствия результатов поставленным целям.
Важнейшим условием стабилизации экономики России и вывода ее на новые рубежи развития является нормализация инвестиционной программы. В этой связи особую актуальность приобретает теоретическое обоснование сущности инвестиционной программы и выявление его специфики. Поскольку инвестиции играют ключевую роль в общем росте экономики, то от правильной расстановки акцентов на соотношение инвестиций, инвестиционной деятельности, инвестиционного программы во многом зависит построение модели реальных экономических отношений в инвестиционной сфере и, следовательно, обеспечение эффективности экономического роста.
Актуальность темы в новых условиях экономической реформы определяется, прежде всего, продолжающимся становлением рыночной экономики, что в свою очередь требует перестройки не только форм и методов хозяйствования, но и мышления всех категорий руководителей, маркетологов, экономистов, участвующих в процессе финансово – хозяйственной деятельности.
Объектом исследования выступают инвестиционные проекты, которые разрабатываются на предынвестиционной стадии. Предметом исследования является изучение влияния методов управления рисками на изменение рискованности и эффективности инвестиционных проектов.
Целью работы является разработка основных имитационных моделей инвестиций.
В соответствии с этой целью в работе поставлены и решены следующие задачи:
1. Дать понятие имитационной модели и имитационного моделирования
2. Изучить имитационное моделирование систем массового обслуживания
3. Изучить формирование случайных потоков событий
4. Ознакомиться со способами моделирующих алгоритмов
5. Изучить моделирование системы массового обслуживания
1. Понятие имитационной модели и имитационного
моделирования
Слово имитация (от лат. imitatio
—
подражание) означает подражание, воспроизведение явлений, событий, действий, объектов и т.п. определенным образом. В известном смысле имитация является синонимом термина «модель» (от лат. modulus
— мера, образец), которая определяется как любой образ — материальный или нематериальный (изображение, описание, схема, воспроизведение, материальное воплощение, представитель и т.п.) — изучаемого объекта.
По сути имеющихся определений словосочетание «имитационная модель» не является корректным, однако в середине XX в. оно было введено в практику физического и математического моделирования.
Имитационные модели строят тогда, когда объект моделирования настолько сложен, что описать его поведение, например, математическими уравнениями невозможно или очень трудно. В некоторых случаях такой объект моделирования называют «черным ящиком», т.е. объектом с неизвестной внутренней структурой и, следовательно, с неизвестным механизмом поведения как при воздействии на него извне, так и при внутренних изменениях. В этих случаях имитационная модель позволяет отображать входные воздействия, сходные по параметрам с реальными или желаемыми воздействиями, и, измеряя соответствующую реакцию модели объекта, изучать структуру объекта и его поведение.
Весьма распространены также ситуации, когда с точки зрения математической теории нарушается необходимая строгость описания объекта в целом, так как части последнего могут быть описаны только различными математическими схемами (методами) с различными не стыкующимися критериями или направлениями оптимизации. В этом случае имитационные модели позволяют использовать многокритериальные подходы и условия допустимого компромисса, что способствует в определенной степени разрешению проблем состыковки различных математических методов без нарушения строгости математического описания объекта в целом.
2. Особенности и возможности
имитационного подхода
Сопряжение различных математических методов в рамках имитационной модели упрощается также в связи с тем, что стыковка частей имитационной модели осуществляется не в терминах того или иного математического аппарата, а на языке цифр. Даже если моделирование частей объекта ведется на языках различных математических методов в имитационных моделях соединения частей объекта, оценка целей, критериев их достижения, результатов моделирования осуществляется через матрицы, потоки и иные общематематические понятия, задаваемые или получаемые исключительно в виде числовых, а не аналитических значений. Это, конечно, не означает полной количественной сопоставимости результатов, так как масштабы каждого числового значения могут быть различны, но упрощает процедуры сведения их к сопоставимости.
Построение имитационных моделей не намного сложнее, чем применение стандартных математических схем. Конечно, решить типовую задачу линейного программирования, например на нахождение оптимального плана производства каких-либо изделий на предприятии, максимизирующего прибыль, с применением типового пакета программ на компьютере проще, чем построить имитационную модель этого предприятия с тем же критерием оптимальности. Однако информационность имитационной модели несравненно выше. Она позволяет найти такие характеристики, которые при решении задачи линейного программирования просто отсутствуют.
Таким образом, в большинстве случаев — когда речь не идет о решении простых рутинных проблем, но в постановке задачи стоит вопрос об исследовании сложной, противоречивой динамической системы — весьма целесообразно выбрать имитационную модель.
При имитационном моделировании применяются самые разнообразные математические схемы: конечные и вероятностные автоматы, системы массового обслуживания, агрегативные системы, системы, описываемые дифференциальными уравнениями и марковскими процессами, методы общей теории систем, а также специально сконструированные эвристические подходы.
Применительно к экономическим объектам и процессам наиболее часто используются, на наш взгляд, математические схемы систем массового обслуживания, агрегативных систем, а также эвристические подходы. Кроме того, отдельные элементы метода статистических испытаний или метода Монте-Карло, которые лежат в основе имитационного моделирования, достаточно часто применяются при расчете различных параметров для других типов моделей — эконометрических, моделей кривых роста b т.п. Поэтому и в данной главе будут рассмотрены имитационные модели систем массового обслуживания и агрегативные имитационные модели, а также способы вычисления параметров методом статистических испытаний.
3. Системы массового обслуживания
Рассмотрим основные понятия теории массового обслуживания, занимающейся построением моделей реальных систем обслуживания, производства, банковской деятельности и т.п. Эти математические схемы характеризуются тем, что в некоторые моменты времени (случайные или детерминированные) возникают заявки на обслуживание и имеются специальные устройства (приборы, инструменты) для обслуживания этих заявок, работающие по определенному закону.
Основными понятиями теории массового обслуживания являются: входной поток заявок, обслуживающая система, выходной поток заявок.
Входной поток
заявок (требований на обслуживание) характеризуется определенной организацией и рядом параметров (рис. 1): интенсивностью поступления заявок, т.е. числом заявок, в среднем поступивших в единицу времени, и законом распределения вероятностей моментов прихода заявок в систему.
     Моменты появления заявок Моменты появления заявок
Синхронизирующие моменты
Рис.1. Входной поток заявок
Обслуживающая система
(ОС) представляет собой совокупность устройств (канал, прибор), которые обеспечивают обслуживание заявки, пришедшей в систему. Обслуживающая система характеризуется пропускной способностью (скоростью обслуживания), т.е. числом обслуженных заявок в единицу времени, и
законом распределения времени обслуживания заявок. Примерами таких систем могут служить коммутатор телефонной станции, станок, на котором обрабатываются детали, машины химчистки одежды, оператор сберегательного банка, дежурная справочного бюро и пр.
Поток обслуживающих заявок, выходящих из обслуживающей системы, называется выходным потоком заявок.
Параметром выходного потока является интенсивность.
Всякая система массового обслуживания имеет определенную дисциплину очереди, т.е. порядок обслуживания пришедших заявок. Дело в том, что бывают случаи, когда система обслуживания не в состоянии немедленно обслужить все заявки. В результате образуется очередь из заявок, пришедших на обслуживание. То, в каком порядке заявки из очереди будут поступать в обслуживающую систему, определяется дисциплиной очереди. Например, первой заявка поступила и первой обслуживалась; последней заявка поступила и первой обслуживалась; случайный порядок обслуживания заявок; обслуживание определенных заявок в первую очередь (заявки с приоритетом) и т.п.
Рассмотрим более детально характеристики входного потока заявок (ВПЗ) и простейшие системы массового обслуживания (СМО).
Потоком однородных событий
называют временную последовательность появления заявок на обслуживание при условии, что все заявки являются равноправными. Существуют также потоки неоднородных
событий, когда та или иная заявка обладает каким-то приоритетом.
Если поток однородный, то каждое событие характеризуется только моментом времени его наступления tj. Существуют два способа задания однородных событий. Первый заключается в перечислении всех известных моментов tj, второй — в указании зависимости, позволяющей рассчитать t
j
по предыдущим значениям.
Однако на практике более интересны случайные потоки однородных событий, задаваемые законом распределения, который и характеризует последовательность t1, t2,…tm или последовательность интервалов между случайными событиями ξ1, ξ2…ξm. Совокупность случайных величин {ξ} считается заданной, если при к≥
1 определена совместная функция распределения вида
F
(
z
1,z2,…
zk
) = Р(
ξ
1<
z
,
ξ
2<
z
2,…,
ξk
<
zk
)
или для непрерывной случайной величины соответствующая плотность распределения вероятностей f(z1,z2,…zk)
Часто применяется случайный поток событий с ограниченным последействием
(когда случайные величины ξj являются независимыми).
Существуют также стационарные потоки,
для которых вероятностный режим потока во времени остается неизменным. Это означает, что число заявок, поступивших в СМО в единицу времени, постоянно.
Потоком с отсутствием последействия
называется такой поток, у которого число заявок, поступивших в данный момент времени, не зависит от числа заявок, обслуженных в предыдущий момент времени. Поток с отсутствием последействия является частным случаем потока с ограниченным последействием. Для потока без последействия вероятность Pk(t0,t) наступления k
событий за интервал (t0,t+t) не зависит от возникновения событий до момента t0.
Для потоков с ограниченным последействием совместная функция плотности f(z1,z2,…zk) может быть представлена в виде
f(z1,z2,…zk)= f1(z1),f2(z2),…fk(zk)
Стационарный поток с ограниченным последействием имеет следующее соотношение:
F2(z)=f3(z)=…=fk(z)=f(z)
Это означает, что при j > 1 интервалы ξj имеют одинаковое распределение. Математическое ожидание случайной величины ξj при j> 1
μ=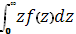 , ,
где μ
имеет смысл средней длины интервала между последовательными заявками.
Для стационарных потоков с ограниченным последействием можно ввести понятие интенсивности потока λ
в виде λ=1/μ
Эта величина характеризует среднее количество событий в единицу времени для данного потока.
Примером стационарного потока с ограниченным последействием является поток с равномерным распределением интервалов времени между заявками.
Функция плотности f
(
z
)
такого потока имеет вид
F
(
z
) =1/
b
, ≤
z
≤
b
.
Такой поток часто используется в практических задачах, возникающих в экономических приложениях.
Ординарным потоком
называется такой поток, в котором невозможно появление двух и более событий одновременно. В практике часто приходится сталкиваться с групповыми заявками, т.е. несколькими событиями, проявляющимися одновременно. Такие потоки не являются одинарными.
В теории СМО весьма большое значение имеет так называемый простейший поток однородных событий,
называющийся потоком Пуассона (пуассоновский поток). Этот поток должен быть стационарным, однородным и без последействия.
Для потока Пуассона вероятность Рк
(
t
)
наступления события за интервал времени длиной / записывается следующим образом:
Pk(t)
=
 , ,
где е
— основание натурального логарифма; λ
t
—
среднее число заявок, поступивших на обслуживание за интервал t
;
k
—
количество заявок за интервал времени t.
Функция плотности вероятности этого потока
F
(
z
) = λ
e
-
λz
, λ = 1/
t
,
где λ
— интенсивность или плотность потока.
Для расчетов параметров СМО на основе потока Пуассона необходимо проверить, соответствует ли поток закону распределения Пуассона. Признаком потока Пуассона является равенство математического ожидания 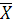 дисперсии дисперсии 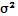 , т.е. , т.е. 
Пусть х —
число заявок, поступивших за единицу времени, т
—
число единиц времени с соответствующим поступлением заявок, п
— общее число единиц времени.
Пример.
Проверить, является ли поток требований в систему распределенным по закону Пуассона.
| х
|
т
|
тх
|
тх2
|
| 0
|
10
|
0
|
0
|
| 1
|
31
|
31
|
31
|
| 2
|
40
|
80
|
160
|
| 3
|
20
|
60
|
180
|
| 4
|
10
|
40
|
160
|
| 5
|
4
|
20
|
100
|
| 6
|
6
|
36
|
216
|
| Итого:
|
121
|
267
|
847
|
Теперь рассчитаем
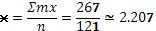
Дисперсия потока

В связи с тем, что, поток можно считать пуассоновским.
Простейший поток и поток с равномерным распределением интервалов времени между последовательными событиями наиболее часто применяются в теории и практике СМО.
Часто используется также ординарный стационарный поток с отсутствием последействия, который называется потоком Эрланга. Потоком Эрланга порядка т
называют поток, для которого

Где λ= /m /m
Поток событий называется регулярным,
если длина интервала между событиями является постоянной величиной. Примерами такого потока могут служить ежедневные сводки о каких-либо событиях (отчеты о дневной выручке в магазине, ежедневная сумма сделок на бирже или прихода средств в банк и т.п.), регламентированный поток деталей, сходящих с конвейера, поток поездов в метро и др.
Если известна длина интервала регулярного потока а,
то данный поток полностью определен во времени и не является случайным. Регулярный поток также является ординарным и стационарным. Однако регулярный поток является потоком с последействием. Интенсивность регулярного потока будет

Потоки событий различного вида могут разряжаться
и объединяться.
К сожалению, эти термины могут применяться только к потокам определенного вида. Например, если интервалы в потоке Эрланга n-го порядка уменьшить в n+1 раз, то интенсивность полученного потока станет равной интенсивности исходного пуассоновского потока, с ростом n
такой поток становится сколь угодно близким к регулярному с той же интенсивностью. Такие нормированные потоки Эрланга дают различные типы потоков с последействием, начиная от потоков без последействия (n= 0) и кончая регулярными (n = ∞).
Если происходит объединение нескольких независимых ординарных потоков с сопоставимыми интенсивностями, то с ростом числа слагаемых потоков объединенный поток приближается к простейшему с возможной нестационарностью. Если слагаемые потоки стационарны, то в пределе получается пуассоновский поток. Интенсивность объединенного потока равна сумме интенсивностей каждого из них.
Поток, получаемый в результате случайного разряжения или объединения пуассоновских потоков, также является пуассоновским.
Как будет показано ниже, используя потоки Эрланга и Пуассона, можно рассчитать аналитически установившиеся значения различных параметров СМО. Однако применение этих потоков в практике имитационного моделирования в чистом виде, без специальной корректировки, учитывающей изменения типа потока, его интенсивности и т.п., крайне ограничено.
Таким образом, вышеприведенные математические описания потоков однородных событий позволяют осуществить формализацию процессов функционирования СМО.
Пусть t ож
— время ожидания обслуживания, тогда в первом случае поступившая заявка может иметь три варианта поведения, а именно: покинуть систему
(
t
0Ж
= 0), встать в очередь
на обслуживание до того момента, пока не освободится свободный канал (tож
= ∞), и, наконец, встать в очередь с ограничением времени ожидания
обслуживания (tож
≠∞).
Исходя из этого СМО подразделяются на системы с отказами (
t
ож
= 0), системы с ожиданием (
t
ож
=∞
) и си
c
темы с ограниченным ожиданием
(0<t
ож
< ∞). Величина tож
является одним из показателей качества СМО.
Рассмотрим теперь время обслуживания заявки
(время занятости линии) tобс
как параметр обслуживающей системы.
Время обслуживания требований является случайной величиной и может изменяться в большом диапазоне. Случайная величина tобС
характеризуется законом распределения, который может определяться на основе статистических испытаний. На практике часто исходят из гипотезы о показательном законе распределения времени обслуживания.
При таком распределении времени обслуживания функция распределения времени обслуживания имеет вид
где θ= —
интенсивность обслуживания одного требования одним обслуживающим устройством; t0
бс — среднее время обслуживания одного требования одним обслуживающим устройством.
При показательном законе распределения времени обслуживания и при наличии n обслуживающих линий одинаковой мощности
Важным параметром СМО является коэффициент загрузки
Величина показывает количество требований, поступающих в систему обслуживания за время обслуживания одного требования одним устройством. В этом случае количество обслуживающих устройств п
должно быть не меньше коэффициента загрузки:
В противном случае очередь будет бесконечно расти.
Ниже приведены расчетные формулы для определения важнейших характеристик качества функционирования СМО при показательном законе распределения времени обслуживания заявок.
1. Вероятность того, что все обслуживающие системы свободны,

2.
Вероятность того, что все обслуживающие устройства заняты,

3. Среднее число устройств, свободных от обслуживания,
4. Коэффициент простоя обслуживающих устройств
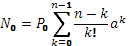
5. Среднее число устройств, занятых обслуживанием,

6. Коэффициент загрузки системы
7. Средняя длина очереди

8. Среднее время ожидания требований в очереди
или
Сущность имитационного моделирования СМО заключается в том, что необходимо построить алгоритмы, вырабатывающие случайные реализации заданных событий или потоков.
Это означает, что нужно проимитировать все входные потоки, задать случайные значения времен обслуживания заявок для каждого канала, а также дисциплину очереди.
4. Вопросы формирования случайных потоков событий
Выше были показаны способы применения простейших случайных потоков событий. Как правило, такие потоки должны обладать свойствами стационарности, отсутствия последействия и однородности. Если выполнить все эти условия, то имитационное моделирование СМО в отличие от аналитического решения сможет дать дополнительно только значения качественных параметров в переходном процессе, т.е. в начальный период функционирования СМО. Установившиеся значения с точностью до инструментальной ошибки должны быть одинаковы.
Вместе с тем можно утверждать, что применение простейших потоков случайных событий
при аналитическом или имитационном моделировании на основе СМО сложных экономических объектов не является эффективным
и, как правило, создает ошибочное представление о качестве функционирования объекта.
В
качестве примера рассмотрим сравнительно простой случай моделирования на основе СМО швейной фабрики. Пусть швейная фабрика имеет 30 машин для шитья одежды. Машины работают две смены — 18 ч. В среднем одна машина шьёт 10 заказов за час, 180 заказов за 2 смены в день. Все 30 машин за 2 смены шьют 5400 заказов. В среднем за день на фабрику поступает от 5000 до 7000 заказов. Требуется определить оптимальное количество работающих машин, длины очередей клиентов и среднее время нахождения в очереди.
Используя введенные выше зависимости, можно вычислить значения среднего числа машин швейной фабрики, свободных от работы No
,
среднюю длину очереди клиентов L
и среднее время ожидания клиентов в очереди tож
. Естественно, что для 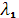 = 5000 заказов/день и = 5000 заказов/день и  = 7000 заказов/день характеристики качества обслуживания будут совершенно различными. Учитывая, что среднее число заявок обслуживаемых в единицу времени , где —
среднее время обслуживания одного заказа одной швейной фабрики, причем θ=1/80 сут., вычислим коэффициент интенсивности нагрузки . Величина = 7000 заказов/день характеристики качества обслуживания будут совершенно различными. Учитывая, что среднее число заявок обслуживаемых в единицу времени , где —
среднее время обслуживания одного заказа одной швейной фабрики, причем θ=1/80 сут., вычислим коэффициент интенсивности нагрузки . Величина 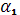 характеризует среднее число машин, которое необходимо иметь, чтобы обслужить за сутки (сутки приняты за единицу времени) все поступившие заказы. Таким образом, необходимо иметь всего 27,7 машины для случая характеризует среднее число машин, которое необходимо иметь, чтобы обслужить за сутки (сутки приняты за единицу времени) все поступившие заказы. Таким образом, необходимо иметь всего 27,7 машины для случая 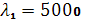 , а для .λ2
= 7000 необходимое количество машин составит более 38 (а2
= 38,8). Чтобы очередь заказчиков не росла безгранично, необходимо выполнить условие a/n<
1, где п —
число машин швейной фабрики. Поскольку в нашем примере на фабрике имеется 30 швейных машин, то , а для .λ2
= 7000 необходимое количество машин составит более 38 (а2
= 38,8). Чтобы очередь заказчиков не росла безгранично, необходимо выполнить условие a/n<
1, где п —
число машин швейной фабрики. Поскольку в нашем примере на фабрике имеется 30 швейных машин, то  . .
Следовательно, для входного потока с  =7000 заказов/день очередь будет безгранично расти. =7000 заказов/день очередь будет безгранично расти.
Рассмотрев итоги приведенных расчетов, мы пришли к следующим выводам.
1. Мы не можем сказать, сколько швейных машин нужно установить, чтобы обслуживать потоки с  =5000, .λ2
= 7000, так как а
меняется от 27,7 до 38,8. =5000, .λ2
= 7000, так как а
меняется от 27,7 до 38,8.
2. В связи с тем, что потоки заявок в системе рассчитаны для средних суток, расчеты величин очереди L
и среднего времени ожидания обслуживания tож
, как и другие качественные параметры, будут рассчитаны неверно, так как интенсивность потока в различные часы суток различна и может меняться до 3—5 раз. Конечно, можно рассчитать эти параметры за каждый час отдельно, но и это будет неверно, так как СМО будет находиться в постоянном переходном процессе. В этом случае входной поток будет не стационарным и с последействием, поскольку математическое ожидание числа заказов в единицу времени будет меняться в 3—5 раз, а число заказов, поступившее, например, в 20 ч, зависит от того, сколько их было фактически за каждый предыдущий час.
3. Цикл работы швейной фабрики равен одному году, так как услуги шитья обладают существенной сезонностью. Имеет место весенний и осенний пики потока заказов, а на лето и зиму приходится снижение интенсивности заказов. Весной одежду меняют с зимней на летнюю, а осенью наоборот. Расчет по средней интенсивности потока заказов ничего хорошего не дает, так как в пик будет перегрузка, а в спад — недогрузка. Разница между ними составляет опять же 3—5 раз.
4. Кроме того, имеет место цикличность работы и в зависимости от дня недели и в течение каждого дня.
На основании этих частных выводов приходим к следующему общему выводу.
Ни один параметр нашей швейной системы не будет найден достоверно как при аналитических расчетах, так и при имитационных, если будут использованы входные потоки Пуассона, обладающие стационарностью, однородностью и отсутствием последействия. Поэтому использование входных потоков такого вида или даже модифицированных в реальных расчетах в чистом виде неприемлемо.
Это означает, что если используется какой-то входной поток, закон распределения которого можно записать в аналитической форме, то он должен быть, по крайней мере, преобразован в поток, учитывающий все необходимые факторы, воздействующие на данную СМО. После этого он становится не однородным, не стационарным с последействием и даже не ординарным.
Если взять поток Пуассона, то вероятность поступления за время t
ровно k
заявок
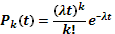
Блоки 2—4 модели должны воздействовать на параметры k
и λ таким образом, чтобы значение скорректированного потока зависело от месяца  ,
дня недели у2
и времени суток у3
: ,
дня недели у2
и времени суток у3
:
Вид конкретной зависимости может быть задан как аналитически, так и таблично или при помощи логических фраз. Только после такого преобразования входного потока можно приступать к имитационному моделированию, например, той же фабрики химчистки.
Выбор размерности входного потока заявок
имеет принципиальное значение при его моделировании. Например, выбранная для нашей швейной фабрики размерность, характеризующая его интенсивность, имеет значение числа заказов в сутки.
Такая размерность не позволяет учитывать изменения интенсивности потока в течение суток, поэтому не является верной. Правильная для нашего случая размерность входного потока заявок на обслуживание всегда должна учитывать тот интервал времени, за который могут произойти какие-либо изменения входного потока
и, в частности, его интенсивности. Для нашего случая размерность должна быть число заказов в час.
Существует также еще один способ получения реальных входных потоков — это использование реальных статистических данных о количестве заявок, поступивших в систему за определенный временной период. Вполне естественным является требование, чтобы длина временного периода не была меньше необходимого цикла моделирования.
Вместе с тем при таком способе формирования входного потока событий возникают проблемы, связанные с воздействием объекта моделирования на входной поток. Если взять наш пример с швейной фабрикой, то последняя обладает конечной мощностью и в период перегрузки каналов очередь заявок на обслуживание обрезается искусственно — прекращается прием заказов на данной фабрике. Такие факты нужно как-то учитывать, например путем добавления потерянных заявок в пиковый период, накладывать какие-то ограничения на модель данной СМО, например уменьшение длины очереди.
Для других объектов таких ограничений может и не быть, поэтому, прежде чем использовать фактическую статистику, необходимо ее проанализировать на предмет возможного влияния объекта моделирования на входной поток.
Входные потоки можно получать также и опросным путем, например в форме изучения спроса на товары и услуги.
Исследование статистических данных для оценки возможности их применения при формировании входных потоков сводится к проведению анализа соответствующего динамического ряда на предмет наличия тренда, сезонности и случайной составляющей.
Обычно их отфильтровывают, измеряют и лишь затем формируют необходимый входной поток. Таким же образом поступают при формировании входных потоков из простейшего потока. Полученные составляющие ряда применяются при формировании модели входного потока.
Несколько слов о цикле моделирования. Для нашего примера моделируемый цикл не может быть меньше одного года, а имитационные реализации должны учитывать данные за каждый час функционирования фабрики. Только при этих условиях можно получить достоверные качественные показатели. Эти показатели не будут одинаковыми в пределах моделируемого цикла. Они будут соответствовать реальным значениям в каждом однотипном интервале времени. Учитывая среднюю длину очереди, среднее время ожидания обслуживания, а также количество фактически загруженных каналов, можно спроектировать, например, такую швейную фабрику, у которой эти параметры соответствуют желаемым целевым показателем. Для различных экономических объектов выбор цикла моделирования может быть другим, но он должен учитывать все или почти все факторы, изменяющие входной поток.
Естественно, что для других экономических объектов модель формирования потока (
t
)
будет совершенно иной, так как экономические факторы могут быть другими. Однако использование потоков без коррекции, как правило, не дает нужных результатов.
Аналогичное заключение можно сделать для показателей интенсивности обслуживания и количества обслуживающих каналов.
Эти показатели также подвергаются воздействию различных экономических факторов, которые следует учитывать. Например, количество каналов обслуживания не может быть постоянной величиной, поскольку в реальной жизни они выходят из строя, подвергаются профилактике, дублированию и другим изменениям. Меняется также их производительность.
5. Моделирующие алгоритмы
Создание моделирующего алгоритма осуществляется на этапе, когда решены все принципиальные вопросы по выбору математического аппарата, описывающего объект, и построению структуры модели в полном объеме. Построение моделирующего алгоритма является способом представления построенной модели, который воспринимает компьютер.
С одной стороны, это чисто техническая задача, не имеющая отношения к построенной модели, а с другой — важная задача, так как моделирующий алгоритм может оказаться неудобным, громоздким или даже влияющим на процесс моделирования.
В настоящее время существуют три способа задания моделирующих алгоритмов: операторный, задаваемый языком программирования
и пакетом прикладных программ.
Для имитационного моделирования обычно применяются специальные языки моделирования или универсальные имитационные модели. Применение языков моделирования и универсальных имитационных моделей является наиболее удобным, однако для лучшего понимания процедур построения моделирующих алгоритмов целесообразно в учебных целях рассмотреть методику построения операторных схем.
Операторы бывают двух видов: арифметические
и логические.
Арифметические выполняют вычисления в широком смысле этого слова и обычно передают управление какому-то одному оператору. Например, запись 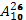 означает «оператор с арифметическим номером 10 передает управление другому оператору с индексом 26». означает «оператор с арифметическим номером 10 передает управление другому оператору с индексом 26».
Логические операторы при передаче им управления проверяют какие-то заданные условия и затем передают управление тому оператору, для которого эти условия выполняются. Например, логический оператор Р20
 означает, что логический оператор означает, что логический оператор 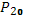 в случае выполнения заданного условия передает управление оператору 22, а в случае невыполнения условий — оператору 10. в случае выполнения заданного условия передает управление оператору 22, а в случае невыполнения условий — оператору 10.
В случае если управление передается данному оператору, то номер оператора, от которого передается управление, записывается слева вверху от символа оператора. Например, запись 38.2
A8
означает, что управление от операторов 38 и 2 передается оператору А18.
Передача управления данному оператору от предыдущего изображается лишь тогда, когда управление передается от нескольких операторов.
Для всех типов операторов, если они следуют друг за другом, обозначение передачи управления опускается.
Окончание вычислений обозначается служебным оператором с индексом Я.
6. Моделирование одноканальной СМО
Рассмотрим процесс моделирования СМО на примере одноканальной системы, т.е. СМО с одним обслуживающим каналом.
Обозначим через г длительность обслуживания заявки в системе. Пусть 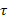 имеет закон распределения f( имеет закон распределения f( ) и является стационарной случайной величиной. Заявки обслуживаются в порядке поступления по очереди, в которой заявки могут находиться не более времени, ) и является стационарной случайной величиной. Заявки обслуживаются в порядке поступления по очереди, в которой заявки могут находиться не более времени, 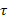 ож
. Величина ож
. Величина 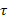 ож
имеет закон распределения ож
имеет закон распределения  .
Предположим, что .
Предположим, что  ож
является независимой величиной для различных заявок. ож
является независимой величиной для различных заявок.
Пусть требуется определить в результате моделирования долю обслуженных заявок, долю заявок, получивших отказ, среднее время ожидания в очереди
и т.п.
Будем рассматривать процесс функционирования в интервале времени [О, Т],
а заявки вне этого интервала в данной СМО не рассматриваются, даже если заявка начала обслуживаться в интервале [0,T], а окончание обслуживания выходит за пределы этого интервала. Такие заявки считаются необслуженными. Заявка получает отказ в обслуживании, если время начала обслуживания tH
< Т,
а время его окончания tCB
> Т.
Введем следующие операторы:
Ф1
— формирование случайных значений моментов ^поступления заявок в систему;
Рг —
проверка условия попадания заявки, появившейся в момент времени  в интервале [О, Т
] в интервале [О, Т
]
Рз
—проверка условия — момент освобождения канала от обслуживания предыдущей заявки;
Ф2
— формирование случайных значений длительности ожидания в очереди в соответствии с законом распределения  ; ;
А5
— вычисления верхней границы интервала  ожидания заявки в очереди; ожидания заявки в очереди;
Р6 —
проверка условия
F
7
— формирование момента начала обслуживания (j—1)-й заявки:
F
8
— формирование момента начала обслуживания j-й заявки:

Ф9 —
формирование времени занятости канала  в соответствии с распределением f( в соответствии с распределением f(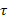 ); );
А10— вычисление момента окончания обслуживания j-й заявки (момент освобождения канала);
Р11
— проверка условия ;
К12—
счетчик количества m
обслуженных заявок;
A
13
—вычисление длительности 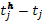 ожидания обслуживания j
-ой
заявки; ожидания обслуживания j
-ой
заявки;
К14
—счетчик числа заявок т,
получивших отказ;
K15 —счетчик числа реализаций N при моделировании;
P16 — проверка условия N
<
N
*,
где N
*
— заданное число реализаций;
F
17
— переход к очередной реализации;
A18 — обработка результатов моделирования;
Я19— окончание вычислений и выдача результатов.
Операторная схема моделирующего алгоритма записывается следующимобразом:
Зададим начальные условия в виде t0
=0, =0, m= 0,  ,
N= 0. ,
N= 0.
Задаются также границы интервала Т,
законы распределения потока заявок, а также f
7. Моделирование многоканальной СМО
Моделирующий алгоритм для многоканальной СМО мало отличается от рассмотренного выше алгоритма для одноканальной СМО.
Предположим, что в отношении входного потока заявок и каналов обслуживающей системы выполняются те же требования, что и для одноканальной СМО. Отличие заключается лишь в том, что вместо одного канала имеется п
идентичных параллельных каналов.
Заявка, поступившая в СМО, обслуживается на том канале, который первым был определен как свободный (правило определения свободного канала может быть и другим). Если все каналы заняты, то заявка становится в очередь и ждет, но не более установленного времени . Если время ожидания больше чем, то она покидает СМО. Для составления моделирующего алгоритма такой СМО заменим операторы Рз,
 алгоритма моделирования одноканальной СМО на алгоритма моделирования одноканальной СМО на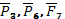 , у которых величина заменена на величину mintCB
,
под которой будем понимать наименьшее время обслуживания любого из п
каналов многоканальной СМО. , у которых величина заменена на величину mintCB
,
под которой будем понимать наименьшее время обслуживания любого из п
каналов многоканальной СМО.
Введем также дополнительно оператор A
2
0,
который вычисляет минимальное значение tCB
,
т.е. mintCB
.
Операторы А1о
и Р11
заменяем на операторы 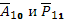 , которые вместо tjCB
содержат tjkсв
, где k
— индекс номера канала. , которые вместо tjCB
содержат tjkсв
, где k
— индекс номера канала.
Моделирующий алгоритм для многоканальной СМО запишется следующим образом:

Рассмотренные простейшие одноканальная и многоканальная СМО могут быть использованы как элементы более сложной имитационной модели, например модели банка, объединения предприятий или целой отрасли. В этом случае эти элементы формализуются на языке систем и используются как составные части более сложной системы. Принципы функционирования составных частей (подсистем) соответствуют тем, которые приняты для той математической схемы, которой определяется процесс функционирования.
ЗАКЛЮЧЕНИЕ
При выполнении контрольной работы поставленная передо мной цель была достигнута, задачи решены.
1. Дать понятие имитационной модели и имитационного моделирования
Слово имитация (от лат. imitatio
—
подражание) означает подражание, воспроизведение явлений, событий, действий, объектов и т.п. определенным образом. В известном смысле имитация является синонимом термина «модель» (от лат. modulus
— мера, образец), которая определяется как любой образ — материальный или нематериальный (изображение, описание, схема, воспроизведение, материальное воплощение, представитель и т.п.) — изучаемого объекта.
Имитационные модели строят тогда, когда объект моделирования настолько сложен, что описать его поведение, например, математическими уравнениями невозможно или очень трудно. В некоторых случаях такой объект моделирования называют «черным ящиком», т.е. объектом с неизвестной внутренней структурой и, следовательно, с неизвестным механизмом поведения как при воздействии на него извне, так и при внутренних изменениях.
2. Изучить имитационное моделирование систем массового обслуживания
Основными понятиями теории массового обслуживания являются: входной поток заявок, обслуживающая система, выходной поток заявок.
Входной поток
заявок характеризуется определенной организацией и рядом параметров: интенсивностью поступления заявок, т.е. числом заявок, в среднем поступивших в единицу времени, и законом распределения вероятностей моментов прихода заявок в систему.
Обслуживающая система
(ОС) представляет собой совокупность устройств, которые обеспечивают обслуживание заявки, пришедшей в систему. Обслуживающая система характеризуется пропускной способностью, т.е. числом обслуженных заявок в единицу времени, и
законом распределения времени обслуживания заявок.
Поток обслуживающих заявок, выходящих из обслуживающей системы, называется выходным потоком заявок.
Параметром выходного потока является интенсивность.
3. Изучить формирование случайных потоков событий
Применение простейших потоков случайных событий
при аналитическом или имитационном моделировании на основе СМО сложных экономических объектов не является эффективным
и, как правило, создает ошибочное представление о качестве функционирования объекта.
Выбор размерности входного потока заявок
имеет принципиальное значение при его моделировании. Например, выбранная для нашей фабрики химчистки размерность, характеризующая его интенсивность, имеет значение числа заказов в сутки.
Существует также еще один способ получения реальных входных потоков — это использование реальных статистических данных о количестве заявок, поступивших в систему за определенный временной период. Вполне естественным является требование, чтобы длина временного периода не была меньше необходимого цикла моделирования.
4. Ознакомиться со способами моделирующих алгоритмов
В настоящее время существуют три способа задания моделирующих алгоритмов: операторный, задаваемый языком программирования
и пакетом прикладных программ.
Для имитационного моделирования обычно применяются специальные языки моделирования или универсальные имитационные модели. Применение языков моделирования и универсальных имитационных моделей является наиболее удобным, однако для лучшего понимания процедур построения моделирующих алгоритмов целесообразно в учебных целях рассмотреть методику построения операторных схем.
Операторная схема моделирующего алгоритма представляет собой последовательность операторов, описывающих достаточно крупную группу операций. Используя эти операторы, легко ориентироваться в общей идее построения алгоритма.
5. Изучить моделирование системы массового обслуживания
Моделирование одноканальной СМО. Операторная схема моделирующего алгоритма записываетсяследующимобразом:
Моделирующий алгоритм для многоканальной СМО мало отличается от рассмотренного выше алгоритма для одноканальной СМО.
Моделирующий алгоритм для многоканальной СМО запишется следующим образом:

|