Курсовая работа: Численные методы решения задач управления технологическими процессами

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПИЩЕВЫХ ПРОИЗВОДСТВ»

Кафедра «Автоматика и Электротехника».

Курсовая работа.

«Численные методы решения задач управления технологическими процессами».

Группа: 07-ИУ-4

Студент: Коняхин Е. И.

Преподаватель: Михайлов А. В.

Москва 2010.

Поиск глобального максимума методом равномерного поиска.

Метод равномерного поиска заключается в последовательном вычислении целевой функции при всех допустимых значениях варьируемого параметра x:

Пусть заданная погрешность определения максимального значения .

Тогда для реализации алгоритма поиска следует определить значение в

точках, равномерно относящихся друг от друга на расстоянии , т.е. в точках:

Из полученных значений показателя качества выбирается наибольшее значение (глобальный максимум).

Алгоритм расчета.

Результаты расчета.

Целевая функция имеет вид :

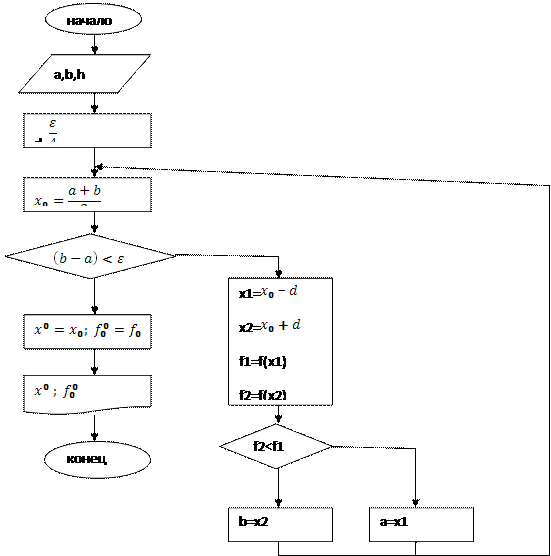
Вывод : при уменьшении заданной погрешности ( точность измерений увеличивается, что позволяет нам получить верное значение глобального максимума. Недостатком метода является то, что одновременно с уменьшением заданной погрешности увеличивается требуемое количество вычислений функции, что приводит к большим затратам машинного времени.

Одномерная оптимизация методом дихотомии.

Этот метод используется для поиска экстремума класса унимодальных функций. Идея метода проста – делить интервал [ a, b] , где расположена точка экстремума , пополам

и отбрасывать ту часть, где экстремума заведомо быть не может. С этой целью достаточно вычислить значение в точках , отстоящих друг от друга на расстояние заданная погрешность определения оптимума. По двум вычисленным значениям и , в силу унимодальности функция легко установить новый интервал неопределенность по следующим условиям ( при поиске максимума):

Таким образом, в результате двух вычислений , промежуток , где содержится экстремум сократится в двое. Следующая пара измерений производится в районе серидины нового интервала неопределенности. Вычисления производятся до тех пор, пока на k -м шаге, после 2 k вычислений длина интервала неопределенности , где находится оптимум, не станет меньше или равна .

Алгоритм расчёта.

ДА

ДА

Результаты расчета .

Целевая функция имеет вид :

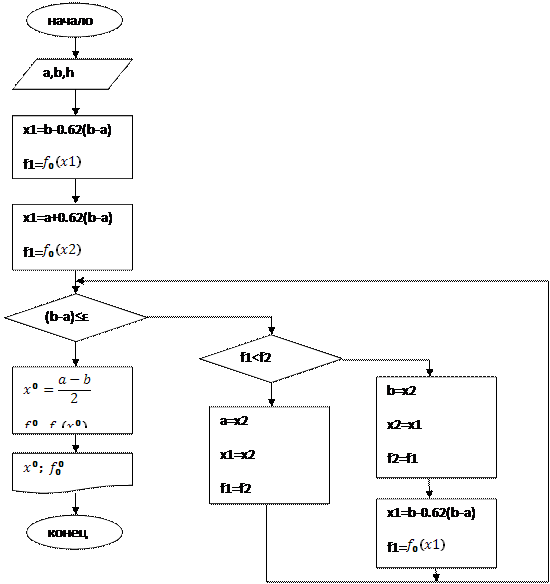
Вывод : как видно метод дихотомии позволяет довольно быстро попадать в район оптимума. И требует меньшего числа расчётов по сравнению с некоторыми другими методами (например : методом равномерного приближения).

Одномерная оптимизация методом золотого сечения.

Интервал неопределенности делится на три отрезка, причем внутренние точки располагаются симметрично по отношению к крайним .

Берутся пробные точки и располагаются следующим образом :

Вычисляется целевая функция в этих точках. В результате анализа двух значений и целевой функции исключается один из подинтервалов, где оптимума заведомо быть не может, и выбирается новый интервал неопределенности, который должен исследовать в дальнейшем.

Поиск оптимума завершается, если после k - го шага длина интервала неопределенности станет меньше или равна .

Алгоритм расчёта.

нет

нет

Результаты расчета .

Целевая функция имеет вид :

Вывод : преимуществом этого метода над методом дихотомии является то, что на каждом шаге вычисляется лишь одно значение , а не два.

Одномерная оптимизация методом поразрядного приближения.

Метод обладает высоким быстродействием. Это достигается тем, что используется алгоритм с переменным шагом поиска. Задаем интервал [ a, b] , содержащий внутри себя точки максимума :

Задается начальное значение и вычисляется . Задается начальный шаг поиска h и кратность изменения шага k в районе оптимума. Производится поиск максимума. Поиск из начальной точки x= осуществляется с постоянным шагом h , после каждого шага вычисляется значение критерия , оно сравнивается с предыдущим и в случае улучшения критерия шаги продолжаются. Движение к оптимуму с неизменным шагом h продолжается до тех пор, пока очередной шаг не окажется неудачным. После этого поиск максима продолжается из последней точки в обратном направлении с шагом в k раз меньше прежнего. Эта процедура будет продолжаться до тех пор, пока не выполнится условие:

, где - заданная погрешность определения оптимума.

Алгоритм расчета.

да

нет

Результаты расчета.

Целевая функция имеет вид :

Вывод: метод является эффективным для измерения оптимума унимодальной функции, причем изменение шага поиска или кратности уменьшения шага ( при неизменной погрешности вычисления на результат практически не влияет).

Одномерная оптимизация методом квадратичной интерполяции.

В предыдущих методах была сделана попытка найти малый интервал, в котором находится оптимум функции f₀ (х) . В этом методе применяется иной подход. Он заключается в построении аппроксимирующей модели оптимизируемой функции (х). Функция может аппроксимирована полиномом второго порядка:

(х) = ах² + Ьх + с

по крайней мере в небольшой области значений, в том числе в области оптимума. При этом положении экстремума (х) определяется по положению экстремума полинома, поскольку последний вычислить проще.

Экстремум функции f_ап (х) как известно расположен в точке: = -Ь/2а.

Положим, что окрестность некоторой исходной точки х=х1 области определения f₀ (х) аппроксимирована полиномом f_ап (х). Задача поиска заключается в определении смещения

= х°_ап – х1

Которое приводит из исходного состояния х = х1 , ближе к экстремуму х = х° . Если f₀ (х) строго квадратичная функция, то смещение после первого шага сразу приведет к. В противном случае достижение х° требует выполнения итерационной процедуры. Для определения смещения нужно определить коэффициенты параболы. Для этого необходимо вычислить значение f₀ (х) в трех точках. Пусть вычисление производится в исходном состоянии х = х1 и в точках, , и при этом получено три значения этой функции

,

где h - полуинтервал интерполяции, малая постоянная величина. Подставляя эти значения в уравнение (х), получаем систему из трех линейных уравнений с тремя неизвестными а, Ь, с :

а(х1 - h)² + Ь(х1 - h) + с =а(х1 - h)² + Ь(х1 - h) + с =

а*х1² + Ь*х1 + с =

а(х1 + h)² + Ь(х1 + h) + с =

Для того, чтобы система имела решение, необходимо чтобы ее определитель не был равен нулю. Это условие выполняется, так как определитель равен: = - 2 h³ 0 так как . Решая систему уравнений, получаем интересующие нас значения параметров а, Ь, с подставляя их в формулу находим положение экстремума параболы

х°_ап = х1 + h( - )/2( - 2 + )

Зная коэффициенты а, Ь, с можно определить и экстремальное значение функции по формуле, которая является оценкой экстремума критерия (х) .

Теперь следует проверить, действительно ли найден экстремум. Для этого достаточно вычислить значение функции цели (х) в предполагаемом экстремуме х=х1+ Δх - х°_ап и сопоставить его с оценкой. Если эти величины отличаются не более чем на ɛ т. е:

| ( х°_ап )- (х°_ап )|

, где ɛ заданная погрешность определения экстремума. При этом = х1 . Если условие не выполняется, тогда следует процесс поиска; т.е. выполнить следующий цикл, но уже построение

аппроксимирующей модели производится в окрестности точки х1= х°_ап . Процедура будет повторяться пока не выполнится условие.

Алгоритм расчета .

Результаты расчета.

Целевая функция имеет вид :

Вывод: расчеты показали, что изменение погрешности определения экстремума ɛ, практически не влияет на точность вычисления в то время, как изменение шага поиска h оказывает значительное влияние. При уменьшении шага точность вычислений улучшается и наоборот, при увеличении шага уменьшается. И в конечном итоге, когда шаг поиска слишком велик для того, чтобы с помощью итерационной процедуры уточнения значений получить результат с заданной погрешностью, программа отказывается производить вычисления.

Оптимизация методом наискорейшего спуска.

Метод наискорейшего спуска предназначен для поиска минимума. Данный метод отличается от метода градиента правилом определения коэффициента шага. Сначала выделяется начальная точка. В пространстве X могут быть выделены области притяжения каждого из локальных минимумов.

Если алгоритм начинает поиск из начальной точки, лежащей в области притяжения некоторого минимума функции против направления градиента. Таким образом, в каждом цикле решается одномерная задача минимизации , после чего шаг находится как

Алгоритм расчета.

Результаты расчета.

Целевая функция имеет вид :

Оптимизация методом линейного программирования.

f₀ (x)=4x+3y

Представим уравнения прямых, составляющих прямоугольник, в виде ограничений для целевой функции и проверим правильность постановки знаков:

1)3x-y≤4

2)x-2y≤-7

3)3x+y≤21

4)-x+4y≤6

Следовательно искомые ограничения:

1)-3x+y-4

2)-x+2y≤7

3)3x+y≤21

4)x-4y≤-6

Точки min и max:

A_min (2;2) C_max (5;6)

min и max функции:

f₀ (x)_min =14

f₀ (x)_max =38

Расчет производится в приложении МАТLАВ.

»f=[4,3]

f = 4 3

»A=[-3,l;-l,2;3,l;l,-4]

A =

-3 1

-1 2

3 1

1 -4

» B=[-4;7;21;-6]

B =

-4

7

21

-6

» [x,y,z]=linprog(f,A,B) Optimization terminated,

x =

2.0000

2.0000

y =

14.0000

z = 1

Решение задачи нелинейного программирования.

Задача №2.

Имеются три продукта n₁ ,n₂ ,n₃ разной цены. Каждый из них содержит определенное количество питательных ингредиентов, причем для нормального потребления требуется u₁ ≥250; u₂ ≥60; u₃ ≥100; u₄ ≥220.

Минимизировать затраты на приобретение продукта.

Расчет производится в приложении МАТLАВ.

a=[-4 -6 -15;-2 -2 0;-5 -3 -4;-7 -3 -12]; »b=[-250-60-100-220];

»f=[44 35 100]

f =

44 35 100

» [x,y,z]=linprog(f,a,b) Optimization terminated. x= 13.2143

16.7857

6.4286

y =

1.8118e+003 z= 1

Задача №3 Вариант№13

Расчет производится в приложении МАТLАВ.

a=[2,5,7,9,12;4,9,16,21,28;7,12_/ 18,27,34;10,18,26,34,42;14_l 23,32,44,51;18,29,39,50,63]

b=[4000;60000;8000;10000;12000;14000]

lb=zeros(5,l)

f=[-10-ll -12-13-14]

»[x,y,z]=linprog(f,a,b,[],[],lb)

Optimization terminated.

x =

777.7778

0.0000

0.0000

0.0000

0.0000

y =

-7.7778e+003

z =

1

Задача №4 Вариант №8

12.

Уваривание рецептурной смеси в змеевиковом уварочном аппарате.

Общий вид зависимости: τвар=f(P пара)

Результаты моделирования: y=178-865,5*x+1629,4*x^2-1025*x^3

Минимизировать время уваривания смеси до влажности 16% при ограничении на давлении в магистрали пара, обусловленного экономической эффективность.

Ограничения: 0,2 <Р пара<0,7 Мпа; f`(Р пара)≤-44

Расчет производится в приложении МАТLАВ.

function f=myfun(x)

function[c,ceq]=ogr(x); c=-865,5+3258,8*x-3075*x^{^} 2+44;

ceq=[];

»[x,y,z]=fmincon(@myfun,[1]_, [],[],[]_, []_, [0_, 7]_, [0,2]_, @ogr)

x =

0

Y =

-687

z =

1

13.

Уваривание рецептурной смеси в змеевиковом уварочном аппарате.

Общий вид зависимости: y отк=f(P апп)

Результаты моделирования: y=47,5-2,01*x+0,03*x^2-0,000015*x^3

Повысить качество смеси, выраженное в заданной взякости 20 Па*с в зависимости от ограничения для температуры в аппарате и частотой вращения мешалки.

Ограничения: 60 <Т апп<76 °С; 15<w лоп<35 об/мин;

Расчет производится в приложении МАТLАВ.

function f=myfun(x)

f=47,5-2,01*x+0,03*x^2-0,00015*x^3;

function[c,ceq]=ogr(x); c=-2,01+0,06*x-0,00045*x^2; ceq=[];

»[x,y_; z]=fmincon(@myfun,[l],[],[],[],[],[65],[93],@ogr)

x =

65.0001

y =

47

z =

1