Контрольная работа: Расчет оптимального уровня цены объема производства и продажи
|
Название: Расчет оптимального уровня цены объема производства и продажи Раздел: Рефераты по маркетингу Тип: контрольная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задача 1 Фирма осуществляет производство и продажу товара через сеть фирменных магазинов. Данные о цене товара и объеме проданных товаров в среднем за сутки в одном из географических сегментов рынка приведены в таблице 1.1. Таблица 1.1 Данные о цене и объеме проданных товаров в среднем за сутки
Необходимо: 1. Проанализировать существующую зависимость между объемом продажи товара и уровнем его цены. 2. Определить коэффициент эластичности между ценой и объемом продажи товара. 3. Определить тесноту связи между ценой и объемом продажи товара. Решение: 1. На основании данных таблицы 1.1, графически изобразим объем продажи товара:
Рис. 1.1 Из рисунка 1.1 видно, что для зависимости может быть использовано уравнение прямой линии Для расчета значений Таблица 1.2. Для расчета значений
Значение коэффициента
подставив данные таблицы 1.2, получим:
Это число показывает теоретическую величину падения объема продаж при увеличении цены на единицу стоимости. Тогда коэффициент
Это число показывает теоретический возможный объем продаж при минимальной цене. Тогда теоретическое уравнение зависимости объема продаж от цены примет вид:
Полученные значения То есть теоретическая зависимость между объемом продаж и ценой равна:
2. Коэффициент эластичности рассчитывается по формуле:
Если Если Используя данные таблицы 1.2 и полученное значение
Это число показывает процент изменения объема продаж при изменении цены на 1%. 3. Теснота связи между показателями цены и объема продаж рассчитывается по формуле:
Если
В данной задаче Так как значение Вывод: 1. Спрос эластичен. Коэффициент эластичности больше единицы и равен 5,26. 2. При таком спросе политика увеличения цены нецелесообразна. Необходимо определять оптимальную цену, при которой размер прибыли от продаж достигнет максимального значения. Задача 2 Для оперативного регулирования цены с учетом установленной эластичности спроса проанализировать затраты на производство и обращение товара на основании следующих исходных данных. Фирма осуществляет производство товара. Данные об объеме производства и суммарных затрат в среднем за сутки приведем в таблице 2.1. Таблица 2.1. Исходные данные об объеме производства и расходов производства в среднем за сутки
Таблица 2.2. Исходные данные об объеме реализации и затрат обращения в среднем за сутки.
Необходимо используя данные таблицы 2.1: 1. Разделить суммарные издержки производства, используя метод "максимальной и минимальной точки". 2. Используя данные таблицы 2.2 разделить суммарные издержки обращения товара с помощью метода наименьших квадратов. 3. Составить математическую модель валовых издержек производства и обращения товара. Решение: 1. Из всей совокупности данных выберем два периода с наименьшим и наибольшим объемом производства. Из таблицы 2.1 видно, что наибольший объем производства в сентябре составил 280 штук. Наименьший объем производства в феврале - он составил 150 штук. Для расчета постоянных и переменных затрат составим вспомогательную таблицу 2.3. Таблица 2.3. Вспомогательная таблица для расчета постоянных и переменных затрат.
Определим ставку переменных издержек (средние переменные расходы в себестоимости единицы продукции) по следующей формуле:
где
Подставив числовые значения, получим ставку переменных издержек:
Общую сумму постоянных издержек
где Определим общую сумму постоянных издержек:
Таким образом, валовые издержки производства
где 2. Метод наименьших квадратов. Позволяет наиболее точно определить состав общих затрат и содержание в них постоянной и переменной составляющих. Таблица 2.2. Исходные данные об объеме реализации и затрат обращения в среднем за сутки.
Согласно данному методу рассчитаем коэффициенты где
Ставка переменных издержек
Для расчета величины Таблица 2.4. Вспомогательная таблица для расчета величины
Используя данные таблицы 2.4, подставив числовые значения, получим ставку переменных издержек:
То есть Тогда переменные издержки на среднесуточный объем продаж
Постоянные издержки
Таким образом, валовые издержки обращения могут быть рассчитаны по формуле:
где Используя результаты предыдущей задачи, определяем, что постоянные издержки на производство и реализацию равны: 967,93+944,63=1912,56 тыс. рублей. Удельные переменные издержки составили: 1,27+1,07=2,34 тыс. руб./шт. Таким образом, валовые издержки производства и обращения могут быть рассчитаны по формуле:
Задача №3 Используя результаты, полученные в задачах №1 и №2 необходимо определить: 1. Оптимальный уровень цены с учетом достижения максимальной прибыли (валовой маржи), предварительно разработав экономико-математическую модель задачи; 2. Объем производства и продажи, обеспечивающий прибыль равную 50 тыс. рублей в день при складывающихся на рынке ценах; 3. Оптимальный уровень цены, обеспечивающий уровень прибыли, равный 50 тыс. рублей в день при уровне производства и реализации равном 3000 и более штук. Решение: 1. Разработаем экономико-математическую модель задачи (формула прибыли):
где Подставляем в формулу значения
Для расчета оптимальной цены возьмем производную полученного выражения и приравняем к нулю:
Тогда оптимальная цена равна:
Для проверки результата проведем дополнительные расчеты в таблице 2.4. Для упрощения расчетов не учитываем значение Таблица 2.4.
Таким образом, оптимальная цена с учетом округления равна 3,1 тыс. руб., при которой валовая маржа достигаем максимума. Значение эластичности спроса позволяет перейти к методу ценообразования на основе обеспечения целевой прибыли. Ставя цель получения определенной прибыли можно определить следующее: 1. объем производства и продаж, обеспечивающих при сложившейся на рынке цене заданный объем прибыли; 2. уровень цены продажи, обеспечивающий при определенном объеме производства и продажи заданный уровень прибыли. 2. Предположим, что необходимо определить количество товара, обеспечивающий прибыль равную 50 тыс. рублей в день при складывающихся на рынке ценах. Определим по формуле:
Тогда: Расчеты объемов производства приведем в таблице 2.5. Таблица 2.5 Расчеты для определения минимального объема продаж
Таким образом, для получения прибыли в день 100 тыс. рублей при продаже по цене 3,1 тыс. руб. необходимо продать 2582 штуки. 3. Предположим необходимо определить оптимальный уровень цены, обеспечивающий уровень прибыли, равный 50 тыс. рублей в день при уровне производства и реализации равном 3000 и более штук. Определяем:
Расчеты среднего уровня цены приведем в таблице 2.6. Таблица 2.6 Расчеты для определения среднего уровня цены
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
,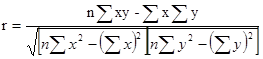
 .
.