| Введение
Теория вероятностей – это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.
История теории вероятности восходит к XVII веку, когда были предприняты первые попытки систематического исследования задач, относящихся к массовым случайным явлениям, и появился соответствующий математический аппарат. С тех пор, многие основы были разработаны и углублены до нынешних понятий, были открыты другие важные законы и закономерности. Множество ученых работало и работает над проблемами теории вероятностей.
Среди них нельзя не обратить внимание на труды Симеона Дени Пуассона ((1781–1840) – французский математик), доказавшего более общую, чем у Якова Бернулли, форму закона больших чисел, а также впервые применившего теорию вероятностей к задачам стрельбы. С именем Пуассона связан один из законов распределения, играющий большую роль в теории вероятностей и ее приложениях.
Число наступлений определённого случайного события за единицу времени, когда факт наступления этого события в данном эксперименте не зависят от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, и не влияет на будущее. А испытания производятся в стационарных условиях, то для описания распределения такой случайной величины обычно используют закон Пуассона (данное распределение впервые предложено и опубликовано этим учёным в 1837 г.).
Этот закон можно также описывать как предельный случай биноминального распределения, когда вероятность p осуществления интересующего нас события в единичном эксперименте очень мала, но число экспериментов m, производимых в единицу времени, достаточно велико, а именно такое, что в процессе p 0 и m 0 и m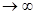 произведение mp стремится к некоторой положительной постоянной величине произведение mp стремится к некоторой положительной постоянной величине  (т.е. mp (т.е. mp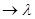 ). ).
Поэтому закон Пуассона часто называют также законом редких событий.
Распределение Пуассона в теории вероятностей
Функция и ряд распределения
Распределение Пуассона – это частный случай биномиального распределения (при n
>> 0 и при p
–> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
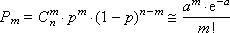
где a
= n
· p
– параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
Pm
= Cn
m
· pm
· (1 – p
)n
– m
может быть написан, если положить p
= a
/n
, в виде

или

Так как p
очень мало, то следует принимать во внимание только числа m
, малые по сравнению с n
. Произведение

весьма близко к единице. Это же относится к величине
  
очень близка к e
–a
. Отсюда получаем формулу:
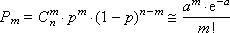
 число Эйлера (2,71…). число Эйлера (2,71…).
 , ,
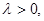 
Для производящей функции  величины величины 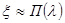 имеем: имеем:
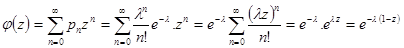
Интегральная функция вероятности распределения равна

Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины, количество телефонных звонков в call-центре или количество обращений к веб-серверу за заданный период времени.
Ряд распределения случайной величины Х, распределенной по закону Пуассона, выглядит следующим образом:
| хm
|
0
|
1
|
2
|
…
|
m
|
…
|
| Pm
|
e-a
|

|

|
…
|

|
…
|
На рис. 1 представлены многоугольники распределения случайной величины Х
по закону Пуассона, соответствующие различным значениям параметра а
.

Для начала убедимся, что последовательность вероятностей, может представлять собой ряд распределения, т.е. что сумма всех вероятностей Р
m
равна единице.
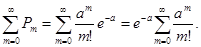
Используем разложение функции ех
в ряд Маклорена:

Известно, что этот ряд сходится при любом значении х
, поэтому, взяв х=а
, получим

следовательно

Числовые характеристики положения о распределении Пуассона
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
По определению, когда дискретная случайная величина принимает счетное множество значений:
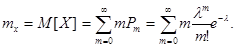
Первый член суммы (соответствующий m
=0
) равен нулю, следовательно, суммирование можно начинать с m
=1
:

Таким образом, параметр а
представляет собой не что иное, как математическое ожидание случайной величины Х
.
Кроме математического ожидания, положение случайной величины характеризуется модой и медианой.
Модой случайной величины называется её наиболее вероятное значение.
Для непрерывной величины модой называется точкой локального максимума функции плотности распределения вероятностей. Если многоугольник или кривая распределения имеют один максимум (рис. 2 а), то распределение называется унимодальным, при наличии более одного максимума – мультимодальным (в частности, распределение, имеющее две моды, называется бимодальным). Распределение, имеющее минимум, называется антимодальным (рис. 2 б)
F(x) Pi
 
xmod
x 0 x1
x2
x3
x4
x
Наивероятнейшим значением случайной величины называется мода, доставляющая глобальный максимум вероятности для дискретной случайной величины или плотности распределения для непрерывной случайной величины.
Медиана – это такое значение хl
, которое делит площадь под графиком плотности вероятности пополам, т.е. медиана является любым корнем уравнения. Математическое ожидание может не существовать, а медиана существует всегда и может быть неоднозначно определенной.
Медианой случайной величины 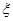 называется такое её значение называется такое её значение
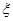 = x med
, что P ( = x med
, что P (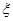 < x med
) = Р ( < x med
) = Р (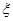 > x med
) = > x med
) =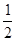 . .
Числовые характеристики разброса
Дисперсией случайной величины Х называют математической ожидание квадрата отклонения случайной величины от ее математического ожидания:

Однако, удобнее ее вычислять по формуле:

Поэтому найдем сначала второй начальный момент величины Х
:

По ранее доказанному

кроме того,

следовательно,

Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а.
Это свойство распределения Пуассона часто применяют на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против подобной гипотезы.
Дисперсия  имеет размерность квадрата случайной величины, что не удобно. Поэтому в качестве показателя рассеяния используют также величину имеет размерность квадрата случайной величины, что не удобно. Поэтому в качестве показателя рассеяния используют также величину 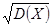 . .
Средним квадратическим отклонением (стандартным отклонением или стандартом)  случайной величины Х называется арифметическое значение корня квадратного из её дисперсии: случайной величины Х называется арифметическое значение корня квадратного из её дисперсии:
 . .

Стремление получить безразмерную характеристику степени рассеивания случайной величины, не зависящую от масштаба измерения исходных параметров случайных явлений, привело также к понятию коэффициента вариации случайной величины.
Коэффициент вариации – это отношение (в%) среднеквадратического отклонения к соответственному математическому ожиданию:

(предполагается, что  ) )

Асимметрия и эксцесс распределения Пуассона
Третий центральный момент  служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, её делят на служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, её делят на 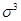 , где , где 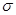 - среднее квадратическое отклонение случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины: - среднее квадратическое отклонение случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины:
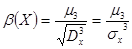 . .
Найдем третий центральный момент через начальные моменты по формуле:
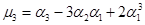
Моменты   и и  : :
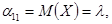  . .
Найдем третий начальный момент  : :
 . .
Обозначим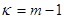 . Тогда . Тогда



Подставляя  в формулу для вычисления в формулу для вычисления  , получаем , получаем

Таким образом, третий центральный момент случайной величины 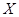 также равен параметру распределения Пуассона также равен параметру распределения Пуассона 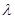 . Найдем коэффициент асимметрии: . Найдем коэффициент асимметрии:
 . .
Коэффициент асимметрии случайной величины, имеющей распределение Пуассона, больше нуля.
Четвертый центральный момент 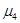 служит для характеристики крутости (островершинности или плосковершинности) распределения. служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом эксцесса) случайной величины называется число
  , ,
где  - центральный момент четвертого порядка. - центральный момент четвертого порядка.
Можно показать, что
 . .
Так как  , то эксцесс распределения Пуассона всегда положителен. , то эксцесс распределения Пуассона всегда положителен.
Дополнительные характеристики распределения Пуассона
I. Начальным моментом порядка k случайной величины Х
называют математическое ожидание величины Х
k
:
αk
=
M
(
Xk
).
В частности, начальный момент первого порядка равен математическому ожиданию:
α1
=
M
(
X
)=
a
.
II. Центральным моментом порядка k
случайной величины Х
называют математическое ожидание величины [
X
-
M
(
X
)]
k
:
μ
k
=
M
[
X
-
M
(
X
)]
k
.
В частности, центральный момент 1-ого порядка равен 0:
μ1
=М [
X
-
M
(
X
)]=0,
центральный момент 2-ого порядка равен дисперсии:
μ2
=
M
[
X
-
M
(
X
)]2
=
a
.
III. Для случайной величины Х
, распределенной по закону Пуассона, найдем вероятность того, что она примет значение не меньшее заданного k. Эту вероятность обозначим Rk
:
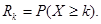
Очевидно, вероятность Rk
может быть вычислена как сумма
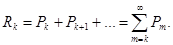
Однако значительно проще определить ее из вероятности противоположного события:

В частности, вероятность того, что величина Х
примет положительное значение, выражается формулой

Распределение Пуассона в математической статистике
Точечная оценка параметра распределения Пуассона
Наилучшей точечной оценкой параметра  является является



Т.е.  , или , или  . .
Отсюда следует, что
 . .
Интервальная оценка распределения Пуассона
Пусть х1,
х2
, … хn
– независимые наблюдения, каждое из которых распределено по закону Пуассона, т.е. при  > 0 вероятность > 0 вероятность
Р , ,
где х = 0,1,2, … и  – неизвестный параметр (интенсивность текучести). – неизвестный параметр (интенсивность текучести).
Оценим параметр  с помощью доверительного интервала. с помощью доверительного интервала.
Тогда доверительный интервал для 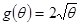 , соответствующий доверительной вероятности , соответствующий доверительной вероятности  , при достаточно большом n будет иметь вид , при достаточно большом n будет иметь вид

для любого значения  . Поэтому, если n достаточно велико и . Поэтому, если n достаточно велико и
 , ,
то
 . .
Пример условия, при котором возникает распределение Пуассона
Как уже говорилось, многие задачи практики приводят к распределению Пуассона. Рассмотрим одну из типичных задач такого рода.
Пусть на оси абсцисс Ох
случайным образом распределяются точки (рис. 3). Допустим, что случайное распределение точек удовлетворяет следующим условиям:
1) Вероятность попадания того или иного числа точек на отрезок l
зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределены на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность, т.е. математическое ожидание числа точек, приходящихся на единицу длины, через λ
.
2) Точки распределяются на оси абсцисс независимо друг от друга, т.е. вероятность попадания того или иного числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним.
3) Вероятность попадания на малый участок Δх
двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
Выделим на оси абсцисс определенный отрезок длины l
и рассмотрим дискретную случайную величину Х
– число точек, попадающих на этот отрезок. Возможные значения величины будут 0,1,2,…,
m
,…
Так как точки попадают на отрезок независимо друг от друга, то теоретически не исключено, что их там окажется сколь угодно много, т.е. данный ряд продолжается неограниченно.
Докажем, что случайная величина Х
распределена по закону Пуассона. Для этого надо подсчитать вероятность Р
m
того, что на отрезок попадет ровно m
точек.
Сначала решим более простую задачу. Рассмотрим на оси Ох
малый участок Δх
и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожидание числа точек, попадающих на этот участок, очевидно, равно λ·Δх
(т. к. на единицу длины попадает в среднем λ
точек). Согласно условию 3 для малого отрезка Δх
можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание λ·Δх
числа точек, попадающих на участок Δх
, будет приближенно равно вероятности попадания на него одной точки (или, что в данных условиях равнозначно, хотя бы одной).
Таким образом, с точностью до бесконечно малых высшего порядка, при Δх→0
можно считать вероятность того, что на участок Δх
попадет одна (хотя бы одна) точка, равной λ·Δх
, а вероятность того, что не попадет ни одной, равной 1-
c
·Δх
.
Воспользуемся этим для вычисления вероятности Pm
попадания на отрезок l
ровно m
точек. Разделим отрезок l
на n
равных частей длиной  Условимся называть элементарный отрезок Δх
«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятность того, что отрезок Δх
окажется «занятым», приближенно равна λ·Δх
= Условимся называть элементарный отрезок Δх
«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятность того, что отрезок Δх
окажется «занятым», приближенно равна λ·Δх
=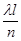 ; вероятность того, что он окажется «пустым», равна 1- ; вероятность того, что он окажется «пустым», равна 1- .
Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n
отрезков можно рассмотреть как n
независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью p
= .
Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n
отрезков можно рассмотреть как n
независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью p
= . Найдем вероятность того, что среди n
отрезков будет ровно m
«занятых». По теореме о повторных независимых испытаниях эта вероятность равна . Найдем вероятность того, что среди n
отрезков будет ровно m
«занятых». По теореме о повторных независимых испытаниях эта вероятность равна
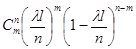 , ,
или обозначим λ
l
=
a
:
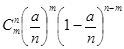 . .
При достаточно большом n
эта вероятность приближенно равна вероятности попадания на отрезок l
ровно m
точек, т. к. попадание двух или больше точек на отрезок Δх
имеет пренебрежимо малую вероятность. Для того, чтобы найти точное значение Р
m
, нужно перейти к пределу при n
→∞:

Учитывая, что

и
 , ,
получаем, что искомая вероятность выражается формулой

где а=λl
, т.е. величина Х
распределена по закону Пуассона с параметром а=λl
.
Надо отметить, что величина а
по смыслу представляет собой среднее число точек, приходящееся на отрезок l
.
Величина R
1
(вероятность того, что величина Х
примет положительное значение) в данном случае выражает вероятность того, что на отрезок l
попадет хотя бы одна точка: R
1
=1-
e
-
a
.
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой областью был отрезок l
на оси абсцисс. Однако этот вывод легко можно распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
1) точки распределены в поле статистически равномерно со средней плотностью λ
;
2) точки попадают в неперекрывающиеся области независимым образом;
3) точки появляются поодиночке, а не парами, тройками и т.д.,
то число точек Х
, попавших в любую область D
(плоскую или пространственную), распределяется по закону Пуассона:
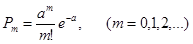 , ,
где а
– среднее число точек, попадающих в область D
.
Для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности (λ=
const
) несущественно. Если выполнены два других условия, то закон Пуассона все-равно имеет место, только параметр а
в нем приобретает другое выражение: он получается не простым умножением плотности λ
на длину, площадь или объем, а интегрированием переменной плотности по отрезку, площади или объему.
Примеры из практики
1. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение. Т.к. по условию n
=1000
достаточно велико, а m
=0,002
мало, можно воспользоваться распределением Пуассона:

где а=
np=1000·0,002=2
.
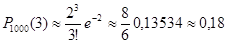
2.
При испытании легированной стали на содержание углерода вероятность того, что в случайно взятой пробе процент углерода превысит допустимый уровень, равна р=0,01. Считая применимым закон редких явлений, вычислить, сколько в среднем необходимо испытать образцов, чтобы с вероятностью р=0,95 указанный эффект наблюдался по крайней мере 1 раз.
Решение. События «указанный эффект наблюдался по крайней мере один раз» (обозначим через Р
) и «указанный эффект не наблюдался ни одного раза» (обозначим через Q
), очевидно, являются противоположными. Следовательно, P
+
Q
=1
, откуда
Р=1-
Q
=1-
Pn
(0)=1-
e
-
a
.
По условию Р=0,95
, следовательно
е-а
=0,05,
а=
np
=3,
откуда
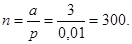
Таким образом, искомое среднее число образцов, которое необходимо испытать, – 300 штук.
3.
Вероятность выигрыша по одному лотерейному билету р=0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью Р, не меньшей, чем 0,98?
Решение. Вероятность выигрыша мала, а число билетов, которое нужно купить, очевидно, велико, поэтому случайное число выигрышных билетов имеет приближенно распределение Пуассона.
События «ни один из купленных билетов не является выигрышным» и «хотя бы один билет – выигрышный» – противоположные. Поэтому сумма вероятностей этих событий равна единице:
Р
n
(0)+
P
=1, или Р=1-Р
n
(0)=1- =1-е-а
. =1-е-а
.
По условию, Р≥0,98
, или 1-е-а
≥0,98
. Откуда е-а
≤0,02
.
По таблице найдем е-3,9
=0,02
. Т.к. функция е-х
– убывающая, предыдущее неравенство выполняется при а≥3,9
, или np
≥3,9
. Отсюда n
≥3,9/0,01=390
.
Таким образом, надо купить не менее 390 билетов, чтобы выиграть хотя бы по одному из них.
4.
Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятность того, что за две секунды на АТС не поступит ни одного вызова; за две секунды на АТС поступит меньше двух вызовов.
Решение. Среднее число вызовов за две секунды равно:

Вероятность того, что на станцию в течение 2-ух секунд не поступит ни одного вызова равна:

Событие, состоящее в поступлении менее двух вызовов, означает, что на станцию либо не поступило ни одного вызова, либо поступил только один. Таким образом, вероятность поступления менее 2-ух вызовов за то же время равна:
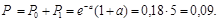
5.
Случайная величина Х – число электронов, вылетающих с нагретого катода электронной лампы в течение времени t, λ – среднее число электронов, испускаемых в единицу времени. Определить вероятность того, что за время t число испускаемых электронов будет меньше m (m
Î
N).
Решение. λ
– среднее число электронов, t
– время испускания, следовательно, а=λ
t
.
P=
6. С накаленного катода за единицу времени вылетает в среднем q(t) электронов, где t – время, протекшее с начала опыта. Найти вероятность того, что за промежуток времени длительности τ, начинающийся в момент t0, с катода вылетит ровно m электронов.
Решение. Находим среднее число электронов а
, вылетающих с катода за данный отрезок времени:

По вычисленному, а
определяем искомую вероятность:
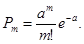
Заключение
В заключение хочется отметить то, что распределение Пуассона является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.
Многие задачи практики сводятся, в конечном счете, к распределению Пуассона. Его особое свойство, заключающееся в равенстве математического ожидания и дисперсии, часто применяют на практике для решения вопроса, распределена случайная величина по закону Пуассона или нет.
Также важен тот факт, что закон Пуассона позволяет находить вероятности события в повторных независимых испытаниях при большом количестве повторов опыта и малой единичной вероятности.
Список использованной литературы
1. Н.Ш. Кремер «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2004.
2. C.А. Айвазян, В.С. Мхитарян «Теория вероятностей и прикладная статистика»: Учеб. пособие. М., 2001.
3. Е.С. Кочетков «Теория вероятностей и математическая статистика»: Учеб. пособие. М., 2001.
4. В.А. Фигурин «Теория вероятности и математическая статистика»: Учеб. пособие. – Мн. ООО «Новое знание», 2000.
5. Л.П. Трошин «Теория вероятностей», МЭСИ. М.: 2004.
6. В.Е. Гмурман «Теория вероятностей и математическая статистика». Учеб. пособие. М.: высшее образование, 2006.
|