| Содержание
Введение
1. Экономическая сущность задачи
2. Исходные данные
3. Метод динамического программирования
4. Метод полного перебора вариантов
5. Интуитивные распределения
5.1. Равномерное распределение
5.2. Метод наибольшей плановой эффективности
5.3. Самостоятельное интуитивное распределение
Заключение
Литература
Цель работы - изучение экономической сущности и математической формализации задачи определения оптимального варианта распределения заданной суммы капитальных вложений между несколькими предприятиями отрасли, выпускающими взаимозаменяемую продукцию.
В отрасли имеется М
предприятий, выпускающих однотипную взаимозаменяемую продукцию, спрос на которую пока не удовлетворяется полностью. С целью увеличения выпуска данной продукции на модернизацию этих предприятий выделена сумма капиталовложений в размере Х
тыс. руб. Каждому предприятию с номером m=1, 2, …,
M
может быть выделена сумма Xm
>=0
, при этом сумма капиталовложений распределяется полностью, т.е.
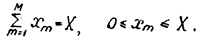 (1) (1)
Оптимизация распределения капиталовложений производится по критерию максимума суммарного прироста выпуска продукции всеми предприятиями
 (2) (2)
Здесь gm
(
xm
)
- прирост выпуска продукции на предприятии с номером m
при условии, что ему выделена сумма капиталовложений xm
.
Исходными данными для решения задачи служат выполненные на каждом предприятии расчеты по обоснованию зависимостей прироста выпуска от размера капиталовложений gm
(
xm
).
Как правило, эти зависимости не удается получить в аналитической форме (в виде непрерывных и аналитических функций) и они представляются таблично, значениями функций при заданных дискретных значениях аргумента.
Для упрощения дальнейших вычислений будем считать, что величины xm
кратны некоторой дискрете h=
X/
N
где N - число дискрет в распределяемой сумме X. Дискрета h
задается заранее, исходя из разумного компромисса между желательной точностью и трудоемкостью расчетов. Уменьшение величины дискреты h
, вообще говоря, увеличивает точность, но при этом растет трудоемкость подготовки исходной информации и её последующей обработки.
С учетом принятого допущения величина капиталовложений xm
меняемся дискретно, принимая значения xm
=nh,
n=0, 1, …,
N.
Каждое предприятие рассчитывает и представляет в министерство (N+1) М
значений, которые удобно свести в табл.1.
При построении табл.1.1 принято М
= 5; Х
= 300 тыс. руб.; N
= 6; h
= 50 тыс. руб.
Таблица 1 - Прирост выпуска продукции при заданной величине капиталовложений, тыс. руб.
| Величина капиталовложений тыс. руб.
|
Порядковый номер предприятия
|
| 1
|
2
|
3
|
4
|
5
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| 0
|
0
|
0
|
0
|
0
|
0
|
| 50
|
30
|
20
|
20
|
40
|
30
|
| 100
|
83
|
75
|
61
|
62
|
72
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| 150
|
98
|
100
|
112
|
97
|
108
|
| 200
|
127
|
150
|
140
|
134
|
122
|
| 250
|
158
|
165
|
152
|
160
|
148
|
| 300
|
195
|
20
|
180
|
185
|
190
|
Идея метода динамического программирования состоит в том, что выделенная сумма Х
распределяется не между всеми М
предприятиями (иначе получается полный перебор), а между двумя "предприятиями": последним предприятием (имеющем номер М
) и группой из (М
-1) - го предшествующего предприятия, для которого оптимальное распределение между ними любой частичной суммы уже известно. Это соответствует решению основного функционального уравнения динамического программирования М
-го, последнего шага
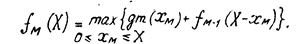 (3) (3)
Здесь fM
(
X) -
максимальный суммарный прирост продукции, получаемый от М
предприятий при оптимальном распределении суммы Х
между M
-тым и группой из (М
-1) - го первых предприятий, при условии, что выделяемая им частичная сумма (Х-ХМ
)
распределяется оптимально;
fM
-1
(
X-ХМ
)
- максимальный суммарный прирост продукции, получаемый от (М
-1) - го первых предприятий при оптимальном распределении между ними частичной суммы (Х-ХМ
),
оставшейся, от М-го предприятия.
Решить уравнение (3) невозможно, так как функция fM
-1
(
X-ХМ
)
неизвестна. Однако её можно выразить с помощью основного функционального уравнения для (М-1) - го шага через функцию максимального суммарного прироста продукции, получаемого при оптимальном распределении частичных сумм в группе из (М-2) - х первых предприятий
 (4) (4)
Снова неизвестна функция fM
-2
(
nh-ХМ-1
)
однако, используя основное fM
-3
(
nh-ХМ-2
)
функциональное уравнение, её можно определить аналогично через функцию и т.д. Эта процедура рекуррентных подстановок неизвестных функций максимального суммарного прироста продукции заканчивается точно через М
шагов. Действительно, на последнем шаге подстановок (его номер m
=1) получаем основное функциональное уравнение динамического программирования в виде
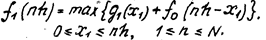 (5) (5)
Функция f0
(
nh-Х1
)
формально есть максимальный прирост продукции при оптимальном распределении частичной суммы (nh-Х1
)
в группе, состоящей из "0" предприятий. Естественно, такой группе, в которой нет ни одного предприятия, никаких средств не выделяется поэтому
f0
(nh-Х1
) =0 (6)
Отсюда следует, что на первом шаге основное функциональное уравнение имеет следующее решение:
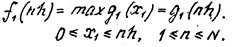 (7) (7)
Это означает, что на первом шаге, когда рассматривается только одно первое предприятие, любая частичная сумма nh
выделяется ему целиком, так как ее некому, кроме него, распределять. Таким образом, оптимальное управление на первой шаге
X1
*
(nh) = nh (8)
Представим найденное решение основного функционального уравнения на первом шаге в виде табл.2.
Таблица 2 - Определение оптимальных управлений и максимальных прирос продукции на первом шаге
| Частичная распределяемая сумма
|
Сумма, выделяемая первому предприятию
|
Оптимальное управление
|
Максимальный прирост продукции
|
| 0
|
50
|
100
|
150
|
200
|
250
|
300
|
| 0
|
0
|
0
|
0
|
| 50
|
30
|
50
|
30
|
| 100
|
83
|
100
|
83
|
| 150
|
-
|
98
|
150
|
98
|
| 200
|
127
|
200
|
127
|
| 250
|
158
|
250
|
158
|
| 300
|
195
|
300
|
195
|
В табл.2 заполнена числами только главная диагональ. Эти числа берутся из табл.1 исходных данных для первого предприятия. Пустые клетки левее главной диагонали показывают, что на 1-м шаге вся частичная сумма nh
целиком отдается первому предприятию, так как на атом шаге других предприятий нет. Пустые клетки справа от главной диагонали показывают, что не может распределяться частичная сумма, большая имеющейся.
ШАГ 1 тривиален, однако важен в том отношении, что позволяет начать процесс рекуррентного вычисления на последующих шагах по основному функциональному уравнению
fm
(nh) =max{gm
(xm
) +fm
-1
(nh-xm
) }, n=1, 2, …, N;
0<=xm<=nh, m=1, 2, …, M.
ШАГ 2. Распределение частичных сумм между вторым предприятием и группой из "одного первого предприятия". Для второго шага основное функциональное уравнение имеет вид
F2
(nh) =max{g2
(x2
) +f1
(nh-x2
) },
0<=x2
<=nh; 1<=n<=N
Его решение представлено в табл.3
Таблица 3 - Определение оптимальных управлений и максимальных приростов продукции на 2-м шаге.
| Частичная распределяемая сумма
|
Сумма, выделяемая второму предприятию
|
Оптимальное управление
|
Максимальный прирост продукции
|
| 0
|
50
|
100
|
150
|
200
|
250
|
300
|
| 0
|
0+0
0
|
0
|
0
|
| 50
|
0+30
30
|
20+0
20
|
0
|
30
|
| 100
|
0+83
83
|
20+30
50
|
75+0
75
|
0
|
83
|
| 150
|
0+98
98
|
20+83
103
|
75+30
105
|
100+0
100
|
100
|
105
|
| 200
|
0+127
127
|
20+98
118
|
75+83
158
|
100+30
130
|
150+0
150
|
100
|
158
|
| 250
|
0+158
158
|
20+127
147
|
75+98
173
|
100+83
183
|
150+30
180
|
165+0
165
|
150
|
183
|
| 300
|
0+195
195
|
20+158
178
|
75+127
204
|
100+98
198
|
150+83
233
|
165+30
195
|
200+0
200
|
200
|
233
|
В клетках таблицы записываются через знак "+" 2 числа, равные g2
(
x2
)
и f1
(
nh-
x2
).
Величины g2
(
x2
)
берутся из табл.1, а величины f1
(
nh-
x2
)
из последнего столбца табл.2.
В последнем столбце табл.3 проставлены максимумы сумм в соответствующих строках, предшествующем столбце - соответствующая этому максимуму оптимальная величина капитальных вложений, выделяемых второму предприятию.
ШАГ 3. Зная оптимальное распределение всех частичных сумм между первыми двумя предприятиями, перейдем к их распределению между третьим предприятием и группой из первых двух (табл.4).
Таблица 4 - Определение оптимальных управлений и максимальных прирост продукции на 3-м шаге
Частичная распределяемая сумма
|
Сумма, выделяемая третьему предприятию
|
Оптимальное управление
|
Максимальный прирост продукции
|
| 0
|
50
|
100
|
150
|
200
|
250
|
300
|
| 0
|
0+0
0
|
0
|
0
|
| 50
|
0+30
30
|
20+0
20
|
0
|
30
|
| 100
|
0+83
83
|
20+30
50
|
61+0
61
|
0
|
83
|
| 150
|
0+105
105
|
20+83
103
|
61+30
91
|
112+0
112
|
150
|
112
|
| 200
|
0+158
158
|
20+105
125
|
61+83
144
|
112+30
142
|
140+0
140
|
0
|
158
|
| 250
|
0+183
183
|
20+158
178
|
61+105
166
|
112+83
195
|
140+30
170
|
152+0
0
|
150
|
195
|
| 300
|
0+233
233
|
20+183
203
|
61+158
219
|
112+105
217
|
140+83
233
|
152+30
182
|
180+0
180
|
0
|
233
|
ШАГ 4. Определение оптимального распределения на 4-м шаге.
Таблица 5 - Определение оптимальных управлений и максимальных приростов продукции на 4-м шаге
Частичная распределяемая сумма
|
Сумма, выделяемая четвертому предприятию
|
Оптимальное управление
|
Максимальный прирост продукции
|
| 0
|
50
|
100
|
150
|
200
|
250
|
300
|
| 0
|
0+0
0
|
0
|
0
|
| 50
|
0+30
30
|
40+0
40
|
50
|
40
|
| 100
|
0+83
83
|
40+40
80
|
62+0
62
|
0
|
83
|
| 150
|
0+112
112
|
40+83
123
|
62+40
102
|
97+0
97
|
50
|
123
|
| 200
|
0+158
158
|
40+112
152
|
62+83
145
|
97+40
137
|
134+0
134
|
0
|
163
|
| 250
|
0+195
195
|
40+158
198
|
62+112
174
|
97+83
180
|
134+40
174
|
160+0
160
|
50
|
198
|
| 300
|
0+233
233
|
40+195
235
|
62+158
220
|
97+112
220
|
134+83
217
|
160+40
200
|
185+0
185
|
50
|
235
|
ШАГ 5. Определение оптимального распределения на 5-м шаге.
Таблица 6 - Определение оптимальных управлений и максимальных приростов продукции на 5-м шаге
Частичная распределяемая сумма
|
Сумма, выделяемая пятому предприятию
|
Оптимальное управление
|
Максимальный прирост продукции
|
| 0
|
50
|
100
|
150
|
200
|
250
|
300
|
| 0
|
0+0
0
|
0
|
0
|
| 50
|
0+40
40
|
30+0
30
|
0
|
40
|
| 100
|
0+83
83
|
30+40
70
|
72+0
72
|
0
|
83
|
| 150
|
0+123
123
|
30+83
113
|
72+40
112
|
108+0
108
|
0
|
123
|
| 200
|
0+158
158
|
30+123
153
|
72+83
155
|
108+40
148
|
122+0
122
|
0
|
158
|
| 250
|
0+198
198
|
30+158
188
|
72+123
195
|
108+83
191
|
122+40
162
|
148+0
148
|
0
|
198
|
| 300
|
0+235
235
|
30+198
228
|
72+158
230
|
108+123
231
|
122+83
205
|
148+40
188
|
190+0
190
|
0
|
235
|
Результаты расчетов на всех 5-и шагах представим в виде табл.7.
Таблица 7 - Сводная таблица оптимальных управлений и максимальных приростов продукции
| Распределяемая сумма
|
Номер шага распределения
|
| 1
|
2
|
3
|
4
|
5
|
| x1
*
|
f1
|
x2
*
|
F2
|
x3
*
|
f3
|
x4
*
|
f4
|
x5
*
|
f5
|
| 0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 50
|
50
|
30
|
0
|
30
|
0
|
30
|
50
|
40
|
0
|
40
|
| 100
|
100
|
83
|
0
|
83
|
0
|
83
|
0
|
83
|
0
|
83
|
| 150
|
150
|
98
|
100
|
105
|
150
|
112
|
50
|
123
|
0
|
123
|
| 200
|
200
|
127
|
100
|
158
|
0
|
158
|
0
|
158
|
0
|
158
|
| 250
|
250
|
158
|
150
|
183
|
150
|
195
|
50
|
198
|
0
|
198
|
| 300
|
300
|
195
|
200
|
233
|
0
|
233
|
50
|
235
|
0
|
235
|
Таблица 8 - Оптимальное распределение частичных сумм между 5-ю предприятиями.
| Распределяемая сумма
|
Выделяемые предприятиям суммы
|
Макс. Суммарный прирост продукции
|
| 1
|
2
|
3
|
4
|
5
|
| 0
|
0
|
0
|
0
|
0
|
0
|
| 50
|
0
|
0
|
0
|
50
|
0
|
40
|
| 100
|
100
|
0
|
0
|
0
|
0
|
83
|
| 150
|
100
|
50
|
0
|
0
|
0
|
123
|
| 200
|
100
|
100
|
0
|
0
|
0
|
158
|
| 250
|
100
|
100
|
0
|
50
|
0
|
198
|
| 300
|
100
|
0
|
150
|
50
|
0
|
235
|
Оптимальное распределение суммы 300 тыс. руб.:
| X1
*
|
100
|
x2
*
|
0
|
x3
*
|
150
|
x4
*
|
50
|
x5
*
|
0
|
Максимальный прирост выпуска продукции при оптимальном распределении равен 235 тыс. руб. Эта величина находится на пересечении строки "Распределяемая сумма - 300"' и столбцов 5-го шага. Задача решена.
Самый простой способ решения распределительных задач подобного типа состоит в полном переборе всех возможных вариантов распределения исходной суммы между предприятиями и выбор того варианта, при котором суммарный прирост выпуска продукции будет максимальным. Недостатком метода полного перебора является то, что число вариантов распределения быстро растет при увеличении количества предприятий и уменьшении дискреты распределения.
По условиям варианта имеем 6 предприятий и 7 дискрет.
Таблица 9 - Расчет числа вариантов распределения между 6-ю предприятиями суммы 300 тыс. руб. с дискретой 37,5 тыс. руб. по методу полного перебора
| №
|
Тип распределения
|
Число вариантов
|
| 1
|
Одному - 300
|
С6
1
=6
|
| 2
|
Одному - 262,5, другому - 37,5
|
С6
1
С5
1
=30
|
| 3
|
Одному - 225, другому - 75
|
С6
1
С5
1
=30
|
| 4
|
Одному - 225, другому - 37,5, третьему - 37,5
|
С6
1
С5
2
=60
|
| 5
|
Одному - 187,5, другому - 112,5
|
С6
1
С5
1
=30
|
| 6
|
Одному - 187,5, второму - 75, третьему - 37,5
|
С6
1
С5
2
С5
2
=120
|
| 7
|
Одному - 187,5, трем по - 37,5
|
С6
1
С5
2
=60
|
| 8
|
Двум по - 150
|
С6
2
=60
|
| 9
|
Одному - 150, второму - 112,5, третему - 37,5
|
С6
1
С5
1
С4
1
=60
|
| 10
|
Одному - 150, второму - 75, двум по - 37,5
|
С6
1
С5
1
С4
2
=180
|
| 11
|
Одному - 150, двум по - 75
|
С6
1
С5
2
=60
|
| 12
|
Одному - 150, четырем по - 37,5
|
С6
1
С5
4
=30
|
| 13
|
Двум по - 112,5 другому - 75
|
С6
2
С4
1
=68
|
| 14
|
Двум по - 112,5 двум по - 37,5
|
С6
2
С4
2
=90
|
| 15
|
Одному - 112,5, второму - 75, трем по - 37,5
|
С6
1
С5
1
С4
3
=120
|
| 16
|
Одному - 112,5, двум по - 75, третьему - 37,5
|
С6
1
С5
2
С3
2
=180
|
| 17
|
Одному - 112,5, пятерым по - 37,5
|
С6
1
С5
5
=6
|
| 18
|
Четырем по - 75
|
С6
4
=15
|
| 19
|
Трем по - 75, двум по - 37,5
|
С6
3
С3
2
=60
|
| 20
|
Двум по - 75, четырем по - 37,5
|
С6
2
С4
4
=15
|
| Итого вариантов: 1287
|
Число вариантов распределения методом полного перебора можно также подсчитать по формуле коэффициентов биномиального распределения
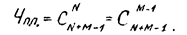 (9) (9) Сколько вариантов распределения пришлось рассмотреть при использовании метода динамического программирования?
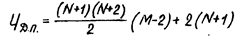 (10) (10)
В нашем случае это составило 1287 вариантов, т.е. по сравнению с методом полного перебора число рассматриваемых вариантов сократилась более чем в 60 раза.
При равномерном распределении суммы в 300 тыс. руб. между 5-ю предприятиями получается, что каждому из них нужно выделить по 60 тыс. руб.
Используя данные о приросте выпуска продукции на предприятиях при выделении им 50 и 100 тыс. соответственно, рассчитаем прирост выпуска продукции при выделении им по 60 тыс. рублей.
Из рис.1 можно найти прирост продукции при выделении предприятию 60-ти тыс. руб.
Величина прироста при распределении суммы капитальных вложений по 60тыс. руб. определяется путем решения ряда пропорций.
Для первого предприятия 50/10=53/y- y=10,6 величина прироста на дополнительные 10 тыс. руб. капитальных вложений. Всего прирост будет равен 40,6.
Для второго предприятия 50/10=55/y- y=11 50/10=22/y- y=4,4 величина прироста на дополнительные 10 тыс. руб. капитальных вложений. Всего прирост будет равен 44,4
Для третьего предприятия 50/10=41/y- y=8,2 величина прироста на дополнительные 10 тыс. руб. капитальных вложений. Всего прирост будет равен 28,2.
Для четвертого предприятия 50/10=22/y- y=4,4 величина прироста на дополнительные 10 тыс. руб. капитальных вложений. Всего прирост будет равен 44,4.
Для пятого предприятия 50/10=42/y- y=8,4 величина прироста на дополнительные 10 тыс. руб. капитальных вложений. Всего прирост будет равен 38,4.
Рисунок 1 - Равномерное распределение капиталовложений

Итак максимальный прирост при равномерном распределении равен.
38,4+44,4+28,2+40,6+31=182,6тыс. руб.
При этом методе вся сумма 300тыс. руб. отдается предприятию с наибольшей плановой эффективностью, то есть тому, которое при капиталовложениях 300тыс. руб. дает максимальный прирост продукции. По данным таблицы 1 видно, что это предприятие № 2. Если ему выделить 300тыс. руб., то максимальный прирост продукции будет 200 тыс. руб.
Из предположения о том, что при увеличении суммы капиталовложений, выделяемых конкретному предприятию, увеличивается прирост продукции, которое оно дает.
Распределение базирующее на основе оценки фондорентабельности каждого вложения
.
Для осуществления данного распределения рассчитаем фондорентабельность. Всех вложений в предприятие. Расчеты представим в таблице 10.
Таблица 10 - фондорентабельность капиталовложений
| Распределяемая сумма
|
Фондорентабельность предприятий
|
| 1
|
2
|
3
|
4
|
5
|
| 0
|
0
|
0
|
0
|
0
|
0
|
| 50
|
0,60
|
0,40
|
0,40
|
0,80
|
0,60
|
| 100
|
0,83
|
0,75
|
0,61
|
0,62
|
0,72
|
| 150
|
0,65
|
0,67
|
0,75
|
0,65
|
0,72
|
| 200
|
0,64
|
0,75
|
0,70
|
0,67
|
0,61
|
| 250
|
0,63
|
0,66
|
0,61
|
0,64
|
0,59
|
| 300
|
0,65
|
0,07
|
0,60
|
0,62
|
0,63
|
Проанализировав величину фондорентабельности выделим максимальные. Максимальная эффективность вложений достигается при вложении во второе предприятие 50 тыс. руб., далее в четвертое 100 тыс. руб., в третье 150 тыс. руб.
Экономический эффект увеличения выпуска продукции.
40+83+112=235.
Таким образом интуитивное распределение с применением методик финансового анализа дало оптимальное распределение.
При выделяемой сумме 300тыс. руб. между пятью предприятиями и с дискретой 50тыс. руб, распределение капиталовложений методом динамического программирования дает оптимальное распределение капиталовложений, которое дает прирост продукции 235тыс. руб.
| X1
*
|
0
|
x2
*
|
50
|
x3
*
|
100
|
x4
*
|
0
|
x5
*
|
150
|
При методе динамического программирования число рассматриваемых вариантов - 198, а если бы задача решалась методом полного перебора, то число вариантов возросло бы до 1287.
Равномерное распределение дает максимальный прирост продукции -182,6тыс. руб.
Выделение всей суммы капиталовложений предприятию с наибольшей эффективностью дает прирост продукции 200тыс. руб.
Интуитивное распределение (сформулированное самостоятельно) дает прирост продукции 235тыс. руб.
1. Мешковой Н.П. Лабораторные работы по экономике промышленности: Челябинск 2001.
2. Стандарты предприятия. Курсовые и дипломные проекты. Общие требования к оформлению: Челябинск 2007.
|