Министерство образования Республики Беларусь
Гомельский Государственный университет имени Франциска Скорины
Курсовая работа
«Дифференциальные системы, эквивалентные автономным системам с известным первым интегралом»
Гомель 2006
Реферат
Курсовая работа состоит из 19 страниц, 3-х источников.
Ключевые слова: эквивалентная система, первый интеграл дифференциальной системы, отражающая функция, эквивалентность систем в смысле совпадения отражающих функций, непрерывно дифференцируемая функция, непрерывная скалярная нечётная функция.
Целью курсовой работы является нахождение связи между первым интегралом системы и эквивалентными системами.
Содержание
Введение
Отражающая функция
Первый интеграл дифференциальной системы и условия его существования
Возмущения дифференциальных систем, не изменяющих временных симметрий
Общее решение
Заключение
Список использованных источников
Введение
В курсовой работе мы находим связь между первым интегралом и эквивалентными системами.
В результате приходим к теореме,
которая звучит так:
Пусть  первый интеграл системы первый интеграл системы  , , 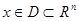 (1). Если (1). Если 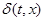 , удовлетворяет уравнению , удовлетворяет уравнению 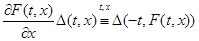 , то указанная система эквивалентна системе , то указанная система эквивалентна системе 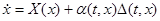 , , 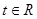 , , 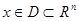 (2). И если, кроме того (2). И если, кроме того 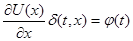 , где , где  - некоторая функция ( - некоторая функция ( -может равняться const), тогда первый интеграл системы (2) выражается следующей формулой -может равняться const), тогда первый интеграл системы (2) выражается следующей формулой 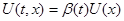 , где , где 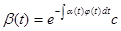 и и 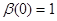 . .
Отражающая функция
Определение. Рассмотрим систему
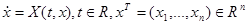 (1) (1)
cчитая, что правая часть которой непрерывна и имеет непрерывные частные производные по 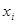 . Общее решение в форме Коши обозначено через . Общее решение в форме Коши обозначено через 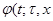 ). Через ). Через 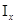 обозначим интервал существования решения обозначим интервал существования решения 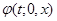 . .
Пусть
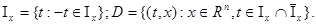
Отражающей функцией
системы (1) назовём дифференцируемую функцию 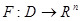 , определяемую формулой , определяемую формулой
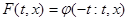
Для отражающей функции справедливы свойства:
1.) для любого решения 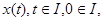 системы (1) верно тождество системы (1) верно тождество
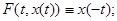
2.) для отражающей функции F любой системы выполнены тождества
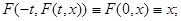
3) дифференцируемая функция 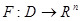 будет отражающей функцией системы (1) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных будет отражающей функцией системы (1) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных
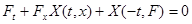
и начальному условию
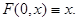
Рассмотрим систему 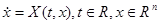 (1*) считая, что её правая часть непрерывно дифференцируемая. Будем говорить, что множество систем вида (1*) образует класс эквивалентности, если существует дифференцируемая функция (1*) считая, что её правая часть непрерывно дифференцируемая. Будем говорить, что множество систем вида (1*) образует класс эквивалентности, если существует дифференцируемая функция 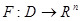 со свойствами: 1) отражающая функция со свойствами: 1) отражающая функция 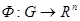 любой системы из рассматриваемого множества совпадает в области определения любой системы из рассматриваемого множества совпадает в области определения 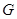 с функцией с функцией 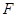 ; 2) Любая система вида (1*), отражающая функция ; 2) Любая система вида (1*), отражающая функция 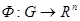 которая совпадает в области которая совпадает в области 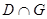 с функцией с функцией 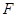 , содержится в рассматриваемом множестве. , содержится в рассматриваемом множестве.
Две системы вида (1*), принадлежащие одному классу эквивалентности, будем называть эквивалентными
. Допуская определённую вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию 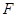 при этом будем называть отражающей функцией класса, а класс – соответствующим отражающей функции при этом будем называть отражающей функцией класса, а класс – соответствующим отражающей функции 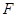 . .
Первый интеграл дифференциальной системы и условия его существования
Рассмотрим систему 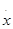 = = 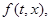 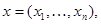 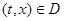 (1)
с непрерывной в области в функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы
(1) в области G, если для любого решения x(t), t (1)
с непрерывной в области в функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы
(1) в области G, если для любого решения x(t), t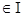 , системы (1), график которого расположен в G функция U (t, x(t)), t , системы (1), график которого расположен в G функция U (t, x(t)), t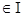 , постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t. , постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.
Пусть V (t, x), V:G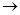 R
, есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V R
, есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V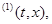 V V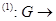 R,
определяемую равенством R,
определяемую равенством
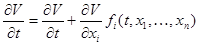 . .
Обозначим V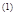 (t, x(t)) (t, x(t))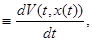 t t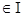 . .
Лемма
Дифференцируемая функция U (t, x), U:G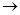 R
,
представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U R
,
представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U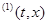 в силу системы (1) тождественно в G обращается в нуль. в силу системы (1) тождественно в G обращается в нуль.
Необходимость. Пусть U (t, x) есть первый интеграл системы (1). Тогда для любого решения x(t) этой системы на основании определения, будем иметь тождества
U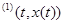  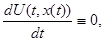
Откуда при t=t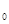 получим равенство U получим равенство U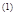 (t (t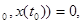 справедливое при всех значениях t справедливое при всех значениях t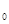 и x(t и x(t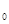 ). Необходимость доказана. ). Необходимость доказана.
Достаточность. Пусть теперь U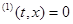 при всех (t, x) при всех (t, x)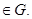 Тогда для любого решения x(t) системы (1) из определения будем иметь тождества Тогда для любого решения x(t) системы (1) из определения будем иметь тождества

а с ним и достаточность.
Из определения первого интеграла следует, что постоянная на G функция также является первым интегралом системы (1). По этому первым интегралом на G будем называть функцию 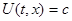 , для которой выполняется неравенство , для которой выполняется неравенство
 и и 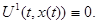
Функцию U(x) будем называть стационарным первым интегралом
системы (1), если она не зависит от t и является первым интегралом системы (1).
Возмущения дифференциальных систем, не изменяющие временных симметрий
Наряду с исходной дифференциальной системой
  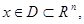 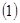
будем рассматривать множество возмущённых систем
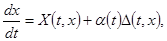  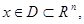 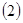
где 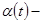 непрерывная скалярная нечётная функция, а непрерывная скалярная нечётная функция, а 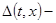 произвольная непрерывно дифференцируемая вектор-функция. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем (1) и (2). При совпадении отражающих функций двух систем совпадают их операторы сдвига на симметричном промежутке вида произвольная непрерывно дифференцируемая вектор-функция. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем (1) и (2). При совпадении отражающих функций двух систем совпадают их операторы сдвига на симметричном промежутке вида 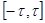 и, значит, для периодических систем совпадают их отображения за период и, значит, для периодических систем совпадают их отображения за период 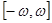 . .
Как известно, отражающая функция системы (1) обязана удовлетворять соотношению
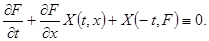 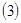
Если  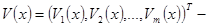 вектор-функция, а вектор-функция, а 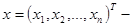
вектор-столбец, то полагаем
  , , 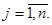
Лемма 1.
Для любых трёх вектор-функций 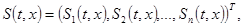 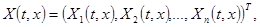 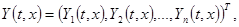 из которых функция из которых функция 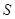 дважды непрерывно дифференцируема, а функции дважды непрерывно дифференцируема, а функции 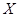 и и 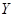 дифференцируемы, имеет место тождество дифференцируемы, имеет место тождество
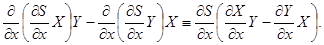 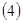
Лемма 2
.
Пусть 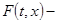 отражающая функция системы отражающая функция системы 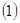 с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор функции с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор функции 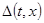 функция функция
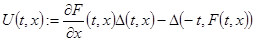 
удовлетворяет тождеству
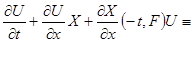
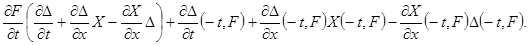 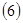
Доказательство. Учитывая соотношение 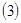 , простыми выкладками установим тождества , простыми выкладками установим тождества
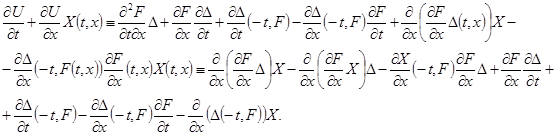
К первым двум слагаемым последней части этого тождества применим тождество 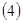 . Тогда после несложных формальных преобразований придём к соотношению . Тогда после несложных формальных преобразований придём к соотношению
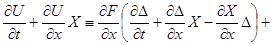
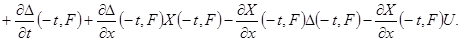
Прибавим к левой и правой частям этого соотношения выражение 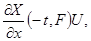 придём к нужному нам тождеству придём к нужному нам тождеству 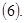
Лемма доказана.
Теорема 1
Пусть вектор-функция 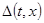 является решением дифференциального уравнения в частных производных является решением дифференциального уравнения в частных производных
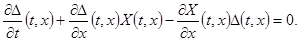 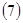
Тогда возмущённая дифференциальная система
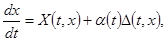   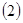 , ,
где 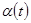 - произвольная непрерывная скалярная нечётная функция, эквивалентна дифференциальной системе - произвольная непрерывная скалярная нечётная функция, эквивалентна дифференциальной системе 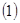 . .
Доказательство.
Пусть 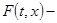 отражающая функция системы отражающая функция системы 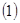 . Следовательно, эта функция удовлетворяет дифференциальному уравнению . Следовательно, эта функция удовлетворяет дифференциальному уравнению 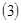 . Покажем, что она удовлетворяет и тождеству . Покажем, что она удовлетворяет и тождеству
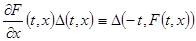 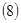
Для этого введём функцию 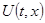 по формуле по формуле 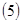 . Согласно лемме 2, эта функция удовлетворяет тождеству . Согласно лемме 2, эта функция удовлетворяет тождеству 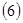 . При условиях доказываемой теоремы с учётом соотношения . При условиях доказываемой теоремы с учётом соотношения 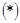 это тождество переписывается в виде это тождество переписывается в виде
 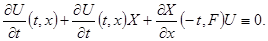
Кроме того, поскольку для всякой отражающей функции 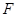 верно тождество верно тождество 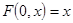 , имеет место соотношения , имеет место соотношения
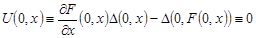 . .
Таким образом, функция 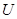 является решением задачи Коши является решением задачи Коши
 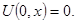
Решение этой задачи существует и единственно. Следовательно, имеет место тождество 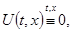 влекущее за собой тождество влекущее за собой тождество  . .
Теперь покажем, что отражающая функция 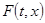 системы системы 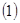 является также и отражающей функцией системы является также и отражающей функцией системы 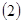 . Для этого нужно проверить выполнение основного соотношения . Для этого нужно проверить выполнение основного соотношения 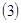 , которое в данном случае должно быть переписано в виде , которое в данном случае должно быть переписано в виде
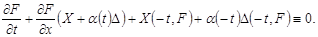 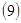
Действительно, последовательно преобразовывая левую часть последнего соотношения и учитывая нечётность функции 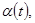 приходим к следующей цепочке тождеств: приходим к следующей цепочке тождеств:

Оба слагаемых, стоящих в квадратных скобках, тождественно равны нулю. Первое – в силу того, что для отражающей функции системы 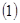 верно тождество верно тождество 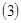 , второе – потому, что при условиях теоремы верно тождество , второе – потому, что при условиях теоремы верно тождество 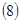 . Следовательно, тождество . Следовательно, тождество 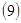 выполняется и функция выполняется и функция 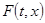 является отражающей функцией системы является отражающей функцией системы 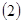 . Теорема доказана. . Теорема доказана.
А теперь рассмотрим пример.
Пример
Рассмотрим систему
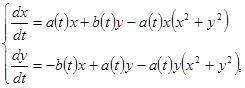
в которой непрерывные и 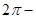 периодические функции периодические функции 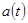 , , 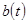 таковы, что таковы, что 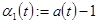 и и 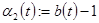 – нечётные функции. – нечётные функции.
Эта система эквивалентна стационарной системе
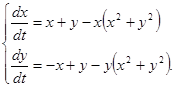
Здесь 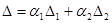 и и  , , 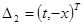 , ,
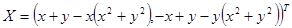 . .
Так как стационарная система имеет асимптотически устойчивый предельный цикл 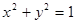 , которому соответствуют , которому соответствуют 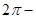 периодические решения, то из сказанного следует, что все решения периодические решения, то из сказанного следует, что все решения 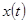 , , 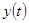 рассматриваемой системы, начинающиеся при рассматриваемой системы, начинающиеся при 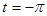 на окружности на окружности 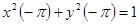 , являются , являются 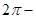 периодическими, а каждое из остальных решений, кроме нулевого, при периодическими, а каждое из остальных решений, кроме нулевого, при 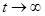 стремится к одному из указанных периодических. стремится к одному из указанных периодических.
Общее решение системы
Рассмотрим две дифференциальные системы
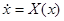 , , 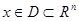 (1) (1)
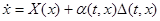 , , 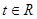 , , 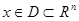 , (2) , (2)
где 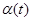 - непрерывная скалярная нечётная функция, - непрерывная скалярная нечётная функция, 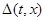 -произвольная непрерывно дифференцируемая функция. -произвольная непрерывно дифференцируемая функция.
Лемма 1
Для любой нечётной функции 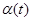 , определённой в окрестности , определённой в окрестности  , справедливо , справедливо 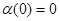 . .
Доказательство.
Так как 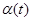 - непрерывная нечётная функция, то - непрерывная нечётная функция, то 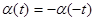 и и
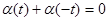 при при 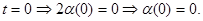
Лемма 2
Пусть 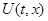 есть первый интеграл системы есть первый интеграл системы 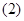 . Тогда . Тогда 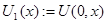 есть первый интеграл системы есть первый интеграл системы 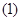 . .
Доказательство. Т.к. 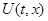 есть первый интеграл системы есть первый интеграл системы 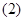 , то его производная в силу системы равна , то его производная в силу системы равна  , т.е. , т.е. 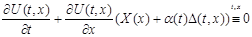 . .
Полагая здесь  , получаем , получаем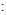 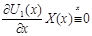 , что и означает что , что и означает что 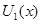 первый интеграл системы первый интеграл системы 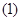
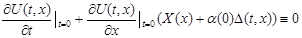 . .
Теорема 1.
Пусть  – отражающая функция системы – отражающая функция системы 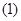 и и 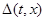 удовлетворяет следующему соотношению удовлетворяет следующему соотношению 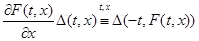 (3) (3)
Тогда система 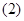 эквивалентна системе эквивалентна системе 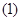 в смысле совпадения отражающих функций. в смысле совпадения отражающих функций.
Доказательство. Поскольку  отражающая функция системы отражающая функция системы 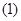 , то , то 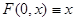  (4). Рассмотрим выражение (4). Рассмотрим выражение 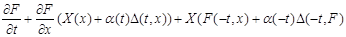
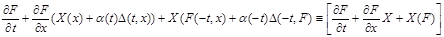 (равно (равно  т.к. т.к. 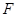 отражающая функция системы отражающая функция системы 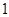 )+ )+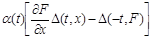 (равно (равно  по по 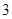 ) )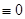 (4) (4)
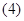 означает, что означает, что 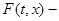 отражающая функция системы отражающая функция системы 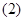 . Поскольку у систем . Поскольку у систем 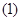 и и 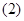 отражающие функции совпадают, то системы отражающие функции совпадают, то системы 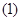 и и 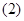 эквивалентны в смысле совпадения отражающих функций. эквивалентны в смысле совпадения отражающих функций.
Введём такие обозначения
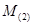 и и 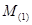 - семейства функций, являющиеся решениями систем - семейства функций, являющиеся решениями систем 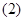 и и 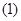 , соответственно , соответственно 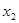 и и 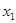 - решение систем - решение систем 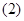 и и 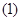 соответственно. соответственно.
Лемма 4
Пусть 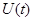 первый интеграл системы первый интеграл системы 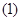 . Если выполнено соотношение . Если выполнено соотношение 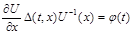 (5), где (5), где 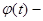 некоторая функция, то некоторая функция, то 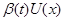 есть первый интеграл системы есть первый интеграл системы 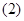 , где , где 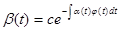 . .
Доказательство. Так как 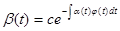 , то , то 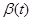 удовлетворяет уравнению удовлетворяет уравнению 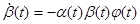 , так как , так как 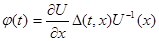 , то , то 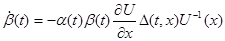 . Умножим обе части справа на . Умножим обе части справа на 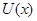 , получим , получим 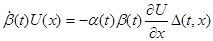 . Перенесём всё в левую часть и к левой части прибавим выражение . Перенесём всё в левую часть и к левой части прибавим выражение 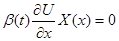 . Так как . Так как  - первый интеграл, получим - первый интеграл, получим 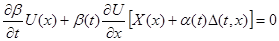 . Т.е. производная функции . Т.е. производная функции 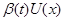 в силу системы в силу системы 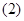 равна равна  , а это означает, что , а это означает, что 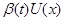 есть первый интеграл системы есть первый интеграл системы 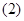 . Ч.т.д. . Ч.т.д.
Лемма 5
. Если  удовлетворяет следующему уравнению в частных производных: удовлетворяет следующему уравнению в частных производных:
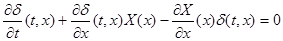 (6), где (6), где 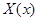 - правая часть системы (1), - правая часть системы (1), 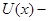 первый интеграл (2), то система (1) эквивалентна системе (2), у которой первый интеграл (2), то система (1) эквивалентна системе (2), у которой 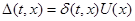 в смысле совпадения отражающей функции. в смысле совпадения отражающей функции.
Доказательство. Умножим (6) на скалярную функцию 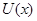 , получим: , получим:
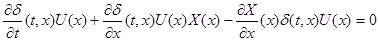 (7) (7)
Так как 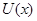 - первый интеграл системы (1), то - первый интеграл системы (1), то
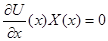 (8) (8)
Прибавим (7) к (8) и преобразуем, получим:  . Таким образом, . Таким образом, 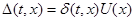 удовлетворяет теореме 1 (если удовлетворяет теореме 1 (если 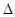 удовлетворяет удовлетворяет 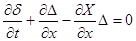 , то (1) эквивалентно (2) и значит, если , то (1) эквивалентно (2) и значит, если  , то система (2) эквивалентна системе (1). , то система (2) эквивалентна системе (1).
Теорема 2
Пусть 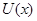 первый интеграл системы (1). Если первый интеграл системы (1). Если  , удовлетворяет уравнению (6), то система (1) эквивалентна системе (2). И если, кроме того , удовлетворяет уравнению (6), то система (1) эквивалентна системе (2). И если, кроме того 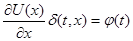 (9), где (9), где 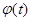 - некоторая функция ( - некоторая функция (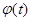 -может равняться const), тогда первый интеграл системы (2) выражается следующей формулой -может равняться const), тогда первый интеграл системы (2) выражается следующей формулой 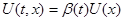 , где , где 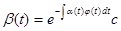 и и 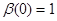 . .
Доказательство.
Доказательство 1-й части теоремы прямо  из леммы 3. из леммы 3.
Требуется доказать вторую часть теоремы. Найдём производную  в силу системы (2) в силу системы (2)
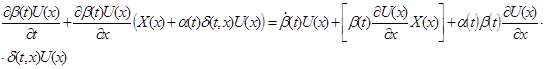 и и
обозначим её (*).
Выражение в […]=0, так как 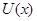 -первый интеграл системы (1), -первый интеграл системы (1), 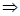 (*) преобразуется в следующее выражение (*) преобразуется в следующее выражение 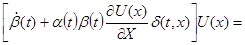
[так как 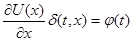 ]= ]=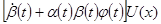 (**) (**)
Так как 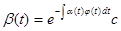 удовлетворяет уравнению удовлетворяет уравнению 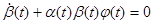 , то таким образом (**)=0, что и означает, что , то таким образом (**)=0, что и означает, что 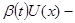 первый интеграл системы (2). Требование первый интеграл системы (2). Требование 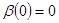 вытекает из леммы 2
. вытекает из леммы 2
.
Лемма
Пусть системы 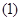 и и 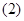 эквивалентны в смысле совпадения отражающих функций. Пусть эквивалентны в смысле совпадения отражающих функций. Пусть 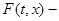 их отражающая функция и пусть их отражающая функция и пусть 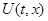 есть первый интеграл системы есть первый интеграл системы 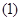 , тогда U , тогда U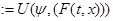 ,
, 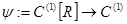 , , 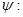 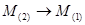 и и 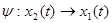 . .
Доказательство. Возьмём произвольное решение 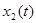 системы системы 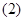 . Покажем, что на нём U
обращается в постоянную. . Покажем, что на нём U
обращается в постоянную.
Действительно, т. к. 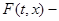 отражающая функция, то отражающая функция, то  . По определению функции . По определению функции 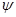 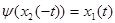 и т. к. и т. к. 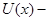 первый интеграл системы первый интеграл системы 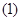 , то U , то U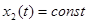 .
.
То, что U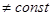 очевидно. Действительно, возьмём любую функцию
очевидно. Действительно, возьмём любую функцию 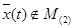 . Обозначим . Обозначим 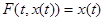 по свойству отражающей функции по свойству отражающей функции 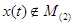 . .
Обозначим 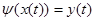 , так как , так как 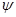 только функциям из только функциям из 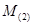 сопоставляет функции из сопоставляет функции из 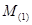 , то , то 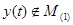 и по определению первого интеграла и по определению первого интеграла 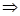 U
отлична от U
отлична от 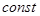 и обращается в и обращается в 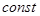 только вдоль решений системы только вдоль решений системы 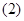 . А это и означает, что U
– первый интеграл системы . А это и означает, что U
– первый интеграл системы 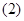 . .
(U
удовлетворяет лемме 2).
Лемма даёт понимание первого интеграла и взаимосвязи первых интегралов возмущённой и не возмущённой систем.
Заключение
В данной работе рассмотрены эквивалентные системы. Сформулирована теорема, которая говорит об эквивалентности систем. Сформулированы и доказаны леммы, которые применяются для доказательства теоремы.
Сформулированы определения дифференциальных систем, эквивалентных систем в смысле совпадения отражающих функций, первого интеграла, определение отражающей функции и общие свойства отражающей функции.
Список использованных источников
1. Мироненко В.И. Линейная зависимость функций вдоль решений дифференциальных уравнений. – Мн., Изд-во БГУ им. В.И. Ленина, 1981, 50 – 51 с.
2. Мироненко В.И. Отражающая функция и периодические решения дифференциальных уравнений. – Мн.: изд-во «Университетское», 1986, 11,17 – 19 с.
3. Мироненко В.В. Возмущения дифференциальных систем, не изменяющие временных симметрий. 2004 г.
|