| Курсова робота
"Вивчення систем, еквівалентних системам з відомим типом крапок спокою"
Реферат
Курсова робота складається з _____ сторінок, 3-х джерел.
Ключові слова: вложима система, з відомим типом крапок спокою, перший інтеграл диференціальної системи, функція, клас систем еквівалентних системі з відомим типом крапок спокою.
Метою курсової роботи є дослідження системи з відомим типом крапок спокою, знаходження першого інтеграла системи, застосування теореми про еквівалентність диференціальних систем.
Зміст
Введення
1. Визначення вложимої системи. Умови вложимості
2. Загальне рішення системи
3. Знаходження першого інтеграла диференціальної системи й умови його існування
4. Функція, що відбиває
5. Застосування теореми про еквівалентність диференціальних систем
Висновок
Список джерел
У курсовій роботі розглядається вложима система з відомим типом крапок спокою. Як відомо система є вложимою, якщо будь-який компонент цієї системи вложима, тобто система вложима тоді й тільки тоді, коли множина її рішень є підмножиною множини рішень деякої лінійної стаціонарної системи.
В 1-2 м пунктах розглядається вложима система, з відомим типом крапок спокою. Далі перевіряємо чи є x і y загальним рішенням нашої системи рівнянь.
В 3-м ми знаходимо перший інтеграл системи й перевіряємо виконання тотожності.
В 4-м пункті досліджуємо функції, що відбивають
В 5-м пункті застосовуємо теорему про еквівалентність диференціальних систем
Розглянемо диференціальну систему
 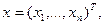  D. (1) D. (1)
Будемо називати i-ю компоненту x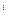 системи (1) вложимої, якщо для будь-якого рішення x (t) = (x системи (1) вложимої, якщо для будь-якого рішення x (t) = (x (t),…,x (t),…,x (t)),t (t)),t , цієї системи функція x , цієї системи функція x t t , є многочленом. У такий спосіб i-я компонента системи (1) вложима тоді й тільки тоді, коли для кожного рішення x (t) цієї системи існує лінійне стаціонарне рівняння виду , є многочленом. У такий спосіб i-я компонента системи (1) вложима тоді й тільки тоді, коли для кожного рішення x (t) цієї системи існує лінійне стаціонарне рівняння виду

  , (2) , (2)
для якого є рішенням. Загалом кажучи, порядок і коефіцієнти рівняння (2) залежать від вибору рішення є рішенням. Загалом кажучи, порядок і коефіцієнти рівняння (2) залежать від вибору рішення  . В окремому випадку, коли компонента . В окремому випадку, коли компонента  будь-якого рішення будь-якого рішення  системи (1) є одночасно й рішенням деякого, загального для всіх рішень системи (1) є одночасно й рішенням деякого, загального для всіх рішень  рівняння (2), компоненту рівняння (2), компоненту  системи (1) будемо називати сильно вложимої у рівняння (2). системи (1) будемо називати сильно вложимої у рівняння (2).
Розглянемо вложиму систему
 (1) (1)
(b>0 і а-постійні) із загальним рішенням
 , якщо з , якщо з 0; 0;
x=0, y=at+c , якщо з=0, де постійні з, з , якщо з=0, де постійні з, з , зі , зі зв'язані співвідношенням з зв'язані співвідношенням з (b+c (b+c +c +c ) =a ) =a , має два центри в крапках , має два центри в крапках  і і  . .  Рішення: Рішення:
Підставимо загальне рішення

у нашу систему (1) одержимо

 
=
 =c (c =c (c cosct-c cosct-c sinct) = sinct) =
a- 
Для стислості розпишемо знаменник і перетворимо
x +y +y
+b=
 

 
=a+c (c sinct+c sinct+c cosct) cosct)
a- 

Одержуємо, що x і y є загальним рішенням системи.
Розглянемо систему  = f (t, x), x= (x = f (t, x), x= (x ,…,x ,…,x ), (t,x) ), (t,x)  (1)
с безперервної в області в функцією f. Функція U (t, x), задана в деякої під області G області D, називається першим інтегралом системи
(1) в області G, якщо для будь-якого рішення x (t), t (1)
с безперервної в області в функцією f. Функція U (t, x), задана в деякої під області G області D, називається першим інтегралом системи
(1) в області G, якщо для будь-якого рішення x (t), t , системи (1), графік якого розташований в G функція U (t, x (t)), t , системи (1), графік якого розташований в G функція U (t, x (t)), t , постійна, тобто U (t, x (t)) залежить тільки від вибору рішення x (t) і не залежить від t. , постійна, тобто U (t, x (t)) залежить тільки від вибору рішення x (t) і не залежить від t.
Нехай V (t, x), V: G R
, є деяка функція. Похідній від функції V у силу системи (1) назвемо функцію V R
, є деяка функція. Похідній від функції V у силу системи (1) назвемо функцію V V V R,
обумовлену рівністю R,
обумовлену рівністю
V (t, x (t)) (t, x (t))  t t . .
Лема 1.
Для будь-якого рішення x (t), t , системи (1), графік якого розташований в G, має місце тотожність , системи (1), графік якого розташований в G, має місце тотожність
V  t t . .
Без доказу.
Лема 2.
Функція U (t, x), U: G R,
являє собою перший інтеграл системи (1) тоді й тільки тоді, коли похідна U R,
являє собою перший інтеграл системи (1) тоді й тільки тоді, коли похідна U у силу системи (1) тотожно в G звертається в нуль. у силу системи (1) тотожно в G звертається в нуль.
Необхідність. Нехай U (t, x) є перший інтеграл системи (1). Тоді для будь-якого рішення x (t) цієї системи, застосовуючи лему 1 будемо мати тотожності
U  
Звідки при t=t одержимо рівність U одержимо рівність U (t (t справедливе при всіх значеннях t справедливе при всіх значеннях t і x (t і x (t ). Необхідність доведена. ). Необхідність доведена.
Достатність. Нехай тепер U при всіх (t, x) при всіх (t, x)  Тоді для будь-якого рішення x (t) системи (1) на підставі леми 1 будемо мати тотожності Тоді для будь-якого рішення x (t) системи (1) на підставі леми 1 будемо мати тотожності

а з ним і достатність.
З визначення першого інтеграла треба, що постійна на G функція також є першим інтегралом системи (1). Перший інтеграл U (t, x) будемо називати на G, якщо при всіх (t, x)  виконується нерівність. виконується нерівність.

Функцію U (x) будемо називати стаціонарним першим інтегралом
системи (1), якщо вона не залежить від t і є першим інтегралом системи (1).
Знайдемо перший інтеграл нашої системи:

Піднесемо до квадрата й виразимо з

y




Покладемо  , одержимо , одержимо





Перевіримо, що функція   - це перший інтеграл системи (1), тобто перевіримо виконання тотожності - це перший інтеграл системи (1), тобто перевіримо виконання тотожності  (2) (2)
Знайдемо похідні по t, x, y
  
 
   
 
Після вище зроблених перетворень одержуємо, що функція   - це перший інтеграл системи (1), 2) Покладемо - це перший інтеграл системи (1), 2) Покладемо  , тобто , тобто  , де , де  , Q , Q 
3) Перевіримо виконання тотожності:
 (3), де (3), де 
Перетворимо (3).
 [у нашім випадку [у нашім випадку  ] = ] =
 
  = =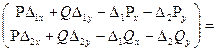
[з огляду на всі зроблені позначення] =
=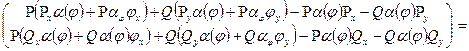
=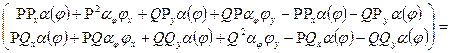
=
[через те, що  котре у свою чергу як ми вже показали їсти тотожний нуль] котре у свою чергу як ми вже показали їсти тотожний нуль] 
Таким чином, тотожність (3) щире.

4.
Функція, що відбиває
Визначення. Розглянемо систему
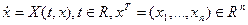 (5) (5)
вважає, що права частина якої безперервна й має безперервні частки похідні по 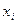 . Загальне рішення у формі Коші позначений через . Загальне рішення у формі Коші позначений через  ). Через ). Через  позначимо інтервал існування рішення позначимо інтервал існування рішення 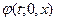 . Нехай . Нехай

функцією, що
відбиває, системи (5) назвемо функцію 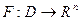 , обумовлену формулою , обумовлену формулою
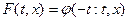
Для функції, що відбиває, справедливі властивості:для будь-якого рішення 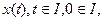 системи (5) вірна тотожність системи (5) вірна тотожність
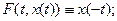
для функції, що відбиває, F будь-якої системи виконані тотожності
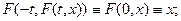
3) функція  буде функцією, що відбиває, системи (5) тоді й тільки тоді, коли вона задовольняє системі рівнянь у частинних похідних буде функцією, що відбиває, системи (5) тоді й тільки тоді, коли вона задовольняє системі рівнянь у частинних похідних
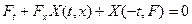
і початковій умові
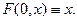
Одержуємо 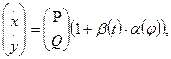 де де  - будь-яка непарна безперервна функція. - будь-яка непарна безперервна функція.
Поряд з диференціальною системою 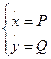 (1) розглянемо обурену систему (1) розглянемо обурену систему (2), де (2), де  - будь-яка безперервна непарна функція. Відомо по [3], що диференціальна система - будь-яка безперервна непарна функція. Відомо по [3], що диференціальна система  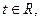  (3) еквівалентна обуреній системі (3) еквівалентна обуреній системі 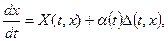 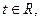 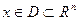 (4), де (4), де  безперервна скалярна непарна функція задовольняючому рівнянню безперервна скалярна непарна функція задовольняючому рівнянню 
Тому що вище вже показано, що функція  де де  {є перший інтеграл} задовольняє цьому рівнянню, те справедлива наступна теорема. {є перший інтеграл} задовольняє цьому рівнянню, те справедлива наступна теорема.
Теорема 1.
Система 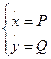 (1) еквівалентна системі (1) еквівалентна системі 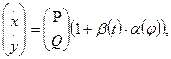 (2) у змісті збігу функції, що відбиває. (2) у змісті збігу функції, що відбиває.
Тому що система 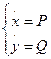 (1) має дві особливі крапки, у кожній з яких перебуває центр, те й система (1) має дві особливі крапки, у кожній з яких перебуває центр, те й система 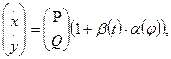 (2) має центри в цих крапках. (2) має центри в цих крапках.
У даній курсовій роботі розглянута вложима система з відомим типом крапок спокою, перевірене задоволення загального рішення нашій системі, знайдені перший інтеграл і перевірений виконання тотожності, потім за допомогою теореми 1 доведена еквівалентність диференціальних систем. Сформульовано визначення вложимої системи, першого інтеграла, що відбиває функції й загальні властивості функції, що відбиває. Сформульована теорема за допомогою якої ми довели еквівалентність нашої системи з диференціальною системою.
1. Мироненко В.І. Лінійна залежність функцій уздовж рішень диференціальних рівнянь. - К., 2001.
2. Мироненко В.І. Функція, що відбиває, і періодичні рішення диференціальних рівнянь. - К., 2004.
3. Мироненко В.І. Збурювання диференціальних систем, що не змінюють тимчасових симетрій. - К., 2004 р.
|