Министерство образования Республики Беларусь
Учреждение образования
"Гомельский государственный университет им. Ф. Скорины"
Математический факультет
Кафедра МПМ
Методика введения понятия производной функции
Реферат
Исполнитель:
Студентка группы М-33 Бондорчук А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Лебедева М.Т.
Гомель 2007
Содержание
Введение
1. Образовательные цели изучения производной функции
2. Различные подходы к введению понятия производной функции в курсе средней школы
3. Методическая схема изучения производной
4. Изучение приложения производной в курсе школьной математики
Заключение
Литература
Цель изучения курса алгебры и начала анализа в 10-11 в.в. систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовки необходимого апорта для изучения геометрии и физики.
Курс характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началом анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения: уровень строгости изложения определяется с учётом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах.
При изучении темы "Производная" проявляются известные трудности, связанные с осуществлением предельных переходов. Важно поэтому придать изложению возможно более наглядный и конкретный характер.
Включённые в курс сведения о пределах имеют вспомогательный характер, они не обходимы для вывода формул производных. Основное внимание должно быть уделено не формальному применению теорем о пределах, а сознательному проведению предельных переходов для приближённого вычисления значений конкретных функций и их приращений. Многочлены невысоких степеней и их частных -наиболее простой объект для иллюстрации идеи предельного перехода.
Определению производной функции как предела разностного отношения предшествует рассмотрению особенностей поведения графиков гладких функций, приводящее к понятию касательной. Производная функции появляется сначала как тангенс угла наклона касательной к оси абсцисс. Тем самым с понятием производной на первом этапе связывается наглядный образ – касательная. Предельные переходы появляются как средство вычисления производной.
При изучении применения производной существенная роль отводится наглядным представлениям о производной. Опора на геометрический и механический смысл делают интуитивно ясными критерии возрастания и убывания функций, признаки максимума минимума.
Решение тестовых задач физического, геометрического и практического содержания с применением производной позволяет учащимся ознакомиться со всеми этапами решения прикладных задач: составление математической модели (перевод задачи на язык функций), решение полученной задачи средствами математического анализа, и наконец, интерпретация полученного решения в терминах исходной задачи.
Различные подходы к введению производной определяются логической связью этого понятия с более общим понятием предела функции в точке.
Логический подход при введении производной в качестве базисного понятия использует определение предела функции в точке. Так в учебных программах по математике 1968 года, используя этот подход, определяли это понятие: 1) исходя из арифметического толкования предела функции (определение по Коши или на языке абсолютной погрешности):

2) исходя из операции предела функции в точке через окрестности (топологическое): a- предельная точка множества E, т.е. a- предельная точка множества E, т.е.

В действующих школьных программах по математике при введении производной функции используют исторический подход, т.е. первоначально формируются понятия производной, и только затем, как обобщение, понятие предела функции. При таком подходе большое внимание уделяется практическим аспектам изучения производной.
I.Привести подводящую задачу, раскрывающую физический смысл понятия производной:
свободное падение тела, которое не является равномерным. Охарактеризуем скорость падения в каждый данный момент времени t , т.е. введём понятие мгновенной скорости свободного падения тела. Известно, что средняя скорость определяется отношением  , причём чем меньше значение , причём чем меньше значение  , тем менее "заметно" изменение средней скорости падения. При , тем менее "заметно" изменение средней скорости падения. При  , отношение , отношение  стремится к значению мгновенной скорости. Таким образом мгновенная скорость характеризует скорость изменения пути стремится к значению мгновенной скорости. Таким образом мгновенная скорость характеризует скорость изменения пути  в момент времени t. в момент времени t.
В общем случае, с любым реальным процессом может быть связана задача:
Пусть  -параметр данного процесса, зависимости от x ; найти скорость изменения параметра -параметр данного процесса, зависимости от x ; найти скорость изменения параметра  в момент, когда в момент, когда 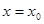 . Решение задачи сводится к нахождению отношения приращения параметра . Решение задачи сводится к нахождению отношения приращения параметра 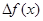 , соответствующую приращению , соответствующую приращению  . .
II.Сформулировать определение понятия производной.
Так как в определении отсутствует понятие предела, то первоначально следует сформировать у учащихся понятие приращения как изменения и аргумента и функции.
Например:

После рассмотрения геометрического смысла производной вводим определение:
Производной функции в точке 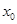 называется число, к которому стремится разностное отношение: называется число, к которому стремится разностное отношение:
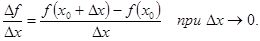
Полезен небольшой анализ формулировки определения, позволяющий чётче выделить признаки данного понятия: 1) число, 2) к которому стремится разностное отношение 
3) при 
Закреплению определения производной способствует вопрос: "Как найти производную функции  в точке в точке 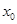 ?", ответ на который может быть дан в форме алгоритма: 1) значению ?", ответ на который может быть дан в форме алгоритма: 1) значению 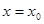 придаём приращение придаём приращение 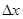 ; 2) находим приращение функции ; 2) находим приращение функции  в точке в точке 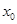  ; 3) составляем разностное соотношение; 4) находим число ; 3) составляем разностное соотношение; 4) находим число  (если такое число существует), к которому стремится (если такое число существует), к которому стремится  при при 
III
. Конкретизировать понятие производной (путём вычисления производной по определению: выяснение её геометрического смысла, графическое отыскание производной)
Первый пример на выяснение производной полезно выполнить на двух уровнях: а) 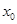 задано конкретным числом; б) задано конкретным числом; б) 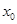 берётся в общем виде. берётся в общем виде.
Например: Дана функция  . Найти её производную в точке: а) x=2; б) . Найти её производную в точке: а) x=2; б)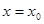
а) Придадим приращение 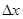 в точке х=2, новое (приращённое) значение аргумента –(2+ в точке х=2, новое (приращённое) значение аргумента –(2+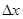 ). Найдём приращение функции: ). Найдём приращение функции:
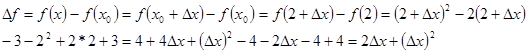
Вычислим разность отношения

Оно стремится к 2 при 
б)  , приращённое значение аргумента : , приращённое значение аргумента : 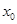 + +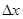
 . .
Составим разностные отношение: 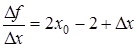 , которые при , которые при  стремится к числу стремится к числу  . .
Для конкретизации понятия производной может быть использован графический метод, суть которого в следующем:
1) На примере функции покажите, что разностное отношение  есть функция с аргументом есть функция с аргументом  . Охарактеризуйте эту функцию. Обратимся к рассмотренному примеру: . Охарактеризуйте эту функцию. Обратимся к рассмотренному примеру:
 , ,  , , 
Наша функция возрастающая, т.е. если
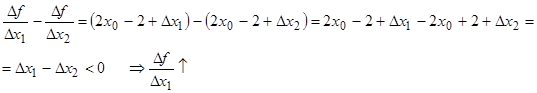
2) Постройте график функции  и с его помощью покажите число, к которому стремится отношение и с его помощью покажите число, к которому стремится отношение  при при  . Пусть . Пусть
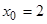 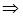 

3) Мотивировать необходимость теорем о вычислении производной, сформулировать и доказать эти теоремы.
4) Рассмотреть приложение производной.
Понятие непрерывной функции
Остановимся на понятии непрерывной функции: функция  стремится к числу стремится к числу 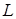 при при  ( ( ), если разность ), если разность 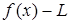 сколь угодно мала, т.е. сколь угодно мала, т.е.  становится меньше любого фиксированного становится меньше любого фиксированного  при уменьшении при уменьшении  . Нахождение числа . Нахождение числа 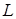 по функции по функции  называется предельным переходом. называется предельным переходом.
Этим названием уже пользовались, давая определения производной. Предельный переход – новая операция для нахождения неизвестных величин. Так, например, функция  называется непрерывной в точке
x
0
, если называется непрерывной в точке
x
0
, если 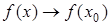 при при  или или
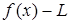 = = . .
В учебнике "Алгебры и начала анализа 10-11 класс" формулируются правила новой операции:
1) Если функция  непрерывна в точке непрерывна в точке  , то , то 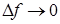 при при 
2) Если функция  имеет производную в точке имеет производную в точке  , то: , то: 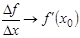 при при 
3) Пусть  , , 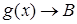 при. при.  Тогда при Тогда при  : :
а) 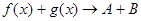 ; ;
б)  ; ;
в)  , если , если  . .
Метод интервалов
Приложения производной начинаются с рассмотрения приложения непрерывной функции: "Если на интервале  функция функция  непрерывна и не обращается в нуль, то на этом интервале она сохраняет постоянный знак! " Эта теорема применяется в решении неравенств методом интервалов. В более "сильных" классах можно заменить нахождение знака данной функции на каждом из интервалов проведением кривой знаков ", которая берет свое начало в правом верхнем углу, если знак коэффициента при старшей степени непрерывна и не обращается в нуль, то на этом интервале она сохраняет постоянный знак! " Эта теорема применяется в решении неравенств методом интервалов. В более "сильных" классах можно заменить нахождение знака данной функции на каждом из интервалов проведением кривой знаков ", которая берет свое начало в правом верхнем углу, если знак коэффициента при старшей степени  положителен, и в правом нижнем углу в противном случае (вспомнить аналогию с расположением ветвей параболы для функции положителен, и в правом нижнем углу в противном случае (вспомнить аналогию с расположением ветвей параболы для функции  ). ).
Например: решить неравенство
 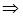  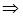 

Ответ: 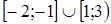 . .
Исследование свойств функции с помощью производной
Рассматриваются примеры разрывной функции:  , непрерывной, но не дифференцируемой в точке, функции , непрерывной, но не дифференцируемой в точке, функции 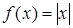 . .
При исследовании свойств функции с помощью производной опираются на такие известные теоремы математического анализа, как теоремы Лагранжа, Ферма и Вейерштрасса. Формула Лагранжа как иллюстрация геометрического смысла производной приводится в пункте 19 "Касательная к графику функции" и, немного позже, с ее применением формулируется достаточные признаки возрастания и убывания функции:
 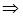  ; ;  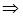 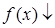 , т.к. , т.к.  , ,
где  - формула Лагранжа. - формула Лагранжа.
Методическая схема изучения достаточных признаков возрастания и убывания функции:
· поставить учебную проблему;
· подвести учащихся к формулировке признака с помощью геометрической иллюстрации;
· сформулировать признак, привести краткую запись его условия и заключения.
· привести доказательство признака с помощью формулы Лагранжа;
· закрепить доказательство путем выделения в нем составляющих шагов.
Например, подведение учащихся к формулировке признака возрастания функции конкретно- индуктивным методом можно осуществить следующим образом, обращаясь к учащимся, учитель говорит: "Можно ли охарактеризовать поведение функции с помощью производной? ". Рассмотрим рисунок


Как ведет себя функция  ? ?
Здесь приведен график функции, которая в каждой точке промежутка (a,b) имеет положительную производную. Что можно сказать о поведении функции на данном промежутке? Высказывается предположение, что функция возрастает. Справедливо ли это? Для ответа на этот вопрос приводятся примеры других функций, производная которых положительна на некотором промежутке:
 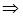  , ,  ; ;
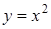 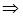  , ,  . .
На основе индуктивного обобщения рассмотренных примеров формулируется соответствующий признак.
Т.о. методическая схема изучения достаточных признаков возрастания и убывания функции:
· поставить учебную проблему;
· подвести учащихся к формулировке признака с помощью геометрической иллюстрации;
· сформулировать признак, привести краткую запись его условия и заключения.
· привести доказательство признака с помощью формулы Лагранжа;
· закрепить доказательство путем выделения в нем составляющих шагов.
1. К.О. Ананченко "Общая методика преподавания математики в школе", Мн., "Унiверсiтэцкае",1997г.
2.Н.М.Рогановский "Методика преподавания в средней школе", Мн., "Высшая школа", 1990г.
3.Г.Фройденталь "Математика как педагогическая задача",М., "Просвещение", 1998г.
4.Н.Н. "Математическая лаборатория", М., "Просвещение", 1997г.
5.Ю.М.Колягин "Методика преподавания математики в средней школе", М., "Просвещение", 1999г.
6.А.А.Столяр "Логические проблемы преподавания математики", Мн., "Высшая школа", 2000г.
|