Вариант №10 Задание №1
Определить реакции опор горизонтальной балки от заданной нагрузки
Дано:

Решение:
Рассмотрим равновесие балки АВ
(рис. 1).
К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции.
Активные
(заданные) силы:
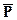 , ,  , , 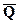 , пара сил с моментом М
, где , пара сил с моментом М
, где
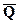 - сосредоточенная сила, заменяющая действие распределенной вдоль отрезка АС нагрузки интенсивностью - сосредоточенная сила, заменяющая действие распределенной вдоль отрезка АС нагрузки интенсивностью  . .
Величина
 . .
Линия действия силы 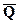 проходит через середину отрезка СD. проходит через середину отрезка СD.
Силы реакции
(неизвестные силы):
 , ,  , ,  - реакции жесткой заделки. - реакции жесткой заделки.
Для полученной плоской произвольной системы сил можно составить три уравнения равновесия:
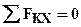 , ,  , ,  . .
Задача является статически определимой, так как число неизвестных сил ( , , , ,  ) - три - равно числу уравнений равновесия. ) - три - равно числу уравнений равновесия.
Поместим систему координат XY
в точку А, ось AX
направим вдоль балки. За центр моментов всех сил выберем точку В.
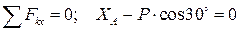 (1) (1)
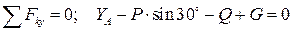 (2) (2)
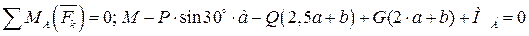 (3) (3)
Решая систему уравнений, найдем  , ,  : :
Из (1):

Из (2):

Из (3):
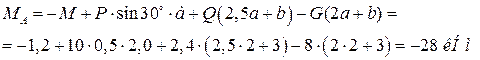
Модуль реакции опоры А
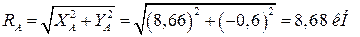
Для проверки правильности решения составляем уравнение моментов всех сил относительно точки В:



Ответ:  . .
Вариант №10 Задание №2

Определение реакции опор и давления
в промежуточном шарнире составной
конструкции.
Дано:

Решение:
Решение:
Рис. 1
Рассмотрим равновесие всей конструкции (рис. 1). К ней приложены:
активные силы
 пара сил с моментом М, пара сил с моментом М,
где 
силы реакции:
 , ,  , - заменяют действие шарнирно-неподвижной опоры А; , - заменяют действие шарнирно-неподвижной опоры А;
 , ,  - реакции шарнира С; - реакции шарнира С;
 - заменяет действие шарнирно-неподвижной опоры В - заменяет действие шарнирно-неподвижной опоры В
 Расчетная схема Расчетная схема
Рис. 2
Решение.
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня АС и раму в целом. Проведем координатные оси  и изобразим действующие на стержень силы: сосредоточенный момент М и реакции шарнира С и изобразим действующие на стержень силы: сосредоточенный момент М и реакции шарнира С 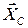 и и 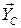 , реакции опоры А ( , реакции опоры А ( и и  ), равномерно распределенная нагрузка, которую заменяем силой ), равномерно распределенная нагрузка, которую заменяем силой 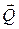 , приложенной в середине участка длиной а
(численно , приложенной в середине участка длиной а
(численно  ), силы ), силы и и  , реакции шарнира С ( , реакции шарнира С (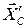 и и 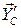 ), направленные противоположно реакциям ), направленные противоположно реакциям 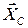 и и 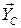 , составляющие , составляющие  , ,  реакции опоры В. Для полученной плоской системы сил составляем шесть уравнений равновесия: реакции опоры В. Для полученной плоской системы сил составляем шесть уравнений равновесия:
 (1) (1)  (2) (2)
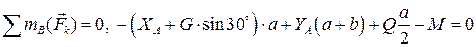 (3) (3)
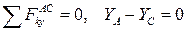 (4) (4)
 (5) (5)
 (6) (6)
  Из уравнения (2) находим Из уравнения (2) находим 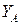 : :
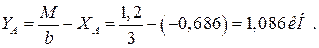
Из уравнения (3) находим YА
:
 
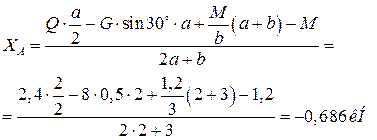
Из уравнения (1) находим ХС
:
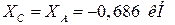
Из уравнения (4) находим YС
:
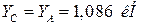
Из уравнения (5) находим XВ
:

Из уравнения (6) находим YВ
:

Проверка: 
Ответ:
ХА
= - 0,686 кН, YA
= 1,086 кН, ХС
= - 0,686 кН,
YС
= 1,086 кН, ХB
= 0,986 кН, YB
= 1,986 кН. Знаки указывают на то, что силы направлены так, как показано на рисунке, кроме силы  и и 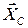 . .

Вариант №10 Задание №3
Кинематика точки.
Дано: 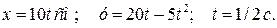
Решение:
Для определения уравнения траектории точки исключим из заданных уравнений движения время 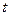 . .

Определим местоположения точки при t = 1/2 с.

Скорость точки найдем по ее проекциям на координатные оси:

 ; ;

и при 
 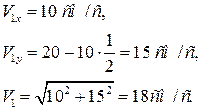 (2) (2)
Аналогично найдем ускорение точки:


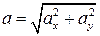
и при 


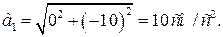 (3) (3)
Касательное ускорение найдем, дифференцируя по времени равенство
 . .
Получим
 (4) (4)
Числовые значения всех величин, входящих в правую часть выражения (4), определены и даются равенствами (2) и (3). Получаем
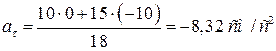 . .
Нормальное ускорение точки
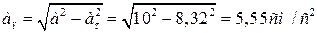 . .
Радиус кривизны траектории
 . .
Вариант №10 Задание №4
 Дано: Дано:
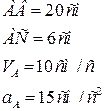
Решение:
1). Определение скоростей точек и угловой скорости АВ.
Вектор скорости  направлен вдоль направляющих ползуна В. Модуль направлен вдоль направляющих ползуна В. Модуль  найдем, применив теорему о проекциях скоростей на прямую АВ. найдем, применив теорему о проекциях скоростей на прямую АВ.

Для определения скорости 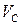 строим мгновенный центр скоростей (МЦС Р) который находится на пересечении перпендикуляров восстановленных к векторам строим мгновенный центр скоростей (МЦС Р) который находится на пересечении перпендикуляров восстановленных к векторам  в точках А и В. Направление в точках А и В. Направление  определяем направлением вектора определяем направлением вектора  . Вектор скорости . Вектор скорости  направлен перпендикулярно РС в сторону направлен перпендикулярно РС в сторону  , и численно , и численно 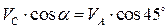 , ,
где 
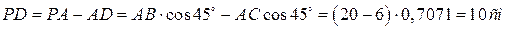

 . .
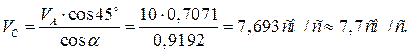
Угловая скорость звена АВ:

2) Определение ускорений точек звена и углового ускорения звена.
Согласно теореме об ускорениях точек плоской фигуры
 , где , где 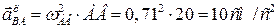 - вектор направлен от В к А. Вектор ускорения - вектор направлен от В к А. Вектор ускорения 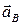 направлен вдоль направляющих ползуна В. Вектор направлен вдоль направляющих ползуна В. Вектор 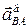 перпендикулярен прямой АВ. перпендикулярен прямой АВ.
Спроектируем векторное уравнение  на ось х
: на ось х
:
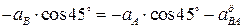 , откуда , откуда
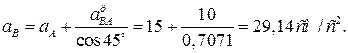
Спроектируем векторное уравнение на ось у
:
 , откуда , откуда
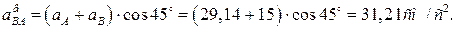
Угловое ускорение 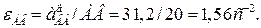
Определяем ускорение точки С:
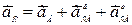 . .
Здесь
 ; ;
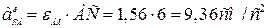
Модуль ускорения точки С находим способом проекций:
 . .
Вычисляем
 ; ;
 . .
Итак,

|