Сортировка данных в массиве
В этом разделе будет рассмотрен знаменитый алгоритм ''быстрой'' сортировки, по праву считающийся самым быстрым среди неспециализированных алгоритмов сортировки. Для сравнения мы также рассмотрим один из алгоритмов сортировки, имеющих более низкую эффективность, но и более простых алгоритмов – сортировку вставками.
Сортировка вставками
Сортировка вставками похожа на процесс тасования карточек с именами. Регистратор заносит каждое имя на карточку, а затем упорядочивает карточки по алфавиту, вставляя карточку в верхнюю часть стопки в подходящее место. Опишем этот процесс на примере нашего пятиэлементного списка A = 50, 20, 40, 75, 35 (рисунок 1).
В функцию InsertionSort передается массив A и длина списка n. Рассмотрим i-ый проход (1<i<n-1). Подсписок от A[0] до A[i-1] уже отсортирован по возрастанию. В качестве вставляемого (TARGET) выберем элемент A[i] и будем продвигать его к началу списка, сравнивая с элементами A[i-1], A[i-2] и т.д. Просмотр заканчивается на элементе A[j], который меньше или равен TARGET, или находится в начале списка (j = 0). По мере продвижения к началу списка каждый элемент сдвигается вправо (A[j] = A[j-1]). Когда подходящее место для A[i] будет найдено, этот элемент вставляется в точку j.

Рис. 1
// Сортировка вставками упорядочивает подсписки A[0]...A[i], 1 <= i <= n-1. Для
// каждого i A[i] вставляется в подходящую позицию A[j]
template <class T>
void InsertionSort(T A[], int n)
{
int i, j;
T temp;
// i определяет подсписок A[0]...A[i]
for (i=1; i<n; i++)
{
// индекс j пробегает вниз по списку от A[i] в процессе
// поиска правильной позиции вставляемого значения
j = i;
temp = A[i];
// обнаружить подходящую позицию для вставки, сканируя подсписок,
// пока temp < A[j-1] или пока не встретится начало списка
while (j > 0 && temp < A[j-1])
{
// сдвинуть элементы вправо, чтобы освободить место для вставки
A[j] = A[j-1];
j--;
}
// точка вставки найдена; вставить temp
A[j] = temp;
}
}
|
Вычислительная эффективность сортировки вставками
Сортировка вставками требует фиксированного числа проходов. На n-1 проходах вставляются элементы от A[1] до A[n-1]. На i-ом проходе вставки производятся в подсписок A[0]–A[i] и требуют в среднем i/2 сравнений. Общее число сравнений равно
| 1/2 + 2/2 + 3/2 + ... + (n-2)/2 + (n-1)/2 = n(n-1)/4 |
В отличие от других методов, сортировка вставками не использует обмены. Сложность алгоритма измеряется числом сравнений и равна O(n2). Наилучший случай – когда исходный список уже отсортирован. Тогда на i-ом проходе вставка производится в точке A[i], а общее число сравнений равно n-1, т.е. сложность составляет O(n). Наихудший случай возникает, когда список отсортирован по убыванию. Тогда каждая вставка происходит в точке A[0] и требует i сравнений. Общее число сравнений равно n(n-1)/2, т.е. сложность составляет O(n2).
В принципе, алгоритм сортировки вставками можно значительно ускорить. Для этого следует не сдвигать элементы по одному, как это продемонстрировано в приведенном выше примере, а находить нужный элемент с помощью бинарного поиска, описанного в предыдущем номере (то есть, в цикле разбивая список на две равные части, пока в списке не останется один-два элемента), а для сдвижки использовать функции копирования памяти. Такой подход дает довольно высокую производительность на небольших массивах. Основным узким местом в данном случае является само копирование памяти. Пока объем копируемых данных (около половины размера массива) соизмерим с размером кэша процессора 1 уровня, производительность этого метода довольно высока. Но из-за множественных непроизводительных повторов копирования, этот способ менее предпочтителен, чем метод «быстрой» сортировки, описанный в следующем разделе. Этот же метод можно рекомендовать в случае относительно статичного массива, в который изредка производится вставка одного-двух элементов.
«Быстрая» сортировка
Итак, мы рассмотрели алгоритм сортировки массива, имеющий сложность порядка O(n2). Алгоритмы, использующие деревья (турнирная сортировка, сортировка посредством поискового дерева), обеспечивают значительно лучшую производительность O(n log2n). Несмотря на то, что они требуют копирования массива в дерево и обратно, эти затраты покрываются за счет большей эффективности самой сортировки.
Широко используемый метод пирамидальной сортировки также обрабатывает массив «на месте» и имеет эффективность O(n log2n). Однако «быстрая» сортировка, которую изобрел К.Хоар, для большинства приложений превосходит пирамидальную сортировку и является самой быстрой из известных до сих пор.
Описание «быстрой» сортировки
Как и для большинства алгоритмов сортировки, методика «быстрой» сортировки взята из повседневного опыта. Чтобы отсортировать большую стопку алфавитных карточек по именам, можно разбить ее на две меньшие стопки относительно какой-нибудь буквы, например K. Все имена, меньшие или равные K, идут в одну стопку, а остальные – в другую.
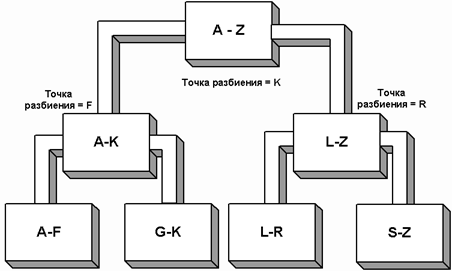
Рис.2
Затем каждая стопка снова делится на две. Например, на рисунке 2 точками разбиения являются буквы F и R. Процесс разбиения на все меньшие и меньшие стопки продолжается.
В алгоритме «быстрой» сортировки применяется метод разбиения с определением центрального элемента. Так как мы не можем позволить себе удовольствие разбрасывать стопки по всему столу, как при сортировке алфавитных карточек, элементы разбиваются на группы внутри массива. Рассмотрим алгоритм «быстрой» сортировки на примере, а затем обсудим технические детали. Пусть дан массив, состоящий из 10 целых чисел:
| A = 800, 150, 300, 600, 550, 650, 400, 350, 450, 700 |
Фаза сканирования
Массив имеет нижнюю границу, равную 0 (low), и верхнюю границу, равную 9 (high). Его середина приходится на 4 элемент (mid). Первым центральным элементом является A[mid] = 550. Таким образом, все элементы массива A разбиваются на два подсписка: Sl и Sh. Меньший из них (Sl) будет содержать элементы, меньшие или равные центральному. Подсписок Sh будет содержать элементы большие, чем центральный. Поскольку заранее известно, что центральный элемент в конечном итоге будет последним в подсписке Sl, мы временно передвигаем его в начало массива, меняя местами с A[0] (A[low]). Это позволяет сканировать подсписок A[1]--A[9] с помощью двух индексов: scanUp и scanDown. Начальное значение scanUp соответствует индексу 1 (low+1). Эта переменная адресует элементы подсписка Sl. Переменная scanDown адресует элементы подсписка Sh и имеет начальное значение 9 (high). Целью прохода является определение элементов для каждого подсписка.

Рис.3
Оригинальность «быстрой» сортировки заключается во взаимодействии двух индексов в процессе сканирования списка. Индекс scanUp перемещается вверх по списку, а scanDown – вниз. Мы продвигаем scanUp вперед и ищем элемент A[scanUp] больший, чем центральный. В этом месте сканирование останавливается, и мы готовимся переместить найденный элемент в верхний подсписок. Перед тем, как это перемещение произойдет, мы продвигаем индекс scanDown вниз по списку и находим элемент, меньший или равный центральному. Таким образом, у нас есть два элемента, которые находятся не в тех подсписках, и их можно менять местами.
| Swap (A[scanUp], A[scanDown]); // менять местами партнеров |
Этот процесс продолжается до тех пор, пока scanUp и scanDown не зайдут друг за друга (scanUp = 6, scanDown = 5). В этот момент scanDown оказывается в подсписке, элементы которого меньше или равны центральному. Мы попали в точку разбиения двух списков и указали окончательную позицию для центрального элемента. В нашем примере поменялись местами числа 600 и 450, 800 и 350, 650 и 400 (см. рисунок 4).
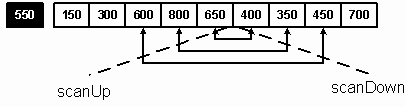
Рис.4
Затем происходит обмен значениями центрального элемента A[0] с A[scanDown]:
В результате у нас появляются два подсписка A[0] – A[5] и A[6] – A[9], причем все элементы первого подсписка меньше элементов второго, и последний элемент первого подсписка является его наибольшим элементом. Таким образом, можно считать, что после проделанных операций подсписки разделены элементом А[5] = 550 (рисунок 5). Если теперь отсортировать каждый подсписок по отдельности, то у нас получится полностью отсортированный массив. Заметьте, что по сути оба этих подсписка являются такими же массивами, как и исходный, поэтому к ним можно применить тот же самый алгоритм. Применение того же алгоритма к частям массива называется рекурсивной фазой.
Рекурсивная фаза
Одним и тем же методом обрабатываются два подсписка: Sl(A[0] – A[4]) и Sh(A[6] – A[9]). Элемент А[5] обрабатывать не надо, так как он уже находится на своем месте.
Тот же алгоритм применяется для каждого подсписка, разбивая эти подсписки на меньшие части, пока в подсписке не останется одного элемента или пока подсписок не опустеет.

Рис.5
Алгоритм QuickSort
Этот рекурсивный алгоритм разделяет список A[low]--A[high] по центральному элементу, который выбирается из середины списка
mid = (high + low) / 2;
pivot = A[mid];
|
После обмена местами центрального элемента с A[low], задаются начальные значения индексам scanUp = low + 1 и scanDown = high, указывающим на начало и конец списка, соответственно. Алгоритм управляет этими двумя индексами. Сначала scanUp продвигается вверх по списку, пока не превысит значение scanDown или пока не встретится элемент больший, чем центральный.
while (scanUp <= scanDown && A[scanUp] <= pivot)
scanUp++;
|
После позиционирования scanUp индекс scanDown продвигается вниз по списку, пока не встретится элемент, меньший или равный центральному.
while (pivot < A[scanDown])
scanDown--;
|
По окончании этого цикла (и при условии что scanUp < scanDown) оба индекса адресуют два элемента, находящихся не в тех подсписках. Эти элементы меняются местами.
| Swap(A[scanUp], A[scanDown]); |
Обмен элементов прекращается, когда scanDown становится меньше, чем scanUp. В этот момент scanDown указывает начало левого подсписка, который содержит меньшие или равные центральному элементы. Индекс scanDown становится центральным. Взять центральный элемент из A[low]:
| Swap(A[low], A[scanDown]); |
Для обработки подсписков используется рекурсия. После обнаружения точки разбиения мы рекурсивно вызываем QuickSort с параметрами low, mid-1 и mid+1, high. Условие останова возникает, когда в подсписке остается менее двух элементов, так как одноэлементный или пустой массив упорядочивать не нужно.
// Swap меняет местами элементы массива. Соответствующий тип данных
// должен поддерживать операцию «=».
template <class T>
void Swap(T & el1, T & el2)
{
T tmp = el1;
el1 = el2;
el2 = tmp;
}
// QuickSort принимает в качестве параметров массив
// и предельные значения его индексов
template <class T>
void QuickSort(T A[], int low, int high)
{
// локальные переменные, содержащие индекс середины - mid,
// центральный элемент и индексы сканирования
T pivot;
int scanUp, scanDown;
int mid;
// если диапазон индексов не включает в себя
// как минимум два элемента, завершить работу
if(high - low <= 0)
return;
else if(high - low == 1)
{
// если в подсписке два элемента, сравнить их между собой
// и поменять местами при необходимости
if(A[high] < A[low])
Swap(A[low], A[high]);
return;
}
// Рассчитать индекс середины и поместить значение соответствующего
// элемента массива в переменную pivot.
mid = (low + high)/2;
pivot = A[mid];
// Поменять местами центральный и начальный элементы списка.
Swap(A[mid], A[low]);
// Инициализировать индексы scanUp и scanDown.
scanUp = low + 1;
scanDown = high;
// Искать элементы, расположенные не в тех подсписках.
// Остановиться при scanDown < scanUp.
do
{
// Продвигаться вверх по первому подсписку. Остановиться,
// когда scanUp укажет на второй подсписок или если
// указываемый этим индексом элемент > центрального.
while(scanUp <= scanDown && A[scanUp] <= pivot)
scanUp++;
// Продвигаться вниз по второму подсписку. Остановиться,
// когда scanDown указжет на элемент >= центральному.
while(A[scanDown] > pivot)
scanDown--;
// Если индексы все еще в своих подсписках, то они указывают
// на два элемента, находящихся не в тех подсписках.
if(scanUp < scanDown)
{
// Поменять их местами
Swap(A[scanUp], A[scanDown]);
}
}
while(scanUp < scanDown);
// Скопировать элемент на который указывает точка разбиения
// в первый элемент первого подсписка, ...
A[low] = A[scanDown];
// а центральный элемент в точку разбиения
A[scanDown] = pivot;
// если первый подсписок (low...scanDown-1) имеет 2 или более
// элемента, выполнить для него рекурсивный вызов QuickSort
if(low < scanDown-1)
QuickSort(A, low, scanDown-1);
// если второй подсписок (scanDown+1...high) имеет 2 или более
// элемента, выполнить для него рекурсивный вызов QuickSort
if(scanDown+1 < high)
QuickSort(A, scanDown+1, high);
}
|
Вычислительная сложность «быстрой» сортировки
Общий анализ эффективности «быстрой» сортировки достаточно труден. Будет лучше показать ее вычислительную сложность, подсчитав число сравнений при некоторых идеальных допущениях. Допустим, что n – степень двойки, n = 2k (k = log2n), а центральный элемент располагается точно посередине каждого списка и разбивает его на два подсписка примерно одинаковой длины.
При первом сканировании производится n-1 сравнений. В результате создаются два подсписка размером n/2. На следующей фазе обработка каждого подсписка требует примерно n/2 сравнений. Общее число сравнений на этой фазе равно 2(n/2) = n. На следующей фазе обрабатываются четыре подсписка, что требует 4(n/4) сравнений, и т.д. В конце концов процесс разбиения прекращается после k проходов, когда получившиеся подсписки содержат по одному элементу. Общее число сравнений приблизительно равно
| n + 2(n/2) + 4(n/4) + ... + n(n/n) = n + n + ... + n = n * k = n * log2n |
Для списка общего вида вычислительная сложность «быстрой» сортировки равна O(n log2 n). Идеальный случай, который мы только что рассмотрели, фактически возникает тогда, когда массив уже отсортирован по возрастанию. Тогда центральный элемент попадает точно в середину каждого подсписка.
Если массив отсортирован по убыванию, то на первом проходе центральный элемент обнаруживается на середине списка и меняется местами с каждым элементом как в первом, так и во втором подсписке. Результирующий список почти отсортирован, алгоритм имеет сложность порядка O(n log2n).

Рис.6
Наихудшим сценарием для «быстрой» сортировки будет тот, при котором центральный элемент все время попадает в одноэлементный подсписок, а все прочие элементы остаются во втором подсписке. Это происходит тогда, когда центральным всегда является наименьший элемент. Рассмотрим последовательность 3, 8, 1, 5, 9.
На первом проходе производится n сравнений, а больший подсписок содержит n-1 элементов. На следующем проходе этот подсписок требует n-1 сравнений и дает подсписок из n-2 элементов и т.д. Общее число сравнений равно:
| n + n-1 + n-2 + ... + 2 = n(n+1)/2 - 1 |
Сложность худшего случая равна O(n2), т.е. не лучше, чем для сортировок вставками и выбором. Однако этот случай является патологическим и маловероятен на практике. В общем, средняя производительность «быстрой» сортировки выше, чем у всех рассмотренных нами сортировок.
Алгоритм QuickSort выбирается за основу в большинстве универсальных сортирующих утилит. Если вы не можете смириться с производительностью наихудшего случая, используйте пирамидальную сортировку – более устойчивый алгоритм, сложность которого равна O(n log2n) и зависит только от размера списка.
Сравнение алгоритмов сортировки массивов
Мы сравнили алгоритмы сортировки, испытав их на массивах, содержащих 4000, 8000, 10000, 15000 и 20000 целых чисел, соответственно. Время выполнения измерено в тиках (1/60 доля секунды). Среди всех алгоритмов порядка O(n2) время сортировки вставками отражает тот факт, что на i-ом проходе требуется лишь i/2 сравнений. Этот алгоритм явно превосходит все прочие сортировки порядка O(n2). Заметьте, что самую худшую общую производительность демонстрирует сортировка методом пузырька. Результаты испытаний показаны в таблице 1 и на рисунке 7.
Для иллюстрации эффективности алгоритмов сортировки в экстремальных случаях используются массивы из 20000 элементов, отсортированных по возрастанию и по убыванию. При сортировке методом пузырька и сортировке вставками выполняется только один проход массива, упорядоченного по возрастанию, в то время как сортировка посредством выбора зависит только от размера списка и производит 19999 проходов. Упорядоченность данных по убыванию является наихудшим случаем для пузырьковой, обменной и сортировки вставками, зато сортировка выбором выполняется, как обычно.
| n |
Обменная сортировка |
Сортировка выбором |
Пузырьковая сортировка |
Сортировка вставками |
| 4 000 |
12.23 |
17.30 |
15.78 |
5.67 |
| 8 000 |
49.95 |
29.43 |
64.03 |
23.15 |
| 10 000 |
77.47 |
46.02 |
99.10 |
35.43 |
| 15 000 |
173.97 |
103.00 |
223.28 |
80.23 |
| 20 000 |
313.33 |
185.05 |
399.47 |
143.67 |

Рис.7 Сравнение сортировок порядка O(n2)
| n |
Обменная сортировка |
Сортировка выбором |
Пузырьковая сортировка |
Сортировка вставками |
| 8 000 (упорядочен по возрастанию) |
185.27 |
185.78 |
0.03 |
0.05 |
| 8 000 (упорядочен по убыванию) |
526.17 |
199.00 |
584.67 |
286.92 |
В общем случае QuickSort является самым быстрым алгоритмом. Благодаря своей эффективности, равной O(n log2n), он явно превосходит любой алгоритм порядка O(n2). Судя по результатам испытаний, приведенных в следующей таблице, он также быстрее любой из сортировок порядка O(n log2n), рассмотренных нами в прошлом номере. Обратите внимание, что эффективность «быстрой» сортировки составляет O(n log2n) даже в экстремальных случаях. Зато сортировка посредством поискового дерева становится в этих случаях O(n2) сложной, так как формируемое дерево является вырожденным.
| n |
Турнирная сортировка |
Сортировка посредством дерева |
Пирамидальная сортировка |
"Быстрая" сортировка |
| 4 000 |
0.28 |
0.32 |
0.13 |
0.07 |
| 8 000 |
0.63 |
0.68 |
0.28 |
0.17 |
| 10 000 |
0.90 |
0.92 |
0.35 |
0.22 |
| 15 000 |
1.30 |
1.40 |
0.58 |
0.33 |
| 20 000 |
1.95 |
1.88 |
0.77 |
0.47 |
| 8 000 (упорядочен по возрастанию) |
1.77 |
262.27 |
0.75 |
0.23 |
| 8 000 (упорядочен по убыванию) |
1.65 |
275.70 |
0.80 |
0.28 |
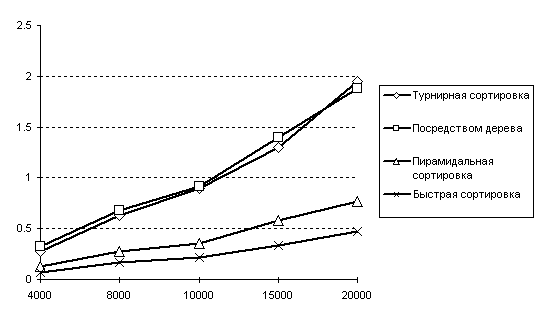
Рис.8 Сравнение сортировок порядка O(n log2n)
Сравнение сортировок
Эта программа осуществляет сравнение алгоритмов сортировки данных, представленных на рисунках 7 и 8. Здесь мы приводим только базовую структуру программы. Хронометраж производится с помощью функции TickCount, возвращающей число 1/60 долей секунды, прошедших с момента старта программы.
#include <iostream.h>
#include "arrsort.h"
// Перечислимый тип, описывающий начальное состояние массива данных.
enum Ordering {randomorder, ascending, descending};
// Перечислимый тип, идентифицирующий алгоритм сортировки.
enum SortType
{
SortTypeBegin,
exchange = SortTypeBegin,
selection,
bubble,
insertion,
tournament,
tree,
heap,
quick,
SortTypeEnd = quick
};
// копировать n-элементныймассив y вмассив x
void Copy(int *x, int *y, int n)
{
for (int i=0; i<n; i++)
*x++ = *y++;
}
// Общая сортирующая функция, которая принимает исходный массив
// с заданной упорядоченностью элементов и применяет указанный
// алгоритмсортировки.
void Sort(int a[], int n, SortType type, Ordering order)
{
long time;
cout << "Сортировка " << n;
// Вывести тип упорядоченности.
switch(order)
{
case random:
cout << " элементов. ";
break;
case ascending:
cout << " элементов, упорядоченных по возрастанию. ";
break;
case descending:
cout << " элементов, упорядоченных по убыванию. ";
break;
}
// засечьвремя
time = TickCount();
// Выполнить сортировку и вывести ее тип...
switch(type)
{
case exchange:
ExchangeSort(a, n);
cout << "Сортировкаобменом: ";
break;
case selection:
SelectionSort(a, n);
cout << "Сортировкавыбором: ";
break;
case bubble: . . . . . . .
case insertion: . . . . . . .
case tournament: . . . . . . .
case tree: . . . . . . .
case heap: . . . . . . .
case quick: . . . . . . .
}
// Подсчитать время выполнения в секундах.
time = TickCount() - time;
cout << time/60.0 << endl;
}
// Выполняет сортировку массива с n элементами,
// расположенных в порядке, определяемом параметром order.
void RunTest(int n, Ordering order)
{
int i;
int *a, *b;
SortType stype;
RandomNumber rnd;
// Выделить память для двух n-элементных массивов a и b.
a = new int [n];
b = new int [n];
// Определить тип упорядоченности данных.
if(order == randomorder)
{
// Заполнить массив b случайными числами.
for(i=0; i<n; i++)
b[i] = rnd.Random(n);
}
else
{
// Данные, отсортированные по возрастанию.
for(i=0; i<n; i++)
b[i] = i;
}
else
{
// данные, отсортированные по убыванию.
for(i=0; i<n; i++)
b[i] = n - 1 - i;
}
else
{
// Копировать данные в массив a. Поочередно выполнить сортировку для
// каждоготипа.
for(stype = SortTypeBegin; stype <= SortTypeEnd; stype = SortType(stype+1))
{
Copy(a, b, n);
Sort(a, n, stype, order);
}
}
// Удалить оба динамических массива.
delete [] a;
delete [] b;
}
// Отсортировать 4 000-, 8 000-, 10 000-, 15 000- и 20 000-элементный массивы,
// заполненные случайными числами.
// Затем сначала отсортировать 20 000-элементный массив, упорядоченный
// по возрастанию, а потом по убыванию.
void main(void)
{
int nelts[5] = {4000, 8000, 10000, 15000, 20000};
int = i;
cout.precision(3);
cout.setf(ios::fixed | ios::showpoint);
for(i= 0; i<5; i++)
RunTest(nelts[i], randomorder);
RunTest(20000, ascending);
RunTest(20000, descending);
|
|