| ПРОГНОЗИРОВАНИЕ КРИТИЧЕСКОГО ОБЪЕМА
Для массовых расчетов может быть рекомендован метод Лидерсена, возможности и точность которого, однако, не следует переоценивать. По методу Лидерсена критический объем рассчитывается с использованием корреляции:
 ,(5.17) ,(5.17)
где v
- парциальные вклады, значения которых, выраженные в кубических см3
/моль, приведены в табл. 5.2. Расчет достаточно прост и не требует дополнительного комментария.
ПРОГНОЗИРОВАНИЕ АЦЕНТРИЧЕСКОГО ФАКТОРА
Фактор ацентричности
был предложен в 1955 г. Питцером в качестве коррелирующего параметра, характеризующего ацентричность, или несферичность молекулы. Анализируя зависимость приведенного давления насыщенного пара различных веществ от приведенной температуры, Питцер с сотрудниками установили, что для аргона, криптона, ксенона, азота, кислорода, окиси углерода, метана и некоторых других веществ эта зависимость описывается практически одним уравнением. Однако расширение этого списка соединениями других классов дает серию практически прямых линий, наклоны которых различаются. Питцер и др. приняли приведенное давление насыщенного пара 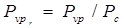 при определенной приведенной температуре при определенной приведенной температуре  в качестве характеристики вещества. При этих температурах приведенное давление инертных газов, выбранных в качестве простого вещества, составляет примерно 0,1. На основании этого наблюдения было сформулировано определение нового параметра - ацентрического фактора
как описывающего отклонение значения приведенного давления пара для определенного вещества от приведенного давления пара вещества сравнения в следующем виде: в качестве характеристики вещества. При этих температурах приведенное давление инертных газов, выбранных в качестве простого вещества, составляет примерно 0,1. На основании этого наблюдения было сформулировано определение нового параметра - ацентрического фактора
как описывающего отклонение значения приведенного давления пара для определенного вещества от приведенного давления пара вещества сравнения в следующем виде:
 (при Tr
=0,7),(5.18) (при Tr
=0,7),(5.18)
где  - давление насыщенного пара вещества при приведенной температуре Tr
=0,7. - давление насыщенного пара вещества при приведенной температуре Tr
=0,7.
По определению Питцера ацентрический фактор является “мерой отклонения функций межмолекулярного потенциала от функций межмолекулярного потенциала сферических молекул вещества сравнения”. Значение
= 0 соответствует сферической симметрии в разреженном газе. Отклонения от поведения, характерного для простого вещества, очевидны, если
> 0. Для одноатомных газов ацентрический фактор близок к нулю. Для метана он еще очень мал. Однако для углеводородов с высокой молекулярной массой значение
возрастает и резко увеличивается с ростом полярности молекул.
Диапазон варьирования ацентрического фактора - от нуля до единицы.
В настоящее время ацентрический фактор широко используется в качестве параметра, который в известной степени характеризует сложность строения молекулы в отношении как ее геометрии, так и полярности. В соответствии с рекомендациями [5, 6, 19] применимость корреляций, включающих фактор ацентричности, должна ограничиваться нормальными газами и жидкостями, их не следует использовать для прогнозирования свойств сильно полярных или ассоциированных жидкостей.
Здесь следует заметить, что опыт нашей работы позволяет заключить, что приведенное выше ограничение является излишне категоричным. При соблюдении определенных условий корреляции с
могут использоваться и применительно к названным группам органических веществ.
Значения ацентрического фактора для многих веществ вычислены на основе лучших экспериментальных данных по упругостям паров, Tc
и Pc
соединений и содержатся в Приложении.
При отсутствии сведений об
для его прогнозирования могут использоваться:
· уравнение Эдмистера
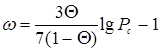 ;(5.19) ;(5.19)
· уравнение Ли-Кеслера
 ,(5.20) ,(5.20)
· уравнение Амброуза-Уолтона
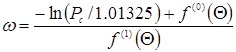 ,(5.21) ,(5.21)
где 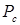 - критическое давление, выраженное в физических атмосферах;
- критическое давление, выраженное в физических атмосферах;
= 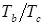 - приведенная нормальная температура кипения вещества; - приведенная нормальная температура кипения вещества;
 - нормальная температура кипения вещества в градусах Кельвина;
- нормальная температура кипения вещества в градусах Кельвина;
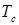 - критическая температура в градусах Кельвина.
- критическая температура в градусах Кельвина.
f
(0)
,
f
(1)
– определены в описании метода Амброуза-Уолтона (раздел 7.3)
Завершая рассмотрение материала по критическим свойствам и критериям подобия, остановимся еще на одном важном и общем вопросе. Он касается критериев подобия. В настоящее время их предложено довольно много, мы познакомились с одним из них - ацентрическим фактором. В разд. 7 рассматривается еще один критерий подобия - и коэффициент Риделя. Оба критерия применяются весьма широко. Тем не менее универсальных подходов к выбору того или иного критерия подобия пока не создано, а значит, работы в этом направлении будут продолжены. Мы считаем целесообразным повторить те требования, которые перечислены Уэйлесом в его монографии [19] и относятся к дополнительным параметрам или критериям подобия:
· Эти параметры должны соотноситься с молекулярной структурой и электростатическими свойствами молекулы.
· Их можно определить при минимальном количестве экспериментальных данных.
· Критические свойства не должны оказывать непосредственное воздействие на их значения.
· При оценке этих параметров надо избегать использования данных о P-V-T
, так как в противном случае теряется смысл приведенного уравнения.
Дополнительные параметры должны быть функцией температуры, предпочтительно приведенной.
Можно соглашаться или нет с перечисленными требованиями, но совершенно очевидно, что всему их комплексу не отвечает ни ацентрический фактор, ни критерий Риделя. Мало того, нам представляется ясным, что одной из причин успеха в их применении является именно согласованность их величин с критическими параметрами и P-T данными. В качестве носителя связи с P-T данными выступает температура кипения при одном из давлений, чаще при атмосферном.
Таким образом, развитие методов прогнозирования потребует, вероятно, и уточнения требований к критериям подобия.
6. ПРОГНОЗИРОВАНИЕ плотности газа и жидкости [6, 17-18]
Перед тем как перейти к прогнозированию, следует напомнить, что в зависимости от принятых температуры и давления вещество может находиться либо в насыщенном, либо в ненасыщенном состоянии. Давление над насыщенной жидкостью равно давлению ее насыщенного пара при данной температуре
. Давление над ненасыщенной, переохлажденной или сжатой жидкостью больше давления ее насыщенного пара при избранной для расчета температуре. Для каждой из названных областей P-V-T
пространства существуют самостоятельные подходы к прогнозированию плотности.
Прогнозирование плотности индивидуальных веществ с использованием коэффициента сжимаемости
Пример 6.1
Для изобутилбензола, имеющего критическую температуру 650 К, критическое давление 31 атм и ацентрический фактор 0,378, рассчитать с использованием таблиц Ли-Кеслера (табл. 4.6, 4.7):
· коэффициент сжимаемости при 500, 657 и 1170 К и давлении 1-300 атм,
· плотность при 500, 657 и 1170 К и давлении 1-300 атм;
дать графические зависимости:
· коэффициента сжимаемости от давления при указанных температурах,
· плотности от давления при указанных температурах.
Решение
Используем разложение Питцера (уравн. 4.34) и табл. 4.6, 4.7 для коэффициента сжимаемости.
1. Вычислим значения приведенных температур:
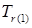 = 500/600 =0,769; = 500/600 =0,769;  = 657/650 =1,01; = 657/650 =1,01;  = 1170/650 =1,80. = 1170/650 =1,80.
2. Вычислим значения приведенных давлений:
 = 1/31 =0,03226; = 1/31 =0,03226;  = 300/31 =9,677. = 300/31 =9,677.
Поскольку диапазон интересующих приведенных давлений совпадает с диапазоном  , рассмотренных Ли-Кеслером, используем информацию о , рассмотренных Ли-Кеслером, используем информацию о  и и  для дискретных значений для дискретных значений  , представленных в табл. 4.6, 4.7. , представленных в табл. 4.6, 4.7.
Каждое из значений  и и 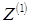 получено линейной интерполяцией по температуре. Так, при 500 К ( получено линейной интерполяцией по температуре. Так, при 500 К (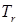 = 0,769) и = 0,769) и 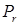 = 0,010 для = 0,010 для  имеем имеем
(0,9935-0,9922)/(0,80-0,75)·(0,769-0,75)+0,9922 = 0,9927.
Прогнозирование плотности насыщенных жидкости и пара с использованием уравнений состояния вещества
Нахождение условий насыщения из уравнений состояния представляет собой достаточно сложную задачу, решение которой зачастую невозможно без привлечения вычислительной техники и специального программного обеспечения. Для простых уравнений состояния, таких как уравнение Ван-дер-Ваальса, эта задача может быть решена путем несложных вычислений. Однако необходимо помнить, что на практике при помощи уравнения Ван-дер-Ваальса можно лишь качественно оценить состояние насыщения. Для более точного представления насыщения разработаны другие уравнения состояния и специальные методы.
В данном пособии на примере уравнения Ван-дер-Ваальса рассмотрен подход к нахождению давления насыщения и объемов насыщения жидкости и пара (точки, принадлежащие бинодали), а также условий, определяющих метастабильные состояния вещества (точки экстремумов изотермы).
Пример 6.3
Для изобутилбензола при температурах 400, 500, 600 и 640 К, используя уравнение Ван-дер-Ваальса, рассчитать давление пара и объемы насыщения жидкости и пара. Определить также области метастабильных состояний пара и жидкости при указанных температурах. Критическая температура равна 650 К, критическое давление - 31 атм.
Решение
1. Запишем принцип Максвелла:
Площадь =  .(6.1) .(6.1)
Выразим из уравнения Ван-дер-Ваальса значение давления и подставим его в подинтегральное выражение. Получим
 .
(6.2) .
(6.2)
В данном случае имеется возможность найти аналитическое решение определенного интеграла
 .(6.3) .(6.3)
Теперь задача сводится к отысканию значения P sat
, при котором выражение 6.3 обратится в тождество. При его нахождении нам потребуется неоднократно определять значения объемов жидкости и пара для заданного P, т.е. находить решения (корни) кубического уравнения.
2. Перепишем уравнение Ван-дер-Ваальса в виде полинома по объему
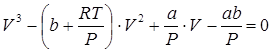 .(6.4) .(6.4)
Корни данного уравнения можно найти, воспользовавшись формулами Кардано. Для этого перейдем к приведенному виду кубического уравнения, выполнив следующие преобразования. Обозначим коэффициенты в уравнении (6.4) через
 ; ;  ; ; 
и сделаем замену неизвестного V на Y:
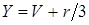 ; ;
тогда уравнение (6.4) примет приведенный вид
 ,(6.5) ,(6.5)
где  ; ; 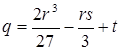 . .
Число действительных решений кубического уравнения зависит от знака дискриминанта
 .(6.6) .(6.6)
Если в > 0, то уравнение имеет одно действительное решение; если в < 0, то - три действительных решения; и если в = 0, то уравнение имеет либо два действительных решения, одно из которых двукратное, либо одно действительное трехкратное решение (последнее в случае p = q = 0).
В данном примере рассматривается область P-V-T пространства, где сосуществуют пар и жидкость. Для этой области уравнение Ван-дер-Ваальса имеет три действительных решения (дискриминант уравнения (6.5) меньше нуля). При использовании формул Кардано в оригинальном виде корни уравнения выражаются через комплексные величины. Избежать этого можно, если ввести следующие обозначения:
 , , 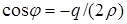 .(6.7) .(6.7)
Тогда решениями приведенного уравнения (6.5) будут
 ;(6.8) ;(6.8)
 ;(6.9) ;(6.9)
 ,(6.10) ,(6.10)
от которых заменой
 (6.11) (6.11)
снова можно перейти к решениям кубического уравнения (6.4).
3. Вычислим характеристические константы уравнения Ван-дер-Ваальса. Для удобства вычислений примем следующие единицы измерения: V - л/моль , P - атм, Т - К. Тогда R = 0,08206 л·атм/(моль·К);
a = 27·0,082062·6502/(64·31)=38,72 л·атм;
b = 0,08206·650/(8·31)=0,2151 л.
4. Давление насыщения находится методом последовательных приближений. В качестве первого приближения при Т = 400 К примем давление насыщения равным 10 атм.
5. Рассчитаем значения коэффициентов уравнения (6.4):
 = –(0,2151+0,08206·400/10) = – 3,4975; = –(0,2151+0,08206·400/10) = – 3,4975;
 = 38,72/10 = 3,872; = 38,72/10 = 3,872;
 = – (38,72·0,2151/10) = – 0,8329. = – (38,72·0,2151/10) = – 0,8329.
6. Далее вычислим коэффициенты приведенного кубического уравнения (6.5) и значение дискриминанта D:
 = [3·3,872–(–3,4975)2]/3 = – 0,2055; = [3·3,872–(–3,4975)2]/3 = – 0,2055;
 = 2·(–3,4975)3/27–(–3,4975·3,872)/3+(–0,8329)=0,5121; = 2·(–3,4975)3/27–(–3,4975·3,872)/3+(–0,8329)=0,5121;
 = (–0,2055/3)3+(0,5121/2)2 = 0,0652. = (–0,2055/3)3+(0,5121/2)2 = 0,0652.
Значение дискриминанта (D) получилось положительным, что говорит о единственном действительном решении уравнения (6.5). Следовательно, значение давления выбрано неверно.
7. Предположим, что давление насыщения равно 1 атм. Повторим вычисления в пунктах 5 и 6.
 = –(0,2151+0,08206·400/1) = –33,04; = –(0,2151+0,08206·400/1) = –33,04;
 = 38,72/1 = 38,72; = 38,72/1 = 38,72;
 = –(38,72·0,2151/1) = –8,329; = –(38,72·0,2151/1) = –8,329;
 =[3·38,72 –(–33,04)2]/3 = –325,2; =[3·38,72 –(–33,04)2]/3 = –325,2;
 = 2·(–33,04)3/27 –(–33,04·38,72)/3+(–8,329) = –2254; = 2·(–33,04)3/27 –(–33,04·38,72)/3+(–8,329) = –2254;
 = (–325,2/3)3+(–2254/2)2 = –3632. = (–325,2/3)3+(–2254/2)2 = –3632.
Значение в отрицательное, следовательно, уравнение имеет три действительных решения.
8. Найдем эти решения, но прежде вычислим вспомогательные величины 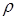 и и
 = [–(–325,2)3/27]1/2 = 1129; = [–(–325,2)3/27]1/2 = 1129;
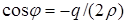 = –(–2254)/(2·1129) = 0,9982; = –(–2254)/(2·1129) = 0,9982;
 = arccos (0,9982) = 0,0600 радиан; = arccos (0,9982) = 0,0600 радиан;
 = 2·(1129)1/3·cos(0,0600/3) = 20,82; = 2·(1129)1/3·cos(0,0600/3) = 20,82;
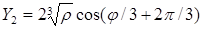 = 2·(1129)1/3 cos(0,0600/3 + 2·3,14/3) = –10,75; = 2·(1129)1/3 cos(0,0600/3 + 2·3,14/3) = –10,75;
 = 2·(1129)1/3 cos (0,0600/3 + 4·3,14/3) = –10,09. = 2·(1129)1/3 cos (0,0600/3 + 4·3,14/3) = –10,09.
9. Перейдем к решениям уравнения (6.4), воспользовавшись (6.11).
 = 20,82 –(–33,04/3) = 31,8 л/моль; = 20,82 –(–33,04/3) = 31,8 л/моль;
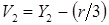 = –10,75 –(–33,04/3) = 0,263 л/моль; = –10,75 –(–33,04/3) = 0,263 л/моль;
 = –10,09 –(–33,04/3) = 0,923 л/моль. = –10,09 –(–33,04/3) = 0,923 л/моль.
При 400 К и 1 атм объем пара (V1
) составляет 31,8 л/моль, объем жидкости (V2
) – 0,263 л/моль. V3
= 0,923 – третий корень уравнения, не имеющий физического смысла.
10. Вычислим значение левой части выражения (6.3), для этого имеются все необходимые величины:
 = 0,08206·400 ln[(31,8–0,2151)/ = 0,08206·400 ln[(31,8–0,2151)/
/(0,263– 0,2151)] + 38,72·(1/31,8–1/0,263)–1·(31,8–0,263) = 35,53.
При избранном давлении (1 атм ) выражение (6.3) в тождество не обращается, т.е. левая и правая части не равны друг другу. Необходимо принять другое значение давления насыщения.
В пунктах 5-10 вычисления производились с округлением промежуточных величин на каждом шаге вычислений до значений, записанных в формулах. Далее приводятся результаты вычислений с точностью в 16 десятичных разрядов, и округление выполнено только при представлении окончательных величин.
11. Примем Psat
= 3 атм. Повторим вычисления в пунктах 5-10. При 400 К и 3 атм объем пара составляет 9,878 л/моль, объем жидкости – 0,282 л/моль. Левая часть выражения (6.3) равна  = 1,0515. Тождество не выполняется, но степень отклонения от него существенно уменьшилась. = 1,0515. Тождество не выполняется, но степень отклонения от него существенно уменьшилась.
12. Подбор давления насыщения следует продолжить. Теперь имеется два значения для левой части выражения (6.3) при соответствующих давлениях. Используя эти величины, можно оценить значение давления для следующего расчета путем линейной интерполяции.
 = 1–(1–3)/(35,53–1,0515)·35,53 = 3,061 атм.
= 1–(1–3)/(35,53–1,0515)·35,53 = 3,061 атм.
13. Повторим вычисления (пункты 5-12) для Psat
= 3,061 атм. Получим:
 =
9,658 л/моль; =
9,658 л/моль;  =
0,282 л/моль;
=
0,282 л/моль; 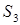 =
0,473. Новое значение давления – 3,111 атм. =
0,473. Новое значение давления – 3,111 атм.
После 5 итераций, исключая расчет при Psat
= 10 атм, имеем:
T =
400 K; P
sat =
3,112 атм;  =
9,480 л/моль;
=
9,480 л/моль;  = 0,282 л/моль;
= 0,282 л/моль; 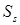 =
8,7·10-5. Полученные значения давления и объемов жидкости и пара соответствуют условиям насыщения. =
8,7·10-5. Полученные значения давления и объемов жидкости и пара соответствуют условиям насыщения.
14. Результаты расчета для других температур приведены в табл. 6.3.
Таблица 6.3
| Т
, К
|
Psat
, атм
|
 , л/моль
, л/моль
|
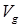 , л/моль
, л/моль
|
| 400
|
3,112
|
0,282
|
9,480
|
| 500
|
9,888
|
0,322
|
3,235
|
| 600
|
22,328
|
0,410
|
1,322
|
| 640
|
29,127
|
0,515
|
0,850
|
15. Область метастабильных (пересыщенных) состояний пара и жидкости занимает пространство между бинодалью и спинодалью. Точки на изотермах, принадлежащие бинодали, определены выше, и их значения приведены в табл. 6.3.
Для определения конфигурации спинодали воспользуемся соотношением
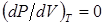 , ,
т.е. условиями экстремальности для соответствующих точек изотермы. Далее продифференцируем уравнение Ван-дер-Ваальса по объему (при Т = const) и преобразуем полученное выражение к полиному по V. Получим кубическое уравнение (6.12), корни которого могут быть найдены изложенным выше способом (п.п. 5-9):
 .(6.12) .(6.12)
16. Для 400 К имеем следующие значения коэффициентов уравнения (6.12):
 = –[2·38,72/(0,08206·400)] = –2,3593; = –[2·38,72/(0,08206·400)] = –2,3593;
 = [4·38,72·0,2151/(0,08206·400)] = 1,0149; = [4·38,72·0,2151/(0,08206·400)] = 1,0149;
 = –[2·38,72·0,21512/(0,08206·400)] = –0,1092. = –[2·38,72·0,21512/(0,08206·400)] = –0,1092.
Коэффициенты приведенного кубического уравнения (6.5) соответственно равны:
 = [3·1,0149 –(–2,3593)2]/3 = –0,8405; = [3·1,0149 –(–2,3593)2]/3 = –0,8405;
 = 2·(–2,3593)3/27 –(–2,3593·1,0149)/3 + (–0,1092) = –0,2838; = 2·(–2,3593)3/27 –(–2,3593·1,0149)/3 + (–0,1092) = –0,2838;
 = (–0,8405/3)3 + (–0,2838/2)2 = –0,0019. = (–0,8405/3)3 + (–0,2838/2)2 = –0,0019.
Значение в отрицательное, следовательно, уравнение имеет три действительных решения.
17. Найдем значения корней уравнения (6.12) при 400 К. Для этого выполним последовательно следующие вычисления:
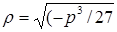 = [–(–0,8405)3/27]1/2 = 0,1483; = [–(–0,8405)3/27]1/2 = 0,1483;
 = –(–0,2838)/(2·0,1483) = 0,9568; = –(–0,2838)/(2·0,1483) = 0,9568;
 = arccos (0,9568) = 0,2950 радиан; = arccos (0,9568) = 0,2950 радиан;
 = 2·(0,1483)1/3 cos(0,2950/3) = 1,0535; = 2·(0,1483)1/3 cos(0,2950/3) = 1,0535;
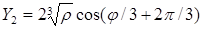 = 2·(0,1483)1/3 cos(0,2950/3 + 2·3,14/3) = –0,6159; = 2·(0,1483)1/3 cos(0,2950/3 + 2·3,14/3) = –0,6159;
 = 2·(0,1483)1/3 cos(0,2950/3 + 4·3,14/3) = –0,4388; = 2·(0,1483)1/3 cos(0,2950/3 + 4·3,14/3) = –0,4388;
 = 1,0535 –(–2,3593/3) = 1,840 л/моль; = 1,0535 –(–2,3593/3) = 1,840 л/моль;
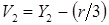 = –0,6159 –(–2,3593/3) = 0,171 л/моль; = –0,6159 –(–2,3593/3) = 0,171 л/моль;
 = –0,4388 –(–2,3593/3) = 0,348 л/моль. = –0,4388 –(–2,3593/3) = 0,348 л/моль.
Наибольший корень 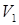 = 1,840 л/моль соответствует максимуму на изотерме 400 К и ограничивает метастабильные состояния пара слева. Корень = 1,840 л/моль соответствует максимуму на изотерме 400 К и ограничивает метастабильные состояния пара слева. Корень  , равный 0,171 л/моль, не имеет физического толкования, поскольку его значение меньше параметра b в уравнении Ван-дер-Ваальса. И, наконец, корень , равный 0,171 л/моль, не имеет физического толкования, поскольку его значение меньше параметра b в уравнении Ван-дер-Ваальса. И, наконец, корень  соответствует минимуму на изотерме 400 К и отделяет слева область пересыщенной жидкости от абсолютно неустойчивых состояний. соответствует минимуму на изотерме 400 К и отделяет слева область пересыщенной жидкости от абсолютно неустойчивых состояний.
18. Давление в системе при соответствующем объеме пересыщенного пара ( ) и пересыщенной жидкости ( ) и пересыщенной жидкости ( ) находится из уравнения Ван-дер-Ваальса подстановкой в него требуемых значений температуры и объема. ) находится из уравнения Ван-дер-Ваальса подстановкой в него требуемых значений температуры и объема.
 = (0,08206·400)/(1,840–0,215)–38,72/1,8402 = 8,763 атм; = (0,08206·400)/(1,840–0,215)–38,72/1,8402 = 8,763 атм;
 = (0,08206·400)/(0,348–0,215)–38,72/0,3482 = –72,928 атм. = (0,08206·400)/(0,348–0,215)–38,72/0,3482 = –72,928 атм.
19. Результаты расчета для прочих температур приведены в табл. 6.4.
| Т, К
|
 , атм
, атм
|
 , л/моль
, л/моль
|
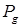 , атм
, атм
|
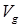 , л/моль
, л/моль
|
| 400
|
-72,928
|
0,348
|
8,763
|
1,840
|
| 500
|
-20,124
|
0,397
|
14,913
|
1,324
|
| 600
|
17,803
|
0,482
|
24,103
|
0,929
|
| 640
|
28,798
|
0,563
|
29,347
|
0,750
|
|