Задача 1 (5)
Производится контроль партии из 4 изделий. Вероятность изделия быть неисправным равна 0,1. Контроль прекращается при обнаружении первого неисправного изделия. Х – число обследованных приборов. Найти:а) ряд распределения Х б)функцию распределения F(X), в ответ ввести F(3.5). в) m(x) г) d(x) д) p(1.5<X<3.5).
Решение
Пусть событие А – состоит в том, что изделие исправно, и соответственно 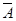 - неисправно. По условию, вероятность - неисправно. По условию, вероятность  , значит p(A)=1- , значит p(A)=1- . Случайная величина Х – число обследованных приборов – может принимать значения 0(если первый же прибор неисправен),1,2,3,4. . Случайная величина Х – число обследованных приборов – может принимать значения 0(если первый же прибор неисправен),1,2,3,4.
Найдем соответствующие вероятности:

Составим ряд распределения Х:
| Х |
0 |
1 |
2 |
3 |
4 |
| р |
0,1 |
0,09 |
0,081 |
0,0729 |
0,6561 |
Х – дискретная случайная величина. Найдем функцию распределения F(x)=P(X

Значение F(3.5)=0.34391
Математическое ожидание дискретной случайной величины 
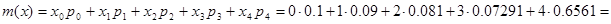

Дисперсия 

Вероятность 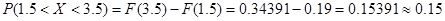
Задача 2(2
). События А и В независимы. Вероятность наступления хотя бы одного из них равна 0,94. Найти Р(А), если Р(В)=0,7. Ответ записать в виде десятичной дроби.
Решение.
Вероятность наступления суммы событий Р(А+В)=Р(А)+Р(В)-Р(АВ). Но так как события А и В независимы, то Р(АВ)=Р(А)Р(В).
Имеем Р(А+В)=0,94 (наступает событие А или событие В или оба); Р(В)=0,7
0,94=Р(А)+0,7- Р(А)
0,3Р(А)=0,94-0,7=0,24
Р(А)= - вероятность наступления А. - вероятность наступления А.
Задача 3(6).
Дана плотность распределения случайной величины Х:

Найти а)константу А б)функцию распределения F(x), в ответ ввести F(0); F(0.5) в) m(x) г)d(x)
д) P(0<X<0.5).
Решение.
Константу А найдем из условия для р(х) :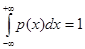
Имеем 
 Отсюда Отсюда  . .
Функция распределения непрерывной случайной величины 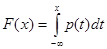
Для  p(x)=0, F(x)=0 p(x)=0, F(x)=0
Для -
Для 

Математическое ожидание непрерывной случайной величины 
Имеем 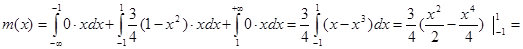

Дисперсия непрерывной случайной величины 
Имеем

Вероятность
Задача 4(2).
Дана плотность распределения вероятностей системы (X,Y).

Найти а)константу С;б)р1(х),р2(у); в) mx; г)my ;д)Dx; е)Dy; ж)cov(X,Y); з)rxy; и)F(-1,5); к) M(X|Y=1)
Решение.
Плотность системы случайных величин должна удовлетворять условию:

В нашем случае  ; ;  ; ; 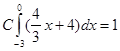 ; ; 

  Y Y
  B 4 B 4
-3 A 0 X
б) Плотности р1(х),р2(у):


в) Математические ожидания:
 
г) Дисперсии:
   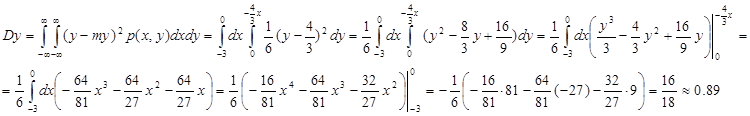 ж) Ковариация ж) Ковариация
  з) Коэффициент корреляции з) Коэффициент корреляции
 
и) Значение F(-1,5)
Функция распределения системы случайных величин
 . (1) . (1)
 (-1,5) Y (-1,5) Y
    5 5
B
  D4 4 D4 4
D1 D0
  A X A X
 -3 -1 O -3 -1 O
D2 D3
В областях D1,D2,D3,D4 которые не пересекаются с треугольником АВО значениеP(x,y)=0
Вычисляя F(-1,5) представим двойной интеграл в виде суммы интегралов:


к) Математическое ожидание M(x|y=1)

|