| МЭИ (ТУ)
Филиал в городе Смоленске
Кафедра ТОЭ
Лабораторная работа
Простые цепи синусоидального тока
Группа : ОЭС-09
Бригада : № 10 Студент: Бабурченков М. А.
Преподаватель: Зезюлькин Г. Г.
Смоленск 2010 г.
I. Краткое содержание работы
В работе исследуются соотношения между синусоидальными напряжениями и токами при последовательном и параллельном соединении резистивных, индуктивных и емкостных элементов цепи. По экспериментальным данным производится определение параметров последовательной и параллельной схем замещения реальных элементов цепи, строятся векторные диаграммы токов и напряжений. Для последовательной резонансной цепи исследуются переменные режимы при изменении индуктивности. Все расчеты и анализ экспериментальных результатов выполняются с использованием символического (комплексного) метода. Работа может выполняться на сильноточном стенде.
II. Подготовка к работе
1. U=40B
I=0,4A
f=80 град
а) последовательная схема замещения катушки.
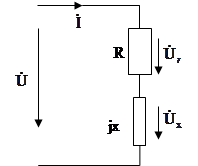
Z=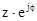 , где z – полное сопротивление. , где z – полное сопротивление.
z=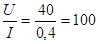 (Ом) (Ом)
Комплексное сопротивление Z можно представить в виде
Z=zcosf+jzsinf=R+jX
R (активное сопротивление) = zcosf = 100cos800
= 17,4 (Ом)
X (реактивное сопротивление) = zsinf = 100sin800
= 98,5 (Ом)
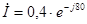 (A) (A)
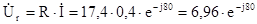 (B) (B)
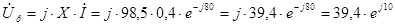 (B) (B)
б) параллельная схема замещения катушки.
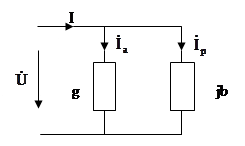
По определению комплексной проводимости имеем:
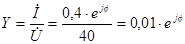 (См) (См)
Комплексную проводимость можно представить в виде:
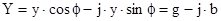
g = ycosf - активная проводимость.
b = ysinf - реактивная проводимость.
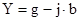
g = 0,01.
cos800
= 0,0017 (См)
b = 0,01.
sin800
= 0,0098 (См)
По закону Ома: 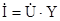
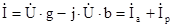 , ,
где 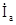 - активная составляющая тока, - активная составляющая тока, 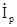 - реактивная составляющая тока. - реактивная составляющая тока.
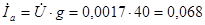 (А) (А)
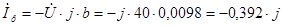 (А) (А)
U = 40 B
R = 50 Ом
С = 160 мкФ
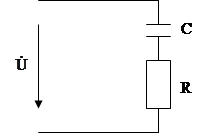
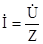
Z = R - 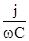 Z = 50 - Z = 50 - 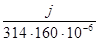 = 50 – 20.
j = = 50 – 20.
j = 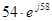
z = 54 (Ом)
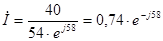 (A) (A)
4. 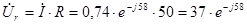 (B); U (B); U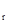 =37(B) =37(B)
 (B); Uc
=14,8(B) (B); Uc
=14,8(B)
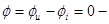
5. f = 50 Гц
I = 1 A
R = 40 Ом
C = 160.
10-6
Ф
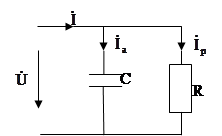
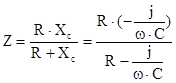
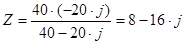
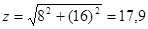 (Ом) (Ом)
I = 1 A
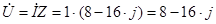 (B) (B)
U = 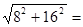 17,9 (B) 17,9 (B)
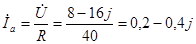 Ia
=0,447(A) Ia
=0,447(A)
Ip
= 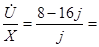 Ip
= (A) Ip
= (A)
6. R = 40 Ом
C = 160.
10-6
Ф
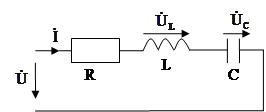
Входное сопротивление цепи на частоте 50 Гц будет чисто активным при резонансе. Условием наступления резонанса в данной схеме является
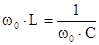 , ,
где w0
– резонансная частота.
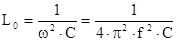 L0
= 15,8 (мГн) L0
= 15,8 (мГн)
III. Рабочее задание.
1.
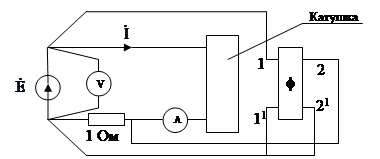
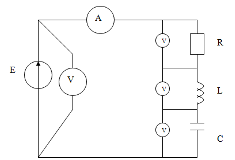
рис. 1
А) последовательная схема замещения.
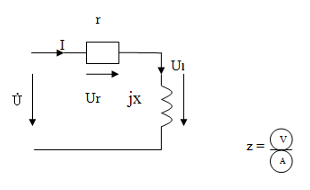
r = z·cosf =
x = z·sinf =
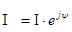 = =
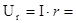
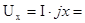
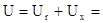
Б) параллельная схема замещения
   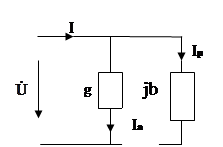 y == y ==
g = y·cosφ =
b = y·sinφ =
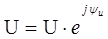 = =

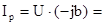
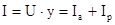 = =
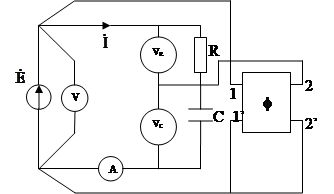
рис. 2
| параметр
|
Измеренное значение
|
Расчетное значение
|
| I
|
| UC
|
| UR
|
| f
|
3.
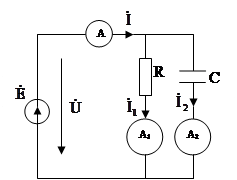
рис. 3
| параметр
|
Измеренное значение
|
Расчетное значение
|
| U
|
| I
|
| IR
|
| IC
|
| Xl, Ом I, A
|
UR, B
|
UL, B
|
UC, B
|
|