| Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Пензенский государственный педагогический университет им. В. Г. Белинского
Кафедра прикладной математики и информатики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине «Дискретная математика »
на тему: «Реализация основных операций над графами, представленных в виде матриц смежностей»
| Автор:
|
Бабаджанов Б. Ю.
|
| Специальность:
|
Математическое обеспечение и администрирование информационных систем.
|
| Группа:
|
МП-21.
|
| Курс:
|
2
|
| Руководитель:
|
Тобольченко В.М.
|
ПЕНЗА 2010
Задания.
Реализовать представление графа с помощью матрицы смежности. Реализовать основные операции над графами (дополнение графа, объединение графов, добавление ребра в граф, удаление вершины из графа, удаление ребра из графа, добавление вершины в граф).
Реферат
Пояснительная записка содержит 30 листов, 7 рисунков, 2 таблиц, 3 приложений на 12 листах.
Дискретная Математика, ИНФОРМАТИКА, ПРОГРАММИРОВАНИЕ,ООП, С++, ГРАФ, ОПЕРЦИИ НАД ГРАФАМИ, дополнение графа, объединение графов, соединение графов, добавление ребра в граф, стягивание подграфа, удаление вершины из графа, удаление ребра из графа, добавление вершины в граф.
В работе реализован граф виде матрицы смежности на языке программирование С++. Написан код для вычисление основных операций над графами.
Содержание
.
Задания. - 2 -
Реферат.. - 3 -
Содержание. - 4 -
Введение.. - 5 -
1 Разработка программы для реализации графа. - 6 -
1.1 Анализ математических требований. - 8 -
1.2 Кодирование. - 18 -
1.3 Тестирование. - 19 -
Заключение. - 21 -
ПРИЛОЖЕНИЕ А. - 22 -
ПРИЛОЖЕНИЕ Б. - 23 -
ПРИЛОЖЕНИЕ В. - 28 -
Список литературы: - 32 -
Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок. Очень долго она находилась в стороне от главных направлений исследований ученых, была в царстве математики на положении Золушки, чьи дарования раскрылись в полной мере лишь тогда, когда она оказалась в центре общего внимания.
Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г. Толчок к развитию теория графов получила на рубеже ХIX и ХХ столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства. Графы стали использоваться при построении схем электрических цепей и молекулярных схем. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы ХХ столетия.
В последнее время графы и связанные с ними методы исследований органически пронизывают на разных уровнях едва ли не всю современную математику. Теория графов рассматривается как одна из ветвей топологии; непосредственное отношение она имеет также к алгебре и к теории чисел. Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине, географии. Широкое применение находят графы в таких областях, как программирование, теория конечных автоматов, электроника, в решении вероятностных и комбинаторных задач, нахождении максимального потока в сети, кратчайшего расстояния, максимального паросочетания, проверки планарности графа и др. Как особый класс можно выделить задачи оптимизации на графах. Математические развлечения и головоломки тоже являются частью теории графов, например, знаменитая проблема четырех красок, интригующая математиков и по сей день. Теория графов быстро развивается, находит все новые приложения и ждет молодых исследователей.
1 Разработка программы для
реализации графа.
Приведенные ниже этапы создания программы.
I этап. Создание любой программы начинается с постановки задачи или анализа требования. Изначально задача поставлена в терминах предметной области, и приведена в термины, более близкие к программированию.
В ходе работе:
• описаны исходные данные и результаты (типы, форматы, точность, способ передачи, ограничения);
• описаны задачи, реализуемой программой;
• способ обращения к программе;
• описаны возможные аварийные ситуации и ошибки пользователя.
Таким образом, функции, входные и выходные данные.
II этап. Проектирование (определение общей структуры и взаимодействия модулей). На этом этапе применилось технология нисходящего проектирования программы, основная идея которого теоретически проста: разбиение задачи на подзадачи меньшей сложности, которые можно рассматривать раздельно. При этом используется метод пошаговой детализации. Очень важной на этом этапе является спецификация интерфейсов, то есть способов взаимодействия подзадач.
III этап. Кодирование. Процесс программирования также организовался по принципу «сверху вниз»: вначале кодируются модули самого верхнего уровня и составляются тестовые примеры для их отладки. Таким образом, сначала создавался логический скелет программы.
Этапы проектирования и программирования совмещены во времени: в идеале сначала проектируется и кодируется верхний уровень, затем — следующий, и так далее. Такая стратегия применяется потому, что в процессе кодирования может возникнуть необходимость внести изменения, отражающиеся на модулях нижнего уровня.
IV этап. Тестирование. Этот этап записан последним, но это не значит, что тестирование не должно проводиться на предыдущих этапах. Проектирование и программирование обязательно должны сопровождаться написанием набора тестов — проверочных исходных данных и соответствующих им наборов эталонных реакций.
Необходимо различать процессы тестирования и отладки программы. Тестирование — процесс, посредством которого проверяется правильность программы. Тестирование носит позитивный характер, его цель — показать, что программа работает правильно и удовлетворяет всем проектным спецификациям. Отладка — процесс исправления ошибок в программе, при этом цель исправить все ошибки не ставится. Исправляют ошибки, обнаруженные при тестировании. При планировании следует учитывать, что процесс обнаружения ошибок подчиняется закону насыщения, то есть большинство ошибок обнаруживается на ранних стадиях тестирования, и чем меньше в программе осталось ошибок, тем дольше искать каждую из них.
Для исчерпывающего тестирования программы необходимо проверить каждую из ветвей алгоритма. Общее число ветвей определяется комбинацией всех альтернатив на каждом этапе. Это конечное число, но оно может быть очень большим, поэтому программа разбивается на фрагменты, после исчерпывающегося тестирования которых, они рассматриваются как элементарные узлы более длинных ветвей. Кроме данных, обеспечивающих выполнение операторов в требуемой последовательности, тесты должны содержать проверку граничных условий Отдельно проверяется реакция программы на ошибочные исходные данные.
В программе проверена каждая из ветвей алгоритма. Общее число ветвей определено комбинацией всех альтернатив на каждом этапе. Отдельно проверена реакция программы на ошибочные исходные данные.
1.1 Анализ математических требований.
Матрица смежности — один из способов представления графа в виде матрицы.
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица Aразмера n, в которой значение элемента aij равно числу ребёр из i-й вершины графа в j-ю вершину.
Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины.
Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.
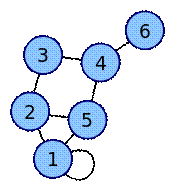
Ниже приведён пример (рис 1.) неориентированного графа и соответствующей ему матрицы смежности A. Этот граф содержит петлю вокруг вершины 1, так что, в зависимости от конкретных приложений, элемент a11 может считаться равным либо единице (как показано ниже), либо двум.
| Граф
|
Матрица смежности
|
| 
|
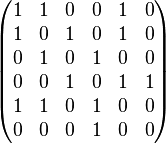
|
Рисунок 1– Граф и представления графа в виде матрицы.
Матрица смежности полного графа Kn содержит единицы во всех своих элементах, кроме главной диагонали, на которой расположены нули.
Матрица смежности пустого графа, не содержащего ни одного ребра, состоит из одних нулей.
Матрица смежности неориентированного графа симметрична, а значит обладает действительными собственными значениями и ортогональным базисом из собственных векторов. Набор её собственных значений называется спектром графа, и является основным предметом изучения спектральной теории графов.
Два графа G1 и G2 с матрицами смежности A1 и A2 являются изоморфными если и только если существует перестановочная матрица P, такая что
PA1P-1 = A2.
Из этого следует, что матрицы A1 и A2 подобны, а значит имеют равные наборы собственных значений, определители и характеристические многочлены. Однако обратное утверждение не всегда верно — два графа с подобными матрицами смежности могут быть неизоморфны.
Если A — матрица смежности графа G, то матрица Am
обладает следующим свойством: элемент в i-й строке, j-м столбце равен числу путей из i-й вершины в j-ю, состоящих из ровно m ребер.
Матрица смежности и списки смежности являются основными структурами данных, которые используются для представления графов в компьютерных программах
Использование матрицы смежности предпочтительно только в случае неразряженных графов, с большим числом ребёр, так как она требует хранения по одному биту данных для каждого элемента. Если граф разрежён, то большая часть памяти напрасно будет тратиться на хранение нулей, зато в случае неразряженных графов матрица смежности достаточно компактно представляет граф в памяти, используя примерно n2 / 8 байт памяти, что может быть на порядок лучше списков смежности.
В алгоритмах, работающих со взвешенными графами (например в алгоритме Флойда-Уоршелла), элементы матрицы смежности вместо чисел 0 и 1, указывающих на присутствие или отсутствие ребра, часто содержат веса самих ребер. При этом на место отсутствующих ребер ставят некоторое специальное граничное значение (англ. sentinel), зависящее от решаемой задачи, обычно 0 или 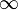 . .
В нашей работе анализ требований есть анализ основных требований теорий графов. В нашей работе был разработан представление графа в виде матрицы смежности и представлены основные операции над графами. Рассмотрим следующие элементы теорий графов.
Операции над графами и их свойства.
Удаление вершины
 из графа G приводит к подграфу из графа G приводит к подграфу 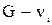 , содержащему все вершины графа G, за исключением , содержащему все вершины графа G, за исключением 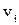 , и все рёбра графа G, не инцидентные , и все рёбра графа G, не инцидентные 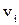 . Другими словами, . Другими словами, 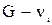 есть максимальный подграф графа G, не содержащий есть максимальный подграф графа G, не содержащий 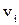 . .
Удаление ребра ej из графа G приводит к основному подграфу, содержащему все рёбра графа G, за исключением ej, т.е. G–ej есть максимальный подграф графа G, не содержащий ej.
Удаление произвольного множества вершин или рёбер из G определяется как последовательное удаление всех элементов этого множества.
Если 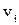 и и 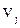 не смежны в G, то добавление ребра не смежны в G, то добавление ребра 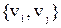 ( (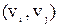 ) образует наименьший надграф графа G, содержащий ребро ) образует наименьший надграф графа G, содержащий ребро 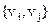 ( (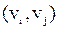 ). ).
Эти понятия иллюстрируются на рис. 2.1.1.
Рис. 2.1.1–Примеры графов
Существуют графы, для которых результат удаления вершины или ребра, а также добавления ребра не зависит от выбора вершины или ребра. Для графа G, обладающего этим свойством, обозначим соответствующие графы через G–v, 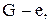 G+e, см. рис. 2.1.2. G+e, см. рис. 2.1.2.
Рис. 2.1.2–Удаление и добавление дуги в граф.
Удаление вершины х3 показано на рис. 2.2.3,б (для исходного графа, изображенного на рис. 2.2.3,а). Матрица смежности исходного графа представлена на таблице 1а). Результирующая матрица смежности графа после выполнения операции удаления вершины хi получается путем удаления соответствующего i- го столбца и i-ой строки из исходной матрицы и "сжимания" матрицы по вертикали и горизонтали начиная с (i+1)- го столбца и (i+1)-ой строки (таблица 1б).В дальнейшем элементы графа могут быть переобозначены.

Рисунок 2.2.2–Преставление графов графически и с помощи матриц.

Рисунок 2.2.3––Преставление графов графически .
| a.
|
| X1
|
X2
|
X3
|
X4
|
X5
|
| X1
|
1
|
| X2
|
1
|
1
|
| X3
|
1
|
1
|
| X4
|
1
|
| X5
|
1
|
1
|
| б.
|
| X1
|
X2
|
X4
|
X5
|
| X1
|
1
|
| X2
|
1
|
| X4
|
| X5
|
1
|
1
|
| в.
|
| X1
|
X2
|
X3
|
X4
|
X5
|
| X1
|
1
|
| X2
|
1
|
| X3
|
1
|
1
|
| X4
|
| X5
|
1
|
1
|
| г.
|
| X1-2
|
X3
|
X4
|
X5
|
| X1-2
|
1
|
1
|
1
|
| X3
|
1
|
1
|
| X4
|
1
|
| X5
|
1
|
1
|
Таблица 1–Матрицы смежности графов.
| д.
|
| X1-2
|
X3
|
X4
|
X5
|
| X1-2
|
1
|
1
|
| X3
|
1
|
1
|
| X4
|
1
|
| X5
|
1
|
1
|
| е.
|
| X1-2
|
X3-4
|
X5
|
| X1-2
|
1
|
1
|
| X3
|
1
|
| X5
|
1
|
1
|
| |
Таблица 1–Матрицы смежностей графов.
Удаление ребра
или удаление дуги. Если ai -дуга графа G = = (X, A), то G-ai – подграф графа G, получающийся после удаления из G дуги ai . Заметим, что концевые вершины дуги ai не удаляются. Удаление изграфа множества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дуг a4 и a7 показано на рис. 2.2.3,в. Результирующая матрица смежности графа после выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы (таблица 1в).
Стягивание.
Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф, изображенный на рис. 2.2.3,д получен стягиванием дуги a1 , а на рис. 2.2.3,е – стягиванием дуг a1 ,a6 и a7 . Соответствующие результирующие матрицы смежности показаны в таблицах 1д и 1е.
Пересечение графов
G1 и G2 , обозначаемое как G1  G2 , представляет собой граф G4 = (Х1 G2 , представляет собой граф G4 = (Х1  Х2, A1 Х2, A1  A2). Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2 . Операция пересечения графов G1 A2). Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2 . Операция пересечения графов G1  G2 показана на рис. 2.2.2,в, а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.2.г. G2 показана на рис. 2.2.2,в, а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.2.г.
Дополнение.
Пусть G(V,E) – обыкновенный граф. Дополнение 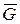 графа G (также обыкновенный граф) имеет в качестве множества вершин множество V, любые две несовпадающие вершины в графа G (также обыкновенный граф) имеет в качестве множества вершин множество V, любые две несовпадающие вершины в 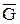 смежны тогда и только тогда, когда они не смежны в G. На рис. 3.1.1 изображены графы смежны тогда и только тогда, когда они не смежны в G. На рис. 3.1.1 изображены графы 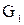 , , 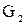 и их дополнения и их дополнения 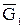 и и 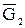 соответственно. соответственно.

Рисунок. 3.1.1–Дополнение графов.
Очевидно, что 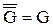 и и 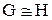 тогда и только тогда, когда тогда и только тогда, когда 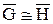 . .
Граф, изоморфный своему дополнению, называется самодополнительным. Например, 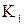 и граф, изображённый на рис. 3.1.2, – самодополнительные. и граф, изображённый на рис. 3.1.2, – самодополнительные.
Рисунок. 3.1.2–Самодополнительные графы.
Теорема Пусть G – обыкновенный граф с матрицей смежности вершин А. Тогда матрицей смежности вершин графа 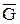 является матрица является матрица 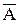 , образованная поэлементным логическим отрицанием матрицы А, исключая диагональные элементы, которые остаются нулевыми. , образованная поэлементным логическим отрицанием матрицы А, исключая диагональные элементы, которые остаются нулевыми.
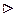 Если число вершин графа G равно p, то матрицы А и Если число вершин графа G равно p, то матрицы А и 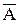 имеют одинаковую размерность имеют одинаковую размерность 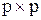 . Если G – неориентированный обыкновенный граф, то элемент . Если G – неориентированный обыкновенный граф, то элемент 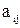 ( (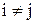 ) матрицы А равен 1, если вершины ) матрицы А равен 1, если вершины 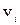 и и 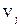 смежны, и 0 в противном случае. Так как смежны, и 0 в противном случае. Так как 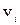 и и 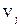 ( (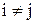 ) смежны в ) смежны в 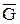 тогда и только тогда, когда они не смежны в G, то тогда и только тогда, когда они не смежны в G, то 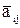 равно 1 (0) в равно 1 (0) в 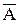 тогда и только тогда, когда тогда и только тогда, когда 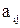 равно 0 (1) в А. равно 0 (1) в А.
Если G – обыкновенный орграф, то элемент 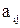 ( (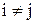 ) матрицы А равен 1, если существует дуга ) матрицы А равен 1, если существует дуга 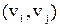 в G, и 0 в противном случае. Элемент в G, и 0 в противном случае. Элемент 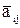 ( (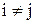 ) в ) в 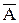 равен 1 (0) тогда и только тогда, когда не существует (существует) дуга равен 1 (0) тогда и только тогда, когда не существует (существует) дуга 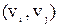 в G, т.е. элемент в G, т.е. элемент 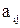 равен 0 (1) в А. равен 0 (1) в А.
 в А и в А и  в в 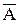 , т. к. G и , т. к. G и 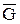 – обыкновенные графы. – обыкновенные графы.
Матрицы смежности вершин А графа 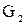 и и  графа графа  , изображённых на рис. 3.1.3, имеют вид: , изображённых на рис. 3.1.3, имеют вид:
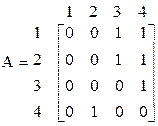 , , 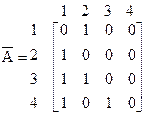 . .
Правильность построения матрицы 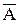 можно легко проверить по рис. 3.1.3 можно легко проверить по рис. 3.1.3
Объединение графов
G1 и G2 , обозначаемое как G1 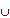 G2 , представляет такой граф G3 = (Х1 G2 , представляет такой граф G3 = (Х1  Х2, A1 Х2, A1  A2), что множество его вершин является объединением Х1 и Х2 , а множество ребер – объединением A1 и A2 . ГрафG3 , полученный операцией объединения графов G1 и G2 , показан на рис. 2.2.1,д, а его матрица смежности – на рис. 2.2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2 . A2), что множество его вершин является объединением Х1 и Х2 , а множество ребер – объединением A1 и A2 . ГрафG3 , полученный операцией объединения графов G1 и G2 , показан на рис. 2.2.1,д, а его матрица смежности – на рис. 2.2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2 .
Объединение графов.
Пусть 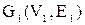 и и 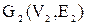 – произвольные графы. Объединением – произвольные графы. Объединением 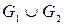 графов графов 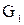 и и 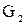 называется граф со множеством вершин называется граф со множеством вершин 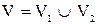 и множеством рёбер и множеством рёбер 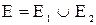 . .
Операция объединения графов обладает следующими свойствами, которые следуют из её определения и свойств операции объединения множеств:
для любых графов 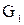 и и 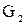 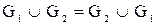 – свойство коммутативности; – свойство коммутативности;
для любых графов 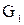 , , 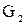 и и 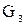 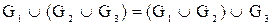 – свойство ассоциативности. – свойство ассоциативности.
Операция объединения распространяется на любое конечное число графов по индукции: 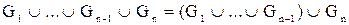 . .
Операция объединения графов может быть выполнена в матричной форме.
Теорема . Пусть 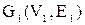 и и 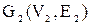 – два графа (ориентированные или неориентированные одновременно), и пусть – два графа (ориентированные или неориентированные одновременно), и пусть  и и  – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа 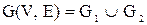 является матрица А, полученная поэлементным взятием максимального элемента вспомогательных матриц А1¢ и А2¢. Матрицы Аi¢, i=1,2, получаются из является матрица А, полученная поэлементным взятием максимального элемента вспомогательных матриц А1¢ и А2¢. Матрицы Аi¢, i=1,2, получаются из 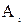 с помощью добавления нулевых строк и столбцов, соответствующих вершинам, отсутствующим в с помощью добавления нулевых строк и столбцов, соответствующих вершинам, отсутствующим в 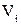 , но присутствующим в , но присутствующим в 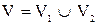 . .
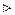 По определению графа По определению графа 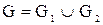 его матрица смежности А имеет размерность его матрица смежности А имеет размерность 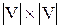 . Построим вспомогательные графы . Построим вспомогательные графы 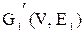 и и 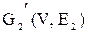 . Очевидно, что их матрицами смежности вершин будут . Очевидно, что их матрицами смежности вершин будут 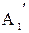 и и 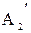 соответственно. Очевидно также, что соответственно. Очевидно также, что 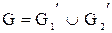 . Для каждой пары вершин . Для каждой пары вершин 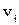 и и 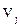 из V в из V в 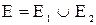 входит максимальное число рёбер, соединяющих их в входит максимальное число рёбер, соединяющих их в 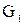 и и 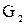 , что и определяет значение элемента , что и определяет значение элемента 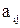 матрицы А. матрицы А.
Следствие. Если элементы матриц смежности вершин 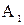 и и 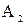 графов графов 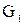 и и 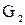 принимают только значения 0 и 1, то операция взятия максимального элемента для нахождения матрицы смежности вершин принимают только значения 0 и 1, то операция взятия максимального элемента для нахождения матрицы смежности вершин 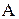 графа графа 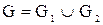 соответствует логической сумме элементов. соответствует логической сумме элементов.
Соединение графов
Эта операция была введена А.А. Зыковым. Пусть 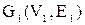 и и 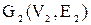 – два одновременно неориентированных или ориентированных графа с непересекающимися множествами вершин. Соединение графов – два одновременно неориентированных или ориентированных графа с непересекающимися множествами вершин. Соединение графов 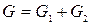 состоит из состоит из 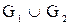 и всех рёбер в случае неориентированного графа (пар нестрого параллельных дуг в случае орграфа), соединяющих вершины из и всех рёбер в случае неориентированного графа (пар нестрого параллельных дуг в случае орграфа), соединяющих вершины из 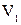 с вершинами из с вершинами из 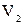 . В частности, . В частности, 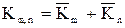 , по определению полного двудольного графа. Эта операция иллюстрируется на рис. 3.2.1, где , по определению полного двудольного графа. Эта операция иллюстрируется на рис. 3.2.1, где 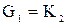 и и 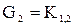 . .
Рис. 3.2.1–Соединение графов.
Операция соединения
графов обладает следующими свойствами, которые следуют из её определения и свойств операции объединения:
для любых графов 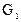 и и 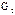 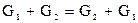 – свойство коммутативности; – свойство коммутативности;
для любых графов 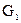 , , 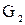 и и 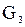 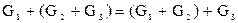 – свойство ассоциативности. – свойство ассоциативности.
Операцию соединения можно распространить по индукции на любое конечное число графов, все множества вершин которых различны: G1+…+Gn–1+Gn=(G1+…+Gn–1)+Gn.
1.2 Кодирование.
В программе реализован граф в виде матрице смежности. Использован класс «MatrixGraph». Анализировав требования было разработано меню понятный для пользователя.(приложение «А» рис.А4)
Класс «MatrixGraph».
Переменные класса:
int** graph;– Инициализация динамического массива.
int vertexNumber; Число вершин графа.
Методы класса.
Таблица 2– Методы класса «Polya».
| Название
|
Входные данные
|
Выходные данные
|
Описание
|
| MatrixGraph();
|
int
|
-
|
Инициализирует динамический массив.
|
| ShowUnion();
|
MatrixGraph a
|
Void
|
Вывод на экран объединение двух графов.
|
| ComplementGraph();
|
-
|
Void
|
Дополнение графа.
|
| addArc();
|
int from, int to
|
void
|
Добавление дуги в граф.
|
| deleteArc();
|
int from, int to
|
Void
|
Удаление дуги из граф.
|
| addNode();
|
int n
|
Void
|
Добавление вершины
|
| deleteNode();
|
int n,bool flag
|
Void
|
Удаление вершины
|
| hasArc();
|
int from, int to
|
Int
|
Проверка на наличие дуги
|
| Size()
|
int
|
Возвращает значение количества вершин.
|
| PrintMatrix();
|
void
|
Вывод на экран матрицу смежности графа.
|
В функции «Main» инициализируется два графа, и выводиться меню. В меню предложены основные операции над графами.
Код программы проекта приведен в приложении «Б».
1.3 Тестирование.
В Проекте программа неоднократно тестировалась. Тестировался инициализация динамической матрицы. Тестировались также такие части программы как:
1.Добавление дуги в матрицу А.
2.Удаление дуги из матрицы А.
3. Добавление вершину в матрицу А.
4. Удаление вершину из матрицы A.
5.Вывод объединения А и B.
6.Вывод дополнения А.
При запуске приложение выводиться меню при соответственном выборе натурального числа, запускается соответствующая операция над графами. Соответственно:
1.Добавить дугу в матрицу А.
2.Удалить дугу из матрицы А.
3.Добавить дугу в матрицу B.
4.Удалить дугу из матрицы B.
5.Добавить вершину в матрицу А.
6.Удалить вершину из матрицы A.
7.Вывод объединения А и B.
8.Вывод дополнения А.
9.Выход…
Все результаты должны были соответствовать законам теории графов.
1. Добавление дуги в матрицу – проверяется методом класса правильность веденных значений вершин между которыми должно установиться смежность. Если значение корректны устанавливается дуга.
2. Удаление дуги из матрицы –также проводиться на корректность значений вершин и удаляется дуга.
3. Добавление вершины– проверяется значение веденное пользователем. Если значение вершины существует в матрице, проверяется было ли удалено раньше эта вершина, если да соответственно производиться добавление в противном случаи оставляется все без изменение. В случаи не существование вершины матрица увеличивается в размере.
4. Удаление вершины – производиться зачеркивание соответствующих элементов матрицы.
5. Объединение двух графов - Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2 .
Результаты тестирование выбора типа операции и соответственно выполнения операции над графами показаны в приложении «В» на рисунке В5-В11.
В результате выполнения курсовой работы была разработана консольная программа, реализующая представление графа в виде матрицы смежности. Также были реализованы следующие операции:
· дополнение графа;
· объединение графов;
· добавление ребра в граф.
· удаление вершины из графа
· удаление ребра из графа
· добавление вершины в граф
Все поставленные задачи были осуществлены. Навыки, полученные при написании программы, могут быть применены в дальнейшем при написании более сложных программ.
Разумеется, методы и сферы применения графов не ограничиваются тем, что представлено в этой работе, так как были рассмотрены только базовые, наиболее известные методы.
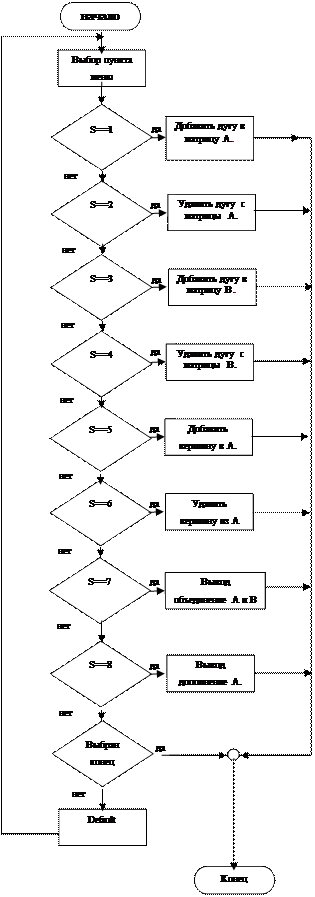
Рисунок A4 – Алгоритм меню.
Файл
MatrixGraph
.
h
#pragma once
class MatrixGraph
{
int** graph;
int vertexNumber;//число вершин
public:
MatrixGraph(int);
void ShowUnion(MatrixGraph a);
void ComplementGraph(); //дополнение
void addArc(int,int);//добавление дуги
void deleteArc(int,int);
void addNode(int);
void deleteNode(int,bool);
int hasArc(int,int);// проверка дуги
int Size(){return vertexNumber;}
void PrintMatrix();
};
Файл
MatrixGraph.cpp
#include "StdAfx.h"
#include "MatrixGraph.h"
MatrixGraph::MatrixGraph(int n)
{
graph=new int*[vertexNumber=n];
for(int i=0;i<n;i++)
{
graph[i]=new int[n];
for(int j=0;j<n;j++)
{
graph[i][j]=0;
}
}
}
void MatrixGraph::addNode(int n)
{
int temp_n=n,countVertex;
temp_n--;
int** tempgraph;
if(temp_n<=0)
{
return;
}
if(temp_n>0&&temp_n<vertexNumber)
{
if(graph[temp_n][temp_n]==-1)
{
deleteNode(temp_n,false);
}
}
else
{
countVertex=n-vertexNumber;
n=countVertex+vertexNumber;
tempgraph=new int*[n];
for(int i=0;i<n;i++)
{
tempgraph[i]=new int[n];
for(int j=0;j<n;j++)
{
tempgraph[i][j]=0;
}
}
for(int i=0;i<vertexNumber;i++)
{
for(int j=0;j<vertexNumber;j++)
{
tempgraph[i][j]=graph[i][j];
}
}
delete [] graph;
graph=tempgraph;
vertexNumber+=countVertex;
}
}
void MatrixGraph::deleteNode(int n,bool flag)
{
if(n<0||n>=vertexNumber)
{
return;
}
if(flag)
{
for(int i=0;i<vertexNumber;i++)
{
for(int j=0;j<vertexNumber;j++)
{
graph[i][n]=-1;
graph[n][j]=-1;
}
}
}
else
{
for(int i=0;i<vertexNumber;i++)
{
for(int j=0;j<vertexNumber;j++)
{
graph[i][n]=0;
graph[n][j]=0;
}
}
}
}
void MatrixGraph::PrintMatrix()
{
for(int i=0; i<=vertexNumber; i++)
{
cout.width(3);
if(i==0){cout<<" "; i++;}
cout<<"X"<<i;
}
cout<<endl<<endl;
for(int i=0;i<vertexNumber;i++)
{
cout.width(4);
cout<<"X"<<i+1;
for(int j=0;j<vertexNumber;j++)
{
cout.width(4);
if(graph[i][j]==-1)
{
cout<<"#";
}
else
{
cout<<graph[i][j];
}
}
cout<<endl<<endl;
}
}
void MatrixGraph::addArc(int from,int to)
{
if(from<0||from>=vertexNumber||to<0||to>=vertexNumber)
return;
graph[from][to]=1;
}
void MatrixGraph::deleteArc(int from,int to)
{
if(from<0||from>=vertexNumber||to<0||to>=vertexNumber)
return;
graph[from][to]=0;
}
int MatrixGraph::hasArc(int from,int to)
{
if(from<0||from>=vertexNumber||to<0||to>=vertexNumber)
return false;
return graph[from][to];
}
void MatrixGraph::ComplementGraph()
{
for(int i=0;i<vertexNumber;i++)
{
for(int j=0;j<vertexNumber;j++)
{
if(graph[i][j]==0)
{
graph[i][j]=1;
}
else
{
if(graph[i][j]==1)
{
graph[i][j]=0;
}
}
}
}
for(int i=0;i<vertexNumber;i++)
{
for(int j=0;j<vertexNumber;j++)
{
if(i==j)
{
graph[i][j]=0;
}
}
}
}
void MatrixGraph:: ShowUnion(MatrixGraph a)
{
int max,min;
a.Size()>vertexNumber ? max=a.Size():max=vertexNumber;
a.Size()<vertexNumber? min=a.Size():min=vertexNumber;
MatrixGraph c(max);
for(int i=0;i<max;i++)
{
for(int j=0;j<max;j++)
{
if(a.hasArc(i,j)==1|| hasArc(i,j)==1)
{c.addArc(i,j); }
}
}
c.PrintMatrix();
}
Файл «Kursach.cpp»
#include "stdafx.h"
#include<windows.h>
#include<iostream>
#include"MatrixGraph.h"
using namespace std;
void main()
{
SetConsoleCP(1251);
SetConsoleOutputCP(1251);
MatrixGraph a(6),b(6);
a.addArc(0,1);
a.addArc(1,2);
a.addArc(1,4);
a.addArc(2,3);
a.addArc(3,2);
a.addArc(4,0);
cout<<"Матрица А."<<endl;
a.PrintMatrix();
b.addArc(0,1);
b.addArc(1,4);
b.addArc(4,0);
b.addArc(4,3);
cout<<"Матрица B."<<endl;
b.PrintMatrix();
int n,from,to,vertex;
do
{
cout.width(3);
cout<<"///////////////////////////////////////\n";
cout<<"// 1.Добавить дугу в матрицу А. //\n";
cout<<"// 2.Удалить дугу из матрицы А. //\n";
cout<<"// 3.Добавить дугу в матрицу B. //\n";
cout<<"// 4.Удалить дугу из матрицы B. //\n";
cout<<"// 5.Добавить вершину в матрицу А. //\n";
cout<<"// 6.Удалить вершину из матрицы A. //\n";
cout<<"// 7.Вывод объединения А и B. //\n";
cout<<"// 8.Вывод дополнения А. //\n";
cout<<"// 9.Выход... //\n";
cout<<"///////////////////////////////////////\n";
cin>>n;
switch(n)
{
case 1:cout<<"Ведите вершины.\n";
cin>>from>>to;
from--;to--;
a.addArc(from,to);
a.PrintMatrix();break;
case 2:cout<<"Ведите вершины.\n";
cin>>from>>to;
from--;to--;
a.deleteArc(from,to);
a.PrintMatrix();break;
case 3:cout<<"Ведите вершины.\n";
cin>>from>>to;
from--;to--;
b.addArc(from,to);
b.PrintMatrix();break;
case 4:
cout<<"Ведите вершины.\n";
cin>>from>>to;
from--;to--;
b.deleteArc(from,to);
b.PrintMatrix();break;
case 5:cout<<"Ведите вершину.\n";
cin>>vertex;
//vertex--;
a.addNode(vertex);
a.PrintMatrix();break;
case 6:cout<<"Ведите вершину.\n";
cin>>vertex;
vertex--;
a.deleteNode(vertex,true);
a.PrintMatrix();break;
case 7:a.ShowUnion(b);break;
case 8:a.ComplementGraph();
a.PrintMatrix();
case 9:cout<<"Выход...\n";break;
default: cout<<"Попробуйте еще\n";
}
}while(n!=9);
}
 Результаты тестирования. Результаты тестирования.
Рисунок B5–Вывод матрицы А , B и операций над графами.

Рисунок B6–Вывод выполнение операции добавление дуги.
 
а) б)

с)
Рисунок B7–Вывод выполнение операции удаление и добавление вершины матрицы.

Рисунок B8–Вывод выполнение операции объединение А и В.

Рисунок B9–Вывод выполнение операции дополнение А .

Рисунок B10–Вывод выполнение операции удаление дуги.

Рисунок В11– Выход из меню.
1. Лафоре Р. Oобъектно-ориентированное программирование в С++. Классика Computer Science. 4-ое изд. /Р.Лафоре–СПб.: Питер, 2004.-924с.:ил.
2. Герберт Шилдт. С++ руководство для начинающих. 2-ое издание. / Пер. с англ. — М. : Издатель-ский дом "Вильяме", 2005. — 672 с. : ил. — Парал. тит. англ.
3. Герберт Шилдт. Полный справочник по С++, 4-е издание. . Пер. с англ. — М. : Издательский дом "Вильяме", 2006. — 800 с. : ил. — Парал. тит. англ.
15ВЫ 5-8459-0489-7 (рус.)
4.Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4
|