Лабораторная работа: Електромагнітна сумісність
|
Название: Електромагнітна сумісність Раздел: Рефераты по физике Тип: лабораторная работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ Кафедра ЕПМ РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА З «ЕЛЕКТРОМАГНІТНОЇ СУМІСНОСТІ» Виконав: ст.гр. ЕСЕ – 08м Овсянніков М.А. Перевірив: проф. Курінний Е.Г. Донецьк – 2008 ІМІТАЦІЯ БАЗОВОГО ГРАФІКА ЗАВАДИ
Таблиця 1 – Початкові дані для обробки базового графіка, мм
Графік завад є випадковим, тому що він утворюється великою кількістю електроприймачів. Практичне заняття № 2 СТАТИСТИЧНА ОБРОБКА БАЗОВОГО ГРАФІКА Мета – визначення статистичної функції розподілу і її характеристик. 2.1 За даними табл.1 розраховую наступні числові характеристики базового графіка: - середнє значення
y
c
= - ефективне значення
y
е
= - дисперсія
Dy
= - стандарт σy
= - коефіцієнт форми
k
ф
= де i – індекс підсумування від 0 до N . 2.2 Знаходжу статистичну функцію F розподілу ординат базового графіка. Таблиця 2 – Статистична функція розподілу базового графіка
За даними стовпців 1 (абсциси) і 4 (ординати) викреслюю графік 1.
Рисунок 2.1 – Статистична функція розподілу базового графіка 2.3 Знаходжу ymin мінімальне і ymax максимальне значення випадкової величини згідно з інтегральною імовірністю 95%, якій відповідають імовірності Ex = 0,05 для мінімального і Ex = 0,95 для максимального значень.
ymin =32,5 мм; ymax =132,5 мм. З табл. 1 виписую найменшу у м і найбільшу у М ординати – повинно бути: у м < y min , у М > y max . у м =18 мм; у М =145 мм. 18<32,5 145>132,5 Умова виконується. Висновки: 1. Випадковий графік має невипадкові характеристики. 2. Використання згідно з ГОСТ 13109-97 практично достовірних значень показників ЕМС дозволяє заощаджувати капітальні вкладення на забезпечення ЕМС. Практичне заняття № 3 АПРОКСИМАЦІЯ СТАТИСТИЧНОЇ ФУНКЦІЇ РОЗПОДІЛУ Мета – перевірка можливості апроксимації статистичної (опитної) функції розподілу теоретичними імовірнісними розподілами: рівномірним і нормальним. Критерій перевірки.
Відповідність теоретичної функції розподілу F (у)
статистичній
де N – кількість дослідів (N 0 = 50) 3.1 Рівномірний закон розподілу характеризується прямолінійною функцією розподілу F п (у) у межах
де – y c = 85 мм, σy = 33 мм беремо з практичної роботи №2. Теоретичний діапазон змінення k п = y пМ – y пм =142-28=114 мм. (3.3) Наносимо точки а і b з координатами (у пм , 0) і (у пМ , 1) на графік статистичної функції, який зображений на рис. 3.1. Ці точки з'єднуємо прямою. Перевіряємо можливість прийняття рівномірного розподілу для апроксимації статистичної функції розподілу за критерієм Колмогорова:
3.2 Нормальний закон розподілу характеризується функцією розподілу F
н
(у
) від – до табл. 3.1.
У верхній частині таблиці у < у с , тому ці значення є від'ємними. З таблиці Б.1 по абсолютним величинам | z | знаходимо значення Φ(| z | ) і заносимо їх до табл. 3.1. Шукані значення функції нормального розподілу
У нижній частині таблиці при у > у с аргумент z є позитивним. У цьому випадку знайдені з таблиці Б.1 значення Φ (| z | ) заносимо зразу в останній стовпець, оскільки
Нижня частина стовпця Φ(| z | ) не заповнюється. Перевіряємо можливість прийняття рівномірного розподілу для апроксимації статистичної функції розподілу за критерієм Колмогорова:
Таблиця 3.1 – Функція розподілу нормального закону
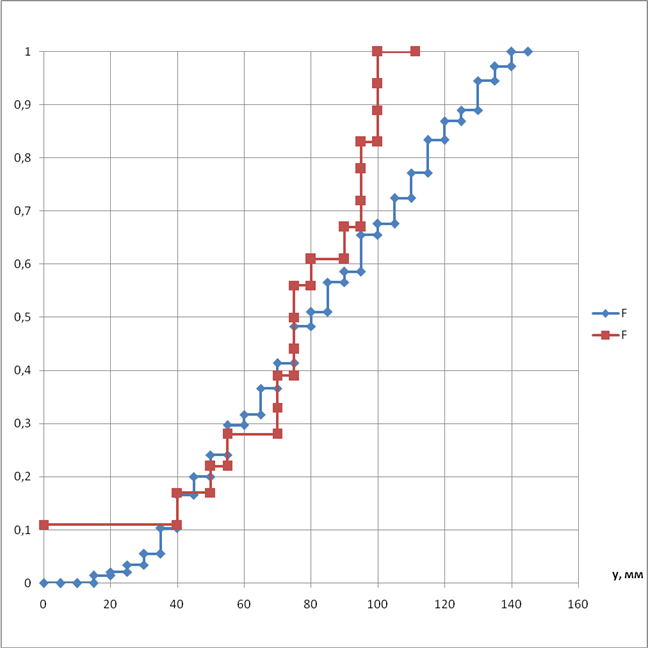
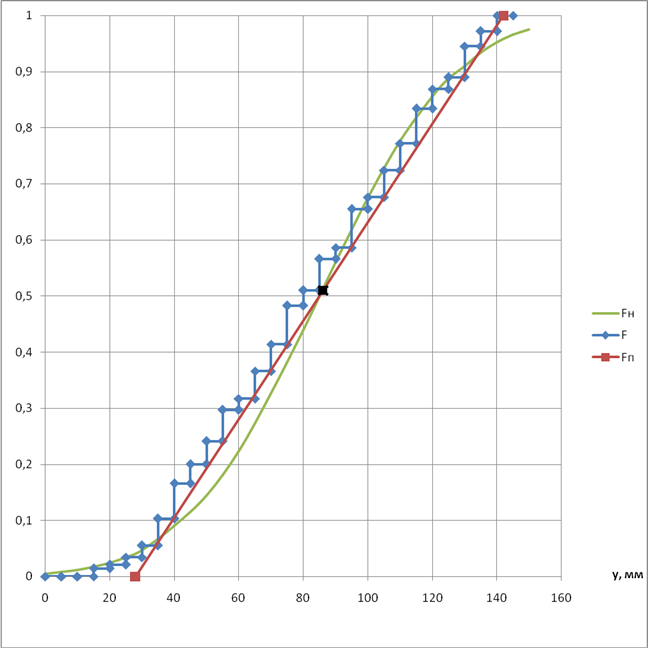
Рисунок 3.1 – Функції розподілу: 3.3 Зіставляємо розрахункові значення: статистичні і теоретичні. Розходження вважається прийнятим, якщо воно не перевищує 10% від найбільш можливої ординати – 150 мм. Таблиця 3.2 – Зіставлення розрахункових значень
Мінімальні і максимальні розрахункові значення: - для рівномірного розподілу
де дані беремо з п.3.1, - для нормального розподілу
Розраховуємо відносні розходження: - для рівномірного розподілу
- для нормального розподілу
Висновки: 1. Згідно до розрахунків рівномірний і нормальний розподіли є прийнятними за критерієм Колмогорова, тому ми приймаємо нормальний закон, як такий, що за фізичним змістом більш відповідає умовам опиту. 2. За розрахунками абсолютні величини не перевищують допустиме значення розходження 10%. Практичне заняття № 4 ОЦІНЮВАННЯ ЕМС ЗА НОРМАМИ НА ВІДХИЛЕННЯ НАПРУГИ Мета – перевірка дотримання норм стандарту [1] на однохвилинні відхилення напруги. 4.1 Базовий графік (гр. з пр. з. № 1) вважається графіком змінення за часом t діючих значень U напруги у відносних одиницях (в.о.). Зв'язок між ординатами у у мм і напругою дається співвідношеннями:
U = 1 + 0,0008·y . (4.1) 4.2 Базовий графік напруги розбиваємо на однохвилинні ділянки: для цього через кожні 40 мм проводимо вертикальні лінії. Для першої ділянки перевіряємо точність візуальної обробки шляхом розрахунку точного значення:
де підсумовуються квадрати 8 перших значень з табл. 1. Таким чином, графік у θ (t) є ступеневим з кількістю ступенів Ν = 720/40 =18. Величини ступенів заносимо у стовпець 2 табл. 4,1, у якій i – номер ступеня (стовпець 1). В стовпці 3 їх розташовуємо у порядку зростання – позначення у θз . У стовпець 4 заносять значення функції розподілу
перше з яких дорівнює 1/40 = 0,025, а останнє – одиниці. Таблиця 4.1 – Дані для розрахунку однохвилинних напруг
Мінімальне розрахункове значення у θmin та максимальне значення у θmax знаходимо з табл. 4.1. Підставивши їх в одну з формулу (4.1), отримаємо мінімальне U θmin і максимальне U θmax розрахункові значення однохвилинних напруг U θ у в.о. ( в стандарті [1] – U у ):
у θmin =40 мм, у θmax =115 мм, U θmin = 1 + 0,0008 · у θmin =1+0,0008·40=1,03, U θmax = 1 + 0,0008· у θmax =1+0,0008·115=1,09. U θmin ≥ 0,95 – виконується, U θmax ≤ 1,05 – не виконується. Порівняємо значення U min та U max (які перерахуємо за формулою (4.1) для у min =32,5 мм та у max =132,5 мм) з U θmin і U θmax : U min = 1 + 0,0008·32,5 =1,026, U max = 1 + 0,0008·132,5=1,11. U θmin ≥ U min , U θmax ≤ U max
Рисунок 4.1 – Статистична функція розподілу базового графіка та функція розподілу відхилення напруги Висновки: 3. Норми стандарту [1] на однохвилинні відхилення напруги не виконуються, тому що максимальне значення відхилення напруги перевищує допустимі 5%. 4. Однолінійне усереднення зменшує диапозон змінення графіка. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
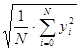 = 91 мм;
= 91 мм;
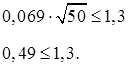
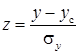 . (3.4)
. (3.4)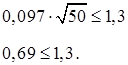
 , (4.2)
, (4.2)