| Министерство образования и науки Российской Федерации
Вятский государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и МПМ
Дипломная работа
Метризуемость топологических пространств
Выполнила
студентка 5 курса
математического факультета
Побединская Татьяна Викторовна
_______________________________
(подпись)
Научный руководитель
к.ф.-м.н., доцент кафедры математического анализа и МПМ Варанкина Вера Ивановна
_______________________________
(подпись)
Рецензент
_______________________________
(подпись)
Допущена к защите в ГАК
Зав. кафедрой______________________________к.п.н., доцент Крутихина М.В.
(подпись)
«_____» _______________2004 г.
Декан факультета_________________________к.ф.-м.н., доцент Варанкина В.И.
(подпись)
«_____» _______________2004 г.
КИРОВ
2004
Содержание
Введение. 3
Глава I. Основные понятия и теоремы.. 4
Глава II. Свойства метризуемых пространств. 10
Глава III. Примеры метризуемых и неметризуемых пространств. 21
Библиографический список. 24
Тема дипломной работы – «Метризуемость топологических пространств».
В первой главе работы вводятся основные определения, связанные с понятиями метрического и топологического пространств.
Во второй главе рассматриваются и доказываются следующие свойства метризуемых пространств:
1. Метризуемое пространство хаусдорфово.
2. Метризуемое пространство нормально.
3. В метризуемом пространстве
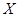 выполняется первая аксиома счетности. выполняется первая аксиома счетности.
4. Метризуемое пространство совершенно нормально.
5. Для метризуемого пространства 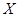 следующие условия эквивалентны: следующие условия эквивалентны:
1) 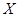 сепарабельно, сепарабельно,
2) 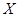 имеет счетную базу, имеет счетную базу,
3) 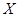 финально компактно. финально компактно.
6. Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.
7. Произведение счетного числа метризуемых пространств метризуемо.
В третьей главе рассматриваются примеры метризуемых и неметризуемых пространств.
Глава
I. Основные понятия и теоремы
Определение.
Метрическим пространством
называется пара 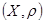 , состоящая из некоторого множества (пространства) , состоящая из некоторого множества (пространства) 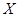 элементов (точек) и расстояния, то есть однозначной неотрицательной действительной функции элементов (точек) и расстояния, то есть однозначной неотрицательной действительной функции 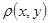 , определенной для любых , определенной для любых  и и 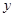 из из 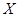 и удовлетворяющей трем условиям: и удовлетворяющей трем условиям:
1) 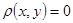 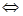 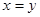 (аксиома тождества); (аксиома тождества);
2) 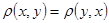 (аксиома симметрии); (аксиома симметрии);
3) 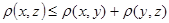 (аксиома треугольника). (аксиома треугольника).
Определение.
Пусть 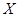 – некоторое множество. Топологией в – некоторое множество. Топологией в 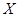 называется любая система
называется любая система 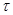 его подмножеств его подмножеств 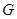 , удовлетворяющая двум требованиям: , удовлетворяющая двум требованиям:
1. Само множество 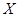 и пустое множество принадлежат и пустое множество принадлежат 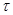 . .
2. Объединение 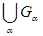 любого (конечного или бесконечного) и пересечение любого (конечного или бесконечного) и пересечение 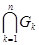 любого конечного числа множеств из любого конечного числа множеств из 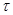 принадлежат принадлежат 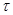 . .
Множество 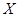 с заданной в нем топологией с заданной в нем топологией 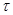 , то есть пара , то есть пара 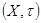 , называется топологическим
пространством. , называется топологическим
пространством.
Множества, принадлежащие системе 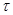 , называются открытыми. , называются открытыми.
Множества 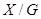 , дополнительные к открытым, называются замкнутыми
множествами топологического пространства , дополнительные к открытым, называются замкнутыми
множествами топологического пространства 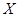 . .
Определение.
Совокупность 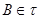 открытых множеств топологического пространства называется базой
топологического пространства
открытых множеств топологического пространства называется базой
топологического пространства 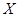 , если всякое открытое множество в , если всякое открытое множество в 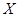 может быть представлено как объединение некоторого числа множеств из может быть представлено как объединение некоторого числа множеств из 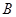 . .
Теорема 1.
Всякая база 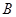 в топологическом пространстве в топологическом пространстве 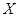 обладает следующими двумя свойствами: обладает следующими двумя свойствами:
1)
любая точка 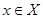 содержится хотя бы в одном содержится хотя бы в одном 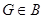 ; ;
2)
если  содержится в пересечении двух множеств содержится в пересечении двух множеств 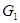 и и 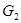 из из 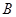 , то существует такое , то существует такое 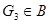 , что , что 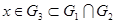 . .
Определение.
Открытым шаром или окрестностью точки 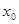 радиуса радиуса 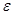
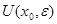 в метрическом пространстве в метрическом пространстве 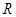 называется совокупность точек называется совокупность точек 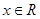 , удовлетворяющих условию , удовлетворяющих условию 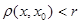 . При этом . При этом 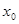 – центр шара, – центр шара, 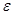 – радиус шара. – радиус шара.
Утверждение 1.
Для любого  , принадлежащего , принадлежащего 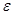 -окрестности точки -окрестности точки 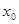 , существует окрестность радиуса , существует окрестность радиуса  , включенная в , включенная в 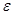 -окрестность точки -окрестность точки 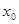 . .
Доказательство.
Выберем в качестве  : :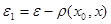 . .
Достаточно доказать для произвольного 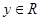 импликацию импликацию 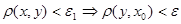 . Действительно, если . Действительно, если 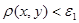 , то , то 
Получаем, что 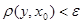 , что и требовалось доказать. , что и требовалось доказать.
Теорема 2.
Совокупность всех открытых шаров образуют базу некоторой топологии.
Доказательство.
Проверим свойства базы (теорема 1).
· Свойство первое очевидно, так как для любого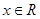 выполняется выполняется 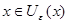 для любого для любого 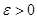 . .
· Проверим второе свойство.
Пусть 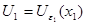 , , 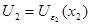 и и 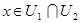 , тогда, воспользовавшись утверждением 1, найдем такое , тогда, воспользовавшись утверждением 1, найдем такое 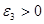 , что , что 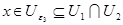 Теорема доказана. Теорема доказана.
Определение.
Топологическое пространство 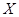 метризуемо
, если существует такая метрика метризуемо
, если существует такая метрика  на множестве на множестве 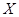 , что порожденная этой метрикой топология совпадает с исходной топологией пространства , что порожденная этой метрикой топология совпадает с исходной топологией пространства 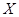 . .
Аксиомы отделимости
Аксиома 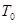 . Для любых двух различных точек топологического пространства окрестность хотя бы одной из них не содержит другую.
. Для любых двух различных точек топологического пространства окрестность хотя бы одной из них не содержит другую.
Аксиома 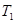 . Каждая из двух произвольных точек пространства имеет окрестность, не содержащую вторую точку.
. Каждая из двух произвольных точек пространства имеет окрестность, не содержащую вторую точку.
Предложение.
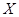 является является 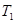 - пространством тогда и только тогда, когда для любого - пространством тогда и только тогда, когда для любого 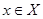 множество множество 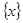 замкнуто. замкнуто.
Доказательство.
Необходимость.
Пусть 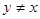 . Так как . Так как 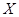 является является 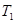 -пространством, то существует окрестность -пространством, то существует окрестность 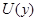 , не содержащая , не содержащая  . .
Рассмотрим 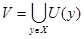
Докажем, что  . Применим метод двойного включения: . Применим метод двойного включения:
· Очевидно, что 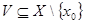 по построению множества по построению множества 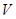 . .
· 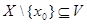 . .
Пусть 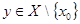 отсюда для любого отсюда для любого 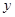 отличного от отличного от 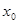 существует окрестность существует окрестность 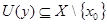 , значит , значит 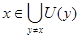 , тогда , тогда 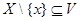 . .
Множество 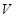 - открыто, как объединение открытых множеств. - открыто, как объединение открытых множеств.
Тогда множество 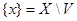 - замкнуто, как дополнение открытого множества. - замкнуто, как дополнение открытого множества.
Достаточность.
Рассмотрим 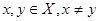 . По условию . По условию 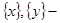 замкнутые множества. Так как замкнутые множества. Так как 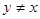 , то , то 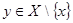 . Множество . Множество 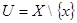 -открыто как дополнение замкнутого и не содержит -открыто как дополнение замкнутого и не содержит  . Аналогично доказывается существование окрестности точки . Аналогично доказывается существование окрестности точки 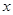 , не содержащей точку , не содержащей точку 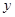
Что и требовалось доказать.
Аксиома  ( аксиома Хаусдорфа). Любые две точки пространства имеют непересекающиеся окрестности.
( аксиома Хаусдорфа). Любые две точки пространства имеют непересекающиеся окрестности.
Аксиома  .
Любая точка и не содержащее ее замкнутое множество имеют непересекающиеся окрестности. .
Любая точка и не содержащее ее замкнутое множество имеют непересекающиеся окрестности.
Определение.
Пространства, удовлетворяющие аксиомам 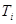 ( (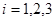 ) называются ) называются 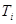 -пространствами
( -пространствами
(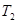 -пространства называют также хаусдорфовыми пространствами
). -пространства называют также хаусдорфовыми пространствами
).
Определение.
Пространство называется нормальным
или 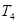 -пространством
, если оно удовлетворяет аксиоме -пространством
, если оно удовлетворяет аксиоме 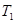 , и всякие его два непустые непересекающиеся замкнутые множества имеют непересекающиеся окрестности. , и всякие его два непустые непересекающиеся замкнутые множества имеют непересекающиеся окрестности.
Определение.
Система окрестностей называется определяющей системой окрестностей точки 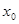 , если для любой окрестности
, если для любой окрестности  точки точки 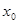 найдется окрестность из этой системы, содержащаяся в найдется окрестность из этой системы, содержащаяся в 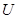 . .
Определение.
Если точка 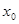 топологического пространства имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполняется первая аксиома счетности
. Если это верно для каждой точки пространства, то пространство называется пространством с первой аксиомой счетности. топологического пространства имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполняется первая аксиома счетности
. Если это верно для каждой точки пространства, то пространство называется пространством с первой аксиомой счетности.
Определение.
Две метрики 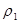 и и 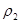 на множестве на множестве 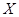 называются эквивалентными
, если они порождают на нем одну и ту же топологию. называются эквивалентными
, если они порождают на нем одну и ту же топологию.
Пример.
На плоскости  для точек для точек 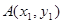 и и 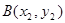 определим расстояние тремя различными способами: определим расстояние тремя различными способами:
1. 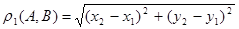 , ,
2.  , ,
3. 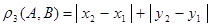 . .
· Введенные расстояния являются метриками. Проверим выполнимость аксиом метрики для введенных расстояний.
1. 1) 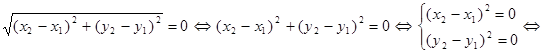
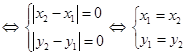
2) так как 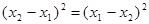 и и  , то вторая аксиома очевидна: , то вторая аксиома очевидна: 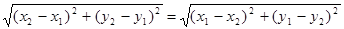
3) рассмотрим точки 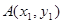 , ,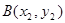 , ,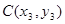 и докажем следующее неравенство: и докажем следующее неравенство:
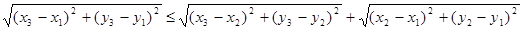 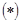
Возведем это неравенство в квадрат:
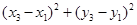 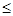 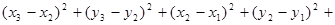
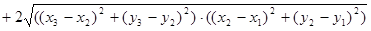 . .
Так как 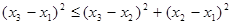 и и 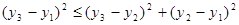 (поскольку (поскольку 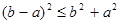 ) и выражение ) и выражение  есть величина неотрицательная, то неравенство есть величина неотрицательная, то неравенство 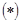 является верным. является верным.
2. 1) 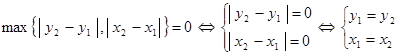
2) так как 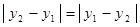 и и 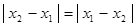 , то вторая аксиома очевидна: , то вторая аксиома очевидна: 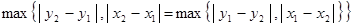 . .
3) рассмотрим точки 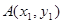 , ,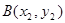 , ,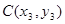 и докажем следующее неравенство: и докажем следующее неравенство: 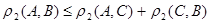 . .
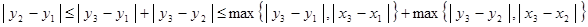
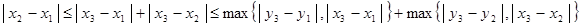
Тогда и 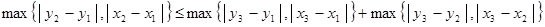 . .
3. 1) 
2) так как 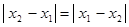 и и 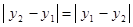 , то вторая аксиома очевидна: , то вторая аксиома очевидна:
 . .
3) рассмотрим точки 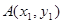 , ,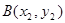 , ,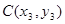 . .
Неравенство: 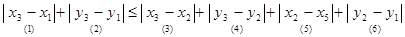 - очевидно. - очевидно.
· Введенные метрики 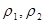 и и 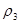 эквивалентны, то есть задают одну и ту же топологию. эквивалентны, то есть задают одну и ту же топологию.
Пусть метрика 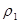 порождает топологию порождает топологию 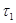 , , 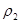 - топологию - топологию 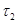 и и 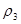 - топологию - топологию 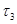 . Достаточно показать два равенства. . Достаточно показать два равенства.
Покажем, что 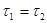 . .
Рассмотрим множество, 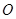 открытое в открытое в 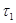 и покажем, что и покажем, что 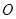 открыто в открыто в 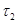 . Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в . Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в 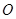 . Шар в . Шар в 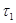 - квадрат, шар в - квадрат, шар в 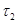 - круг. А квадрат всегда можно заключить в круг. Тогда - круг. А квадрат всегда можно заключить в круг. Тогда 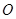 открыто и в открыто и в 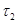 . .
Аналогично доказывается, что 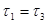 . А тогда и . А тогда и 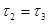 . .
Глава
II. Свойства метризуемых пространств
Свойство 1.
Метризуемое пространство хаусдорфово.
Доказательство.
Пусть  . Возьмем . Возьмем 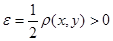 . Докажем, что . Докажем, что 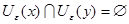 . .
Предположим, что 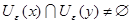 , тогда существует , тогда существует 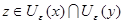 , т.е. , т.е. 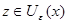 и и 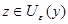 . Тогда, . Тогда, 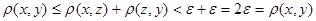 . Получили противоречие. Следовательно, . Получили противоречие. Следовательно, 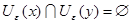 . .
Следствие.
Метризуемое пространство является 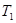 - пространством. - пространством.
Определение.
Расстоянием от точки 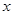 до множества до множества 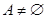 в метрическом пространстве называется в метрическом пространстве называется 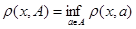 . .
Утверждение 2.
Пусть множество 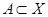 фиксировано; тогда функция фиксировано; тогда функция 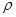 , сопоставляющая каждой точке , сопоставляющая каждой точке 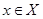 расстояние расстояние 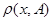 , непрерывна на пространстве , непрерывна на пространстве  . .
Доказательство.
Воспользуемся определением непрерывности: функция 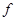 называется непрерывной в точке называется непрерывной в точке 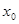 , если , если 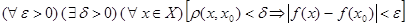 . .
Из неравенства 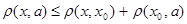 , где , где 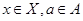 , получаем , получаем  . Аналогично . Аналогично 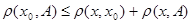 . Из полученных неравенств следует . Из полученных неравенств следует  . .
Для произвольного 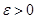 возьмем возьмем 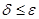 . Тогда из неравенства . Тогда из неравенства 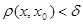 следует следует  . Непрерывность . Непрерывность 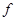 доказана. доказана.
Лемма.
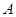 – замкнутое множество в метрическом пространстве – замкнутое множество в метрическом пространстве 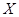 . Для любого . Для любого 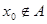 расстояние от расстояние от 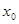 до множества до множества 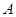 положительно. положительно.
Доказательство.
Множество 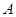 замкнуто, отсюда следует, что множество замкнуто, отсюда следует, что множество 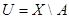 - открыто. Так как точка - открыто. Так как точка 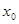 принадлежит открытому множеству принадлежит открытому множеству 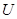 , то существует такое , то существует такое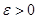 , что , что 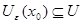 . Так как . Так как 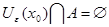 , то , то 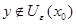 для некоторого для некоторого 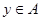 . Поэтому . Поэтому 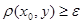 для любого для любого 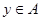 . Следовательно, . Следовательно, 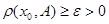 , что и требовалось доказать. , что и требовалось доказать.
Свойство 2.
Метризуемое пространство нормально.
Доказательство.
По доказанному метризуемое пространство является
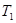 -пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества -пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества 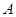 и и 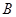 имеют непересекающиеся окрестности. имеют непересекающиеся окрестности.
Так как 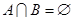 и множество и множество 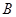 замкнуто по условию, то для любого замкнуто по условию, то для любого  по лемме по лемме 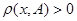 . .
Обозначим 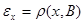 и и 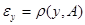 для произвольных для произвольных  и и 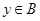 . .
Множества 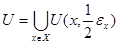 и и 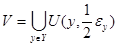 открыты как объединения открытых шаров в открыты как объединения открытых шаров в  и содержат соответственно множества и содержат соответственно множества 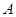 и и 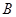 . .
Следовательно, 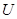 - окрестность множества - окрестность множества 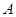 , ,  - окрестность множества - окрестность множества 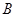 . .
Докажем, что 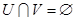 . .
Предположим, что 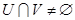 , то есть , то есть 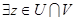 . Тогда из условия . Тогда из условия 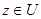 следует, что следует, что 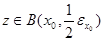 для некоторого для некоторого 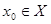 . Отсюда . Отсюда  . .
Аналогично получаем 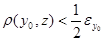 для некоторого для некоторого 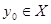 . Для определенности пусть . Для определенности пусть 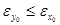 . Тогда . Тогда 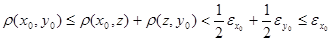 . .
Получаем 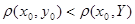 , для некоторой точки , для некоторой точки 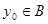 , что невозможно в силу определения расстояния от точки до множества. , что невозможно в силу определения расстояния от точки до множества.
Следовательно 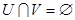 . Таким образом, . Таким образом,  является является 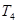 -пространством, а, значит, нормальным пространством. Теорема доказана. -пространством, а, значит, нормальным пространством. Теорема доказана.
Свойство 3.
В метризуемом пространстве
 выполняется первая аксиома счетности. выполняется первая аксиома счетности.
Доказательство.
Пусть 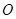 - произвольное открытое множество, содержащее точку - произвольное открытое множество, содержащее точку 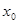 . Так как открытые шары образуют базу топологии метрического пространства, то . Так как открытые шары образуют базу топологии метрического пространства, то 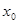 содержится в содержится в 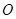 вместе с некоторым открытым шаром, то есть вместе с некоторым открытым шаром, то есть 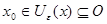 для некоторых для некоторых 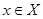 и и 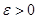 . По утверждению 1 найдется такое . По утверждению 1 найдется такое 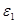 , что , что 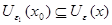 . .
Возьмем 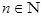 , для которого , для которого 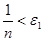 . Тогда . Тогда  . Таким образом открытые шары . Таким образом открытые шары 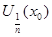 , , 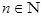 образуют определяющую систему окрестностей точки образуют определяющую систему окрестностей точки 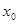 . Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать. . Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.
Определение.
Множеством типа
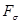 или просто или просто 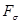 - множеством
пространства - множеством
пространства 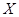 называется всякое множество называется всякое множество 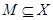 , являющееся объединением счетного числа замкнутых (в , являющееся объединением счетного числа замкнутых (в  ) множеств. ) множеств.
Определение.
Множеством типа 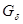 или просто
или просто 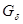 - множеством
пространства - множеством
пространства 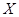 называется всякое множество называется всякое множество 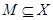 , являющееся пересечением счетного числа открытых (в , являющееся пересечением счетного числа открытых (в  ) множеств. ) множеств.
Очевидно, что множества типа 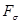 и и 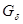 являются взаимно дополнительными друг для друга.
являются взаимно дополнительными друг для друга.
Определение.
Нормальное пространство, в котором всякое замкнутое множество является множеством типа 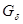 , называется совершенно нормальным
.
, называется совершенно нормальным
.
Утверждение 3.
Нормальное пространство является совершенно нормальным тогда и только тогда, когда всякое открытое множество, принадлежащее этому пространству, является множеством типа 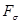 . .
Свойство 4.
Метризуемое пространство совершенно нормально.
Доказательство.
Пусть 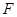 - непустое замкнутое множество в - непустое замкнутое множество в 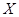 . Тогда . Тогда 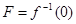 для непрерывной функции для непрерывной функции 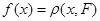 (непрерывность ее установлена в утверждении 2). Обозначим (непрерывность ее установлена в утверждении 2). Обозначим 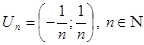 , множества , множества 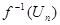 открыты в открыты в 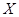 как прообразы открытых множеств при непрерывном отображении. Докажем, что как прообразы открытых множеств при непрерывном отображении. Докажем, что  . .
Пусть  , тогда , тогда  . Так как . Так как 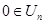 для любого для любого 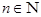 , то , то  для любого для любого 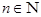 . Отсюда . Отсюда 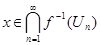 . .
Обратно. Пусть 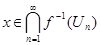 , тогда , тогда  для любого для любого 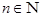 . Отсюда . Отсюда 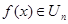 для любого для любого 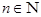 , поэтому , поэтому 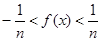 для любого для любого 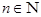 , тогда , тогда 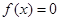 , значит , значит 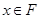 . Таким образом множество . Таким образом множество 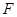 является множеством типа является множеством типа 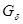 .
.
Определение.
Множество 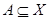 всюду плотно в всюду плотно в  , если любое непустое открытое в
, если любое непустое открытое в  множество содержит точки из множество содержит точки из 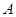 . .
Определение.
Топологическое пространство  называется сепарабельным
, если оно имеет счетное всюду плотное подмножество. называется сепарабельным
, если оно имеет счетное всюду плотное подмножество.
Определение.
Семейство γ открытых в  множеств образуют покрытие пространства множеств образуют покрытие пространства  , если
, если  содержится в объединении множеств этого семейства. содержится в объединении множеств этого семейства.
Определение.
Топологическое пространство  называется финально компактным
, если из любого его открытого покрытия можно выделить счетное подпокрытие. называется финально компактным
, если из любого его открытого покрытия можно выделить счетное подпокрытие.
Свойство 5.
Для метризуемого пространства  следующие условия эквивалентны: следующие условия эквивалентны:
1)  сепарабельно, сепарабельно,
2)  имеет счетную базу, имеет счетную базу,
3)  финально компактно. финально компактно.
Доказательство.
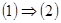
Пусть 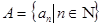 - счетное всюду плотное множество в - счетное всюду плотное множество в 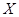 , , 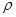 - метрика в - метрика в 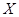 . Множество окрестностей . Множество окрестностей 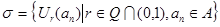 счетно. Докажем, что счетно. Докажем, что 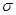 - база топологии в - база топологии в  . Пусть . Пусть 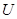 - произвольное открытое в - произвольное открытое в  множество, множество, 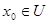 . Тогда . Тогда 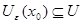 для некоторого для некоторого 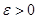 . Рассмотрим рациональное число . Рассмотрим рациональное число  , для которого , для которого 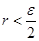 и точку и точку 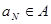 , для которой , для которой 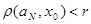 . .
Докажем, что 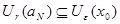 . Пусть . Пусть 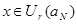 . Так как . Так как 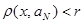 , то , то 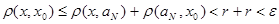 . Тогда . Тогда  . Таким образом, для произвольного . Таким образом, для произвольного 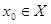 и открытого множества и открытого множества 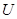 нашелся элемент из нашелся элемент из 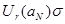 , такой, что , такой, что  . Следовательно . Следовательно 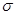 - база топологии. - база топологии.
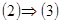 Пусть Пусть 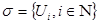 - счетная база в - счетная база в  . Рассмотрим произвольное открытое покрытие множества . Рассмотрим произвольное открытое покрытие множества 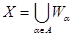 , , 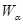 - открыты для любого - открыты для любого 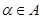 ( (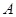 - индексное множество). Для любого - индексное множество). Для любого  существует существует 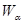 , для которого , для которого 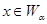 . Так как . Так как 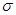 - база, то найдется такое - база, то найдется такое 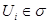 , что , что 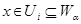 . Тогда . Тогда 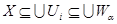 . Поскольку база . Поскольку база 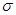 счетна, то счетна, то  покрывается счетным числом соответствующих множеств покрывается счетным числом соответствующих множеств 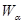 . Таким образом, . Таким образом,  - финально компактно. - финально компактно.
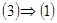 Для каждой точки Для каждой точки 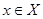 рассмотрим окрестности рассмотрим окрестности 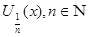 , которые образуют покрытие пространства , которые образуют покрытие пространства  . В силу финальной компактности . В силу финальной компактности 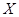 из этого покрытия можно выделить счетное подпокрытие из этого покрытия можно выделить счетное подпокрытие 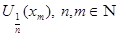 . В каждом из этих множеств выберем точку . В каждом из этих множеств выберем точку 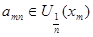 . Множество точек . Множество точек 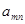 счетно, докажем, что оно плотно в счетно, докажем, что оно плотно в  . Пусть . Пусть 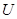 - произвольное открытое множество в - произвольное открытое множество в 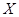 , , 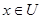 , тогда , тогда 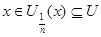 для некоторого для некоторого 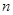 . Существует элемент подпокрытия . Существует элемент подпокрытия 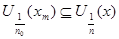 . Тогда . Тогда 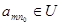 , то есть любое непустое открытое множество в , то есть любое непустое открытое множество в 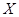 содержит точку этого множества. Что и требовалось доказать. содержит точку этого множества. Что и требовалось доказать.
Определение.
Диаметром непустого множества
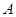 в метрическом пространстве в метрическом пространстве 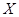 называется точная верхняя грань множества всех расстояний между точками множества называется точная верхняя грань множества всех расстояний между точками множества 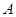 и обозначается и обозначается 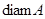 . .
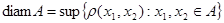 . .
Если 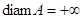 , то множество , то множество 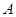 называют неограниченным. называют неограниченным.
Определение.
Метрика  метрического пространства метрического пространства 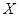 называется ограниченной
, если называется ограниченной
, если 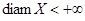 . .
Свойство 6.
Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.
Доказательство.
Пусть метрика  порождает топологию топологического пространства порождает топологию топологического пространства 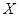 . Положим . Положим 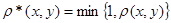 для любых для любых 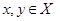 . .
Докажем следующее:
1. 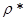 -метрика на -метрика на 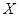 ; ;
2. метрики 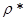 и и  эквивалентны; эквивалентны;
3. 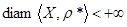 . .
1. Проверим выполнимость аксиом.
1) 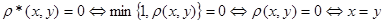 ; ;
2)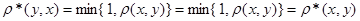 ; ;
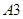 : Докажем, что : Докажем, что 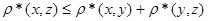 . .
Известно, что  . .
· Если 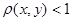 и и  , то , то  и и 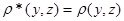 , тогда , тогда 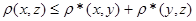 . Так как . Так как 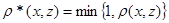 , то , то 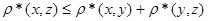 . .
· Если 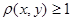 или или 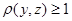 , то , то 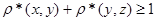 , а , а 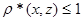 , тогда , тогда 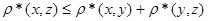 . .
2. Пусть 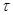 - топология, порожденная метрикой - топология, порожденная метрикой  , а , а  - топология, порожденная метрикой - топология, порожденная метрикой 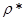 . Докажем, что . Докажем, что  . .
Пусть  - открытое множество в - открытое множество в 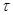 , докажем, что множество , докажем, что множество 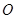 открыто в открыто в  . Для любого . Для любого  существует существует 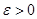 такое, что такое, что 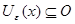 . Можно считать, что . Можно считать, что 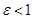 . Тогда . Тогда 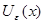 является окрестностью в является окрестностью в 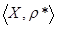 того же радиуса того же радиуса 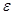 . Следовательно, . Следовательно, 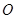 открыто в топологии открыто в топологии  . .
В обратную сторону доказательство проводится аналогично.
Из всего выше сказанного следует, что метрики 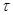 и и 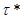 эквивалентны. эквивалентны.
3. Из формулы  следует, что следует, что 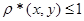 для любых для любых 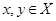 . Отсюда . Отсюда 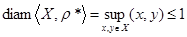 . .
Определение.
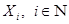 - топологические пространства, - топологические пространства,  . Тихоновским произведением топологических пространств . Тихоновским произведением топологических пространств
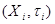 называется топологическое пространство называется топологическое пространство 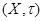 , в котором базу топологии образуют множества , в котором базу топологии образуют множества  , где , где 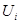 открыто в открыто в 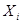 для любого для любого 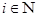 и и 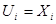 для всех индексов кроме конечного их числа. для всех индексов кроме конечного их числа.
Свойство 7.
Произведение счетного числа метризуемых пространств метризуемо.
Доказательство.
Пусть 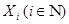 - метризуемые топологические пространства. По лемме на каждом множестве - метризуемые топологические пространства. По лемме на каждом множестве 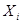 существует ограниченная метрика существует ограниченная метрика 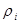 соответственно. соответственно.
Рассмотрим 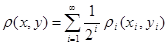 . .
Покажем:
1.  является метрикой на является метрикой на 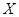 и и 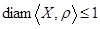 . .
2. топология, порожденная метрикой  , совпадает с топологией произведения пространств , совпадает с топологией произведения пространств 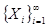 . .
1. Проверим выполнимость аксиом метрики.
1) 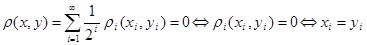 (так как (так как 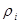 - метрика по условию). - метрика по условию).
2) 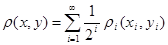 , , 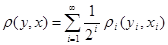 . .
Так как 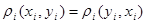 ( (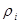 -метрика по условию), то -метрика по условию), то 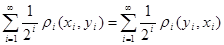 , тогда , тогда 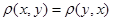 . .
3) Докажем, что 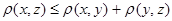 . .
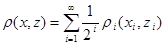 , , 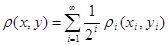 , , 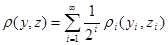 . Но так как выполняется неравенство . Но так как выполняется неравенство 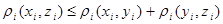 , то будет выполняться неравенство: , то будет выполняться неравенство:
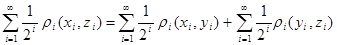 , тогда , тогда 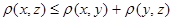 . .
Теперь докажем, что 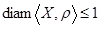 . .
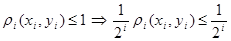 , где , где 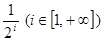 геометрическая прогрессия, а геометрическая прогрессия, а  , тогда , тогда 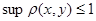 . .
2. 1) Покажем, что каждое множество 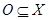 , открытое в топологии, индуцированной метрикой , открытое в топологии, индуцированной метрикой  , открыто и в топологии произведения. , открыто и в топологии произведения.
Рассмотрим произвольную точку 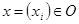 . Существует такое . Существует такое  , что , что 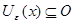 . Далее достаточно найти положительное число . Далее достаточно найти положительное число 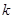 и открытые множества и открытые множества 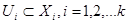 , такие, что , такие, что 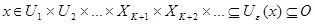 . .
Пусть 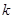 - положительное целое число, удовлетворяющее условию: - положительное целое число, удовлетворяющее условию:
 . .
Для 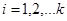 положим положим  и и 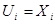 для для 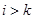 . .
Для каждой точки 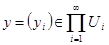 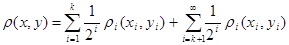 . Рассмотрим полученные суммы. Так как . Рассмотрим полученные суммы. Так как 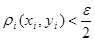 , где , где 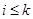 , то , то 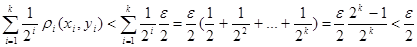 . Так как . Так как 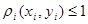 для любых для любых 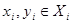 , то , то  . Тогда . Тогда 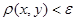 , т.е. , т.е. 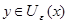 . Таким образом . Таким образом 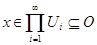 . Следовательно, множество . Следовательно, множество 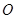 открыто в тихоновской топологии произведения. открыто в тихоновской топологии произведения.
2) Пусть множество 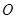 открыто в топологии произведения. Докажем, что оно открыто в топологии, порожденной метрикой открыто в топологии произведения. Докажем, что оно открыто в топологии, порожденной метрикой  . .
Требуется доказать, что для любой точки  найдется такое найдется такое  , что , что  . .
Так как множество 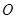 открыто в топологии произведении, то открыто в топологии произведении, то 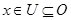 для некоторого множества для некоторого множества 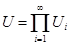 , где , где 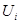 - открыто в - открыто в 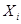 и и  для любого для любого 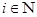 и и 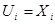 для всех индексов для всех индексов 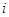 кроме конечного их числа. Поскольку кроме конечного их числа. Поскольку  и и 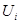 открыто в открыто в 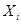 , то , то 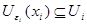 для конечного числа индексов, для которых для конечного числа индексов, для которых 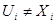 . Пусть . Пусть 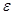 - наименьший из этих значений - наименьший из этих значений 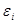 . Докажем, что . Докажем, что 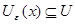 . Возьмем произвольное . Возьмем произвольное 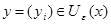 . Тогда . Тогда 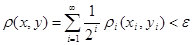 . Отсюда . Отсюда 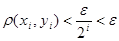 для любого для любого  . Это означает, что . Это означает, что 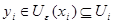 для любого для любого 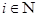 . Получили . Получили 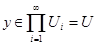 . Следовательно, множество . Следовательно, множество 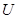 открыто в топологии, индуцируемой метрикой открыто в топологии, индуцируемой метрикой  . Теорема доказана. . Теорема доказана.
Глава
III. Примеры метризуемых и неметризуемых пространств
1. Дискретное топологическое пространство.
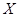 - произвольное непустое множество. Открытым назовем любое подмножество в - произвольное непустое множество. Открытым назовем любое подмножество в  . Очевидно, при этом выполнены все аксиомы топологического пространства. Рассмотрим . Очевидно, при этом выполнены все аксиомы топологического пространства. Рассмотрим 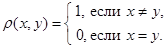 Для любого Для любого 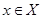 множество множество 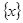 открыто, так как открыто, так как 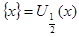 . Следовательно, открыто и любое подмножество в . Следовательно, открыто и любое подмножество в 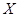 как объединение одноэлементных множеств. Вывод: дискретное топологическое пространство – метризуемо. как объединение одноэлементных множеств. Вывод: дискретное топологическое пространство – метризуемо.
2. Двоеточия.
 . Рассмотрим топологии на . Рассмотрим топологии на 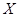 . .
1)  - простое двоеточие. - простое двоеточие.
2) 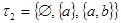 - связное двоеточие. - связное двоеточие.
3) 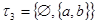 - слипшееся двоеточие. - слипшееся двоеточие.
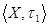 - метризуемо, так как топология - метризуемо, так как топология 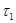 - дискретная. - дискретная.
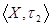 , , 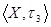 - неметризуемы, так как не являются хаусдорфовыми. - неметризуемы, так как не являются хаусдорфовыми.
3. Стрелка
(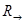 ). ).
В 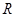 открытыми назовем открытыми назовем  и множества вида и множества вида 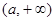 , где , где 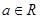 . Очевидно, при этом выполнены все аксиомы топологического пространства. Топологическое пространство . Очевидно, при этом выполнены все аксиомы топологического пространства. Топологическое пространство 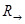 не является хаусдорфовым, а значит неметризуемо. не является хаусдорфовым, а значит неметризуемо.
4. Окружности Александрова
(пространство 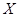 ). ).
Открытые множества в  : :
первого рода
: интервал на малой окружности 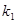 плюс его проекция на большую окружность плюс его проекция на большую окружность 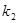 , из которой выброшено конечное число точек. , из которой выброшено конечное число точек.
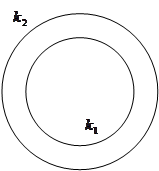 второго рода
: каждая точка на большой окружности открыта. второго рода
: каждая точка на большой окружности открыта.
1. Множество 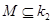 замкнуто в замкнуто в 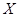 тогда и только тогда, когда тогда и только тогда, когда 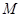 - конечно. - конечно.
Доказательство.
Очевидно, что любое конечное множество 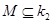 замкнуто как дополнение открытого. Пусть
замкнуто как дополнение открытого. Пусть 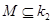 и и 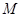 - бесконечно. Докажем, что - бесконечно. Докажем, что 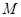 - незамкнуто. - незамкнуто.
Так как 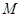 - бесконечно, то оно содержит счетное подмножество, которое можно рассмотреть как последовательность точек, принадлежащих - бесконечно, то оно содержит счетное подмножество, которое можно рассмотреть как последовательность точек, принадлежащих 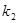 . Эта последовательность ограничена в . Эта последовательность ограничена в 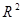 , по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность. Так как , по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность. Так как  замкнуто в замкнуто в 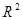 , то предел этой последовательности , то предел этой последовательности 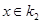 . Пусть . Пусть 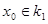 - точка, для которой - точка, для которой 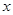 является проекцией на является проекцией на  . Возьмем произвольное открытое в . Возьмем произвольное открытое в 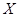 множество
множество 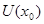 , содержащее точку , содержащее точку 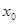 . Тогда исходя из структуры открытых множеств первого рода получаем, что . Тогда исходя из структуры открытых множеств первого рода получаем, что 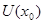 содержит бесконечно много точек множества содержит бесконечно много точек множества  , т.е. , т.е. 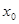 является предельной точкой множества является предельной точкой множества 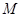 . При этом . При этом 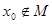 . Следовательно, . Следовательно, 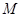 - незамкнуто. - незамкнуто.
2. Множество 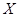 не совершенно нормально. не совершенно нормально.
Доказательство.
Пусть дуга 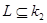 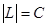 . Множество . Множество  открыто, как объединение открытых одноэлементных множеств. Замкнутыми в открыто, как объединение открытых одноэлементных множеств. Замкнутыми в  являются по доказанному лишь конечные множества. Но счетное объединение конечных множеств счетно. Следовательно являются по доказанному лишь конечные множества. Но счетное объединение конечных множеств счетно. Следовательно 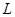 открыто и не является множеством типа открыто и не является множеством типа  . Таким образом множество . Таким образом множество 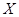 неметризуемо.
неметризуемо.
1. Александров П.С., Пасынков Б.А. Введение в теорию размерности. – М.: Наука, 1973.
2. Энгелькинг Р. Общая топология – М.: Мир, 1986.
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М. Наука, 1989.
|