РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
СПЕЦИАЛЬНОСТЬ «Менеджмент организаций »
К О Н Т Р О Л Ь Н А Я Р А Б О Т А
По предмету: Экономико-математический практикум
Выполнил:
Студент 2 курса
4 семестр
Рахимова Лидия Рустамовна
Ташкент,2009
Задача № 1
Условно стандартная задача линейного программирования
Необходимо выполнить в указанном порядке следующие задания.
1. Найти оптимальный план прямой задачи:
а) графическим методом;
б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
2. Построить двойственную задачу.
3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
4. Найти оптимальный план двойственной задачи по первой теореме двойственности, используя окончательную симплекс-таблицу, полученную при решении прямой задачи (см. п. 1б). Проверить утверждение «значения целевых функций пары двойственных задач на своих оптимальных решениях совпадают».
5. Двойственную задачу решить симплекс-методом, затем, используя окончательную симплекс-таблицу двойственной задачи найти оптимальный план прямой задачи по первой теореме двойственности. Сравнить результат с результатом, который был получен графическим методом (см. п. 1а).
6. Найти оптимальное целочисленное решение:
а) графическим методом;
б) Методом Гомори.
Сравнить значения функций целочисленного и нецелочисленного решений
4
Решение задачи 1
1. Найдем оптимальный план решения графическим методом:
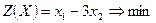 ; ;
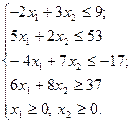
Построим на координатной плоскости Ох
1
х
2
граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе):
  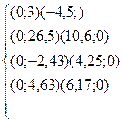
Область допустимых решений определяется многоугольником ОАВС
D
(см. график 1).
Для линий уровня х
1
- 3х
2
= h
(h
— const) строим нормальный вектор 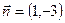 . Перпендикулярно нормальному вектору построим одну из линий уровня (на рис. 1 она проходит через начало координат) Так как задача на минимум, то перемещаем линию уровня в направлении вектора . Перпендикулярно нормальному вектору построим одну из линий уровня (на рис. 1 она проходит через начало координат) Так как задача на минимум, то перемещаем линию уровня в направлении вектора 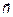 до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L
3
и L
4
, т. е. через точку до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L
3
и L
4
, т. е. через точку 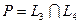 . Для определения координат точки P
решаем систему уравнений . Для определения координат точки P
решаем систему уравнений
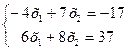 . .
Получаем х
1
= 5,3, х
2
= 0,6. Это и будет оптимальным решением данной задачи, которому соответствует минимальное значение целевой функции Z
min
=3,5




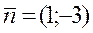 
 
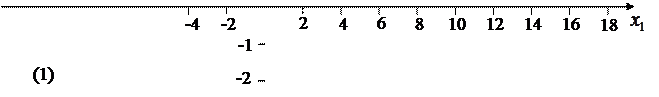
График № 1
1б) Перейдем к расширенной задаче:
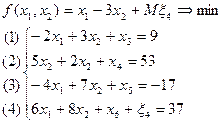
Данная расширенная задача имеет начальное опорное решение 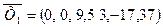 с базисом с базисом 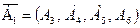 . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении: . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении:
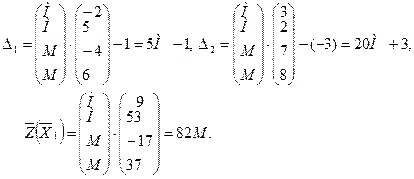
Расчеты проведем в таблице (Табл. 1)
Таблица 1
| 1 |
-3 |
0
|
0 |
0 |
0 |
M |
| Б
|
Сб
|
В
|
А
1
|
А
2
|
А
3
|
А
4
|
А
5
|
А
6
|
А
7
|
| А
3
|
0 |
9 |
-2 |
3 |
1 |
0 |
0 |
0 |
0 |
| А
4
|
0 |
53 |
5 |
2 |
0 |
1 |
0 |
0 |
0 |
| А
5
|
0 |
17 |
4 |
-7 |
0 |
0 |
1 |
0 |
0 |
| ←
|
А
7
|
М
|
37 |
6 |
8 |
0 |
0 |
0 |
1 |
1 |
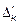 |
0 |
–1 |
3 |
0 |
0 |
0 |
0 |
0 |
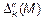 |
37 |
6 |
8 |
0 |
0 |
0 |
0 |
0 |
Начальное опорное решение не является оптимальным, так как в задаче на минимум имеются положительные оценки. Выбираем номер вектора А
k
, вводимого в базис опорного решения, и вектора А
l
, выводимого из базиса. Наибольшая положительная оценка соответствует А2
, за разрешающий элемент выбираем коэффициент 8 и выполняем преобразование Жордана.
Вектор А2
выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем второе опорное решение 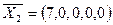 с базисом с базисом 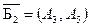 (табл. 1.3). Целевая функция (табл. 1.3). Целевая функция 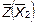 =-3М
-21. Это решение не является оптимальным, так как есть положительная оценка. =-3М
-21. Это решение не является оптимальным, так как есть положительная оценка.
Таблица 1
| Б
|
Сб
|
B
|
А
1
|
А
2
|
А
3
|
А
4
|
А
5
|
А
6
|
|
| А2
|
-3
|
3,0 |
-0,7 |
1,0 |
0,3 |
0,0 |
0,0 |
0,0 |
0,0 |
| А
4
|
0
|
47,0 |
6,3 |
0,0 |
-0,7 |
1,0 |
0,0 |
0,0 |
0,0 |
| А
5
|
0
|
38,0 |
-0,7 |
0,0 |
2,3 |
0,0 |
1,0 |
0,0 |
0,0 |
| a7
|
М
|
13,0 |
11,3 |
0,0 |
-2,7 |
0,0 |
0,0 |
1,0 |
1,0 |
| M+1 |
-9,0 |
1,0 |
0,0 |
-1,0 |
0,0 |
0,0 |
0,0 |
0,0 |
| M+2 |
13,0 |
11,3 |
0,0 |
-2,7 |
0,0 |
0,0 |
0,0 |
0,0 |
| A2
|
-3
|
-2,4 |
-0,6 |
1,0 |
0,0 |
0,0 |
-0,1 |
0,0 |
0,0 |
| a4
|
0
|
57,9 |
6,1 |
0,0 |
0,0 |
1,0 |
0,3 |
0,0 |
0,0 |
| А
3
|
0
|
16,3 |
-0,3 |
0,0 |
1,0 |
0,0 |
0,4 |
0,0 |
0,0 |
| A7
|
М
|
56,4 |
10,6 |
0,0 |
0,0 |
0,0 |
1,1 |
1,0 |
1,0 |
| M+1 |
7,3 |
0,7 |
0,0 |
0,0 |
0,0 |
0,4 |
0,0 |
0,0 |
| M+2 |
56,4 |
10,6 |
0,0 |
0,0 |
0,0 |
1,1 |
0,0 |
0,0 |
| A2
|
-3
|
0,6 |
0,0 |
1,0 |
0,0 |
0,0 |
-0,1 |
0,1 |
0,1 |
| a4
|
0
|
25,1 |
0,0 |
0,0 |
0,0 |
1,0 |
-0,4 |
-0,6 |
-0,6 |
| А
5
|
0
|
17,8 |
0,0 |
0,0 |
1,0 |
0,0 |
0,5 |
0,0 |
0,0 |
| A1
|
1
|
5,3 |
1,0 |
0,0 |
0,0 |
0,0 |
0,1 |
0,1 |
0,1 |
| 3,5 |
0,0 |
0,0 |
0,0 |
0,0 |
0,4 |
-0,1 |
-0,1 |
| 0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
-1,0 |
-1,0 |
Целевая функция после второй итерации равна 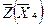 = 3,5. Все оценки отрицательные, план оптимален. = 3,5. Все оценки отрицательные, план оптимален.
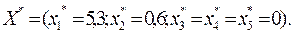
Оптимальный план исходной задачи Х*=
(х1
*
=5,3; х2
*
=0,6). Минимальное значение целевой функции исходной задачи =3,5.
Ответ: minZ
(X
*
) =3,5.
2. Двойственная задача
Двойственная задача имеет вид.
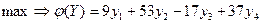
при условиях

3. Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
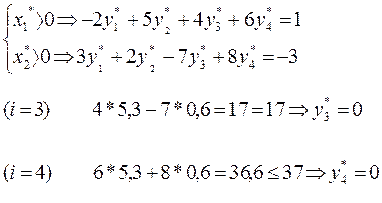
Откуда следует:
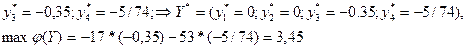
4.
Оптимальный план двойственной задачи найдем, используя окончательную симплекс-таблицу прямой задачи (Табл.1)
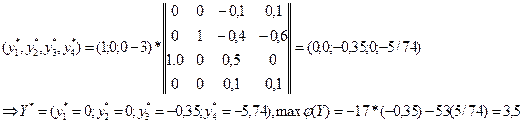
Максимальное значение функции двойственной задачи совпадает с минимальным значением функции прямой задачи, что подтверждает первую теорему двойственности.
Проанализируем решение задачи
, используя условия дополняющей нежесткости (вторую теорему двойственности). Подставляем координаты оптимального решения двойственной задачи Y
* = (0;0;-0,35;-0,068), в систему ограничений.
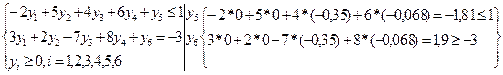
Ответ: Z
(X
) =3,5 при Х
* = (0;0;-0,35;-0,068).
Задача № 2
Каноническая задача
В каждом варианте приведены таблицы, в которых записаны условия канонической задачи линейного программирования на минимум, т. е.
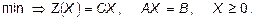
В первой строке помещены коэффициенты целевой функции. В остальных строках, в первых пяти столбцах, находятся векторы условий, а в последнем столбце записан вектор ограничений. В правом верхнем углу таблицы указана цель задачи.
Необходимо последовательно выполнить следующие задания.
1. Задачу решить графическим методом.
2. Применяя симплекс-метод, решить задачу, т.е. найти ее оптимальный план 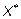 и минимальное значение целевой функции и минимальное значение целевой функции 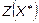 или установить, что задача не имеет решения. Начальный план рекомендуется искать методом искусственного базиса. или установить, что задача не имеет решения. Начальный план рекомендуется искать методом искусственного базиса.
3. Построить двойственную задачу. Если вектор 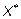 найден, вычислить оптимальный план найден, вычислить оптимальный план 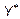 двойственной задачи, используя первую теорему двойственности двойственной задачи, используя первую теорему двойственности 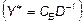 . Вычислить максимальное значение функции . Вычислить максимальное значение функции 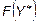 . .
4. Провести анализ полученного решения, применяя условия дополняющей нежесткости.
Если 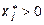 ,то ,то  . .
Если 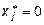 , то , то 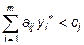 . .
| 14 |
| 1 |
-5 |
6 |
8 |
-2 |
min |
| 11 |
7 |
1 |
12 |
5 |
16 |
| 14 |
10 |
0 |
3 |
8 |
17 |
| 13 |
2 |
9 |
4 |
6 |
15 |
Решение задачи 2
Представим исходные данные задачи в виде:
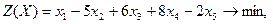
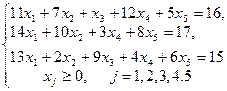
Проверяем, применим ли графический метод при решении данной задачи.
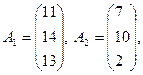
линейно независимы, так как их координаты непропорциональны. Поэтому ранг системы векторов-условий r
= 3. Находим n
-r
=5 - 3 = 2 £ 2. Следовательно, метод применим.
1. Приведём систему уравнений-ограничений к равносильной, разрешённой методом Жордана–Гаусса. Преобразуем систему уравнений методом Жордана-Гаусса до получения общего решения (табл. 2.1).
Таблица 2.1.
| № итерац.
|
x1
|
x2
|
x3
|
x4
|
x5
|
bi
|
(1)
|
11 |
7 |
1 |
12 |
5 |
16 |
| 14 |
10 |
0 |
3 |
8 |
17 |
| 13 |
2 |
9 |
4 |
6 |
15 |
(2)
|
-45,00
|
-33,00
|
1,00
|
0,00
|
-27,00
|
-52,00
|
| 4,67
|
3,33
|
0,00
|
1,00
|
2,67
|
5,67
|
| -5,67
|
-11,33
|
9,00
|
0,00
|
-4,67
|
-7,67
|
(3)
|
2,25
|
0,75
|
1,00
|
10,13
|
0,00
|
5,38
|
| 1,75
|
1,25
|
0,00
|
0,38
|
1,00
|
2,13
|
| 2,50
|
-5,50
|
9,00
|
1,75
|
0,00
|
2,25
|
| (4)
|
-12,21
|
32,57
|
-51,07
|
0,00
|
0,00
|
-7,64
|
| 1,21
|
2,43
|
-1,93
|
0,00
|
1,00
|
1,64
|
| 1,43
|
-3,14
|
5,14
|
1,00
|
0,00
|
1,29
|
| (5)
|
0,24
|
-0,64
|
1,00
|
0,00
|
0,00
|
0,15
|
| 1,68
|
1,20
|
0,00
|
0,00
|
1,00
|
1,93
|
| 0,20
|
0,14
|
0,00
|
1,00
|
0,00
|
0,52
|
Общее решение системы уравнений имеет вид
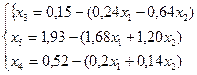
Учитывая, что все переменные неотрицательны, перейдем от уравнений к неравенствам из общего решения системы.
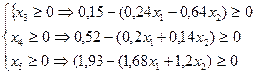
откуда получим систему неравенств с двумя переменными
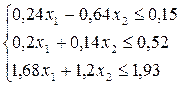
Целевую функцию выразим через свободные переменные
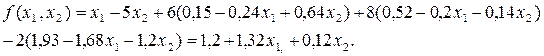
Окончательно получим стандартную задачу линейного программирования с двумя переменными
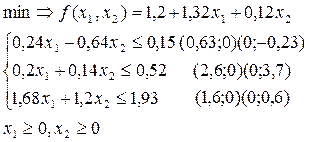
Строим область допустимых решений (график 2). Любая точка многоугольника 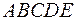 удовлетворяет системе неравенств. Вершина удовлетворяет системе неравенств. Вершина 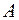 является точкой входа семейства прямых является точкой входа семейства прямых 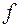 в область решений, следовательно, в этой точке она принимает минимальное значение. в область решений, следовательно, в этой точке она принимает минимальное значение.
В свою очередь, 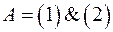 =(1,32;0,12). =(1,32;0,12).
Решая систему уравнений получаем х1
=2,2, х2
=0,6. Это и будет оптимальным решением данной задачи, которому соответствует минимальное значение целевой функции Z
min
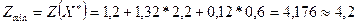 . .

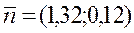
 A A
А 
(3)
график 2
2.
Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса
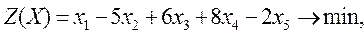
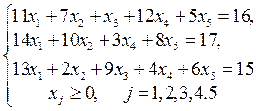
Составим расширенную задачу. В левые части уравнений системы ограничений вводим неотрицательные искусственные переменные с коэффициентом +1. Удобно справа от уравнений записать вводимые искусственные переменные. В первое уравнение вводим переменную х
6
, во второе — переменную х
7
, в третье – х8
. Данная задача — задача на нахождение минимума. Получаем
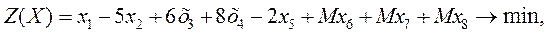
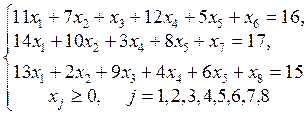
Данная расширенная задача имеет начальное опорное решение 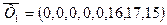 с базисом с базисом 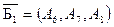 . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении: . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении:
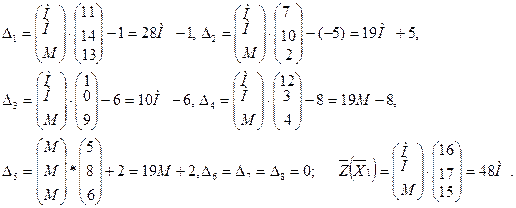
Записываем исходные и расчетные данные в симплексную таблицу (табл.2.2).
Таблица 2.2
| 1 |
-5 |
6 |
8 |
-2 |
М
|
M |
M |
| Б
|
Сб
|
А
0
|
А
1
|
А
2
|
А
3
|
А
4
|
А
5
|
А
6
|
A7
|
A8
|
| А
6
|
М
|
16 |
11 |
7 |
1 |
12 |
5 |
1 |
0 |
0 |
| A7
|
M |
17 |
14 |
10 |
0 |
3 |
8 |
0 |
1 |
0 |
| ←
|
А
8
|
М
|
15 |
13 |
2 |
9 |
4 |
6 |
0 |
0 |
1 |
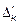 |
0 |
-1 |
5 |
-6 |
-8 |
2 |
0 |
0 |
0 |
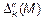 |
48 |
28 |
19 |
10 |
19 |
19 |
0 |
0 |
0 |
Начальное опорное решение не является оптимальным, так как в задаче на минимум имеются положительные оценки. Выбираем номер вектора А
k
, вводимого в базис опорного решения, и вектора А
l
, выводимого из базиса. В столбце «А
3
» (см. табл. 2.1) за разрешающий элемент выбираем коэффициент 9 в третьей строке и выполняем преобразование Жордана.
Вектор А3
выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем первое опорное решение 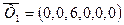 с базисом с базисом 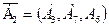 (табл. 2.3). Целевая функция (табл. 2.3). Целевая функция  =31,33М
-10. Это решение не является оптимальным, так как имеются положительные оценки. =31,33М
-10. Это решение не является оптимальным, так как имеются положительные оценки.
Таблица 2.3
| 1 |
-5 |
6 |
8 |
-2 |
М
|
M |
M |
| Б
|
Сб
|
А
0
|
А
1
|
А
2
|
А
3
|
А
4
|
А
5
|
А
6
|
A7
|
A8
|
| А
6
|
М
|
14,33 |
9,56 |
6,78 |
0,00 |
11,56 |
4,33 |
1,00 |
0,00 |
-0,11 |
| A7
|
M |
17,00 |
14,00 |
10,00 |
0,00 |
3,00 |
8,00 |
0,00 |
1,00 |
0,00 |
| ←
|
А
3
|
6
|
1,67 |
1,44 |
0,22 |
1,00 |
0,44 |
0,67 |
0,00 |
0,00 |
0,11 |
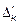 |
10,00 |
-7,67 |
-6,33 |
0,00 |
5,33 |
-6,00 |
0,00 |
0,00 |
-0,67 |
| 31,33 |
13,56 |
16,78 |
0,00 |
14,56 |
12,33 |
0,00 |
0,00 |
-1,11 |
Вводим вектор А
4
в базис, получаем второе опорное решение (таблица 2.4) 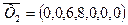 с базисом с базисом 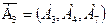 . Целевая функция . Целевая функция 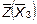 = 3,38+13,28M. Далее в таблице 2.4 приведены расчеты с третьей по пятую итерации. = 3,38+13,28M. Далее в таблице 2.4 приведены расчеты с третьей по пятую итерации.
Таблица 2.4
| 4 |
2 |
-1 |
5 |
1 |
М |
M |
M |
| Б
|
Сб
|
А0 |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
A7 |
A8 |
| a4
|
8
|
1,24 |
0,83 |
0,59 |
0,00 |
1,00 |
0,38 |
0,09 |
0,00 |
-0,01 |
| a7
|
M |
13,28 |
11,52 |
8,24 |
0,00 |
0,00 |
6,88 |
-0,26 |
1,00 |
0,03 |
| a3
|
6
|
1,12 |
1,08 |
-0,04 |
1,00 |
0,00 |
0,50 |
-0,04 |
0,00 |
0,12 |
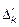 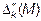
|
3,38 |
-12,08 |
-9,46 |
0,00 |
0,00 |
-8,00 |
-0,46 |
0,00 |
-0,62 |
| 13,28 |
1,52 |
8,24 |
0,00 |
0,00 |
6,88 |
-1,26 |
0,00 |
-0,97 |
| a4 |
8 |
0,52 |
0,20 |
0,14 |
0,00 |
1,00 |
0,00 |
0,10 |
-0,05 |
-0,01 |
| a5 |
-2 |
1,93 |
1,68 |
1,20 |
0,00 |
0,00 |
1,00 |
-0,04 |
0,15 |
0,00 |
| a3 |
6 |
0,15 |
0,24 |
-0,64 |
1,00 |
0,00 |
0,00 |
-0,02 |
-0,07 |
0,11 |
| 18,84 |
1,33 |
0,13 |
0,00 |
0,00 |
0,00 |
-0,76 |
1,16 |
-0,58 |
| 0,00 |
-10,00 |
0,00 |
0,00 |
0,00 |
0,00 |
-1,00 |
-1,00 |
-1,00 |
| a1 |
1 |
2,60 |
1,00 |
0,69 |
0,00 |
5,04 |
0,00 |
0,51 |
-0,27 |
-0,06 |
| a5 |
-2 |
-2,42 |
0,00 |
0,04 |
0,00 |
-8,44 |
1,00 |
-0,89 |
0,61 |
0,10 |
| a3 |
6 |
-0,47 |
0,00 |
-0,80 |
1,00 |
-1,20 |
0,00 |
-0,14 |
-0,01 |
0,13 |
| 4,19 |
0,00 |
-0,79 |
0,00 |
-6,68 |
0,00 |
-1,44 |
1,53 |
-0,51 |
| 25,99 |
0,00 |
6,90 |
0,00 |
50,35 |
0,00 |
4,07 |
-3,75 |
-1,56 |
Целевая функция после пятой итерации равна 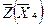 = 4,19. Положительных оценок нет, план оптимален. Ответ: minZ
(X
*
) =4,2. = 4,19. Положительных оценок нет, план оптимален. Ответ: minZ
(X
*
) =4,2.
3.Построим двойственную задачу
Используя вторую симметричную пару двойственных задач, составим задачу, двойственную к исходной:
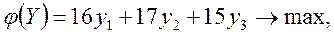
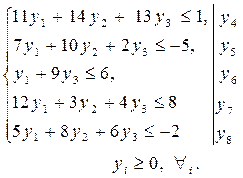
Вводим неотрицательные дополнительные переменные у
4
, у
5
, у
6
у
7
, у
8
для приведения задачи к каноническому виду:
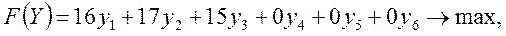
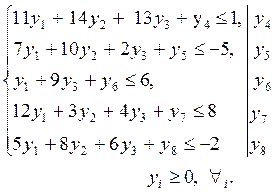
Находим начальное опорное решение Y
1
= (0,0,0,1,-5,6,8,-2) с базисом Б1
= (А
4
, А
5
, А
6
, А
7
, А
8
). Решение задачи симплексным методом приведено в табл. 2.5. (расчеты табл.2.2. и табл.2.4.)
Таблица 2.5
| 1 |
-5 |
6 |
8 |
-2 |
М
|
M |
M |
| Б
|
Сб
|
А
0
|
А
1
|
А
2
|
А
3
|
А
4
|
А
5
|
А
6
|
A7
|
A8
|
| ←
|
А
6
|
М
|
16 |
11 |
7 |
1 |
12 |
5 |
1 |
0 |
0 |
| A7
|
M |
17 |
14 |
10 |
0 |
3 |
8 |
0 |
1 |
0 |
| А
8
|
М
|
15 |
13 |
2 |
9 |
4 |
6 |
0 |
0 |
1 |
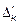 |
0 |
-1 |
5 |
-6 |
-8 |
2 |
0 |
0 |
0 |
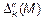 |
48 |
28 |
19 |
10 |
19 |
19 |
0 |
0 |
0 |
| a1 |
1 |
2,60 |
1,00 |
0,69 |
0,00 |
5,04 |
0,00 |
0,51 |
-0,27 |
-0,06 |
| a5 |
-2 |
-2,42 |
0,00 |
0,04 |
0,00 |
-8,44 |
1,00 |
-0,89 |
0,61 |
0,10 |
| a3 |
6 |
-0,47 |
0,00 |
-0,80 |
1,00 |
-1,20 |
0,00 |
-0,14 |
-0,01 |
0,13 |
|
|
4,19 |
0,00 |
-0,79 |
0,00 |
-6,68 |
0,00 |
-1,44 |
1,53 |
-0,51 |
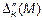 |
25,99 |
0,00 |
6,90 |
0,00 |
50,35 |
0,00 |
4,07 |
-3,75 |
-1,56 |
Приведем оптимальное решение прямой задачи
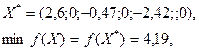
Окончательный базис, соответствующий оптимальному решению прямой задачи, состоит из векторов А2
А3
А4
поэтому базисная матрица имеет вид

Решение прямой задачи начиналось с единичного базиса А6,
А7
,А8
. Поэтому в окончательной таблице указанные столбцы преобразуются в матрицу 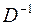 , обратную к базисной матрице , обратную к базисной матрице  , следовательно, , следовательно,

Оптимальный план двойственной найдем из соотношения
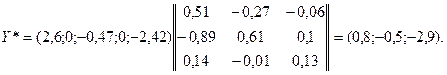
Откуда 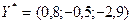 При этом плане максимальное значение функции двойственной задачи составляет величину равную При этом плане максимальное значение функции двойственной задачи составляет величину равную
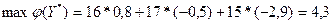
Максимальное значение целевой функции двойственной задачи совпадает с минимальным значением целевой функции прямой задачи.
5. Проанализируем решение задачи
, используя условия дополняющей нежесткости (вторую теорему двойственности).
Подставляем координаты оптимального решения двойственной задачи 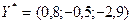 в систему ограничений. в систему ограничений.
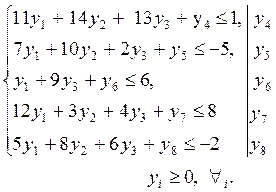
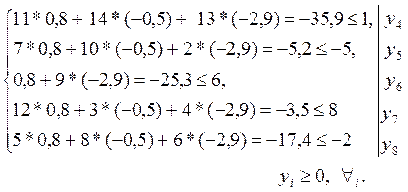
Первое, третье и пятое ограничения выполняются как строгие неравенства, следовательно, их координаты оптимального решения исходной задачи равны нулю:  . Учитывая это, первую, вторую и пятую координаты оптимального решения Х
*
находим при совместном решении уравнений-ограничений исходной задачи: . Учитывая это, первую, вторую и пятую координаты оптимального решения Х
*
находим при совместном решении уравнений-ограничений исходной задачи:
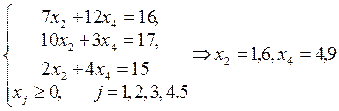
Ответ: Z
(X
) = 4,2 при Х
* = (0;1,6; 0;4,9;0).
Задача № 3
Транспортная задача
Ниже приведены числовые данные транспортных задач. Стоимость перевозки единицы продукции записаны в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу. Требуется построить начальный план методами: «северо-западного угла», «минимального элемента», «двойного предпочтения», методом Фогеля. Из каждого плана найти оптимальный план методом потенциалов.
| 24 |
| 34 |
30 |
39 |
29 |
18 |
82 |
| 40 |
35 |
45 |
41 |
10 |
36 |
| 36 |
38 |
41 |
50 |
8 |
79 |
| 14 |
10 |
13 |
10 |
12 |
80 |
| 77 |
60 |
22 |
68 |
50 |
Решение.
1.Метод северо-западного угла.
Исходные данные задачи сведем в таблицу (табл. 3.1).
Таблица 3.1.
| Поставщики |
Потребители |
Запасы |
 |
 |
 |
 |
 |
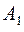 |
34 |
30 |
39 |
29 |
18 |
82
|
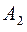 |
40 |
35 |
45 |
41 |
10 |
36
|
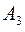 |
36 |
38 |
41 |
50 |
8 |
79
|
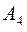 |
14 |
10 |
13 |
10 |
12 |
8
0
|
| Потребности |
77
|
60
|
22
|
6
8
|
50
|
Решение. Построим опорный план задачи методом северо-западного угла.
Объем перевозки 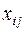 и последовательность заполнения матрицы и последовательность заполнения матрицы 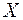 будем записывать в соответствующие клетки табл. 3.2. будем записывать в соответствующие клетки табл. 3.2.
Цифры, стоящие в скобках над объемами перевозок, обозначают номер шага, на котором определяются эти перевозки.
1. х11
(1)
=min(82,77)=77. Потребности первого потребителя удовлетворены, исключаем его. Запасы первого поставщика уменьшились на х11
(1)
и стали равны (82-77=5) 5.
2. х12
(1)
=min(5,60)=5. Запасы первого поставщика исчерпаны, исключим первую строку. Второй потребитель удовлетворил свои потребности на 5 единиц, его спрос уменьшился на величину х11
(1)
и стал равным 55.
3. х22
(3)
=min(36,55)=36. После третьего шага ресурсы поставщика А2
исчерпаны. Спрос потребителя B2
равен b2
(3)
=55-36=19.
4. х23
(4)
=min(79,19)=19. Следует исключить потребителя B2.
Ресурсы поставщика А3
(4)
= a3
– х23
(4)
=79-19=60 составляет 60 единиц.
5. х33
(5)
=min(60,22)=22. Потребитель В3
полностью удовлетворил свой спрос, исключаем столбец 3.
6. х34
(6)
=min(38,68)=38. Следует исключить поставщика А3
, запасы которого исчерпаны. Спрос потребителя В4
в4
(6)
– х34
(5)
=68-38=30 составляет 30 единиц.
7. х44
(7)
=min(80,30)=30. Спрос четвертого потребителя удовлетворен. Запасы поставщика А4
составляет
80-30=50.
8. х45
(8)
=min(50,50)=0. Запасы исчерпаны, потребности удовлетворены.
Опорный
план построен (табл. 3.2).
Таблица 3.2.
| 34
|
3
0
|
3
9
|
29
|
18
|
| 77(1)
|
5(2)
|
82
|
| 4
0
|
35
|
4
5
|
41
|
10
|
| 36(3)
|
36
|
| 36
|
3
8
|
41
|
50
|
8
|
| 19(4
)
|
22(5)
|
38(6)
|
79
|
| 1
4
|
1
0
|
1
3
|
1
0
|
1
2
|
| 30(7)
|
50(
8
)
|
8
0
|
| 7
7
|
60
|
22
|
6
8
|
50
|
Суммарные транспортные издержки на перевозку продукции от поставщиков к потребителю составляют

2.Метод минимального элемента.
Исходные данные
| поставщики |
потребители |
Запасы |
| В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
34 |
30 |
39 |
29 |
18 |
82
|
| А2
|
40 |
35 |
45 |
41 |
10 |
36
|
| А3
|
36 |
38 |
41 |
50 |
8 |
79
|
| А4
|
14 |
10 |
13 |
10 |
12 |
8
0
|
| потребности |
77
|
60
|
22
|
6
8
|
50
|
1. 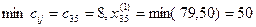 Объем запасов и потребностей после первого шага уменьшается на величину: х31
(1)
=50; Объем запасов и потребностей после первого шага уменьшается на величину: х31
(1)
=50; 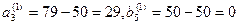 . Запасы пятого поставщика исчерпаны, потребности первого потребителя уменьшились на 50 единиц и стали равны 29, исключаем пятый столбец. . Запасы пятого поставщика исчерпаны, потребности первого потребителя уменьшились на 50 единиц и стали равны 29, исключаем пятый столбец.
2. 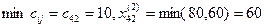 .Объем запасов и потребностей после второго шага уменьшается на величину: х42
(2)
=60; .Объем запасов и потребностей после второго шага уменьшается на величину: х42
(2)
=60;  . Потребности пункта В2
удовлетворены, исключим из рассмотрения второй столбец. . Потребности пункта В2
удовлетворены, исключим из рассмотрения второй столбец.
3. 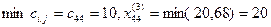 . Объем запасов и потребностей после третьего шага уменьшается на величину: х44
(3)
=20; . Объем запасов и потребностей после третьего шага уменьшается на величину: х44
(3)
=20; 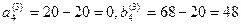 . Запасы пункта А4
исчерпаны, исключим из рассмотрения четвертую строку. . Запасы пункта А4
исчерпаны, исключим из рассмотрения четвертую строку.
4.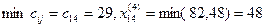 .
Корректируем объемы запасов и потребностей после четвертого шага: .
Корректируем объемы запасов и потребностей после четвертого шага: 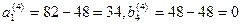 . Потребности пункта В4
удовлетворены, исключим четвертый столбец.
. Потребности пункта В4
удовлетворены, исключим четвертый столбец.
5. 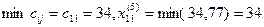 .
После пятого шага запасы поставщика А1
будут исчерпаны, исключаем первую строку. Потребности В1
равны: .
После пятого шага запасы поставщика А1
будут исчерпаны, исключаем первую строку. Потребности В1
равны: 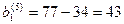 . .
6.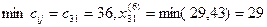 .
После шестого шага запасы третьего поставщика будут исчерпаны .
После шестого шага запасы третьего поставщика будут исчерпаны 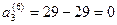 , потребности первого потребителя равны
, потребности первого потребителя равны 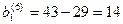 . Исключаем третью строку.
. Исключаем третью строку.
7. 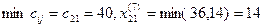 .
После седьмого шага запасы второго поставщика будут равны .
После седьмого шага запасы второго поставщика будут равны 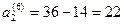 , потребности первого потребителя удовлетворены.
, потребности первого потребителя удовлетворены.
8. 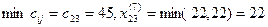 .
После восьмого шага запасы и потребности будут удовлетворены. .
После восьмого шага запасы и потребности будут удовлетворены.
Потребности всех потребителей удовлетворены, запасы поставщиков исчерпаны. После седьмого шага мы получили исходный опорный план 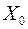 (Табл.3.3). (Табл.3.3).
Х0
Таблица 3.3.
| 34
|
30
|
39
|
29
|
18
|
| 34(5)
|
48(4)
|
82
|
| 40
|
35
|
45
|
41
|
10
|
| 14(7)
|
22(8)
|
36
|
| 36
|
38
|
41
|
50
|
8
|
| 29(6)
|
50(1)
|
79
|
| 14
|
10
|
13
|
10
|
12
|
| 60(2)
|
20(3)
|
80
|
| 77
|
60
|
22
|
68
|
50
|
Также как и в предыдущем случае, номер шага помещен в скобках над объемами перевозок. Суммарные транспортные расходы, соответствующие данному плану перевозок равны
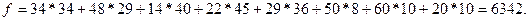
По сравнению с расчетом по методу северо-западного угла суммарные транспортные расходы уменьшились с 8452 у.е. до 6342 у.е.
Для проверки плана на оптимальность составим систему уравнений, следуя условию — для базисных переменных сумма потенциалов равна тарифу. Значение одного из потенциалов зададим произвольно (пусть 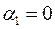 ), последовательность вычисления остальных потенциалов указана ниже: 1), 2),…, 8). ), последовательность вычисления остальных потенциалов указана ниже: 1), 2),…, 8).
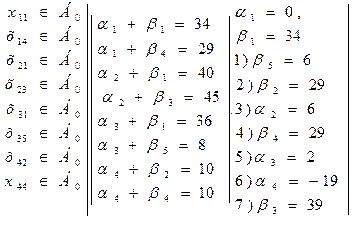
Потенциалы поставщиков  поместим слева от таблицы, а потенциалы потребителей поместим слева от таблицы, а потенциалы потребителей 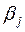 – сверху над таблицей (табл.3.4). – сверху над таблицей (табл.3.4).
Таблица 3.4
| 34 |
29 |
39 |
29 |
6 |
| 0 |
34 |
30 |
39 |
29 |
18 |
| 34(5)
|
48(4)
|
82
|
| -1 |
0 |
-12 |
| 6 |
40 |
35 |
45 |
41 |
10 |
| 14(
7
)
|
22(8)
|
36
|
| 0 |
-6 |
-2 |
| 2 |
36 |
38 |
41 |
50 |
8 |
| 29(6)
|
50(
1
)
|
79
|
| -7 |
0 |
-19 |
| -19 |
14 |
10 |
13 |
10 |
12 |
| 60(2)
|
20(
3
)
|
80
|
| 1 |
7 |
-25 |
| 77
|
60
|
22
|
68
|
50
|
Для небазисных переменных вычислим оценки по формуле:
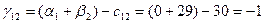
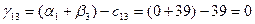
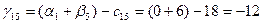

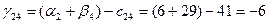
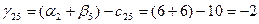
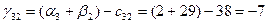
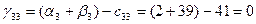 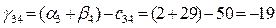
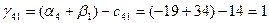
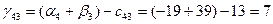
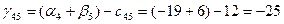
Значения оценок поместим в левом нижнем углу незанятых клеток табл. 3.4. Фиксируем наибольшую положительную оценку. В данном случае: 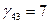 . Разрешающей объявим коммуникацию (4,3). Строим цикл пересчета, который показан в табл. 3.4 пунктирной линией. . Разрешающей объявим коммуникацию (4,3). Строим цикл пересчета, который показан в табл. 3.4 пунктирной линией.
Величина корректировки ρ=(58,79)=58. Вносим изменение в план: перевозки отрицательного полуцикла уменьшаем на 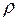 , а перевозки положительного полуцикла увеличиваем на эту же величину, остальные перевозки оставим без изменения. Переменная х11
вводится в базис со значением =58,переменная х14
выводится из базиса. Получим план , а перевозки положительного полуцикла увеличиваем на эту же величину, остальные перевозки оставим без изменения. Переменная х11
вводится в базис со значением =58,переменная х14
выводится из базиса. Получим план 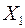 (табл. 3.5). (табл. 3.5).
План 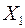 Таблица 3.5 Таблица 3.5
| 34 |
29 |
39 |
29 |
6 |
| 0 |
34 |
30 |
39 |
29 |
18 |
| 34(5)
|
48(4)
|
82
|
| -1 |
0 |
-12 |
| 6 |
40 |
35 |
45 |
41 |
10 |
| 14(
7
)
|
22 |
36
|
| 0 |
-6 |
-2 |
| 2 |
36 |
38 |
41 |
50 |
8 |
| 29(6)
|
50(
1
)
|
79
|
| -7 |
0 |
-19 |
| -19 |
14 |
10 |
13 |
10 |
12 |
| 60(2)
|
20(
3
)
|
80
|
| 1 |
7 |
-25 |
| 77
|
60
|
22
|
68
|
50
|
Значение функции уменьшилось на (38*16-9*38=290) и стало: 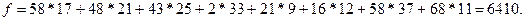
План не оптимален. Заново вычисляем потенциалы и оценки (табл. 3.6). Наибольшая положительная оценка– это 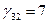 , план не оптимален. Строим цикл пересчета и определяем величину корректировки плана ρ=(48,58)=48. , план не оптимален. Строим цикл пересчета и определяем величину корректировки плана ρ=(48,58)=48.
Таблица 3.6
План X2
| 34 |
29 |
39 |
29 |
6 |
| 0 |
34 |
30 |
39 |
29 |
18 |
| 14 |
68(4)
|
82
|
| -1 |
0 |
-12 |
| 6 |
40 |
35 |
45 |
41 |
10 |
| 36 |
36
|
| 0 |
-6 |
-2 |
| 2 |
36 |
38 |
41 |
50 |
8 |
| 65 |
14 |
79
|
| -7 |
0 |
-19 |
| -19 |
14 |
10 |
13 |
10 |
12 |
| 12 |
46(2)
|
22 |
80
|
| 1 |
7 |
-25 |
| 77
|
60
|
22
|
68
|
50
|
Значение функции и соответственно транспортные расходы составили 
Положительных оценок нет, план Х2
оптимален.
3. Метод Фогеля
В табл. 3.4 показаны последовательность определения базисных переменных, наборы разностей 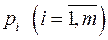 в строках справа от таблицы, а в строках справа от таблицы, а 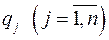 в столбцах снизу под таблицей. в столбцах снизу под таблицей.
План Х0
Таблица 3.4
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 34
|
30
|
39
|
29
|
18
|
11 |
11 |
11 |
11 |
11 |
11 |
- |
- |
| 34(6)
|
48(5)
|
82
|
| 40
|
35
|
45
|
41
|
10
|
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
| 14(7)
|
22(8)
|
36
|
| 36
|
38
|
41
|
50
|
8
|
28 |
2 |
- |
- |
- |
- |
- |
- |
| 29(2)
|
50(1)
|
79
|
| 14
|
10
|
13
|
10
|
12
|
2 |
2 |
2 |
2 |
- |
- |
- |
- |
| 12(4)
|
68(3)
|
80
|
| 77
|
60
|
22
|
68
|
50
|
| Этап 1 |
20 |
20 |
26 |
19 |
2 |
| Этап 2 |
20 |
20 |
26 |
19 |
- |
| Этап 3 |
20 |
20 |
26 |
19 |
- |
| Этап 4 |
20 |
20 |
26 |
12 |
- |
| Этап 5 |
20 |
- |
26 |
- |
- |
| Этап 6 |
20 |
- |
26 |
- |
- |
| Этап 7 |
16 |
- |
26 |
- |
- |
| Этап 8 |
- |
- |
26 |
- |
- |
Суммарные транспортные расходы, соответствующие данному плану перевозок равны
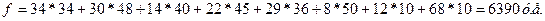 . .
Сравним расчеты, проделанные тремя методами. Транспортные расходы, рассчитанные:
1) методом северо-западного угла составили 8452 у.е.,
2) методом минимального элемента соответственно 6342 у.е.,
3) пересчитанные по методу потенциалов – 6118 у.е.,
4) методом Фогеля соответственно – 6390 у.е.
Наименьшие транспортные расходы составили расходы, рассчитанные по методу потенциалов.
Задача № 4
Сетевая задача
Ниже приведено 10 вариантов транспортной задачи в сетевой постановке. Каждая задача изображена в виде неориентированного связного графа. На ребрах проставлены значения тарифов 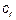 , на вершинах (в кружках) — значения запасов-потребностей , на вершинах (в кружках) — значения запасов-потребностей 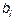 . Построить пробный допустимый план, проверить его на оптимальность. В случае необходимости довести до оптимального плана методом потенциалов. . Построить пробный допустимый план, проверить его на оптимальность. В случае необходимости довести до оптимального плана методом потенциалов.
Решение.
Построим пробный опорный план (рис.1).
Рис. 1. Пробный план перевозок по сети.
В качестве начальной выберем вершину 12, которая является поставщиком с запасами в 20 единиц продукции. Из этой вершины отправим транзитом через 13 с запасами 45 ед. и 10 вершину с запасами 30 единиц в 8 вершину и удовлетворяем её потребности в 40 единиц. Оставшиеся 55 единиц отправим в 6 вершину с потребностями 40 единиц, оставшиеся 15 единиц отправляем в 5 вершину с потребностями 10 единиц, оставшиеся 5 единиц направим в 1 вершину, потребности которой составляют 35 единиц.
Из 11 вершины с запасами 45 единиц направим транзитом через 9 вершину , всего запасов стало 75 единиц, направим их транзитом через 7 вершину в 4 вершину, потребности которой составляют 40 единиц, оставшиеся 35 единиц направим во 2 вершину и удовлетворим ее потребности.
Из 3 вершины с запасами 30 единиц направим транзитом через 7 вершину в 1 вершину, потребности которой удовлетворим.
В результате проведенных операций все запасы вывезены, потребности всех потребителей удовлетворены.
В результате проведенных операций все запасы вывезены, потребности всех потребителей удовлетворены. Число базисных ребер здесь равно 11, число вершин 13.
Итак, полученный план является опорным, так как удовлетворяет всем требованиям опорного плана. Значение функции, которое соответствует построенному плану равно
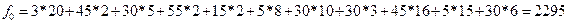 . .
Проверку плана на оптимальность осуществим с помощью метода потенциалов.
Одной из вершин (например, 1) зададим произвольное значение потенциала α1
=0. Запишем его около вершины 1.
Затем, двигаясь по базисным ребрам, вычисляем потенциалы остальных вершин.
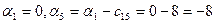 ; ; 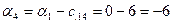
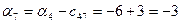 ; ;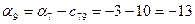 ; ;
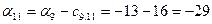 ; ;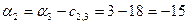 ; ;
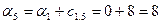 ; ;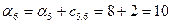
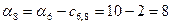 ; ;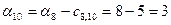 ; ;
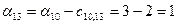 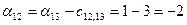
После вычисления потенциалов находим оценки для небазисных ребер: (1,2), (2,4),(2,7), (3,7),(7,12), (7,8), (10,12),(4,6). Они определяются по формуле и равны соответственно:
 ; ;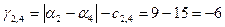 ; ;
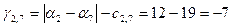 ; ;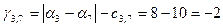 ;. ;.
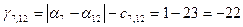 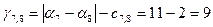
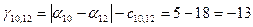 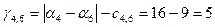
Есть три положительные оценки, значит построенный опорный план не оптимальный.
Наибольшая оценка 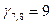 . Ребро (7,8), объявляем разрешающим, направляем разрешающую стрелку (пока пустую) от вершины с меньшим потенциалом к вершине с большим потенциалом, т.е. от 7–й вершины к 8–й (на рис. 2 разрешающая стрелка намечена пунктиром). В результате получаем цикл пересчета, замыкающийся на ребре (7,8). Цикл пересчета на рис.2 намечен сплошной линией. . Ребро (7,8), объявляем разрешающим, направляем разрешающую стрелку (пока пустую) от вершины с меньшим потенциалом к вершине с большим потенциалом, т.е. от 7–й вершины к 8–й (на рис. 2 разрешающая стрелка намечена пунктиром). В результате получаем цикл пересчета, замыкающийся на ребре (7,8). Цикл пересчета на рис.2 намечен сплошной линией.
Рис.3. пересчет перевозок по потенциалам
Во второй строке выписываем ребра, принадлежащие циклу пересчета. В первой строке, над ребрами с помощью стрелок укажем направление перевозок, а в третьей строке – объем перевозимого груза. В четвертой строке полученной конструкции запишем 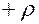 , если направление перевозки совпадает с разрешающей стрелкой и , если направление перевозки совпадает с разрешающей стрелкой и  , в противном случае. , в противном случае.

Изменяем распределение поставок. Определяем 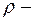 величину корректировки плана. Поскольку перевозки х8,10
,х11,9
направлены против разрешающей стрелки, величина величину корректировки плана. Поскольку перевозки х8,10
,х11,9
направлены против разрешающей стрелки, величина 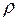 полагается меньшей из них полагается меньшей из них 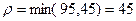
Включаем в базис ребро (7,8), а объем перевозки полагаем равным величине корректировки 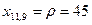 Ребро (7,9) исключаем из базиса. Ребро (7,9) исключаем из базиса.
После пересчета получим значение функции:
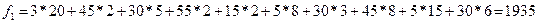
Задача № 5
Задача о назначениях
Ниже приведены таблицы, в клетках которых проставлены элементы матрицы эффективностей 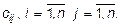 задачи о разборчивой невесте. Решить задачу методом потенциалов и венгерским методом. задачи о разборчивой невесте. Решить задачу методом потенциалов и венгерским методом.
| 44 |
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
Решение.
1. Метод потенциалов.
Начальный вариант выбора 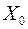 найдем методом максимального элемента (Табл. 5.1). найдем методом максимального элемента (Табл. 5.1).
Шаг 1. Максимальным элементом является с3,4
=49. Назначим третьей невесте четвертого жениха. Вычеркнем третью строку.
Шаг 2. Из невычеркнутых элементов матрицы максимальным элементом является с5,8
=49. Назначим пятой невесте восьмого жениха. Вычеркнем пятую строку.
Шаг 3. Из невычеркнутых элементов матрицы максимальным элементом является с6,2
=49. Шестая невеста выбирает второго жениха, вычеркиваем шестую строку.
Шаг 4. Из невычеркнутых элементов матрицы максимальным элементом является с4,3
=48.Четвертая невеста выбирает третьего жениха, вычеркиваем четвертую строку.
Шаг 5. Из невычеркнутых элементов матрицы максимальным элементом является с8,6
=46. Восьмая невеста выбирает шестого жениха, вычеркиваем восьмую строку.
Шаг 6. Из невычеркнутых элементов матрицы максимальным элементом является с7,1
=45. Седьмая невеста выбирает первого жениха, вычеркиваем седьмую строку.
Шаг 7. Из невычеркнутых элементов матрицы максимальным элементом является с1,4
=41. Но четвертого жениха уже выбрала третья невеста, поэтому в клетку (1,4) поместим 0. В дальнейшем, х1,4
=0 будем считать базисной переменной. Вычеркнем четвертый столбец.
Шаг 8. Из невычеркнутых элементов матрицы максимальным элементом является с1,7
=38. Первая невеста назначается седьмому жениху, вычеркиваем первую строку.
Шаг 9. Из невычеркнутых элементов матрицы максимальным элементом является с2,7
=38. Но седьмой жених уже выбран, поэтому в клетку (2,7) поместим 0. Х2,7
=0 - базисная переменная. Вычеркнем седьмой столбец.
Шаг 10. Из невычеркнутых элементов матрицы максимальным элементом является с2,8
=36. На восьмой жених уже выбран, поэтому в клетку (2,8) поместим 0. Х2,8
=0 - базисная переменная. Вычеркнем восьмой столбец.
Шаг 11. Из невычеркнутых элементов матрицы максимальным элементом является с2,1
=35. Но первый жених уже занят, поэтому в клетку (2,1) поместим 0. Х2,1
=0 - базисная переменная. Вычеркнем первый столбец.
Шаг 12. Из невычеркнутых элементов матрицы максимальным элементом является Х2,3
=26. Но третий жених уже занят, поэтому в клетку (2,3) поместим 0. Х2,3
=0 - базисная переменная. Вычеркнем третий столбец.
Шаг 13. Из невычеркнутых элементов матрицы максимальным элементом является Х1,5
=23. Но пятый жених уже занят, поэтому в клетку (1,5) поместим 0. Х1,5
=0 - базисная переменная. Вычеркнем пятый столбец.
Шаг 14. Из невычеркнутых элементов матрицы максимальным элементом является с2,2
=20. Но второй жених уже занят, поэтому в клетку (2,2) поместим 0. Х2,2
=0 - базисная переменная. Вычеркнем второй столбец.
Шаг 15. Из невычеркнутых элементов матрицы максимальным элементом является с2,5
=17. Вторая невеста назначается пятому жениху, вычеркиваем вторую строку.
В табл. 5.1 номер шага, на котором были получены базисные переменные, указан в скобках. После 15 шага получим пробный вариант назначения Х0
: х1,7
=х2,5
= х3,4
=х4,3
=х5,8
=х6,2
= х7,1
=х8,6
=1. Это означает, что первая невеста выходит замуж за седьмого жениха, вторая невеста за пятого жениха, третья невеста за четвертого жениха, четвертая невеста за третьего жениха, пятая невеста за восьмого жениха, шестая невеста за второго жениха, седьмая невеста за первого жениха, восьмая невеста за шестого жениха.
Таблица 5.1.
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 0
(
7
)
|
0(13)
|
1
(
8)
|
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 0(11)
|
0(14)
|
0(12)
|
1
(
15
)
|
0
(
7)
|
0
(
10)
|
| 12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 1(1)
|
| 28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 1(4)
|
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 1
(
2
)
|
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 1(
3
)
|
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 1
(
6
)
|
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
| 1
(
5
)
|
Суммарная эффективность, отвечающая полученному варианту выбора равна:
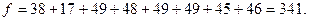 условных единиц эффективности условных единиц эффективности
Вариант выбора 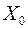 проверим на оптимальность. Для этого вычислим потенциалы и оценки. проверим на оптимальность. Для этого вычислим потенциалы и оценки.
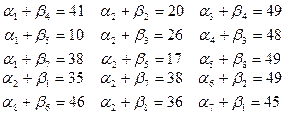
Отсюда вычислим потенциалы:
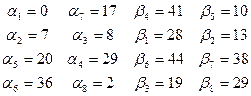
Для небазисных переменных вычислим оценки по соответствующей формуле:
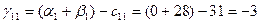
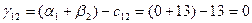
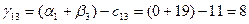
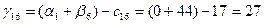
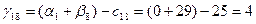
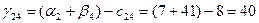
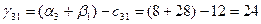

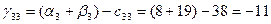 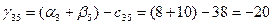
И так далее расчеты по соответствующим формулам и данным приведены в таблице 5.2.
Таблица 5.2
| Х0
|
28
|
13
|
19
|
41
|
10
|
44
|
38
|
29
|
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 0
|
0
(
7
)
|
0(13)
|
1
(
8)
|
| Оценка
1
|
-3
|
0
|
8
|
27
|
4
|
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 7
|
0(11)
|
0(14)
|
0(12)
|
1
(
15
)
|
0
(
7)
|
0
(
10)
|
| Оценка
2
|
40 |
37 |
| 8
|
12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 1(1)
|
| Оценка
3
|
24 |
-16 |
-11 |
-20 |
30 |
36 |
24 |
| 29 |
28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 1(4)
|
| Оценка
4
|
29 |
21 |
27 |
-5 |
44 |
41 |
46 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 20
|
1
(
2
)
|
| Оценка
5
|
11 |
11 |
0 |
15 |
4 |
44 |
14 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 36 |
1(
3
)
|
| Оценка
6
|
42 |
36 |
75 |
26 |
50 |
29 |
49 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 17 |
1
(
6
)
|
| Оценка
7
|
3
|
31 |
37 |
-3 |
40 |
21 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
| 2 |
1
(
5
)
|
| Оценка
8
|
-6 |
-11 |
8 |
-19 |
16 |
7 |
17 |
Cреди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок 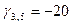 Строим цикл пересчета: (3,5), (2,5), (1,7), (1,4), (3,5) замыкающийся на разрешающей клетке. Вычислим величину корректировки Строим цикл пересчета: (3,5), (2,5), (1,7), (1,4), (3,5) замыкающийся на разрешающей клетке. Вычислим величину корректировки 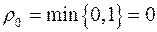 . Базисный нуль 03,5
перемещается в клетку (1,7), переменная х1,7
включается в базис, а переменная х3,5
выходит из базиса. Получим новую комбинацию расстановки единиц и нулей (Табл. 5.3). Суммарная эффективность равна: . Базисный нуль 03,5
перемещается в клетку (1,7), переменная х1,7
включается в базис, а переменная х3,5
выходит из базиса. Получим новую комбинацию расстановки единиц и нулей (Табл. 5.3). Суммарная эффективность равна:
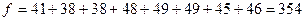 условных единиц эффективности условных единиц эффективности
Таблица 5.3
| Х0
|
28
|
13
|
19
|
41
|
10
|
44
|
38
|
29
|
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 0
|
1
(
7
)
|
0(13)
|
0
(
8)
|
| Оценка
1
|
-3
|
0
|
8
|
27
|
4
|
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 7
|
0(11)
|
0(14)
|
0(12)
|
0
(
15
)
|
1
(
7)
|
0
(
10)
|
| Оценка
2
|
40 |
37 |
| 28
|
12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 1
(
7
)
|
| Оценка
3
|
44 |
4 |
9 |
20 |
50 |
56 |
44 |
| 29 |
28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 1(4)
|
| Оценка
4
|
29 |
21 |
27 |
-5 |
44 |
41 |
46 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 20
|
1
(
2
)
|
| Оценка
5
|
11 |
11 |
0 |
15 |
4 |
44 |
14 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 36 |
1(
3
)
|
| Оценка
6
|
42 |
36 |
75 |
26 |
50 |
29 |
49 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 17 |
1
(
6
)
|
| Оценка
7
|
3
|
31 |
37 |
-3 |
40 |
21 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
| 2 |
1
(
5
)
|
| Оценка
8
|
-6 |
-11 |
8 |
-19 |
16 |
7 |
17 |
Заново вычисляем потенциалы и оценки.
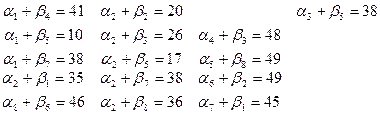
Отсюда вычислим потенциалы:
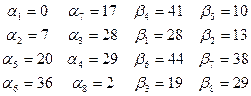
Для небазисных переменных вычислим оценки в таблице 5.3.
Среди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок 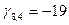 Строим цикл пересчета: (8,4), (2,4), (2,2), (8,2),(8,4) замыкающийся на разрешающей клетке. Вычислим величину корректировки Строим цикл пересчета: (8,4), (2,4), (2,2), (8,2),(8,4) замыкающийся на разрешающей клетке. Вычислим величину корректировки 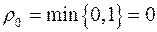 . Базисная переменная х2,2
=0 перемещается в клетку (8,4), переменная х8,4
включается в базис, а переменная х2,2
выходит из базиса. (Табл. 5.4). . Базисная переменная х2,2
=0 перемещается в клетку (8,4), переменная х8,4
включается в базис, а переменная х2,2
выходит из базиса. (Табл. 5.4).
Таблица 5.4
| Х1
|
28
|
13
|
19
|
41
|
10
|
44
|
38
|
29
|
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 0
|
1
(
7
)
|
0(13)
|
0
(
8)
|
| Оценка
1
|
-3
|
0
|
8
|
27
|
4
|
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 7
|
0(11)
|
0(12)
|
0
(
15
)
|
1
(
7)
|
0
(
10)
|
| Оценка
2
|
40 |
37 |
| 28
|
12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 1
(
7
)
|
| Оценка
3
|
44 |
4 |
9 |
20 |
50 |
56 |
44 |
| 29 |
28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 1(4)
|
| Оценка
4
|
29 |
21 |
27 |
-5 |
44 |
41 |
46 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 20
|
1
(
2
)
|
| Оценка
5
|
11 |
11 |
0 |
15 |
4 |
44 |
14 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 36 |
1(
3
)
|
| Оценка
6
|
42 |
36 |
75 |
26 |
50 |
29 |
49 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 17 |
1
(
6
)
|
| Оценка
7
|
3
|
31 |
37 |
-3 |
40 |
21 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
| 2 |
0(14)
|
1
(
5
)
|
| Оценка
8
|
-6 |
-11 |
8 |
-19 |
16 |
7 |
17 |
Суммарная эффективность не изменилась и равна:
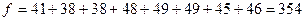 условных единиц эффективности условных единиц эффективности
Заново вычисляем потенциалы и оценки. Расчеты оценок приведены в таблице 5.5.
Среди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок 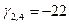 Строим цикл пересчета: (2,4), (2,5), (5,5), (5,2),(2,2) замыкающийся на разрешающей клетке. Вычислим величину корректировки Строим цикл пересчета: (2,4), (2,5), (5,5), (5,2),(2,2) замыкающийся на разрешающей клетке. Вычислим величину корректировки 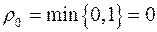 . Базисная переменная х5,2
=0 перемещается в клетку (2,4), переменная х2,4
включается в базис, а переменная х5,2
выходит из базиса. (Табл. 5.5). . Базисная переменная х5,2
=0 перемещается в клетку (2,4), переменная х2,4
включается в базис, а переменная х5,2
выходит из базиса. (Табл. 5.5).
Таблица 5.5
| Х2
|
28
|
13
|
19
|
41
|
10
|
44
|
38
|
29
|
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 0
|
1
(
7
)
|
0(13)
|
0
(
8)
|
| Оценка
1
|
-3
|
0
|
8
|
27
|
4
|
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 7
|
0(11)
|
0(12)
|
0
(
15
)
|
1
(
7)
|
0
(
10)
|
| Оценка
2
|
40 |
37 |
| 28
|
12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 1
(
7
)
|
| Оценка
3
|
44 |
4 |
9 |
20 |
50 |
56 |
44 |
| 29 |
28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 1(4)
|
| Оценка
4
|
29 |
21 |
27 |
-5 |
44 |
41 |
46 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 20
|
1
(
2
)
|
| Оценка
5
|
11 |
11 |
0 |
15 |
4 |
44 |
14 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 36 |
1(
3
)
|
| Оценка
6
|
42 |
36 |
75 |
26 |
50 |
29 |
49 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 17 |
1
(
6
)
|
| Оценка
7
|
3
|
31 |
37 |
-3 |
40 |
21 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
| 21 |
0(14)
|
1
(
5
)
|
| Оценка
8
|
6 |
11 |
20 |
29 |
26 |
29 |
Заново вычисляем потенциалы и оценки. Расчеты оценок приведены в таблице 5.5.
Отрицательных оценок нет. Назначение Х2
оптимально, обозначим его через Х2
*
.
Суммарная эффективность, отвечающая полученному варианту назначения равна:
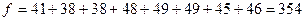 условных единиц эффективности условных единиц эффективности
Назначение Х2
оптимально. Итак, оптимальный вариант назначения имеет вид:
х1,4
=1 (первая невеста выберет четвертого жениха),
х2,7
=1 (вторая невеста выберет седьмого жениха),
х3,5
=1 (третья невеста выбрала пятого жениха),
х4,3
=1 (четвертая невеста выбрала третьего жениха),
х5,8
=1 (пятая невеста выберет восьмого жениха),
х6,2
=1 (шестая невеста выберет второго жениха),
х7,1
=1 (седьмая невеста выберет первого жениха),
х8,6
=1 (восьмая невеста выберет шестого жениха).
При этом варианте назначений получим максимальную эффективность 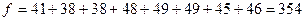 единиц эффективности. единиц эффективности.
2.
Венгерский метод.
Предварительный этап. Исходная матрица
C
:
| 31 |
13 |
11 |
41 |
10 |
17 |
38 |
25 |
| 35 |
20 |
26 |
8 |
17 |
14 |
38 |
36 |
| 12 |
37 |
38 |
49 |
38 |
22 |
10 |
13 |
| 28 |
21 |
48 |
43 |
44 |
29 |
26 |
12 |
| 37 |
22 |
39 |
46 |
26 |
20 |
44 |
49 |
| 22 |
49 |
19 |
2 |
20 |
30 |
45 |
16 |
| 45 |
27 |
5 |
21 |
30 |
21 |
34 |
23 |
| 43 |
33 |
20 |
29 |
3 |
46 |
33 |
21 |
Шаг 1. Обозначим через 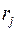 наибольший элемент столбца наибольший элемент столбца 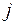 матрицы матрицы 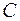 (r1
=45, r2
=49, r3
=48, r4
=49, r5
=44, r6
=46, r7
=45, r8
=49). Каждый элемент (r1
=45, r2
=49, r3
=48, r4
=49, r5
=44, r6
=46, r7
=45, r8
=49). Каждый элемент 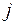 -го столбца вычтем из -го столбца вычтем из 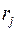 , результаты вычислений будем помещать на место вычитаемого. Аналогичные преобразования проводим в остальных столбцах. Получим неотрицательную матрицу , результаты вычислений будем помещать на место вычитаемого. Аналогичные преобразования проводим в остальных столбцах. Получим неотрицательную матрицу  , в каждом столбце которой есть хотя бы один нуль. , в каждом столбце которой есть хотя бы один нуль.
| C1
= |
14
|
36
|
37
|
8
|
34
|
29
|
7
|
24
|
| 10
|
29
|
22
|
41
|
27
|
32
|
7
|
13
|
| 33
|
12
|
10
|
0
|
6
|
24
|
35
|
36
|
| 17
|
28
|
0
|
6
|
0
|
17
|
19
|
37
|
| 8
|
27
|
9
|
3
|
18
|
26
|
1
|
0
|
| 23
|
0
|
29
|
47
|
24
|
16
|
0
|
30
|
| 0
|
22
|
43
|
28
|
14
|
25
|
11
|
23
|
| 2
|
16
|
28
|
20
|
41
|
0
|
12
|
25
|
Шаг 2. Преобразуем матрицу 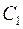 . Для этого обозначим через . Для этого обозначим через 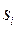 минимальный элемент строки минимальный элемент строки 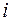 , который последовательно вычтем из элементов той же строки, результаты поместим на место уменьшаемого. Наименьший элемент первой строки матрицы , который последовательно вычтем из элементов той же строки, результаты поместим на место уменьшаемого. Наименьший элемент первой строки матрицы 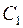 равен 7. Проведем вычисления для элементов первой строки: (d11
=7, d12
=29, d13
=30, d14
=1, d15
=27, d16
=22, d17
=0, d18
=17). Такие же вычисления проведем для остальных строк, получим неотрицательную матрицу равен 7. Проведем вычисления для элементов первой строки: (d11
=7, d12
=29, d13
=30, d14
=1, d15
=27, d16
=22, d17
=0, d18
=17). Такие же вычисления проведем для остальных строк, получим неотрицательную матрицу 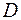 , в каждом столбце и каждой строке которой есть хотя бы один нуль. , в каждом столбце и каждой строке которой есть хотя бы один нуль.
| D= |
7
|
29
|
30
|
1
|
27
|
22
|
0
*
|
17
|
| 3
|
22
|
15
|
34
|
20
|
25
|
0
|
6
|
| 33
|
12
|
10
|
0
*
|
6
|
24
|
35
|
36
|
| 17
|
28
|
0
*
|
6
|
0
|
17
|
19
|
37
|
| 8
|
27
|
9
|
3
|
18
|
26
|
1
|
0
*
|
| 23
|
0
*
|
29
|
47
|
24
|
16
|
0
|
30
|
| 0
*
|
22
|
43
|
28
|
14
|
25
|
11
|
23
|
| 2
|
16
|
28
|
20
|
41
|
0
*
|
12
|
25
|
Основной этап.
После второго шага предварительного этапа получим неотрицательную матрицу 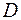 , эквивалентную матрице эффективностей , эквивалентную матрице эффективностей 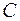 : :
П.1. В первом столбце матрицы 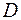 отметим звездочкой 0*
7,1
,во втором столбце – 06,2
, в третьем столбце – 04,3
, в четвертом столбце – 0*
3,4
, в шестом столбце – 08,6
, в седьмом столбце – 01,7 ,
в восьмом столбце – 05,8.
Нули в пятом столбце – 04,5
нельзя отметить звездочкой, так как они лежат в строке, в которой уже есть нуль со звездочкой – 04,3,
. Число звездочек равно семи, что меньше размерности матрицы (8), переходим к п.2. отметим звездочкой 0*
7,1
,во втором столбце – 06,2
, в третьем столбце – 04,3
, в четвертом столбце – 0*
3,4
, в шестом столбце – 08,6
, в седьмом столбце – 01,7 ,
в восьмом столбце – 05,8.
Нули в пятом столбце – 04,5
нельзя отметить звездочкой, так как они лежат в строке, в которой уже есть нуль со звездочкой – 04,3,
. Число звездочек равно семи, что меньше размерности матрицы (8), переходим к п.2.
| D= |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
| 7
|
29
|
30
|
1
|
27
|
22
|
0
*
|
17
|
| 3
|
22
|
15
|
34
|
20
|
25
|
0
’
|
6
|
| 33
|
12
|
10
|
0
*
|
6
|
24
|
35
|
36
|
| 17
|
28
|
0
*
|
6
|
0
’
|
17
|
19
|
37
|
+ |
| 8
|
27
|
9
|
3
|
18
|
26
|
1
|
0
*
|
| 23
|
0
*
|
29
|
47
|
24
|
16
|
0
’
|
30
|
| 0
*
|
22
|
43
|
28
|
14
|
25
|
11
|
23
|
| 2
|
16
|
28
|
20
|
41
|
0
*
|
12
|
25
|
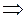 ε=2 ε=2
П.2. Помечаем знаком «+» сверху столбцы: 1, 2, 3, 4,6, 7,8 и считаем эти столбцы занятыми. Незанятый нуль находитсяв четвертой строке пятого столбца 04,5 ,
во второй строке и шестой строках седьмого столбца. Помечаем их штрихом 0'
4,5 ,
0'
2,7 ,
0'6,7
. Переходим к пункту 3.
П.3. Столбец 3 считаем незанятым и знак «+» сверху снимаем (обводим в рамку), а четвертую строку объявляем занятой и помечаем знаком «+» справа. Возвращаемся к третьему абзацу п.2.
П.2. Незанятых нулей нет, переходим к п.5.
П.5. Среди незанятых элементов находим минимальный, который обозначим через 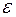 , ε=d3,5
=6. Преобразуем матрицу , ε=d3,5
=6. Преобразуем матрицу 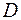 : незанятые элементы уменьшим на 6; дважды занятые увеличим на 6; остальные элементы оставим без изменения. Получим матрицу : незанятые элементы уменьшим на 6; дважды занятые увеличим на 6; остальные элементы оставим без изменения. Получим матрицу  , в которой имеется один незанятый нуль, переходим к четвертому абзацу п.2. , в которой имеется один незанятый нуль, переходим к четвертому абзацу п.2.
| + |
+ |
+ |
+ |
+ |
+ |
+ |
D1
=
|
7
|
29
|
24
|
1
|
21
|
22
|
0
*
|
17
|
| 3
|
22
|
9
|
34
|
14
|
25
|
0
’
|
6
|
+ |
| 33
|
12
|
4
|
0
*
|
0
’
|
24
|
35
|
36
|
| 23
|
34
|
0
*
|
12
|
0
’
|
23
|
25
|
43
|
+ |
| 8
|
27
|
3
|
3
|
12
|
26
|
1
|
0
*
|
| 23
|
0
*
|
23
|
47
|
18
|
16
|
0
’
|
30
|
| 0
*
|
22
|
37
|
28
|
8
|
25
|
11
|
23
|
| 2
|
16
|
22
|
20
|
35
|
0
*
|
12
|
25
|
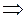
П.2. Незанятый нуль находится в третьей строке пятого столбца 03,5
. Помечаем штрихом 0'
3,5
. Во второй строке седьмого столбца находится нуль со штрихом. Помечаем штрихом 0'
2,7
и считаем седьмой столбец незанятым, знак «+» сверху снимаем, а вторую строку объявляем занятой и помечаем знаком «+» справа.
| + |
+ |
+ |
+ |
+ |
+ |
+ |
D2
=
|
7
|
29
|
24
|
1
|
21
|
22
|
0
*
|
17
|
| 3
|
22
|
9
|
34
|
14
|
25
|
0
’
|
6
|
+ |
| 33
|
12
|
4
|
0
*
|
0
’
|
24
|
35
|
36
|
| 23
|
34
|
0
*
|
12
|
0
’
|
23
|
25
|
43
|
+ |
| 8
|
27
|
3
|
3
|
12
|
26
|
1
|
0
*
|
| 23
|
0
*
|
23
|
47
|
18
|
16
|
0
’
|
30
|
| 0
*
|
22
|
37
|
28
|
8
|
25
|
11
|
23
|
| 2
|
16
|
22
|
20
|
35
|
0
*
|
12
|
25
|
П.5. Переходим к пункту 2. Помечаем звездочкой 0*6,5,
штрихом 0'
8,3,
0'
2,7
. В третьей нет  , следовательно, переходим к пункту 4, ε=d6,4
=7 после преобразований, получим матрицу D3 , следовательно, переходим к пункту 4, ε=d6,4
=7 после преобразований, получим матрицу D3
| + |
+ |
+ |
+ |
+ |
+ |
+ |
D3
=
|
7
|
29
|
24
|
1
|
21
|
22
|
0
*
|
17
|
| 3
|
22
|
9
|
34
|
14
|
25
|
0
’
|
6
|
+ |
| 33
|
12
|
4
|
0
*
|
0
’
|
24
|
35
|
36
|
| 23
|
34
|
0
*
|
12
|
0
’
|
23
|
25
|
43
|
+ |
| 8
|
27
|
3
|
3
|
12
|
26
|
1
|
0
*
|
| 23
|
0
*
|
23
|
47
|
18
|
16
|
0
’
|
30
|
| 0
*
|
22
|
37
|
28
|
8
|
25
|
11
|
23
|
| 2
|
16
|
22
|
20
|
35
|
0
*
|
12
|
25
|
П.4. Строим цепочку из нулей. Начиная от только что отмеченного штрихом нуля (0’
2,7
), идем по строке до  5,2
цепочка состоит из двух элементов Ц: 07,2,
0’
5,2
. В матрице такие цепочки обозначают так 5,2
цепочка состоит из двух элементов Ц: 07,2,
0’
5,2
. В матрице такие цепочки обозначают так  . После преобразования получим новый набор нулей со звездочкой ( . После преобразования получим новый набор нулей со звездочкой ( ), который содержит на одну звездочку больше, чем предыдущий набор. ), который содержит на одну звездочку больше, чем предыдущий набор.
Проводим следующие пересчеты.
Процесс окончен, так как число нулей со звездочкой равно размерности матрицы эффективности.
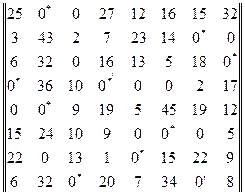
Оптимальный вариант выбора (1,2)(2,7)(3,8)(4,1)(5,4),(6,6),(7,5),(8,3). Это значит, что первая невеста выберет второго жениха, вторая невеста седьмого жениха, третья –восьмого, четвертая первого, пятая четвертого, шестая – шестого, седьмая невеста пятого жениха, а восьмая невеста выберет третьего жениха.
При этом максимальная суммарная эффективность (суммарная продолжительность жизни всех семей) равна:  (единиц эффективности) (единиц эффективности)
|