По имеющимся исходным данным выявить и оценить на основе регрессионных моделей производственные связи. Провести расчет прогнозных значений показателей, когда уровень факторных показателей на 30% превышают средние величины исходных данных.
Исходные данные представлены в таблице:
| №
|
Удой молока на среднегодовую корову, кг
|
Расход кормов на 1 корову, корм. ед.
|
Удельный вес чистопородных коров в стаде, %
|
Себестоимость молока за 1 кг, руб.
|
| 1 |
3280 |
48,20 |
61 |
0,313 |
| 2 |
2920 |
43,10 |
54 |
0,413 |
| 3 |
5140 |
60,70 |
70 |
0,268 |
| 4 |
4630 |
60,10 |
67 |
0,310 |
| 5 |
4950 |
59,40 |
71 |
0,309 |
| 6 |
5000 |
52,50 |
74 |
0,288 |
| 7 |
2790 |
44,00 |
45 |
0,357 |
| 8 |
4340 |
54,20 |
68 |
0,247 |
| 9 |
4160 |
53,20 |
65 |
0,305 |
| 10 |
2660 |
46,40 |
51 |
0,376 |
| 11 |
2960 |
47,10 |
52 |
0,351 |
| 12 |
3230 |
46,10 |
57 |
0,356 |
| 13 |
3480 |
53,90 |
58 |
0,312 |
| 14 |
3230 |
53,40 |
52 |
0,415 |
| 15 |
2370 |
39,40 |
44 |
0,411 |
| 16 |
2610 |
40,20 |
50 |
0,380 |
| 17 |
3000 |
45,50 |
52 |
0,326 |
| 18 |
2960 |
41,40 |
49 |
0,341 |
| 19 |
3100 |
47,80 |
53 |
0,398 |
| 20 |
2720 |
46,30 |
57 |
0,405 |
Необходимо определить тесноту связи между данными признаками. Для этого вначале воспользуемся коэффициентом корреляции рангов Спирмэна. Этот показатель основан на корреляции не самих значений коррелируемых признаков, а их рангов. Для его расчета присвоим ранги значениям соответствующих признаков, затем найдем их разность d. Эти вычисления отразим в нижеследующих таблицах. Далее вычислим непосредственно сам коэффициент, который равен: 
, ( n – число наблюдаемых пар значений признаков.)
Расчетные таблицы для определения коэффициента корреляции рангов Спирмэна
| Удой молока на среднегодовую корову, кг |
Себестоимость молока за 1 кг, руб. |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 3280 |
0,313 |
8 |
13 |
-5 |
25 |
| 2920 |
0,413 |
15 |
2 |
13 |
169 |
| 5140 |
0,268 |
1 |
19 |
-18 |
324 |
| 4630 |
0,31 |
4 |
15 |
-11 |
121 |
| 4950 |
0,309 |
3 |
16 |
-13 |
169 |
| 5000 |
0,288 |
2 |
18 |
-16 |
256 |
| 2790 |
0,357 |
16 |
8 |
8 |
64 |
| 4340 |
0,247 |
5 |
20 |
-15 |
225 |
| 4160 |
0,305 |
6 |
17 |
-11 |
121 |
| 2660 |
0,376 |
18 |
7 |
11 |
121 |
| 2960 |
0,351 |
13,5 |
10 |
3,5 |
12,25 |
| 3230 |
0,356 |
9,5 |
9 |
0,5 |
0,25 |
| 3480 |
0,312 |
7 |
14 |
-7 |
49 |
| 3230 |
0,415 |
9,5 |
1 |
8,5 |
72,25 |
| 2370 |
0,411 |
20 |
3 |
17 |
289 |
| 2610 |
0,38 |
19 |
6 |
13 |
169 |
| 3000 |
0,326 |
12 |
12 |
0 |
0 |
| 2960 |
0,341 |
13,5 |
11 |
2,5 |
6,25 |
| 3100 |
0,398 |
11 |
5 |
6 |
36 |
| 2720 |
0,405 |
17 |
4 |
13 |
169 |
| n = 20 |
∑ d 2
= |
2398 |
| ρ = |
-0,803 |
Из выше приведенного можно сказать о сильной обратной связи между удоем молока и себестоимостью, т.е. при увеличении удоя себестоимость молока снижается.
| Расход кормов на 1 корову, корм.ед. |
Себестоимость молока за 1 кг, руб. |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 48,2 |
0,313 |
9 |
13 |
-4 |
16 |
| 43,1 |
0,413 |
17 |
2 |
15 |
225 |
| 60,7 |
0,268 |
1 |
19 |
-18 |
324 |
| 60,1 |
0,31 |
2 |
15 |
-13 |
169 |
| 59,4 |
0,309 |
3 |
16 |
-13 |
169 |
| 52,5 |
0,288 |
8 |
18 |
-10 |
100 |
| 44 |
0,357 |
16 |
8 |
8 |
64 |
| 54,2 |
0,247 |
4 |
20 |
-16 |
256 |
| 53,2 |
0,305 |
7 |
17 |
-10 |
100 |
| 46,4 |
0,376 |
12 |
7 |
5 |
25 |
| 47,1 |
0,351 |
11 |
10 |
1 |
1 |
| 46,1 |
0,356 |
14 |
9 |
5 |
25 |
| 53,9 |
0,312 |
5 |
14 |
-9 |
81 |
| 53,4 |
0,415 |
6 |
1 |
5 |
25 |
| 39,4 |
0,411 |
20 |
3 |
17 |
289 |
| 40,2 |
0,38 |
19 |
6 |
13 |
169 |
| 45,5 |
0,326 |
15 |
12 |
3 |
9 |
| 41,4 |
0,341 |
18 |
11 |
7 |
49 |
| 47,8 |
0,398 |
10 |
5 |
5 |
25 |
| 46,3 |
0,405 |
13 |
4 |
9 |
81 |
| n = 20 |
∑ d 2
= |
2202 |
| ρ = |
-0,656 |
Так как значение коэффициента отрицательно, следовательно, имеем обратную связь между расходом кормов на 1 корову и себестоимостью молока.
Удельный вес чистопородных коров в стаде, %
|
Себестоимость молока за 1 кг, руб. |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 61 |
0,313 |
7 |
13 |
-6 |
36 |
| 54 |
0,413 |
11 |
2 |
9 |
81 |
| 70 |
0,268 |
3 |
19 |
-16 |
256 |
| 67 |
0,31 |
5 |
15 |
-10 |
100 |
| 71 |
0,309 |
2 |
16 |
-14 |
196 |
| 74 |
0,288 |
1 |
18 |
-17 |
289 |
| 45 |
0,357 |
19 |
8 |
11 |
121 |
| 68 |
0,247 |
4 |
20 |
-16 |
256 |
| 65 |
0,305 |
6 |
17 |
-11 |
121 |
| 51 |
0,376 |
16 |
7 |
9 |
81 |
| 52 |
0,351 |
13 |
10 |
3 |
9 |
| 57 |
0,356 |
9 |
9 |
0 |
0 |
| 58 |
0,312 |
8 |
14 |
-6 |
36 |
| 52 |
0,415 |
13 |
1 |
12 |
144 |
| 44 |
0,411 |
20 |
3 |
17 |
289 |
| 50 |
0,38 |
17 |
6 |
11 |
121 |
| 52 |
0,326 |
13 |
12 |
1 |
1 |
| 49 |
0,341 |
18 |
11 |
7 |
49 |
| 53 |
0,398 |
12 |
5 |
7 |
49 |
| 57 |
0,405 |
9 |
4 |
5 |
25 |
| n = 20 |
∑ d 2
= |
2260 |
| ρ = |
-0,699 |
Имеется обратная зависимости между удельным весом чистопородных коров в стаде и себестоимостью молока.
| Удой молока на среднегодовую корову, кг |
Расход кормов на 1 корову, корм.ед. |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 3280 |
48,2 |
8 |
9 |
-1 |
1 |
| 2920 |
43,1 |
15 |
17 |
-2 |
4 |
| 5140 |
60,7 |
1 |
1 |
0 |
0 |
| 4630 |
60,1 |
4 |
2 |
2 |
4 |
| 4950 |
59,4 |
3 |
3 |
0 |
0 |
| 5000 |
52,5 |
2 |
8 |
-6 |
36 |
| 2790 |
44 |
16 |
16 |
0 |
0 |
| 4340 |
54,2 |
5 |
4 |
1 |
1 |
| 4160 |
53,2 |
6 |
7 |
-1 |
1 |
| 2660 |
46,4 |
18 |
12 |
6 |
36 |
| 2960 |
47,1 |
13,5 |
11 |
2,5 |
6,25 |
| 3230 |
46,1 |
9,5 |
14 |
-4,5 |
20,25 |
| 3480 |
53,9 |
7 |
5 |
2 |
4 |
| 3230 |
53,4 |
9,5 |
6 |
3,5 |
12,25 |
| 2370 |
39,4 |
20 |
20 |
0 |
0 |
| 2610 |
40,2 |
19 |
19 |
0 |
0 |
| 3000 |
45,5 |
12 |
15 |
-3 |
9 |
| 2960 |
41,4 |
13,5 |
18 |
-4,5 |
20,25 |
| 3100 |
47,8 |
11 |
10 |
1 |
1 |
| 2720 |
46,3 |
17 |
13 |
4 |
16 |
| n = 20 |
∑ d 2
= |
172 |
| ρ = |
0,871 |
Полученное значение коэффициента корреляции рангов Спирмэна свидетельствует о сильной прямой связи между удоем молока и расходом кормов на 1 корову, т.е. при увеличении расхода кормов в пересчете на 1 корову увеличивается и удой молока на среднегодовую корову.
| Удой молока на среднегодовую корову, кг |
Удельный вес чистопородных коров в стаде, % |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 3280 |
61 |
8 |
7 |
1 |
1 |
| 2920 |
54 |
15 |
11 |
4 |
16 |
| 5140 |
70 |
1 |
3 |
-2 |
4 |
| 4630 |
67 |
4 |
5 |
-1 |
1 |
| 4950 |
71 |
3 |
2 |
1 |
1 |
| 5000 |
74 |
2 |
1 |
1 |
1 |
| 2790 |
45 |
16 |
19 |
-3 |
9 |
| 4340 |
68 |
5 |
4 |
1 |
1 |
| 4160 |
65 |
6 |
6 |
0 |
0 |
| 2660 |
51 |
18 |
16 |
2 |
4 |
| 2960 |
52 |
13,5 |
13 |
0,5 |
0,25 |
| 3230 |
57 |
9,5 |
9 |
0,5 |
0,25 |
| 3480 |
58 |
7 |
8 |
-1 |
1 |
| 3230 |
52 |
9,5 |
13 |
-3,5 |
12,25 |
| 2370 |
44 |
20 |
20 |
0 |
0 |
| 2610 |
50 |
19 |
17 |
2 |
4 |
| 3000 |
52 |
12 |
13 |
-1 |
1 |
| 2960 |
49 |
13,5 |
18 |
-4,5 |
20,25 |
| 3100 |
53 |
11 |
12 |
-1 |
1 |
| 2720 |
57 |
17 |
9 |
8 |
64 |
| n = 20 |
∑ d 2
= |
142 |
| ρ = |
0,893 |
Значение положительно, поэтому имеемхарактеризует сильную прямую связь между удоем молока и удельным весом чистопородных коров в стаде и показывает, что вариация результативного признака на 89,3 % обусловлена вариацией факторного признака (согласно коэффициенту Спирмэна).
| Расход кормов на 1 корову, корм.ед. |
Удельный вес чистопородных коров в стаде, % |
Ранги |
Разность рангов в = Nx - Ny |
d2
|
| x |
y |
Nx
|
Ny
|
| 48,2 |
61 |
9 |
7 |
2 |
4 |
| 43,1 |
54 |
17 |
11 |
6 |
36 |
| 60,7 |
70 |
1 |
3 |
-2 |
4 |
| 60,1 |
67 |
2 |
5 |
-3 |
9 |
| 59,4 |
71 |
3 |
2 |
1 |
1 |
| 52,5 |
74 |
8 |
1 |
7 |
49 |
| 44 |
45 |
16 |
19 |
-3 |
9 |
| 54,2 |
68 |
4 |
4 |
0 |
0 |
| 53,2 |
65 |
7 |
6 |
1 |
1 |
| 46,4 |
51 |
12 |
16 |
-4 |
16 |
| 47,1 |
52 |
11 |
13 |
-2 |
4 |
| 46,1 |
57 |
14 |
9 |
5 |
25 |
| 53,9 |
58 |
5 |
8 |
-3 |
9 |
| 53,4 |
52 |
6 |
13 |
-7 |
49 |
| 39,4 |
44 |
20 |
20 |
0 |
0 |
| 40,2 |
50 |
19 |
17 |
2 |
4 |
| 45,5 |
52 |
15 |
13 |
2 |
4 |
| 41,4 |
49 |
18 |
18 |
0 |
0 |
| 47,8 |
53 |
10 |
12 |
-2 |
4 |
| 46,3 |
57 |
13 |
9 |
4 |
16 |
| n = 20 |
∑ d 2
= |
244 |
| ρ = |
0,817 |
О сильной прямой зависимости между расходом кормов в пересчете на 1 корову и удельным весом чистопородных коров в стаде говорит значение коэффициента. Чем выше удельный вес, тем выше расход кормов.
Но следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, а не самих значений признаков, он менее точен по сравнению с линейным коэффициентом корреляции. Воспользуемся последним.
Воспользуемся программным пакетом Stata 7.
Корреляционная матрица имеет вид:
. corrudkormvessst
(obs=20)
| ud korm ves sst
-------------+------------------------------------
ud | 1.0000
korm | 0.8851 1.0000
ves | 0.9401 0.8290 1.0000
sst | -0.7875 -0.6497 -0.7587 1.0000
· ud
– удой молока на среднегодовую корову,
· korm
– расход кормов на 1 корову,
· ves
– удельный вес чистопородных коров в стаде,
· sst
– себестоимость молока за 1 кг.
Можно сделать вывод, что присутствует обратная связь между себестоимостью и удоем молока (r = - 0,79), себестоимостью и удельным весом (r = - 0,76),себестоимостью и расходом кормов (r = - 0,65).Имеется сильная прямая связи между удоем молока и расходом кормов (r = 0,89), удоем молока и удельным весом (r = 0,94), расходом кормов и удельным весом (r = 0,83). Если сравнивать значения, полученные линейным коэффициентом корреляции и ранговым коэффициентом Спирмэна, то расхождения не превысят 8 %. В большинстве же своем погрешность составляет около 1 %.
Теперь проверим коэффициенты корреляции на значимость:
. pwcorr ud korm ves sst
| ud korm ves sst
-------------+------------------------------------
ud | 1.0000
korm | 0.8851 1.0000
ves | 0.9401 0.8290 1.0000
sst | -0.7875 -0.6497 -0.7587 1.0000
Всекоэффициентызначимы.
Построим модель.
Так как значения удоя молока и значения других показателей отличаются на порядок, то будем использовать вместо переменной «удой молока» переменную натурального логарифма удоя молока.
Рассмотрим в качестве результативного фактора себестоимость молока за 1 кг, поскольку важен расчет именно себестоимости и определение от каких факторов и насколько она зависит. Удой молока, расход кормов на 1 корову и удельный вес чистопородных коров в стаде могут повлиять на значение себестоимости.
Приведем графики зависимости себестоимости от каждого из факторов:
От логарифма удоя молока
От расхода кормов на 1 корову
От удельного веса чистопородных коров в стаде
Графики демонстрируют нам обратную зависимость между результативным фактором – себестоимостью и объясняющим фактором, что подтверждается значениями коэффициентов корреляции.
Вначале рассмотрим линейную модель по всем факторам:
. reg sst lnud korm ves
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.37
Model | .031800232 3 .010600077 Prob > F = 0.0005
Residual | .016350718 16 .00102192 R-squared = 0.6604
-------------+------------------------------ Adj R-squared = 0.5968
Total | .04815095 19 .002534261 Root MSE = .03197
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.2305787 .1162704 -1.98 0.065 -.4770609 .0159036
korm | .0026417 .0025775 1.02 0.321 -.0028223 .0081057
ves | -.0000138 .0024772 -0.01 0.996 -.0052651 .0052376
_cons | 2.088534 .7538614 2.77 0.014 .4904194 3.686649
------------------------------------------------------------------------------
Хотя у этой модели и достаточно хороший коэффициент детерминации и согласно F-критерию Фишера оно значимо, параметры при переменных lnud, korm, ves не значимы по t-критерию Стьюдента с P-значениями 0.065, 0.321 и 0.996. Значит, эта модель не подходит.
Построим модель вида: 
. reg sst lnud1 korm1 ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.32
Model | .031744654 3 .010581551 Prob > F = 0.0005
Residual | .016406296 16 .001025393 R-squared = 0.6593
-------------+------------------------------ Adj R-squared = 0.5954
Total | .04815095 19 .002534261 Root MSE = .03202
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 14.46292 6.110319 2.37 0.031 1.509625 27.41622
korm1 | -5.633853 5.967609 -0.94 0.359 -18.28462 7.016912
ves1 | .6831225 6.892859 0.10 0.922 -13.92909 15.29533
_cons | -1.33304 .6029802 -2.21 0.042 -2.611301 -.0547791
------------------------------------------------------------------------------
Видим что коэффициент детерминации хорош - 0,659 и по F-критерию Фишера уравнение значимо. Но параметры при переменных korm1, ves1 не значимы по t-критерию Стьюдента с P-значениями 0.359 и 0.922. Значит, эта модель не подходит.
Будем рассматривать различные комбинации переменных при включении в модель. Построим модель вида: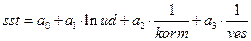 
. reg sst lnud korm1 ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.09
Model | .031497211 3 .01049907 Prob > F = 0.0006
Residual | .016653739 16 .001040859 R-squared = 0.6541
-------------+------------------------------ Adj R-squared = 0.5893
Total | .04815095 19 .002534261 Root MSE = .03226
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.2065493 .0898758 -2.30 0.035 -.3970775 -.0160212
korm1 | -5.156249 5.939941 -0.87 0.398 -17.74836 7.435864
ves1 | 1.094516 6.895036 0.16 0.876 -13.52231 15.71134
_cons | 2.109487 .8816345 2.39 0.029 .2405058 3.978469
------------------------------------------------------------------------------
Так же как и в предыдущих моделях, значение R-квадрата хорошее, уравнение значимо по F-критерию Фишера, но одновременно с этим параметры при переменных korm1, ves1 с P-значениями 0.398 и 0.876 соответственно не значимы по t-критерию Стьюдента. Также отбросим эту модель.
Построим модель вида: 
. reg sst lnud1 korm ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.60
Model | .032029999 3 .010676666 Prob > F = 0.0004
Residual | .016120951 16 .001007559 R-squared = 0.6652
-------------+------------------------------ Adj R-squared = 0.6024
Total | .04815095 19 .002534261 Root MSE = .03174
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 15.74117 6.497854 2.42 0.028 1.966333 29.516
korm | .0027978 .0025644 1.09 0.291 -.0026386 .0082341
ves1 | .0207899 6.780318 0.00 0.998 -14.35284 14.39442
_cons | -1.732706 .8136604 -2.13 0.049 -3.457589 -.0078235
------------------------------------------------------------------------------
R-квадрат хорош- 0,665, уравнение значимо согласно F-критерию Фишера. Но при этом параметры при переменных korm, ves1 с P-значениями 0.291 и 0.998 соответственно не значимы по t-критерию Стьюдента. Также отбросим эту модель.
Рассмотрим модель: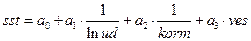 
. reg sst lnud1 korm1 ves
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.31
Model | .031738225 3 .010579408 Prob > F = 0.0005
Residual | .016412725 16 .001025795 R-squared = 0.6591
-------------+------------------------------ Adj R-squared = 0.5952
Total | .04815095 19 .002534261 Root MSE = .03203
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 14.53007 7.378598 1.97 0.066 -1.111856 30.172
korm1 | -5.544031 5.927707 -0.94 0.364 -18.11021 7.022147
ves | -.0001462 .002454 -0.06 0.953 -.0053485 .005056
_cons | -1.322613 .969369 -1.36 0.191 -3.377583 .7323579
------------------------------------------------------------------------------
Как и в предыдущих моделях, несмотря на значимость уравнения и хорошее значение коэффициента детерминации, эту регрессионную модель мы также отбросим, так как в ней незначимы параметры при переменных lnud1, korm1, ves согласно t-критерию Стьюдента.
Рассмотрим модель:
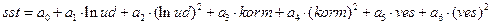
. reg sst lnud lnud2 korm korm2 ves ves2
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 6, 13) = 4.52
Model | .032557159 6 .005426193 Prob > F = 0.0109
Residual | .015593791 13 .001199522 R-squared = 0.6761
-------------+------------------------------ Adj R-squared = 0.5267
Total | .04815095 19 .002534261 Root MSE = .03463
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -5.729043 9.44621 -0.61 0.555 -26.13634 14.67825
lnud2 | .341597 .5910669 0.58 0.573 -.9353253 1.618519
korm | .0132344 .0388671 0.34 0.739 -.0707327 .0972016
korm2 | -.0001134 .0004041 -0.28 0.783 -.0009865 .0007596
ves | .0150622 .0364293 0.41 0.686 -.0636385 .0937629
ves2 | -.0001446 .0003466 -0.42 0.683 -.0008934 .0006042
_cons | 23.57414 36.19652 0.65 0.526 -54.62369 101.772
------------------------------------------------------------------------------
Эта модель также не подходит, поскольку параметры при всех переменных не значимы согласно t-критерию Стьюдента.
Рассмотрим модель: 
. reg sst lnud2 korm2 ves2
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.39
Model | .031819188 3 .010606396 Prob > F = 0.0005
Residual | .016331762 16 .001020735 R-squared = 0.6608
-------------+------------------------------ Adj R-squared = 0.5972
Total | .04815095 19 .002534261 Root MSE = .03195
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud2 | -.0150021 .0079436 -1.89 0.077 -.0318418 .0018377
korm2 | .000028 .0000263 1.07 0.302 -.0000277 .0000838
ves2 | 2.49e-06 .0000227 0.11 0.914 -.0000457 .0000507
_cons | 1.258054 .4178871 3.01 0.008 .3721731 2.143935
------------------------------------------------------------------------------
И в этой модели параметры при переменных не значимы по t-критерию Стьюдента. Отбрасываем эту модель.
Воспользуемся процедурой пошагового отбора регрессоров при построении множественной регрессии. При этом из исходного набора объясняющих переменных будут включаться в число регрессоров в первую очередь те переменные, которые имеют больший уровень значимости. Вначале включим в набор переменных переменную  , а затем переменную  .
. sw reg sst lnud korm ves korm1 ves1 lnud2 korm2 ves2,pe(0.05)
begin with empty model
p = 0.0000 < 0.0500 adding lnud
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 31.70
Model | .030711968 1 .030711968 Prob > F = 0.0000
Residual | .017438982 18 .000968832 R-squared = 0.6378
-------------+------------------------------ Adj R-squared = 0.6177
Total | .04815095 19 .002534261 Root MSE = .03113
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.1672727 .0297095 -5.63 0.000 -.22969 -.1048553
_cons | 1.703191 .241499 7.05 0.000 1.19582 2.210561
------------------------------------------------------------------------------
В итоге получили модель  . Это уравнение значимо согласно F-критерию Фишера, и параметр при переменной lnud и константа значимы по t-критерию Стьюдента. 63,78 % суммы квадратов отклонений переменной sst от среднего значения объясняется переменными модели. А при увеличении удоя молока на 2,72 % себестоимость снижается на 0,17 %.
. sw reg sst lnud1 korm ves korm1 ves1 lnud2 korm2 ves2,pe(0.05)
begin with empty model
p = 0.0000 < 0.0500 adding lnud1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
Получили модель 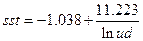 . Это уравнение значимо по F-критерию Фишера, и параметр при переменной lnud1 и константа значимы по t-критерию Стьюдента. 64,03 % суммы квадратов отклонений переменной sst от среднего значения объясняется переменными модели.
Сделаем выбор между этими двумя моделями. Представим критерии выбора модели в следующей таблице:
| Модель |
Критерий |
| R-квадрат |
Скорректированный R-квадрат |
Акейка |
Шварца |
σост
|
|
0.6378 |
0.6177 |
-13,9896 |
-6,89499 |
0,0302959 |
|
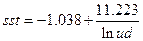0.6403 |
0.6203 |
-14,0032 |
-6,90180 |
0,03019289 |
Из данной таблицы видно, что по всем критериям гиперболическая модель лучше линейной.
Проверим регрессию на автокорреляцию остатков:
. regdw sst lnud1,t(lnud1) force
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
Durbin-Watson Statistic = 2.460766
Проверка на автокорреляцию дает удовлетворительное значение статистики Дарбина-Уотсона 2,46 (автокорреляция отсутствует), так как  , где  (табличное значение). Это означает, что ошибки независимы между собой.
Построим график остатков регрессии от оцененной зависимой переменной:
. fit sst lnud1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
. rvfplot, c(m)
Можно предположить наличие гетероскедастичноти, поскольку разброс значений остатков увеличивается с ростом значений себестоимости молока. Проверим этот факт с помощью теста Бреуша-Пагана:
. hettest
Cook-Weisberg test for heteroskedasticity using fitted values of sst
Ho: Constant variance
chi2(1) = 0.01
Prob > chi2 = 0.9328
Тест Бреуша-Пагана подтверждает наличие гетероскедастичности, потому что гипотеза о постоянстве дисперсий отклоняется.
Скорректируем стандартные ошибки по Навье-Весту, учитывая гетероскедастичность:
. newey sst lnud1, lag(0) force
Regression with Newey-West standard errors Number of obs = 20
maximum lag : 0 F( 1, 18) = 60.26
Prob > F = 0.0000
------------------------------------------------------------------------------
| Newey-West
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud
1 | 11.2229 1.445712 7.76 0.000 8.18557 14.26023
_cons | -1.038311 .1784612 -5.82 0.000 -1.413244 -.6633776
------------------------------------------------------------------------------
Изменились доверительные интервалы для параметров переменных модели.
Итак, имеем модель:  ,
(sst-себестоимость молока за 1 кг, руб) ;
lnud-логарифм удоя молока на среднегодовую корову, кг.
Себестоимость не зависит ни от расхода кормов на 1 корову, ни от удельного веса чистопородных коров в стаде. Выявлена обратная пропорциональность между себестоимостью молока и логарифмом удоя молока, а следовательно, и просто удоем молока. Стандартная ошибка переменной  составляет 1.4457, а константы – 0.1785. Доверительный интервал для переменной – [ 8.1856 ; 14.2602 ], для константы – [ -1.4132 ; -0.6634 ].
Рассчитаем прогнозные значения показателей, когда уровень факторных показателей на 30 % превышает средние величины исходных данных. Средний показатель удоя молока на среднегодовую корову равен 3476.5 кг. Превышение этого значения на 30 % составляет 4519.45 кг. Прологарифмируя, получим: lnud = 8.416. Тогда, согласно модели, себестоимость при таком значении удоя молока составит 0,296 руб. за 1 кг.
|