Задача №5
Оборот и издержки обращения двадцати шести торговых предприятий за отчетный период составили (тыс. руб.):
| Магазины, № п/п |
Оборот |
Издержки обращения |
Магазины, № п/п |
Оборот |
Издержки обращения |
| 1 |
4010 |
878 |
14 |
980 |
246 |
| 2 |
5305 |
1010 |
15 |
5500 |
1045 |
| 3 |
3720 |
740 |
16 |
3470 |
729 |
| 4 |
950 |
233 |
17 |
5008 |
951 |
| 5 |
2430 |
588 |
18 |
6950 |
1251 |
| 6 |
3992 |
838 |
19 |
1440 |
360 |
| 7 |
2903 |
653 |
20 |
5590 |
1060 |
| 8 |
4902 |
1029 |
21 |
3704 |
775 |
| 9 |
5404 |
973 |
22 |
2325 |
553 |
| 10 |
3940 |
788 |
23 |
2635 |
580 |
| 11 |
4010 |
862 |
24 |
3990 |
854 |
| 12 |
5307 |
991 |
25 |
5740 |
1081 |
| 13 |
2870 |
654 |
26 |
3610 |
784 |
Для выявления зависимости между размером оборота и издержками обращения произведите группировку магазинов по размеру оборота, образовав четыре группы магазинов с равными интервалами. В каждой группе и в целом подсчитайте:
1) число магазинов;
2) размер оборота – всего и в среднем на один магазин;
3) издержки обращения – всего и в среднем на один магазин;
4) уровень издержек обращения  . .
Решение оформите в разработочной и групповой таблицах. Сделайте выводы, укажите вид группировки.
Решение:
Определим величину интервала каждой группы по формуле:
 , n=4 , n=4

Составим таблицу для интервалов
| № группы |
1 |
2 |
3 |
4 |
| Интервал |
950-2450 |
2450-3950 |
3950-5450 |
5450-6950 |
Сформируем разработочную таблицу
| № группы |
Группы магазинов по обороту |
№ магазина в списке |
Оборот, тыс. руб. |
Издержки обращения, тыс. руб. |
| 4 |
950 |
233 |
| 1 |
950-2450 |
5 |
2430 |
588 |
| 14 |
980 |
246 |
| 19 |
1440 |
360 |
| 22 |
2325 |
553 |
| Итого по гр.1
|
5
|
8125
|
1980
|
| 3 |
3720 |
740 |
| 7 |
2903 |
653 |
| 10 |
3940 |
788 |
| 2 |
2450-3950 |
13 |
2870 |
654 |
| 16 |
3470 |
729 |
| 21 |
3704 |
775 |
| 23 |
2635 |
580 |
| 26 |
3610 |
784 |
| Итого по гр.2
|
8
|
26852
|
5703
|
| 1 |
4010 |
878 |
| 2 |
5305 |
1010 |
| 6 |
3992 |
838 |
| 3 |
3950-5450 |
8 |
4902 |
1029 |
| 9 |
5404 |
973 |
| 11 |
4010 |
862 |
| 12 |
5307 |
991 |
| 17 |
5008 |
951 |
| 24 |
3990 |
854 |
| Итого по гр.3
|
9
|
41928
|
8386
|
| 15 |
5500 |
1045 |
| 4 |
5450-6950 |
18 |
6950 |
1251 |
| 20 |
5590 |
1060 |
| 25 |
5740 |
1081 |
| Итого по гр.4
|
4
|
23780
|
4437
|
| Всего
|
26
|
100685
|
20506
|
На основе разработочной группировочной таблицы составим итоговую аналитическую таблицу
| № группы |
Группы магазинов |
Число магазинов |
Оборот, тыс .руб. |
Издержки обращения, тыс. руб. |
Уровень издержек обращения, % |
| Всего |
в среднем на 1 магазин |
Всего |
в среднем на 1 магазин |
| 1 |
950-2450 |
5 |
8125 |
1625 |
1980 |
396 |
24,4 |
| 2 |
2450-3950 |
8 |
26852 |
3356,5 |
5703 |
712,875 |
21,2 |
| 3 |
3950-5450 |
9 |
41928 |
4658,67 |
8386 |
931,78 |
20 |
| 4 |
5450-6950 |
4 |
23780 |
5945 |
4437 |
1109,25 |
18,7 |
| Итого |
26 |
100685 |
3872,5 |
20506 |
788,69 |
20,4 |
Выводы: группировка показала наличие зависимости издержек обращения в зависимости от оборота – с ростом оборота растут издержки обращения, а также направление этой зависимости ‑ с ростом значений факторного признака также растут значения результативного признака.
Задача №10
Предприятие закупило у акционерного общества шерсть для переработки:
| Вид шерсти |
Выход чистой шерсти, % |
Количество шерсти, кг |
| фактический |
стандартный |
Тонкая
Полутонкая
Полугрубая
Грубая
|
40
38
42
60
|
35
39
41
58
|
600
260
400
1700
|
Определите по каждому виду и в целом:
1) количество стандартной шерсти;
2) долю каждого вида в общем объеме закупленной шерсти;
3) темп роста закупок, если в прошлом периоде закупили у акционерного общества 3050 кг.
Решение:
1) Для определения количества стандартной шерсти по каждому виду шерсти рассчитаем коэффициент пересчета для каждого вида шерсти, а затем умножим его на количество закупленной шерсти. Результаты расчетов занесем в таблицу.
| Вид шерсти |
Выход чистой шерсти, % |
Количество шерсти, кг |
Коэффициент пересчета |
Количество стандартной шерсти, кг |
| фактический |
стандартный |
| Тонкая |
40 |
35 |
600 |
1,143 |
685,714 |
| Полутонкая |
38 |
39 |
260 |
0,974 |
253,333 |
| Полугрубая |
42 |
41 |
400 |
1,024 |
409,756 |
| Грубая |
60 |
58 |
1700 |
1,034 |
1758,621 |
Тогда общий объем в условно-натуральных единицах составит
685,714+253,333+409,756+1758,621=3107,424 кг
2) Доля каждого вида закупленной шерсти находится как отношение каждого вида шерсти к общему ее количеству, выраженное в процентах. Расчеты проведем в таблице:
| Вид шерсти |
Количество стандартной шерсти |
| кг |
% |
| Тонкая |
685,714 |
22,07 |
| Полутонкая |
253,333 |
8,15 |
| Полугрубая |
409,756 |
13,19 |
| Грубая |
1758,621 |
56,59 |
3) Рассчитаем темп роста закупок:
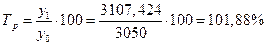 , т.е. объем закупок в текущем году увеличился на 1,88%. , т.е. объем закупок в текущем году увеличился на 1,88%.
Задача №20
Сведения о ценах и количестве проданного товара А по данным регистрации цен на рынке города:
| Цена за 1 кг, руб. |
Продано кг за |
| 22.06 |
22.07 |
22.08 |
22.09 |
июль |
август |
сентябрь |
| 10 |
14 |
12 |
12 |
3000 |
3500 |
3200 |
Определите:
1) среднемесячные цены за июль, август, сентябрь;
2) среднеквартальную цену товара А.
Решение:
Определим средние цены по формуле средней арифметической простой:
за июль:  руб. руб.
за август:  руб. руб.
за сентябрь:  руб. руб.
Средняя цена за квартал вычисляется по формуле средней арифметической взвешенной:
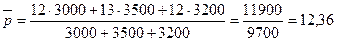 руб. руб.
Задача №23
С целью изучения вариации размеров торговой площади магазинов произведено 5%-ное выборочное обследование по методу случайного бесповторного отбора. Результаты обследования представлены следующими данными:
| Группы магазинов по торговой площади, кв. м |
Число магазинов |
| До 40 |
2 |
| 40-60 |
4 |
| 60-100 |
9 |
| 100-200 |
10 |
| Свыше 200 |
5 |
| Итого |
30 |
Определите:
1) средний размер торговой площади одного магазина;
2) дисперсию и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборки, а также интервал, в котором находится средний размер торговой площади всех магазинов.
Сделайте выводы.
Решение:
Для проведения расчетов нужно преобразовать интервальный ряд в дискретный. Центр интервала определяем по формуле средней арифметической простой. Величины первого и последнего открытых интервалов условно примем равными величинам второго и предпоследнего интервалов соответственно. Результаты вычислений запишем в таблицу:
| Группы магазинов по торговой площади, м2
|
Число магазинов
f
|
Среднее значение интервала,
x
|
x×f |
x2
×f |
| до 40 |
2 |
30 |
60 |
1800 |
| 40-60 |
4 |
50 |
200 |
10000 |
| 60-100 |
9 |
80 |
720 |
57600 |
| 100-200 |
10 |
150 |
1500 |
225000 |
| свыше 200 |
5 |
250 |
1250 |
312500 |
| Итого |
30 |
3730 |
606900 |
1. Рассчитаем среднее значение торговой площади по формуле средней арифметической взвешенной
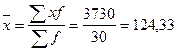 м2 м2
2. Рассчитаем дисперсию


Среднее квадратическое отклонение равно  м2 м2
3. Рассчитаем коэффициент вариации: 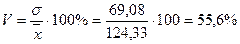
4. Предельная ошибка для генеральной средней в случае бесповторного отбора вычисляется по формуле:
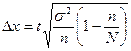 , где s2
- дисперсия, n - объем выборки, N - объем генеральной совокупности, а t – коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,997 t=3). , где s2
- дисперсия, n - объем выборки, N - объем генеральной совокупности, а t – коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,997 t=3).
Т.к. выборка 5%-ная, то отношение 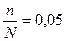 . Подставим известные данные в формулу: . Подставим известные данные в формулу:

Пределы для генеральной средней задаются неравенствами:

Таким образом, интервал, в котором находится средний стаж работы всех работников предприятия, будет
124,33 – 36,88 £ a £ 124,33 + 36,88
87,45 £ a £ 161,21
Выводы: колеблемость торговой площади, определяемая коэффициентом вариации, значительна (более 50%). С вероятностью 0,997 можно утверждать, что средняя торговая площадь всей генеральной совокупности лежит в пределах от 87,45 до 161,21 м2
.
Задача №32
Производство хлеба и хлебобулочных изделий в области характеризуется следующими данными:
| Год |
Произведено хлеба, тыс. т |
| 1 |
166,6 |
| 2 |
141,0 |
| 3 |
128,9 |
| 4 |
121,2 |
| 5 |
120,0 |
Определите:
1) вид динамического ряда;
2) средний уровень динамического ряда;
3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;
4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.
Результаты расчетов представьте в таблице. Изобразите динамичес-кий ряд на графике. Сделайте выводы.
Решение:
1) динамический ряд – интервальный, т.к. уровни ряжа приведены за определенный промежуток времени (в данном случае, за год);
2) т.к. данный ряд интервальный, то средний уровень вычисляем по формуле средней арифметической
 тыс. тонн тыс. тонн
3) рассчитаем абсолютные приросты, темпы роста и прироста, а также абсолютное содержание 1% прироста. Результаты расчетов удобно поместить в таблицу
| Год |
Произведено хлеба, тыс. т. |
Абсолютный прирост |
Темп роста |
Темп прироста |
Абсолютное содержание 1% прироста |
| цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
| 1 |
166,6 |
| 2 |
141 |
-25,6 |
-25,6 |
84,63% |
84,63% |
-15,37% |
-15,37% |
1,666 |
| 3 |
128,9 |
-12,1 |
-37,7 |
91,42% |
77,37% |
-8,58% |
-22,63% |
1,41 |
| 4 |
121,2 |
-7,7 |
-45,4 |
94,03% |
72,75% |
-5,97% |
-27,25% |
1,289 |
| 5 |
120 |
-1,2 |
-46,6 |
99,01% |
72,03% |
-0,99% |
-27,97% |
1,212 |
Для расчета были использованы следующие формулы:
а) цепные показатели
Dy (ц.с.)=yi
-yi
-1
Тр
(ц.с.)=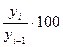
Тпр
(ц.с.)=Тр
(ц.с.) – 100
б) базисные показатели
Dy(б.с.)=yi
-y0
Тр
(б.с.)= 
Тпр
(б.с.)=Тр
(б.с.) – 100
 - абсолютное содержание одного процента прироста - абсолютное содержание одного процента прироста
4) рассчитаем средние показатели ряда
Средний абсолютный прирост
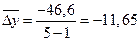
Средний темп роста
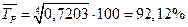
Средний темп прироста
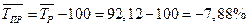
Изобразим динамический ряд на графике
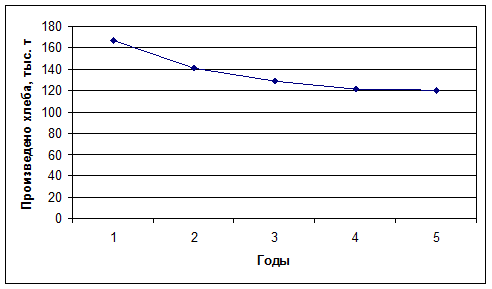
Выводы: динамический ряд является строго убывающим, о чем свидетельствуют все отрицательные цепные абсолютные приросты. Таким образом, объем производства хлеба и х/б изделий области неуклонно снижался. При этом среднегодовое значение производства хлеба составило 135,54 тыс. тонн. Ежегодное снижение производства хлеба составило в среднем 11,64 тыс. тонн, среднегодовой темп роста составил 92,12%, т.е. уровни ряда ежегодно уменьшались в среднем на 7,88%.
Задача №48
Реализация яблок за два периода составила:
Сорт
яблок
|
Продано, кг |
Цена 1 кг, руб. |
| базисный период |
отчетный период |
базисный период |
отчетный период |
| А |
100 |
120 |
35 |
30 |
| В |
210 |
260 |
28 |
22 |
Определите:
1) индивидуальные индексы цен и физического объема продаж;
2) общий индекс цен;
3) общий индекс физического объема продаж;
4) общий индекс оборота в действующих ценах;
5) абсолютную сумму прироста оборота – всего, в том числе за счет изменения цен и количества проданных товаров.
Сделайте выводы.
Решение:
1) Индивидуальные индексы рассчитываются как отношение величин в отчетном и базисном периоде:  , , 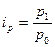 . .
Для расчетов общих индексов заполним вспомогательную таблицу
| Сорт яблок |
Продано, кг |
Цена 1 кг, руб. |
Индивидуальные индексы |
p1
q1
|
p0
q0
|
p0
q1
|
| базисный период |
отчетный период |
базисный период |
отчетный период |
физического объема |
цен |
| А |
100 |
120 |
35 |
30 |
1,200 |
0,857 |
3600 |
3500 |
4200 |
| Б |
210 |
260 |
28 |
22 |
1,238 |
0,786 |
5720 |
5880 |
7280 |
| Итого |
310 |
380 |
9320 |
9380 |
11480 |
2) Общий индекс цен Пааше
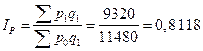 или 81,18% или 81,18%
3) Общий индекс физического объема продаж
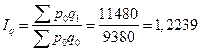 или 122,39% или 122,39%
4) Общий индекс оборота в действующих ценах
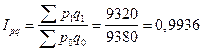 или 99,36% или 99,36%
5) абсолютная сумма изменения оборота непродовольственных товаров
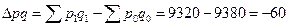 руб., в том числе руб., в том числе
за счет динамики цен  руб. руб.
за счет динамики физического объема  руб. руб.
Выводы: в отчетном году оборот от продажи яблок уменьшился на 0,64%. Уменьшение оборота произошло за счет уменьшения цен на 18,82%, но за счет увеличения физического объема продажи оборот увеличился на 22,39%, что в абсолютном выражении составило -60 руб. всего, в том числе за счет уменьшения цен - на -2160 руб. и за счет увеличения физического объема – на +2100 руб.
Задача №46
Продажа безалкогольных напитков предприятием составила (тыс. руб.):
| Квартал |
Первый год |
Второй год |
Третий год |
| 1-й |
113 |
106 |
120 |
| 2-й |
268 |
276 |
292 |
| 3-й |
454 |
498 |
505 |
| 4-й |
168 |
187 |
208 |
Для анализа сезонности продажи безалкогольных напитков исчислите индексы сезонности. Изобразите сезонную волну графически. Сделайте выводы.
Решение:
Определим средние показатели. Результаты расчетов запишем в таблицу.
| Квартал |
Первый год |
Второй год |
Третий год |
Итого |
Среднее |
| 1 |
113 |
106 |
120 |
339 |
113 |
| 2 |
268 |
276 |
292 |
836 |
278,6667 |
| 3 |
454 |
498 |
505 |
1457 |
485,6667 |
| 4 |
168 |
187 |
208 |
563 |
187,6667 |
| Итого |
1003 |
1067 |
1125 |
3195 |
1065 |
| Среднее |
250,75 |
266,75 |
281,25 |
798,75 |
266,25 |
Теперь можно рассчитать индекс сезонности как отношение ежеквартальных средних значений за 3 года к общему среднему (266,25). Результаты расчетов запишем в таблицу.
| Квартал |
Индекс сезонности |
| 1 |
42,44% |
| 2 |
104,66% |
| 3 |
182,41% |
| 4 |
70,49% |
Отобразим сезонную волну на графике

Выводы: на основе расчетов видно, что в первом квартале продажа безалкогольных напитков имеет наименьшее значение (индекс сезонности равен 42,44%), затем она увеличивается и достигает максимума в 3 квартале (индекс сезонности 182,41%). В 4 квартале происходит снижение продаж до 70,49% от среднего уровня продаж.
Задача №65
Данные об обороте и уровне издержек обращения по шести магазинам:
| № торгового предприятия |
Оборот,
тыс. руб.
|
Уровень издержек
обращения, %
|
| 1 |
207,9 |
30,1 |
| 2 |
258,3 |
28,8 |
| 3 |
309,7 |
25,3 |
| 4 |
340,3 |
23,5 |
| 5 |
359,4 |
24,0 |
| 6 |
542,9 |
22,0 |
Для изучения зависимости уровня издержек обращения от товарооборота вычислите линейное уравнение связи. Для оценки тесноты связи рассчитайте линейный коэффициент корреляции. Сделайте выводы.
Решение:
Уравнение регрессии, связывающее факторный и результативный показатели, записывается в виде:
 , ,
где a0
и a1
- параметры уравнения регрессии, которые находятся из системы двух линейных уравнений
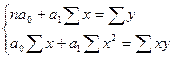
Составим уравнение регрессии. Для этого заполним вспомогательную расчетную таблицу
| № п/п |
X |
Y |
X2
|
Y2
|
X×Y |
 |
| 1 |
207,9 |
30,1 |
43222,41 |
906,01 |
6257,79 |
28,72 |
| 2 |
258,3 |
28,8 |
66718,89 |
829,44 |
7439,04 |
27,51 |
| 3 |
309,7 |
25,3 |
95914,09 |
640,09 |
7835,41 |
26,26 |
| 4 |
340,3 |
23,5 |
115804,1 |
552,25 |
7997,05 |
25,52 |
| 5 |
359,4 |
24 |
129168,4 |
576 |
8625,6 |
25,06 |
| 6 |
542,9 |
22 |
294740,4 |
484 |
11943,8 |
20,62 |
| Итого |
2018,5
|
153,7
|
745568,3
|
3987,79
|
50098,69
|
153,70
|
На основе итоговых значений составим систему нормальных уравнений и найдем ее решение:

Решая эту систему, получим, что a1
=-0,024, a0
=33,75
Таким образом, уравнение регрессии имеет вид:  =33,75-0,024x =33,75-0,024x
Используя полученное уравнение, вычислим выравненные значения уровня издержек обращения  и занесем их в таблицу. и занесем их в таблицу.
Рассчитаем линейный коэффициент корреляции r. Для расчета коэффициента корреляции можно воспользоваться следующей формулой:


Выводы: т.к. r<0, то линейная связь обратная, т.е. с ростом факторного признака (оборот) результативный признак уменьшается (уровень издержек обращения). Т.к. rÎ[0,7;0,9], то линейная связь сильная.
Найденное значение коэффициента корреляции очень высокое, поэтому найденное уравнение регрессии 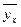 =33,75-0,024x можно использовать для прогноза уровня издержек обращения при наличии данных об изменении оборота магазина. =33,75-0,024x можно использовать для прогноза уровня издержек обращения при наличии данных об изменении оборота магазина.
Список литературы
1. Практикум по теории статистики: Учеб. пособие для экон. спец. вузов [Р.А. Шмойлова, А.Б. Гусынин, В.Г. Минашкин, Н.А. Садовникова]; Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.
2. Курс социально-экономической статистики / Под ред. Назарова М.Г. - М.: Финстатинформ, 2002.
3. Общая теория статистики: Учеб. для вузов по направлению и спец. «Статистика» / И.И. Елисеева, М.М. Юзбашев; под ред. И.И. Елисеевой. – 5-е изд., перераб. доп. – М.: Финансы и статистика, 2005.
|