Задача №1
Исходные данные:
| № наблю-дения |
Уровень фактора (или тип региона) |
| Кировская область |
Архангельск. область |
Республика Карелия |
Ленинград. Область |
Калинингр. область |
Псковская область |
Новгород-ская область |
| 1 |
2,90 |
3,90 |
4,90 |
2,10 |
6,10 |
7,00 |
8,00 |
| 2 |
2,10 |
5,00 |
3,50 |
6,90 |
10,0 |
10,00 |
1,00 |
| 3 |
10,30 |
2,80 |
4,00 |
2,00 |
15,1 |
12,10 |
1,10 |
| 4 |
4,90 |
8,90 |
3,00 |
3,10 |
5,00 |
5,90 |
2,00 |
| 5 |
4,00 |
4,10 |
1,90 |
5,90 |
5,10 |
6,10 |
2,00 |
| 6 |
2,90 |
4,90 |
1,20 |
7,90 |
6,00 |
5,10 |
1,10 |
| 7 |
1,10 |
1,50 |
4,10 |
6,10 |
5,00 |
6,10 |
1,19 |
| 8 |
2,30 |
3,90 |
3,00 |
2,70 |
6,10 |
8,90 |
1,10 |
| 9 |
2,00 |
1,80 |
2,90 |
7,00 |
3,10 |
5,00 |
3,19 |
| 10 |
1,00 |
3,00 |
5,90 |
3,00 |
2,00 |
5,91 |
| 11 |
1,00 |
2,50 |
2,90 |
5,20 |
3,10 |
4,80 |
| 12 |
1,10 |
3,90 |
5,00 |
13,00 |
10,90 |
1,00 |
| 13 |
1,01 |
4,50 |
5,00 |
3,00 |
5,10 |
0,19 |
| 14 |
1,91 |
1,91 |
2,00 |
2,10 |
1,00 |
1,00 |
| 15 |
1,09 |
1,10 |
9,00 |
3,00 |
| 16 |
1,10 |
1,10 |
8,10 |
2,10 |
| 17 |
2,10 |
1,90 |
15,9 |
2,90 |
| 18 |
2,91 |
2,10 |
6,20 |
1,00 |
| 19 |
2,09 |
2,20 |
| 20 |
3,90 |
| 21 |
2,90 |
| 22 |
2,10 |
| 23 |
2,50 |
Решение:
1. Находим сумму квадратов всех наблюдений (Q1), сумму квадратов итогов по столбцам, деленных на число наблюдений в соответствующем столбце (Q2), квадрат общего итога, деленный на число всех наблюдений (Q3).
№
наблю-дения
|
Квадрат наблюдений |
| Кировская область |
Архан-гельская. область |
Республика Карелия |
Ленинград. Область |
Калинингр. область |
Псковская область |
Новго-родская область |
| 1 |
8,41 |
15,21 |
24,01 |
4,41 |
37,21 |
49,00 |
64,00 |
| 2 |
4,41 |
25,00 |
12,25 |
47,61 |
100,00 |
100,00 |
1,00 |
| 3 |
106,90 |
7,84 |
16,00 |
4,00 |
228,01 |
146,41 |
1,21 |
| 4 |
24,01 |
79,21 |
9,00 |
9,61 |
25,00 |
34,81 |
4,00 |
| 5 |
16,00 |
16,81 |
3,61 |
34,81 |
26,01 |
37,21 |
4,00 |
| 6 |
8,41 |
24,01 |
1,44 |
62,41 |
36,00 |
26,01 |
1,21 |
| 7 |
1,21 |
2,25 |
16,81 |
37,21 |
25,00 |
37,21 |
1,41 |
| 8 |
5,29 |
15,21 |
9,00 |
7,29 |
37,21 |
79,21 |
1,21 |
| 9 |
4,00 |
3,24 |
8,41 |
49,00 |
9,61 |
25,00 |
10,17 |
| 10 |
0 |
1,00 |
9,00 |
34,81 |
9,00 |
4,00 |
34,92 |
| 11 |
0 |
1,00 |
6,25 |
8,41 |
27,04 |
9,61 |
23,04 |
| 12 |
0 |
1,21 |
15,21 |
25,00 |
169,00 |
118,81 |
1,00 |
| 13 |
0 |
1,02 |
20,25 |
25,00 |
9,00 |
26,01 |
0,03 |
| 14 |
0 |
3,64 |
3,64 |
4,00 |
4,41 |
1,00 |
1,00 |
| 15 |
0 |
1,18 |
0 |
1,21 |
0 |
81,00 |
9,00 |
| 16 |
0 |
1,21 |
0 |
1,21 |
0 |
65,61 |
4,41 |
| 17 |
0 |
4,41 |
0 |
3,61 |
0 |
252,81 |
8,41 |
| 18 |
0 |
8,46 |
0 |
4,41 |
0 |
38,44 |
1,00 |
| 19 |
0 |
4,36 |
0 |
0 |
0 |
0 |
4,84 |
| 20 |
0 |
15,21 |
0 |
0 |
0 |
0 |
0 |
| 21 |
0 |
8,41 |
0 |
0 |
0 |
0 |
0 |
| 22 |
0 |
4,41 |
0 |
0 |
0 |
0 |
0 |
| 23 |
0 |
6,25 |
0 |
0 |
0 |
0 |
0 |
| Q1-сумма квадратов |
2997,78 |
| кол-во наблю-дений |
9 |
23 |
14 |
18 |
14 |
18 |
19 |
115 |
| Q2 |
19,759 |
10,893 |
11,063 |
20,223 |
53,036 |
62,897 |
9,256 |
187,127 |
| 26,068 |
2. Вычисляем оценку дисперсии фактора:

3. Вычисляем оценку дисперсии, связанной со случайностью:
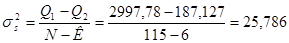
4. Рассчитываем значение F-статистики (статистики Фишера):
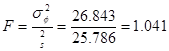
5. Проверяем значимость фактора (q =0,05; h1
= K-1; h2
= N-K)
F = 2,29, так как расчетное меньше табличного, с вероятностью 0,95 можно утверждать, что связь между сроком окупаемости и типом региона не существенна.
6. Строим диаграмму средних значений сроков окупаемости для всех рассматриваемых регионов.
Средние сроки окупаемости:
| Показатель |
Кировская область |
Архангельск. область |
Республика Карелия |
Ленинград. Область |
Калинингр. область |
Псковская область |
Новго-родская область |
| Ср.срок окупаемости |
3,54 |
2,76 |
3,17 |
3,93 |
6,27 |
7,08 |
2,36 |

Согласно таблицы и диаграммы самый маленький срок окупаемости инвестиционных проектов сложился в Новгородской области, следовательно, данная область является приоритетной.
Задача 2
Исходные данные:
| Моменты времени (дни) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
| -60 |
-40 |
-20 |
0 |
20 |
40 |
60 |
| Расчет для варианта(убрать) |
340+510 |
400+59 |
440+610 |
430+69 |
520+79 |
570+710 |
550+89 |
| У-физ.объем товарооборота (шт.) |
850 |
459 |
1050 |
499 |
599 |
1280 |
639 |
Решение.
1. Изобразить данные графически.

2. Составить уравнение линейной регрессии.
3. Для расчета параметров уравнения регрессии (yt
= a0
+ a1
t) составляем вспомогательную таблицу:
| Моменты времени (дни) |
У-физ.объем товарооборота (шт.) |
t |
t^2 |
y*t |
Урасч. |
У^2 |
| 0 |
850 |
-60 |
3600 |
-51000 |
708,24 |
722500 |
| 20 |
459 |
-40 |
1600 |
-18360 |
728,16 |
210681 |
| 40 |
1050 |
-20 |
400 |
-21000 |
748,08 |
1102500 |
| 60 |
499 |
0 |
0 |
0 |
768 |
2493001 |
| 80 |
599 |
20 |
400 |
11980 |
787,92 |
358801 |
| 100 |
1280 |
40 |
1600 |
51200 |
807,84 |
1638400 |
| 120 |
639 |
60 |
3600 |
38340 |
827,76 |
408321 |
| ∑ |
5376 |
0 |
11200 |
11160 |
5376 |
6934204 |
Для нахождения a0
и a1
составляем систему уравнений:
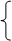 ∑у =n*a0
+ a1
∑t ∑у =n*a0
+ a1
∑t
∑уt =a0
∑t + a1
∑t2
Так как при t =60мин = 0, ∑t=0, система принимает вид:
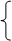 5376 =7*a0 5376 =7*a0
11160 = a1
*11200
Откуда:
a0
= 768 и a1
= 0,996
Уравнение регрессии имеет вид:
yt
= 768 + 0,996 t
Задача 3
Исходные данные:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 231+8 |
171+10 |
291+8 |
309+10 |
317+28 |
362+210 |
351+8+10 |
361+10+8 |
| Спрос |
239 |
181 |
299 |
319 |
345 |
572 |
369 |
379 |
Решение
1. Находим среднее значение, среднее квадратичное отклонение, коэффициенты автокорреляции (для лагов τ=1;2) и частный коэффициент автокорреляции 1-го порядка.
2. - среднее значение:

- среднее квадратическое отклонение:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| У |
239 |
181 |
299 |
319 |
345 |
572 |
369 |
379 |
| У-Уср |
239 |
181 |
299 |
319 |
345 |
572 |
369 |
379 |
| (У-Уср)^2 |
57121 |
32761 |
89401 |
101761 |
119025 |
327184 |
136161 |
143641 |
| ∑(У-Уср)^2 |
1007055 |

- Найдем коэффициент автокорреляции r(τ) временного ряда (для лага τ=1), т.е. коэф-т корреляции между последовательностями семи пар наблюдений:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Уt |
239 |
181 |
299 |
319 |
345 |
572 |
369 |
| Уt+ τ |
181 |
299 |
319 |
345 |
572 |
369 |
379 |
Вычисляем необходимые суммы:
∑ Уt = 239+181+…+369 =2319
∑ Уt2
= 2392
+ 1812
+ … + 3692
= 860449
∑ Уt+ τ = 181+ 299+ … +379 = 2464
∑ У2
t+ τ = 1812
+2992
+ … +3792
=949934
∑ Уt *Уt+ τ = 239*181 + 181*299 + … + 369*3729=851073
Находим коэффициент автокорреляции:

- Найдем коэффициент автокорреляции r(τ) временного ряда (для лага τ=2), т.е. коэф-т корреляции между последовательностями шести пар наблюдений:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
| Уt |
239 |
181 |
299 |
319 |
345 |
572 |
| Уt+ τ |
299 |
319 |
345 |
572 |
369 |
379 |
Вычисляем необходимые суммы:
∑ Уt = 239+181+…+572 =1955
∑ Уt2
= 2392
+ 1812
+ … + 5722
= 727253
∑ Уt+ τ = 299+ 319+ … +379 = 2283
∑ У2
t+ τ = 2992
+3192
+ … +3792
=917173
∑ Уt *Уt+ τ = 239*299 + 181*319 + … + 572*379 =758916
Находим коэффициент автокорреляции:

Для определения частного коэффициента корреляции 1-го порядка найдем коэффициент автокорреляции между членами ряда Уе+1
и Уе+2
:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
| Уt+ 1 |
181 |
299 |
319 |
345 |
572 |
369 |
| Уt+ 2 |
299 |
319 |
345 |
572 |
369 |
379 |
Вычисляем необходимые суммы:
∑ Уt+1= 181+299+…+369 =2080
∑ У2
t +1= 1812
+ 2992
+ … + 3692
= 806293
∑ Уt+ 2 = 299+ 319+ … +379 = 2283
∑ У2
t+ 2 = 2992
+3192
+ … +3792
=917173
∑ Уt+1 *Уt+ 2 = 181*299 + 299*319 + … + 369*379 =807814
Находим коэффициент автокорреляции:
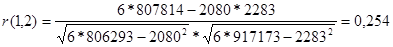
- Найдем частный коэффициент автокорреляции 1-го порядка:
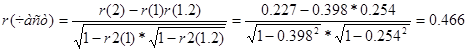
3. Найти уравнение неслучайной составляющей (тренда) для временного ряда, полагая тренд линейным.
4. Находим коэффициенты для системы нормальных уравнений:
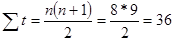



Система нормальных уравнений имеет вид:
 8b0
+ 36b1
= 2703 8b0
+ 36b1
= 2703
36b0
+ 204b1
= 13546
Отсюда находим b0
= 189,068;b1
=33,068
Уравнение тренда:
Yt
= 189,068+33,068t
То есть спрос ежегодно увеличивается в среднем на 33.068 ед.
5. Провести сглаживание временного ряда методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания m = 3 года.
6. у2
= 1/3 (у1
+ у2
+ у3
) = 1/3 (239+181+299)=239,7
7. у3
= 1/3 (у2
+ у3
+ у4
) = 1/3 (181+299+319)=266,3
У4
=1/3(у3
+ у4
+ у5
)=1/3(299+572+345)=405.3
У5
=1/3(y4
+y5
+y6
)=1/3(319+345+572)=412
У6
=1/3(у5
+ у6
+ у7)
=1/3(345+572+369)=428,7
У7
=1/3(у6
+ у7
+ у8)
=1/3(572+369+379)=440
В результате получим сглаженный ряд:
| Год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Уt |
- |
239,7 |
266,3 |
405,3 |
412,0 |
428,7 |
440,0 |
- |
8. Дать точечную и с надежностью 0,95 интервальную оценки прогноза среднего и индивидуального значений спроса на некоторый товар в момент времени t=взятый год. (Полагаем, что тренд линейный, а возмущения удовлетворяют требованиям классической модели).
По полученному выше уравнению регрессии Yt
= 189,068 + 33,068t оценим условное математическое ожидание. Оценкой у(9) является групповая средняя:
Уt=9
= 189,068 + 33,068*9 =486,68(ед)
Составим вспомогательную таблицу для оценки дисперсии.
| Год |
У |
Уt |
еt = У-Уt |
et-1 |
et *et-1 |
et ^2 |
| 1 |
239 |
222,1 |
16,9 |
0,0 |
0,0 |
285,6 |
| 2 |
181 |
252,2 |
-74,2 |
16,9 |
-1253,98 |
5505,6 |
| 3 |
299 |
288,3 |
10,7 |
-74,2 |
-793,94 |
114,5 |
| 4 |
319 |
321,3 |
2,3 |
10,7 |
24,6 |
5,3 |
| 5 |
345 |
354,4 |
-9,4 |
2,3 |
-21,62 |
88,4 |
| 6 |
572 |
387,5 |
184,5 |
-9,4 |
-1734,3 |
34040,3 |
| 7 |
269 |
420,5 |
-51,5 |
184,5 |
-9501,8 |
2652,3 |
| 8 |
379 |
453,6 |
-74,6 |
-51,5 |
384,19 |
5565,2 |
| 9439,02 |
48257,2 |
Вычислим оценку s2
дисперсии 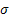 ^ ^
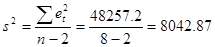
Вычислим оценку дисперсии групповой средней:


Значение t0.95;6
= 2,45, критерий Стьюдента. Теперь находим интервальную оценку прогноза среднего значения спроса:
486,68 – 2,45*69,76 ≤у(9)≤ 486,68+2,45*69,76
Или
315,77≤у(9)≤ 657,59
Для нахождения интервальной оценки прогноза индивидуального значения вычислим дисперсию его оценки:

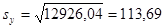
Теперь находим интервальную оценку:
486,68-2,45*113,69 ≤ у*
(9) ≤ 486,68+2,45*113,69
Или
208,14 ≤ у*
(9) ≤ 765,22
Вывод:
Следовательно, с надежностью 0,95 среднее значение спроса на товар на 9-й год будет заключено от 315,77 до 657,59 (ед.), а его индивидуальное значение – от 208,14до 765,22 (ед.)
|