Министерство образования и науки Украины
Национальная академия природоохранного и курортного строительства
Факультет экономики и менеджмента
Кафедра экономической кибернетики
Курсовая работа
по дисциплине «Моделирование экономики»
на тему: «Производственные функции»
Выполнила:
студентка 5 курса
группы ЭК-502
Томас М.А.
Проверил:
Клевец Н.И.
Симферополь, 2010 г.
Содержание
1. Производственные функции. Определение и назначение.
3
1.2 Применение производственных функций.3
1.3 Основные требования, предъявляемые к производственным функциям.6
1.4 Основные формы представления производственных функций.11
1.5 Моделирование научно-технического прогресса.16
1.6 Методы определения параметров производственных функций.20
Пример выполнения лабораторной работы
.. 22
Построение производственной функции Кобба – Дугласа. 22
Вопросы для самопроверки
. 25
Список литературы:26
1. Производственные функции. Определение и назначение.
Производственная функция
(функция производства) представляет уравнение, связывающее переменные величины затрат (ресурсов, факторов производства) с величиной выпуска продукции (в дальнейшем просто «выпуска»). Понятия выпуска и факторов производства конкретизируются в зависимости от характера и масштаба рассматриваемой производственной единицы, цели исследования, доступной информации. Например, выпуск может измеряться в натуральных или стоимостных показателях, в реальных или потенциальных величинах. А ресурсы могут рассматриваться либо фактически затраченные, либо имеющиеся в распоряжении на начало периода производства. Число факторов в производственной функции не обязательно ограничивается заранее, однако требуется их сопоставимость по характеру воздействия на выпуск и уровню агрегирования [14].
В экономическом моделировании наиболее широко представлены макроэкономические производственные функции
. Эти функции являются агрегатными производственными функциями, характеризующими зависимость показателя совокупного общественного продукта или иного обобщающего показателя от основных факторов производства. В качестве основных факторов производства обычно рассматриваются объем капитала, рабочей силы, а также земли. В ряде макроэкономических производственных функций в качестве отдельного фактора учитывается также воздействие научно-технического прогресса. Макроэкономические производственные функции исследуются самостоятельно или включаются в сложные эконометрические модели.
1.2 Применение производственных функций.
Производственные функции применяются для анализа влияния различных сочетаний факторов на объем выпуска и решения прогнозных и плановых задач в следующих случаях:
• для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант, который отражает текущие связи между экономическими показателями);
• для анализа и прогнозирования соотношения объемов факторов и объемов выпуска в разные моменты времени (динамический вариант, т. е. выявление тенденций экономического развития).
Для отдельного предприятия (фирмы) или отрасли, выпускающей однородный продукт, часто рассматриваются многофакторные производственные функции, связывающие объем валового выпуска (измеренного в натуральных единицах) с затратами:
• рабочего времени по различным видам трудовой деятельности;
• различных видов сырья, энергии, полуфабрикатов, комплектующих изделий (измеренных, как и выпуск, в натуральных единицах).
Такие функции характеризуют действующую технологию или спектр возможных технологий. В отдельной фирме производственная функция описывает максимальный объем выпуска продукции, которую эта фирма в состоянии произвести при каждом сочетании используемых факторов производства.
При построении производственных функций крупных отраслей, регионов или народного хозяйства обычно пользуются стоимостными измерителями (как правило, в постоянных ценах), а выпуск измеряют конечным (а не валовым) продуктом. Кроме того, в этих функциях исключают или сводят к минимуму учет текущих затрат, а также включают небольшое количество переменных (по сравнению с микроэкономическим уровнем). Макроэкономические производственные функции, как правило, содержат 2-4 фактора производства, например, живой труд, основные средства, научно-технический прогресс, обобщающий показатель вовлекаемых природных ресурсов.
Многофакторные микроэкономические производственные функции применяются в технико-экономических расчетах и отражают реально действующие или потенциально допустимые производственные технологии,
например, для определения возможных вариантов развития предприятий.
В прикладных исследованиях основное направление использования производственных функций — прогнозирование
(особенно средне- и долгосрочное) и перспективное планирование.
Для агрегатных экономических единиц производственная функция строится в предположении, что соответствующий объект моделируется как единое предприятие, функционирующее по принципу «затраты ресурсов — выпуск продукции» или «имеющиеся ресурсы — результаты деятельности». В первом случае рассматриваются потоки ресурсов, а во втором — их общие объемы, запасы. Тем самым принимается гипотеза о целостности объекта, моделируемого с помощью производственной функции, о его неделимости. Для большинства производственных функций эта гипотеза существенна и с формальной точки зрения, ибо не удается воспользоваться одной и той же производственной функцией для представления объекта в целом и в виде совокупности образующих его производственных единиц. Другими словами, непосредственное агрегирование для производственной функции, как правило, неосуществимо. Исключение составляют производственные функции, в которые факторы входят в виде линейной комбинации. Поэтому анализ экономической деятельности как агрегата и как совокупности предприятий ведется изолированно, а совмещение полученных результатов и их интерпретация представляют самостоятельные и, главным образом, содержательные задачи. Отраслевые производственные функции могут отображать функционирование отрасли как целого, либо отображают деятельность ее среднего предприятия. В первом случае производственная функция связывает временные ряды отраслевых агрегатов выпуска и ресурсов, а внутренняя структура отрасли обычно не учитывается. Во втором случае производственная функция «пространственно» измеряет показатели для образующих отрасль предприятий. Объединение этих подходов в рамках одного эконометрического исследования технически сложно и требует более жестких предположений о характере эмпирических данных [2].
Производственная функция является обобщением таких традиционных экономических показателей как производительность труда, фондоотдача, материалоемкость и т. п. Иногда, вместо производственных функций используются соотношения, связывающие между собой не объемы, а темпы прироста ресурсов и выпуска или темпы и объемы одновременно. Такие соотношения обычно называются темповыми производственными функционалами. Широко распространения в экономико-математических исследованиях они не получили.
1.3 Основные требования, предъявляемые к производственным функциям.
Производственная функция, устанавливающая зависимость объема производства от наличия или потребления ресурсов, называется функцией выпуска.
Частными случаями производственной функции являются:
• функция издержек
, описывающая связь между объемом выпуска и издержками производства;
• инвестиционная функция
, описывающая зависимость необходимых инвестиций от производственной мощности будущего предприятия.
Формально производственная функция может быть записана следующим образом:
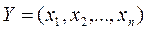
где Y
— объем выпуска;  — объем ресурса — объем ресурса  . .
Предполагается, что функция 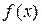 удовлетворяет некоторым условиям, вытекающим из общеэкономических соображений. Вид функции и некоторые ограничения на значения параметров вытекают, как правило, из теоретических представлений о структуре и функционировании моделируемого объекта, а конкретные численные значения параметров находятся в результате обработки, имеющейся в распоряжении исследователя информации. удовлетворяет некоторым условиям, вытекающим из общеэкономических соображений. Вид функции и некоторые ограничения на значения параметров вытекают, как правило, из теоретических представлений о структуре и функционировании моделируемого объекта, а конкретные численные значения параметров находятся в результате обработки, имеющейся в распоряжении исследователя информации.
Это могут быть:
• результаты пространственных выборок, данные о технико-экономических характеристиках используемых, потенциально доступных или проектируемых технологий, агрегатов, производственных комплексов (в этом случае рассматриваются статические модели);
• временные ряды (ряды динамики) или результаты пространственно-временных выборок показателей ресурсов и выпуска (тогда речь идет о динамических моделях) [5].
Параметры функции оцениваются, в основном, методами корреляционно- регрессионного анализа. Полученные таким образом производственные функции представляют статистические зависимости между ресурсами и выпуском. Причем, часто оценка погрешности такова, что пользоваться полученными зависимостями на практике не представляется возможным, особенно в случае множественной регрессии. Поэтому полученные зависимости отражают только предполагаемые тенденции развития и обладают низкой достоверностью. В работах западных экономистов неоклассического направления значения параметров производственной функции часто определяют исходя из гипотезы:
• о равенстве отношения предельных производительностей ресурсов, отношению цен на них. Например, в качестве «цены труда» рассматривают среднюю ставку заработной платы, а «цены капитала» — норму процента;
• о равенстве эластичностей выпуска по ресурсам и долей их владельцев в доходе.
Иногда производственную функцию записывают в более общем виде:

Тогда последнее выражение называют уравнением производственной поверхности. Его можно обобщить на случай совместного производства нескольких видов продукции:
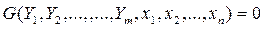
Но такие многопродуктовые производственные поверхности встречаются лишь в сугубо теоретических работах.
Производственная поверхность
— это геометрическое представление производственной функции. В простейшем двумерном случае (один ресурс — один продукт) применяется термин «производственная кривая». Эта кривая позволяет оценить объем производства продукта при наличии определенного количества ресурсов [15].
Если факторов и товаров более одного, например n
, т
,
то можно говорить уже не кривой, а о некоторой гиперповерхности, описывающей все возможные комбинации рассматриваемых товаров, которые можно произвести при полном использовании имеющихся факторов производства. Эта гиперповерхность соединяет точки, показывающие, что дальнейшее наращивание выпуска одного товара возможно только за счет сокращения выпуска других. Примером может служить граница области допустимых значений в задаче линейного программирования. Другой термин для обозначения этого понятия: кривая (поверхность) производственных возможностей [12].
Производственная функция может быть также представлена множеством изоквант, связанных с различными уровнями объема производства.
Общепринятого мнения, каким именно набором свойств, вытекающих из общеэкономических соображений, должна обладать производственная функция, не существует. Однако обычно требуется, чтобы она обладала всеми или хотя бы некоторыми из следующих свойств:
1. т.е. выпуск невозможен при отсутствии ресурсов; т.е. выпуск невозможен при отсутствии ресурсов;
2. Если  , для , для  , то , то  , т.е. при увеличении затрат всех ресурсов выпуск также растет; , т.е. при увеличении затрат всех ресурсов выпуск также растет;
3.  , т. е. при увеличении затрат любого из ресурсов, при неизменном количестве остальных, выпуск не сокращается; , т. е. при увеличении затрат любого из ресурсов, при неизменном количестве остальных, выпуск не сокращается;
4.  , т.е. с увеличением затрат любого из ресурсов, при неизменном количестве остальных, эффективность вовлечения в производство дополнительной его единицы не возрастает (принцип убывающей отдачи последовательных вложений); , т.е. с увеличением затрат любого из ресурсов, при неизменном количестве остальных, эффективность вовлечения в производство дополнительной его единицы не возрастает (принцип убывающей отдачи последовательных вложений);
5.  , т.е. эффективность затрат любого из ресурсов при увеличении затрат какого-либо другого ресурса и неизменном количестве остальных, не снижается; , т.е. эффективность затрат любого из ресурсов при увеличении затрат какого-либо другого ресурса и неизменном количестве остальных, не снижается;
6. 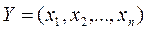 — строго квазивогнута; — строго квазивогнута;
7. 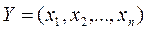 — вогнута (выпукла вверх). — вогнута (выпукла вверх).
Это более жесткая формулировка принципа убывающей отдачи последовательных вложений, из которой, в частности, следует свойство 4;
8. 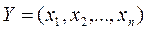 — однородна степени — однородна степени 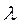 , т.е. , т.е.

При  с увеличением масштабов производства его эффективность растет (растущая отдача или экономия от масштаба), при с увеличением масштабов производства его эффективность растет (растущая отдача или экономия от масштаба), при 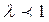 — падает (падающая отдача или потери от масштаба, при — падает (падающая отдача или потери от масштаба, при  — не меняется. В одних случаях значение — не меняется. В одних случаях значение  оценивается статистически, в других на него накладываются априорные оценивается статистически, в других на него накладываются априорные
ограничения. В подавляющем большинстве малоразмерных моделей экономического роста предполагается, что 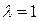 . .
Однако не все производственные функции и не при всех значениях входящих в них переменных обладают перечисленными свойствами. Иногда, хотя и редко, применяют производственные функции, для которых не выполняются первые три свойства, хотя они наиболее «естественны». Часто требуется, чтобы производственная функция обладала указанными свойствами не при всех, а лишь при
«экономически осмысленных» или реально достижимых значениях переменных. Множество таких значений называют экономической областью.
Иногда требуется, чтобы производственная функция, помимо указанных выше свойств, обладала и некоторыми другими. Так, довольно часто, например, используется так называемые асимптотические условия. Состоит оно в том, что значение функции равно нулю при нулевом значении любого из аргументов, например, для случая двухфакторной макроэкономической производственной функции.
Однородную производственную функцию произвольной степени
часто называют неоклассической, если она имеет:
• положительные первые частные производные;
• отрицательные вторые частные производные;
• положительные вторые смешанные производные по всем факторам производства.
Производственная функция позволяет рассчитать ряд важных характеристик:
1) предельная производительность (предельный продукт) фактора j,  . Данный показатель показывает, насколько увеличивается выпуск при увеличении затрат фактора jна одну единицу, при неизменном количестве остальных факторов; . Данный показатель показывает, насколько увеличивается выпуск при увеличении затрат фактора jна одну единицу, при неизменном количестве остальных факторов;
2) частная эластичность выпуска по фактору j(частная факторная эластичность),  . Показывает, на сколько процентов увеличится выпуск при увеличении затрат фактора jна 1% и при неизменном количестве остальных факторов. Частная эластичностьпредставляет отношение предельной производительностик средней; . Показывает, на сколько процентов увеличится выпуск при увеличении затрат фактора jна 1% и при неизменном количестве остальных факторов. Частная эластичностьпредставляет отношение предельной производительностик средней;
3) эластичность производства
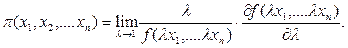
Эластичность производства показывает, на сколько процентов увеличится выпуск при увеличении на 1% затрат каждого фактора. Этот показатель является локальной характеристикой эффекта масштаба производства.
Очевидно, что

4) предельная норма замены (замещения) фактора jфактором i.
Этот показатель определяет количество фактора j ,
которое требуется для замены одной единицы фактора jпри сохранении на неизменном уровне объема выпуска и количества остальных факторов.
Обычно обозначается 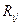 и, по определению, равна: и, по определению, равна:
 при при 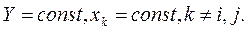
Очевидно, что 
5) эластичность замены (замещения) фактора jфактором i.
Наряду с предельной нормой замещения этот показатель характеризует возможности замены одного фактора другим. В простейшем случае определяется как
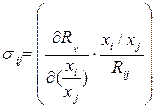 при при 
Существует и ряд других определений эластичности замещения для многофакторных производственных функций. Все существующие определения эквивалентны только для двухфакторных линейно-однородных производственных функций. В этом случае все они приводят к формуле:
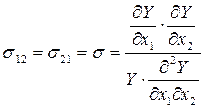
С помощью производственных функций изучается взаимозаменяемость факторов производства, которая может быть неизменной либо переменной (т. е. зависимой от объемов ресурсов).
Соответственно, функции делят на два вида:
- спостояннойэластичностьюзамены (CES — Constant Elasticity of Substitution);
- спеременнойэластичностьюзамены (VES — Variable Elasticity of Substitution).
1.4 Основные формы представления производственных функций.
В настоящее время математиками-аналитиками предложено множество конкретных производственных функций.
Чаще всего используются следующие:
1) линейная  ; ;
2) леонтьевская 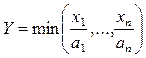
3) Кобба-Дугласа ; ;
4) с постоянной эластичностью замещения. В простейшем варианте эта функция имеет вид:

Наиболее популярной и в теоретических, и в прикладных исследованиях
является функция Кобба-Дугласа:
она сочетает простоту математической записи, очевидную экономическую интерпретацию и относительную легкость определения численных значений ее параметров. Особенность этой мультипликативно-степенной формы производственной функции состоит в том, что если один из сомножителей равен нулю, то результат обращается также в нуль. Это
свойство соответствует тому факту, что в большинстве случаев для производства необходимы все факторы и при отсутствии одного из них выпуск продукции невозможен. Например, даже в самом автоматизированном производстве нельзя обойтись без cоответствующего персонала. В самой общей форме (форма называется канонической) мультипликативно-степенная функция записывается в следующем виде:
 или или 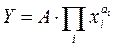
Коэффициент A
учитывает размерность, которая, в свою очередь, зависит от выбранной единицы измерений затрат и выпуска. Сомножители от первого до n-го могут иметь различное содержание в зависимости от того, какие факторы оказывают влияние на общий результат (т. е. выпуск продукции). Например, в производственной функции, которая применяется для изучения экономики в
целом, в качестве результативного показателя можно принять объем конечного продукта, а в качестве сомножителей — основные факторы производства:
• численность занятого населения  ; ;
• величину основного и оборотного капитала  ; ;
• площадь используемой земли  ; ;
С помощью функции Кобба-Дугласа была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20-30 годов XX века:
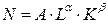
где N
— национальный доход; А
— коэффициент размерности;  и К
— соответственно объемы приложенного труда и капитала; и К
— соответственно объемы приложенного труда и капитала; , , — коэффициенты эластичности производства по труду L
и капиталу К.
Функция Кобба-Дугласа используется для описания объема производства в зависимости от числа занятых (наряду с капиталом): — коэффициенты эластичности производства по труду L
и капиталу К.
Функция Кобба-Дугласа используется для описания объема производства в зависимости от числа занятых (наряду с капиталом):
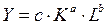
где Y
— объем производства; К
— величина капитала; L
— численность занятых; с
— постоянный параметр производительности; а —
коэффициент эластичности производства по отношению к величине капитала; b
— коэффициент эластичности производства по отношению к численности занятых. Сумма коэффициентов эластичности а + b
характеризует эффект масштаба производства:
• возрастающий, если а +
b
>
1;
• постоянный, если а +
b
=1;
• убывающий, если а +
b
<
1.
Хотя сумма а +
b
может принимать любые значения, чаще всего предполагается неизменный масштаб производства. В связи с этим предположением, один параметр определяется через другой:
b
= 1 - а.
В «классической» производственной функции Кобба-Дугласа  = 0,33, = 0,33,  = 0,67. = 0,67.
Среди моделей, характеризующих влияние демографического фактора на экономическое развитие, выделяются динамические модели, основанные на предположении, что технологические изменения влияют на объем производства непосредственно (модель Р. Солоу):

где t
— календарный год; 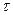 — постоянный темп технического развития. — постоянный темп технического развития.
Второй метод учета технического развития предполагает изменение влияния отдельных факторов производства, которое моделируется с помощью динамического изменения коэффициентов эластичности (модель М. Брауна):

Третий метод основан на том, что техническое развитие приводит к качественному изменению внутри факторов производства (модель В. Солоу):

где индекс * отражает качественные изменения в физическом или человеческом капитале.
Степенные коэффициенты (параметры) мультипликативно-степенной производственной функции показывают ту долю в процентном приросте конечного продукта, которую вносит каждый из сомножителей (или на сколько процентов возрастет продукт, если затраты соответствующего ресурса увеличить на один процент). Эти параметры являются коэффициентами эластичности производства относительно затрат соответствующего ресурса. Если сумма коэффициентов составляет 1, то это означает однородность функции: она возрастает пропорционально росту количества ресурсов. Но возможны и такие случаи, когда сумма параметров больше (или меньше) единицы. Это показывает, что увеличение затрат к непропорционально большему (или непропорционально меньшему) росту выпуска (эффект от масштаба производства).
В динамическом варианте применяются разные формы производственной функции.
Например, в двухфакторном случае:
 , где множитель A(t)
— обычно возрастает во времени, отражая общий рост эффективности факторов производства в динамике. , где множитель A(t)
— обычно возрастает во времени, отражая общий рост эффективности факторов производства в динамике.
Дальнейшая адаптация производственной функции может заключаться в использовании переменных коэффициентов эластичности.
Наиболее гибкой и содержательной считается CES-функция, частным случаем которой являются функции Кобба-Дугласа, однако в общем случае оценка ее параметров затруднена.
Примеры других производственных функций приводятся для случая двух факторов Y =f(K,
L
), где К
— капитал, a L
— объемы приложенного труда (затраты живого труда). Значительное число производственных функций получены в результате комбинации различных вариантов приведенных выше четырех функций. Срединих:
1) функция с линейной эластичностью замещения
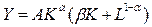
Эта функция выводится из предположения, что эластичность замещения линейно зависит от фондовооруженности. Для этой производственной функции эластичность замены (замещения) фактора К
фактором L
равна
 ; ;
2) многорежимная функция

Эта функция выводится из предположения, что эластичности выпуска по ресурсам представляют  - уровневые ступенчатые функции фондовооруженности (для эластичности по капиталу — убывающую, для эластичности по труду — возрастающую). - уровневые ступенчатые функции фондовооруженности (для эластичности по капиталу — убывающую, для эластичности по труду — возрастающую).
Среди неоднородных производственных функций наиболее часто используется квадратичная функция
 , ,
а также функция

называемая функцией Солоу, или функцией Хилхорста. Достоинства этой производственной функции заключаются в том, что ее верификация позволяет проверить гипотезу об однородности. Если  и и  оказываются близкими, эта гипотеза принимается, в противном случае — отвергается. оказываются близкими, эта гипотеза принимается, в противном случае — отвергается.
Описываемые производственной функцией соотношения носят статистический характер, т. е. проявляются только в среднем, в большой массе наблюдений, поскольку реально на результат производства воздействуют не только анализируемые факторы, но и множество неучтенных в этом виде модели.
1.5 Моделирование научно-технического прогресса.
Важнейшей проблемой использования производственных функций является учет в них фактора технического прогресса.
Моделирование научно-технического прогресса развивается в двух направлениях:
1) анализ динамики сквозных агрегатных показателей, измеряющих
экономический рост;
2) изучение процессов появления и распространения нововведений.
Анализ динамики сквозных агрегатных показателей тесно связан с политэкономическими теориями и, в частности, с таким понятием, как производственная функция. В первой трети XX века экономистами было отмечено, что темп прироста производительности труда превышает темп роста фондовооруженности в среднем за период, близкий к продолжительности экономического цикла. С позиций теории факторов производства, когда рассматриваются два основных фактора — труд и капитал (иногда к ним добавляют третий — природный), объяснить такой рост экономики не удается. Поэтому был сделан вывод о существовании еще одного фактора, влияющего на экономический рост — технического прогресса.
В соответствии с теорией австрийского экономиста Й. Шумпетера, считавшего, что изменение технологии происходит под воздействием внешних (по отношению к экономике) возмущений, на долю технического прогресса стали относить ту часть экономического роста, которую нельзя объяснить традиционно рассматриваемыми экономическими факторами. Так возникла идея измерения технического прогресса в виде «остатка», получившая широкое распространение. Эта идея была разработана с помощью аппарата производственных функций и послужила базой для построения многочисленных моделей технического прогресса. Начальные попытки состояли в изучении отношения выпуска  к той его части, которая соответствовала «вкладу» труда к той его части, которая соответствовала «вкладу» труда  и капитала и капитала  : :
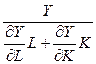
Рост этого отношения интерпретировался как оценка результирующего «вклада» технического прогресса. В реальной экономике возможны разнообразные воздействия на динамику выпуска со стороны изменений в технологии. Так, технология, положительно влияющая на темпы роста в данный момент, может в дальнейшем стать тормозом для роста. И наоборот, технология, требующая в данный момент значительных расходов, может стать через какое-то время
прогрессивной и производительной.
Производственные функции стали средством адекватного представления
роли технического прогресса и способов его измерения. Интерпретировать результаты развития экономики было удобнее в темповых характеристиках. Если переменные производственной функции типа Кобба-Дугласа 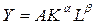 считать зависящими от времени, то ее легко преобразовать в линейное соотношение между темпами прироста: считать зависящими от времени, то ее легко преобразовать в линейное соотношение между темпами прироста:
 , ,
где , , — темпы прироста. — темпы прироста.
В 1939 году голландский экономист Я. Тинберген предложил учитывать время в производственной функции типа Кобба-Дугласа:
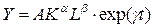
«Остаток», который рассматривался западными экономистами еще до Тинбергена, получил удобное выражение. Концепция Шумпетера была формализована, а соотношение между темпами приобрело вид:

Производственная функция, для которой  = 0,25, = 0,25,  = 0,75, интерпретируется следующим образом: = 0,75, интерпретируется следующим образом:
• увеличение на 1% основных фондов (основного капитала) ведет к приросту (при фиксированной численности занятых) на 0,25%;
• увеличение на 1% численности занятых вызывает соответственно прирост выпуска на 0,75%.
Когда технический прогресс вводится в производственную функцию с помощью множителя, не зависящего от рассматриваемых в ней факторов, говорят о нейтральном техническом прогрессе.
Однако отделить, например, в производственной функции типа Кобба-Дугласа 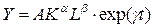 у.), нейтральный технический прогресс, выражаемый параметром у,
от так называемой экономии на масштабах производства с помощью экономических процедур практически невозможно. у.), нейтральный технический прогресс, выражаемый параметром у,
от так называемой экономии на масштабах производства с помощью экономических процедур практически невозможно.
При моделировании технического прогресса отдельно оценивают производственную функцию для различных периодов (возможно и небольших). В этом случае пользуются понятием технологических сдвигов. Так, если для производственной функции Кобба-Дугласа, соответствующей более позднему периоду, отношение 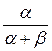 увеличилось по сравнению с его значением в предыдущем периоде, то говорят о капиталоинтенсивном сдвиге в технологии. В противном случае имеет место трудоинтенсивный сдвиг. увеличилось по сравнению с его значением в предыдущем периоде, то говорят о капиталоинтенсивном сдвиге в технологии. В противном случае имеет место трудоинтенсивный сдвиг.
Известны многочисленные попытки усовершенствовать модельные представления о техническом прогрессе, порождаемые производственными функциями. В частности, введение в модель параметра «срок службы основного капитала» позволило отразить зависимость производительности основных фондов от времени, учесть не только физический, но и моральный износ оборудования.
Применяя модели технического прогресса с производственными
функциями, следует учитывать жесткость предположений, на которых они основаны. Интерпретация результатов, полученных с помощью этих моделей, является решающим этапом исследования. Даже небольшие несоответствия в интерпретации способны породить неадекватные выводы. Чаще всего такие модели применяют при анализе народно-хозяйственной ретроспективы. Однако, сравнивая различные периоды, не следует делать выводы о том, что при более высоких уровнях у (т. е. при более высокой доле интенсивных факторов роста) экономика страны развивалась лучше, т. к.:
1) агрегатные показатели, используемые в производственных функциях, не адекватны приписываемому им в соответствующих моделях смыслу;
2) гипотеза о разделении воздействия на выпуск экстенсивных и интенсивных факторов — абстракция, использование которой допустимо только в тех случаях, когда это оправданно;
3) нет оснований утверждать, что более высокие темпы роста экономики всегда предпочтительнее. В частности, постоянное стремление к поддержанию более высоких темпов сдерживает структурные преобразования и противодействует таким важным составляющим технического прогресса как переход к использованию принципиально новых видов ресурсов и удовлетворение экологических требований;
4) введение технического прогресса в качестве невоспроизводимого фактора практически исключает использование соответствующих моделей для анализа альтернативных стратегий развития народного хозяйства. Тем самым эти модели оказываются непригодными для решения именно тех задач, которые стимулировали развитие макроэкономического моделирования.
Возможность воздействия на научно-технический прогресс с помощью нормативных коэффициентов эффективности капитальных вложений рассматривается с трех точек зрения:
1) установления общего для всей экономики страны норматива эффективности, определяя его из моделей, содержащих производственную функцию с техническим прогрессом;
2) введения норматива для различных отраслей, поскольку каждая из них выполняет в народном хозяйстве свою содержательную функцию и потому установление общего норматива невозможно;
3) анализа эффективности или, точнее, результативности в рамках отдельных проектов и решений с преобладанием аргументов содержательного, главным образом технологического характера.
При интерпретации модельных расчетов приоритет отдается аспектам содержательного характера.
1.6 Методы определения параметров производственных функций.
На практике применяются три основных метода определения параметров макроэкономических производственных функций:
1) на основе обработки рядов динамики (временных рядов);
2) на основе данных о структурных элементах агрегатов;
3) на основе данных о распределении национального дохода (распределительный метод).
При построении производственных функций необходимо избавляться от явлений мультиколлинеарности параметров и автокорреляции — в противном случае неизбежны грубые ошибки.
Рассмотрим наиболее часто встречающиеся аналитические представления производственных функций.
Линейная производственная функция:
 , ,
где 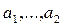  — оцениваемые параметры модели: здесь факторы производства — оцениваемые параметры модели: здесь факторы производства
замещаемы в любых пропорциях.
Функция Кобба-Дугласа
основывается на предположении о понижающейся
предельной отдаче ресурсов, постоянстве коэффициентов эластичности производств по затратам ресурсов. Предельный эффект затрат связан с дополнительным экономическим эффектом (доход, прибыль), вызываемый дополнительной затратой единицы одного ресурса при неизменной величине остальных, т. е. это предел соотношения прироста результата и затрат, которые его вызвали, т. е. частная производная результирующей функции по данному аргументу:
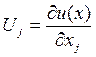 , ,
где 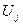 — предельный эффект использования ресурса — предельный эффект использования ресурса  ; ; — функция — функция
полезности (под функцией полезности можно понимать функцию эффективности);  — объем использования ресурса — объем использования ресурса  . .
Эластичность замещения ресурсов в любой точке кривой Кобба-Дугласа равна единице. Хотя данную функцию нельзя отнести к линейным, значения параметров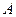 , ,  , ,  можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов. Для этого ее приводят к линейному виду, прологарифмировав обе части уравнения (обычно используются натуральные логарифмы): можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов. Для этого ее приводят к линейному виду, прологарифмировав обе части уравнения (обычно используются натуральные логарифмы):

Модификация функции, учитывающей технический прогресс, достигается введением дополнительного сомножителя 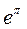 , где , где  - темп технического прогресса (константа). - темп технического прогресса (константа).
Из гипотезы о том, что эластичности замещения между всеми факторами постоянны, выводится CES-функция:
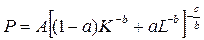
В этом случае эластичность замещения ресурсов не зависит ни от , ни от , ни от 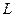 и, следовательно, постоянна и, следовательно, постоянна

Отсюда и происходит название функции. Функция CES, как и функция Кобба-Дугласа, исходит из допущения о постоянном убывании предельной нормы замещения используемых ресурсов. Между тем эластичность замещения капитала трудом и, наоборот, замены труда капиталом в функции Кобба-Дугласа, равная единице, здесь может принимать различные значения, не равные единице, хотя она и является постоянной. Наконец, в отличие от функции Кобба-Дугласа, логарифмирование функции CES не приводит к линейному виду, что вынуждает использовать для оценки параметров более сложные методы нелинейного регрессионного анализа.
Функция VES (один из вариантов):

Здесь эластичность замещения принимает различные значения в зависимости от уровня капиталовооруженности труда  , откуда и происходит название функции [15]. , откуда и происходит название функции [15].
Пример выполнения лабораторной работы
Построение производственной функции Кобба – Дугласа
Определить параметры ПФКД по заданным значениям затрат труда и основных фондов и выпуска продукции.
Найти параметры функции Кобба - Дугласа по данным таблицы:

Формируем векторы-столбцы затрат и матрицу выхода продукции:
 
 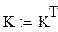
Построим матрицу значений производственной функции:
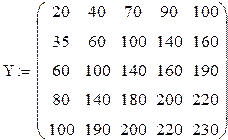
Сформируем функцию Кобба – Дугласа:

Неизвестные параметры ПФКД определим путем минимизации суммы квадратов уклонений ПФКД от наблюдаемых значений выпуска продукции.

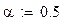 Решим задачу минимизации Решим задачу минимизации 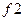 : :
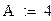   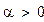
Для оценки точности аппроксимации ПФ вычислим относительное среднеквадратичное отклонение ПФКД от наблюдаемой функции выпуска.
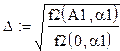

Среднеквадратичную погрешность аппроксимации можно считать приемлемой.
Попытаемся улучшить точность аппроксимации, ослабив требования к параметрам производственной функции. Для этого введем еще один параметр.



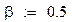 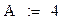
Given  

  

- Сумма показателей степени ПФКД не равна единице.
Вычислим относительную среднеквадратичную погрешность:
Погрешность аппроксимации уменьшилась незначительно. Возможно, более точной окажется ПФ другого типа.
Построим график наблюдаемого значения выпуска и ПФКД с двумя параметрами:

Из графика видно, что наблюдаемое значения выпуска не является гладкой функцией. Это означает, что на выпуск продукции влияют не только труд и капитал, но и другие неучтенные факторы.
Таким образом, в рамках принятой модели, точное описание выпуска продукции не возможно [10].
Вопросы для самопроверки
1. Что такое производственная функция?
2. Какой вид производственных функций наиболее широко представлен в экономическом моделировании?
3. Дайте определение макроэкономической производственной функции.
4. Какие 3 основных метода определения параметров макроэкономической производственной функции вы знаете?
5. Для каких целей применяют производственные функции?
6. Какое основное направление использования производственных функций в прикладных исследованиях?
7. Какие существуют частные случаи производственных функций?
8. Как формально можно записать производственную функцию?
9. Какой общий вид производственной функции?
10. Что такое производственная поверхность?
11. Отличительные черты неоклассической производственной функции?
12. На какие 2 вида делят производственные функции?
13. Какие производственные функции используются чаще всего?
14. Какая из них является наиболее популярной и в теоретических и в прикладных исследованиях? Какой вид она имеет?
15. В каких двух направлениях развивается НТП?
Список литературы:
1. Акофф Рассел Л. Планирование в больших экономических системах.
М., 1972.
2. Басакер Р., Саати Г. Конечные графы и сети. М., 1973.
3. Власов М. П. Моделирование деятельности фирмы с длительным
циклом производства. СПб., 2001.
4. Вильсон А. Дж. Энтропийные методы моделирования сложных
систем. Перев. с англ. М., 1976.
5. Володин А. А. Оптимизационные задачи в экономике. Рязань,
1999.
6. Герловин И. Л. Основы теории всех взаимодействий в веществе.
Л., 1990.
7. Джонстон Р. Дж. География и географы: Пер. с англ. / Под ред.
Э.Б.Алаева. М., 1987.
8. Емельянов А. А. Имитационное моделирование экономических
процессов. М., 2002.
9. Задорожный В. Н Имитационное моделирование, Омск, 1999.
10. Исследование операций: в 2 т. / Пер. с англ., Под ред. Дж. Моу-
дера, С. Элмаграби. М., 1981. Т. 1.
11. Корн Г., Корн Т. Справочник по математике для научных работников
и инженеров. М., 1970.
12. Краковский Ю. М. Имитационное моделирование, Иркутск, 2002.
13. Лопатников Л. И. Экономико-математический словарь. М., 1987.
14. Лопатников Л. И. Экономико-математический словарь: Словарь
современной экономической науки. 5-е изд., перераб. и доп. М., 2003.
15. Интернет
|