|
Многомерное шкалирование.
Содержание
1. Меры различия, типы моделей
2. Неметрическая модель и модель индивидуальных различий
3. Построение математических моделей с помощью компьютера
Список использованной литературы
1. Меры различия, типы моделей
Многомерное шкалирование предлагает геометрическое представление стимулов в виде точек координатного пространства минимально возможной размерности.
Существует два типа моделей: дистанционные и векторные. В дистанционных моделях исходные различия должны быть приближены расстояниями, в большинстве случаев используют привычное евклидово расстояние:
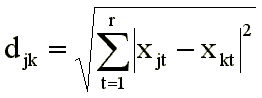
В векторных моделях меры близостей или связей — величины, обратные различиям, аппроксимируются скалярными произведениями векторов, соединяющих точки, соответствующие стимулам, с началом координат:
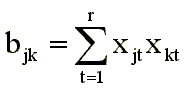
При построении конфигурации стимулов используется аппарат линейной или нелинейной оптимизации. Почему же такая простая модель и формальные методы поиска экстремума позволяют получить содержательно интерпретируемое решение? Почему оси, построенные формальным образом, приобретают смысл хорошо интерпретируемых факторов?
Векторная модель.
Обсудим геометрические свойства векторной модели. Начнем со шкалирования бинарных данных, т. е. высказываний типа «похожи—непохожи». Допустим, что мы имеем матрицу, содержащую информацию о том, что все стимулы не похожи друг на друга. Как можно представить геометрически такую структуру? Стимулы должны располагаться либо на ортогональных прямых, либо в начале координат. В этом случае все скалярные произведения будут нулями.
Перейдем к ситуации наличия нескольких групп похожих между собой стимулов. Стимулы из одной группы должны представляться одной точкой; точки, соответствующие разным группам, должны принадлежать ортогональным прямым. Изолированные стимулы могут быть помещены в начало координат. Тогда скалярные произведения между похожими стимулами будут большими, а скалярные произведения между непохожими стимулами будут нулями.
Ориентируем оси координатного пространства вдоль ортогональных направлений. Тогда каждая ось будет связана с группой похожих между собой стимулов, и фактор, ей соответствующий, будет лежать в основе сходства этих стимулов. Разным группам будут соответствовать ортогональные осп и, следовательно, независимые факторы. Исключение составляют изолированные стимулы, которые могут попасть в начало координат. Чем больше стимулов объединяются в группы, тем меньше измерений необходимо.
Пусть теперь мы располагаем дискретными или непрерывными данными, т. с. получаем оценки о сходствах или связях либо в виде баллов, либо в виде чисел. Допустим, что в этом случае матрица имеет квазиблочпую структуру. Тогда по ней можно разбить все множество на несколько групп так, что стимулы внутри каждой группы будут сильно связаны, а стимулы из разных групп—слабо связаны между собой. Характер отображения будет примерно таким же, как в случае непересекающихся бинарных данных. Однако стимулы из одной группы не будут представляться одной точкой, а будут сконцентрированы в некоторой ее окрестности. Такая структура, вообще говоря, не будет совпадать с ортогональной системой координат, поскольку точки могут лежать несколько в стороне от осей. Однако если связи в группах достаточно сильны, а связи между группами достаточно слабы, то и в этом случае каждое измерение будет связано с одной группой и фактор, ему соответствующий, будет лежать в основе сходства стимулов из этой группы.
На практике сильно структуризованные данные, характеризующие непересекающиеся группы стимулов, встречаются редко, обычно группы имеют пересечения. Имеются стимулы, похожие одновременно на стимулы из двух или нескольких групп. Естественно, что они не попадут на оси, а будут располагаться в пространстве между ними. Характер распределения будет зависеть от матрицы исходных данных. Картина будет тем контрастнее, чем более структуризованы данные, т. е. сильнее внутригрупповые связи и слабее — межгрупповые. Оси будут определяться группами стимулов, которые очень похожи между собой и минимально похожи на стимулы из других групп. Такие стимулы характеризуются большими значениями координат по соответствующим осям. Эти группы стимулов лежат в основе всей структуры. Остальные стимулы, похожие одновременно на стимулы из нескольких групп, должны занять промежуточные положения между этими группами.
Поскольку исходная матрица не является матрицей точных расстояний или скалярных произведений, то все стимулы не могут быть отображены в пространстве, определяемом ортогональными осями, соответствующими изолированным группам. Для их размещения потребуются дополнительные размерности. Если первый тип размерностей определяется большими межгрупповыми различиями и каждая размерность характеризуется значительным разбросом стимулов, то второй тип размерностей возникает за счет того, что субъективные различия между стимулами не могут быть отображены точным образом в пространстве небольшого числа размерностей. Разброс стимулов вдоль размерностей второго типа невелик и во многих случаях им можно пренебречь.
Центрированная векторная модель.
Другой вариант векторной модели — модель центрированных скалярных произведений. На ней основан широко распространенный метод Торгерсона, положивший начало теории многомерного шкалирования. В этой модели полагается, что начало координат помещено в центре тяжести структуры. Исходные близости или связи должны быть аппроксимированы скалярными произведениями векторов, соединяющих точки, соответствующие стимулам, с центром тяжести конфигурации. Матрица исходных близостей предварительно центрируется, так что наряду с положительными числами в ней появляются и отрицательные. Если пронормировать приведенные данные: |ajk
| 1, то их можно рассматривать как коэффициенты корреляции.
Решение, порождаемое моделью центрированных скалярных произведений, отличается от решения, получаемого по обычной векторной модели. В исходной матрице близости (связи) между стимулами могут принимать положительное, нулевое и отрицательное значения; будем приближать их скалярными произведениями. Естественно, что стимулы, характеризующиеся сильными положительными связями (большими мерами близостей), должны концентрироваться в окрестности одной точки, отстоящей на значительном расстоянии от начала координат. Тогда скалярные произведения между соответствующими векторами будут большими. Стимулы, характеризующиеся отрицательными связями, должны находиться по разные стороны от начала координат. Скалярные произведения между ними будут принимать максимальные отрицательные значения, если они будут принадлежать разным концам одной прямой, проходящей через начало координат. Пары стимулов с нулевыми связями должны принадлежать ортогональным прямым; в таком случае скалярные произведения между ними будут нулями. Изолированные стимулы, имеющие нулевые связи со всеми остальными, могут попадать в начало координат.
Большие положительные, отрицательные, а также нулевые связи будут определять основную структуру всей системы. Стимулы, характеризующиеся умеренными связями, будут располагаться между этими основными группами стимулов. Чем слабее связи, тем ближе стимулы к началу координат. Поскольку исходная матрица близостей или связей не является точной матрицей скалярных произведений, то все стимулы не могут быть отображены в пространстве небольшой размерности. Как и в случае предыдущей модели, для компенсации шума в данных потребуются дополнительные размерности, разброс в направлении которых незначителен по сравнению с основными размерностями и им можно пренебречь. Таким образом, модель центрированных скалярных произведений позволяет отобразить структуру системы в координатном пространстве, натянутом на небольшое множество ортогональных прямых. Повернем первоначальные оси пространства и совместим их с этими прямыми. Тогда каждую ось можно интерпретировать как биполярный фактор: справа будут располагаться стимулы, характеризующиеся положительными значениями этого фактора, слева — отрицательными, а в центре — нулевыми. Ортогональные оси будут соответствовать стимулам или группам стимулов, не связанных между собой, поэтому они могут интерпретироваться как независимые факторы. Решение, порождаемое моделью, будет иметь смысловое содержание.
Дистанционная модель.
Посмотрим теперь, какими свойствами обладает дистанционная модель; ограничимся евклидовой метрикой. Начнем опять с системы, в которой все стимулы не похожи друг на друга. Для точной передачи структуры этой системы следует поместить каждый стимул в одну из N вершин многогранника с одинаковыми ребрами (симплекса). Тогда стимулы будут отстоять друг от друга на одинаковом расстоянии.
Пусть имеется несколько изолированных групп- стимулов. Тогда стимулы из одной группы должны быть помещены в одну вершину, и многогранник будет иметь размерность, равную количеству групп. В отличие от векторной модели изолированные стимулы не могут быть все помещены в одну точку — начало координат, каждый из них должен занимать отдельную вершину.
В общем случае произвольной матрицы различий группы похожих между собой стимулов будут сконцентрированы вблизи одной вершины, а стимулы, похожие одновременно на стимулы из двух или нескольких групп, будут располагаться между этими вершинами.
Характер конструкции будет определяться в основном большими различиями между стимулами или группами стимулов. Однако, как и в случае векторной модели, ввиду того, что матрица различий не является точной матрицей расстояний, для передачи структуры потребуются дополнительные размерности. Но разброс стимулов в этих направлениях будет сравнительно мал.
В результате шкалирования необходимо выявить существенные оси, разброс в направлении которых велик, и отбросить несущественные оси, разброс в направлении которых мал. Итак, следуя модели многомерного шкалирования, можно разместить все стимулы в пространстве таким образом, чтобы оси несли смысловую нагрузку и факторы, им соответствующие, лежали в основе сходств или различий между стимулами.
Построенная результирующая конфигурация и полученные размерности отражают данные, занесенные в матрицу близостей или различий. И хотя многомерное шкалирование при своем зарождении было предназначено для анализа высказываний человека, никакой специфики обработки субъективных данных в нем не содержится. Оно в равной мере может использоваться и для анализа объективных данных о близостях или связях. Более того, иногда легче поддаются интерпретации объективные данные, потому что они характеризуют некие объективные связи между объектами. Интерпретация субъективных данных, построенных на основе высказываний одного человека (эксперта, испытуемого), может вызвать значительные затруднения у другого человека (исследователя, экспериментатора).
После анализа механизма шкалирования легко понять, какие же данные следует считать хорошими или, как принято говорить, хорошо структуризованными. Для кластерного анализа хорошо структуризованной является матрица, которая может быть приведена к блочно-диагональному виду. Иными словами, если имеется группа похожих (или сильно связанных) между собой стимулов, то все стимулы этой группы должны быть непохожими на остальные (или слабо связаны). Тогда структура может быть представлена изолированными группами сходных между собой стимулов. В многомерном шкалировании ввиду непрерывности измерений требования на входную информацию более слабые. Если два стимула сходны между собой, то они должны иметь близкие профили сходств со всеми другими стимулами. Это является необходимым условием для их адекватного представления в пространстве небольшого числа измерений.
Хотя модель многомерного шкалирования достаточно проста и интуитивно понятно, какого характера решение следует ожидать, попытки построить конфигурацию точек вручную могут привести к успеху лишь при очень небольшом количестве стимулов и хорошо структуризованной матрице близостей. В общем случае исследователь вынужден прибегнуть к помощи вычислительной машины, а для работы на ней необходимо алгоритмизировать процесс решения задачи. Иногда трудно вручную построить конфигурацию даже для небольшого набора стимулов. Примером такого множества могут служить равнояркие цветовые стимулы, равномерно распределенные по длине волны. Анализ матрицы субъективных различий не позволяет выделить ключевые стимулы, различия между которыми могли бы быть положены в основу всей структуры. Обработка этих данных на ЭВМ приводит к представлению стимулов на окружности — «цветовом круге»; действительно, с точки зрения такой структуры все стимулы равноценны.
Меры различия.
Вывод об экспериментальном эффекте может быть сделан как на основе установления значимой связи между изменениями НП и ЗП, т.е. путем использования мер связи, так и путем установления значимых различий в ЗП между экспериментальным и контрольным условиями, т.е. путем использования мер различий. Выбор тех или иных статистических критериев определяется обоснованным обсуждением адекватности их с точки зрения возможных соотнесений разных видов представления эмпирических результатов и предположений о каузальной зависимости. Если выбраны меры связи, то далее необходимы решения о выборе коэффициента корреляции, соответствующего шкалам измерения психологических переменных и плану соотнесения ЗП с экспериментальными условиями. В случае если выбраны меры различий, то также предполагается ряд решений об их соответствии плану сбора данных и типу показателей ЗП.
При установлении связей между переменными, измеренными в разных шкалах, требуются решения об их преобразованиях (приведение к одному виду, например, на основе их нормирования). Эти и другие решения принимаются не на основе знаний по статистике, а на основе содержательных переходов от целей исследования к поиску процедур, соответствующих установлению необходимых психологических шкал и способов количественной оценки полученных эффектов.
Выявление ковариации или корреляции переменных для выполнения второго условия причинного вывода не означает, что отношение между НП и ЗП должно статистически оцениваться именно на основании использования мер связей. В этом условии имеется в виду установление неслучайного, закономерного соответствия фиксируемых изменений ЗП изменениям в уровнях управляемого (экспериментального) фактора. Статистические выводы о значимых различиях в выборочных показателях ЗП в контрольном и экспериментальном условиях, т.е. использование мер различий для установления экспериментальных эффектов, позволяют установить лишь факт изменений ЗП. Это первый шаг к выводу о результате действия НП. Вторым существенным шагом (при планировании эксперимента и обсуждении его результатов) является обоснование того, что разница в условиях НП экспериментально контролировалась. Обсуждение экспериментальной процедуры с точки зрения того, действительно ли управляемые экспериментатором различия выступают в качестве причинно-действующих условий – лишь один из аспектов принятия решения об установленной зависимости. Другим, не менее важным аспектом является многоплановая оценка валидности эксперимента.
Статистические решения об отвержении нуль-гипотез следует рассматривать только в качестве одного из этапов реализации достоверных выводов об установленной зависимости на основе полученных эмпирических данных. Формальное планирование учитывает этот этап следующим образом. Величина полученного в эксперименте различия (в сравниваемых рядах показателей ЗП) оценивается с точки зрения предполагаемого минимального эффекта, который при заданном уровне значимости (вероятности ошибок первого рода), а также необходимом для этого числе проб или испытуемых (n – величина выборки) принимается в качестве критериального при заключении о неслучайном характере различий в эмпирических выборках показателей.
Статистические решения связаны с количественной оценкой экспериментального эффекта как преодолевающего это минимальное значение. Однако они не означают установления количественных зависимостей, если под таковыми понимать установление количественно представленных отношений между изменениями в уровнях НП и ЗП.
Экспериментальная гипотеза может включать предположения о функциональных отношениях между НП и ЗП как количественных зависимостях. Статистические решения осуществляются и для сравнения качественных уровней НП по соответствующим им показателям ЗП. Иными словами, сама по себе количественная оценка основного результата действия НП не означает, что психологическая гипотеза является количественной.
2. Неметрическая модель и модель индивидуальных различий
Парадоксальная возможность восстановления количественной структуры из числа качественных данных связана с тем обстоятельством, что число пар точек и, следовательно, число порядковых ограничений на их расстоянии возрастает приблизительно как квадрат числа определяемых количественных координат точек. Такие методы называются «неметрическими», поскольку в этом случае используются только порядковые свойства входных данных. Однако выход может достигать большой метрической точности и всегда будет метричным в смысле соответствия аксиомам расстояния.
Такое многомерное неметрическое шкалирование уже достигло в основном современного уровня, когда были введены стандартные методы градиента с целью минимизировать эксплицитно определяемую сумму квадратов как меру отклонения от монотонной зависимости расстояний от субъективных близостей (мера Крускала или «стресс»):

где dij - расстояния между точками на любой конкретной интерации в терминах n•k координат xik точек в k–мерном эвклидовом пространстве; они определяются с помощью обычной формулы расстояния:

dij — числа, которые монотонны с данными сходствами Sij и минимизируют S — «стресс» (меру Крускала) относительно пространственных расстояний dij на каждой итерации.
При заданной пробной размерности пространства стимулов строится начальная конфигурация точек либо произвольно, либо метрическим методом. Тогда при каждой последующей итерации: а) с помощью алгоритма для монотонной регрессии итерации наименьших квадратов определяется наиболее подходящая монотонная последовательность dij; б) оцениваются n∙k частных производных «стресса» по координатам xik; в) координаты корректируются в направлении отрицательного градиента по методу «скорейшего спуска» с помощью формулы хik=xik—αðS/ðxik, где α определяет величину шага итерации. Процесс заканчивается, когда компоненты градиента становятся настолько малыми, что указывает на достаточное приближение к стационарной конфигурации. (Чтобы не попасть в ловушку просто локального минимума, надо использовать несколько начальных «стартовых» конфигураций.) Весь процесс можно повторять в пространствах большей или меньшей размерности, а окончательное решение выбирается с таким расчетом, чтобы получить наилучший баланс между «экономностью» (оценкой возможно меньшего числа параметров), хорошим соответствием и особенно возможностью интерпретации.
Было разработано несколько различных вычислительных программ общего типа. В тех случаях, когда принимались меры по исключению простых локальных минимумов, обычно высокая степень переопределения конечной конфигурации порядковыми ограничениями в данных приводила к тому, что все такие программы, включая и программу автора, оказались способными выдавать существенно одинаковые результаты. Возможно, что наиболее гибкой из таких программ является KYST (что означает: Крускал, Янг, Шепард и Торгёрсон), которая была разработана в «Белл Телефон» на основе более ранних программ этих авторов. Она приспособлена также для весьма общего анализа прямоугольных матриц, в которых по модели «идеал — точки» Кумбса строки соответствуют испытуемым, столбцы — стимулам; каждая позиция в матрице является мерой предпочтения испытуемым данного стимула, интерпретируемого как пространственная близость данного стимула «идеальному» представлению этого стимула испытуемым. При использовании любой из этих программ необходимо избегать следующих ошибок: а) давать решения со слишком большим числом размерностей, которое обеспечивает хорошее соответствие, но не поддается интерпретации и является, возможно, ненадежным, а иногда и «вырожденным» решением; б) позволять вовлечь себя в «ловушку» в виде простого локального минимума, особенно в случае одномерных решений.
Модель индивидуальных различий
DISC У. Марстона основывается на описании наблюдаемого поведения, т.е. того, как человек действует и содержит два очень полезных инструмента:
1. экспресс-диагностику человека в течение первых 10-20 минут общения,
2. объяснение базовых мотиваторов данного человека и, следовательно, его преференций, симпатий и антипатий, шаблонов поведения.
Марстон выбрал 2 критерия, на основе которых он построил свою модель:
• как человек воспринимает мир, в котором действует (как благоприятную или враждебную);
• как человек действует или реагирует в конкретных ситуациях (активно или реактивно).
Если представить эти критерии в виде осей, то при их пересечении получается 4 базовых типа:

Доминирование
(Dominance):
- быстры в действиях и решениях
- нетерпеливы, настойчивы и неутомимы
- открыто говорят то, что думают
- готовы рисковать
- соревновательны, любит вызов и умеет его принимать
Влияние
(Influence):
- открыто выражают свои чувства и эмоции, притягивают к себе эмоции других людей
- обладают высоким творческим потенциалом и нестандартным мышлением
- разговорчивые, обаятельные, обладают повышенной харизмой
- легко доверяют людям, очень дружелюбны, легко заводят друзей
- невнимательны к деталям, импульсивны, мало пунктуальны
Постоянство
(Steadiness):
- умеют внимательно слушать и слышать собеседника
- обидчивы – тонко чувствуют фальши и обман
- любят покой, планомерность и методичность
- отстаивают сложившийся порядок вещей
- в команде будут стараться сохранить гармонию отношений
- сочувствуют и сопереживают, будут пытаться помочь
Соответствие
(Compliance):
- эмоционально зарыты
- демонстрируют собранность и высокую самоорганизованность
- заранее тщательно готовятся, любят системный подход
- анализируют, взвешивают, планируют, предусматривают
- думают о плохом и готовятся к этому
- готовы уступить, чтобы избежать прямого конфликта.
3. Построение математических моделей с помощью компьютера
Для использования ЭВМ при решении прикладных задач прежде всего прикладная задача должна быть "переведена" на формальный математический язык, т.е. для реального объекта, процесса или системы должна быть построена его математическая модель.
Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
Для построения математической модели необходимо:
1. тщательно проанализировать реальный объект или процесс;
2. выделить его наиболее существенные черты и свойства;
3. определить переменные, т.е. параметры, значения которых влияют на основные черты и свойства объекта;
4. описать зависимость основных свойств объекта, процесса или системы от значения переменных с помощью логико-математических соотношений (уравнения, равенства, неравенства, логико-математические конструкций);
5. выделить внутренние связи объекта, процесса или системы с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций;
6. определить внешние связи и описать их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций.
Математическое моделирование, кроме исследования объекта, процесса или системы и составления их математического описания, также включает:
1. построение алгоритма, моделирующего поведение объекта, процесса или системы;
2. проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента;
3. корректировка модели;
4. использование модели.
Математическое описание исследуемых процессов и систем зависит от:
1. природы реального процесса или системы и составляется на основе законов физики, химии, механики, термодинамики, гидродинамики, электротехники, теории пластичности, теории упругости и т.д.
2. требуемой достоверности и точности изучения и исследования реальных процессов и систем.
На этапе выбора математической модели устанавливаются: линейность и нелинейность объекта, процесса или системы, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса. При математическом моделировании сознательно отвлекаются от конкретной физической природы объектов, процессов или систем и, в основном, сосредотачиваются на изучении количественных зависимостей между величинами, описывающими эти процессы.
Математическая модель никогда не бывает полностью тождественна рассматриваемому объекту, процессу или системе. Основанная на упрощении, идеализации она является приближенным описанием объекта. Поэтому результаты, полученные при анализе модели, носят приближенный характер. Их точность определяется степенью адекватности (соответствия) модели и объекта.
Построение математической модели обычно начинается с построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта, процесса или системы. В дальнейшем, в случае необходимости, модель уточняется, делается ее соответствие объекту более полным.
Чем выше требования к точности результатов решения задачи, тем больше необходимость учитывать при построении математической модели особенности изучаемого объекта, процесса или системы. Однако, здесь важно во время остановиться, так как сложная математическая модель может превратиться в трудно разрешимую задачу.
Наиболее просто строится модель, когда хорошо известны законы, определяющие поведение и свойства объекта, процесса или системы, и имеется большой практический опыт их применения.
Более сложная ситуация возникает тогда, когда наши знания об изучаемом объекте, процессе или системе недостаточны. В этом случае при построении математической модели приходится делать дополнительные предположения, которые носят характер гипотез, такая модель называется гипотетической. Выводы, полученные в результате исследования такой гипотетической модели, носят условный характер. Для проверки выводов необходимо сопоставить результаты исследования модели на ЭВМ с результатами натурного эксперимента. Таким образом, вопрос применимости некоторой математической модели к изучению рассматриваемого объекта, процесса или системы не является математическим вопросом и не может быть решен математическими методами.
Основным критерием истинности является эксперимент, практика в самом широком смысле этого слова.
Построение математической модели в прикладных задачах – один из наиболее сложных и ответственных этапов работы. Опыт показывает, что во многих случаях правильно выбрать модель – значит решить проблему более, чем наполовину. Трудность данного этапа состоит в том, что он требует соединения математических и специальных знаний. Поэтому очень важно, чтобы при решении прикладных задач математики обладали специальными знаниями об объекте, а их партнеры, специалисты, – определенной математической культурой, опытом исследования в своей области, знанием ЭВМ и программирования.
Список использованной литературы
1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для втузов. Изд. 9-е , М., Высшая школа, 2003 г.
2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. Изд. 3-е – М., ЮНИТИ-ДАНА, 2007 г.
3. Колемаев В.А. и др. Теория вероятностей и математическая статистика. М.: ИНФРА-М, 1997 г.
4. Мхитарян В.С., Трошин Л.И., Адамова Е.В., Шевченко К.К., Бамбаева Н.Я. Теория вероятностей и математическая статистика / Московский международный институт эконометрики, информатики, финансов и права. – М., 2003 г.
5. Шепард Р.Н. Многомерное шкалирование и безразмерное представление различий // Психологический журнал Том 1 №4 1980
|