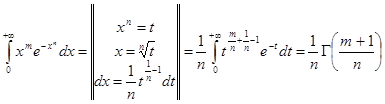Реферат
Целью данной курсовой работы является изучение особых свойств Гамма-функции Эйлера. В ходе работы была изучена Гамма-функция, её основные свойства и составлен алгоритм вычисления с разной степенью точности. Алгоритм был написан на языке высокого уровня - Си. Результат работы программы сверен с табличным. Расхождений в значениях обнаружено не было.
Пояснительная записка к курсовой работе выполнена в объёме 36 листов. Она содержит таблицу значений гамма-функции при некоторых значениях переменных и тексты программ для вычисления значений Гамма-функции и для построения графика, а также 2 рисунка.
Для написания курсовой работы было использовано 7 источников.
Введение
Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.
Такие функции называются интегралами зависящими от параметра. К их числу относятся гамма и бета функции Эйлера.
Бета функции представимы интегралом Эйлера первого рода:
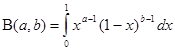
Гамма функция представляется интегралом Эйлера второго рода:

Гамма-функция относится к числу самых простых и значимых специальных функций, знание свойств которой необходимо для изучения многих других специальных функций, например, цилиндрических, гипергеометрических и других.
Благодаря её введению значительно расширяются наши возможности при вычислении интегралов. Даже в случаях, когда конечная формула не содержит иных функций, кроме элементарных, получение её всё же часто облегчает использование функции Г, хотя бы в промежуточных выкладках.
Эйлеровы интегралы представляют собой хорошо изученные неэлементарные функции. Задача считается решённой, если она приводится к вычислению эйлеровых интегралов.
1.
Бэта-функци
я Эйлера
Бэта – функции определяются интегралом Эйлера первого рода:
 = =   (1.1) (1.1)
Он представляет функцию от двух переменных параметров  и и  : функцию B
. Если эти параметры удовлетворяют условиям : функцию B
. Если эти параметры удовлетворяют условиям 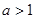 и и  ,то интеграл (1.1) будет несобственным интегралом, зависящим от параметров ,то интеграл (1.1) будет несобственным интегралом, зависящим от параметров  и и  ,причём особыми точками этого интеграла будут точки ,причём особыми точками этого интеграла будут точки  и и 
Интеграл (1.1) сходятся при  .Полагая .Полагая  получим: получим:
 = - = - = =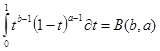
т.e. аргумент  и и  входят в входят в  симметрично. Принимая во внимание тождество симметрично. Принимая во внимание тождество

по формуле интегрирования почестям имеем

Откуда получаем
 = =
(1.2)
При целом b = n последовательно применяя (1.2)
Получим

(1.3)
при целых  = m, = m, = n, имеем = n, имеем
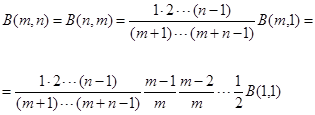
но B(1,1) = 1,следовательно:
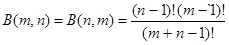
 
Положим в (1.1)  .Так как график функции .Так как график функции  симметрична относительно прямой симметрична относительно прямой  ,то ,то

и в результате подстановки  , получаем , получаем

полагая в(1.1)  ,откуда ,откуда 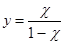 , получим , получим

(1.4)
разделяя интеграл на два в пределах от 0 до 1 и от 1 до  и применение ко второму интегралу подстановки и применение ко второму интегралу подстановки 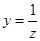 ,получим ,получим
2. Гамма-функция
2.1 Определение
Восклицательный знак в математических трудах обычно означает взятие факториала какого-либо целого неотрицательного числа:
n! = 1·2·3·...·n.
Функцию факториал можно еще записать в виде рекурсионного соотношения:
(n+1)! = (n+1)·n!.
Это соотношение можно рассматривать не только при целых значениях n.
Рассмотрим разностное уравнение
G(z+1)=zG(z).
(2.1)
Несмотря на простую форму записи, в элементарных функциях это уравнение не решается. Его решение называется гамма-функцией. Гамма-функцию можно записать в виде ряда или в виде интеграла. Для изучения глобальных свойств гамма-функции обычно пользуются интегральным представлением.
2.2
Интегральное представление
Перейдем к решению этого уравнения. Будем искать решение в виде интеграла Лапласа:

В этом случае правая часть уравнения (2.1) может быть записана в виде:


Эта формула справедлива, если существуют пределы для внеинтегрального члена. Заранее нам не известно поведение образа [(G)\tilde](p) при p®±¥. Предположим, что образ гамма-функции таков, что внеинтегральное слагаемое равно нулю. После того, как будет найдено решение, надо будет проверить, верно ли предположение о внеинтегральном слагаемом, иначе придется искать G(z) как-нибудь по-другому.
Левая часть равенства (2.1) записывается следующим образом:
 
Тогда уравнение (2.1) для образа гамма-функции имеет вид:

Это уравнение легко решить:
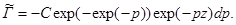
(2.2)
Нетрудно заметить, что найденная функция [(Г)\tilde](p) на самом деле такова, что внеинтегральный член в формуле (2.2) равен нулю.
Зная образ гамма-функции, легко получить и выражение для прообраза:
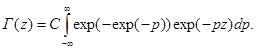
Это неканоническая формула, для того, чтобы привести ее к виду, полученному Эйлером, надо сделать замену переменной интегрирования: t = exp(-p), тогда интеграл примет вид:

Постоянная C выбирается так, чтобы при целых значениях z гамма-функция совпадала с функцией факториал: Г(n+1) = n!, тогда:

следовательно C = 1. Окончательно, получаем формулу Эйлера для гамма-функции:

(2.3)
Эта функция очень часто встречается в математических текстах. При работе со специальными функциями, пожалуй, даже чаще, чем восклицательный знак.
Проверить, что функция, определенная формулой (2.3), действительно удовлетворяет уравнению (2.1), можно, проинтегрировав интеграл в правой части этой формулы по частям:
 
2.3 Область определения и полюсы
В подынтегральной функции интеграла (2.3) при  экспонента exp(-tz
) при R(z
) > 0 убывает гораздо быстрее, чем растет алгебраическая функция t
(z-1)
. Особенность в нуле - интегрируемая, поэтому несобственный интеграл в (2.3) сходится абсолютно и равномерно при R (z) > 0. Более того, последовательным дифференцированием по параметру z
легко убедиться, что Г(z
) - голоморфная функция при R (z
) > 0. Однако, непригодность интегрального представления (2.3) при R (z
) экспонента exp(-tz
) при R(z
) > 0 убывает гораздо быстрее, чем растет алгебраическая функция t
(z-1)
. Особенность в нуле - интегрируемая, поэтому несобственный интеграл в (2.3) сходится абсолютно и равномерно при R (z) > 0. Более того, последовательным дифференцированием по параметру z
легко убедиться, что Г(z
) - голоморфная функция при R (z
) > 0. Однако, непригодность интегрального представления (2.3) при R (z
)  0 не означает, что там не определена сама гамма-функция - решение уравнения (2.1). 0 не означает, что там не определена сама гамма-функция - решение уравнения (2.1).
Рассмотрим поведение Г(z) в окрестности нуля. Для этого представим:

где 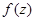 - голоморфная функция в окрестности z = 0
. Из формулы (2.1) следует: - голоморфная функция в окрестности z = 0
. Из формулы (2.1) следует:

Тогда

то есть Г(z) имеет полюс первого порядка при z = 0.
Также легко получить:

то есть в окрестности точки  функция Г(z
) также имеет полюс первого порядка. функция Г(z
) также имеет полюс первого порядка.
Таким же образом можно получить формулу:
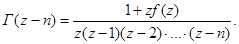
(2.4)
Из этой формулы следует, что точки z = 0,-1,-2,... - простые полюсы гамма-функции и других полюсов на вещественной оси эта функция не имеет. Нетрудно вычислить вычет в точке z = -n, n = 0,1,2,...:

2.4 Представление Ганкеля через интеграл по петле
Выясним, имеет ли гамма-функция нули. Для этого рассмотрим функцию
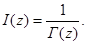
Полюсы этой функции и есть нули функции Г(z).
Разностное уравнение для I(z
) легко получить, воспользовавшись выражением для Г(z
):

Выражение для решения этого уравнения в виде интеграла можно получить так же, как было получено интегральное выражение для гамма-функции - через преобразование Лапласа. Ниже приведены вычисления.ни такие же, как и в п.1).ии теграла будут точки ____________________________________________________________________________

или

После разделения переменных получим:
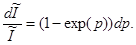
Проинтегрировав получаем:
 или или 
Переход к прообразу Лапласа дает:

В полученном интеграле сделаем замену переменной интегрирования:
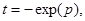 тогда тогда 
Здесь важно заметить, что подынтегральная функция при нецелых значениях z
имеет точку ветвления t
= 0. На комплексной плоскости переменной t
проведем разрез по отрицательной вещественной полуоси. Интеграл по этой полуоси представим как сумму интеграла по верхнему берегу этого разреза от  до 0 и интеграла от 0 до до 0 и интеграла от 0 до  по нижнему берегу разреза. Чтобы интеграл не проходил через точку ветвления, устроим вокруг нее петлю. по нижнему берегу разреза. Чтобы интеграл не проходил через точку ветвления, устроим вокруг нее петлю.

Рис1: Петля в интегральном представлении Ганкеля.
В результате получим:

Чтобы выяснить значение постоянной, вспомним, что I(1) = 1, с другой стороны:

Интегральное представление

(2.5)
называется представлением Ганкеля по петле.
Легко видеть, что функция 1/Г(z
) не имеет полюсов в комплексной плоскости, следовательно, гамма-функция не имеет нулей.
С помощью этого интегрального представления можно получить формулу для произведения гамма-функций. Для этого в интеграле сделаем замену переменной  , тогда: , тогда:


то есть

2.5 Предельная форма Эйлера
Гамма-функцию можно представить в виде бесконечного произведения. Это можно заметить, если в интеграле (2.3) представить
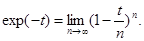
Тогда интегральное представление гамма-функции:

В этой формуле мы можем поменять пределы - предел интегрирования в несобственном интеграле и предел при  внутри интеграла. Приведем результат: внутри интеграла. Приведем результат:

Возьмем по частям этот интеграл:
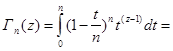


Если провести эту процедуру n раз, получим:

Переходя к пределу, получим предельную форму Эйлера для гамма-функции:

(2.6)
2.6 Формула для произведения
Ниже понадобится формула, в которой произведение двух гамма-функций представляется через одну гамма-функцию. Выведем эту формулу, используя интегральное представление гамма-функций.
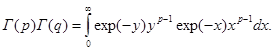
Повторный интеграл представим как двойной несобственный интеграл. Это можно сделать, воспользовавшись теоремой Фубини. В результате получим:
 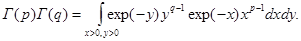
Несобственный интеграл равномерно сходится. Его можно рассматривать, например, как интеграл по треугольнику, ограниченному осями координат и прямой x+y = R при R . В двойном интеграле сделаем замену переменных: . В двойном интеграле сделаем замену переменных:
 
Якобиан этой замены

Пределы интегрирования: u
меняется от 0 до ∞, v
при этом меняется от 0 до 1. В результате получим:

Перепишем опять этот интеграл как повторный, в результате получим:

где Rp
> 0, Rv
> 0.
2. Производная гамма функции
Интеграл

сходится при каждом  ,поскольку ,поскольку  ,и интеграл ,и интеграл   при при  сходится. сходится.
В области 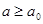 , где , где  - произвольное положительное число, этот интеграл сходится равномерно, так как - произвольное положительное число, этот интеграл сходится равномерно, так как и можно применить признак Вейрштраса. Сходящимся при всех значениях и можно применить признак Вейрштраса. Сходящимся при всех значениях  является и весь интеграл является и весь интеграл  так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом .Легко видеть что интеграл сходится по .Легко видеть что интеграл сходится по в любой области в любой области 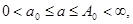 где где  произвольно. Действительно для всех указанных значений произвольно. Действительно для всех указанных значений  и для всех и для всех   ,и так как ,и так как  сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области 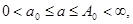 интеграл интеграл 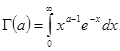 сходится равномерно. сходится равномерно.
Отсюда вытекает непрерывность гамма функции при .Докажем дифференцируемость этой функции при .Докажем дифференцируемость этой функции при  .Заметим что функция .Заметим что функция  непрерывна при непрерывна при  и и , и покажем ,что интеграл : , и покажем ,что интеграл :

сходится равномерно на каждом сегменте 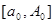 , ,  . Выберем число . Выберем число так , чтобы так , чтобы  ; тогда ; тогда  при при  .Поэтому существует число .Поэтому существует число  такое , что такое , что  и и  на на .Но тогда на .Но тогда на  справедливо неравенство справедливо неравенство

и так как интеграл  сходится, то интеграл сходится, то интеграл  сходится равномерно относительно сходится равномерно относительно  на на  . Аналогично для . Аналогично для  существует такое число существует такое число  , что для всех , что для всех  выполняется неравенство выполняется неравенство  . При таких . При таких  и всех и всех  получим получим  , откуда в силу признака сравнения следует , что интеграл , откуда в силу признака сравнения следует , что интеграл  сходится равномерно относительно сходится равномерно относительно  на на 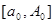 . Наконец , интеграл . Наконец , интеграл

в котором подынтегральная функция непрерывна в области
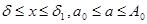 , очевидно, сходится равномерно относительно , очевидно, сходится равномерно относительно  на на 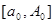 . Таким образом , на . Таким образом , на 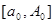 интеграл интеграл

сходится равномерно , а, следовательно , гамма-функция бесконечно дифференцируема при любом  и справедливо равенство и справедливо равенство
  . .
Относительно интеграла 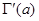 можно повторить те же рассуждения и заключить, что можно повторить те же рассуждения и заключить, что

По индукции доказывается , что Г-функция бесконечно дифференцируема при и для ее я и для ее я  -ой производной справедливо равенство -ой производной справедливо равенство

Изучим теперь поведение  - функции и построим эскиз ее графика. (см. Приложение 1) - функции и построим эскиз ее графика. (см. Приложение 1)
Из выражения для второй производной  -функции видно, что -функции видно, что  для всех для всех  . Следовательно, . Следовательно,  возрастает. Поскольку возрастает. Поскольку 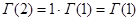 , то по теореме Роля на сегменте [1,2]производная , то по теореме Роля на сегменте [1,2]производная  при при  и и при при  , т. е. Монотонно убывает на , т. е. Монотонно убывает на 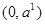 и монотонно возрастает на и монотонно возрастает на  . Далее , поскольку . Далее , поскольку  , то , то  при при  . При . При  из формулы из формулы  следует , что следует , что  при при  . .
Равенство  , справедливое при , справедливое при  , можно использовать при распространении , можно использовать при распространении  - функции на отрицательное значение - функции на отрицательное значение  . .
Положим для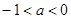 , что , что  . Правая часть этого равенства определена для . Правая часть этого равенства определена для  из (-1,0)
. Получаем, что так продолженная функция из (-1,0)
. Получаем, что так продолженная функция  принимает на (-1,0) отрицательные значения и при принимает на (-1,0) отрицательные значения и при  , а также при , а также при  функция функция 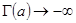 . .
Определив таким образом 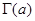 на на 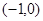 , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением 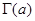 окажется функция, принимающая положительные значения и такая, что окажется функция, принимающая положительные значения и такая, что 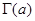  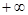 при при  и и  . Продолжая этот процесс, определим функцию . Продолжая этот процесс, определим функцию 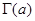 , имеющею разрывы в целочисленных точках , имеющею разрывы в целочисленных точках  (см. Приложение 1.) (см. Приложение 1.)
Отметим еще раз, что интеграл

определяет Г-функцию только при положительных значениях  , продолжение на отрицательные значения , продолжение на отрицательные значения  осуществлено нами формально с помощью формулы приведения осуществлено нами формально с помощью формулы приведения  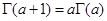 . .
4. Вычисление некоторых интегралов.
Формула Стирлинга
Применим гамма функцию к вычислению интеграла:

где m > -1,n > -1.Полагая , что  ,имеем ,имеем
 
и на основании (2.8) имеем

(4.1)
В интеграле

Где k > -1,n > 0,достаточно положить 
 
Интеграл

Где s > 0,разложить в ряд
  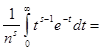
=
где  дзетта функция Римана дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством


Разлагая, в ряд имеем в ряд имеем
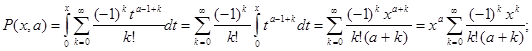

Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
 (4.2) (4.2)
Непрерывна на интервале (-1, ) монотонно возрастает от ) монотонно возрастает от  до до при изменении при изменении  от от  до до и обращаются в 0 при u = 0.Так как и обращаются в 0 при u = 0.Так как

то  при u > 0 и при u < 0 , далее имеем при u > 0 и при u < 0 , далее имеем

И так производная непрерывна и положительна во всем интервале  ,удовлетворяет условию ,удовлетворяет условию

Из предыдущего следует, что существует обратная функция,  определенная на интервале определенная на интервале 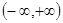 непрерывная и монотонно возрастающая в этом интервале, непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие
 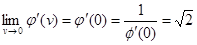
(4.3)
Формулу Стирлинга выведем из равенства

полагая  ,имеем ,имеем

Положим далее  введенная выше обратная функция, удовлетворяющая условиям u = -1при введенная выше обратная функция, удовлетворяющая условиям u = -1при  ,и ,и  при при  .Замечая что(см.4.2) .Замечая что(см.4.2)

имеем
 , ,
полагая на конец ,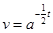 ,получим ,получим

или
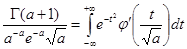
в пределе при  т.е. при т.е. при  (см 4.3) (см 4.3)
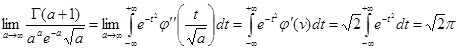
откуда вытекает формула Стирлинга

которую можно взять в виде

(4.4)
где  ,при ,при  
для достаточно больших  полагают полагают

(4.5)
вычисление же производится при помощи логарифмов

если  целое положительное число, то целое положительное число, то  и (4.5) превращается в приближенную формулу вычисления факториалов при больших значениях n и (4.5) превращается в приближенную формулу вычисления факториалов при больших значениях n

приведем без вывода более точную формулу

где в скобках стоит не сходящийся ряд.
5. Примеры вычисления интегралов
Для вычисления необходимы формулы:


Г( ) )
Вычислить интегралы


 
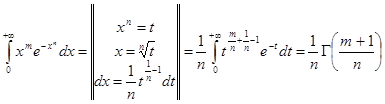

ПРАКТИЧЕСКАЯ ЧАСТЬ
Для вычисления гамма-функции используется аппроксимация её логарифма. Для аппроксимации гамма-функции на интервале x>0 используется следующая формула (для комплексных z):
Г(z+1)=(z+g+0.5)z+0.5
exp(-(z+g+0.5)) [a0
+a1
/(z+1)+a2
/(z+2)+...+an
/(z+n)+eps] [a0
+a1
/(z+1)+a2
/(z+2)+...+an
/(z+n)+eps]
Эта формула похожа на аппроксимацию Стирлинга, но в ней имеется корректирующая серия. Для значений g=5 и n=6, проверено, что величина погрешности ε
не превышает 2*10-10
. Более того, погрешность не превышает этой величины на всей правой половине комплексной плоскости: z > 0.
Для получения (действительной) гамма-функции на интервале x>0 используется рекуррентная формула Г(z+1)=zГ(z) и вышеприведенная аппроксимация Г(z+1). Кроме того, можно заметить, что удобнее аппроксимировать логарифм гамма-функции, чем ее саму. Во-первых, при этом потребуется вызов только одной математической функции - логарифма, а не двух - экспоненты и степени (последняя все равно использует вызов логарифма), во-вторых, гамма-функция - быстро растущая для больших x, и аппроксимация ее логарифмом снимает вопросы переполнения.
Для аппроксимации Ln(Г(х) - логарифма гамма-функции - получается формула:
log(Г(x))=(x+0.5)log(x+5.5)-(x+5.5)+
log(C0
(C1
+C2
/(x+1)+C3
/(x+2)+...+C7
/(x+8))/x)
Значения коэффициентов Ck
- табличные данные (см. в программе).
Сама гамма-функция получается из ее логарифма взятием экспоненты.
Заключение
Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.
Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы
1. Специальные функции и их приложения:
Лебедев И.И.,М.,Гостехтериоиздат,1953
2. Математический анализ часть 2:
Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987
3. Сборник задач по математическому анализу:
Демидович Б.П.,М.,Наука,1966
4. Интегралы и ряды специальные функции:
Прудников А.П., Брычков Ю.А.,М.,Наука,1983
5. Специальные функции:
Кузнецов , М.,”Высшая школа”,1965
6.Асимптотика и специальные функции
Ф.Олвер, М.,Наука,1990.
7.Зоопарк чудовищ или знакомство со спецмальными функциями
О.М.Киселёв,
ПРИЛОЖЕНИЯ
Приложение 1 - График гамма-функции действительного переменного
Приложение 2 – График Гамма-функции
Таблица – таблица значений гамма-функции при некоторых значениях аргумента.
Приложение 3 – листинг программы, рисующий таблицу значений гамма-функции при некоторых значениях аргумента.
Приложение 4 – листинг программы, рисующей график гамма-функции
СОДЕРЖАНИЕ
Реферат............................................................. ...................................3
Введение........................................................... ...................................4
Теоретическая часть…………………………………………………….5
Бета функция Эйлера…………………………………………….5
Гамма функция................................................. ...................................8
2.1. Определение………………………………………………...8
2.2. Интегральное представление………………………………8
2.3. Область определения и полюсы…………………………..10
2.4. Представление Ганкеля через интеграл по петле………..10
2.5. Предельная форма Эйлера………………………………...12
2.6. Формула для произведения………………………………..13
Производная гамма функции ........................ ..................................15
Вычисление интегралов. Формула Стирлинга...........................18
Примеры вычислений интегралов................... ..................................23
Практическая часть…………………………………………………….24
Заключение....................................................... ..................................25
Список литературы……………………………………………..............26
Приложения……………………………………………………………..27
ПРИЛОЖЕНИЕ 1

График гамма-функции действительного переменного
ПРИЛОЖЕНИЕ 2

График Гамма-функции
ТАБЛИЦА
| х |
g(x) |
1.450
1.452
1.454
1.458
1.460
1.462
1.464
1.466
1.468
1.470
1.472
1.474
1.476
1.478
1.480
|
0.8856616058
0.8856432994
0.8856284520
0.8856170571
0.8856091082
0.8856045988
0.8856035228
0.8856058736
0.8856116452
0.8856208314
0.8856334260
0.8856494230
0.8856688165
0.8856916004
0.8857177690
|
ПРИЛОЖЕНИЕ 3
#include<stdio.h>
#include<stdlib.h>
#include<iostream.h>
#include<math.h>
#include<conio.h>
#define CN 8
static double cof[CN]={
2.5066282746310005,
1.0000000000190015,
76.18009172947146,
-86.50532032941677,
24.01409824083091,
-1.231739572450155,
0.1208650973866179e-2,
-0.5395239384953e-5,
};
double GammLn(double x) {
double lg,lg1;
lg1=log(cof[0]*(cof[1]+cof[2]/(x+1)+cof[3]/(x+2)+cof[4]/(x+3)+cof[5]/(x+4)+cof[6]/(x+5)+cof[7]/(x+6))/x);
lg=(x+0.5)*log(x+5.5)-(x+5.5)+lg1;
return lg;
}
double Gamma(double x) {
return(exp(GammLn(x)));
}
void main()
{
double x[8],g[8];
int i,j;
clrscr();
cout<<"vvedite x[1]";
cin>>x[1];
printf("\n\t\t\t_________________________________________");
printf("\n\t\t\t| x |Gamma(x) |");
printf("\n\t\t\t_________________________________________");
for(i=1;i<=8;i++)
{
x[i+1]=x[i]+0.5;
g[i]=Gamma(x[i]);
printf("\n\t\t\t| %f | %f |",x[i],g[i]);
}
printf("\n\t\t\t_________________________________________");
printf("\n Dlia vuhoda iz programmu najmite lybyiy klavishy");
getch();
}
ПРИЛОЖЕНИЕ 4
#include<stdio.h>
#include<graphics.h>
#include<math.h>
#include<conio.h>
Double gam(double x, double eps)
{
Int I, j, n, nb;
Double dze[5]={1.6449340668422643647,
1.20205690315959428540,
1.08232323371113819152,
1.03692775514336992633,
1.01734306198444913971};
Double a=x, y, fc=1.0, s, s1, b;
If(x<=0)
{
Printf (“вы ввели неправильные данные, попробуйте снова\n”); return -1.0;
}
If(x<i)
{
A=x+1.0;
Fc=1.0/x;
}
While (a>=2)
{
A=a-1.0;
Fc=fc*a;
}
A=a-1.0;
If(a==0) return fc;
B=a*a;
S=0;
For (i=0;i<5;i++)
{
S=s+b*dze[i]/(i+2.0);
B=-b*a;
}
Nb=exp((i.0/6.0)*(7.0*log(a)-log(42/0)-log(eps)))+I;
For (n=1;n<=nb;n++)
{
B=a/n;
Si=0;
For(j=0; j<5; j++)
{
Si=si+b/(j+1.0);
B=-b*a/n;
}
S=s+si-log(1.0+a/n);
}
Y=exp(-ce*a+s);
Return y*fc;
}
Main()
}
Double dx,dy, xfrom=0,xto=4, yto=5, h, maxy, miny;
Int n=100, I, gdriver=DETECT, gmode, X0, YN0, X, Y, Y0,pr=0;
Initgraph(&gdriver,&gmode, “ ”);
X0=30;
YN0=getmaxy()-20;
Line(30, getmaxy ()-10,30,30);
Line(20, getmaxy ()-30, getmaxx ()-20, getmaxy ()-30);
X=170;
Y=450;
Do{
Moveto(X,Y);
DO{
Y=Y-1;
Lineto(X,Y);
Y=Y-10;
Moveto(X,Y);
}while (Y>30);
X=X+150;
Y=450;
}while (X<700);
X=30;
Y=366;
Do{
Moveto(X,Y);
Do{
X=X+1;
Lineto(X,Y);
X=X+10;
Moveto(X,Y);
}while (X<=620);
Y=Y-84;
X=30;
}while (y>=30);
X=30+150.0*0,1845;
Moveto(X,30);
For9i=1;i<n,i++)
{
Dx=(4.0*i)/n;
Dy=gam(dx,1e-3);
X=30+(600/0*i)/n;
Y=450-84*dy;
If(Y<30) continue;
Lineto (X,Y);
}
X=30+150.0*308523;
Lineto(X,30);
Line (30,30,30,10);
Line(620,450,640,450);
Line(30,10,25,15);
Line(30,10,25,15);
Line(640,450,635,445);
Line(640,450,635,455);
Line(170,445,170,455);
Line(320,445,320,455);
Line(470,445,470,455);
Line(620,445,620,455);
Line(25,366,35,366);
Line(25,282,35,282);
Line(25,114,35,114);
Line(25,30,35,30);
Outtexty(20,465,"0");
Outtexty(165,465, "1";
Outtexty(315,465, "2";
Outtexty(465,465, "3";
Outtexty(615,465, "4";
Outtexty(630,465, "x";
Outtexty(15,364, "1";
Outtexty(15,280, "2";
Outtexty(15,196, "3";
Outtexty(15,112, "4";
Outtexty(15,30, "5";
Outtexty(15,10, "y";
Getch()
}
|
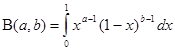

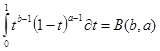


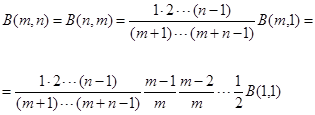











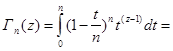

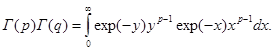


 при
при  так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области
сходится, то выполнены условия признака Вейерштрасса. Таким образом , в области 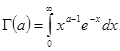 сходится равномерно.
сходится равномерно.
 сходится, то интеграл
сходится, то интеграл  сходится равномерно относительно
сходится равномерно относительно  . При таких
. При таких  сходится равномерно относительно
сходится равномерно относительно 











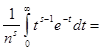

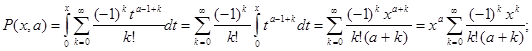
 (4.2)
(4.2)