ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра промышленной теплоэнергетики
Расчетная работа по курсу: ”Специальные главы ГГД”
“Расчет сопла Лаваля”
Вариант№31
Выполнил: студент группы ТЭ-07-2
Татьянин И.Ю.
« » 2009 год
Проверил:
Севастьянов А.В.
« »
2009
год
Липецк,2009
Оглавление:
Расчётное задание…………..……….……………..………………...............…..3
1.Расчет конфузора………………………………………………… 4
2.Расчет диффузора…………………………………………………9
Список используемой литературы………………………………….………13
Исходные данные:
a. газ – ксенон;
b. параметры торможения:
температура газа – 2410 °С, давление 13 МПа;
c. массовый расход – 10 кг/с;
d. скорость на входе в сопло – 15 м/с;
e. угол раскрытия конического диффузора 7°
Определить:
1. Размеры сопла (конфузор рассчитать по формуле Витошинского,  ). ).
2. Распределение по длине сопла диаметра сопла, давления, температуры и плотности газа, локальной скорости звука, приведенного расхода.
Примечание
· Режим истечения расчетный (давление на выходе равно 0,02 МПа).
· Газ принять идеальным.
· Толщиной пограничного слоя и потерями по длине пренебречь.
1.Расчет конфузора.
Проведем расчет первой суживающейся части сопла Лаваля - конфузора.
 , ,
где  - универсальная газовая постоянная, а μ - молярная масса ксенона. - универсальная газовая постоянная, а μ - молярная масса ксенона.
Из уравнения Майера:



Пусть все параметры на входе в сопло имеют индекс 1, а на выходе из сопла –
индекс 2, а параметры торможения индекс 0.
Найдем температуру на входе в сопло, выразив ее через температуру торможения 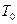 : :

Далее определяем скорость звука на входе в сопло:
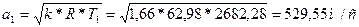 
Находим число Маха для входного сечения:
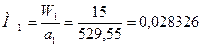
Находим давление на входе в сопло:

Находим отношение давления на выходе из сопла к давлению на входе:

Получаем   можем посчитать критическую скорость. можем посчитать критическую скорость.
Зная параметры торможения можно найти неизвестные из критических и начальных параметров движения газа:  а так же соответствующие габариты сопла: а так же соответствующие габариты сопла: 
Расчет критических параметров:
Так как в критическом сечении  , то , то  с другой стороны: с другой стороны: 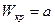 , где а – скорость звука, , где а – скорость звука,  Из данных формул получаем выражение для критической температуры: Из данных формул получаем выражение для критической температуры:
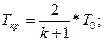
Подобным образом получается формула для критического давления:
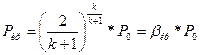
Плотность газа в критическом сечении находим как:
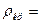
Тогда:




Из уравнения расхода 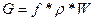 можно найти площадь критического сечение: можно найти площадь критического сечение:
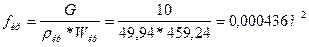
Находим радиус критического сечения:
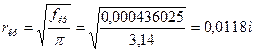
В критическом сечении 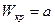  число Маха число Маха 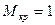 ; ;
Определяем приведенный расход в критическом сечении:  где где 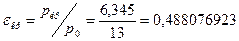
Тогда:
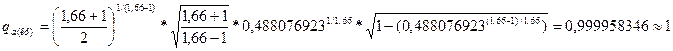
Определение параметров на входе:
Плотность газа во входном сечении находим из уравнения:
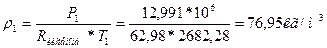
Площадь входного сечения находим по формуле:
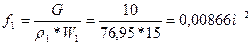
Находим радиус входного сечения:
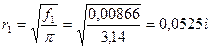
Определяем приведенный расход во входном сечении: 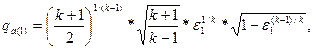 где где 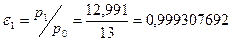
Тогда:

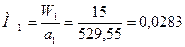
Параметры входного и критического сечений представлены в №1:
Таблица №1
.
 , K , K |
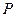 , МПа , МПа |
 , кг/м , кг/м |
 , м/с , м/с |
a, м/с |
M |
 ,м ,м |
r,м |
 |
| Критическое сечение |
2017,3 |
6,345 |
49,94 |
459,24 |
459.24 |
1 |
0,000436 |
0,0118 |
1 |
| Входное сечение |
2682,28 |
12,991 |
76,95 |
15 |
529,55 |
0,0283 |
0,00866 |
0,0525 |
0,0513 |
По условиям расчета, длина конфузора равна:
  
Для последующих расчетов разобьем длину конфузора на 20 одинаковых участков, также разобьем число Маха по длине, тогда получив соответствующий масштаб для  и и  , мы сможем найти значения всех необходимых неизвестных параметров в каждой точке по формулам: , мы сможем найти значения всех необходимых неизвестных параметров в каждой точке по формулам:
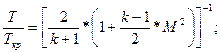

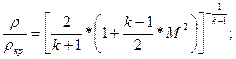
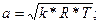
Значения радиусов также найдем, поделив длину конфузора на 20 равных частей, затем подставив получившиеся значения в формулу по формуле Витошинского:
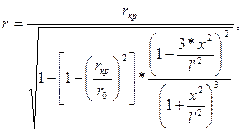
где 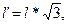  - длина конфузора, - длина конфузора,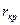 - радиус критического сечения, - радиус критического сечения, 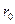 - радиус входного сечения, - радиус входного сечения,  - расстояние от входного сечения до любой точки на оси конфузора, - расстояние от входного сечения до любой точки на оси конфузора, 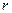 - радиус в искомой точке; - радиус в искомой точке;
 где где 
Шаг длины:
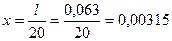
Шаг числа Маха:
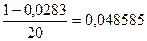
Таблица №2.
| x |
M |
T |
P |
ρ |
a |
r |
qa |
w |
| 0,00000
|
0,02830
|
2682,30009
|
12,99118
|
76,90041
|
529,55254
|
0,05250
|
0,05078
|
14,98634
|
| 0,00315 |
0,07689 |
2677,78536 |
12,93625 |
76,70438 |
529,10669 |
0,04983 |
0,13625 |
40,68037 |
| 0,00630 |
0,12547 |
2669,14254 |
12,83150 |
76,32958 |
528,25213 |
0,04376 |
0,22071 |
66,27979 |
| 0,00945 |
0,17406 |
2656,45140 |
12,67860 |
75,78037 |
526,99478 |
0,03727 |
0,30316 |
91,72608 |
| 0,01260 |
0,22264 |
2639,82768 |
12,47999 |
75,06301 |
525,34326 |
0,03172 |
0,38287 |
116,96242 |
| 0,01575 |
0,27123 |
2619,42050 |
12,23875 |
74,18555 |
523,30873 |
0,02730 |
0,45916 |
141,93441 |
| 0,01890 |
0,31981 |
2595,40906 |
11,95854 |
73,15763 |
520,90470 |
0,02384 |
0,53144 |
166,59053 |
| 0,02205 |
0,36840 |
2567,99884 |
11,64342 |
71,99018 |
518,14676 |
0,02111 |
0,59920 |
190,88267 |
| 0,02520 |
0,41698 |
2537,41741 |
11,29782 |
70,69523 |
515,05230 |
0,01893 |
0,66204 |
214,76651 |
| 0,02835 |
0,46557 |
2503,90995 |
10,92632 |
69,28557 |
511,64028 |
0,01716 |
0,71963 |
238,20181 |
| 0,03150 |
0,51415 |
2467,73475 |
10,53362 |
67,77456 |
507,93087 |
0,01571 |
0,77176 |
261,15266 |
| 0,03465 |
0,56274 |
2429,15870 |
10,12436 |
66,17579 |
503,94520 |
0,01450 |
0,81829 |
283,58760 |
| 0,03780 |
0,61132 |
2388,45302 |
9,70305 |
64,50289 |
499,70503 |
0,01348 |
0,85917 |
305,47968 |
| 0,04095 |
0,65991 |
2345,88919 |
9,27400 |
62,76926 |
495,23248 |
0,01262 |
0,89444 |
326,80639 |
| 0,04410 |
0,70849 |
2301,73536 |
8,84121 |
60,98792 |
490,54976 |
0,01187 |
0,92422 |
347,54960 |
| 0,04725 |
0,75708 |
2256,25307 |
8,40837 |
59,17130 |
485,67895 |
0,01123 |
0,94867 |
367,69539 |
| 0,05040 |
0,80566 |
2209,69453 |
7,97876 |
57,33114 |
480,64175 |
0,01066 |
0,96800 |
387,23383 |
| 0,05355 |
0,85425 |
2162,30030 |
7,55531 |
55,47835 |
475,45933 |
0,01017 |
0,98250 |
406,15876 |
| 0,05670 |
0,90283 |
2114,29751 |
7,14052 |
53,62298 |
470,15214 |
0,00973 |
0,99245 |
424,46746 |
| 0,05985 |
0,95142 |
2065,89853 |
6,73650 |
51,77414 |
464,73980 |
0,00934 |
0,99817 |
442,16042 |
| 0,06300
|
1,00000
|
2017,30000
|
6,34500
|
49,94000
|
459,24096
|
0,00900
|
1,00000
|
459,24096
|
3.Расчет диффузора.
Проведём расчет второй части сопла Лаваля (диффузора).Входными параметрами для диффузора являются критические, которые были ранее определены. Располагая значениями критических параметров можем вычислить параметры на выходе.
Расчет выходных параметров:
Скорость на выходе вычислим по формуле:
 где где 
Тогда:
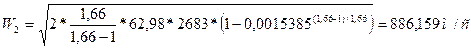
Вычислим коэффициент скорости :

=> число Маха можно найти по формуле:

Выходные параметры рассчитываются формулам:
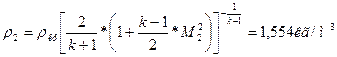 
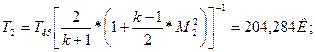

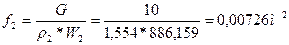
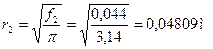
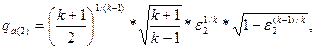 где где 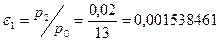
Тогда: 
Параметры на выходе представлены в таблице №3:
Таблица №3.
 , K , K |
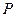 , МПа , МПа |
 , кг/м , кг/м |
 , м/с , м/с |
a, м/с |
M |
 ,м ,м |
r,м |
 |
| Выходное сечение |
204,284 |
0,02 |
1,554 |
886,159 |
146,141 |
6,063723 |
0,00726 |
0,04809 |
0,060062 |
Зная критический и выходной радиусы, и приняв, что диффузор конический (угол раскрытия 7°) можно найти его длину. Длина диффузора вычисляется по формуле:
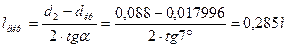
Для расчета промежуточных значений параметров по длине диффузора, разобьем его длину и число Маха на 50 одинаковых частей:
Шаг длины: 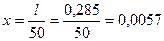
Шаг числа Маха: 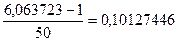
Формулы для расчета промежуточных значений параметров:
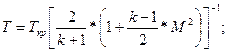


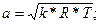
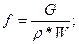

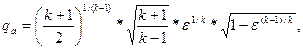 где где 
Значение параметров по длине диффузора№4:
Таблица №4
| X,м |
M |
T,К |
P, МПа |
Ρ,кг/м3
|
а ,м/с |
r,м |
d,м |
qa |
W,м/с |
| 0,00000
|
1,00000
|
2017,30000
|
6,34500
|
49,94000
|
459,24096
|
0,01178
|
0,02357
|
1,00000
|
459,24096
|
| 0,00570 |
1,10127 |
1916,12597 |
5,57477 |
46,19450 |
447,57663 |
0,01183 |
0,02365 |
0,99280 |
492,90471 |
| 0,01140 |
1,20255 |
1816,25444 |
4,87255 |
42,59582 |
435,75634 |
0,01194 |
0,02389 |
0,97325 |
524,01832 |
| 0,01710 |
1,30382 |
1718,79199 |
4,24141 |
39,18087 |
423,90353 |
0,01213 |
0,02425 |
0,94421 |
552,69533 |
| 0,02280 |
1,40510 |
1624,57049 |
3,68067 |
35,97294 |
412,12091 |
0,01236 |
0,02473 |
0,90827 |
579,07020 |
| 0,02850 |
1,50637 |
1534,18074 |
3,18710 |
32,98422 |
400,49181 |
0,01265 |
0,02530 |
0,86764 |
603,28976 |
| 0,03420 |
1,60765 |
1448,00976 |
2,75583 |
30,21818 |
389,08198 |
0,01298 |
0,02596 |
0,82415 |
625,50638 |
| 0,03990 |
1,70892 |
1366,27794 |
2,38116 |
27,67179 |
377,94178 |
0,01335 |
0,02670 |
0,77928 |
645,87272 |
| 0,04560 |
1,81020 |
1289,07352 |
2,05709 |
25,33742 |
367,10831 |
0,01375 |
0,02751 |
0,73416 |
664,53788 |
| 0,05130 |
1,91147 |
1216,38310 |
1,77768 |
23,20436 |
356,60757 |
0,01419 |
0,02838 |
0,68966 |
681,64472 |
| 0,05700 |
2,01274 |
1148,11760 |
1,53731 |
21,26001 |
346,45638 |
0,01466 |
0,02931 |
0,64641 |
697,32820 |
| 0,06270 |
2,11402 |
1084,13372 |
1,33084 |
19,49086 |
336,66409 |
0,01515 |
0,03030 |
0,60485 |
711,71431 |
| 0,06840 |
2,21529 |
1024,25120 |
1,15362 |
17,88309 |
327,23415 |
0,01567 |
0,03135 |
0,56525 |
724,91968 |
| 0,07410 |
2,31657 |
968,26645 |
1,00153 |
16,42310 |
318,16530 |
0,01622 |
0,03244 |
0,52779 |
737,05155 |
| 0,07980 |
2,41784 |
915,96299 |
0,87097 |
15,09782 |
309,45274 |
0,01679 |
0,03358 |
0,49254 |
748,20797 |
| 0,08550 |
2,51912 |
867,11934 |
0,75883 |
13,89489 |
301,08894 |
0,01738 |
0,03477 |
0,45952 |
758,47825 |
| 0,09120 |
2,62039 |
821,51485 |
0,66242 |
12,80279 |
293,06441 |
0,01800 |
0,03600 |
0,42869 |
767,94345 |
| 0,09690 |
2,72167 |
778,93381 |
0,57942 |
11,81087 |
285,36825 |
0,01863 |
0,03727 |
0,39997 |
776,67701 |
| 0,10260 |
2,82294 |
739,16832 |
0,50788 |
10,90941 |
277,98864 |
0,01929 |
0,03857 |
0,37328 |
784,74532 |
| 0,10830 |
2,92421 |
702,02014 |
0,44610 |
10,08954 |
270,91319 |
0,01996 |
0,03992 |
0,34851 |
792,20836 |
| 0,11400 |
3,02549 |
667,30180 |
0,39267 |
9,34322 |
264,12926 |
0,02065 |
0,04131 |
0,32555 |
799,12023 |
| 0,11970 |
3,12676 |
634,83716 |
0,34638 |
8,66321 |
257,62413 |
0,02136 |
0,04273 |
0,30428 |
805,52977 |
| 0,12540 |
3,22804 |
604,46156 |
0,30619 |
8,04295 |
251,38521 |
0,02209 |
0,04418 |
0,28458 |
811,48103 |
| 0,13110 |
3,32931 |
576,02169 |
0,27124 |
7,47659 |
245,40013 |
0,02283 |
0,04567 |
0,26634 |
817,01374 |
| 0,13680 |
3,43059 |
549,37521 |
0,24078 |
6,95885 |
239,65688 |
0,02359 |
0,04719 |
0,24946 |
822,16379 |
| 0,14250 |
3,53186 |
524,39032 |
0,21418 |
6,48499 |
234,14382 |
0,02437 |
0,04874 |
0,23383 |
826,96355 |
| 0,14820 |
3,63314 |
500,94519 |
0,19090 |
6,05079 |
228,84977 |
0,02516 |
0,05032 |
0,21936 |
831,44232 |
| 0,15390 |
3,73441 |
478,92736 |
0,17050 |
5,65243 |
223,76399 |
0,02597 |
0,05193 |
0,20595 |
835,62657 |
| 0,15960 |
3,83568 |
458,23313 |
0,15257 |
5,28652 |
218,87624 |
0,02679 |
0,05357 |
0,19352 |
839,54027 |
| 0,16530 |
3,93696 |
438,76694 |
0,13679 |
4,95000 |
214,17675 |
0,02762 |
0,05525 |
0,18199 |
843,20515 |
| 0,17100 |
4,03823 |
420,44077 |
0,12287 |
4,64014 |
209,65624 |
0,02847 |
0,05694 |
0,17129 |
846,64090 |
| 0,17670 |
4,13951 |
403,17357 |
0,11057 |
4,35447 |
205,30588 |
0,02934 |
0,05867 |
0,16136 |
849,86541 |
| 0,18240 |
4,24078 |
386,89069 |
0,09968 |
4,09081 |
201,11734 |
0,03021 |
0,06042 |
0,15213 |
852,89493 |
| 0,18810 |
4,34206 |
371,52340 |
0,09002 |
3,84715 |
197,08268 |
0,03110 |
0,06220 |
0,14355 |
855,74427 |
| 0,19380 |
4,44333 |
357,00839 |
0,08143 |
3,62172 |
193,19442 |
0,03201 |
0,06401 |
0,13556 |
858,42689 |
| 0,19950 |
4,54461 |
343,28732 |
0,07379 |
3,41292 |
189,44548 |
0,03292 |
0,06584 |
0,12812 |
860,95510 |
| 0,20520 |
4,64588 |
330,30642 |
0,06697 |
3,21930 |
185,82917 |
0,03385 |
0,06770 |
0,12119 |
863,34011 |
| 0,21090 |
4,74716 |
318,01608 |
0,06088 |
3,03956 |
182,33914 |
0,03479 |
0,06958 |
0,11472 |
865,59218 |
| 0,21660 |
4,84843 |
306,37055 |
0,05543 |
2,87251 |
178,96944 |
0,03574 |
0,07149 |
0,10868 |
867,72071 |
| 0,22230 |
4,94970 |
295,32757 |
0,05054 |
2,71710 |
175,71441 |
0,03671 |
0,07342 |
0,10304 |
869,73429 |
| 0,22800 |
5,05098 |
284,84812 |
0,04615 |
2,57236 |
172,56871 |
0,03769 |
0,07538 |
0,09776 |
871,64082 |
| 0,23370 |
5,15225 |
274,89609 |
0,04220 |
2,43742 |
169,52730 |
0,03868 |
0,07735 |
0,09283 |
873,44754 |
| 0,23940 |
5,25353 |
265,43812 |
0,03864 |
2,31149 |
166,58543 |
0,03968 |
0,07936 |
0,08820 |
875,16111 |
| 0,24510 |
5,35480 |
256,44328 |
0,03543 |
2,19385 |
163,73858 |
0,04069 |
0,08138 |
0,08387 |
876,78767 |
| 0,25080 |
5,45608 |
247,88295 |
0,03253 |
2,08385 |
160,98251 |
0,04171 |
0,08343 |
0,07981 |
878,33285 |
| 0,25650 |
5,55735 |
239,73057 |
0,02991 |
1,98090 |
158,31318 |
0,04275 |
0,08550 |
0,07599 |
879,80187 |
| 0,26220 |
5,65863 |
231,96151 |
0,02753 |
1,88445 |
155,72679 |
0,04379 |
0,08759 |
0,07240 |
881,19955 |
| 0,26790 |
5,75990 |
224,55291 |
0,02537 |
1,79401 |
153,21974 |
0,04485 |
0,08970 |
0,06903 |
882,53031 |
| 0,27360 |
5,86117 |
217,48350 |
0,02341 |
1,70913 |
150,78861 |
0,04592 |
0,09183 |
0,06586 |
883,79828 |
| 0,27930 |
5,96245 |
210,73353 |
0,02163 |
1,62941 |
148,43017 |
0,04699 |
0,09399 |
0,06288 |
885,00726 |
| 0,28500
|
6,06372
|
204,28459
|
0,02000
|
1,55445
|
146,14137
|
0,04808
|
0,09617
|
0,06006
|
886,16078
|
Рассматривая выходное сечение, и знвчения, посчитанные ранее по формулам, совпадают со значениями представленными в таблице (последняя строка На основании таблиц (таблица №2 и таблица №4) построены распределения:
1. давления по длине сопла -
2. температуры по длине сопла - 
3. плотности по длине сопла - 
4. локальной скорости звука по длине сопла - 
5. приведенного расхода по длине сопла - 
где 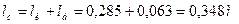 . .
Список используемой литературы:
1. В. Н. Юренев, П. Д. Лебедев. Теплотехнический справочник, т.2, Москва, «Энергия», 1976 г.
2. М.Е. Дейч, А.Е. Зарянкин. Гидрогазодинамика. Москва, «Энергоатомиздат», 1984 г.
3. И.Л. Повх. Техническая гидромеханика. Ленинград, Машиностроение, 1976 г.
4. В.Н. Зубарев, А.Д. Козлов, В.М. Кузнецов и др.; Теплофизические
свойства технически важных газов. Москва, «Энергоатомиздат», 1989 г.
5. Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению. Ленинград, Машиностроение, 1977г.
|