ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОСИЙСКОЙ ФЕДЕРАЦИИ
Государственное Образовательное Учреждение Высшего Профессионального Образования «Воронежский Государственный Технический Университет» (ГОУВПО «ВГТУ»)
Кафедра: Высшей математики и физико-математического моделирования
КУРСОВАЯ РАБОТА
по дисциплине «Математика»
«Метрические характеристики графа»
Выполнил: студент группы
РК-051 Жищенко С.А.
Руководитель: Ускова Н.Б.
Оценка:
Дата защиты:
Воронеж 2006 г.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОСИЙСКОЙ ФЕДЕРАЦИИ
Государственное Образовательное Учреждение Высшего Профессионального Образования «Воронежский Государственный Технический Университет» (ГОУВПО «ВГТУ»)
Кафедра: Высшей математики и физико-математического моделирования
Задание на курсовую работу по дисциплине «Математика»
Исполнитель: Жищенко С.А.
Руководитель: Ускова Н.Б.
«Метрические характеристики графа»
Тема курсовой работы утверждена постановлением по РТФ от 3.10.06, №6.
Задание: дано два графа, построить их матрицы смежности и инцидентности, определить их метрические характеристики.
Срок выдачи курсовой работы:
Срок сдачи:
Задание принял ст. гр. РК-051 Жищенко С.А.
Руководитель__________
Воронеж, 2006.
Содержание
Понятие «граф»..........................................................................................5
Матричное представление графов............................................................9
Операции над графами..............................................................................11
Маршруты, цепи, циклы............................................................................12
Метрические характеристики графа.........................................................15
Приложение теории графов в различных областях науки и техники...16
Практическая часть....................................................................................18
Листинг программы...................................................................................21
ПОНЯТИЕ "ГРАФ"
Пусть V – непустое множество, V(2)
– множество всех его двухэлементных подмножеств. Пара (V,E), где E – произвольное подмножество множества V(2)
, называется графом (неориентированным графом). Элементы множества V называются вершинами графа, а элементы множества E – ребрами. Итак, граф – это конечное множество V вершин и множество E ребер, E⊂V(2)
.
Термин «граф» впервые появился в книге выдающегося венгерского математика Д. Кёнига в 1936 г., хотя начальные задачи теории графов восходят еще к Эйлеру (XVIII в.).
Множества вершин и ребер графа G обозначается соответственно VG и EG. Вершины и ребра графа называются его элементами. Число |VG| вершин графа G называется его порядком и обозначается |G|.
Если |G|=n,|EG|=m, то граф называют (n, m)-графом.
Говорят, что две вершины u и v графа смежны, если множество {u, v} является ребром, и не смежны в противном случае. Если e={u, v}– ребро, то вершины u и v называют его концами. В этой ситуации говорят также, что ребро e соединяет вершины u и v.
Два ребра называются смежными, если они имеют общий конец.
Вершина v и ребро e называются инцидентными, если v является одним из концов ребра e, и не инцидентными в противном случае.
Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Множество всех вершин графа G, смежных с некоторой вершиной v, называется окружением вершины v и обозначается NG(v) или просто N(v).
Графы удобно изображать в виде рисунков (геометрических графов). Геометрический граф в пространстве n-мерном евклидовом пространстве εn
есть множество точек пространства εn
и множество E простых кривых, таких: 1) что каждая замкнутая кривая в E содержит только одну точку v множества V; 2) каждая незамкнутая кривая в E содержит ровно две точки множества V, которые являются ее граничными точками; 3) кривые в E не имеют общих точек кроме точек из множества V. При этом точки множества V соответствуют вершинам графа, а соединяющие пары точек линии – ребрам.
Граф G называется полным, если любые две его вершины смежны. Полный граф порядка n обозначается Kn.
Граф называется вырожденным (пустым), если любые две его вершины не смежны (т.е. у него нет ребер).
Пусть G и H графы, а ϕ: VG→VH – биекция. Если для любых вершин u и v их образы ϕ(u) и ϕ(v) смежны в H тогда и только тогда, когда u и v смежны в G, то эта биекция называется изоморфизмом графов G и H, асами графы G и H – изоморфными. Изоморфные графы будем обозначать G≅H (атакже H G). G).
Если граф G изоморфен геометрическому графу G', то G' называется геометрической реализацией графа G.
Очевидно, что отношение изоморфизма графов является эквивалентностью. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой элементов, но именно это игнорируется при введении понятия "граф".
В некоторых ситуациях все же приходится различать изоморфные графы, и тогда полезно понятие "помеченного графа". Граф порядка n называется помеченным, если его вершинам присвоены некоторые метки, например 1, 2, ..., n. Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин – с множеством чисел {1, 2, ..., n }), определим равенство помеченных графов G и H одного и того же порядка: G=H тогда и только тогда, когда EG =EH.
При необходимости подчеркнуть, что рассматриваемые графы различаются лишь с точностью до изоморфизма, говорят:"абстрактный граф".
Иногда рассмотренное выше понятие "граф" оказывается недостаточным и приходится рассматривать более общие объекты, в которых две вершины могут соединяться более чем одним ребром. Так возникает понятие "мультиграф". Мультиграф – это пара (V, E), где V– непустое множество (вершин), а E– семейство подмножеств множества V(2)
(ребер). Употребление термина "семейство" вместо "множество" означает, что элементы множества V(2)
могут в E повторяться, т.е. допускаются кратные ребра.
Дальнейшее обобщение состоит в том, что кроме кратных ребер допускаются еще петли, т.е. ребра, соединяющую вершину саму с собой. Псевдограф – это пара (V, E), где V– непустое множество (вершин), а E– некоторое семейство неупорядоченных пар (ребер), не обязательно различных.
Изучаются также ориентированные графы. Тогда множество V(2)
заменяется декартовым квадратом V2
, состоящим из упорядоченных пар элементов множества V. Ориентированный граф (или орграф)– это пара (V, A), где V– множество вершин, A– множество ориентированных ребер, которые называются дугами, A V2
. V2
.
Если a=(v1, v2) – дуга, то вершины v1 и v2 называются ее началом и концом соответственно.
Аналогично неориентированному определяется ориентированный мультиграф. Рассматриваются также смешанные графы, у которых есть и дуги, инеориентированные ребра. Заменяя каждую пару (u, v) из множества E, ориентированного (или смешанного) графа G неупорядоченной парой {u, v}, состоящей из тех же элементов uи v, получаем ассоциированный с G=(V, E) графом псевдограф H=(V, E0
). Также говорят, что граф H есть основание графа G.
Орграф называется турниром, если его основание является полным графом.
Для всех рассмотренных обобщений понятия "граф" аналогично вводится понятие изоморфизма как биекции между множествами вершин, сохраняющей смежность, кратности ребер, петли и направления дуг.


Рис.3. Граф Петерсена

Пусть G – граф, w: EG→R+
вещественнозначная функция, ставящая в соответствие каждому ребру e неотрицательное число w(e)– вес ребра e. Пару (G, w) назовем взвешенным графом. Под весом любого подграфа (возможно, несобственного) взвешенного графа будем понимать сумму весов его ребер.
МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ГРАФОВ
Пусть G –помеченный граф порядка n, VG={1, 2, ... , n}. Определим бинарную nЧn-матрицу A=A(G), положив

A(G) называется матрицей смежности графа G. Это симметричная матрица с нулями на диагонали. Число единиц в строке равно степени соответствующей вершины.
Очевидно, что соответствие G→A(G) определяет биекцию множества помеченных графов порядка n на множество бинарных симметричных nЧn-матриц с нулевой диагональю.
 Аналогично определяются матрицы смежности A мульти- и псевдографов: ik равно числу ребер, соединяющих вершины i и k (при этом петля означает два ребра). Аналогично определяются матрицы смежности A мульти- и псевдографов: ik равно числу ребер, соединяющих вершины i и k (при этом петля означает два ребра).
Также определяется матрица смежности A(G) ориентированного графа.
Очевидно, что если A(G)– матрица смежности орграфа G порядка n, то

т.е. число единиц в i-й строке матрицы A(G) равно полустепени исхода i-й вершины, а число единиц в k-м столбце равно полустепени захода k-й вершины.
Теорема. Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов.
Теорема верна также для мультиграфов, псевдографов и орграфов.
Пусть G –(n, m)-граф, VG={1, 2, ... , n} EG={e1, e2,... , em}. Определим бинарную nЧm-матрицу I=I(G) условиями

Матрица I называется матрицей инцидентности графа G. В каждом ее столбце ровно две единицы, равных столбцов нет. Как и выше, соответствие G→I(G) является биекцией множества помеченных (n, m)-графов с занумерованными ребрами на множество nЧm-матриц, удовлетворяющих описанным условиям.
Матрица инцидентности I для орграфа:

Теорема. Графы изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга произвольными перестановками строк и столбцов.
Теорема верна также для мультиграфов, псевдографов и орграфов.
Свойства матриц смежности и инцидентности:
1) Сумма элементов матрицы A(G), где G=(V, E)– мультиграф, V={v1, v2, ..., vn}, по i-йстроке (или по i-му столбцу) равна δ(vi). 2) Сумма элементов матрицы A(G), где G=(V, E)– ориентированный псевдограф,
V={v1, v2, ... , vn}, по i-йстроке и по i-му столбцу соответственно равны δ(vi), δ(vi).
3) Пусть G– ориентированный мультиграф с непустым множеством дуг. Тогда: а) сумма строк матрицы I(G) является нулевой строкой; б) любая строка матрицы I(G) является линейной комбинацией остальных строк; в) ранг матрицы I(G) не превосходит n–1; г) для любого контура матрицы Gсумма столбцов матрицы I(G), соответст-вующих дугам, входящим в этот контур, равна нулевому столбцу.
4) Пусть G– мультиграф с непустым множеством ребер. Тогда при покоординат-ном сложении по модулю 2: а) сумма строк матрицы I(G) является нулевой строкой; б) любая строка матрицы I(G) является суммой остальных строк; в) для любого цикла в Gсумма столбцов матрицы I(G), соответствующих реб-рам, входящим в этот цикл, равна нулевому столбцу.
ОПЕРАЦИИ НАД ГРАФАМИ
Граф H называется подграфом графа G, если VH VG, EH VG, EH EG. Если H – под-граф графа G, то говорят, что H содержится в G. Подграф называется собственным, если он отличен от самого графа. EG. Если H – под-граф графа G, то говорят, что H содержится в G. Подграф называется собственным, если он отличен от самого графа.
Подграф H называется остовным подграфом графа G, если VH =VG.
Если множество вершин подграфа H есть U, а множество его ребер совпадает с множеством всех ребер графа G, оба конца которых принадлежат U, то H называется подграфом, порожденным множеством вершин U, и обозначается G(U).
Если множество ребер подграфа H есть E' EG, а множество его вершин совпадает с множеством всех концов ребер из E' вершин графа G, то подграф H называется подграфом, порожденным множеством ребер E' и обозначается G(E'). EG, а множество его вершин совпадает с множеством всех концов ребер из E' вершин графа G, то подграф H называется подграфом, порожденным множеством ребер E' и обозначается G(E').
Пусть v – вершина графа G. Тогда операцию построения графа H=G–v называют удалением вершины v. Построенный в результате этой операции граф H содержит все ребра множества ЕG кроме инцидентных вершине v, а VH =VG\{v}.
Пусть e – ребро графа G. Тогда операцию построения графа H=G–e называют удалением ребра e. Построенный в результате этой операции граф H содержит все вершины графа G, а EH =EG\{e}.
Удаление вершины или ребра, а также переход к подграфу – это операции, с помощью которых можно из имеющегося графа получать другие графы с мень-шим числом элементов.
Рассмотрим теперь операции, позволяющие получать из имеющихся графов графы с большим числом элементов.
Если вершины u и v графа G=(VG, EG) не смежны, то говорят, что граф H=(VH, EH) получен из графа G добавлением ребра e={u, v}, если VH =VG и EH = EG{e}, то пишут H=G+e.
Граф H называется объединением (или наложением) графов F и G, если H =VF∩VG и EH =EF∩EG. В этой ситуации пишут H=F∩G. Объединение F∩G называется дизъюнктивным, если VF
∩ VG
=∅. Аналогично определяются объединение и дизъюнктивное объединение любого множества графов, причем в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.
Пусть G1=(V1, E1) и G2=(V2, E2). Тогда произведением графов (обозначается G1ЧG2) называется такой граф G, для которого VG =V1ЧV2– декартово произведе-ние множеств вершин исходных графов, а EG определяется следующим образом: вершины (u1, u2) и (v1, v2) смежны в графе G тогда и только тогда, когда u1=v1, а u2 и v2 смежны в G2, или u2=v2, а u1 и v1 смежны в G1
МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ
Чередующаяся последовательность v1, e1, v2, e2, ... , en, vn+1 вершин и ребер графа такая, что ei =vivi+1 (i=1, n ), называется маршрутом, соединяющим вершины 1 и vn+1 (или (v1vn+1)-маршрутом). Очевидно, что для задания маршрута в графе достаточно задать последовательность v1, v2, ..., vn+1. его вершин, либо последовательность e1, e2,... , en его ребер.
Вершина v называется достижимой из вершины u, если существует (u, v)-маршрут. Любая вершина считается достижимой из себя самой.
Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Маршрут (1) называется циклическим, если v1=vn+1. Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом. Число ребер в маршруте называется его длиной. Цикл длины 3 часто называют треугольником. Длина всякого цикла не менее трех, если речь идет о простом графе, поскольку в таком графе нет петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
Свойства маршрутов, цепей и циклов:
1) Всякий незамкнутый (u, v)-маршрут, содержит в себе простую (u, v)-цепь. В частности, любая (u, v)-цепь, содержит в себе простую (u, v)-цепь. Причем, если (u, v)-маршрут содержит в себе вершину w (w≠u и w≠v), то в общем случае, простая (u, v)-цепь может не содержать в себе вершину w.
2) Всякий непростой цикл можно разбить на два или более простых. Причем для замкнутого маршрута такое утверждение не верно.
3) Всякая непростая (u, v)-цепь, может быть разбита на простую (u, v)-цепь и один или более простых циклов. Причем для незамкнутого маршрута такое утверждение не верно.
4) Для любых трех вершин u, w, v из существования (u, w)-цепи их и (w, v)-цепи, следует существование (u, v)-цепи. Причем может не существовать (u, v)-цепи, содержащей вершину w.
5) Объединение двух несовпадающих простых (u, v)-цепей содержит простой цикл. 6) Если граф содержит 2 несовпадающих цикла с общим ребром e, то после удаления этого ребра граф по-прежнему содержит цикл.
Если два графа изоморфны:
1) то они одного порядка;
2) у них одинаковое количество ребер;
3) для произвольного i,0≤i≤n–1, (n – порядок графов) количество вершин степени i, у обоих графов одинаковое;
4) у них совпадают обхваты;
5) у них одинаковое количество простых циклов минимальной длины (по количеству ребер).
Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Очевидно, что для связности графа необходимо и достаточно, чтобы в нем для какой-либо фиксированной вершины u и каждой другой вершины v существовал (u, v)-маршрут.
Теорема. Граф G=(V,E) связен тогда и только тогда, когда множество его вершин нельзя разбить на два непустых подмножества V1 и V2 так, чтобы обе граничные точки каждого ребра находились в одном и том же множестве.
Всякий максимальный связный подграф графа G называется связной компонентой (или компонентой) графа G. Слово "максимальный" означает максимальный относительно включения, т.е. не содержащийся в связном подграфе с большим числом элементов. Множество вершин связной компоненты называется областью связности.
Для ориентированного графа вводится понятие ориентированного маршр-та – это последовательность вида (1), в которой ei=(vi,vi+1). Аналогом цепи в этой ситуации служить путь (ориентированная цепь). Аналогом цикла служит контур (ориентированный цикл).
Орграф называется сильносвязным, если любые две его вершины достижимы друг из друга. Орграф называется одностороннесвязным, если для любой пары его вершин по меньшей мере одна достижима из другой. Орграф называется сла-босвязным, если любые две вершины его основания соединены маршрутом. Орг-раф называется несвязным, если его основание несвязный псевдограф.
Теорема. Орграф является сильносвязным тогда и только тогда, когда в нем есть остовной циклический маршрут.
Необходимость. Пусть G – сильносвязный орграф и T=(v0, x1, v1,..., xn, v0) – его циклический маршрут, проходящий через максимально возможное число вершин. Если этот маршрут не является остовным, то возьмем вне его вершину v. Так как G – сильносвязный орграф, то существуют маршруты T1=(v0, y1, ..., v), T2=(v, z1, ..., v0). Но тогда циклический маршрут T’=(v0, x1, v1, ..., xn, v0, y1, ..., v, z1, ..., v0) содержит большее число вершин, чем T, что противоречит выбору маршру-та T. Следовательно, T – остовной маршрут.
Достаточность. Пусть u и v – две произвольные вершины орграфа G, а T=(v0, x, ..., v, y, ..., u, z, ..., v0) – циклический маршрут. Тогда u достижима из v спомо-щью маршрута (v, y, ..., u)– части маршрута T,– а v из u – с помощью маршрута (u, z,..., v0, x, ..., v).3
Теорема. Орграф является одностороннесвязным тогда и только тогда, когда в нем есть остовной маршрут.
Теорема. Орграф является слабосвязным тогда и только тогда, когда в его основание есть связный псевдограф.
Сильносвязной компонентой орграфа называется его максимальный относи-тельно включения сильносвязный подграф
МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГРАФА
Пусть G– связный граф, а uи v– две его несовпадающие вершины. Длина кратчайшего (u, v)-маршрута называется расстоянием между вершинами uи vи обозначается d(u, v). Положим d(u, u)=0. Очевидно, что введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:
1. d(u, v)≥0;
2. d(u, v)=0 тогда и только тогда, когда u=v;
3. d(u, v)=d(v, u);
4. d(u, v)+ d(v, w)=d(u, w)(неравенство треугольника).
Для фиксированной вершины u величина e(u)=max в (uv)называется эксцентриситетом вершины u. Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается через d(G). Тем самым
dG =max e(u)
Вершина v называется периферийной, если e(v)=d(G). Простая цепь длины d(G), расстояние между концами которой равно d(G), называется диаметральной цепью.
Минимальный из эксцентриситетов вершин связного графа называется его радиусом и обозначается через r(G).
Очевидно, что радиус графа не больше его диаметра.

Вершина v называется центральной, если e(v)=r(G). Множество всех центральных вершин графа называется его центром. Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин. Например, центр простой цепи Pn при четном числе вершин n состоит ровно из двух вершин, а при нечетном – из одной; для цикла же Cn все вершины являются центральными.
Задача нахождения центральных вершин графа постоянно возникает в практической деятельности людей. Пусть, например, граф представляет сеть дорог, т.е. вершины его соответствуют отдельным населенным пунктам, а ребра – дорогам между ними. Требуется оптимально разместить больницы, магазины. В подобных ситуациях критерий оптимальности часто заключается в оптимизации «наихудшего» случая, т.е. в минимизации расстояния от места обслуживания до наиболее удаленного пункта. Следовательно, местами размещения должны быть центральные вершины графа.
Реальные задачи (их называют минимаксными задачами размещения) отличаются от идеальной тем, что приходится ещё учитывать другие обстоятельства – фактические расстояния между отдельными пунктами, стоимость, время проезда и прочее. Для того чтобы учесть это, используют взвешенные графы.
ПРИЛОЖЕНИЕ ТЕОРИИ ГРАФОВ В РАЗЛИЧНЫХ ОБЛАСТЯХ НАУКИ И ТЕХНИКИ.
Информация.
Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Химия
Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов, молекулы которых задаются формулой:
Cn
H2n
+2
Все атомы углеводорода четырехвалентны, все атомы водорода одновалентны. Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа.
Электротехника.
Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
ПРАКТИЧЕСКАЯ ЧАСТЬ
a)

Матрица смежности:

Матрица инцидентности:

Матрица расстояний:
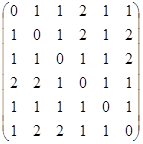
Эксцентриситеты вершин:
e(x1
)=2
e(x2
)=2
e(x3
)=2
e(x4
)=2
e(x5
)=1
e(x6
)=2
Передаточные числа вершин:
p(x1
)=6
p(x2
)=7
p(x3
)=6
p(x4
)=7
p(x5
)=5
p(x6
)=7
Диаметр графа равен 2, радиус – 1. Центр графа находится в вершине X5
. Медианы графа: x2
, x4
, x6
.
б)
Матрица смежности:

Матрица инцидентности:

Матрица расстояний:

Эксцентриситеты вершин:
e(x1
)=2
e(x2
)=2
e(x3
)=2
e(x4
)=1
e(x5
)=2
Передаточные числа вершин:
p(x1
)=5
p(x2
)=5
p(x3
)=5
p(x4
)=4
p(x5
)=5
Диаметр графа равен 2, радиус – 1. Центр графа находится в вершине X4
. Медианы графа: x1
, x2
, x3
, x5
.
ЛИСТИНГ ПРОГРАММЫ
usescrt;
var
A:array[1..100,1..100] of byte;
E,P:array[1..100] of byte;
n,i,j,m,d,r:byte;
begin
clrscr;
writeln('Enter quantity of tops the column and his matrix of a distance.');
readln(n);
writeln;
for j:=1 to n do
for i:=1 to n do
readln(A[i,j]);
clrscr;
for j:=1 to n do
for i:=1 to n do
if i=n
then writeln(A[i,j])
else write(A[i,j],' ');
writeln;
writeln;
for j:=1 to n do
begin
m:=A[1,j];
for i:=1 to n do
begin
if m<A[i,j]
then m:=A[i,j];
end;
E[j]:=m;
end;
for j:=1 to n do
for i:=1 to n do
P[j]:=P[j]+A[i,j];
d:=E[1];
for i:=1 to n do
if d<E[i]
then d:=E[i];
r:=E[1];
for i:=1 to n do
if r>E[i]
then r:=E[i];
for j:=1 to n do
writeln('e(x',j,')=',E[j]);
writeln;
for j:=1 to n do
writeln('p(x',j,')=',P[j]);
writeln;
writeln('d(G)=',d);
writeln('r(G)=',r);
writeln;
writeln('The centers the column:');
for i:=1 to n do
if r=E[i]
then write('x',i,' ');
writeln;
writeln('Medians the column:');
m:=P[1];
for i:=1 to n do
if m<P[i]
then m:=P[i];
for i:=1 to n do
if m=P[i]
then write('x',i,' ');
readkey;
end.
|