МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КОНТРОЛЬНАЯ РАБОТА
на тему:
«Концептуальные и материальные основы системной методологии принятия решений»
СОДЕРЖАНИЕ
1. Введение…………………………………………………………………….3
2. Основные понятия и определения теории принятия решений………….4
3. Система предпочтений лица, принимающего решения…………………6
4. Методология разработки управленческого решения……………………9
4.1. Методы разработки управленческих решений: аналитические, статистические, математические…………………………………………9
4.2. Методы разработки управленческих решений: активизирующие, эвристические и метод сценариев………………………………………10
4.3. Методы разработки управленческих решений: экспертные методы…………………………………………………………………….11
5. Классификация и типология управленческих решений………………..13
6. Технология и организация разработки решений………………………..14
6.1. Организация процесса разработки решения……………………….14
6.2. Организация выполнения принятых решений……………………..15
6.3. Организация процесса коллективного принятия решений……….16
7. Моделирование процесса разработки решения………………………...18
8. Разновидности математических моделей……………………………….20
8.1. Динамические модели………………………………………………20
8.2. Балансовые модели………………………………………………….20
8.3. Поиск равновесия……………………………………………………20
9. Постановка задачи векторной оптимизации……………………………22
10. Множество Эджворта – Парето………………………………………….24
10.1. Модель многокритериального выбора……………………………24
10.2. Аксиомы разумного выбора……………………………………….24
10.3. Аксиома Парето…………………………………………………….26
10.4. Принцип Эджворта—Парето……………………………………...27
1. ВВЕДЕНИЕ
Дисциплина, изучающая процессы принятия решений и методы, которые используют управленцы, чтобы делать оптимальный выбор в ситуациях с высоким уровнем неопределенности и риска. Она занимается, с одной стороны, описанием того, как на практике решаются проблемные ситуации, а с другой - разработкой стратегий, использование которых обеспечит принятие наилучших решений в будущем.
Теория принятия решений сформировалась на базе научного менеджмента. В области принятия руководящих решений традиционно существовало своеобразное разделение труда, при котором одни - академические ученые - изучали, как следует управлять, а другие - администраторы - осуществляли управление на практике. Однако еще пионеры в области теории управления, такие, как Вудро Вильсон и Леонард Уайт, выступали за создание теории, способной сделать практику руководства государственными учреждениями более рациональной.
Впервые модели теории принятия решений были использованы в исследованиях государственного управления в 1947 г., когда в журнале "Паблик администрейшн ревью" появилась статья Герберта Саймона "Поговорки управления". Саймон утверждал, что принятие решений - это суть процесса управления и что прогресс в области менеджмента можно обеспечить, обучая руководителей методам принятия рациональных решений, а не пытаясь изобрести какие-то идеальные организационные структуры.
Теория принятия решений вышла на первый план в 1960-х гг., благодаря развитию менеджмента, исследований операций, вычислительной техники и системного анализа. Именно эта дисциплина, изучающая создание математических моделей реальности, оказала основное влияние на развитие компьютерного моделирования социальных процессов.
Данная теория используется менеджерами и аналитиками для того, чтобы структурировать описание проблем и оценивать возможные варианты их решения. Так, теория игр, одно из ответвлений этой дисциплины, широко используется экспертами из Госдепартамента США при прогнозировании возможного развития событий на международной арене. Другая дочерняя область - оценка риска - нашла применение в практике регулирующих учреждений, таких, как Агентство по защите окружающей среды, определяющего стандарты экологической безопасности.
2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
В данной работе следует использовать и придерживаться смысла следующих основных понятий: управление, ЛПР, проблема или задача (управления), решение, цель (управления, деятельности), операция (кибернетическая), альтернатива, активные ресурсы, результат, модель, условия (разработки решений).
Обращаю внимание на то, что эти основные понятия следует воспринимать только как термины, а не как строгие определения. Причин тому, как минимум две.
Во-первых, для некоторых категорий ТПР просто нет строгих определений. Во-вторых, любое определение всегда достаточно косвенно, а ТПР — динамическая, бурно развивающаяся наука, которая постоянно пересматривает свой понятийный и методический аппарат. Следовательно, нет необходимости учить наизусть те слова, посредством которых толкуется смысл основных понятий, однако обязательно следует глубоко проникнуться теми мыслями и образами, которые за этими словами стоят, уметь их интерпретировать.
Управление
. Как уже отмечалось, решение проблемы, стоящей перед ЛПР, возможно только путем направления и задействования активных ресурсов для исполнения конкретных заданий или работ. Ничто само по себе не делается. Людям, принимающим участие в операции, нужно указать, где, когда, что и с помощью чего сделать, каковы требования качеству выполняемых заданий или работ, каковы допустимые вариации от намеченных заданий и при каких форс-мажорных обстоятельствах следует принять экстренные меры, каковы эти меры и проч. Все это объединяется одним понятием "управление". Управлять — это значит направлять кого-либо или что-либо к намеченной цели для достижения желаемого результата.
Главное требование к качеству управления — это его непрерывность.
Решение
. Обычно одну и ту же задачу можно решить разными способами. Однако качество исхода операции, т. е. значения ее результатов, зависит не только от качества активных ресурсов и условий их применения, но и от качества способа задействования этих ресурсов в этих условиях. В этой связи в данном случае слово "решение" чаще всего будет интерпретироваться как наилучший способ разрешения проблемы, стоящей перед ЛПР, как наиболее предпочтительный способ достижения намеченной ЛПР цели. Следовательно, значение слова "решение" в нашем случае будет несколько отличаться от того значения, которое ему приписывается, например, в математике, когда говорят о решении математической задачи. В математике правильное решение правильно поставленной задачи всегда одно и то же, независимо от того, кто и в каких условиях эту задачу решает. Математическое решение всегда объективно. В отличие от него решение проблемы — субъективно, так как разные ЛПР могут выбрать разные, понравившиеся именно им способы разрешения проблемы. Да к тому же условия решения проблемы накладывают существенный отпечаток на выбор ЛПР: одно и то же ЛПР в разных условиях может предпочесть в общем случае неодинаковый способ устранения проблемы.
Цель
. Формализованное описание того желаемого состояния, достижение которого отождествляется в сознании ЛПР с решением проблемы или задачи. Цель описывается в виде требуемого результата.
Альтернатива.
Это условное наименование какого-то из возможных (допустимых в соответствии с законами природы и предпочтениями ЛПР) способов достижения цели. Каждая отдельная альтернатива отличается от других способов решения проблемы последовательностью и приемами задействования активных ресурсов, т. е. специфическим набором указаний кому, что, где с помощью чего и к какому сроку сделать.
Активные ресурсы
— это все то, что может быть использовано ЛПР для решения проблемы. Главными из активных ресурсов всегда следует считать людей, время, финансы (деньги) и расходные материалы, имеющиеся в распоряжении ЛПР.
Результат
. Под результатом будем понимать специальную форму описания наиболее важных для ЛПР характеристик исхода операции. При исследовании операции степень предпочтительности (или, наоборот, непредпочтительности) ее результатов представляют в наиболее подходящей для этого шкале: числовой, количественной или качественной.
Условия разработки решений.
Каждая проблема всегда связана с конкретной обстановкой, ситуацией и вполне определенным комплексом условий. Проблема всегда решается в рамках существующего положения вещей. Анализируя тот или иной способ достижения цели, ЛПР должно четко представлять закономерности, связывающие ход и исход операции с принятыми решениями. Совокупность представлений об этих закономерностях, конечно, воспринимается ЛПР в упрощенной, модельной форме. Некоторые из закономерностей удается фиксировать в строго формальном виде.
3. СИСТЕМА ПРЕДПОЧТЕНИЙ ЛИЦА, ПРИНИМАЮЩЕГО РЕШЕНИЯ
Принятие решений в организациях - это чрезвычайно сложный процесс, который сопровождается психологическими, организационными и техническими трудностями. Задачи принятия решений редко формулируются в «чистом» виде, когда четко задано множество альтернатив, имеющих определенные оценки по известным показателям. В этом случае остается лишь сравнить эти альтернативы между собой при помощи какого-либо метода и выбрать среди них наилучшую или удовлетворительную. Однако в реальной жизни все не так просто. Дело в том, что перед тем, как сделать выбор, необходимо провести огромную работу - выполнить диагноз решаемой проблемы, собрать информацию об альтернативах и факторах, влияющих на результаты решений, оценить последствия каждой альтернативы, организовать (если это необходимо) их коллективное обсуждение и решить много других задач. Выполнить весь объем этой работы одному человеку не под силу. Поэтому в принятии решений обычно участвуют разные люди или группы людей, исполняющие в этом процессе определенные роли. Среди них выделяют пять основных ролей:
• владелец проблемы
• лицо, принимающее решение
• активная группа
• эксперт
• аналитик
Владелец проблемы.
В любой реальной задаче выбора существует человек, который отвечает за решение возникшей проблемы. Он называется владельцем проблемы. Можно сказать, что владелец проблемы - это человек, который, по мнению окружающих или своему служебному положению, должен решать проблему и нести ответственность за принятые решения. Эти решения обычно непосредственно влияют на положение и благосостояние владельца проблемы. Например, владельцы всех проблем в организациях - это руководители организаций, которые, однако, могут поручить решение этих проблем другим людям, делегируя им часть своих полномочий.
Лицо, принимающее решение
. Ключевая роль в процессе принятия решений — лицо, принимающее решение (ЛПР), которое далеко не всегда является владельцем проблемы, ЛПР - это индивид или группа людей, которые реально осуществляют выбор и несут ответственность за принятые решения в соответствии со своими полномочиями. Если решение принимается группой людей, то в этом случае можно использовать термин «группа, принимающая решение» (ГПР).
Если говорить о соотношении ролей владельца проблемы и ЛПР, то на практике возможны три различных ситуации:
1. Владелец проблемы и ЛПР - один и тот же человек.
В этом случае владелец проблемы никому не доверяет ее решение, кроме себя самого. Конечно, при этом он может собирать информацию, общаясь со своими подчиненными, советоваться с ними, прибегать к услугам экспертов и аналитиков, но окончательное решение владелец проблемы всегда принимает самостоятельно.
2. Владелец проблемы входит в состав группы, принимающей решение.
В этой ситуации владелец проблемы является лишь одним из нескольких человек, принимающих участие в ее решении. Причем, несмотря на более высокий статус и положение внутри группы, владелец проблемы имеет равные права с другими участниками обсуждения. В этом случае он не может принять решение единолично и соглашается с любым решением, принятым всей группой.
3. Владелец проблемы и ЛПР - разные люди.
Такие ситуации возникают, если владелец проблемы, например руководитель организации, «перекладывает» принятие решений на других людей (своих подчиненных, консультантов, экспертов) и дает им для этого необходимые полномочия. В этом случае владелец проблемы не снимает с себя ответственности, но заранее соглашается с любым решением, которое будет принято другим человеком или группой.
Активные группы
. На принятие решений может сильно влиять позиция активных групп. Активная группа - это группа людей, имеющих общие интересы по отношению к решаемой проблеме. Как правило, роль активной группы исполняют другие организации, которые так или иначе заинтересованы в решении возникшей проблемы. Например, активной группой можно считать общественную организацию по защите окружающей среды, протестующую против решения о строительстве нового промышленного предприятия в экологически чистом районе. Активной группой может быть конкурирующая организация, которая пытается помешать осуществлению ваших планов и предлагает «договориться», т.е. найти компромиссное решение проблемы. Конечно, теоретически ЛПР может исходить только из своих интересов и не обязано учитывать мнение активных групп, но практически такая позиция может привести к обострению конфликта и нежелательным последствиям в будущем. Поэтому разумное ЛПР всегда принимает во внимание интересы активных групп, учитывая их позиции и критерии выбора в процессе принятия решений.
Эксперты
. В процессе принятия решений важную роль играют эксперты - люди, которые профессионально лучше, чем ЛПР, знают отдельные аспекты проблемы и выступают в роли источника информации, необходимой для принятия решения. К экспертам обычно обращаются, чтобы выяснить причины возникшей проблемы, разработать варианты ее решения, оценить каждую альтернативу и сделать прогноз развития событий. Например, принимая решение о разработке нового товара, ЛПР может обратиться за советом к экспертам-маркетологам, которые лучше представляют ситуацию на рынке и могут оценить уровень спроса на этот товар. Принимая решение о вложении денег в ценные бумаги, ЛПР может обратиться за информацией к специалистам фондового рынка, которые оценят ожидаемый доход и риск инвестиций.
Предоставляя необходимую информацию, эксперты высказывают свое субъективное мнение. Однако если эксперт, будучи профессионалом в своем деле, беспристрастно оценивает ситуацию, тощего оценки близки к объективным. При этом всегда следует помнить, что экспертная информация - это не решение, а лишь полезная информация, помогающая принять решение. Принимать решение на основе своих предпочтений может только ЛПР. Эксперты отвечают только за свои рекомендации. В общем случае мнения экспертов и ЛПР могут не совпадать.
Аналитики
. В подготовке сложных решений, имеющих обычно стратегический характер, принимают участие аналитики (или консультанты по принятию решений). Их роль заключается в рациональной организации процесса принятия решений. Аналитики выполняют следующие основные функции:
• оказание помощи ЛПР и владельцу проблемы в правильной постановке задачи;
• выявление ролей и позиций активных групп;
• организация работы с экспертами;
• выявление предпочтений ЛПР;
• разработка и применение методов принятия решений.
Аналитик, в отличие от эксперта, обычно не дает никаких личных оценок, а только помогает ЛПР уяснить свои предпочтения, взвесить все «за» и «против» и прийти к разумному компромиссу.
Важнейшая задача и специфика работы аналитика состоит в изучении и выявлении системы предпочтений ЛПР
. Опытный руководитель, как правило, четко представляет свои цели, сразу уясняет суть проблемы и вырабатывает основные варианты ее решения. Однако результаты многих исследований показывают, что ЛПР без дополнительной аналитической поддержки часто используют упрощённые или противоречивые правила и критерии выбора. Причины такого поведения заключаются не только в индивидуальных особенностях ЛПР, но и в том, что существуют объективные ограничения человеческой системы переработки информации. Именно поэтому возникают многие ошибки и противоречия человека в процессе принятия решений. Чтобы их избежать, можно обратиться к услугам аналитика, который должен помочь ЛПР последовательно и логично выразить свои предпочтения и принять окончательное решение.
Главный инструмент аналитика
- методы принятия решений, которые в хорошем смысле «механизируют» мышление ЛПР и определяют порядок получения и обработки всей необходимой информации. Правильно построенные методы принятия решений позволяют выявить предпочтения ЛПР, сравнить между собой все альтернативы и служат своеобразным усилителем человеческих возможностей.
4. МЕТОДОЛОГИЯ РАЗРАБОТКИ УПРАВЛЕНЧЕСКОГО РЕШЕНИЯ
4.1. Методы разработки управленческих решений: аналитические, статистические, математические
В теории разработки управленческих решений выделяются следующие группы методов: аналитические, статистические, математические, эвристические, активирующие, экспертные, методы сценариев и дерева решений. Каждый метод основан на исследовании специально разработанных моделей, которые периодически проверяются на достоверность, точность и эффективность.
Основная задача каждой модели – упростить процесс разработки решения. Точность определяется соответствием моделируемых процедур и операций при разработке решений реальным процессам.
Метод аналитических зависимостей
предусматривает использование формул, графиков, диаграмм, логических соотношений, которые являются типовыми, объективно существующими и выработанными теорией и практикой в течение многих лет. Каждый руководитель должен знать кривые спроса и предложения, зависимость стиля управления от характеристик организации, качества решений от полноты информации и т.д. Часть закономерностей руководители отыскивают сами методом проб и ошибок, и это уже их интеллектуальная собственность. Основу аналитического метода составляет наблюдение, обобщение, анализ и синтез, абстрагирование, формализация, теория вероятности и математическая статистика, теория массового обслуживания.
Статистические методы
основаны на использовании информации о прошлом удачном опыте ряда организаций в какой-либо сфере деятельности. Данные методы реализуются путем сбора, обработки и анализа статистических материалов.
Статистические методы на стадии разработки управленческого решения
Статистические методы на стадии выбора управленческого решения
 Организация Организация
|
|
 Набор практических и возможных результатов Набор практических и возможных результатов
|
Выбор окончательного решения |
Математические методы
лучше всего представлены математическим программированием, которое позволяет рассчитывать лучший вариант решения по критерию оптимальности:
Разработчик решения вводит в компьютер набор ситуаций, подлежащих изменению в соответствии с целью, критерии выбора решений и с помощью математических соотношений либо получает новое решение, либо выбирает подходящее на основе имеющегося набора альтернативных решений.
4.2. Методы разработки управленческих решений: активизирующие, эвристические и метод сценариев
Активизирующие методы
принятия решений делятся на две группы. Методы психологической активизации включают конференции идей, методы мозговой атаки, метод вопросов
. Методы подключения новых интеллектуальных источников включают теоретико-игровые методы, метод наставничества, работу с консультантами
.
Методы психологической активизации созданы в 40-е годы и широко известны во всем мире. Метод конференции идей
основан на стимулировании процесса мышления на уровне подсознания, когда команде численностью до 10 человек на 30 – 40 минут даются варианты решения 2 – 3 взаимосвязанных идей. Если требуется большее количество вариантов идей, применяется интеллектуальный штурм типа мозговой атаки
, когда команда численностью до 10 человек за 30 – 40 минут дает до 100 вариантов идей, от прагматических до еретических. Метод контрольных вопросов
основан на наборе предварительно сформулированных вопросов, ответы на которые формируют новый подход к решениям: что можно убавить или добавить, увеличить и т.д.
Вторая группа активизирующих методов применяется, когда имеется большой объем информации и недостаток времени для ее осмысления. Теоретико-игровые
методы основаны на использовании ПК и материала для поддержки управленческих решений, заменяющих совещания. Метод наставничества
и работа с консультантами
позволяют значительно сократить срок разработки и повысить качество решений.
При разработке управленческих решений для нетиповых, творческих задач применяются эвристические методы. Это новые условия, в которых оказывается руководитель или специалист, когда «не работают» формализованные методы и используются приемы, основанные на опыте Сократа. Суть этих методов – извлечение скрытой в подсознании информации путем стимулирования мышления посредством искусно наводящих вопросов. Существует множество вариантов эвристического приема. Для наглядности приведем один из них – пятнадцатишаговый эвристический прием:
1.Постановка задачи в обобщенном виде.
2. Конкретизация задачи для места и времени.
3. Формулирование обратной задачи, т.е. определение того, что должно быть в конце.
4. Подключение внешних структур.
5. Оценивание и критика внешних структур.
6. Поиск условий и факторов решения проблемы.
7. Что получилось при пересмотре от конца к началу?
8. Сближение с целью.
9. Составление модели.
10. Поиск аналогичных решений.
11. Рассмотрение модели с различных сторон.
12. Возвращение к условиям задачи.
13. Предположение конфликта.
14. Какие еще есть идеи?
15. К чему приведет суть решения, что придется переструктурировать?
Заключение.
В случае большого размера организации и необходимости решать стратегические задачи используется метод сценариев. Суть его состоит в представлении задачи в виде многообразного ее прохождения через ситуации, конфликты, неудовольствия и прогноз возможных результатов решения как эпилога в сценарии. Сценарий обсуждается на совещании заинтересованных в его реализации лиц.
4.3. Методы разработки управленческих решений: экспертные методы
Экспертные методы основаны на совокупном мнении специалистов чаще в пересекающихся областях деятельности: социологии, психологии, математике, логике и т.д. Основные условия применения экспертных методов следующие:
1. Наличие квалифицированных в данной области специалистов для формирования экспертной комиссии;
2. Принятие условия, что решения, принимаемые комиссией, являются безусловными для участников, представивших на оценку свой вариант решения.
Основные направления принятия экспертных оценок:
а) определение целей и выбор приоритетности на дереве целей;
б) составление экспертного прогноза по возможному развитию ситуаций;
в) участие в составлении рейтинговых оценок;
г) нахождение наиболее важного критерия для оценки эффективности принимаемых решений;
д) принятие коллективных решений методом Дельфи, мозговых штурмов и др., где требуется заключение экспертов.
В настоящее время разработано несколько приемов выработки экспертных оценок.
5. КЛАССИФИКАЦИЯ И ТИПОЛОГИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
Для совершенствования разработки управленческих решений используется классификация решений. Чаще всего на практике встречаются следующие группы управленческих решений: по функциональной направленности – планирующие, организующие, координирующие, контролирующие; по источнику возникновения – ситуационные, по предписанию, программные, инициативные; по организации разработки – индивидуальные, коллегиальные, коллективные; по направлению воздействия – внутренние и внешние; по времени действия – стратегические, тактические, оперативные; по сфере действия – экономические, социальные, организационные, научные; по масштабу воздействия – комплексные и частные; по способу фиксации – письменные, на электронных носителях, устные; по числу критериев – одно- и многокритериальные; по методу переработки информации – алгоритмические и эвристические; по глубине воздействия – одно- и многоуровневые; по характеру реализации – уравновешенные, импульсивные, инертные, рискованные, осторожные; по форме представления – указание, акт, протокол, инструкция, договор, соглашение, план, контракт, оферта, акцепт, положение, правило, модель.
Определенный интерес представляет типология управленческих решений, когда все их многообразие можно условно объединить в три типа в зависимости от степени формализации проблемы, творческого вклада руководителя в разработку решения и степени стереотипности ситуации.
В зависимости от степени формализации выделяются следующие типы решений:
- хорошо структурированные, когда зависимости между элементами ситуации численно определимы;
- слабоструктурированные, содержащие как количественные, так и качественные элементы;
- неструктурированные, когда количественные зависимости неизвестны.
В зависимости от творческого вклада руководителя в разработку решений различаются:
- рутинные решения, принимаемые по стандартной программе;
- селективные решения, когда известно число возможных вариантов ответов, задача руководителя – сделать правильный выбор;
- адаптационные, рассчитанные на непредусмотренные трудности и требующие личной инициативы и творчества;
- инновационные решения, необходимые для решения сложных проблем.
С учетом стереотипности ситуаций принято выделять программируемые (стандартные) и непрограммируемые решения, принимаемые в новых ситуациях.
Знание типологии управленческих решений помогает руководителю правильно выбрать технологию решения проблемы.
6. ТЕХНОЛОГИЯ И ОРГАНИЗАЦИЯ РАЗРАБОТКИ РЕШЕНИЙ
6.1. Организация процесса разработки решения
Теория и практика управления дает следующие рекомендации по организации процесса разработки управленческих решений.
Основные принципиальные моменты следующие:
- соблюдение принципа иерархии, координация усилий, контроль за соподчиненностью по уровням при разработке решений;
- создание целевых групп на временной основе для использования знаний и опыта каждого, кто может участвовать в процессе разработки решений;
- формирование инструктивных материалов по проведению формальных процедур при разработке управленческих решений, не усложняя ими процессы и процедуры принятия инновационных управленческих решений;
- создание системы планирования процесса разработки решений, включающей разработку таких элементов плана, как сроки, ресурсы, ответственные за этапы, разделы, вопросы.
Функции, выполняемые руководителем по организации разработки решения, заключаются в следующем:
- управление общим процессом выработки решений;
- определение сущности задачи, участие в ее конкретизации, в выборе критериев оценки решений;
- окончательный выбор решения;
- организация внедрения управленческого решения.
Ряд организаций ведет системный специальный учет управленческих проблемных ситуаций и способов их разрешения. Для этого многие организации формируют картотеки, состоящие из следующих карточек:
- карточки проблемной ситуации (характеристика ситуации, главная цель принятия решения, ограничения на принятие решения);
- технологической карты принятия решения, в которой отмечена логическая последовательность принятия решения, названы основные альтернативные решения;
- карточки решения, в которой после его принятия отмечается: причина возникновения проблемы, возможные концептуальные последствия непринятия решения, лицо, принимающее решение, вовлеченные лица, организации, первичная информация, необходимая для принятия решения, лицо, ответственное за исполнение решения.
В работе Л. Зайверта «Ваше время – в ваших руках» даются следующие рекомендации:
Задачи А
Весьма важные задачи.
Составляют 15% всех
задач и 65% общей их
значимости |
|
Задачи В
Важные задачи.
Составляют 20% всех
задач и 20% значимости |
|
Задачи С
Менее важные задачи.
Составляют 65% всех
задач и 15% значимости |
|
 |
 |
 |
Выполнять руководителю,
не перепоручать |
Частично поручать |
Перепоручать, сокращать, выдерживать |
6.2. Организация выполнения принятых решений
Организация выполнения управленческих решений – это комплекс работ по их эффективному внедрению. Теорией и практикой разработаны принципиальные моменты, которые надо учитывать при выполнении принятых решений.
Прежде всего, необходимо расчленить общую программу действий на отдельные участки для соисполнителей. Затем надо довести задание до исполнителей и подготовить их к исполнению задания. Наконец, важную роль играет побуждение руководителей к его добросовестному исполнению. Формы реализации решений, т.е. доведение их до исполнителей, – это предписание, деловая беседа, убеждение, разъяснение, принуждение, наставление, сообщение, личный пример, обучение, совет, деловая игра, совещание, заседание и др.
Каждое отдельное задание руководитель «проигрывает» сам, ставя себя на место исполнителя в соответствующие условия. Во избежание неэффективной организации выполнения принятых решений рекомендуется придерживаться следующих рекомендаций:
1) обеспечивать соответствие каждой задачи деловым и психологическим особенностям исполнителей, для чего необходимо объективно оценивать их опыт и профессионализм;
2) добиваться взаимного доверия исполнителей общей задачи, организационными мерами обеспечивать однородность мотивов; система стимулов должна ориентировать исполнителей на качественное выполнение частей во имя цельного замысла;
3) мобилизовать коллектив на выполнение задания, а затем и плана организационно-технических мероприятий по реализации решения.
Основные моменты, которые затрудняют процесс разработки и принятия решения:
- недостаток и необъективность информации;
- ошибки собственного опыта и предпочтений;
- слабые собственные управленческие способности;
- неумение организовать процессы принятия и реализации решений.
Чтобы обеспечить эффективность процесса разработки и принятия решений, надо руководствоваться следующими рекомендациями:
1) люди никогда не берут на себя ответственность добровольно, и этого ждать от них не следует;
2) нельзя пускать на самотек процессы согласования на всех этапах, включая совещания и заседания, во избежание вмешательства в этот процесс возмущающих факторов;
3) никогда нельзя во всем полагаться на память, многие вещи надо фиксировать в записной книжке, ноутбуках;
4) учитывая, что самый высокий уровень навыков принятия решений требуется политикам, стратегам, военным, специалистам делового администрирования, необходимо для достижения этого уровня осваивать и пополнять знания по теории разработки управленческих решений.
6.3. Организация процесса коллективного принятия решений
Эволюция управленческой деятельности в зарубежном менеджменте имеет тенденцию к развитию групповых форм разработки решений. Причиной этому послужили процессы демократизации и повышения сложности решаемых проблем. Процесс коллективной выработки идей в современных западных фирмах осуществляется с помощью специально создаваемых команд, состоящих из групп специалистов различных сфер деятельности. Распространены комитеты как совещательные консультативные группы, кружки качества, целевые команды, комиссии и т.д.
Принятие решений в специально созданной группе приводит к появлению определенной линии поведения исполнителей и руководителей. В любом творческом коллективе, как показывают исследования, около 5% творческих личностей, 25% эрудитов, 20% аналитиков и 50% рядовых исполнителей. Руководители творческих групп характеризуются как демократы, пессимисты, диктаторы или организаторы.
Групповое решение предпочтительнее индивидуального в следующих случаях:
- если по этическим соображениям решение нельзя принимать кулуарно;
- если для принятия решения полезна их независимая экспертная оценка;
- когда руководитель затрудняется сам предложить альтернативные решения в достаточном количестве и т.д.
Исследования показали и негативные факты группового принятия решений, приводящие к появлению конформизма и «группового единомыслия».
Основные признаки приближения такого явления следующие:
- появление излишнего оптимизма и иллюзии независимости коллектива;
- коллективное устремление сметать на пути все возражения, противоположные групповому;
- безусловная вера в принятые коллективом принципы, открытое давление на сопротивляющихся мнению, иллюзия единодушия по принципу подавляющего большинства и т.д.
Во избежание появления «группового единомыслия» руководителю не следует создавать условий, удобных для возникновения таких ситуаций, стараться поощрять в коллективе разные мнения и не глушить голос меньшинства, чаще занимать нейтральную позицию и сохранять беспристрастность.
Любое коллективное творчество основано на индивидуальных мыслительных процессах, разработанные решения совместно оцениваются и сравниваются. Для принятия стратегических решений эффективен метод Дельфи; при необходимости выработать «100 идей за 100 минут» используется мозговой штурм; хорошо «работает» метод контрольных вопросов, конференции идей, коллективного блокнота, ассоциаций, морфологического ящика и другие.
7. МОДЕЛИРОВАНИЕ ПРОЦЕССА РАЗРАБОТКИ РЕШЕНИЯ
Для процедуры разработки управленческого решения руководителю и аппарату управления необходимо осуществить следующие действия:
1. Оформить документацию о начале выполнения работ с указанием конкретного задания, состава персонала и системы его подчинения, времени исполнения решений, промежуточных этапов контроля и размера выделяемых ресурсов.
2. Разработчикам решения разъяснить содержание организационных документов о начале выполнения работ по разработке решения.
3. Разработчикам решения разъяснить их права, ответственность и полномочия.
4. Обсудить с разработчиками неучтенные детали для успешного выполнения работ.
5. Акцентировать внимание на важности задания и значении его качественного исполнения.
6. После окончания разработки решения провести контроль со стороны юриста на соответствие его действующему законодательству и уставным документам организации.
7. Получить заключение о выполнимости вариантов и заключение экспертов об общей и экологической (если требуется) безопасности реализации решения.
Процедуры согласования управленческого решения с вышестоящими органами, заказчиками, клиентами следующие:
1. Оформить документацию на физических и юридических лиц, с которыми необходимо согласовать решение, временные периоды согласования.
2. Документально оформить акт согласования.
Процедуры принятия решения:
1. Документально подтвердить отсутствие в вариантах решения противоречивости.
2. Документально оформить набор критериев для выбора решения: наименования и значения.
3. Документально зафиксировать отклонения параметров решения от запланированных критериев.
4. Документально оформить процедуру принятия решения с указанием даты, ответственных лиц.
Процедуры утверждения решения:
1. Оформить документацию о физических и юридических лицах, у которых нужно утвердить решение.
2. Документально оформить акт утверждения.
Процедуры организации выполнения решения:
1. Оформить документацию о начале реализации решения с указанием необходимых элементов.
2. Разъяснить исполнителю содержание и порядок выполнения задания.
3. Разъяснить исполнителям их права, ответственность и полномочия при выполнении задания.
4. Обсудить с исполнителями неучтенные факторы для успешного выполнения работ.
5. Акцентировать внимание на важности предстоящей работы, выделить средства для реализации решения.
6. Активизировать работу исполнителей по эффективной реализации решения.
7.Осуществлять контроль за ходом реализации задания.
8. Сдать документацию по реализованному решению в архив.
8. РАЗНОВИДНОСТИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
8.1. Динамические модели.
Динамические модели стали развиваться во многом благодаря развитию вычислительной техники, так как связаны с необходимостью решать большое число (сотни) уравнений за короткий промежуток времени. Эти уравнения являются более или менее сложными математическими описаниями того, как функционирует исследуемая система и даются они в форме выражений для “уровней” различных типов, “темп” изменения которых регулируется управляющими функциями. Уравнения для уровней описывают накопление в системе таких, например, величин, как вес, количество энергии, количество организмов, а уравнения для темпов управляют изменением этих уровней во времени. Управляющие функции отражают правила, регулирующие функционирование системы. В динамических моделях часто используются уравнения неразрывности - соотношения между потоками переменной в какую-то часть системы и из нее со скоростью изменения этой переменной.
8.2. Балансовые модели
.
Балансовые модели представляют моделируемый объект как совокупность неких потоков вещества и энергии, баланс которых рассчитывается на каждом шаге моделирования. Являются разновидностью динамических моделей. В настоящее время эти модели получили очень широкое распространение благодаря наглядности и сравнительно простой реализации. Однако применение их возможно лишь при решении, общеметодологических вопросов: баланс каких веществ является наиболее важным для рассмотрения; насколько целесообразно подробно прослеживать потоки данного вещества; как, выразить смену режимов трансформация веществ и т.п.
8.3. Поиск равновесия.
Этот подход основан на постулате о том, что любая большая система может иметь состояние равновесия. Например, в экономических системах это равновесие между спросом и предложением (по Н.Д.Кондратьеву – это равновесие «1-го порядка»), равновесие в структуре цен (равновесие 2-го порядка), равновесие основных капитальных благ» - промышленных изделий, сооружений, квалифицированной рабочей силы, технологий, источников энергии и т.д. (равновесие 3-го порядка).
В экологии может рассматриваться равновесие между определенной численностью хищников и их жертв, между загрязнением окружающей среды и ее способностью к самовосстановлению.
Поиск равновесия очень важен для исследования экономических и экологических систем. При этом следует различать динамическое и статическое равновесие.
Динамическое («подвижное») равновесие предполагает непрерывный обмен веществом и энергией между системой веществ и энергии, поглощаемых и выделяемых системой одинаковы. При динамическом равновесии сохраняется соответствие между частями системы, все размеры которой одновременно меняются.
Статическое равновесие означает сохранение того же соответствия при неизменных размерах (величинах) частей системы и системы в целом. Можно проиллюстрировать поиск равновесия на примере определения состояния насыщения рынка. Для этого было предложено уравнение
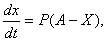
где х – количество товара, t - время, А,Р – константы.
Эта функция описывается «затухающей кривой». Было показано, что она описывает ряд общественных и экономических процессов, например, насыщение рынка книгами по специальным дисциплинам и т.п., если выполняются такие условия, как
- незаменимость товара,
- неизменность цен;
- отсутствие спекулятивных перепродаж;
- приобретение каждым покупателем равного количества;
- отсутствие повторных покупок товара.
Разумеется, это достаточно примитивное уравнение, которое не соответствует подвижному и динамическому равновесию. Для построения более адекватных моделей с равновесием необходимо использование обратных связей
9. ПОСТАНОВКА ЗАДАЧИ ВЕКТОРНОЙ ОПТИМИЗАЦИИ
В реальных задачах выбора наиболее предпочтительного решения, возникающих на практике, как правило, присутствуют несколько критериев оптимальности. Можно привести много примеров, когда требуется найти решение, для которого достигались наилучшие значения сразу по нескольким критериям. Наиболее распространенная задача, которую мы решаем очень часто (не облекая ее в термины оптимизации) - это поиск покупки, которая была как можно качественнее и как можно дешевле.
Задачи выбора некоторого решения из множества допустимых решений с учетом нескольких критериев оптимальности называют многокритериальной задачей оптимизации.
Многокритериальные задачи широко распространены в техническом проектировании, например, задача проектирования компьютера с максимальным быстродействием, максимальным объемом оперативной памяти и минимальным весом или задача проектирования электрического двигателя с максимальной мощностью, максимальным коэффициентом полезного действия, минимальным весом и минимальными затратами электротехнической стали (естественно, при ограничениях на необходимые параметры проектируемых устройств). Реальные многокритериальные управленческие задачи также широко распространены, лозунг экономики СССР 80-х гг. - «максимум качества при минимуме затрат», несмотря на его одиозность, выражал сущность большинства проблем управления.
Под многокритериальной задачей зачастую понимают не собственно вербальное описание задачи, а ее модель, а именно: «многокритериальная задача – математическая модель принятия оптимального решения по нескольким критериям. Эти критерии могут отражать оценки различных качеств объекта или процесса, по поводу которых принимается решение».
Формально многокритериальная задача как модель задается в виде:
 , (9.1) , (9.1)
где в - множество допустимых решений. F(x) – векторная функция векторного аргумента x, которую можно представить как F(x)={f1(x), f2(x), … , fk(x) }, где f1(x), f2(x), … , fk(x) – скалярные функции векторного аргумента x, каждая их которых является математическим выражением одного критерия оптимальности. Так как в данной модели используется векторная целевая функция, ее зачастую называют задачей векторной оптимизации. Очевидно, что задача (9.1) не принадлежит классу задач математического программирования, т.к. модели этого класса задач содержат всегда только одну целевую функцию векторного аргумента.
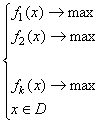
Сущность поставленной задачи состоит в нахождении такого ее допустимого решения, которое в том или ином смысле максимизирует (минимизирует) значения всех целевых функций fi(x), i=1,k. Существование решения, буквально максимизирующего все целевые функции, является редким исключением. (Если вспомнить пример о поиске одновременно очень качественной и очень дешевой покупки, то становится понятным, что нахождение такого решения – редкая удача, но, гораздо более часто, это неразрешимая задача).
Отсюда следует, что принципиальным моментом при решении такого рода задач является предварительная договоренность, а что считать самым предпочтительным решением, т.е. надо договориться об используемом принципе оптимальности. Ранее используемый принцип оптимальности «хорошо то, что доставляет наибольшее (наименьшее) значение имеющемуся единственному критерию оптимальности» в многокритериальных задачах очевидно «не работает».
Задача векторной оптимизации в общем случае не имеет строго математического решения. Для получения того или иного ее решения необходимо использовать дополнительную субъективную информацию специалиста в данной предметной области, которого принято называть лицом принимающим решение (ЛПР), в английском языке - decision maker. Это означает, что при решении задачи разными специалистами с привлечением различных источников информации, скорей всего будут получены различные ответы.
Задачи векторной оптимизации, в настоящее время принято рассматривать в рамках теории принятия решений, основной особенностью задач которой является наличие неопределенности. Эта неопределенность не может быть исключена с помощью различных приемов моделирования и объективных расчетов. В многокритериальных задачах неопределенность состоит в том, что неизвестно, какому критерию отдать предпочтение и в какой степени. Для устранения этой неопределенности необходимо, во-первых, сформулировать специальный принцип оптимальности, а также привлечь дополнительную субъективную информацию ЛПР, основанную на его опыте и интуиции.
10. МНОЖЕСТВО ЭДЖВОРТА – ПАРЕТО
10.1. Модель многокритериального выбора
Пусть имеются шкалы (непустые абстрактные множества) Y1 ,Y2 ,...,Ym
( m > 1). Они могут быть как конечными, так и бесконечными. На каждом множестве Yi будем считать заданным некоторое бинарное отношение fi, обладающее свойствами иррефлексивности, транзитивности и слабой связности i = 1,2,...,m. Слабая связность отношения fi означает, что для любых двух элементов s,t Yi, s ≠ t , выполняется либо соотношение s
fi t
, либо соотношениеt
fi s
. Отношениеfi
можно трактовать как отношение строгого предпочтения на множестве значений i -го критерия. Оно асимметрично.
Yi, s ≠ t , выполняется либо соотношение s
fi t
, либо соотношениеt
fi s
. Отношениеfi
можно трактовать как отношение строгого предпочтения на множестве значений i -го критерия. Оно асимметрично.
Введем в рассмотрение декартово произведение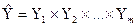 . Его элементы называют вариантами. Выбор осуществляется из множества
. Его элементы называют вариантами. Выбор осуществляется из множества  в соответствии с определенной функцией выбора; он представляет собой некоторое подмножество множества A и обозначается далее Sel (A). Напомним, что однозначное отображение
в соответствии с определенной функцией выбора; он представляет собой некоторое подмножество множества A и обозначается далее Sel (A). Напомним, что однозначное отображение  называют функцией выбора, если для любого подмножества
называют функцией выбора, если для любого подмножества  , выполняется включение
, выполняется включение  . По определению функции выбора в случае y′≠y′′ одновременно равенства Sel ({y′, y′′}) ={y′}, Sel ({y′, y′′})={y′′} выполняться не могут.
. По определению функции выбора в случае y′≠y′′ одновременно равенства Sel ({y′, y′′}) ={y′}, Sel ({y′, y′′})={y′′} выполняться не могут.
Заметим, что в общем случае для некоторых A возможно равенство  , которое означает, что выбор является пустым. Другими словами, при предъявлении некоторых A вместо реального выбора из этого множества может иметь место «отказ от выбора».
, которое означает, что выбор является пустым. Другими словами, при предъявлении некоторых A вместо реального выбора из этого множества может иметь место «отказ от выбора».
10.2. Аксиомы разумного выбора
Сформулируем определенные требования к функциям выбора, которые можно назвать аксиомами разумного выбора. Как будет показано в следующих разделах, при выполнении этих требований всегда имеет место принцип Эджворта—Парето. Тем самым, аксиомы разумного выбора выделяют определенный достаточно широкий класс многокритериальных задач, в которых успешный выбор обязательно должен осуществляться в пределах множества Парето. Это означает, для указанного класса задач оптимальность по Парето является необходимым условием приемлемости выбираемых вариантов. Тогда как за пределами этого класса (т. е. тогда, когда хотя бы одна из аксиом разумного выбора нарушается) наилучший выбор не обязан быть парето-оптимальным.
Аксиома 1
. Для любых трех вариантов y′, y′′, y′′′ , удовлетворяющих равенствам Sel ({y′, y′′}) = {y′} и Sel ({y′′, y′′′}) = {y′′}, всегда выполняется Sel ({y′, y′′′}) = {y′}.
, удовлетворяющих равенствам Sel ({y′, y′′}) = {y′} и Sel ({y′′, y′′′}) = {y′′}, всегда выполняется Sel ({y′, y′′′}) = {y′}.
Аксиома 1 устанавливает определенную естественную последовательность (логичность) в ходе осуществления выбора. Это свойство на языке бинарных отношений предпочтения носит название транзитивности.
Следует однако заметить, что при определенных обстоятельствах поведение человека, осуществляющего выбор, может оказаться несовместимым с аксиомой 1. Дело в том, что человек не всегда ведет себя разумно! Специалистам в области принятия решений давно известны случаи нарушения некоторыми индивидами свойства транзитивности, когда из трех предлагаемых решений первое предпочитается второму, второе предпочитается третьему, но при выборе из первого и третьего предпочтение отдается не первому, а третьему решению.
Аксиома 2
. Для любых двух вариантов y′, y′′ , таких, что
, таких, что
y′ = ( ),
),
y′′ = ( ),
), 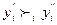 ,
,
всегда выполняется равенство
Sel ({y′, y′′}) = {y′}, i =1,2, ...,m .
Согласно аксиоме 2 вариант (и только этот вариант), являющийся более предпочтительным по какой-то одной компоненте по сравнению с другим вариантом при прочих равных условиях (т. е. при совпадении всех остальных компонент) обязательно будет выбран из данной пары.
Определение 1
. Условимся говорить, что i-й критерий независим по предпочтению от остальных критериев, если из выполнения для некоторых двух вариантов  и
и 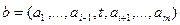 , s ≠ t , принадлежащих множеству
, s ≠ t , принадлежащих множеству  и связанных соотношением Sel ({a,b}) = {a}, всегда следует равенство Sel ({a′,b′}) = {a′}, в котором варианты
и связанных соотношением Sel ({a,b}) = {a}, всегда следует равенство Sel ({a′,b′}) = {a′}, в котором варианты  и
и 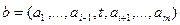 образованы с помощью произвольных компонент
образованы с помощью произвольных компонент  , удовлетворяющих включению a′,b′
, удовлетворяющих включению a′,b′ .
.
Утверждение.
Если выполнена аксиома 2, то каждый критерий независим по предпочтению от остальных.
Доказательство
. Зафиксируем произвольный номер i {1,2,...,m} .
{1,2,...,m} .
Пусть по условию для некоторых a,b имеет место равенство Sel ({a,b}) = {a} . Благодаря s ≠ t и слабой связности отношения
имеет место равенство Sel ({a,b}) = {a} . Благодаря s ≠ t и слабой связности отношения  , могут иметь место лишь два случая: t
, могут иметь место лишь два случая: t  s или s
s или s t . Первый из них на самом деле невозможен, так как тогда на основании аксиомы 2 выполнялось бы равенство Sel ({a,b}) = {b} , противоречащее условиям Sel ({a,b}) = {a} и a ≠ b . Во втором случае согласно той же аксиоме 2 равенство Sel ({a′,b′}) = {a′} всегда будет выполнено для всех a′,b′
t . Первый из них на самом деле невозможен, так как тогда на основании аксиомы 2 выполнялось бы равенство Sel ({a,b}) = {b} , противоречащее условиям Sel ({a,b}) = {a} и a ≠ b . Во втором случае согласно той же аксиоме 2 равенство Sel ({a′,b′}) = {a′} всегда будет выполнено для всех a′,b′ из определения 1. Утверждение доказано.
из определения 1. Утверждение доказано.
Аксиомы 1−2 накладывают определенные ограничения на функцию выбора в пределах всего множества  , тогда как следующая аксиома относится к выбору из фиксированного подмножества вариантов.
, тогда как следующая аксиома относится к выбору из фиксированного подмножества вариантов.
Зафиксируем некоторое непустое подмножество  , которое будем называть множеством возможных вариантов
.
, которое будем называть множеством возможных вариантов
.
Всюду далее будем считать, что Sel (Y) ≠ 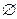 . Это означает, что какой-
. Это означает, что какой-
то выбор из множества возможных вариантов Y обязательно должен быть
произведен. При этом выбранными могут оказаться один, несколько или же бесконечное число вариантов.
Аксиома 3
. Для любой пары вариантов y′,y′′ Y , y′ ≠ y′′, таких, что Sel ({y′, y′′}) = {y′} , всегда выполняется y′′
Y , y′ ≠ y′′, таких, что Sel ({y′, y′′}) = {y′} , всегда выполняется y′′ Sel(Y) .
Sel(Y) .
Аксиома 3 требует, чтобы вариант, не выбираемый в некоторой паре, не выбирался и из всего множества возможных вариантов Y .
Эта аксиома определенным образом связана с обратным условием Кондорсе [Айзерман и др. 1990], которое формулируется следующим образом:
y′′ Sel (Y)
Sel (Y)  y′′
y′′ Sel ({y′, y′′}) для всех y ′
Sel ({y′, y′′}) для всех y ′ Y.
Y.
Заметим, что включение y′′ Sel ({y′, y′′}) в общем случае не исключает возможности y′
Sel ({y′, y′′}) в общем случае не исключает возможности y′ Sel ({y′, y′′}).
Sel ({y′, y′′}).
Очевидно, обратное условие Кондорсе для множества Y может быть
переписано в эквивалентной форме:
y′′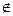 Sel ({y′, y′′}) для некоторого y′
Sel ({y′, y′′}) для некоторого y′ Y
Y  y′′
y′′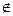 Sel (Y), (1)
Sel (Y), (1)
где y′′ Y . Сравнивая аксиому 3 с импликацией (1) и принимая во внимание, что
Y . Сравнивая аксиому 3 с импликацией (1) и принимая во внимание, что
Sel ({y′, y′′}) = {y′}, y′ ≠ y′′  y′′
y′′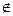 Sel ({y′, y′′}),
Sel ({y′, y′′}),
можно сделать вывод о том, что выполнение обратного условия Кондорсе влечет справедливость аксиомы 3, но не наоборот.
10.3. Аксиома Парето
Прежде чем формулировать аксиому Парето, введем следующее определение.
Определение 2
. Бинарное отношение  , заданное на декартовом произведении
, заданное на декартовом произведении  при помощи эквивалентности
при помощи эквивалентности
y′  y′′
y′′  [(
[(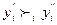 или
или  ) для всех i =1,2, ...,m] и y′ ≠ y′′ ,
) для всех i =1,2, ...,m] и y′ ≠ y′′ ,
где  ,
,  , будем называть отношением Парето.
, будем называть отношением Парето.
Аксиома Парето
. Для двух любых вариантов y′,y′′ Y, связанных соотношением y′
Y, связанных соотношением y′  y′′ , всегда имеет место равенство
y′′ , всегда имеет место равенство
Sel ({y′, y′′}) = {y′}.
Как видим, аксиома Парето выражает собой определенное правило выбора из двух вариантов, находящихся друг с другом в отношении Парето. Согласно этому правилу если один вариант является более предпочтительным по сравнению с другим по какому-то одному или нескольким компонентам, то при прочих равных условиях (т. е. при совпадении всех остальных компонент данных двух вариантов) выбранным должен оказаться именно тот вариант, у которого имеются более предпочтительные компоненты. С точки зрения здравого смысла такое правило представляется вполне естественным.
Очевидно, из аксиомы Парето следует выполнение аксиомы 1, но не наоборот.
Лемма
. Аксиома Парето является следствием аксиом 1 и 2.
Доказательство
. Предположим, что для некоторых произвольно выбранных двух вариантов y′,y′′ Y выполняется соотношение y′
Y выполняется соотношение y′  y′′ . Не уменьшая общности последующего рассмотрения, предположим, что выполнение y′
y′′ . Не уменьшая общности последующего рассмотрения, предположим, что выполнение y′  y′′ означает, что для некоторого 1
y′′ означает, что для некоторого 1 l
l  m справедливо
m справедливо
 .
.
Благодаря аксиоме 2 имеем равенства:
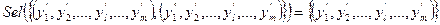 ,
,
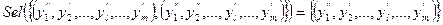 ,
,
………………………
 .
.
Отсюда, последовательно применяя аксиому 1, получаем
 . (2)
. (2)
А так как  , k = l
+1,...,m, то (2) принимает вид требуемого равенства Sel ({y′, y′′}) = {y′}.
, k = l
+1,...,m, то (2) принимает вид требуемого равенства Sel ({y′, y′′}) = {y′}.
10.4. Принцип Эджворта—Парето
Далее понадобятся два понятия, непосредственно связанные с множеством возможных вариантов Y .
Определение 3
. Множество парето-оптимальных вариантов
(множество Парето) обозначается P(Y) и определяется равенством:
P(Y) = {y*  Y| не существует y
Y| не существует y Y, такого, что y
Y, такого, что y y*} .
y*} .
Определение 4
. Множество недоминируемых вариантов
обозначим Ndom(Y)
и определим равенством:
Ndom(Y) = {y* Y| не существует y
Y| не существует y Y, y ≠ y*, такого, что Sel ({y, y*}) = {y}}.
Y, y ≠ y*, такого, что Sel ({y, y*}) = {y}}.
Теорема (принцип Эджворта—Парето)
. Для любой функции выбора Sel(
 ), подчиненной аксиомам 1–3, справедливо включение:
), подчиненной аксиомам 1–3, справедливо включение:
Sel(Y)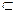 P(Y ) .
P(Y ) .
Доказательство
. Зафиксируем произвольную функцию выбора Sel ( ), удовлетворяющую аксиомам 1–3.
), удовлетворяющую аксиомам 1–3.
Сначала установим справедливость включения:
Z-Sel (Y) 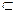 Ndom(Y).
Ndom(Y).
С этой целью произвольно выберем вариант y′′ Sel (Y) и предположим противное: y′′
Sel (Y) и предположим противное: y′′ Ndom(Y). Тогда по определению 4 найдется такой вариант y′
Ndom(Y). Тогда по определению 4 найдется такой вариант y′ Y , что y′ ≠ y′′ и Sel ({y′, y′′}) = {y′}. Благодаря аксиоме 3 последнее равенство влечет y′′
Y , что y′ ≠ y′′ и Sel ({y′, y′′}) = {y′}. Благодаря аксиоме 3 последнее равенство влечет y′′ Sel (Y). Это противоречит начальному допущению y′′
Sel (Y). Это противоречит начальному допущению y′′ Sel (Y). Таким образом, включение (4) доказано.
Sel (Y). Таким образом, включение (4) доказано.
Теперь проверим включение
Ndom (Y)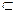 P(Y).
P(Y).
Для этого произвольно выберем вариант y  Ndom (Y). Допустим противное: y
Ndom (Y). Допустим противное: y 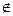 P(Y). Отсюда по определению 3 следует, что найдется такой вариант y′
P(Y). Отсюда по определению 3 следует, что найдется такой вариант y′ Y , для которого верно соотношение y′
Y , для которого верно соотношение y′ y. В условиях доказываемой теоремы благодаря лемме справедлива аксиома Парето. На основании этой аксиомы из соотношения y′
y. В условиях доказываемой теоремы благодаря лемме справедлива аксиома Парето. На основании этой аксиомы из соотношения y′ y вытекает равенство Sel ({y, y′}) = {y′} , причем y ≠ y′. Следовательно, y
y вытекает равенство Sel ({y, y′}) = {y′} , причем y ≠ y′. Следовательно, y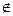 Ndom (Y). Полученное не совместимо с начальным предположением y
Ndom (Y). Полученное не совместимо с начальным предположением y Ndom (Y). Таким образом, включение (5) выполнено. Из (4)–(5) немедленно следует (3).
Ndom (Y). Таким образом, включение (5) выполнено. Из (4)–(5) немедленно следует (3).
Теорема доказана.
Замечание.
Как указано ранее, в (3) считается, что Sel(Y) ≠ 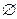 .
.
Теорему 1 можно выразить следующим образом: произвольный выбор из множества возможных вариантов, подчиненный аксиомам 1–3, должен осуществляться в пределах множества Парето.
В целом требования, накладываемые аксиомами 1–3 на характер осуществляемого выбора, можно интерпретировать как разумное поведение лица, принимающего решение (ЛПР) в процессе выбора. Поэтому согласно доказанной теореме принцип Эджворта - Парето всегда выполняется, если поведение ЛПР разумно. А поскольку именно разумное поведение является наиболее распространенным, то этим обстоятельством можно объяснить чрезвычайно широкое и успешное применение «наивного» принципа Эджворта - Парето в принятии решений, теории игр, математической экономике и других областях, когда в любой задаче многокритериального выбора поиск наилучшего решения предлагается ограничить лишь пределами множества Парето.
|