Лекція 9
Лінії передач для інтегральних схем.
В інтегральній електроніці використовуються в основному плоскі лінії.
1. Симетрично – смушкова лінія (ССЛ): вона відкрита, тому має втрати.

2. Не симетрично – смушкова лінія (НСЛ):

3. Мікросмушкова лінія (microstrip line) – МСЛ. Тут ємність дуже велика, енергія сконцентрована. Підкладка з діелектрика 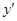 . Лінія двоповерхова – це не дуже зручно. . Лінія двоповерхова – це не дуже зручно.
4. Щілинна лінія (slot line). Вона є одноповерховою:
5. Компланарний хвильовід – все в одній площині.
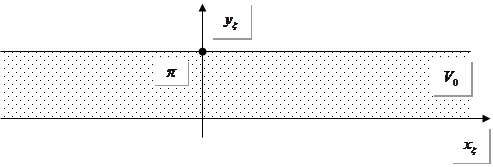
Поля в несиметрично – смушковій лінії.
Складність розв’язання цієї задачі полягає в тому, що граничні умови тут – нерегулярні; не можна покласти, що на поверхні 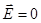 . Використовують наближені методи; зокрема конформних відображень. . Використовують наближені методи; зокрема конформних відображень.

Наближення
: Існує Т – хвиля (нехтуємо випромінюванням). Використаємо симетрію задачі. Цікавимося випромінюванням на краю.
 Треба розв’язати задачу: знайти розв’язок рівняння Лапласа у верхній площині з напівнескінченним розрізом. Використаємо метод конформних відображень: тут застосовується інтегральне конформне перетворення Кристофеля – Шварца. Треба розв’язати задачу: знайти розв’язок рівняння Лапласа у верхній площині з напівнескінченним розрізом. Використаємо метод конформних відображень: тут застосовується інтегральне конформне перетворення Кристофеля – Шварца.
Розглянемо ламану лінію, що в точці а
змінює напрямок на кут  : :
 . Якщо є два зломи, то . Якщо є два зломи, то  , де , де  , ,  , , 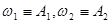 . В нашій конкретній задачі ламану можна подати у вигляді: . В нашій конкретній задачі ламану можна подати у вигляді:
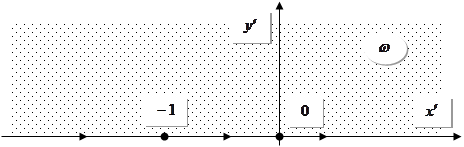 Кут відраховується проти годинникової стрілки від наступного напрямку до попереднього. Кут відраховується проти годинникової стрілки від наступного напрямку до попереднього. 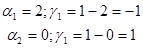 , ,  , перенесемо точки: , перенесемо точки:  . .
Проінтегрувавши отримаємо шукане перетворення: 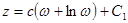 . Константи . Константи 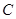 та та  визначаються з умов: визначаються з умов: 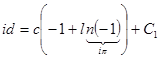 , отже , отже 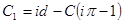 . Умовою . Умовою  ми не можемо скористатися, бо одержимо ми не можемо скористатися, бо одержимо  . Використаємо фізичні міркування: . Використаємо фізичні міркування:

Загальний вид відображення  ; бо область інваріанта відносно зсуву вздовж ОХ (трансляційна симетрія). ; бо область інваріанта відносно зсуву вздовж ОХ (трансляційна симетрія).
Зрозуміло, у нашій задачі область при 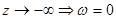 . При . При  перетворення набуває вигляду: перетворення набуває вигляду:  . Порівнюючи з . Порівнюючи з  , , 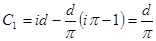 . Отже шукане перетворення: . Отже шукане перетворення: 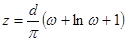 . .
Для того, щоб знайти розв’язок у верхній півплощині, необхідно перетворити її в конденсатор, використовуючи перетворення зворотне до 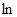 : :  . Тоді відображення, що перетворить вихідну область ( . Тоді відображення, що перетворить вихідну область (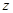 ) (край конденсатора) у конденсатор ( ) (край конденсатора) у конденсатор (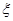 ), має вигляд: ), має вигляд: 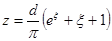 . .
Тепер необхідно розв’язати рівняння у плоскому конденсаторі та скористатись зворотнім перетворенням: 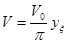 , ,  . . 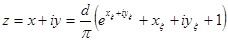 . .
Таким чином: 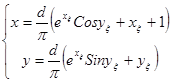 . .
Запишемо рівняння еквіпотенційних поверхонь:  . .
ЕПП 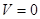 переходить в переходить в  . .
ЕПП  переходить в переходить в  . .
Таким чином, отримаємо таку картину еквіпотенціальних поверхонь:
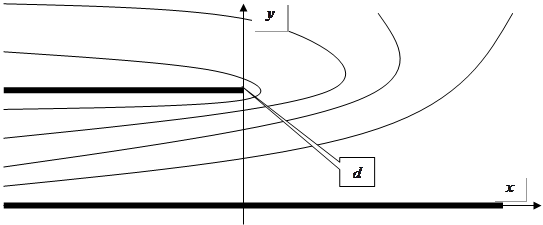
Тепер знайдемо електричні силові лінії. Ці лінії перпендикулярні ЕПП, однак ми знайдемо їх в аналітичний спосіб. Очевидно, в (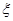 ) такі силові лінії, як на малюнку. Знайдемо образ цих ліній у просторі ( ) такі силові лінії, як на малюнку. Знайдемо образ цих ліній у просторі (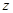 ). Наприклад, ). Наприклад,  , , . Отримаємо картину ЕП в ( . Отримаємо картину ЕП в ( ): ):

Часто важливо знайти напруженість поля в певній точці: 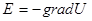 . .
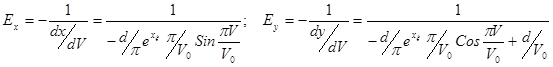
|