Міністерство освіти та науки України
Прикарпатський університет імені Василя Стефаника
Фізичний факультет
Кафедра фізики твердого тіла
Дипломна робота
Халькогеніди свинцю і сполуки на їх основі
м. Івано-Франківськ
2007
Вступ
|
| 1 Система Pb-S |
| 2 Константи рівноваги квазіхімічних реакцій утворення власних атомних дефектів Френзеля у кристалах Pb-S |
| 2.1.Експеремент |
| 2.2 Квазіхімічний аналіз |
| 2.3 Обговорення результатів |
| 3 Розрахунок констант рівноваги квазіхімічних реакцій утворення власних атомних дефектів у халькогенідах свинцю на основі експериментальних даних про границі області гомогенності |
| 3.1 Квазіхімічне моделювання |
4. Залежність властивостей плівок  від термодинамічних параметрів від термодинамічних параметрів |
| Висновки |
| Література |
| Додаток |
ВСТУП
Халькогеніди свинцю і сполуки на їх основі знаходять широке застосування у напівпровідниковій техніці (інфрачервоні пристрої оптоелектроніки, лазери, термогенератори). Досягнення сучасних технологій дозволяють отримати такі тонкі епітаксійні шари халькогенідів свинцю, які близькі за своїми характеристиками до об'ємних монокристалів і мають ряд унікальних властивостей, що значно розширює використання їх в науці і техніці.
При одержанні тонких плівок із парової фази за ефективним і поширеним методом "гарячої стінки" технологічні фактори відіграють вирішальну роль у формуванні електричних і оптичних властивостей плівок PbS, які визначаються дефектною кристалічною структурою і в значній мірі власними точковими дефектами плівок. Дефектна підсистема істотно змінюється при подальшій термічній обробці плівок у вакуумі, в атмосфері різних газів, під дією зовнішніх полів. Незважаючи на численні публікації в цьому напрямку, на даний час ряд важливих питань ще залишається нез'ясованим.
При вивченні процесу дефектоутворення в плівках, отриманих методом гарячої стінки, використовують частинні кристалохімічні моделі з різними комбінаціями поодиноких переважних дефектів, відносно яких досі немає єдиної думки і стійких уявлень про їх вид і зарядові стани. У розглянутих сполуках спостерігається схильність до самокомпенсації і виникає необхідність в одночасному врахуванні більш широкого спектра зарядових станів власних точкових дефектів. Електрофізичні властивості плівок сильно залежать від типу використаних підкладок, що не знайшло ще свого пояснення, крім припущень про слабо вивчені механічні напруження, які виникають в процесі вирощування плівок на різних підкладках. Актуальними залишаються ще додаткові теоретичні і експериментальні дослідження для з'ясування основних механізмів квазіхімічних реакцій утворення металічної фази при синтезі плівок халькогенідів свинцю квазірівноважними методами і впливу на дефектну підсистему PbS електрично активних газів.
Дослідження закономірностей вакуумного відпалу тонких плівок халькогенідів свинцю є актуальним у зв'язку з розробкою технологічних методів виготовлення на їх основі оптоелектронних приладів в ІЧ - області спектра. Можливість стимуляції окремих стадій процесу відпалу за рахунок поєднання термічних і нетермічних дій дозволило б підвищити ефективність цього процесу для створення потрібних для мікроелектроніки структур з необхідними електрофізичними параметрами. Виникнення двошарової p-n-структури в плівках PbS при ізотермічному вакуумному відпалі вимагає додаткового теоретичного розгляду. Не достатньо ще вивчено вплив зовнішніх електричного і магнітного полів на процес відпалу плівок типу PbS, ревипаровування летких компонентів з поверхневого шару плівок і вплив дифузійних процесів на концентрацію носіїв струму і власних дефектів при вакуумному відпалі плівок PbS.
1 Система Рb-S
Т-х-проеція діаграми стану системи показана на рис. 1.1. В системі знайдено одну сполуку – моносульфід свинцю РbS, що плавиться конгруентно при 1386 К [10]. Ліквідус в області складів 50-100% атомного вмісту сірки не був раніше визначений у зв’язку з високою пружністю пари сірки [2]. На рис. 1.4 ця частина діаграми побудована за даним роботи [11], де проводився диференціальний термічний аналіз під тиском 5·106
Па. Була знайдена область розслоювання з протяжністю від 70,5 до 99,1 % атомного вмісту сірки при монотектичній температурі 1072 К. У присутності сульфіду свинцю сірка плавиться при 387±1 К, що співпадає з температурою плавлення чистої сірки в межах похибки експерименту. Перетворення орторомбічної модифікації проходило при 374±2 К. Ліквідус для області складів 0-50% атомного вмісту сірки побудований за даними робіт [10, 12, 13], які знаходяться в добрій відповідності. Крива ліквідусу побудована за даними термічного аналізу [10], при екстраполяції добре сходиться з кривою ліквідусу, що знайдена з даних хімічного аналізу за розчинністю сірки в рідкому свинцю для сплавів з вмістом сірки 10% [13]. Для області менше 1% атомного вмісту сірки, її розчинність в рідкому свинцю відмічається при таких температурах і складах: 923 К і 0,59% атомного вмісту сірки, 873 К і 0,33; 833 К і 0,16; 773 К і 0,08; 723 К і 0,03% атомного вмісту сірки [13]. Так як між 20 і 40% атомного вмісту сірки точки кривої ліквідусу лежать майже на горизонтальній лінії, в ряді робіт не виключалась можливість існування області розслоювання в рідкому стані для цього інтервалу складів [2]. Склад евтектики зі сторони свинцю лежить при 0,0017% атомного вмісту сірки і одержаний екстраполяцією лінії ліквідусу [13]. Температура плавлення евтектики практично співпадає з температурою плавлення чистого свинцю.

Рис. 1.1. Фазова діаграма системи Pb-S: 1 – [10]; 2 – [13]; 3 – [12].
Т-х-проекція Р-Т-х діаграми поблизу 50% атомного вмісту сірки досліджувалась в роботі [14]. Монокристалічні зразки сульфіду свинцю відпалювались при заданому тиску сірки протягом часу, достатнього для приведення системи в рівновагу. Відпал проводився в двотемпературній печі, і необхідний тиск пари сірки підтримувався або регулюванням температури в резервуарі з сіркою, або застосуванням суміші водню з сірководнем. В останньому випадку тиск пари сірки розраховувався за ступенем дисоціації сірководню. Потім з
разокзагартовувався водою, визначалась концентрація носіїв і склад зразка. Зразок досліджувався на ознаки плавлення. Подібні досліди повторювали через кожні 5-10 К при постійному тиску пари сірки до того часу, поки зразок не починав плавитись.
Будувалась залежність складу твердої фази від температури відпалу, і шляхом екстраполяції до точки плавлення визначався склад, що відповідає солідусу. Повторення подібних вимірювань для різних значень тиску пари сірки дає повну лінію солідусу.
Лінія ліквідусу визначалась аналогічним способом. Зразки відпалювалися при температурі вище точки плавлення, і склад їх визначався шляхом хімічного аналізу. Екстраполяція до температури плавлення давала склад рідкої фази в точці плавлення, що відповідає даному тиску пари сірки. Таким методом визначається лінія ліквідусу тільки для свинцю, так як зі сторони сірки тиск пари сірки великий, і розплав втрачає її при кристалізації. Тому склад, знайдений з аналізу охолодженого зразка, помітно відрізняється від складу конденсованої фази при високих температурах. Лінія ліквідусу в цій області визначається класичним методом термічного аналізу в контейнерах з малим вільним об'ємом.
В роботах [15, 16] лінія солідусу зі сторони свинцю визначалася методом, що використовує явище мікроосадження і розчинення надстехіометричного свинцю, зв'язаного з ретроградною розчинністю свинцю в сульфіді свинцю. Монокристали сульфіду свинцю були одержані методом Бріджмена з розплаву стехіометричного складу. Так як кристали охолоджувались до кімнатної температури дуже повільно, частина надстехіометричного свинцю осідала в середині кристалу у вигляді дисперсної другої фази, яка була електрично нейтральною. Процес осадження оборотній, і, коли кристали знову піддали відпалу в вакуумі або в атмосфері інертного газу, розчинність свинцю збільшувалась з ростом температури. Швидкість розчинення залежала від температури відпалу. При досягненні рівноваги кількість надстехіометричного свинцю,який залишається в гратці, визначаєтьсякривою солідусу і температурою відпалу, а надлишок свинцю присутній в кристалі у вигляді мікроосаду. Зразки потім загартовувались до кімнатної температури із швидкістю, яка була достатньою, щоб попередити осадження в процесі загартування. Виміряна концентрація носіїв відповідала складу, що відповідає солідусу при температурі відпалу. Метод обмежений температурами, при яких, по-перше, концентрація надлишкового свинцю у вихідних монокристалах переважає розчинність; по-друге, швидкість розчинення і осадження достатньо велика для того, щоб рівновага була досягнута за час відпалу; по-третє, швидкість осадження атомів свинцю недостатньо висока для загартування після відпалу. В роботі [16] було показано, що задовільні результати одержуються в інтервалі температур 623-1123 К.
Метод мікро осадження і розчинення, що використовується для визначення лінії солідусу у випадку ретроградної розчинності, має ту суттєву перевагу, що час, необхідний для досягнення рівноваги, значно менший, ніж у випадку встановлення рівноваги із зовнішнім газовим середовищем. Для прикладу можна привести наступні дані: в роботі [16], де використовувався метод мікроосаджень, для досягнення рівновагибув потрібен відпал протягом 0,5 і 2 год. при 773 і 973 K відповідно. Якщо відпал проводився в парі сірки [16], час, потрібний для досягнення рівноваги з зовнішнім газовим середовищем, складав 7 і 60 год. при 100 і 800 K відповідно. Область гомогенності сульфіду свинцю визначалась також методом Бребрика, описаним раніше для телуриду олова. Монокрнсталічні зразки сульфіду свинцю урівноважувалися через газову фазу з двофазними сплавами, які знаходились при температурі відпалу в твердо-рідкому стані [17]. Результати всіх досліджень подані на рис. 1.2.

Рис. 1.2. Т-х- проекція системи Pb-S поблизу сполуки PbS
1 – [14]; 2 – [15]; 3 – [16]; 4 – [17]; 5 – [17].
Склад, що відповідає максимуму на кривій ліквідусу, містить надлишок свинцю в кількості 3×10-4
ат./моль. Сульфід свинцю має вузьку область гомогенності, розчинність надстехіометричного свинцю і сірки в сульфіді свинцю складають близько 3×10-4
ат/моль (973 K).
Р-Т-проекція діаграми стану системи Рb-S подана на рис. 1.3. Лінія трифазової рівноваги обмежує область стійкості твердого сульфіду свинцю. При температурах нижче 1023 K і високих тисках пари сірки трифазова лінія практично співпадає з лінією тиску насиченої пари чистої сірки. 3 боку сірки трифазова лінія досягає максимуму тиску пари сірки – 1,32×105
Па – при 1070 К. При низьких температурах і низьких тисках лінія трифазової рівноваги відповідає тиску пари сірки, який може бути одержаний із тиску пари чистого свинцю за допомогою співвідношення
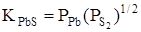 |
(1.1) |
KPbS
є константою рівноваги наступної реакції:
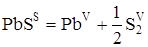 |
(1.2) |
Парціальні тиски пари сірки, що відповідають стехіометричному складу, показані суцільною лінією FG, яка ділить область всередині трифазової петлі на обласпь n-типу (багату свинцем) і р-типу (багату сіркою).
Тиск пари  над сульфідом свинцю, що сублімується конгруентно описується рівнянням [9] над сульфідом свинцю, що сублімується конгруентно описується рівнянням [9]
 , , |
(1.3) |
а парціальні тиски 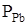 і і 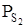 , що відповідають конгруентній сублімації, рівняннями [19] , що відповідають конгруентній сублімації, рівняннями [19]
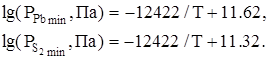 |
(1.4) |
На рис. 1.3 показані склади рівного відхилення від стехіометрії в сторону надлишку свинцю і надлишку сірки. Із збільшенням температури лінії однакової концентрації носіїв наближаються до стехіометичної лінії і для достатньо низьких концентрацій носіїв зливаються з нею. Лінія стереометричного складу перетинає петлю трифазової рівноваги при 1350 К.
Ця температура нижче максимальної температури плавлення, яка дорівнює 1400 К [14] і відповідає складу, що містить надлишок свинцю в твердій фазі близько 6×1018
см-3
.
Лінія МN на рис. 1.3 відноситься до парціальних тисків сірки 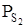 в рівновазі із зразками, що сублімуються конгруентно. Вона визначається із виразу : в рівновазі із зразками, що сублімуються конгруентно. Вона визначається із виразу :
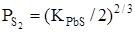 , , |
(1.7) |
який виводиться із умови, що характеризує пару стехіометричного складу, 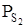 =1/2 =1/2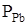 і із константи рівноваги реакції (1.2) і із константи рівноваги реакції (1.2) 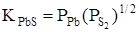 . Склад, що сублімується конгруентно, містить надлишок свинцю відносно стехіометричного складу близько 3×10-4
ат/моль при 1173 К і лежить на стороні n-типу. Складу, що випаровується конгруентно, відповідає мінімум на кривій залежності від загального тиску, який складається з парціальних тисків пари сірки і пари свинцю . Склад, що сублімується конгруентно, містить надлишок свинцю відносно стехіометричного складу близько 3×10-4
ат/моль при 1173 К і лежить на стороні n-типу. Складу, що випаровується конгруентно, відповідає мінімум на кривій залежності від загального тиску, який складається з парціальних тисків пари сірки і пари свинцю 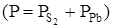 . .
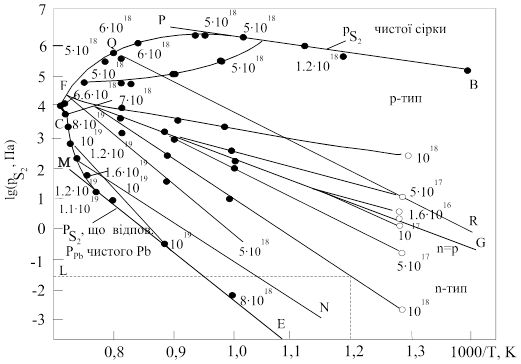
Рис. 1.3. P-Т- проекція системи Pb-S [18]
Pb – температурна залежність тиску чистої сірки в припущенні існування тільки молекул S2
; DE – 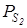 , що відповідає Р чистого свинцю, розрахована за рівнянням (1.1); QR – температурна залежність тискупари молекул PbS; FG – температурна залежність , що відповідає Р чистого свинцю, розрахована за рівнянням (1.1); QR – температурна залежність тискупари молекул PbS; FG – температурна залежність 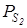 для твердої фази стехіометричного складу; MN – лінія для твердої фази стехіометричного складу; MN – лінія 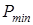 , парціальний тиск , парціальний тиск 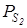 в рівновазі із зразками, що сублімуються конгруентно; С – максимальна точка плавлення PbS; BAFCDE – в рівновазі із зразками, що сублімуються конгруентно; С – максимальна точка плавлення PbS; BAFCDE – 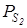 , що відповідає лінії трифазової рівноваги. , що відповідає лінії трифазової рівноваги.
2 Константи квазіхімічних реакцій утворення власних атомних
дефектів Френкеля у кристалах PbS
2.1 Експеримент
Вихідний сульфід свинцю синтезували сплавленням свинцю (С–000) і сірки (В-5) у вакуумованих кварцових ампулах. Термічний відпал синтезованих кристалів у парах сірки проводився за загальновідомою методикою двотемпературного відпалу, при якому в один кінець кварцової ампули поміщали розплавлені сірку, а в інший – кристали PbS. Парціальний тиск пари сірки задавався температурою його нагріву в одній зоні ампули. Температуру відпалу кристалів PbS задавали іншою зоною. Після відпалу ампули із зразками швидко загартовували у крижаній воді.
Концентрацію носіїв струму в таких зразках визначали на основі холлівських вимірювань при 300 К. Експериментальні результати залежності концентрації носіїв струму у відпалених кристалах PbS від парціального тиску при різних температурах відпалу зображено на рис.2.1[2].
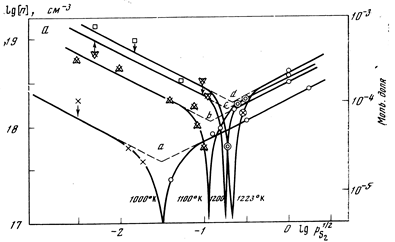
Рис.2.1. Експериментальні ізотерми концентрації носіїв струму кристалів PbS від парціального тиску сірки при різних температурах відпалів [2].
2.2. Квазіхімічний аналіз
Рівноважний стан власних атомних дефектів кристалів PbS при їх термодинамічному відпалі у парі сірки можна описати системою кристалохімічних рівнянь (див. табл.). Тут: S – тверда фаза; V – пара; 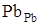 , , 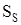 – атоми у вузлі; – атоми у вузлі;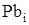 – міжвузловий атоми; – міжвузловий атоми; 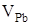 – вакансії; е – електрони, h – дірки; +, – – знак заряду. – вакансії; е – електрони, h – дірки; +, – – знак заряду.
У запропонованій моделі (табл.): реакція І відображає утворення пари Френкеля у металевій підґратці; ІІ – перехід сірки з пари в кристал; IІІ – ІV – реакції іонізації утворених дефектів; V – реакція виникнення власної провідності та VI – рівняння електронейтральності у випадку утворення однозарядних дефектів у катіонній підгратці.
Дана система рівнянь дозволяє розрахувати концентрацію дефектів (міжвузлових атомів свинцю 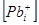 , вакансій свинцю , вакансій свинцю  ) чи концентрацію носіїв струму n(p), якщо відомі константи Kа
, Kb
, Ki
, КF
, ) чи концентрацію носіїв струму n(p), якщо відомі константи Kа
, Kb
, Ki
, КF
, 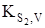 . .
Якщо ж відома з експерименту концентрація носіїв струму, то можна визначити константи рівноваги реакцій утворення власних атомних дефектів.
Таблиця 2.1
Реакції та константи рівноваги К=К0
exp (–DH/kT) утворення атомних дефектів Френкеля у кристалах PbS
Для визначення констант рівноваги реакцій (ІІI – V) скористалися зонною теорією для невироджених напівпровідників. Константи рівноваги реакцій іонізації дефектів визначали згідно [3] за формулами:
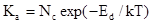 , , |
(2.4) |
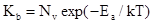 , , |
(2.5) |
де Еd
, Ea
- енергії іонізації донорних і акцепторних точкових дефектів, які близькі до нуля (0,01 еВ). Густини станів в дозволених зонах Nc
i Nv
можна розрахувати за формулами :
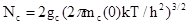 , , |
(2.6) |
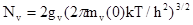 . . |
(2.7) |
Тут 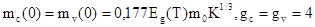 . .
де K=12, mc
(0) - маса електрона в зоні провідності, mv
(0) - маса дірки в валентній зоні, m0
- маса вільного електрона, Eg
- ширина забороненої зони [4]:
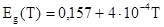 . . |
(2.8) |
Константа рівноваги власної провідності дорівнює [3]:
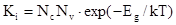 . . |
(2.9) |
Значення КF
, 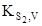 знайшли, апроксимуючи експериментальні залежності концентрації носіїв струму від тиску сірки (рис.1) виразом (3). Одержані значення знайдених констант наведено у таблиці. Використовуючи знайдені константи, побудували залежності концентрації дефектів (міжвузлових атомів свинцю знайшли, апроксимуючи експериментальні залежності концентрації носіїв струму від тиску сірки (рис.1) виразом (3). Одержані значення знайдених констант наведено у таблиці. Використовуючи знайдені константи, побудували залежності концентрації дефектів (міжвузлових атомів свинцю  вакансій свинцю вакансій свинцю 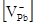 ) та концентрації носіїв струму n(p) від температури відпалу та парціального тиску пари сірки, які зображено на рис.2.2-5.2 ) та концентрації носіїв струму n(p) від температури відпалу та парціального тиску пари сірки, які зображено на рис.2.2-5.2

Рис.2.3. Залежність розрахованих значень концентрації носіїв струму (1–n(p)), міжвузлових атомів свинцю (2–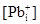 ) та вакансій свинцю (3- ) та вакансій свинцю (3-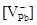 ) в кристалах PbS від температури відпалу ( ) в кристалах PbS від температури відпалу (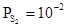 Па). Па).
2.3. Обговорення результатів
При відпалі кристалів PbS у парі сірки змінюється як концентрація, так і вид дефектів (рис.2–5). Так, зокрема, результати теретичного аналізу вказують на те, що збільшення парціального тиску сірки (рис. 2.1), як і зменшення температури відпалу (рис. 3.5), зумовлюють
Рис. 2.4. Залежність концентрації носіїв струму PbS від парціального тиску сірки (суцільна лінія- розрахунок згідно (3.3) з використанням знайдених значень констант рівноваги, точки – експеримент) при температурі відпалу Т, К: 1-1000, 2-1100, 3-1200.

Рис.2.5. Залежність розрахованих згідно (3.3) значень концентрації носіїв струму PbS з використанням знайдених значень констант рівноваги від температури відпалу при парціальному тиску сірки  , Па: 1 - 10-4
, 2 - 10-2
, 3 - 1. , Па: 1 - 10-4
, 2 - 10-2
, 3 - 1.
топологічно ідентичні зміни. Для випадку збільшення парціального тиску сірки спостерігається зменшення концентрації електронів, конверсія провідності з n–на p–тип (термодинамічний n–p–перехід) і подальше зростання концентрації дірок. А у випадку підвищення температури відпалу спочатку відбувається спадання концентрації дірок, аж до моменту настання n–p–переходу, а потім зростання концентрації електронів (рис. 3,5). При цьому в області малих тисків концентрація визначається міжвузловими атомами свинцю (n = 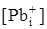 ), а в області високих тисків – концентрацією вакансій свинцю (p = ), а в області високих тисків – концентрацією вакансій свинцю (p = 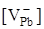 ) (рис.2.2). ) (рис.2.2).
3.
Розрахунок констант рівноваги квазіхімічних реакцій утворення
власних атомних дефектів у халькогенідах свинцю на основі
експериментальних даних про границі області гомогенності
3.1 Квазіхімічне моделювання
Таблиця 3.1
Реакції та константи рівноваги К=К0
exp (–DH/kT) утворення переважаючих атомних дефектів у халькогенідах свинцю PbS
| № п/п |
Рівняння |
Константа рівноваги |
| 1 |
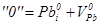 |
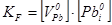 |
| 2 |
 |
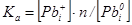 |
| 3 |
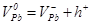 |
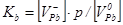 |
| 4 |
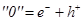 |
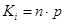 |
| 5 |
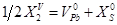 |
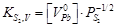 |
| 6 |
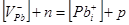 |
Припускалося, що в халькогенідах свинцю переважаючим є дефектоутворення у катіоній підгратці за механізмом Френкеля. Згідно [6], процес дефектоутворення в PbS можна описати системою квазіхімічних реакцій (таблиця 3.1). Тут реакція (1) описує утворення пари Френкеля, (2)-(3) – іонізацію утворених дефектів, (4) – збудження власної провідності. Реакція (5) описує проникнення атомів халькогену з парової фази у кристал з утворенням нейтральної 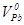 металічної вакансії, а (6) – рівняння повної електронейтральності. металічної вакансії, а (6) – рівняння повної електронейтральності.
Границі області гомогенності халькогенідів свинцю для надлишку атомів свинцю і халькогену можна розрахувати за формулами[11]:
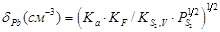
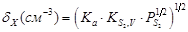
|
(3.1) |
де К – константи відповідних квазіхімічних реакцій (див. таблицю 3.1).
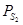 – парціальний тиск пари сірки, що відповідає трифазовій рівновазі тверде тіло – рідина – газ в системі свинець - сірка. – парціальний тиск пари сірки, що відповідає трифазовій рівновазі тверде тіло – рідина – газ в системі свинець - сірка.
Вирази (3.1) дозволяють розрахувати границі області гомогенності якщо відомі константи Ka
, Kb
, Ki
, КF
, 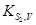 . Навпаки, якщо границі області гомогенності відомі з експерименту, то можна визначити константи рівноваги реакцій утворення власних атомних дефектів. Проте, ця задача є досить складною. Для її спрощення константи Ka
, Kb
, Ki
розраховували теоретично, використовуючи зонну теорію невироджених напівпровідників. Константи рівноваги реакцій іонізації дефектів визначали за формулами: . Навпаки, якщо границі області гомогенності відомі з експерименту, то можна визначити константи рівноваги реакцій утворення власних атомних дефектів. Проте, ця задача є досить складною. Для її спрощення константи Ka
, Kb
, Ki
розраховували теоретично, використовуючи зонну теорію невироджених напівпровідників. Константи рівноваги реакцій іонізації дефектів визначали за формулами:
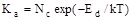 |
(3.2) |
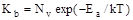 |
(3.3) |
Таблиця 3.2
Значення параметрів, які використовувались при розрахунках констант Ka
, Kb
, Ki
[1,2,15]
| Сполука |
Носії струму |
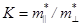 |
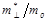 (300 К) (300 К) |
Eg
, еВ |
низькі
температури
|
високі темпера-тури |
| PbS |
n |
1,3 |
0,160 |
0,275+4,5×10–4
Т |
0,45 |
| p |
1,4 |
0,150 |
де Еd
, Ea
- енергії іонізації донорних і акцепторних точкових дефектів, які брали рівними 0,01 еВ. Густини станів в дозволених зонах Nc
i Nv
можна розрахувати за формулами :
Nc
= 2(2p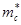 kT/h2
)3/2 kT/h2
)3/2
|
(3.4) |
Nv
= 2(2p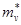 kT/h2
)3/2 kT/h2
)3/2
|
(3.5) |
де 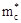 , , 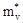 -ефективна маса електрона в зоні провідності і дірки в валентній зоні відповідно, m0
- маса вільного електрона. -ефективна маса електрона в зоні провідності і дірки в валентній зоні відповідно, m0
- маса вільного електрона.
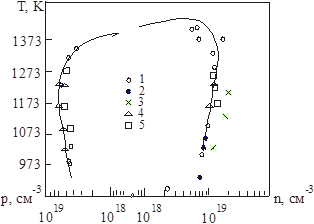
Рис. 3.1.
Область гомогенності PbS [2]
Температурну залежність ефективної маси густини станів для електронів і легких дірок визначали за формулою
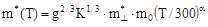 |
(3.6) |
де 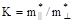 ; gc
= gv
= 4 ; gc
= gv
= 4
Вважали, що ефективна маса важких дірок не залежить від температури.
Значення параметрів, які використовувались при розрахунках наведені в таблиці 3.2.
Константу рівноваги реакції збудження власної провідності одержимо з виразу
| Ki
= Nc
Nv
×exp(–Eg
/kT). |
(3.7) |
де Eg
- ширина забороненої зони.
Таблиця 3.3
Константи рівноваги К = К0
exp (–DH/kT) утворення атомних дефектів у халькогенідах свинцю PbS
№
п/п
|
Ka
|
Kb
|
Ki
|
KF
|
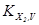 |
При-мітка |
K0
,
см-3
|
DH, еВ |
K0
,
см-3
|
DH, еВ |
K0
,
см-6
|
DH, еВ |
K0
,
см-6
|
DH, еВ |
K0
,
см-6
,Па-1/2
|
DH, еВ |
| PbS |
| 1 |
1,4×1021
|
0,14 |
1,4×1021
|
0,14 |
4,8×1041
|
1,0 |
2,1×1042
|
2,5 |
1,5×1016
|
0,50 |
[6] |
| 2 |
1,5×1020
|
0,12 |
1,5×1020
|
0,12 |
2,3×1040
|
0,83 |
5,8×1040
|
1,80 |
4,3×1016
|
0,20 |
* |
*) – легкі дірки;
**) – важкі дірки.
На відміну від більшості напівпровідників в халькогенідів свинцю ширина забороненої зони в області низьких температур лінійно зростає, а при температурах вищих 500 К лінійність температурної залежності порушується і ширина забороненої зони прямує до сталого значення (таблиця 3.2).
Отримавши таким чином константи Ka
, Kb
, Ki
, значення констант КF
, 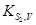 знайшли апроксимуючи експериментальні залежності границь області гомогенності від температури (рис. 3.1) виразами (3.1). Результати оцінки знайшли апроксимуючи експериментальні залежності границь області гомогенності від температури (рис. 3.1) виразами (3.1). Результати оцінки 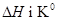 наведені в таблиці 3.3. наведені в таблиці 3.3.
4. Залежність властивостей плівок 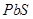 від термодинамічних від термодинамічних
параметрів
Модель 
Таблиця 4.1.
| № |
Реакція |
Константа рівноваги |
| I |
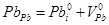 |
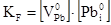 |
| II |
 |
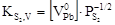 |
| III |
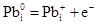 |
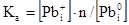 |
| IV |
 |
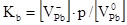 |
| V |
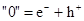 |
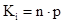 |
| VI |
 |
 |
(4.1) |
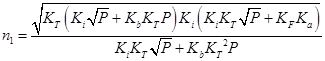
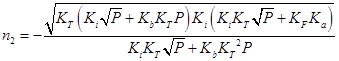
|
(4.2) |
 Рис.4.1 Ізотерми концентрації носів заряду 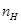 в плівках в плівках 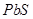 , ,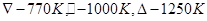
 Рис.4.2. Ізобари концентрації носів заряду  в плівках в плівках  , ,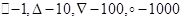
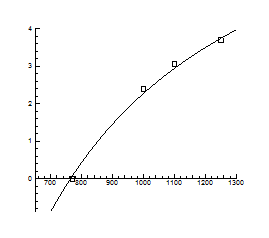 Рис.4.3. Залежність тиску інверсії від температури
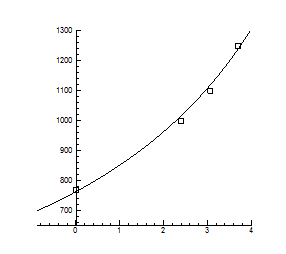 Рис.4.4. Залежність температури інверсії від тиску
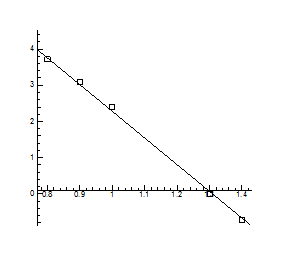 Рис.4.5. P-Т- проекція системи Pb-S
Модель 
Таблиця 4.2.
| № |
Реакція |
Константа рівноваги |
| I |
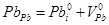 |
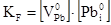 |
| II |
 |
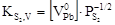 |
| III |
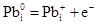 |
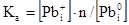 |
| IV |
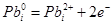 |
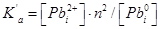 |
| V |
 |
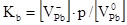 |
| VI |
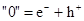 |
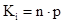 |
| VII |
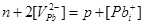 |
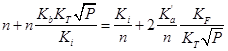 |
(4.3) |
 Рис.4.6. Ізотерми концентрації носів заряду 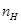 в плівках в плівках 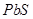 , , 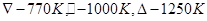
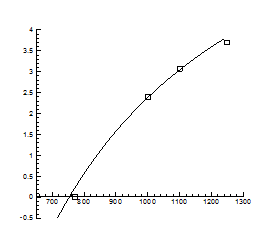 Рис.4.7. Залежність тиску інверсії від температури
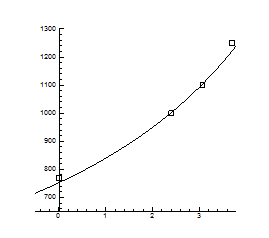 Рис.4.8. Залежність температури інверсії від тиску
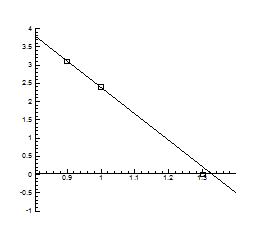 Рис.4.9. P-Т- проекція системи Pb-S
Модель 
Таблиця 4.3.
| № |
Реакція |
Константа рівноваги |
| I |
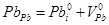 |
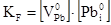 |
| II |
 |
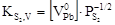 |
| III |
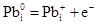 |
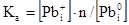 |
| IV |
 |
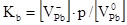 |
| V |
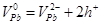 |
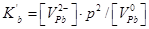 |
| VI |
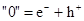 |
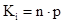 |
| VII |
 |
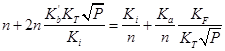 |
(4.4.) |
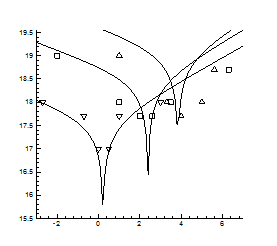 Рис.4.10. Ізотерми концентрації носів заряду 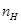 в плівках в плівках 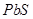 , , 
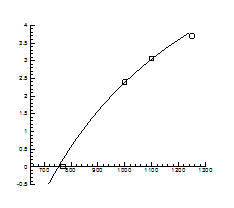 Рис.4.11. Залежність тиску інверсії від температури
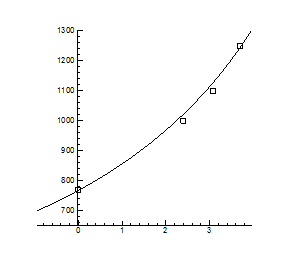 Рис.4.12. Залежність температури інверсії від тиску
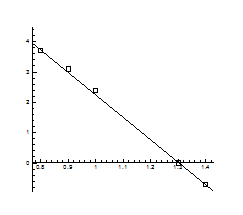 Рис.4.13. P-Т - проекція системи Pb-S
Модель 
Таблиця 4.4.
| № |
Реакція |
Константа рівноваги |
| I |
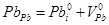 |
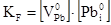 |
| II |
 |
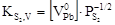 |
| III |
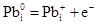 |
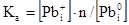 |
| IV |
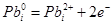 |
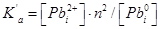 |
| V |
 |
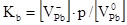 |
| VI |
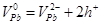 |
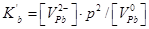 |
| VII |
 |
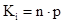 |
| VIII |
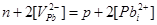 |
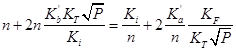 |
(4.5) |
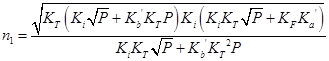
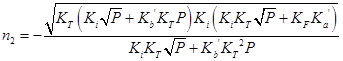
|
(4.6) |
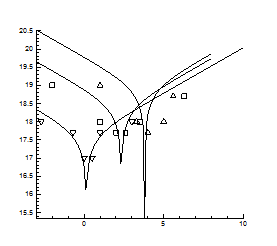 Рис.4.14. Ізотерми концентрації носів заряду 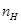 в плівках в плівках 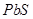 , , 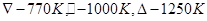
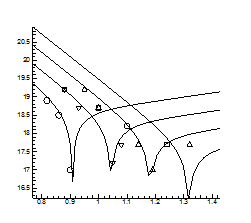 Рис.4.15. Ізобари концентрації носів заряду 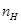 в плівках в плівках 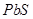 , ,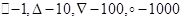
 Рис.4.16. Залежність тиску інверсії від температури
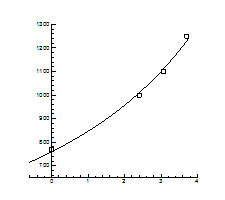 Рис.4.17. Залежність температури інверсії від тиску
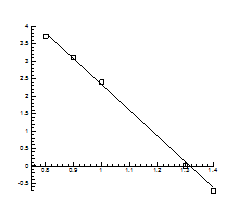 Рис.4.18. P-Т - проекція системи Pb-S
Модель 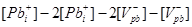
Таблиця 4.5.
| № |
Реакція |
Константа рівноваги |
| I |
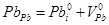 |
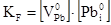 |
| II |
 |
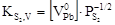 |
| III |
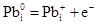 |
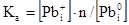 |
| IV |
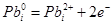 |
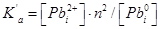 |
| V |
 |
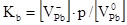 |
| VI |
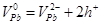 |
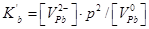 |
| VII |
 |
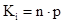 |
| VIII |
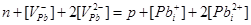 |
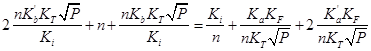 |
(4.7) |
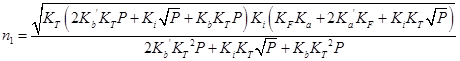

|
(4.8) |
 Рис.4.19. Ізотерми концентрації носів заряду 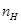 в плівках в плівках  , , 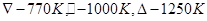
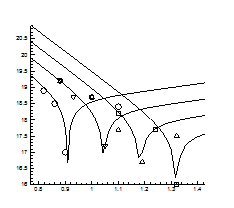 Рис.4.20. Ізобари концентрації носів заряду 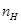 в плівках в плівках 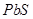 , ,
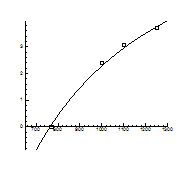 Рис.4.21. Залежність тиску інверсії від температури
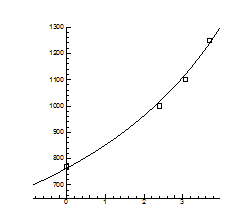 Рис.4.22. Залежність температури інверсії від тиску
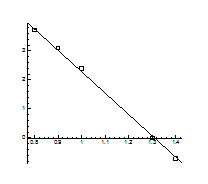 Рис.4.23. P-Т - проекція системи Pb-S
Таблиця 4.6.
| № |
Реакція |
Константа рівноваги |
Теоретичні |
Розраховані |
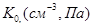 |
 |
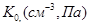 |
 |
| I |
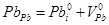 |
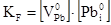 |
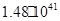 |
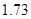 |
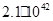 |
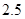 |
| II |
 |
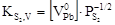 |
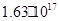 |
 |
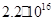 |
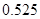 |
| III |
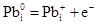 |
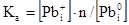 |
 |
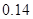 |
 |
 |
| IV |
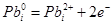 |
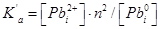 |
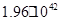 |
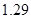 |
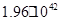 |
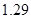 |
| V |
 |
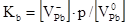 |
 |
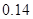 |
 |
 |
| VI |
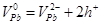 |
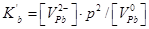 |
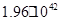 |
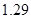 |
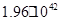 |
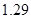 |
| VII |
 |
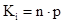 |
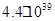 |
 |
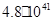 |
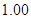 |
Література:
[1] Ю.М.Равич, Б.А.Ефимова, Н.А.Смирнов, Методы исследования полупроводников в применении к халькогенидам свинца PbTe, PbSe, PbS, Наука, М. (1968)
[2] Н.Х.Абрикосов, Л.Е.Шалимова. Полупроводниковые материалы на основе соединений АIV
ВVI
. Наука, М. (1975).
[3] И.М.Раренко, Д.М. Фреик. Полупроводниковые материалы и приборы инфракрасной техники
. ЧДУ, Черновцы (1980).
[4] Ф.Ф.Сизов. Твердые растворы халькогенидов свинца и олова и фотоприемники на их основе // Зарубеж. электрон. техника
, 24
, сс.3-48 (1977).
[5] H.Holloway. Thin Films IV-VI semiconductor photodiodes // Phys. Thin Films
, 11
, pp.105-203 (1980).
[6] Ф.Крегер, Химия несовершенных кристаллов, Мир, М. (1969).
[7] В.П.Зломанов, О.В.Матвеев, А.В.Новоселова. Физико-химическое исследование селенида свинца // Вестник МГУ. Химия
, 5
, cc.81-89 (1967).
[8] В.П.Зломанов, О.В.Матвеев, А.В.Новоселова. Определение констант равновесий дефектов в селениде свинца // Вестник МГУ. Химия
, 6
, cc.67-71 (1968).
[9] А.В.Новоселова, В.П.Зломанов. Физико-химическое исследование селенида свинца // Неорган. материалы
, 3(8)
, cc.1323-1329 (1967).
[10] А.М.Гаськов, О.В.Матвеев, В.П.Зломанов, А.В.Новоселова. Исследование теллурида свинца // Неорган. материалы
. 4(11)
, cc. 1889-1894 (1969)
[11] А.М.Гаськов, В.П.Зломанов, А.В.Новоселова. Область гомогенности теллурида свинца // Неорган. материалы
. 15(8)
, cc.1476-1478 (1979)
[12] В.П.Зломанов, А.М.Гаськов. Собственные и примесные дефекты в соединениях группы AIV
BVI
// Рост полупроводниковых кристаллов и плёнок: новые методики, критерии функциональной пригодности материалов, Новосибирск
, сс.116-133 (1984).
[13] В.П.Зломанов. P-T-x-диаграммы двухкомпонентных систем.
МГУ, М. (1980).
[14] В.П.Зломанов, А.В.Новоселова. Р-Т-х-диаграммы состояния системы металл-халькоген.
Наука, М. (1987).
[15] Е.Д. Девяткова, В.А.Саакян. Температурная зависимость ширины запрещенной зоны твердых растворов PbTex
Se1-x
// ФТТ
. 10(5)
, сс. 1563–1565 (1968).
np
restart:with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> for T from 700 to 1300 by 25 do
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(2.2e16*exp((-0.52)/((1.380662e-23/1.60219e-19)*T)));
> n:=ki^(1/2);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,p);
> Data:=[op(Data),[evalf(1000/T),evalf(log10(P))]];
> od:
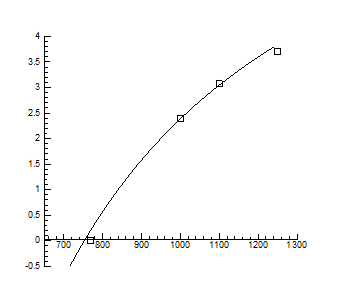
> Data1:=[[1.4,-5/7], [0.8,3+5/7], [0.9,3.1], [0.9,3.1], [1,2.4], [1.3,0]];
> A:=plot(Data1, style=point,symbol=circle,color=black):
> B:=plot(Data,x=0.7..1.5,y=-2..4):
> display(A,B);

константа
> restart:
> with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> T:=1250;
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(1.63e27*exp((-0.2)/((1.380662e-23/1.60219e-19)*T)));
> n:=0.75*10^18;
> p:=10^(4);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,kt);
> plot(Data):
> plot(f(x),x=0..1):
> Q:=n+n*kb/ki*kt*p^(-1/2)=ki/n+ka/n*kf/kt*p^(1/2);
> ln(2.041*10^9);
> with(stats):
> fit[leastsquare[[x,y], y=a/x+b, {a,b}]]([[770,1250],[21.436,39.055]]);
> evalf(exp(67.3188));
> k:=(1.380662e-23/1.60219e-19);
> 35329.7*k;
Nx(p) T=const
> restart:
> with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> z:=100;
> v1:=1;
> v:=5;
> T:=770;
> for p1 from -3 to 10 by 0.1 do
> ka:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(v1*4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(z*2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(z^(1/2)*2.2e16*exp((-0.525)/((1.380662e-23/1.60219e-19)*T)));
> p:=10^(p1);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> N:=solve(Q,n)[2];
> Nx:=abs(N-ki/N);
> G:=N*kb/ki*kt*p^(1/2);
> Data:=[op(Data),[(p1),evalf(log10(Nx))]];
> od:
> DataE:=[[3,18],[-2.7,18],[1,17.7],[-0.7,17.7], [0,17], [0.5,17]];
> A:=plot(Data):
> B:=plot(DataE, style=point,symbol=circle):
> display(A,B);

Nx(T) P= const
> restart:
> with(plots):
> Data1:=[]:
> Data:=[]:
> Ki:=ko(-h/kT);
> z:=100;
> v1:=1;
> v:=5;
> p1:=0:
> for T from 700 to 1300 by 10 do
> ka:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(v1*4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(z*2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(z^(1/2)*2.2e16*exp((-0.525)/((1.380662e-23/1.60219e-19)*T)));
> p:=10^(p1);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> N:=solve(Q,n)[2];
> Nx:=abs(N-ki/N);
> G:=N*kb/ki*kt*p^(1/2);
> Data:=[op(Data),[(1000/T),evalf(log10(Nx))]];
> od:
> DataE:=[[0.88,19.2], [1.0,18.7], [1.1,18.2], [1.24,17.7], [1.32,16]];
> A:=plot(Data):
> B:=plot(DataE, style=point,symbol=circle):
> display(A,B);

restart:with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> for T from 700 to 1300 by 25 do
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(2.2e16*exp((-0.52)/((1.380662e-23/1.60219e-19)*T)));
> n:=ki^(1/2);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,p);
> Data:= [op(Data),[evalf(1000/T),evalf(log10(P))]];
> Data1:= [op(Data),[T),evalf(log10(P))]];
od:
> Data3:=[[1.4,-5/7], [0.8,3+5/7], [0.9,3.1], [0.9,3.1], [1,2.4], [1.3,0]];
> A:=plot(Data):
> B:=plot(Data1):
> C:=plot(Data2):
> display(A,C);
> display(B,C);
 |