Содержание:

I Введение...................................................................................................... 3

Вступление................................................................................................. 3

Треугольники............................................................................................. 4

II Основная часть.......................................................................................... 8

Общие сведения о тригонометрических функциях............................ 8

Теоремы.................................................................................................... 13

Теорема о площади треугольника:................................................... 13

Теорема синусов:................................................................................. 14

Теорема косинусов:............................................................................. 16

Задачи........................................................................................................ 17

III Заключение............................................................................................ 20

Список литературы.................................................................................... 21

IВведение

Вступление

Геометрия - одна из самых древних и интересных наук, занимающаяся изучением геометрических фигур. Наш мир невозможно представить без их существования. Эта наука имеет огромный запас различных теорем, которые постоянно применяются как при решении математических задач, так и в жизни. Больше всего меня заинтересовали теоремы синусов и косинусов, которые применяются при решении произвольных треугольников. Цель данного реферата - уметь доказывать теоремы косинусов и синусов, применять их в решении задач, выбирать правильный ход решения при их использовании, знать, где данные теоремы применяются в жизни.

Треугольники

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.

Виды треугольников :

· Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

· Треугольник, у которого все стороны равны, называется равносторонним или правильным.

· Треугольник называется прямоугольным , если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой , две другие стороны называются катетами .

· Треугольник называется остроугольным , если все три его угла – острые, то есть меньше 90°

· Треугольник называется тупоугольным, если один из его углов – тупой, то есть больше 90°.

Бермудский Треугольник - широко известная аномальная зона. Расположен он в границах между Бермудскими островами, Майями во Флориде и Пуэрто-Рико. Площадь Бермудского треугольника составляет свыше одного миллиона квадратных километров. Рельеф дна в этой акватории хорошо изучен. На шельфе, который составляет значительную часть этого дна, было проведено множество бурений с целью отыскать нефть и другие полезные ископаемые. Течение, температура воды в разное время года, ее соленость и движение воздушных масс над океаном - все эти природные данные занесены во все специальные каталоги. Этот район не особенно сильно отличается от других похожих географических мест. И, тем не менее, именно в районе Бермудского треугольника загадочно исчезали суда, а затем и самолеты.

Выдвигаются различные гипотезы для объяснения этих исчезновений, от необычных погодных явлений до похищений инопланетянами. Скептики утверждают, однако, что исчезновения судов в бермудском треугольнике происходят не чаще, чем в других районах мирового океана и объясняются естественными причинами.Морские и воздушные суда погибают и в других районах земного шара, иногда бесследно. Неисправность радио или внезапность катастрофы может помешать экипажу передать сигнал бедствия. Поиск обломков в море — непростая задача, особенно в шторм или когда место катастрофы точно неизвестно. Если учесть очень оживлённое движение в районе бермудского треугольника, частые циклоны и штормы, большое количество отмелей, количество случившихся здесь катастроф, которые так и не получили объяснения, не является необычно большим.

Впервые о «таинственных исчезновениях» в бермудском треугольнике упомянул корреспондент Associated Press Джонс, в 1950 году он назвал этот район «морем дьявола». Автором словосочетания «бермудский треугольник» обычно считают Винсента Гладдиса, опубликовавшего в 1964 году в одном из журналов, посвящённых спиритизму, статью «Смертоносный бермудский треугольник».

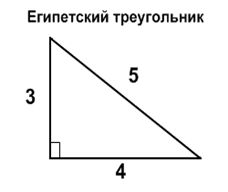Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

Особенностью такого треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.

Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами.

Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

В архитектуресредних веков египетский треугольник применялся для построения схем пропорциональности.

II Основная часть

Общие сведения о тригонометрических функциях

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников.

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Длительную историю имеет понятие синус . Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги. В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completelysinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin(90° - a)). Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Современные обозначения синуса и косинуса знаками sin и cos были впервые введены в 1739 г. швейцарским математиком Иоганном Бернуллив письме к Леонарду Эйлеру, который и стал употреблять их в своих математических работах. Эйлер ввел также обозначения для функций угла х: tg x , ct g x , sec x , cosec x .

Синус, косинус, тангенс, котангенс.

· Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (AB/OB).

· Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе (ОА/OB).

· Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету (AB/OA).

· Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету (ОА/AB) .

Значения тригонометрических функций.

Значения тригонометрических функций для некоторых углов.

	0°(0 рад)	30° (π/6)	45° (π/4)	60° (π/3)	90° (π/2)	180° (π)	270° (3π/2)	360° (2π)
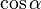					N/A		N/A
	N/A					N/A		N/A

Значения косинуса и синуса на окружности.

Свойства тригонометрических функций

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или основному тригонометрическому тождеству, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно, имеем далее:

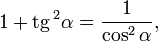
Формулы приведения:

sin(90° - α) = cosα

cos(90° - α) = sinα

sin(180° - α) = sinα

cos(180° - α) = - cosα

Чётность и нечетность функций.

Чётная функция - функция y = f ( x ) называется чётной, если область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство

f (- x ) = f ( x )

Нечётная функция - функция, область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство

f(- x) = - f( x)

Косинус — единственная чётная функция. Остальные три функции — нечётные, то есть:

Теоремы

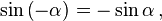
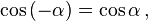
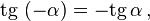
Теорема о площади треугольника:

Дано:

∆ АВС, АВ= с, ВС = a , СА = b , h - высота

Доказать:

S = ½ absinC

Доказательство:

Введём систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх , а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S = ½ ah , где h – высота треугольника. Но h равна ординате точки А , т.е. h = b sinC (т.к. sinC = h / b ) => S = ½ absinC

Ч.т.д.

Теорема синусов:

Дано:

∆АВС АВ= с, ВС= а, СА= b

Доказать :

a/ sinA = b/ sin B = c/ sinC

Доказательство:

По теореме о площади треугольника S= ½ absinC, S = ½ bcsinA, S= ½ acsinB.

Из первых двух равенств получаем ½ absinC = ½ bcsinA,

½ ab sinC = ½ bc sinA │ : ½ b

a sinC = c sinA │: sinA sinC

a/sinA = c/sinC

Точно также из второго и третьего равенства получаем

½ bc sinA = ½ ac sinB │: ½ c

b sinA = a sinB │: sinA sinB

b/sinB = a/sinA

Таккакa/sinA = c/sinC иb/sinB = a/sinA, тоa/sinA= b/sinB= c/sinC.

Ч.т.д.

Замечание:

Отношение стороны треугольника к синусу противолежащего

угла равно диаметру описанной окружности.

a/sinA= b/sinB= c/sinC= 2R

Дано:

R – радиус описанной окружности, ВС = a, BA1 - диаметр

Доказать:

BC/sinA = 2R (BC=2RsinA)

Доказательство:

Проведем диаметр ВА1. Рассмотрим ∆А1ВС, ∟С - прямоугольный => ВС=ВА1×sinA1. Если т.А1 лежит на дуге ВАС, то ∟А1=∟А, если на дуге BDC, то ∟A1= 180° - ∟A. И в том, и в другом случае sinA1 = sinA => BC= BA1*sinA, BC= 2RsinAили BC/sinA= 2R.

Ч.т.д.

Теорема косинусов:

Дано:
∆АВС АВ= с, ВС= а, СА= b

Доказать:

a ² = b ² + c ² − 2bc cosα

Доказательство:

Введем систему координат с началом в точке А. Точка В имеет координаты (с; 0), а точка С(bcosA; bsinA). По формуле расстояния между двумя точками d2 = (x2 – x1)2 + (y2 – y1)2получаем:

ВС² = a ² = (b cosA – c)² +(bsinА- 0) ² ,

a ² = b² cos2A - 2bc cosA + c² + b² sin² A,

a ² = b² (cos2A + sin2A) + c² - 2bc cosA,

a ² = b² + c² – 2bc cosA.

Ч.т.д.

Обобщенная теорема Пифагора.

Теорему косинусов называют иногда обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в ∆АВС ∟А прямой, то cosA = cos 90° = 0 и по a ² = b ² + c ² − 2bc cosα получаем:

a ² = b ² + c ² ,

т.е. квадрат гипотенузы равен сумме квадратов катета.

Задачи

№1

Решение треугольника по двум сторонам и углу между ними.

Дано :

a = 7 см, b = 23cм, ∟ C = 130°

Найти: с , ∟ А, ∟ В

Решение :

c ² = a ² + b ² − 2bc cosC

с = √ 49 + 529 - 2×7×23×(-0,643)» 28

cos A = b ² + c ² − a ² / 2bc

cos A = (529 + 784 – 49) / 2 ×23× 28 » 0,981

∟ А » 11°

∟ В = 180° - (∟ А + ∟ C) = 180°- (11°+130°) » 39°

Ответ: c » 28, ∟ А » 11°, ∟ B » 39°.

№2

Решение треугольника по стороне и прилежащим к ней углам.

Дано:

а= 20 см, ∟ А= 75°, ∟ В= 60°

Найти: ∟ C , b , c

Решение:

∟ C = 180-(60°+75°) = 45°

a /sin A = b /sin B = c /sin C

b = a × (sin B / sin A )

b » 20×(0,866/ 0,966)»17,9

c = a × (sin C / sin A )

c = 20×(0,7/ 0,966)»14,6

Ответ: ∟ C = 45°, b » 17,9 см, c »14,6 см.

№3

Решение треугольника по трем сторонам.

Дано:

а= 7 см, b =2 см, с =8 см

Найти: ∟ А, ∟ В, ∟ С.

Решение:

cos A = (4 + 64 – 49) / 2 × 2 × 8 » 0,981

∟ А » 54°

cos B = (49 + 64 – 4) / 2 × 7 × 8 » 0,973

∟ В » 13°

∟ С = 180° - (54° + 13°) = 113°

Ответ: ∟ А » 54°, ∟ В » 13°, ∟ С = 113°

№4

Измерение высоты предмета.

Предположим, что требуется определить высоту АН какого – то предмета. Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим ∟АВН=a. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = а tg a.

Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: ∟АВН =a, ∟АСВ = b, ∟ВАС = a –b.Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ: АВ = asinb/ sin (a –b). Из прямоугольного треугольника АВН находим высоту АН предмета:

АН = АВ sin a= a sina sinb / sin ( a –b).

№5

Измерение расстояния до недоступной точки (измерение ширины реки).

На местности выберем точку В и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В: ∟А= a и ∟В = b. Эти данные, т.е. с , a и b, позволяют решить ∆АВС и найти искомое расстояние d=AC.

Находим ∟С и sinC : ∟С= 180°- a –b, sin C= sin(180°- a –b) = sin(a+b).

Так как d/sinb = c/sinC, то в = csinb/ sin(a+b).

III Заключение.

Список литературы.

1. Анатасян Л.С., Бутузов В.Ф. Геометрия 7-9 класс – 12-е изд.-М.: Просвещение, 2002г., стр.157-159, 256-261

2. Балк М.Б., Балк Г.Д. «Математика после уроков», М., Просвещение, 1971., стр.56-57

3. Берманд А. Ф. Тригонометрия, 1967г., стр.4-6

4. Макарычев Ю.Н., Миндюк Н.Г. Алгебра 9 класс – 13-е изд.-М.: Просвещение, 2006г., стр.112-114

5. Понарин Я.П. Элементарная геометрия. МЦНМО, 2004., стр. 84-85.

МОУ «Средняя общеобразовательная школа №4 г.Балабаново»

Реферат

на тему:

«Решение треугольников»

Выполнила

ученица 9 б класса

Матвеева Анастасия

учитель

Заречкова Л.И.

г.Балабаново 2010