XIV муниципальная научно-практическая конференция «Ломоносовские чтения »
Изучение методов
интерполяции и аппроксимации
Выполнила учащаяся группы ФМ3.2
Сарманова Снежана Геннадьевна
Научный руководитель: Бородкин
Дмитрий Константинович,
преподаватель информатики Лицея №2
г.Ангарск, 2009
Содержание
1. Аннотация……………………………...…………………………………………………....3
2. Цель, задачи……………………………………………………………………...……….....3
3. Введение………………………………………………………………………..…….……...4
4. Линейная интерполяция………………………………………………………....……...….5
· Теория ………………………………………………………………………….........5
· Блок-схема……………………………………………………………...……………6
· Текст программы……………………………………………………………..….….7
· Пример…………………………………………………………………..……….…..7
5. Квадратичная интерполяция………….………………………………………..…………..8
· Теория…………………………………………………………………….……….. 10
· Блок-схема…………………………………………………………….....…………11
· Текст программы…………………………………………………………….……..12
· Пример……………………………………………………………………………...13
6. Инструкция по работе с программами……………............................................................16
7. Заключение…………………………………………………………………………………17
8. Список литературы………………………………………………………………………...18
Аннотация
В данной работе излагаются основные численные методы решения математических задач, возникающих при исследовании физических и технических проблем. Изложенные методы пригодны как для расчетов на ЭВМ, так и для «ручных» расчетов.
Огромное количество численных методов ставит актуальной задачей не столько создание новых, сколько исследование и классификацию старых, выявление лучших.
Данная работа будет полезна студентам, аспирантам, преподавателям университетов и технических институтов, научным работникам и инженерам-исследователям, а так же всем, кто имеет дело с численными расчетами.
Цель работы:
разработать программы вычисления значений функции f(
x)
для значений х,
не содержащихся в таблице.
Задачи:
· Изучить и проанализировать научную, справочную литературу
· Подобрать наиболее простые и лучшие методы решения уравнений первой и второй степени
· Составить алгоритм решения уравнений в виде блок-схемы
· Разработать программы в системе программирования Borland Turbo Pascal 7.0
Гипотеза:
создание программ для нахождения неизвестных значений функции в системе программирования позволит значительно сократить затраты времени по сравнению с ручными расчетами.
Введение
Если задана функция y (
x),
то это означает, что любому допустимому значению х
сопоставлено значение у
. Но нередко оказывается, что нахождение этого значения очень трудоемко. Например, у(х)
может быть определено как решение сложной задачи, в которой х
играет роль параметра, или у(х)
измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно.
Функция у(х)
может участвовать в каких-либо физико-технических или чисто математических расчетах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х)
приближенной формулой, т. е. подобрать некоторую функцию φ (х),
которая близка в некотором смысле к у(х)
и просто вычисляется. Затем при всех значениях аргумента полагают у(х)
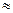φ(х)
. Близость получают введением в аппроксимирующую функцию свободных параметров а={а1
, а2
, …, а
n
}
и соответствующим их выбором. В этом случае используются такие понятия как, аппроксимация
и интерполяция
.
ИНТЕРПОЛЯЦИЯ (от лат. interpolatio — изменение, переделка
) - отыскание промежуточных значений величины по некоторым известным ее значениям. Например, отыскание значений функции f( x
) в точках x, лежащих между точками x0
по известным значениям yi = f( xi) (где i = 0,1,..., n).
Если x
лежит вне интервала ( x0
, xn
), аналогичная процедура называется экстраполяцией
.
Основная цель интерполяции
– получить быстрый (экономичный) алгоритм вычисления значений f(
x)
для значений х,
не содержащихся в таблице.
АППРОКСИМАЦИЯ (от лат. approximo — приближаюсь
) - замена одних математических объектов (наприме
р, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (например
, кривых линий близкими к ним ломаными).
Огромное количество численных методов ставит актуальной задачей не столько создание новых, сколько исследование и классификацию старых, выявление лучших. Именно поэтому в данной работе будут рассмотрены два вида интерполяции – линейная и квадратичная.
Линейная интерполяция
Простейшим и часто используемым видом локальной интерполяции является линейная ( или кусочно-линейная) интерполяция.
Она состоит в том, что заданные точки ( х
i
, у
i
) (
i=0, 1, …,
n
) соединяются прямолинейными отрезками, и функция f(х)
приближается ломаной с вершинами в данных точках.
Рис. пример интерполяции
Уравнения каждого отрезка ломаной в каждом случае разные. Поскольку имеется nинтервалов ( х
i-1
, х
i
), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение, проходящей через точки ( х
i-1
, у
i-1
) и (х
i
,
yi
), в виде
= 
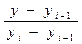Отсюда
y= ai
x + bi
; xi-1
≤ x ≤ xi
, (1)
 ,
bi
=
yi
-1
–
ai
xi
-1
.
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х
, а затем подставить его в формулу (1) и найти приближенное значение функции в этой точке.
Данный алгоритм представлен на рисунке
Нет
 Да
Нет
Текст программы:
Program interpol;
Const N=3;
Var x: array [1..N] of real;
y: array [1..N] of real;
a, b, xр, yр : real;
i: integer;
begin
for i:=1 to N do
begin{ввод данных через массивы
}
writeln (‘x[‘,i,’]=’);
readln (x[i]);
writeln (‘y[‘,i,’]=’);
readln (y[i]);
end;
write (‘vveditex=’); {ввод промежуточного значения}
readln (xр);
for i:=2 to N do
if (x[i-1]<=xp) and (xp<=x[i-1]) then
begin
a:= (y[i] – y[i-1]) / (x[i] – x[i-1]);
b:= y [i-1] – a*x[i-1];
yр:= a*xр + b
else writeln (‘ekstrepolyazia’);
readln;
end;
writeln (‘y=’, yр); {вывод искомого значения}
readln;
end.
Пример
. Найти значение функции y=f(x),
изображенной на рисунке, при х=1
Воспользуемся формулой линейной интерполяции(1). Значение х=1 находится между точками хi
=2 и хi-1
= 0. Отсюда имеем
= 
bi
= yi
-1
– ai
٠xi
-1
= 4 – 0.5٠0=4
у= а٠хр
+b = -0.5 ٠1 + 4 = 3.5
Результаты выполнения программы
На рисунке 1 показан вид окна программы при вводе исходных данных
Рис.1
На рисунке 2 представлен вид окна программы после вывода результатов
Рис.2
Исполнимый модуль программы находится в файле с именем interpol1.
exe
Пример 2.
Если в два часа ночи температура воздуха была +10, а в шесть утра - +25,
то используя линейную интерполяцию можно предположить
что в три часа ночи температура воздуха была равна
(25 - 10) / (6 - 2) * (3 - 2) + 10 = 13.75
Квадратичная интерполяция
В качестве интерполяционной функции на отрезке [х
i-1
,
xi
+
1
] принимается квадратный трехчлен. Такую интерполяцию называют также параболической.
Уравнение квадратного трехчлена
y = ai
x2
+ bi
x + ci
, xi-1
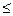 xi
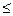xi+1
(2)
содержит три неизвестных коэффициента ai
,
bi
,
ci
, для определения которых необходимы три уравнения. Ими служат условия прохождения параболы (2) через три точки ( xi
-1
,
yi
-1
),
(xi
,
yi
), (xi
+1
,
yi
+1
). Эти условия можно записать в виде
yi-1
= ai
x2
i-1
+ bi
xi-1
+ ci
yi
= ai
x2
i
+ bi
xi
+ ci
(3)
yi
+1
=
ai
x2
i+1
+
bi
xi
+1
+
ci
Данная система уравнений решается методом Крамера.
Определители:
Решение:
Алгоритм нахождения приближенного значения функции с помощью квадратичной интерполяции можно записать в виде структурограммы, как и для случая линейной интерполяции. Вместо формулы (1) нужно использовать (2) с учетом решения системы линейных уравнений (3). Интерполяция для любой точки x є
[xo
,
xn
] приводится по трем ближайшим к ней узлам.
Данный алгоритм представлен на рисунке
Да
Program interpol2;
Const N=3;
Var x: array [1..N] of real;
y: array [1..N] of real;
a, b, c, xр, yр, deltaA, deltaB, deltaC, delta : real;
i: integer;
begin
for i:=1 to N do
begin{ввод данных через массивы
}
writeln (‘x[‘,I,’]=’);
readln (x[i]);
writeln (‘y[‘,I,’]=’);
readln (y[i]);
end;
write (‘vvedite x’); {
ввод
промежуточного
значения
}
readln (xр);
for i:=2 to N do
if (x[i-1]<=xр) and (xр<=x[i-1]) then
begin{вычисления}
delta:= x[i-1]*x[i-1]*x[i] – x[i-1]*x[i-1]*x[i+1]+ x[i-1]*x[i+1]*x[i+1] – x[i-1]*x[i]*x[i] – x[i+1]*x[i+1]*x[i]+ x[i+1]*x[i]*x[i];
deltaA:= x[i+1]*y[i]– x[i-1]*y[i] +y[i-1]*x[i]-x[i+1]*y[i-1] – y[i+1]*x[i]+x[i-1]*y[i+1];
deltaB:=x[i-1]*x[i-1]*y[i] – x[i+1]*x[i+1]*y[i]-
y[i-1]*x[i]*x[i] + y[i+1]*x[i]*x[i] – x[i-1]*x[i-1]*y[i+1] + x[i+1]*x[i+1]*y[i-1];
deltaC:= y[i+1]*x[i-1]*x[i-1]*x[i] – y[i]*x[i-1]*x[i-1]*x[i+1] + y[i]*x[i-1]*x[i+1]*x[i+1]- y[i+1]*x[i-1]*x[i]*x[i] –y[i-1]*x[i+1]*x[i+1]*x[i] + y[i-1]*x[i+1]*x[i]*x[i];
a:= delta/deltaA;
b:=delta/deltaB;
c:= delta/ deltaC;
yр:= a*xр*xр + b*xр +c;
end;
writeln (‘y=’, yр); {вывод искомого значения}
readln;
end.
Пример
. Найти приближенное значение функции y =
f (
x)
при x
= 2.5, если известна следующая таблица её значений:
Найдем приближенное значение функции с помощью формулы квадратичной интерполяции (2) . Составим систему уравнений (3). С учетом ближайших к точке x = 2.5 узлов xi
-1
= 2 , xi
= 3,
xi
+1
= 4. Соответственно yi
-1
= 2 , yi
= 4yi
+1
= 7. Система (3) запишется в виде
22
ai
+ 2bi
+ ci
= 2;
32
ai
+ 3bi
+ ci
= 4
42
ai
+ 4bi
+ ci
= 7.
4 2 1
 9 3 1 = 4٠3-4٠4+2٠16 -2٠9 – 16٠3+ 4٠9= -2
16 4 1
2 2 1
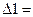 4 3 1 = 2٠3 -2٠4 +2٠3 – 4٠2 - 7٠3 +2٠7= -1
7 4 1
4 2 1
 9 4 1 = 4٠4- 16٠4 -2٠9 + 7٠9 - 4٠7+16٠2= 1
16 7 1
 4 2 2
 9 3 4 =7٠4٠3 – 4٠4٠4 + 4٠2٠16 – 7٠2٠9 – 2٠16٠3 + 2٠4٠9= -2
16 4 7
 
 ; 
 
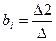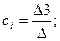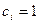
Решая эту систему, находимai
=0.5 , b
i
= -0.5, ci
= 1. Искомое значение функции
y
(2.5)2
٠0.5 + 2.5٠(-0.5) + 1
2.875.
На рисунке 1 показан вид окна программы при вводе исходных данных
Рис.1
На рисунке 2 представлен вид окна программы после вывода результатов
Рис.2
Исполнимый модуль программы находится в файле с именем
interpol2.
exe
Инструкция по работе с программами
Исполнимые модули программ находятся в файле с именами interpol.
exe и
interpol2.
exe
, запускаются на выполнение в операционной системе ее средствами.
После запуска программы пользователь должен ввести исходные данные, как это показано на рисунке 1 (см. стр.8, 14) После ввода исходных данных программа производит вычисления и выводит результат на экран в том же окне, что и исходные данные, как это показано на рисунке 2(см. стр.9,15). Чтобы завершить работу программы, пользователь должен нажать любую клавишу.
Составленные программы решают задачу интерполирования таблично заданной функции с произвольным расположением узлов. Как показывает анализ результатов, вычисления, производимые программами, верны.
Заключение
В данной работе была изучена и проанализирована справочная литература, вследствие чего были выявлены два наиболее простых и удобных вида интерполяции – линейная и квадратичная; созданы программы в системе программирования Borland Turbo Pascal 7.0 для вычисления значений функции f(
x)
и разработан быстрый (экономичный) алгоритм решения этой функции, предоставленный в виде блок-схем.
Список использованных источников
1. Калиткин Н.Н.. Численные методы. – М.: Наука, 1982.
2. Марчук Г.И. Методы вычислительной математики – М.: Наука, 1977.
3. Носач В.В. Решение задач аппроксимации с помощью персональных компьютеров.. М.: Бином, 1994
4. Самарский А.А. Численные методы. – М.: Наука, 1989.
|