Решение задачи о кратчайшем маршруте методом Форда
1. Постановка сетевой транспортной задачи.
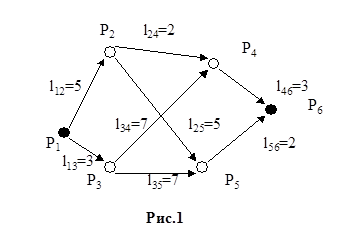
На практике часто встречается задача определения кратчайшего маршрута по заданной сети из начального пункта до конечного пункта маршрута. Транспортная сеть может быть представлена в виде графа (рис.1), дуги которого - транспортные магистрали, а узлы - пункты отправления и назначения. Графически транспортная сеть изображается в виде совокупности n пунктов P1
,P2
,...,Pn
, причем некоторые упорядоченные пары (Pi
,Pj
) пунктов назначения соединены дугами заданной длинны r(Pi
,Pj
)=lij
. Некоторые или все дуги могут быть ориентированы, т.е. по ним возможно движение только в одном направлении, указанном стрелками.
На рис.1 построена ориентированная транспортная сеть, содержащая шесть пунктов P1
,P2
,...,P6
, которые связаны между собой восьмью транспортными путями.
Необходимо определить кратчайший маршрут из пункта P1
в P6
. Определение кратчайшего маршрута состоит в указании последовательности прохождения маршрута через промежуточные пункты и суммарной длинны маршрута.
Например маршрут из пункта P1
в пункт P6
: P1
P2
P4
P6
; L=l12
+l24
+l46
=10.
Постановка задачи приобретает смысл в том случае, если имеется несколько вариантов маршрута из начального пункта в конечный. В этом случае физический смысл функции цели задачи состоит в минимизации общей длинны маршрута, т.е. в определении кратчайшего пути из P1
в Pn
.
2. Описание метода и алгоритма решения.
Метод Форда бал разработан специально для решения сетевых транспортных задач и основан, по существу, на принципе оптимальности.
Алгоритм метода Форда содержит четыре этапа (схема 1). На первом этапе производится заполнение исходной таблицы расстояний от любого i-го пункта в любой другой j-й пункт назначения. На втором этапе определяются для каждого пункта некоторые параметры li
и lj
по соответствующим формулам. Далее на третьем этапе определяются кратчайшие расстояния. Наконец, на четвертом этапе определяются кратчайшие маршруты из пункта отправления Р1
в любой другой пункт назначения Рj
, j=1,2,...,n.
Рассмотрим подробнее каждый из этих четырех этапов.
2.1 Первый этап: Составление исходной таблицы расстояний.
Данная таблица содержит n+1 строк и такое же количество столбцов; Pi
- пункты отправления; Pj
- пункты назначения. Во второй строке и втором столбце проставляется значения параметров li
иlj
, определение значений которых производятся на втором этапе решения задачи. В остальных клетках таблицы проставляются значения расстояний lij
из i-го пункта в j-й пункт. Причем заполняем клетки таблицы, лежащие выше главной диагонали. Если пункт Pi
не соединен отрезком пути с пунктом Pj
, то соответствующая клетка таблицы не заполняется.
2.2 Второй этап: Определение li
и lj
.
Определяется значение параметров в соответствии с формулой:
lj
=min(li
+lij
); i=1,2,...,n; j=1,2,...,n, (1)
где l1
=0.
Эти значения заполняются во второй строке и во втором столбце.
2.3 Третий этап: Определение длинны кратчайших путей.
Возможны два случая определения длинны кратчайших путей из пунктов Pi в пункты Pj
, i=1,2,...,n; j=1,2,...,n.
В первом случае, если выполняются неравенство:
lj
- li
£ lij
; lij
¹0; j=1,2,...,n; j=1,2,...,n, (2)
то значения параметров l1
,...,ln
удовлетворяют условиям оптимальности. Каждое значение lj
есть не что иное, как кратчайшее расстояние от пункта Pi
до пункта Pj
, j=2,3,...,n.
Во втором случае, если для некоторых клеток (i,j) таблицы имеет место неравенство:
lj
- li
> lij
; i=1,...,n; j=1,...,n, (3)
то значения lj
иli
могут быть уменьшены.
Если справедливо (3), тогда исправим значение lj0
, пересчитав его по формуле:
l¢j0
=li0
+li0j0
. (4)
2.4 Четвертый этап: Нахождение кратчайшего пути.
Определения последовательности пунктов кратчайшего маршрута. С этой целью для каждого столбца определяют величину:
lr1,j
= lj
- lr1
, (5)
где lr1,j
берется из таблицы, причем lr1
выбирается так, чтобы выполнилось равенство (5). Таким образом определим r1. Далее продолжим ту же операцию, но будем считать, последней не Pn
, а Pr1
. Будем продолжать до тех пор, пока rn
=1.
Таким образом кратчайший маршрут проходит через Pr1
,Pr2
,...,Prn
, а длинна маршрута Lmin=lr2,r1
+lr3,r2
+...+lrn-1,rn
.
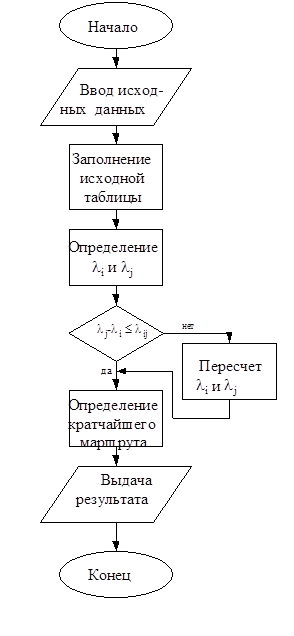
3. Описание программы.
Программа “FORD” написана на языке высокого уровня - Pascal, в интегрированной среде разработки “Turbo Pascal 7.0” фирмы Borland Inc.
Программа предназначена для нахождения кратчайшего пути в сетевом графе по методу Форда. Программа легка в использовании, что достигается за счет использования дружественного интерфейса и иерархического меню. Вначале программы производится ввод данных, затем нахождение кратчайшего маршрута и вычисление его длинны, далее выводится результат. Вывод результатов возможен как в файл, так и на экран.
В программе предусмотрена возможность повторного решения задачи с другими исходными данными.
4. Описание подпрограмм и процедур.
Подпрограммы и функции.
ТИП
|
НАЗВАНИЕ
|
НАЗНАЧЕНИЕ
|
Function
type : real
|
min; |
Вычисляет минимальное значение вектора k[i]; |
| Procedure |
set_graph_mode; |
Устанавливает графический режим; |
| Procedure |
install_firewall; |
Инициализирует огонь; |
| Procedure |
fire; |
Процедура рисования огня; |
| Procedure |
ok; |
Выводит сообщение о корректности операции; |
| Procedure |
notok; |
Выводит сообщение о некорректности операции; |
| Procedure |
check_input_data; |
Проверяет корректность ввода данных; |
| Procedure |
keybord_input; |
Ввод исходных данных с клавиатуры; |
| Procedure |
ramka; |
Выводит рамку по краям экрана; |
| Procedure |
save; |
Сохранение результатов в файл; |
| Procedure |
about_program; |
Выводит информацию о программе; |
| Procedure |
about_method; |
Выводит информацию о методе Форда; |
| Procedure |
output_graph; |
Рисует вершины графа; |
| Procedure |
draw_ways; |
Рисует дуги графа; |
| Procedure |
draw_short_way; |
Рисует кратчайший маршрут; |
| Procedure |
count_point_coord; |
Вычисляет экранные координаты вершин графа; |
| Procedure |
set_font; |
Инициализирует шрифт пользователя; |
| Procedure |
calculate; |
Основное математическое ядро программы; |
| Procedure |
draw_menu; |
Открытие меню; |
| Procedure |
redraw_menu; |
Закрытие меню; |
| Procedure |
main_menu; |
Основной механизм меню; |
| Procedure |
pixel; |
Ставит точку; |
| Procedure |
stars; |
Инициализирует массив со звездами; |
| Procedure |
welcomescreen; |
Заставка; |
4.2 Таблица идентификаторов.
ИМЯ
|
тИП
|
НАЗНАЧЕНИЕ
|
| Константы
|
| menu |
array of string |
Описывает меню программы |
| menuof |
array of byte |
Описывает меню программы |
| menugo |
array of byte |
Описывает меню программы |
| name1 |
string |
Имя файла входных данных |
| name2 |
string |
Имя файла выходных данных |
| xxx |
word |
Размер огня по х |
| yyy |
word |
Размер огня по у |
| xx1 |
word |
Координата х огня |
| yy1 |
word |
Координата у огня |
| messize |
byte |
Размер заглавия |
| title |
array of string |
Заглавие |
| Переменные
|
| mas |
array of real |
Основная матрица вычислений |
| coord_point |
array of real |
Координаты вершин графа |
| i |
integer |
Переменная для организации цикла |
| j |
integer |
Переменная для организации цикла |
| t |
integer |
Используется при расчете пути |
| m |
integer |
Счетчик кол-ва вершин в крат. Пути |
| n |
integer |
Кол-во вершин в графе |
| z |
integer |
Код ошибки |
| x1 |
integer |
Исп. в процедуре вывода на экран |
| y1 |
integer |
Исп. в процедуре вывода на экран |
| x2 |
integer |
Исп. в процедуре вывода на экран |
| y2 |
integer |
Исп. в процедуре вывода на экран |
| kk |
integer |
Промежуточное значение |
| iii |
integer |
Промежуточное значение |
| x |
integer |
Координата х конца отрезка |
| y |
integer |
Координата у конца отрезка |
| lenth |
integer |
Кол-во вершин в кратчайшем маршруте |
| chrus |
integer |
Номер шрифта пользователя |
| z1 |
integer |
Номер графического драйверв |
| z2 |
integer |
Номер графического режима |
| k |
array of real |
Используется для нахождения минимума |
| result |
array of integer |
Номера вершин, которые входят в кратчайший маршрут |
| error_code |
array of byte |
Коды ошибок при вводе данных |
| fire1 |
array of byte |
Хранит цвета огня |
| fire2 |
array of byte |
Матрица промежуточных данных |
| aa |
real |
Используется при вычислении координат вершин графа |
| pi1 |
real |
Используется при вычислении координат вершин графа |
| s |
real |
Хранит промежуточное значение |
| l |
boolean |
Исп. при определении кратчайшего маршрута |
| inputdata |
boolean |
TRUE, если данные вводились |
| calculatedata |
boolean |
TRUE, если данные били обработаны |
| mov |
boolean |
Используется в процедуре меню |
| o |
string |
Используется при вводе с клавиатуры |
| temp |
byte |
Хранит временное значение |
| cursor |
byte |
Координаты курсора меню |
| lastcursor |
byte |
Последние координаты курсора меню |
| menulevel |
byte |
Уровень меню |
| nline |
byte |
Кол-во строк в текушем уровне меню |
| pressed |
char |
Используется при вводе с клавиатуры |
| f1 |
text |
Файловая переменная |
| f2 |
text |
Файловая переменная |
5. Примеры решения контрольных задач.
Исходная таблица расстояний для одного из вариантов ранжированного графа:
| Pi
/Pj
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
X |
5 |
3 |
| 2 |
X |
2 |
5 |
| 3 |
X |
7 |
7 |
| 4 |
X |
3 |
| 5 |
X |
2 |
| 6 |
X |
После обработки таблицы с заданными исходными данными, программа выдает следующие результаты:
- кратчайший маршрут: 1-2-4-6
- длинна кратчайшего маршрута: 10
Исходная таблица расстояний для одного из вариантов не ранжированного графа:
| Pi
/Pj
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
X |
1 |
6 |
2 |
| 2 |
X |
1 |
| 3 |
8 |
X |
| 4 |
2 |
X |
5 |
| 5 |
1 |
3 |
X |
9 |
| 6 |
X |
После обработки таблицы с заданными исходными данными, программа выдает следующие результаты:
- кратчайший маршрут: 1-5-4-2-6
- длинна кратчайшего маршрута: 8
Программа работоспособна при любых других вариантах исходных данных.
6. Выводы.
Анализ алгоритма операций, необходимых при решении сетевой транспортной задачи методом Форда в заданной постановке подтверждает:
Достижение конечного результата производится в четыре этапа.
Каждый этап описывается простыми математическими операциями и может быть записан на одном из языков программирования.
Составлена программа на алгоритмическом языке высокого уровня “Pascal”, позволяющая решать задачу в диалоговом режиме, удобном для пользователя не программиста.
Алгоритм решения транспортной задачи методом Форда является универсальным, что позволяет производить расчёты как с ранжированными, так и с не ранжированными графами (примеры решения задачи приведены на странице 11).
Возможность реализаций для удобства работы пользователя в программе сервисной части.
Возможность неоднократного решения задачи методом Форда при различных исходных данных.
PROGRAM
ford
;
uses
crt,graph;
const
menu:array[0..4,1..6] of string =
(('Ввод данных','Решение задачи','Вывод результата',
'О методе','О программе','Выход'),
('Ввод данных','Просмотр данных','Назад','','',''),
('Экран','Файл','Назад','','',''),
('Клавиатура','Файл','Назад','','',''),
('Да','Нет','','','',''));
menuof:array[0..4] of byte =(6,3,3,3,2);
menugo:array[0..4,1..6] of byte = ((1,0,2,0,0,4), (3,0,0,0,0,0), (0,0,0,0,0,0), (0,0,1,0,0,0), (0,0,0,0,0,0));
name1='input.dat';
name2='output.dat';
xxx=140;
yyy=20;
xx1=10;
yy1=140;
messize=3;
col:array[16..31] of byte=(0,186,113,4,40,41,41,42,42,43,44,69,15,15,15,15);
title:array[0..messize] of string = ('АЛГОРИТМИЧЕСКИЕ МЕТОДЫ',
' ИССЛЕДОВАНИЯ ОПЕРАЦИЙ ', ' ', ' Метод Форда ');
type
matr = array[0..20,0..20] of real;
coord = array [1..20,1..2] of real;
var
mas:matr;
coord_point:coord;
i,j,t,m,n,z,x1,y1,x2,kk,iii,y2,x,y,lenth,chrus,z1,z2:integer;
k:array[1..20] of real;
result:array[1..20] of integer;
error_code:array[1..5] of byte;
fire1:array[1..yyy,1..xxx] of byte;
fire2:array[1..yyy,1..xxx] of byte;
mask:array[1..6] of byte;
starx:array[1..500] of word;
stary:array[1..500] of word;
starc:array[1..500] of byte;
aa,cc,pi1,s:real;
l,inputdata,calculatedata,move:boolean;
o:string;
temp,cursor,lastcursor,menulevel,nline,step:byte;
pressed:char;
f1,f2:text;
FUNCTION min:real;
begin
s:=0;
for i:=1 to n do
if (s=0) and (k[i]<>-1) then s:=k[i]
else if(k[i]<s) and (k[i]<>-1)
then s:=k[i];
min:=s;
end
;
PROCEDURE set_graph_mode;
begin
z1:=installuserdriver('svga256',nil);
initgraph(z1,z2,'');
cleardevice;
end
;
PROCEDURE pixel(x:word;y,col:byte);
begin
asm
mov bx,x
mov cl,y
mov dl,col
mov ax,0a000h
mov es,ax
mov al,0a0h
mul cl
add ax,ax
add bx,ax
mov [es:bx],dl
end
;
end
;
PROCEDURE install_firewall;
begin
for i:=1 to yyy do
for j:=1 to xxx do
begin
fire1[i,j]:=0;
fire2[i,j]:=0;
end
;
end
;
PROCEDURE fire;
begin
for i:=1 to yyy-1 do
for j:=1 to xxx do
begin
pixel(j*2+xx1,i*3+yy1,col[fire1[i,j]]);
pixel(j*2+xx1,i*3+yy1-1,col[fire1[i,j]]);
pixel(j*2+xx1,i*3+yy1-2,col[fire1[i,j]]);
end
;
for j:=1 to xxx do
begin
kk:=random(8);
if kk<3 then fire1[yyy,j]:=16
else fire1[yyy,j]:=round(31-kk);
end
;
for i:=yyy-1 downto 1 do
for j:=2 to xxx-1 do
begin
fire2[i,j]:=round((fire1[i+1,j]+fire1[i+1,j-1]+fire1[i+1,j+1]-random(4))/3);
if (fire2[i,j]<16) or (fire2[i,j]>31) then fire2[i,j]:=16;
end
;
for i:=1 to yyy do
for j:=1 to xxx do
fire1[i,j]:=fire2[i,j];
end
;
PROCEDURE ok;
begin
cleardevice;
setcolor(1);
rectangle(120,100,520,220);
rectangle(100,120,540,200);
setcolor(14);
outtextxy(180,130,'Опeрация произведена');
outtextxy(250,160,'корректно.');
repeat until keypressed;
end
;
PROCEDURE notok;
begin
cleardevice;
setcolor(4);
rectangle(120,100,520,220);
rectangle(100,120,540,200);
setcolor(14);
outtextxy(180,130,'Опeрация произведена');
outtextxy(230,160,'не корректно.');
repeat until keypressed;
end
;
PROCEDURE check_input_data;
begin
inputdata:=true;
for i:=1 to 5 do
error_code[i]:=0;
for i:=0 to n do
begin
if mas[i,1]<>-1 then error_code[1]:=1;
if mas[n,i]<>-1 then error_code[2]:=1;
if mas[i,i]<>-1 then error_code[3]:=1;
end
;
for i:=1 to n do
for j:=1 to n do
begin
if (mas[i,j]<>-1) and (mas[j,i]<>-1) then error_code[4]:=1;
if (mas[i,j]<0) and (mas[i,j]<>-1) then error_code[5]:=1;
end
;
clrscr;
if error_code[1]<>0 then
writeln('Ошибка: Не существует истока.');
if error_code[2]<>0 then
writeln('Ошибка: Не существует стока.');
if error_code[3]<>0 then
writeln('Ошибка: Существует дуга из одной вершины в ту же вершину.');
if error_code[4]<>0 then
writeln('Ошибка: Существует две дуги из одной вершины в другую.');
if error_code[5]<>0 then
writeln('Ошибка: Существует дуга с отрицительной нагрузкой.');
for i:=1 to 5 do
if error_code[i]<>0 then inputdata:=false;
if (z<>0) or (round(n)<>n) or (n<2) or (n>20) then inputdata:=false;
calculatedata:=false;
end
;
PROCEDURE keyboard_input;
begin
z:=0;
closegraph;
clrscr;
write('Введите колличество пунктов(2-20): ');
readln(o);
val(o,n,z);
if (z<>0) or (round(n)<>n) or (n<2) or (n>20) then check_input_data;
writeln(' Введите нагрузку. Если дуга не существует, то нажмите Enter.');
writeln;
for i:=1 to n-1 do
for j:=i to n do
if i<>j then
begin
write(' Введите нагрузку от ',i,'-й вершины до ',j,'-й вершины:');
readln(o);
if o<>'' then val(o,mas[i,j],z)
else mas[i,j]:=-1;
if z<>0 then exit;
end
;
check_input_data;
set_graph_mode;
settextstyle(chrus,0,2);
if inputdata=true then ok
else notok;
end
;
PROCEDURE ramka;
begin
cleardevice;
setcolor(1);
rectangle(30,10,610,470);
rectangle(10,30,630,450);
end
;
PROCEDURE save;
begin
assign(f2,name2);
rewrite(f2);
write(f2,'Кратчайший маршрут: ');
for i:=1 to lenth do
write(f2,result[lenth-i+1]);
writeln(f2,'');
write(f2,'Длинна кратчайшего маршрута: ');
write(f2,round(mas[0,n]));
close(f2);
ok;
end
;
PROCEDURE about_program;
begin
ramka;
settextstyle(chrus,0,5);
setcolor(14);
outtextxy(160,30,'О программе');
settextstyle(chrus,0,1);
setcolor(12);
outtextxy(40,100,'Программа: ');
outtextxy(40,150,'Версия: ');
outtextxy(40,175,'Назначение: ');
outtextxy(40,240,'Автор: ');
outtextxy(40,265,'Дата: ');
setcolor(8);
outtextxy(200,100,'Решение задачи о кратчайшем');
outtextxy(200,120,'маршруте методом Форда.');
outtextxy(200,150,'v1.0');
outtextxy(200,175,'Курсовой проект по дисциплине');
outtextxy(200,195,'"Алгоритмические методы иссле-');
outtextxy(200,215,'дования опираций"');
outtextxy(200,240,’’);
outtextxy(200,265,'декабрь 1998 года');
setcolor(11);
outtextxy(50,395,'для большей информации смотрите README.TXT');
repeat until keypressed;
end
;
PROCEDURE about_metod;
begin
ramka;
settextstyle(chrus,0,5);
setcolor(14);
outtextxy(130,30,'О методе Форда');
settextstyle(chrus,0,1);
setcolor(8);
outtextxy(40,90,'Метод Форда был разработан специально для');
outtextxy(50,110,'решения сетевых транспортных задач и осно-');
outtextxy(50,130,'ван, по существу на принципе оптимальности.');
outtextxy(40,150,'Алгоритм метода Форда содержит четыре этапа.');
outtextxy(50,170,'На первом этапе производится заполнение ис-');
outtextxy(50,190,'ходной таблицы расстояний от любого i-го');
outtextxy(50,210,'пункта в любой другой j-й пункт назначения');
outtextxy(50,230,'На втором этапе определяются для каждого');
outtextxy(50,250,'пункта некоторые параметры Ai и Aj по соот-');
outtextxy(50,270,'ветствующим формулам и правилам. Далее на');
outtextxy(50,290,'третьем этапе определяется кратчайшее рас-');
outtextxy(50,310,'стояние. Наконец, на четвертом этапе опре-');
outtextxy(50,330,'деляются кратчайшие маршруты из пункта');
outtextxy(50,350,'отправления Р1 в любой пункт назначения Рj,');
outtextxy(50,370,'j=2,3,...,n.');
repeat until keypressed;
end
;
PROCEDURE output_graph;
begin
settextstyle(chrus,0,1);
for i:=1 to n do
begin
setcolor(10);
fillellipse(round(coord_point[i,1]),round(coord_point[i,2]),15,15);
setcolor(15);
str(i,o);
if i>9 then outtextxy(round(coord_point[i,1]-12),
round(coord_point[i,2]-12),o)
else outtextxy(round(coord_point[i,1]-7),
round(coord_point[i,2]-12),o);
end
;
repeat until keypressed;
end
;
PROCEDURE draw_ways;
begin
settextstyle(chrus,0,2);
for i:=1 to n do
for j:=1 to n do
if mas[i,j]<>-1 then
begin
x1:=round(coord_point[i,1]);
y1:=round(coord_point[i,2]);
x2:=round(coord_point[j,1]);
y2:=round(coord_point[j,2]);
setcolor(15);
line(x1,y1,x2,y2);
temp:=round(mas[i,j]);
str(temp,o);
setcolor(2);
outtextxy(round((x1+x2)/2+5),round((y1+y2)/2+5),o);
end
;
end
;
PROCEDURE draw_short_way;
begin
for i:=1 to lenth-1 do
begin
setlinestyle(0,0,3);
setcolor(red);
x:=result[i];
y:=result[i+1];
x1:=round(coord_point[x,1]);
y1:=round(coord_point[x,2]);
x2:=round(coord_point[y,1]);
y2:=round(coord_point[y,2]);
line(x1,y1,x2,y2);
end
;
settextstyle(chrus,0,1);
setcolor(14);
outtextxy(50,370,'Кратчайший маршрут: ');
for i:=1 to lenth do
begin
str(result[lenth-i+1],o);
outtextxy(300+i*15,370,o);
end
;
outtextxy(50,400,'Длинна кратчайшего маршрута: ');
str(round(mas[0,n]),o);
outtextxy(420,400,o);
end
;
PROCEDURE count_point_coord;
begin
pi1:=(2*pi)/n;
m:=0;
aa:=3*pi/2;
for i:=1 to n do
begin
coord_point[i,1]:=(cos(aa)*150)+300;
coord_point[i,2]:=(sin(aa)*150)+200;
aa:=aa+pi1;
end
;
end
;
PROCEDURE set_font;
begin
chrus:=installuserfont('fn03');
settextstyle(chrus,0,2);
end
;
PROCEDURE calculate;
begin
for i:=1 to n do
k[i]:=0;
clrscr;
mas[0,1]:=0;
mas[1,0]:=0;
{3}
for j:=2 to n do
begin
for i:=1 to n do
if (mas[0,i]<>-1) and (mas[i,j]<>-1)
then k[i]:=mas[0,i]+mas[i,j]
else k[i]:=-1;
mas[0,j]:=min;
mas[j,0]:=mas[0,j];
end
;
{4}
repeat
l:=true;
for i:=1 to n do
for j:=1 to n do
if (mas[0,j]-mas[0,i]>mas[i,j]) and (mas[i,j]<>-1) then
begin
l:=false;
mas[0,j]:=mas[0,i]+mas[i,j];
end
;
until l;
{5}
j:=n;
m:=1;
t:=0;
for i:=1 to n do
result[i]:=-1;
result[1]:=n;
repeat
inc(m);
for i:=1 to j do
begin
if (mas[i,j]<>-1) and (i<>j) and (mas[i,j]=mas[0,j]-mas[0,i])
then
begin
t:=i;
break;
end
;
end
;
result[m]:=t;
j:=t;
lenth:=m;
until j=1;
calculatedata:=true;
ok;
end
;
PROCEDURE stars;
begin
for i:=1 to 500 do
begin
starx[i]:=round(random(640));
stary[i]:=round(random(480));
starc[i]:=round(31-random(16));
end
;
end
;
PROCEDURE draw_menu;
begin
cleardevice;
for i:=1 to 500 do
putpixel(starx[i],stary[i],starc[i]);
cursor:=1;
lastcursor:=cursor;
for i:=1 to 260 do
begin
setcolor(8);
line(210+i,110,210+i,110);
setcolor(4);
line(200+i,100,200+i,100);
end
;
for j:=1 to nline*30+10 do
begin
setcolor(8);
line(210,110+j,470,110+j);
setcolor(4);
line(200,100+j,460,100+j);
end
;
setcolor(0);
for j:=1 to nline do
outtextxy(220,110+(j-1)*25,menu[menulevel,j]);
end
;
PROCEDURE redraw_menu;
begin
for j:=nline*30+10 downto 1 do
begin
setcolor(0);
line(210,110+j,470,110+j);
line(200,100+j,210,100+j);
setcolor(8);
if j<10 then
begin
setcolor(0);
line(210,100+j,470,100+j);
end
else
line(210,100+j,470,100+j);
end
;
for i:=260 downto 0 do
begin
putpixel(210+i,110,0);
putpixel(200+i,100,0);
end
;
cleardevice;
end
;
PROCEDURE main_menu;
begin
settextstyle(chrus,0,2);
draw_menu;
repeat
setcolor(0);
outtextxy(220,110+(lastcursor-1)*25,menu[menulevel,lastcursor]);
setcolor(7);
outtextxy(220,110+(cursor-1)*25,menu[menulevel,cursor]);
pressed:=readkey;
if pressed=#0 then
begin
pressed:=readkey;
move:=false;
if (pressed=#80) and (cursor=nline) then
begin
lastcursor:=nline; cursor:=1;
move:=true;
end
;
if (pressed=#72) and (cursor=1) then
begin
lastcursor:=1;
cursor:=nline;
move:=true;
end
;
if (pressed=#80) and (cursor<nline) and not(move) then
begin
lastcursor:=cursor;
inc(cursor);
end
;
if (pressed=#72) and (cursor>1) and not(move) then
begin
lastcursor:=cursor;
dec(cursor);
end
;
end
;
until pressed=#13;
redraw_menu;
if cursor=5 then about_program;
if cursor=4 then about_metod;
if (cursor=1) and (menulevel=3) then keyboard_input;
if (cursor=1) and (menulevel=4) then
begin
closegraph;
halt;
end
;
if (cursor=2) and (menulevel=1) and (inputdata=false) then notok;
if (cursor=2) and (menulevel=1) and (inputdata=true) then
begin
count_point_coord;
draw_ways;
output_graph;
end
;
if (cursor=2) and (menulevel=0) and (inputdata=true) then calculate;
if (cursor=2) and (menulevel=0) and (inputdata=false) then notok;
if (cursor=1) and (menulevel=2) and (calculatedata=false) then notok;
if (cursor=1) and (menulevel=2) and (calculatedata=true) then
begin
count_point_coord;
draw_ways;
draw_short_way;
output_graph;
end
;
if (cursor=2) and (menulevel=2) and (calculatedata=true) then save;
if (cursor=2) and (menulevel=2) and (calculatedata=false) then notok;
if (cursor=2) and (menulevel=3) then notok;
menulevel:=menugo[menulevel,cursor];
nline:=menuof[menulevel];
main_menu;
end
;
PROCEDURE welcomescreen;
begin
settextstyle(chrus,0,1);
randomize;
install_firewall;
for i:=0 to messize do
begin
setcolor(4);
outtextxy(10,iii*step+i*30,title[i]);
end
;
repeat
fire;
until keypressed;
end
;
BEGIN
for i:=0 to 20 do
for j:=0 to 20 do
mas[i,j]:=-1;
stars;
inputdata:=false;
calculatedata:=false;
menulevel:=0;
nline:=menuof[menulevel];
z2:=0;
set_graph_mode;
set_font;
welcomescreen;
closegraph;
z2:=2;
set_graph_mode;
main_menu;
repeat until keypressed;
END.
|