Классификация нефтепродуктопроводов и нефтепроводов.
Трубопровод, предназначенный для перекачки нефтей, называется нефтепроводом, а нефтепродуктов – нефтепродуктопроводом. Последние в зависимости от вида перекачиваемого продукта называют бензопроводами, мазутопроводами и т. д.
В зависимости от назначения, территориального расположения и длинны трубопроводы делят на внутренние (внутрибазовые, внутризаводские, внутрицеховые, внутри промысловые), местные (между перекачивающей станцией и нефтебазой, заводом и нефтебазой и т.д.), магистральные.
К магистральным нефтепроводам и нефтепродуктопроводам относятся:
· Нефтепроводы и отводы от них, по которым нефть подается на нефтебазы и перевалочные нефтебазы
· Нефтепродуктопроводы и отводы от них, по которым нефтепродукты с головной насосной станции подаются на нефтебазы.
Магистральный нефтепровод работает круглосуточно в течение всего года. Он имеет относительно большой диаметр и длину. Для перекачки по нему нефтей и нефтепродуктов создается давление 5,0 – 6,5 МПа.
Основные объекты и сооружения магистральных трубопроводов.
Магистральный трубопровод состоит из следующих комплексов сооружений.
1. Подводящих трубопроводов, связывающих источники нефти или нефтепродуктов с головными сооружениями трубопровода. По этим трубопроводам перекачивают нефть от промысла или нефтепродукт от завода в резервуары головной станции.
2. Головной перекачивающей станции, на которой собирают нефть и нефтепродукты, предназначенные для перекачки по магистральному трубопроводу. Здесь производят приемку нефтепродуктов, разделение их по сортам, учет и перекачку на следующую станцию.
3. Промежуточных перекачивающих станций, на которых нефть, поступающая с предыдущей станции, перекачивается далее.
4. Конечных пунктов, где принимают продукт из трубопровода, распределяют потребителям или отправляют далее другими видами транспорта.
5. Линейных сооружений трубопровода. К ним относятся собственно трубопровод, линейные колодцы на трассе, станции катодной и протекторной защиты, дренажные установки, а так же переходы через водные препятствия, железные и автогужевые дороги.
Основной составной частью магистрального трубопровода является собственно трубопровод. Глубину заложения трубопровода определяют в зависимости от климатических и геологических условий, а так же с учетом специфических условий, связанных с необходимостью поддержания температуры перекачиваемого продукта.
На трассе с интервалом 10 – 30 км, в зависимости от рельефа, устанавливают линейные задвижки для перекрытия участков трубопровода в случае аварии. Промежуточные станции размещают по трассе трубопровода согласно гидравлическому расчету. Среднее значение перегона между станциями 100 – 200 км.
Рассмотрим участок трубопровода между двумя промежуточными станциями.
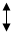    РН
РК РН
РК
D
  L L

Дано:
М = 198 [кг/с] – массовый расход
в = 1,22 [м] – диаметр трубы
К э
= 0,001 [м] – шероховатость трубы
r = 870 [кг/м3
] – плотность
u = 0,59 * 10-4
[м2
/с] - вязкость
Рн
= 5,4 * 106
[кг/мс2
] – давление
L = 1.2 * 105
[м] – длина нефтепровода
С = 1483 [м/с] – скорость света в идеальной жидкости
Т = 293°К – температура
Примем допущения:
1. Жидкость идеальна
2. Процесс стационарный
3. Процесс с распределенными параметрами
4. Трубопровод не имеет отводов
5. Трубопровод не имеет перепадов по высоте
6. Движение нефти в трубопроводе ламинарное
7. Процесс изотермический.
Прежде чем находить математическую модель линейного трубопровода выведем закон сохранения массы и закон сохранения количества движения.
Закон сохранения массы.
Этот закон гласит: масса любой части материальной системы, находящейся в движении, не зависит от времени и является величиной постоянной. Поскольку скорость изменения постоянной величины равна нулю, полная производная по времени от массы любой части рассматриваемой системы будет так же равна нулю. Математически это запишется так:
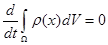 (1) (1)
где r(х) – плотность вещества х = (х1
, х2
, х3
) – координаты точки W - произвольный объем системыdV – дифференциал объема (dV = dx1
+ dx2
+ dx3
)
Это уравнение называется интегральной формой закона сохранения массы.
Движение системы можно задать тремя функциями 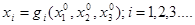 (2) (2)
определяющими в момент времени t при t = t0
точка занимала положение 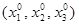 . .
Выразим начальные координаты через текущие 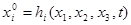 . (3) . (3)
Перейдем от координат 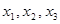 к к 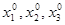 получим: получим:
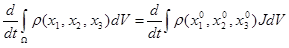 (4) (4)
где J – якобиан преобразования.
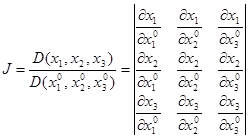 (5) (5)
Делая обратный переход от 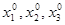 к к 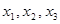 получим: получим:
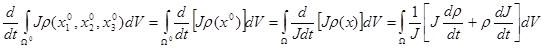 (6) (6)
По правилу дифференцирования определителей получим:
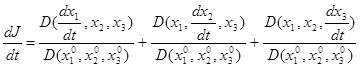 (7) (7)
примем 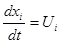
Из этого равенства и определения якобиана следует
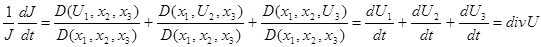 (8) (8)
С учетом этого равенства, уравнение (6) примет вид.
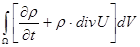 = 0 (9) = 0 (9)
Раскрывая полную производную по времени в подынтегральном выражении по правилу
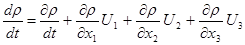 (10) (10)
приведем уравнение (9) к виду
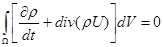 (11) (11)
В силу произвольности выбора множества W из (9) следует, что подынтегральное выражение должно быть равно нулю.
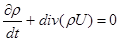 (12) (12)
Эта формула называется законом сохранения массы в дифференциальной форме.
 Для одномерного течения жидкости уравнение примет вид Для одномерного течения жидкости уравнение примет вид
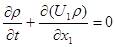 (13) (13)
Закон сохранения количества движения.
Этот закон гласит: скорость изменения количества движения любой части материальной системы, находящейся в движении, равна сумме всех внешних сил. В математическом виде этот закон запишется так:
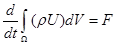 (1) (1)
где 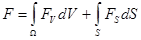 (2) (2)
Fv
– силы обусловленные силовыми полями
Fs
– силы действующие на единицу поверхности.
Подставив (2) в (1) получим интегральную форму записи закона сохранения количества движения
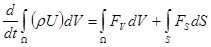 . (3) . (3)
Это векторное уравнение эквивалентно системе из трех уравнений, отражающих закон сохранения количества движения по каждой из координат х1
, х2
, х3
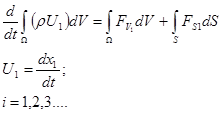 (4) (4)
Пользуясь правилами дифференцирования интеграла, взятого по изменяющемуся объему и объединяя два слагаемых, получим
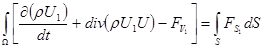 . (5) . (5)
Учитывая 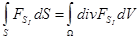 приведем (5) к виду приведем (5) к виду
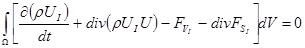 . (6) . (6)
Поскольку это равенство справедливо при произвольном объеме подынтегральное выражение (6) должно быть равно нулю
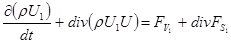 . (7) . (7)
Выражение (7) есть дифференциальная форма записи закона сохранения количества движения.
Для одномерного случая, когда все составляющие сил и скоростей по всем направлениям, кроме оси х1
, равны нулю, уравнения (5) и (7) примет вид
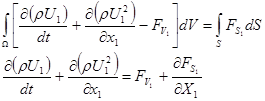 . .
Для написания математической модели линейного нефтепровода будем пользоваться этими двумя законами.
Дифференциальная форма записи линейного нефтепровода.
Рассмотрим динамическую модель нефтепровода. Запишем исходные уравнения законов сохранения массы и количества движения в интегральной форме
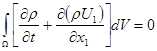 (1) (1)
  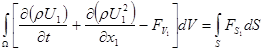 (2) (2)
    В качестве объема W выберем цилиндр, вырезанный из потока двумя перпендикулярными к оси трубы сечениями, отстоящими друг от друга на расстоянии DХ1
. Считая DХ1
малой величиной, уравнения можно записать в виде В качестве объема W выберем цилиндр, вырезанный из потока двумя перпендикулярными к оси трубы сечениями, отстоящими друг от друга на расстоянии DХ1
. Считая DХ1
малой величиной, уравнения можно записать в виде
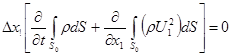 (3) (3)
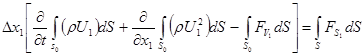 (4) (4)
где S0
– площадь основания выделенного цилиндра
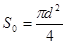 ; в – диаметр трубы. ; в – диаметр трубы.
Считая величины 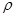 и и 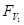 постоянными по сечению и переходя к средней скорости потока v по сечению трубы по правилу постоянными по сечению и переходя к средней скорости потока v по сечению трубы по правилу
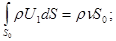 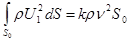 . (5) . (5)
Из уравнений (3) и (4) получим.
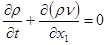 (6) (6)
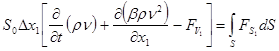 (7) (7)
Коэффициент 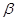 введен для учета профиля скорости по сечению трубы. Для ламинарного течения введен для учета профиля скорости по сечению трубы. Для ламинарного течения 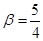 . .
Сила 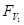 определяется полем сил тяжести определяется полем сил тяжести
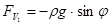 . (8) . (8)
Силу 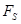 , действующую на поверхность объема интегрирования, разделим на две составляющие: , действующую на поверхность объема интегрирования, разделим на две составляющие:
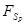 - сила, обусловленная разностью давлений на основании цилиндра - сила, обусловленная разностью давлений на основании цилиндра
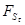 - сила, определяемая трением объема стенки - сила, определяемая трением объема стенки
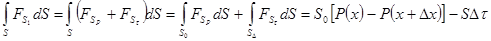 (9) (9)
здесь 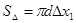 - боковая поверхность цилиндра - боковая поверхность цилиндра
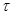 - касательное напряжение трения на стенке трубы - касательное напряжение трения на стенке трубы
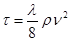 ; ; 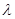 - коэффициент сопротивления. - коэффициент сопротивления.
Раскладывая 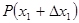 в ряд Тейлора и ограничившись первыми двумя членами, получим. в ряд Тейлора и ограничившись первыми двумя членами, получим.
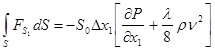 (10) (10)
Подставив (8) и (10) в (7), запишем законы сохранения массы и количества движения для движения жидкости по нефтепроводу в следующем виде:
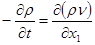 (11) (11)
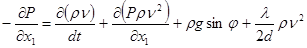 (12) (12)
Введем дополнительное уравнение. Это соотношение между скоростями изменения плотности и давления:
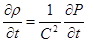 (13) (13)
где С – скорость звука в жидкости.
Второе уравнение можно упростить объединив слагаемые 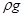 и и 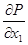 . Такое упрощение возможно, если принять суммарное давление в точке х равным . Такое упрощение возможно, если принять суммарное давление в точке х равным  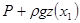 , где , где 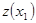 - высота подъема трубопровода от нулевой точки. В нашем случае - высота подъема трубопровода от нулевой точки. В нашем случае 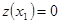 . Слагаемое . Слагаемое 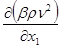 - характеризует изменение давления вдоль трубопровода за счет скорости напора. - характеризует изменение давления вдоль трубопровода за счет скорости напора.
Для несжимаемой жидкости, когда 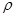 и и 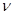 вдоль трубы постоянны, это слагаемое равно нулю. Учитывая уравнение (13), получим обычно используемую математическую модель для описания движения жидкости в линейном трубопроводе: вдоль трубы постоянны, это слагаемое равно нулю. Учитывая уравнение (13), получим обычно используемую математическую модель для описания движения жидкости в линейном трубопроводе:
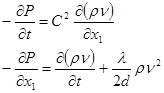 (14) (14)
Система уравнений (14) нелинейна.
Линеаризуем эту систему, приняв во внимание  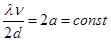
Линеаризованная система имеет вид:
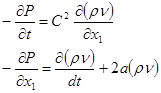 (15) (15)
Приняв во внимание, что в длинном нефтепроводе у нас будут отсутствовать инерционные силы, первое слагаемое во втором уравнении можно принять равным нулю.
Система уравнений примет вид:
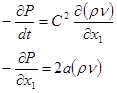 (16) (16)
Перейдем к реальным параметрам трубопровода. 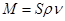 – массовый расход. – массовый расход.
Получим:
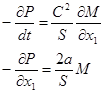 (17) (17)
Примем 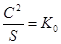 а а 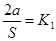 . .
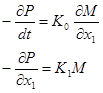 (18) (18)
Система дифференциальных уравнений (18) является математической моделью линейного нефтепровода.
Статический режим работы линейного нефтепровода.
Для рассмотрения статического режима линейного нефтепровода воспользуемся вторым уравнением системы (18)
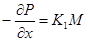 где где 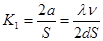 . .
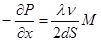
Т.к. 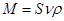 получим. получим.
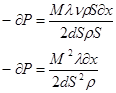
Приняв во внимание то, что  получим. получим.
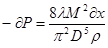
Проинтегрировав это уравнение
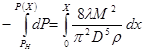
получим: 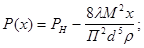 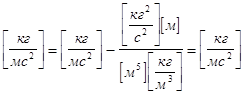
Коэффициент гидравлического сопротивления определяется по формуле А. Д. Альтшуля.
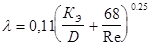 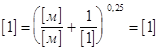
Число Рейнольдса 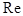 определяется по формуле определяется по формуле 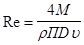 где где 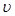 – вязкость. Число Рейнольдса безразмерная величина. – вязкость. Число Рейнольдса безразмерная величина.
Проверим.
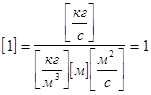
Вычислим число Рейнольдса:
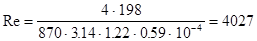 . .
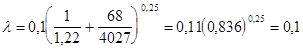
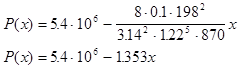
Построим график статического режима линейного трубопровода.

Динамический режим работы линейного нефтепровода.
Допустим, что у нас был установившийся режим, характеризующийся при:
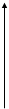 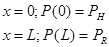 . .
Пусть в какой-то момент времени t = 0 на входе Р
 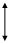 был создан скачек: был создан скачек: 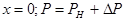 , но давление на , но давление на
выходе нефтепровода не изменилось. Нас будет ин-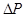
 тересовать как изменится давление в любой точке t тересовать как изменится давление в любой точке t
нефтепровода.
Воспользуемся ранее выведенной системой дифференциальных уравнений (18).
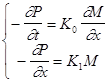 где где 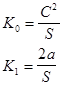 (1) (1)
Дифференцируя второе уравнение по х и учитывая первое, получим уравнение:
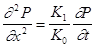 . (2) . (2)
Для упрощения уравнения примем 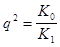 , тогда уравнение запишем: , тогда уравнение запишем:
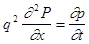 . (3) . (3)
Напишем для него начальные и граничные условия:
Начальные условия: 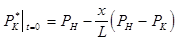 . .
при:  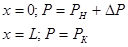
где 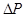 есть единичный скачек. есть единичный скачек.
Решим уравнение (3) используя метод преобразования Лапласа.
Для этого, вместо Р введем вспомогательную величину Р*
, такую что
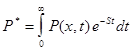 где S - оператор (4) где S - оператор (4)
тогда граничные условия перепишутся в виде:
1. 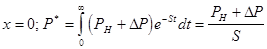
2. 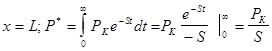 (5) (5)
Умножим обе части уравнения (3) на e-St
и проинтегрируем в пределах от 0 до 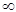 во времени во времени
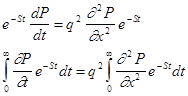 (6) (6)
Рассмотрим левую часть уравнения
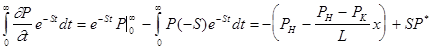 . (7) . (7)
Рассмотрим левую часть уравнения
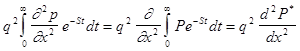 . (8) . (8)
Приравниваем обе части:
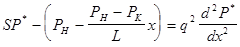
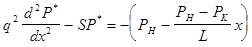 . (9) . (9)
Найдем сначала решение однородного уравнения
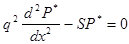 . (10) . (10)
Пусть Р*
определяется как 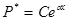 . .
Нам необходимо определить 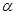 и С и С
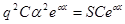 откуда откуда 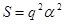 , а , а 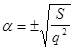 . .
Тогда решением уравнения является
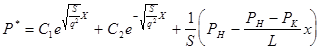 (11). (11).
Для определения коэффициентов С1
и С2
учтем граничные условия
х=0; 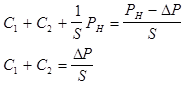 (12) (12)
x = L; 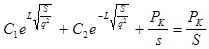 (13) (13)
отсюда выразим значения С1
и С2
: 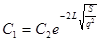 , ,
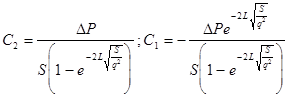 (14). (14).
Подставив найденное значение коэффициентов в (11) окончательно получаем:
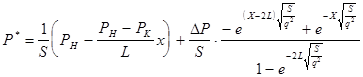 (15). (15).
Применим к выражению (15) обратное преобразование Лапласа
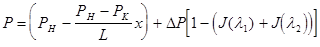 (16) (16)
где 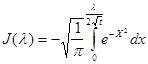 окончательно запишется: окончательно запишется:
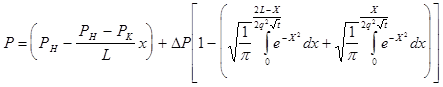 (17). (17).
Разложив подынтегральную функцию в ряд Тейлора, ограничившись первыми двумя членами и взяв интегралы, мы получим конечную формулу:
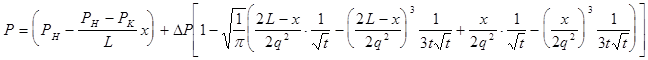
Формула имеет вынужденную и свободную составляющие. Нас интересует поведение свободной составляющей.
Построим график динамического режима линейного нефтепровода (свободной составляющей) в точке х = 60 км.

|