Министерство
образования и науки Республики Казакстан
Акимат г.Алматы
Университет «Туран»
ГОРОДСКОЙ КОНКУРС ШКОЛЬНЫХ НАУЧНЫХ РАБОТ
ДОКЛАД
Секция: математика
Тема: «Сравнительный анализ использования занимательных задач в практической деятельности древнего и coвременного мира»
Школа лицей №8 тел:292-67-47
Класс 10 «А»
Баимбетова Динара
и
Пак Екатерина
Тел: 87016699993
Научный руководитель
Галактионова Любовь Петровна
Алматы - 2010
Данный научный проект включает в себя исследования и сравнительный
анализ использования математических задач на практике в древности и современном мире. В работе рассматривалась математика Древнего Египта, междуречья и Древней Греции, а также новые сферы использования.
Цель исследования.
Целью данного проекта является изучение и анализ занимательных задач древнего и современного мира, выявление сходств и различий.
Гипотеза:
открытия древних математиков используются по сей день, но, благодаря современным ученым, математика достигла еще более высокого уровня, но и это не предел.
Этапы исследования:
изучение достижений математиков Древнего Египта, Междуречья, Древней Греции, использование математики в информационных технологиях, в физике и в быту. Работа с энциклопедиями, материалами Интернет сайтов.
Методика исследования
:
аналитический, описательный методы, сравнение и систематизация данных.
Новизна исследования
:
на основе сравнительного анализа выявлены специфика и особенности использования математических задач во все времена.
В истории науки принято называть первым математиком Фалеса.
Математика является одним из важнейших открытий человечества.
С XVIII в., со времен Эйлера и Лагранжа, математика служит базой для инженерных наук. Все крупные технические достижения – от строительства зданий и мостов до раскрепощения атомной энергии, сверхзвуковой авиации и космических полетов - были бы не возможны без математики. Потребность решать эти грандиозные задачи привела к созданию компьютеров, и на наших глазах происходит новая техническая и информационная революция. Наше время – период невиданного расцвета математики.
Древний мир
Самые ранние математические тексты, известные в наши дни, оставили великие цивилизации древности – Египет и Месопотамия, или Междуречье.
Древний Египет

Уровень древнеегипетской математики был довольно высок. Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян.
Все правила счета древних египтян основывались на умении складывать и вычитать, удваивать числа и дополнять дроби до единицы.
Для дробей были специальные обозначения. Египтяне использовали дроби вида 1/п,
где п
- натуральное число. Такие дроби называются аликвотными. Единственная неаликвотная дробь, которую «признавали» египетские математики, - это 2/3. Действияс дробями составляли особенность египетской арифметики.
В египетских папирусах встречаются также задачи на арифметическую и геометрическую прогрессии, что еще раз подчеркивает теоретический характер древней математики.
Важным достижением геометрической науки египтян было очень хорошее приближение числа π
,которое из формулы для площади круга диаметра d:

Египтяне предполагали, что  (погрешность менее 1 %) (погрешность менее 1 %)
Среди пространственных тел самым «египетским» можно считать пирамиду. Так вот, оказывается, кроме объемов куба, параллелепипеда, призмы и цилиндра египтяне умели вычислять объем усеченной пирамиды, в основаниях которой лежат квадраты со сторонами a
и b
, а высота равна h
. Они применяли формулу

Эта формула считается высшим достижением древнеегипетской математики.
Междуречье
 В Вавилонском царстве всеми расчетами занимались писцы. Школа, где обучались писцы называлась «дом табличек». Для таких школ предназначались специальные математические таблички. Тексты на них можно разделить на два класса: таблицы и задачники. В Вавилонском царстве всеми расчетами занимались писцы. Школа, где обучались писцы называлась «дом табличек». Для таких школ предназначались специальные математические таблички. Тексты на них можно разделить на два класса: таблицы и задачники.
Среди вычислительных задач на клинописных табличках встречаются задачи на арифметические и геометрические прогрессии, представления о которых у вавилонян были более развиты чем у египтян. Методы решения в основном опирались на идеи пропорциональной зависимости и среднего арифметического. Вавилонские писцы знали правило суммирования п
членов арифметической прогрессии:
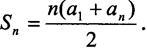
Вавилонские математики умели решать квадратные уравнения, знали теорему в последствии названную как теорема Пифагора, о свойствах прямоугольных треугольников, могли решать достаточно сложные задачи стереометрии.
В клинописных текстах содержатся первые задачи на проценты - ведь Вавилон стоял на пересечении торговых путей, и здесь рано появились денежные знаки и кредит. Было у вавилонян и правило для приближенного вычисления квадратных корней.
Открытия, сделанные математиками Междуречья, поражают своим размахом. Ведь именно здесь появилась первая позиционная система счисления, которая оказалась выше, чем у греков. Здесь впервые была разработана алгебра линейных и квадратных уравнений и рассмотрены первые неопределенные уравнения, возникшие из геометрических задач. Такая тесная связь геометрических задач с алгеброй и теорией чисел - одна из особенностей вавилонской математики.
Фалес и первые доказательства
 Фалес— древнегреческийфилософ и математик,купец и путешественник (он родился в VII в. до н. э.в городе Милеете.). Фалес— древнегреческийфилософ и математик,купец и путешественник (он родился в VII в. до н. э.в городе Милеете.).
Он был первым, кто доказал некоторые геометрические предложения, что превратило геометрию из свода правил в подлинную науку.
Фалес доказал ряд первых теорем геометрии:
равенство вертикальных углов, равенство углов при основании равнобедренного треугольника. Он установил и один из признаков равенства треугольников: если два треугольника имеют равную сторону и два равных угла, прилегающих к этой стороне, то эти треугольники равны.
Фалес не был только «чистым» математиком, он решал и прикладные задачи. Измерив тень от египетской пирамиды и тень от шеста и применив свои теоремы о подобии, он вычислил высоту пирамиды. Так родилась наша наука. Фалес сделал и много открытия в области астрономии.
Архимед

«Архимед»
|
Несомненно, Архимед (около 287 - 212 до н. э.) - самый гениальный ученый Древней Греции. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью. Знание гидравлики позволило Архимеду изобрести винтовой насос для выкачивания воды. Такой насос до недавнего времени применялся на испанских и мексиканских серебреных рудниках.
Самые замечательные математические открытия Архимеда связаны с его методами вычисления площадей и объемов. Архимед вычислил площадь произвольного сегмента параболы.
Архимеду принадлежит много замечательных геометрических открытий. Он научился вычислять стороны вписанного семиугольника; доказал, что наклонное сечение конуса представляет собой эллипс. Формулу нахождения площади треугольника по длинам его сторон:

Называют формулой Герона, но Архимед знал ее раньше.
Кроме того, Архимед построил спираль, называющуюся теперь его именем.
«Арифметика» Диофанта
До наших дней дошли два произведения Диофанта, оба не полностью.
Это: «Арифметика» (шесть книг из тринадцати) и отрывки из трактата «О многоугольных числах». Но о самом авторе не известно почти ничего. Благодаря буквенной символике Диофанта алгебра обрела новый язык, гораздо более оперативный и удобный, чем язык геометрии.
Диофант сделал решительный шаг в алгебре – ввел отрицательные числа и сформулируровал два основных правила преобразования уравнений: правило переноса члена уравнения из одной части уравнения в другую с обратным знаком и правило приведения подобных членов.
Современный мир
Теория информации
С давних пор люди задумывались над тем, как с помощью технических средств упростить и ускорить работу с информацией. Изобретение книгопечатания позволило быстро копировать информацию и облегчило ее хранение. В XIX в. заметно увеличились темпы передачи информации:
сначала пароходы и паровозы стали перевозить почту, затем появился телеграф, а в конце века - телефон. В хх в. информация превратилась в глобальную - ее можно передавать за считанные минуты в любую точку земного шара, причем не только тексты, но и изображения.
В хх в. появились технические устройства и приборы для переработки информации: приборы автоматической телефонной станции (АТС) ,
компьютер.
Любой процесс передачи информации можно представить несложной схемой. От передатчика информации по каналу связи к приемнику информации. В данной схеме основным является надежность и время передачи, преобразования и защита информации.
Различные технические средства обеспечивают необходимое в каждом конкретном случае качество передачи. Их
разрабатывают специалисты по технике связи. Однако большую роль в теории информации играют и математические методы. В их основе лежат принципы измерения информации, с открытия которых и началась теория информации.
Почта при расчетах количества информации может обойтись традиционными физическими мерами - весом и объемом писем и посылок. Но для современных систем таких «грубых» мер недостаточно. При отправке телеграмм мы платим за каждое слово. Чем длиннее телеграмма, тем она дороже не только нам, но и телеграфной службе: длинный текст дольше кодируется в передатчике (т. е. превращается в электрические сигналы), дольше декодируется в приемнике, дольше передается по каналу связи. Итак, при передаче сообщения важна его длина. Но тогда точнее измерять ее не числом слов, а числом букв и цифр, короче говоря - числом символов (знаков).
Представим себе, что мы передаем числа. Тогда число 25 после выражения в электрические сигналы будет выражено пятью знаками в двоичной системе: 11001. в обоих случаях содержание информации одно и то же, но длина записей различна.
Чем больше мощность алфавита, тем короче запись. Самый бедный алфавит - двоичный: он состоит из двух символов, неважно каких. И у большого, и у маленького алфавита есть: свои плюсы и минусы.
Какой алфавит выбрать - решают проектировщики конкретной системы передачи. Но для измерения информации желательно иметь единицы, которые не зависели бы от алфавита. В качестве такой единицы выбрали бит
- единицу минимальной по числу символов двоичной системы кодирования.
Более крупной единицей информации является байт
- запись из восьми битов. Общее количество символов, используемых в обычных текстах, больше чем 27
=256. (На клавиатуре компьютера можно насчитать около 150 знаков.)
При записи обычных текстов каждый символ, как правило, кодируется одним байтом. Следовательно, число байтов примерно равно числу символов; но байтов может быть больше за счет пробелов в тексте.
Измерение информации, основанное на подсчете числа символов в сообщении, необходимо для того, чтобы оценить возможности технических устройств, работающих с ней. Количество информации, установленное таким способом, называют объемом информации.
Объем информации, которая может в них храниться (объем памяти), измеряется в килобайтах
(тысячах байтов) и мегабайтах
(миллионах байтов). Чем больше объем памяти компьютера, тем шире его возможности. Время передачи сообщения по каналу связи зависит не только от длины текста, но и от того, какой объем информации за единицу времени можно передать через канал, или от пропускной способности. Эта величина обычно измеряется в килобайтах в
секунду.
Математические основы информатики
Криптография
Алгоритмы для защиты конфиденциальной информации, включают в себя шифрование.
Теория графов
Основы структур данных и алгоритмов поиска.
Математическая логика
Булева логика и другие способы моделирования логических запросов.
Теория типов
Формальный анализ типов данных и использование этих типов для понимания свойств программ, в частности, их безопасности.
Финансовая математика
Финансовая математика
-
раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами.
Основные направления:
· классическая финансовая математика (проведение процентных расчётов и анализ потоков платежей, применяемые в банковском деле, кредитовании, инвестировании)
· стохастическая финансовая математика, включающая расчёт безарбитражной (или «справедливой») цены финансовых инструментов
· проведение актуарных расчётов (составляющих математическую основу страхования)
· эконометрические расчёты, связанные с прогнозированием поведения финансовых рынков
Преобразования
 
Арифметика
Дифференциальное
Векторный
и интегральное
анализ
исчисление
Анализ
Дифференциальные
Динамические
Теория
Уравнения
системы
хаоса
Арифметика
– Векторный анализ
– Анализ
– Теория меры
– Дифференциальные уравнения
– Динамические системы
– Теория хаоса
– Перечень функций
Пространственные отношения
Более наглядные подходы в математике.
Геометрия
Тригонометрия
Дифференциальная
Топология
геометрия

Фракталы
Геометрия – Тригонометрия – Алгебраическая геометрия – Топология – Дифференциальная геометрия – Дифференциальная топология – Алгебраическая топология – Линейная алгебра – Фракталы.
Заключение
Таким образом проведено сравнительное исследование различных сфер
применения математики. Ученые древности внесли огромный вклад в развитие математики и заложили ее основу. Их
открытия и исследования мы используем и сейчас. Каждый школьник знает теорему Пифагора, на основе математики Древнего Египта мы строим небоскребы, поражающие своей высотой. Но и современная математика не стоит на месте. На основе математики появились такие науки как информатика, экономика и многие другие. Математика не потеряла своего значения: она используется во всех видах деятельности человека, развивается и достигает новых высот.
|